Abstract
This work involves the design optimization of metal–ceramic through the thickness of functionally graded material (FGM) plates subjected to thermomechanical loadings. Constrained optimization was performed for minimum mass and minimum material cost of the FGM plates. The design process of FGM plate structures requires a good choice of metal and ceramic materials and the adequate definition of the components volume fractions through the thickness direction in order to accomplish a certain structural behavior, while optimizing the material costs and/or the plate mass. Here, the optimization problems are solved with the simulated annealing (SA) algorithm, not requiring the calculation of the derivatives of the objective or constraint functions. Constrained single objective optimization cases are studied, and validated with alternative solutions, considering the p-index and the FGM plate thickness as design variables. New optimization cases, involving additionally the metal and ceramic materials as design variables, are presented both for benchmark purposes and to demonstrate the suitability of the SA algorithm to solve those optimization problems.
1. Introduction
The desired thermomechanical behavior of functionally graded material (FGM) metal–ceramic plate structures can be achieved through the proper definition of volume fractions of the constituent materials and the metal and ceramic materials to be used. The wide range of possible metal and ceramic material choice, the gradation of material properties through the thickness of the plate, are variables which need to be specified in order to fulfill the design specifications and to do that an appropriated design optimization computer program would be an important engineering tool. The development and validation of such a program is the aim of the present work.
The review works from Jha et al. [1], Swaminathan et al. [2], Thai and Kim [3] and Gupta and Talha [4], have addressed the theories found in the literature for modelling the deformation, stress, vibration and buckling analyses of functionally graded materials and structures. Gupta and Talha [4] have pointed out that most of the 2D theories for FGM plates considered the transverse shear deformation effect, but very few theories considered both the transverse shear and transverse normal deformation effects. Furthermore, it has been remarked that the 3D analytical solutions for FGM plates are interesting for benchmark purposes, but their solution methods involve mathematical complexities and are time consuming. Those notes are important for the implementation of design optimization programs, since the most appropriate theories have to be chosen, looking for a good compromise between model accuracy and computational efficiency, knowing in advance that many evaluations of the objective functions and constraint equations are necessary. According to those review papers [1,2,3,4] among the research publications, involving FGM structures, there is a lack of research in the area of the design optimization.
Very recently, Nikbakht et al. [5] published a review on the optimization of FGM structures. This review addressed several types of structure constituted from FGM, and noted that the most common optimization design variable in the reviewed researches is the material distribution pattern. Stress distribution, critical buckling load, fundamental frequency and the weight of FGM structures were the most popular objectives, which the researchers have improved through optimization studies. In addition, it was noted that the methodologies based on genetic algorithms (GA) and particle swarm optimization (PSO) are, so far, the most frequently used algorithms. This review also suggested some additional topics for future research in the area, pointing out that there are few optimization studies involving manufacturing aspects or noting that the cost of the design is an important issue and there are few studies using this objective function.
Regarding the structural optimization involving FGM plates and shell structures, in a closer relation with the present work, the following publications can be mentioned. Cho and Shin [6] have used artificial neural networks (ANN) in the optimization of material composition of heat-resisting FGMs. Chen and Tong [7] presented a numerical technique for the sensitivity analysis of the coupled thermomechanical problem of FGM parts by using sequential linear programming (SLP). Goupee and Vel [8] optimized the volume fraction distribution of FGMs using a multi-objective genetic algorithm. Goupee and Vel [9] performed a two-dimensional optimization of material distribution in FGMs using GA. Xia and Wang [10] performed the optimization of the volume fraction and the topology of FGM structures. Icardi and Ferrero [11] presented the minimization of the interlaminar stresses at the interface with the core in sandwich FGM plates. Na and Kim [12,13,14] optimized the stresses and the thermo-mechanical buckling behavior of FGMs by using the quasi-Newton method and the finite difference method as optimizer. Mozafari et al. [15] used the imperialist competitive algorithm (ICA) for the optimization of critical buckling load on FGM plates and performed comparisons with the GA. Kou et al. [16] showed that the PSO method outperforms the classical mathematical programming methods in FGM problems. Noh et al. [17] proposed a reliability-based design optimization (RBDO) to deal with uncertainty in the manufacturing process of FGMs. Vatanabe et al. [18], used topology optimization and homogenization to design FGM piezocomposites for energy-harvesting applications. Ashjari and Khoshravan [19] used GA and PSO in optimization problems and analyzed the accuracy and convergence of those algorithms. Loja [20] used PSO for the maximization of FGM sandwich beam bending stiffness. Taheri and Hassani [21] presented an optimization study of FGMs with the eigenfrequencies as constraints or objective function. Taheri et al. [22] used mathematical programming to solve the optimization problem. Shi and Shimoda [23] presented a shape optimization method to design FGM sandwich structures based in two sets of metal–ceramic materials. Wang et al. [24] presented solutions for the optimization of FGM pressure vessels subjected to thermo-mechanical loading. Roque et al. [25,26] minimized the fundamental natural frequency of FGM beams using differential evolution optimization. Tsiatas and Charalampakis [27] presented a methodology to optimize the natural frequencies of axially functionally graded beams and arches. Shabana et al. [28] studied the minimization of stresses in multi-layer FGM cylinders subjected to pressure loading using the PSO. Lieu and Lee [29] optimized FGM plates in a thermo-mechanical environment using the adaptive hybrid evolutionary firefly algorithm (AHEFA). Lieu et al. [30], optimized the layer thicknesses and the ceramic volume fraction in FGM sandwich plates in free vibration using AHEFA. Jafari et al. [31] compared the performance of a classical KKT optimization method with SA and PSO for the weight minimization of rotating disks. Khorsand and Tang [32] used a combination of a co-evolutionary particle swarm optimization (CPSO) approach coupled with a differential quadrature method to minimize the stresses and displacements in FGM rotating disks. Moita et al. [33] used the feasible arc interior point gradient-based algorithm (FAIPA) for the optimization of general FGM plate-shell structures. Some other authors have used multi-objective optimization approaches applied to the FGM design optimization, where essentially the same design variables and objective functions have been used: Vel and Pelletier [34], Wang et al. [35], Ashjari et al. [36], Franco Correia et al. [37,38] and Moleiro et al. [39], among others.
The SA algorithm has been disregarded by most researchers in favor of the aforementioned optimization methods. Very recently, Morales-Castañeda et al. [40] have presented an improved SA algorithm with better search capacities and tested it in several benchmarking functions, which could lead to future applications. In the present work, the basic SA algorithm is used and its performance in the context of design optimization of FGM plate structures is demonstrated. In addition, the ability of this algorithm to deal with continuous and discrete design variables is verified.
As mentioned in previous works from the authors [37,38], for the design optimization of FGM plate structures, the use of finite element models based on appropriated shear deformation theories is important, seeking a balance between accuracy and computational efficiency. A nine-nodes Lagrangian finite element plate model based on a higher order shear deformation theory, considering the transverse shear and transverse normal deformations and accounting for the temperature dependency of the material properties, has been used in the present work. The constrained optimization is performed for different objectives, namely the mass and cost minimization. Tsai-Hill failure criteria and other structural response constraints or design limitations are considered. The design variables are the index of the power-law distribution in the metal–ceramic graded material, the thickness of the graded material, and also the choice of metal and ceramic materials which can be combined from a discrete set of available materials.
2. Constitutive Relations of the Functionally Graded Material (FGM)
The properties of the FGM material are assumed to vary continuously, through the thickness, from a full metal at the bottom of the plate to a full ceramic at the top of the plate, as represented in Figure 1. The volume fractions of ceramic and metal constituents, and , are obtained by [41]:
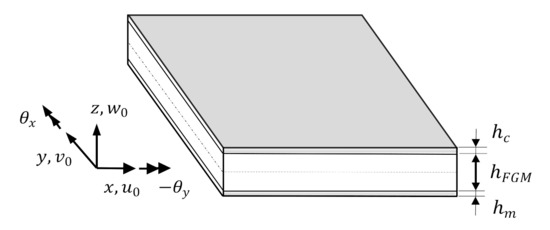
Figure 1.
Geometry definition of the functionally graded metal–ceramic plate with metal and ceramic skins.
The material properties, elastic moduli E and G, Poisson coefficient ν, density , coefficient of thermal expansion , coefficient of thermal conductivity , vary according to Equation (2). The properties can be expressed as a non-linear function of temperature by the expression [37,38,41]:
where are the coefficients of the temperature (in Kelvin) which are given in Table 1, for the relevant materials used in Section 5, and is the corresponding material property at the given temperature . The material properties in FGM plates vary across the thickness of the plate and the temperature variation occurs only in the thickness direction being constant in the x-y plane [38].

Table 1.
Temperature-dependent properties for metal and ceramic materials [42,43].
The relation between stresses and strains is represented by:
where is the elastic stress vector, is the elastic strain vector and is the thermal vector of strains caused by the temperature change . represents the stress-free reference temperature and is the elastic constitutive matrix [41].
3. Finite Element Model
The displacement components at any point in the laminate domain along the directions, respectively, are expanded in a Taylor’s series powers of the thickness coordinate . Each component is a function of coordinates and time, t. The following higher order displacement field is used [44]:
where are the displacements of a generic point in the reference surface, are the rotations of normal to the reference surface about the y and x axes respectively (Figure 1) and are the higher order terms defined at the reference surface, in a total of 11 nodal parameters (HSDT11).
Based on this displacement field, the elastic strains can be written as:
The equilibrium equation for the plate domain can be written as:
where and , are respectively the stiffness and mass matrices, is the displacements vector, which can be related with the strains by means of an appropriate strain-displacement matrix , , and are the accelerations, is the geometric stiffness matrix due to the initial stresses, is the external forces vector and is the vector of forces caused by the thermal effects [37]. For linear static type problems, it gives rise to the general equilibrium equation,
For free vibration analysis, considering the initial stresses on the stiffness, the natural frequencies are determined by solving the eigenvalue problem:
4. Optimization with Simulated Annealing
A general, single objective, optimization problem consists in finding design variables = , which minimize an objective function as:
where denotes a feasible region, which can be defined by inequality constraints:
and bound constraints , where and are, respectively, the lower and upper limits of the design variables. The design variables can also be defined as a discrete set of integer values.
The simulated annealing (SA) algorithm proceeds iteratively as described by Kirkpatrick et al. [45], Corana et al. [46] and Henderson et al. [47], i.e., a new point is accepted or rejected according to the Metropolis criterion: If , the new point is accepted; otherwise the new point is accepted with the probability given by , where is designated as temperature parameter. This acceptance probability is the basic idea behind the search mechanism in SA. The algorithm starts at a user defined temperature and stops at a temperature parameter such that no more improvement in the objective function can be expected. As mentioned by Corana et al. [46], from an optimization point of view, an iterative search accepting only new points with lowest function values is very likely to be stuck in a local minimum. The SA algorithm permits uphill moves under the control of the temperature parameter. The optimality of the final point cannot be guaranteed, but the method has proved to be able to proceed towards a better minima, even in the presence of many local minima. Detailed explanation of the algorithm implementation can be found in Corana et al. [46], Henderson et al. [47] and Goffe et al. [48], among other authors. In the present study, the applicability of the SA algorithm to the design optimization of FGM structures is analyzed and discussed.
5. Numerical Applications
5.1. Design Optimization Studies with a Simply Supported FGM Plate Subjected to Mechanical Loading
The design optimization of a FGM simply supported plate () is considered for validation purposes. Two metal–ceramic combinations are considered: first, stainless steel as the metal and silicon nitride as the ceramic (SUS304/Si3N4); and secondly, stainless steel and aluminum oxide as ceramic (SUS304/Al2O3). The optimization results are compared with alternative single objective optimization results published by Correia et al. [38], obtained with the same finite element model, employing global and local optimization using direct search (GLODS), as described in Custodio and Madeira [49].
The FGM plate () is subjected to a uniformly distributed transverse loading of . The temperature on the metal side is 300 K, the stress-free temperature, and the temperature on the ceramic side 400 K. The material properties are those from Table 1. The material cost for the metal SUS304 is assumed to be 3 USD/kg. The assumed material costs for the ceramics are 50 USD/kg for the Si3N4 and 27.4 USD/kg for the Al2O3, as in the reference [38]. For comparison purposes with the alternative results [38], two design optimization cases are considered: minimization of the mass; and minimization of the material cost. The optimization is constrained with the Tsai-Hill stress failure criteria. The isotropic tensile and compressive strengths, and , respectively, and the shear strength, , are given in Table 2. The constraint equation is expressed as:
being either the material strengths in tension or in compression, ie. or respectively, depending on the sign of the corresponding stress. During the optimization process with the SA algorithm, all intermediate solutions corresponding to non-feasible designs are rejected.

Table 2.
Metal and ceramic material strengths in tension, compression and shear (MPa).
In both optimization cases, results of which are presented in Table 3 and Table 4, two design variables are considered: the power law index, , assuming that: with possible increments of 0.1; and the total thickness of the FGM graded material, hFGM, considering , with possible increments of . From Table 3 and Table 4, a complete validation of the optimal solutions obtained using the simulated annealing algorithm can be verified with the alternative single objective optimal designs obtained by Correia et al. [38] using the same finite element model but different optimization algorithms, as mentioned above.

Table 3.
Optimal designs for the functionally graded material (FGM) SUS304/Si3N4 simply supported square plate for the aforementioned objective functions subject to Tsai–Hill failure constraints with . Two design variables.

Table 4.
Optimal designs for the FGM SUS304/Al2O3 simply supported square plate for the mentioned objective functions subject to Tsai-Hill failure constraints with . Two design variables.
In a second validation case, whose results are presented in Table 5, the objective is the maximization of the fundamental natural frequency, with the desired frequencies falling in the range: . Two design variables are considered: the thickness of the FGM plate graded material, with a lower bound of 5 mm and an upper bound of 60 mm, with possible increments of 0.1 mm; and the power law index, , assuming again that: , with possible increments of 0.1 As before, the solutions not falling in the feasible region are rejected. An excellent agreement with the reference [37] is achieved and a good agreement is also obtained by comparison with the alternative results from Moita et al. [33] using the gradient-based feasible arc interior point algorithm (FAIPA) for the optimization problem and a different finite element model based in a higher-order shear deformation theory. The SA algorithm has shown good accuracy and computational performance dealing with those problems.

Table 5.
Maximum fundamental natural frequency for the FGM SUS304/Si3N4 simply supported square plate. Two design variables. Bounds imposed on the design variables: ; .
5.2. Design Optimization Studies with a Square FGM Plate with Circular Hole Subjected to Thermal Loading
The optimization of an FGM square plate () with a circular hole with diameter is now considered as a design optimization case, with and . The plate is simply supported all round and is subjected to a thermal load through the thickness of the plate, such that the metal side is kept at a stress-free temperature and at the ceramic side the temperature is raised up to a 120 K, while the temperature distribution in the plane is uniform.
In this problem, we are interested in finding the best material choice, from a list of available ceramic and metal materials, the power law index p, and the thicknesses of the FGM material, in order to minimize the material cost of the plate or minimize the mass of the plate. The optimization process is constrained with Tsai–Hill failure criteria and natural frequency constraints. The material properties are defined in Table 1, being temperature dependent. The following, indicative material costs are considered: stainless steel—3 USD/kg; titanium alloy (Ti6Al4V)—30 USD/kg; silicon nitride (Si3N4)—50 USD/kg; alumina (Al2O3)—27.4 USD/kg, based in approximated average market costs.
Two objective functions are considered: the minimization of the overall mass of the plate; and the minimization of the material cost of the plate. Depending on the metal and ceramic materials being used those two objective functions can be contradictory, or not. The solutions not fulfilling the Tsai–Hill failure criteria are rejected. In addition, the natural frequency of the fundamental mode is required to fall in the range: and the solutions not fulfilling this condition are equally rejected.
In a first optimization run, the design variables are: the metal material; the ceramic material; the power law index, p; the thickness of the FGM plate, . The first two design variables are discrete. The material can be chosen from a list of available metal and ceramic materials. The p-index is defined as: , with possible increments of 0.1.
Constraints can be imposed on the materials which can be combined to form the FGM, considering manufacturing limitations for example. The FGM thickness variable has a lower bound of 5 mm and an upper bound of 20 mm, with possible increments of 0.1 mm.
In a second optimization run, two design variables are added: the thickness of the metal lower face, ; and the thickness of the ceramic upper face . The thicknesses are defined as in Figure 1. The metal and ceramic faces have a lower bound of zero and an upper bound of 20 mm, also with increments of 0.1 mm. The total thickness cannot exceed the value of 20 mm.
The optimization results obtained with SA algorithm are presented in Table 6, considering four design variables, i.e., the metal and ceramic materials, the p-index and the FGM thickness, . In Table 7, are shown the optimization results considering six design variables. The results obtained are very similar to the previous ones, since the optimal results have converged to full ceramic or full metal solutions, the optimal thicknesses and are both zero in all cases. The optimal solutions for minimum mass are either the SUS304/Si3N4 FGM with , with 7.3 mm thickness (solution S1) or the Ti6Al4V/Si3N4 FGM with , and 7.3 mm thickness (solutions S5 and S5′). These full ceramic silicon nitride optimal solutions are consequence of the highest Young modulus and lowest density of this ceramic among the considered set, which lead to an optimal solution with lower mass fulfilling the lower limit imposed on the natural frequency constraint. The optimal solution for minimum cost is the SUS304/Al2O3 FGM with and 15.8 mm thickness (solutions S4 and S4′). This is mostly a metal solution, which has the highest mass from all obtained solutions, since the steel SUS304 is the material having the lower cost and the highest density from the considered set. The optimal solutions listed in Table 6 and Table 7 are represented in Figure 2. In some metal and ceramic combinations, the minimization of mass and minimization of cost are conflicting objectives, and therefore the solution to be adopted should be based on a compromise between both objectives. In this case the Ti6Al4V/Si3N4 with 7.3 mm thickness and , which means a Si3N4 full ceramic (solutions S5 and S6), would be the best choice. Whenever metal and ceramic materials have similar prices and similar densities, the mass minimization and cost minimization are not conflicting objectives, and therefore similar solutions are obtained in both optimization problems.

Table 6.
Optimal designs for the simply supported square plate with circular hole, considering different metal–ceramic materials. Bounds imposed on the design variables: ; . Fundamental natural frequency: . Maximum displacement: .

Table 7.
Optimal designs for the simply supported square plate with circular hole with different metal–ceramic materials. Bounds imposed on the design variables: ; ; ; ; . Fundamental natural frequency: Maximum displacement: .
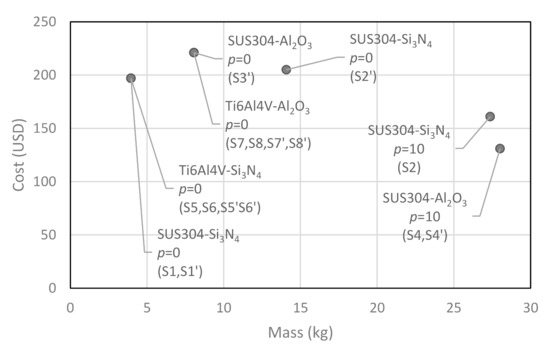
Excellent improvements in the objective functions were obtained, with respect to the initial designs, in all optimization cases. The SA algorithm denoted lower performance when dealing with many design variables (namely for the present problem having 6 design variables), since a huge number of function evaluations are required (more than 50 k). The performance was much more acceptable for problems with lower number of design variables. The ability to deal with both discrete and continuous design variables in the same optimization problem was a remarkable advantage.
5.3. Design Optimization Studies with a Square FGM Plate with Circular Hole Subjected to Mechanical Loading
The optimization of an FGM simply supported square plate () with a circular hole, as in the previous section, is now considered for the minimization of the transversal displacement (δmax) subject to Tsai–Hill stress criteria constraints and also for the minimization of the Tsai–Hill criteria, thus maximizing the strength safety factor. The plate is subjected to a transversal uniform pressure of , causing compression in the metal side and tension in the ceramic side. In these simple optimization problems, the design variables are: the FGM p-index comprised in the range ; the metal material; the ceramic material. The available metal and ceramic materials are the ones listed in Table 1 and Table 2 and the plate thickness is fixed as .
Table 8 shows the optimal design for minimum transversal displacement. The optimal solution corresponds to a full ceramic Si3N4 plate with . Table 9 shows the optimal solution for minimum Tsai–Hill criteria, which is the Ti6Al4V/Si3N4 FGM with . This solution is the one with lower mass, but higher cost. The solution with Ti6Al4V/Al2O3 and the same p-index leads to a slightly higher mass but a slightly lower cost. The performance of the SA with this problem was excellent with convergence requiring less than 10 k function evaluations.

Table 8.
Optimal design for the simply supported square plate with circular hole subject to transversal pressure load, for minimum transversal displacement δmax, considering different metal–ceramic materials.

Table 9.
Optimal design for the simply supported square plate with circular hole subject to transversal pressure load, for minimization of the Tsai–Hill failure criteria, considering different metal–ceramic materials.
6. Conclusions
Design optimization is an important engineering tool for the proper design of FGM structures. The use of the simulated annealing optimization algorithm associated with a finite element model for the structural analysis of through-the-thickness FGM metal–ceramic plate structures, subjected to thermomechanical loadings, has been shown in this paper, as an extension of previous works developed by the authors.
The accuracy of the finite element model was validated in previous works from the authors, namely in references [37,38], against alternative solutions, being exact, numerical or experimental, published by other authors, and therefore this demonstration was omitted here. The optimization results obtained with the SA algorithm have been compared, for validation purposes, in a few numerical cases, with previously published works from the authors, namely with optimization results obtained using a direct search derivative-free algorithm—global and local optimization using direct search (GLODS) and also with optimization results published in [33] obtained with the feasible arc interior point (FAIPA) gradient-based algorithm. The validation of the SA optimization results was excellent, but the computation efforts involved were not comparable since the results obtained with GLODS were included in a multiobjective optimization scheme and, regarding the FAIPA results, the computation time was not available.
In this work, besides the p-index and the thickness of the FGM plate, the choices of metal and ceramic materials have been added as design variables of the optimization problem, with the aim of finding the best metal–ceramic combination from a discrete set of available materials to fulfill an optimization objective, namely the mass minimization, cost minimization and other structural behavior objectives. These design variables have been pointed out in recent reviews as the most important for the design of FGM structures, alongside the need to address the manufacturing limitations which can be easily implemented with the SA. The convergence of the SA to the global optima cannot be guaranteed, but for the validation cases which have been carried out, a good agreement has been verified with respect to the alternative solutions mentioned before. It has been verified as a good performance of the SA algorithm for problems with lower number of design variables. For the optimization problems with higher number of design variables, which involved the p-index, thicknesses, and the materials all together, the computation time required by the SA algorithm was quite high due to the high number of function evaluations which were necessary to obtain convergence. Whenever a lower number of design variables are used in the optimization problem, the SA algorithm showed a good performance.
The numerical examples presented in this paper, involving the optimal design of FGM plate structures subject to thermomechanical loadings, can be used as benchmark solutions, knowing that these studies are, so far, scarce in the literature. Manufacturing constraints, which could be expressed by a feasible discrete set of values for the p-index, and the metal and ceramic materials to be chosen, are easily implemented with the SA algorithm.
Author Contributions
Investigation, writing and review: all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
This work was supported by FCT, Fundação para a Ciência e Tecnologia, through IDMEC, under LAETA, project UIDB/50022/2020.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jha, D.K.; Kant, T.; Singh, R.K. A critical review of recent research on functionally graded plates. Compos. Struct. 2013, 96, 833–849. [Google Scholar] [CrossRef]
- Swaminathan, K.; Naveenkumar, D.T.; Zenkour, A.M.; Carrera, E. Stress, vibration and buckling analyses of FGM plates—A state-of-the-art review. Compos. Struct. 2015, 120, 10–31. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Nikbakht, S.; Kamarian, S.; Shakeri, M. A review on optimization of composite structures Part II: Functionally graded materials. Compos. Struct. 2019, 214, 83–102. [Google Scholar] [CrossRef]
- Cho, J.R.; Shin, S.W. Material composition optimization for heat-resisting FGMs by artificial neural network. Compos. Part A: Appl. Sci. Manuf. 2004, 35, 585–594. [Google Scholar] [CrossRef]
- Chen, B.; Tong, L. Thermomechanically coupled sensitivity analysis and design optimization of functionally graded materials. Comput. Methods Appl. Mech. Eng. 2005, 194, 1891–1911. [Google Scholar] [CrossRef]
- Goupee, A.J.; Vel, S.S. Multi-objective optimization of functionally graded materials with temperature-dependent material properties. Mater. Des. 2007, 28, 1861–1879. [Google Scholar] [CrossRef]
- Goupee, A.J.; Vel, S.S. Two-dimensional optimization of material composition of functionally graded materials using meshless analyses and a genetic algorithm. Comput. Methods Appl. Mech. Eng. 2006, 195, 5926–5948. [Google Scholar] [CrossRef]
- Xia, Q.; Wang, M.Y. Simultaneous optimization of the material properties and the topology of functionally graded structures. Comput. Aided Des. 2008, 40, 660–675. [Google Scholar] [CrossRef]
- Icardi, U.; Ferrero, L. Optimization of sandwich panels with functionally graded core and faces. Compos. Sci. Technol. 2009, 69, 575–585. [Google Scholar] [CrossRef]
- Na, K.S.; Kim, J.H. Volume fraction optimization of functionally graded composite panels for stress reduction and critical temperature. Finite Elem. Anal. Des. 2009, 45, 845–851. [Google Scholar] [CrossRef]
- Na, K.S.; Kim, J.H. Optimization of volume fractions for functionally graded panels considering stress and critical temperature. Compos. Struct. 2009, 89, 509–516. [Google Scholar] [CrossRef]
- Na, K.S.; Kim, J.H. Volume fraction optimization for step-formed functionally graded plates considering stress and critical temperature. Compos. Struct. 2010, 92, 1283–1290. [Google Scholar] [CrossRef]
- Mozafari, H.; Ayob, A.; Kamali, F. Optimization of functional graded plates for buckling load by using imperialist competitive algorithm. Procedia Technol. 2012, 1, 144–152. [Google Scholar] [CrossRef][Green Version]
- Kou, X.Y.; Parks, G.T.; Tan, S.T. Optimal design of functionally graded materials using a procedural model and particle swarm optimization. Comput. Aided Des. 2012, 44, 300–310. [Google Scholar] [CrossRef]
- Noh, Y.J.; Kang, Y.J.; Youn, S.J.; Cho, J.R.; Lim, O.K. Reliability-based design optimization of volume fraction distribution in functionally graded composites. Comput. Mater. Sci. 2013, 69, 435–442. [Google Scholar] [CrossRef]
- Vatanabe, S.L.; Paulino, G.H.; Silva, E.C.N. Design of functionally graded piezocomposites using topology optimization and homogenization—Toward effective energy harvesting materials. Comput. Methods Appl. Mech. Eng. 2013, 266, 205–218. [Google Scholar] [CrossRef]
- Ashjari, M.; Khoshravan, M.R. Mass optimization of functionally graded plate for mechanical loading in the presence of deflection and stress constraints. Compos. Struct. 2014, 110, 118–132. [Google Scholar] [CrossRef]
- Loja, M.A.R. On the use of particle swarm optimization to maximize bending stiffness of functionally graded structures. J. Symb. Comput. 2014, 61, 12–30. [Google Scholar] [CrossRef]
- Taheri, A.H.; Hassani, B. Simultaneous isogeometrical shape and material design of functionally graded structures for optimal eigenfrequencies. Comput. Methods Appl. Mech. Eng. 2014, 277, 46–80. [Google Scholar] [CrossRef]
- Taheri, A.H.; Hassani, B.; Moghaddam, N.Z. Thermo-elastic optimization of material distribution of functionally graded structures by an isogeometrical approach. Int. J. Solids Struct. 2014, 51, 416–429. [Google Scholar] [CrossRef]
- Shi, J.X.; Shimoda, M. Interface shape optimization of designing functionally graded sandwich structures. Compos. Struct. 2015, 125, 88–95. [Google Scholar] [CrossRef]
- Wang, Z.W.; Zhang, Q.; Xia, L.Z.; Wu, J.T.; Liu, P.Q. Stress Analysis and Parameter Optimization of an FGM Pressure Vessel Subjected to Thermo-Mechanical Loadings. Procedia Eng. 2015, 130, 374–389. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Martins, P.A.L.S. Differential evolution for optimization of functionally graded beams. Compos. Struct. 2015, 133, 1191–1197. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Martins, P.A.L.S.; Ferreira, A.J.M.; Jorge, R.M.N. Differential evolution for free vibration optimization of functionally graded nano beams. Compos. Struct. 2016, 156, 29–34. [Google Scholar] [CrossRef]
- Tsiatas, G.C.; Charalampakis, A.E. Optimizing the natural frequencies of axially functionally graded beams and arches. Compos. Struct. 2017, 160, 256–266. [Google Scholar] [CrossRef]
- Shabana, Y.M.; Elsawaf, A.; Khalaf, H.; Khalil, Y. Stresses minimization in functionally graded cylinders using particle swarm optimization technique. Int. J. Press. Vessel. Pip. 2017, 154, 1–10. [Google Scholar] [CrossRef]
- Lieu, Q.X.; Lee, J. Modeling and optimization of functionally graded plates under thermo-mechanical load using isogeometric analysis and adaptive hybrid evolutionary firefly algorithm. Compos. Struct. 2017, 179, 89–106. [Google Scholar] [CrossRef]
- Lieu, Q.X.; Lee, J.; Lee, D.; Lee, S.; Kim, D.; Lee, J. Shape and size optimization of functionally graded sandwich plates using isogeometric analysis and adaptive hybrid evolutionary firefly algorithm. Thin Walled Struct. 2018, 124, 588–604. [Google Scholar] [CrossRef]
- Jafari, S.; Hojjati, M.H.; Fathi, A. Classical and modern optimization methods in minimum weight design of elastic rotating disk with variable thickness and density. Int. J. Press. Vessel. Pip. 2012, 92, 41–47. [Google Scholar] [CrossRef]
- Khorsand, M.; Tang, Y. Design functionally graded rotating disks under thermoelastic loads: Weight optimization. Int. J. Press. Vessel. Pip. 2018, 161, 33–40. [Google Scholar] [CrossRef]
- Moita, J.S.; Araújo, A.L.; Correia, V.F.; Soares, C.M.M.; Herskovits, J. Material distribution and sizing optimization of functionally graded plate-shell structures. Compos. Part B Eng. 2018, 142, 263–272. [Google Scholar] [CrossRef]
- Vel, S.S.; Pelletier, J.L. Multi-objective optimization of functionally graded thick shells for thermal loading. Compos. Struct. 2007, 81, 386–400. [Google Scholar] [CrossRef]
- Wang, C.; Koh, J.M.; Yu, T.; Xie, N.G.; Cheong, K.H. Material and shape optimization of bi-directional functionally graded plates by GIGA and an improved multi-objective particle swarm optimization algorithm. Comput. Methods Appl. Mech. Eng. 2020, 366, 113017. [Google Scholar] [CrossRef]
- Ashjari, M.; Khoshravan, M.R. Multi-objective optimization of a functionally graded sandwich panel under mechanical loading in the presence of stress constraint. J. Mech. Behav. Mater. 2017, 26, 79–93. [Google Scholar] [CrossRef]
- Correia, V.M.F.; Madeira, J.F.A.; Araújo, A.L.; Soares, C.M.M. Multiobjective optimization of ceramic-metal functionally graded plates using a higher order model. Compos. Struct. 2018, 183, 146–160. [Google Scholar] [CrossRef]
- Correia, V.M.F.; Madeira, J.F.A.; Araújo, A.; Soares, C.M.M. Multiobjective optimization of functionally graded material plates with thermo-mechanical loading. Compos. Struct. 2019, 207, 845–857. [Google Scholar] [CrossRef]
- Moleiro, F.; Madeira, J.F.A.; Carrera, E.; Reddy, J.N. Design optimization of functionally graded plates under thermo-mechanical loadings to minimize stress, deformation and mass. Compos. Struct. 2020, 245, 112360. [Google Scholar] [CrossRef]
- Morales-Castañeda, B.; Zaldivar, D.; Cuevas, E.; Maciel-Castillo, O.; Aranguren, I.; Fausto, F. An improved Simulated Annealing algorithm based on ancient metallurgy techniques. Appl. Soft Comput. 2019, 84, 105761. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates-Theory and Applications; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Reddy, J.N.; Chin, C.D. Thermomechanical analysis of functionally graded cylinders and plates. J. Therm. Stress. 1998, 21, 593–626. [Google Scholar] [CrossRef]
- Shen, H.S.; Wang, Z.X. Assessment of Voigt and Mori–Tanaka models for vibration analysis of functionally graded plates. Compos. Struct. 2012, 94, 2197–2208. [Google Scholar] [CrossRef]
- Correia, V.M.F.; Gomes, M.A.A.; Suleman, A.; Soares, C.M.M.; Soares, C.M. Modelling and design of adaptive composite structures. Comput. Methods Appl. Mech. Eng. 2000, 185, 325–346. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gellat, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Corana, A.; Marchesi, M.; Martini, C.; Ridella, S. Minimizing multimodal functions of continuous variables with the Simulated Annealing algorithm. ACM Trans. Math. Softw. 1987, 13, 262–280. [Google Scholar] [CrossRef]
- Henderson, D.; Jacobson, S.H.; Johnson, A.W. The Theory and Practice of Simulated Annealing. In International Series in Operations Research & Management Science; Glover, F., Kochenberger, G.A., Eds.; Springer: Boston, MA, USA, 2003; Volume 57. [Google Scholar] [CrossRef]
- Goffe, W.L.; Ferrier, G.D.; Rogers, J. Global optimization of statistical functions with simulated annealing. J. Econ. 1994, 60, 65–99. [Google Scholar] [CrossRef]
- Custódio, A.L.; Madeira, J.F.A. GLODS: Global and Local Optimization using Direct Search. J. Glob. Optim. 2014, 62, 1–28. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).