Experimental Analysis of Ultrasonic Multiple Scattering Attenuation through the Air with Fine Dust
Abstract
1. Introduction
2. Scattering Attenuation Defined by Independent Scattering Approximation
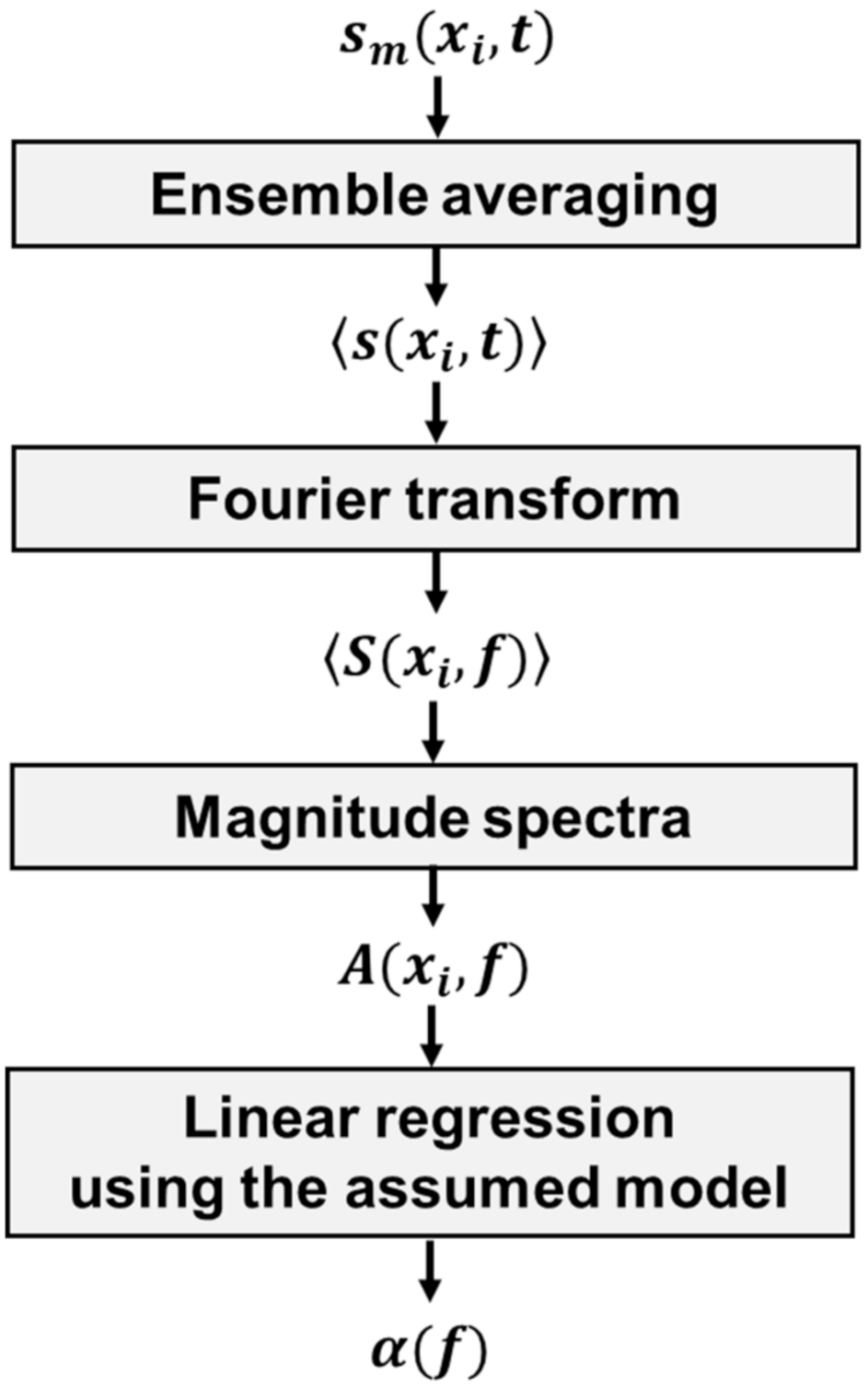
3. Signal Processing
4. Experimental Details
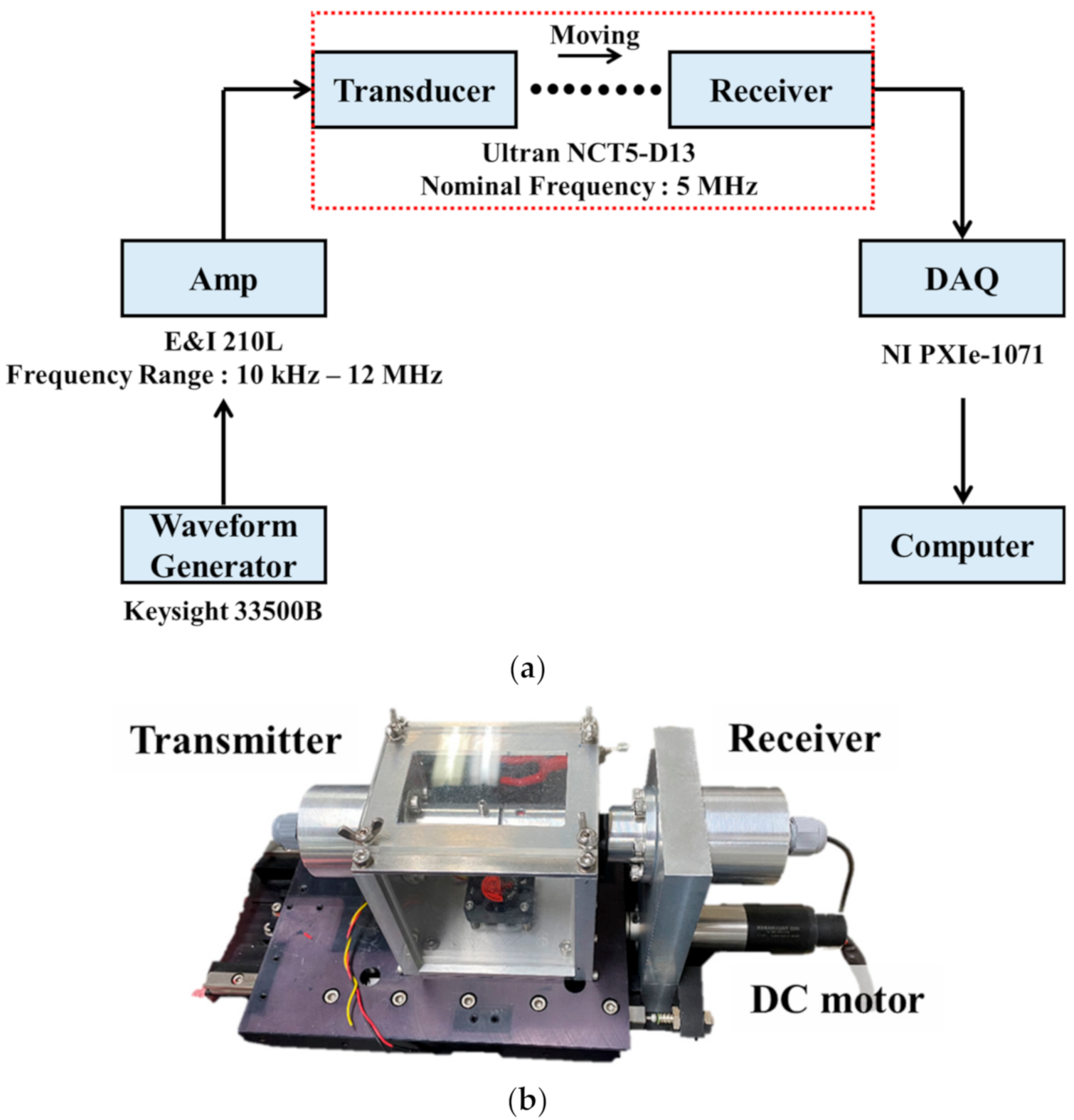
4.1. Ultrasonic Scattering Hardware
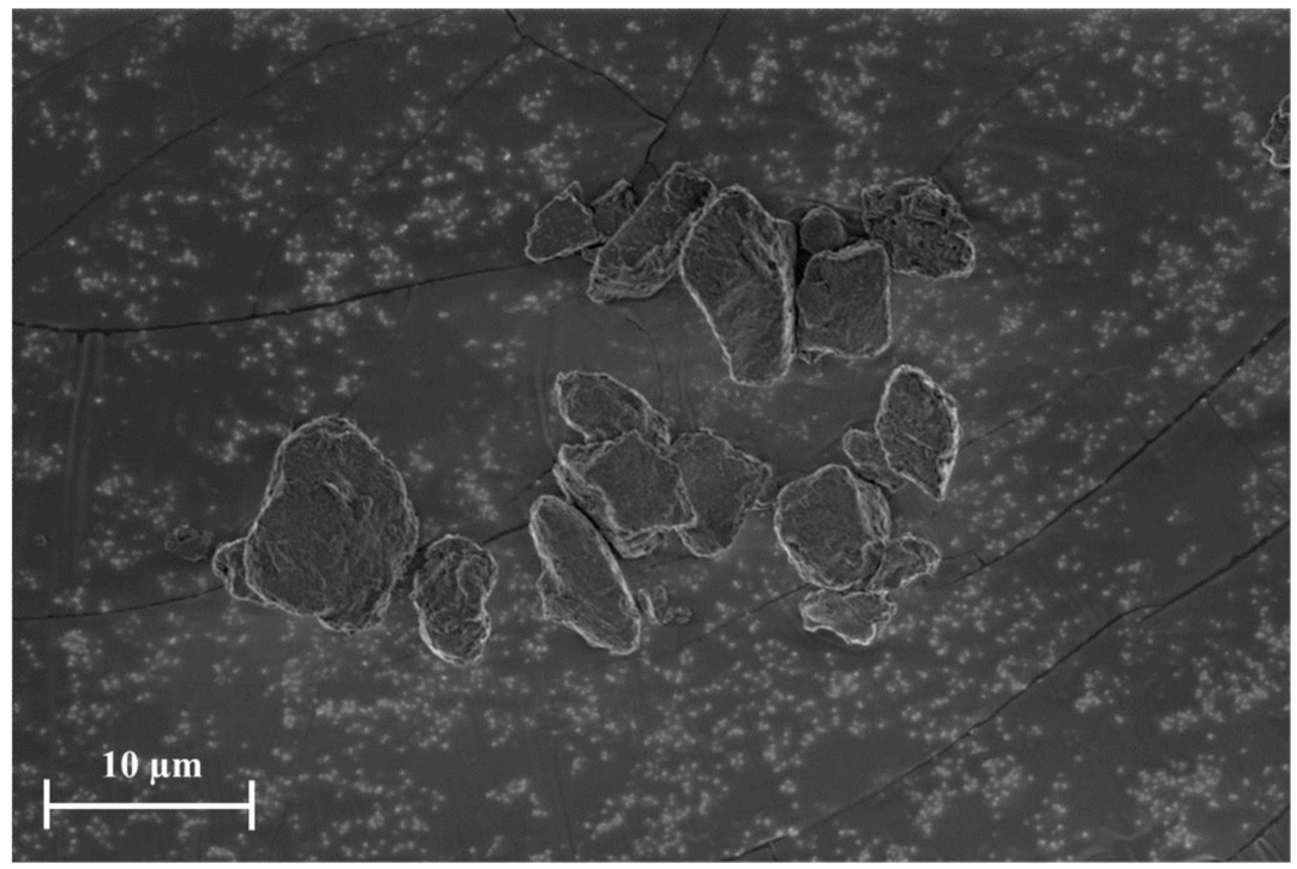
4.2. Fine Dust Materials
4.3. Experimental Procedure
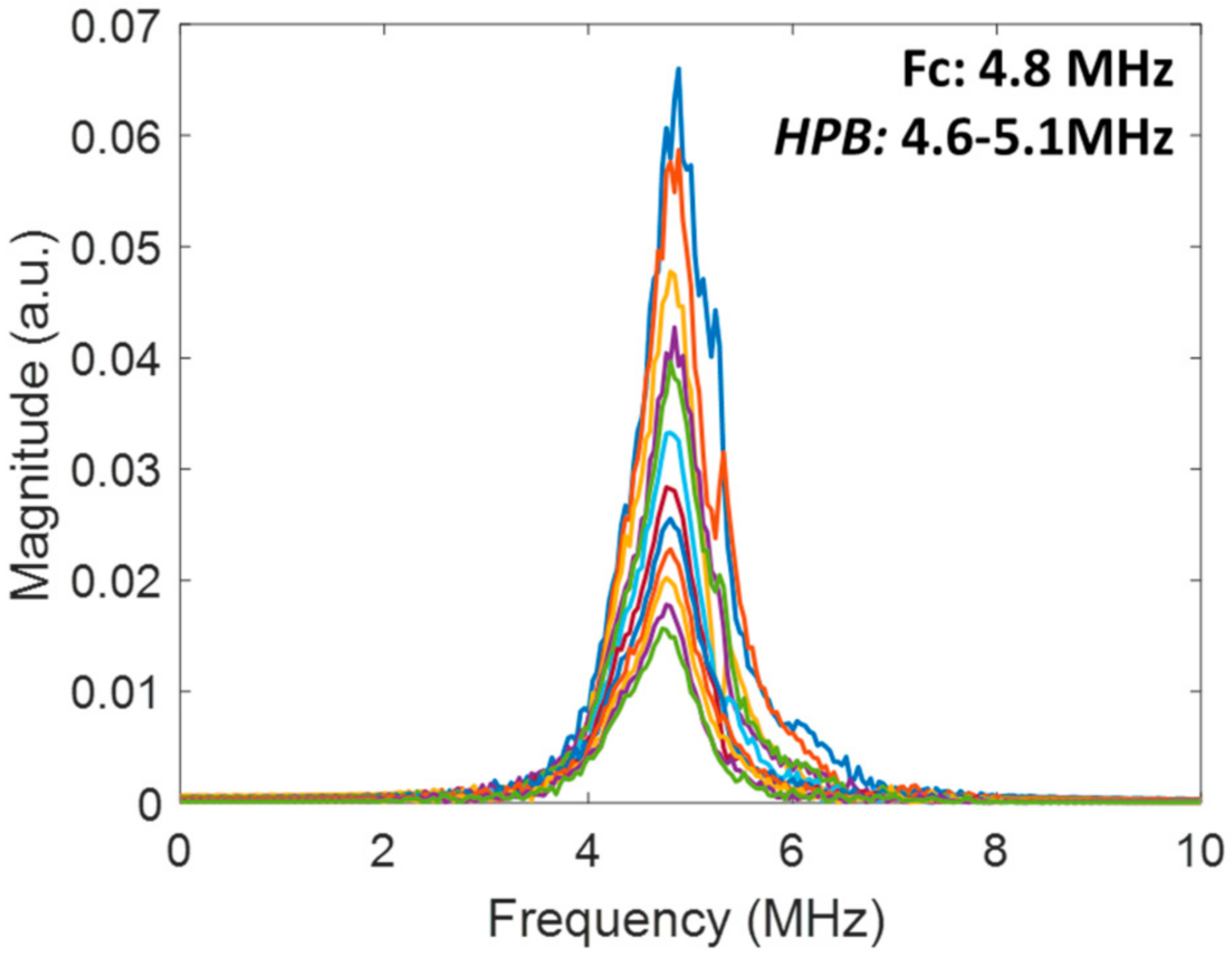
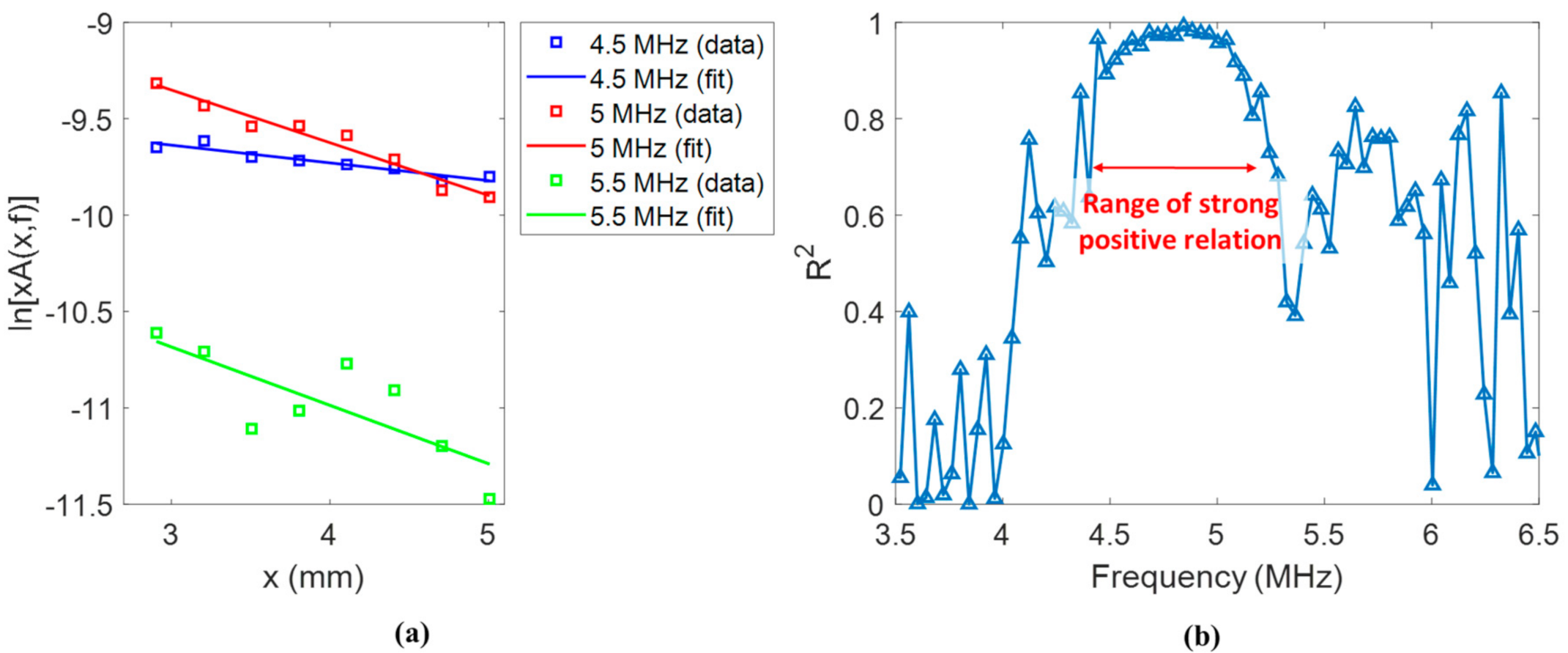
5. Experimental Results
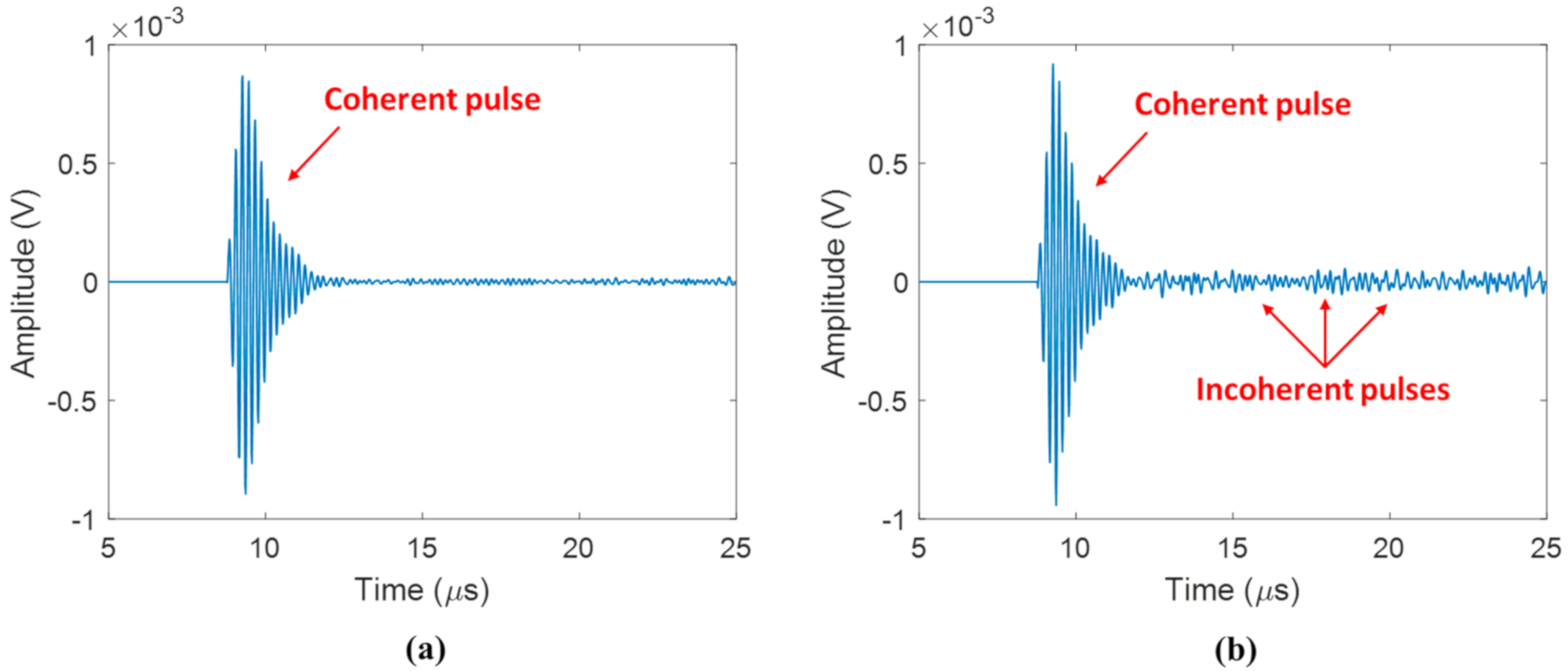
5.1. Multiply Scattered Acoustic Waves
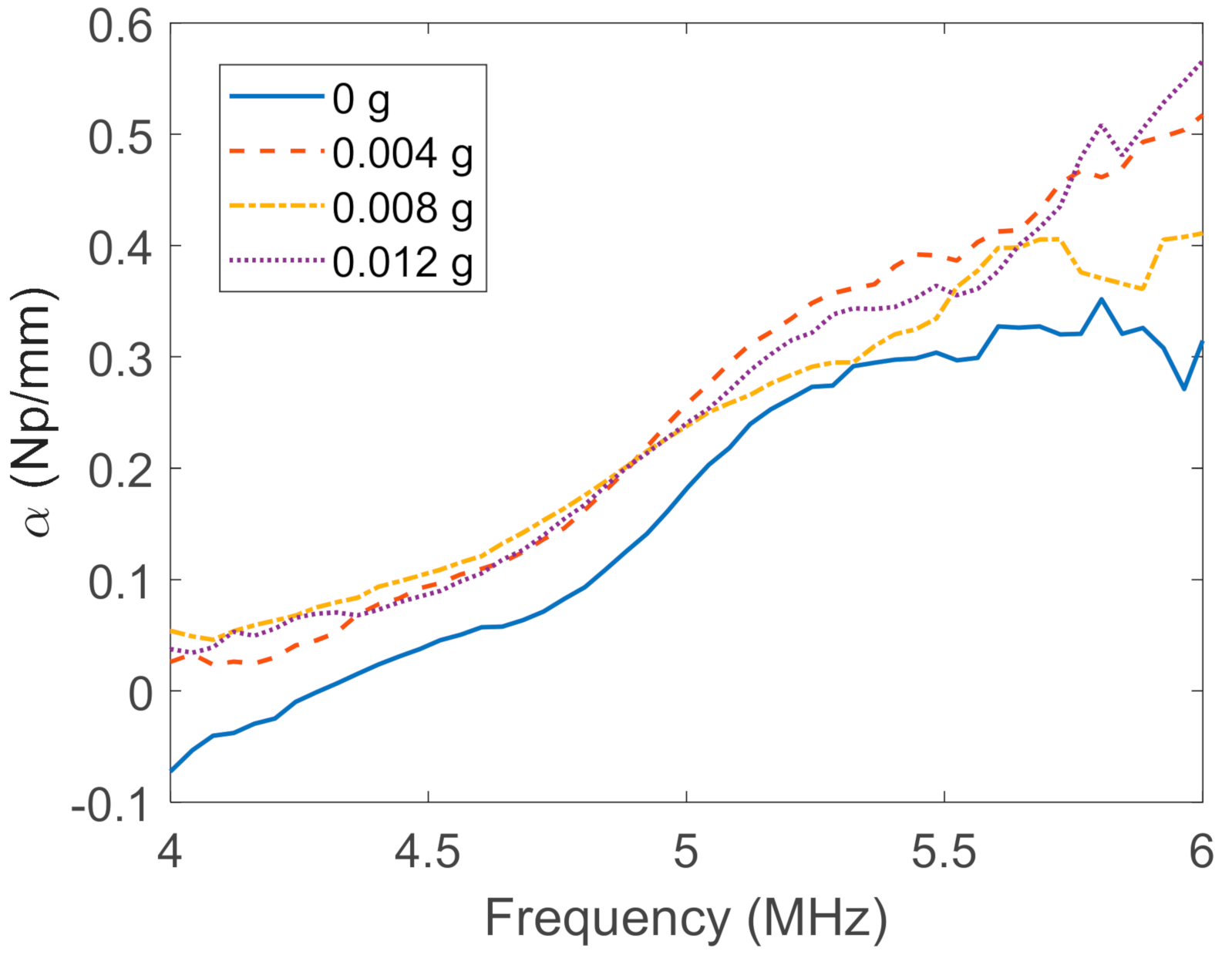
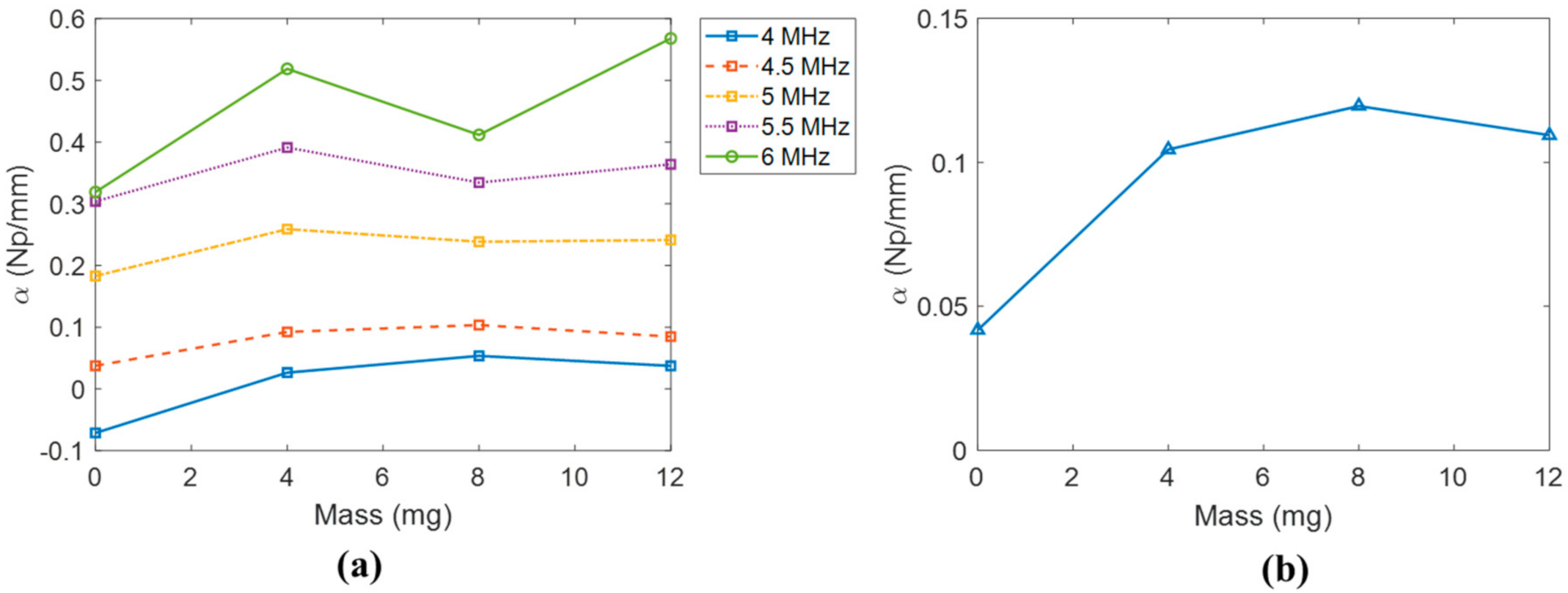
5.2. Scattering Attenuation of Coherent Waves
6. Discussion
7. Conclusions and Future Work
- The developed ultrasonic scattering hardware enables the acquisition of meaningful signal data through air with fine dust (PM 10). The applied ultrasonic wavelength was approximately 68 μm in air and a total of 120 different time series data were obtained per case of the experiment.
- The proposed signal processing approach (including ensemble averaging and Fourier analysis) enables the calculation of scattering attenuation, and the results obtained indicate a correlation between the scattering attenuation and the dosage of fine dust until 0.008 g.
- The range of scattering cross-sections of actual fine dust particles is required to estimate the number of fine dust particles per unit volume. Numerical investigation presented the effect of irregular particle shape on the number density estimation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shridhar, V.; Khillare, P.S.; Agarwal, T.; Ray, S. Metallic species in ambient particulate matter at rural and urban locations of Delhi. J. Hazard. Mater. 2010, 175, 600–607. [Google Scholar] [CrossRef] [PubMed]
- Jim, C.Y.; Chen, W.Y. Assessing the ecosystem service of air pollutant removal by urban trees in Guangzhou (China). J. Environ. Manag. 2008, 88, 665–676. [Google Scholar] [CrossRef] [PubMed]
- Nowak, D.J.; Crane, D.E.; Stevens, J.C. Air pollution removal by urban trees and shrubs in the United States. Urban For. Urban Green. 2006, 4, 115–123. [Google Scholar] [CrossRef]
- Pope, C.A.; Dockery, D.W. Health effects of fine particulate air pollution: Lines that connect. J. Air Waste Manag. Assoc. 2006, 56, 709–742. [Google Scholar] [CrossRef] [PubMed]
- Amaral, S.S.; de Carvalho, J.A.; Costa, M.A.M.; Pinheiro, C. An overview of particulate matter measurement instruments. Atmosphere 2015, 6, 1327–1345. [Google Scholar] [CrossRef]
- Hauck, H.; Berner, A.; Gomiscek, B.; Stopper, S.; Puxbaum, H.; Kundi, M.; Preining, O. On the equivalence of gravimetric PM data with TEOM and beta-attenuation measurements. J. Aerosol Sci. 2004, 35, 1135–1149. [Google Scholar] [CrossRef]
- Giechaskiel, B.; Maricq, M.; Ntziachristos, L.; Dardiotis, C.; Wang, X.; Axmann, H.; Bergmann, A.; Schindler, W. Review of motor vehicle particulate emissions sampling and measurement: From smoke and filter mass to particle number. J. Aerosol Sci. 2014, 67, 48–86. [Google Scholar] [CrossRef]
- Chow, J.C.; Watson, J.G.; Park, K.; Lowenthal, D.H.; Robinson, N.F.; Park, K.; Maglian, K.A. Comparison of particle light scattering and fine particulate matter mass in central california. J. Air Waste Manag. Assoc. 2006, 56, 398–410. [Google Scholar] [CrossRef]
- Lee, C.H.; Oh, S.N. Effect of Atmospheric Humidity on Fine Dust Measurement Using the Light Scattering Method. J. Korean Soc. Hazard Mitig. 2020, 20, 391–399. [Google Scholar] [CrossRef][Green Version]
- Kim, J.H.; Oh, J.; Choi, J.S.; Ahn, J.Y.; Yoon, G.H.; Park, J.S. A Study on the Correction of Optic Scattering PM2.5 by the Gravimetric Method. J. Korean Soc. Urban Environ. 2014, 14, 41–47. [Google Scholar]
- Kim, S.J.; Kang, H.S.; Son, Y.S.; Yoon, S.L.; Kim, J.C.; Kim, G.S.; Kim, I.W. Compensation of Light Scattering Method for Real-Time Monitoring of Particulate Matters in Subway Stations. J. Korean Soc. Atmos. Environ. 2010, 26, 533–542. [Google Scholar] [CrossRef]
- Fu, S.; Lou, W.; Wang, H.; Li, C.; Chen, Z.; Zhang, Y. Evaluating the effects of aluminum dust concentration on explosions in a 20 L spherical vessel using ultrasonic sensors. Powder Technol. 2020, 367, 809–819. [Google Scholar] [CrossRef]
- Kazys, R.; Sliteris, R.; Mazeika, L.; Van den Abeele, L.; Nielsen, P.; Snellings, R. Ultrasonic monitoring of variations in dust concentration in a powder classifier. Powder Technol. 2020, in press. [Google Scholar]
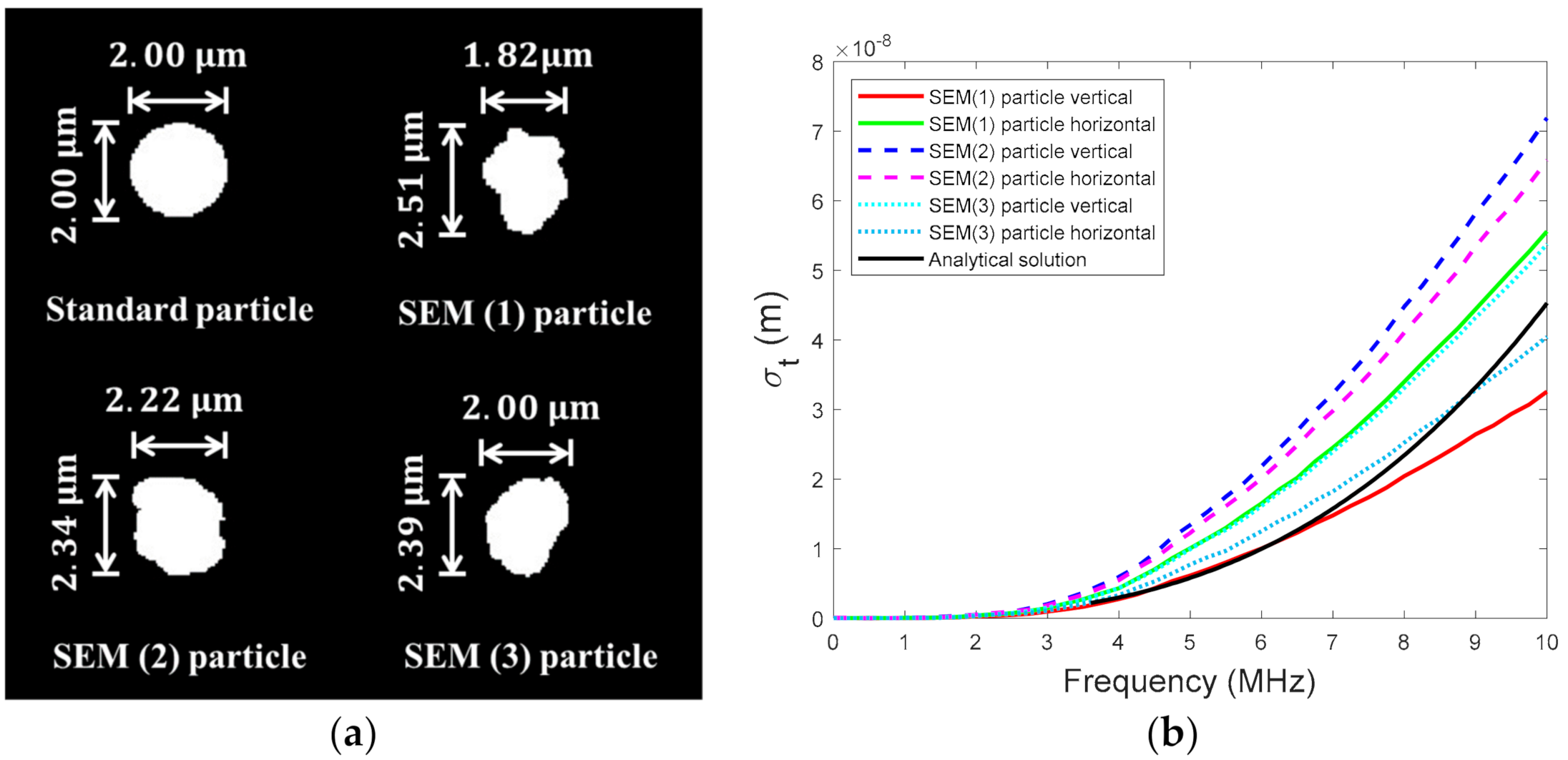
- Song, H.M.; Woo, U.Y.; Choi, H.J. Numerical analysis of ultrasonic multiple scattering for fine dust number density estimation. J. Appl. Sci. 2020. accpeted. [Google Scholar]
- Tourin, A.; Derode, A.; Peyre, A.; Fink, M. Transport parameters for propagating an ultrasonic-pulsed wave in a multiple scattering medium. J. Acoust. Soc. Am. 2000, 108, 503–512. [Google Scholar] [CrossRef]
- Tourin, A.; Fink, M.; Derode, A. Multiple scattering of sound. Waves Random Media 2000, 10, R31–R60. [Google Scholar] [CrossRef]
- Lagendijk, A.; van Tiggelen, B.A. Resonant multiple scattering of light. Phys. Rep. 1996, 29, 143–215. [Google Scholar] [CrossRef]
- Foldy, L.L. The multiple scattering of waves. I. General theory of isotropic scattering by randomly distributed scatterers. Phys. Rev. 1945, 67, 107–119. [Google Scholar] [CrossRef]
- Lax, M. Multiple scattering of waves. II. The effective field in dense systems. Phys. Rev. 1952, 85, 621–629. [Google Scholar] [CrossRef]
- Waterman, P.C.; Truell, R. Multiple scattering of waves. J. Math. Phys. 1961, 2, 512–537. [Google Scholar] [CrossRef]
- Lloyd, P.; Berry, M.V. Wave propagation through an assembly of spheres: IV. Relationship between different multiple scattering theories. Proc. Phys. Soc. 1967, 91, 678–688. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ih, J.-G.; Lee, B.-H. Dispersion of elastic wave in randome particulate composites. J. Acoust. Soc. Am. 1995, 97, 1380–1388. [Google Scholar] [CrossRef]
- Choy, T.C. Effective Medium theory: Principles and Applications; Oxford University Press: New York, NY, USA, 2000; pp. 96–135. [Google Scholar]
- Berge, P.A.; Bonner, B.P.; Berryman, J.G. Ultrasonic velocicty-porosity relationships for sandstone analogs made from fused glass beads. Geophysics 1995, 60, 108–119. [Google Scholar] [CrossRef]
- Treeby, B.E.; Cox, B.T. k-Wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010, 15, 021314. [Google Scholar] [CrossRef] [PubMed]


| Material Properties | ||
| Wave Speed (m/s) | Mass Density (kg/m3) | |
| Air | 343 | 1.2754 |
| Fine dust particle | 343 | 500 |
| Simulation parameters | ||
| Number of grid points (Nx × Ny) | 1500 × 1500 | |
| Grid spacing (dx and dy) | 0.057 μm | |
| Time step (dt) | 0.02 ns | |
| Time duration (T) | 4 μs | |
| Number of sensing points | 3676 (sensor array radius 37.05 μm) | |
| Sensor spacing along y axis | 1.65 μm | |
| CFL condition | 0.1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, U.; Choi, H.; Song, H. Experimental Analysis of Ultrasonic Multiple Scattering Attenuation through the Air with Fine Dust. Appl. Sci. 2021, 11, 694. https://doi.org/10.3390/app11020694
Woo U, Choi H, Song H. Experimental Analysis of Ultrasonic Multiple Scattering Attenuation through the Air with Fine Dust. Applied Sciences. 2021; 11(2):694. https://doi.org/10.3390/app11020694
Chicago/Turabian StyleWoo, Ukyong, Hajin Choi, and Homin Song. 2021. "Experimental Analysis of Ultrasonic Multiple Scattering Attenuation through the Air with Fine Dust" Applied Sciences 11, no. 2: 694. https://doi.org/10.3390/app11020694
APA StyleWoo, U., Choi, H., & Song, H. (2021). Experimental Analysis of Ultrasonic Multiple Scattering Attenuation through the Air with Fine Dust. Applied Sciences, 11(2), 694. https://doi.org/10.3390/app11020694




