5.1. Calibration
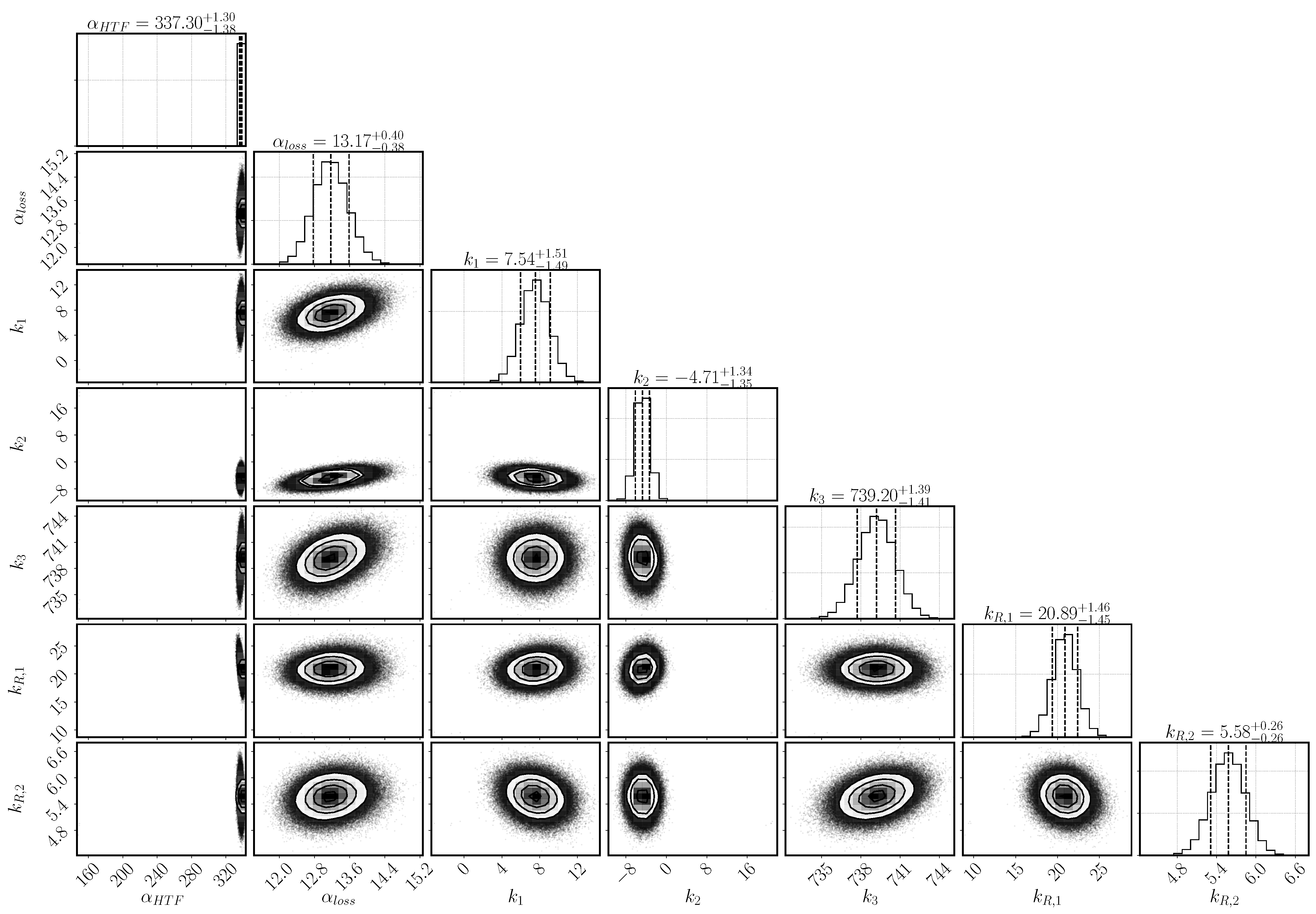
Figure 3 shows the posterior distribution for the parameters and their dependencies. The optimum values and the 95% confidence interval of each parameter are as well listed in
Table 6. All the parameters display a Gaussian posterior distribution, that is, the model output is sensitive to all the selected parameters. Otherwise, the posterior distribution would resemble the prior, uniform distribution. The narrower the width of the Gaussian distribution, the more sensitive the model output is on the respective parameter.
The heat-transfer coefficient has a narrow distribution and lies with as mean value at the upper bond of the selected range. The larger the heat transfer coefficient, the more heat is transported to the heat-transfer channel given the same temperature conditions. The heat transfer is, however, correlated to the heat-loss mechanism that transports the heat to the top of the reactive bed. It is described by the combination of the parameters , and k–k. Both mechanisms depend on the temperature at the boundary of the reactive bed and the outer temperature of both the HTF channel and the vapor vessel. However, the temperature distribution in the HTF channel changes according to the progress of conversion. In early stages, the reaction occurs everywhere in the reactive bed until the local temperature reaches the equilibrium temperature. Afterwards, reaction occurs only where the reaction bed is cooled down. Heat is transported to the HTF channel, where cooler air is injected from the left. The flowing air takes up the heat of the reactive bed. The temperature difference between bed and channel is largest at the inlet and, thus, the reactive material is converted the fastest at this point. Eventually, a reaction front develops between the region, that has already been converted, and the region, where the conditions are still at equilibrium. Only at the front, the conditions of temperature and pressure are such that the chemical reaction can occur. If no heat was lost and all the heat was transported to the HTF channel, the reaction front would move diagonally from the bottom left to the top right corner of the reactive bed. However, heat is also lost at the top boundary dependent on the temperature in the outer vessel and, thus, the reaction is fast also close to the top boundary. In the center of the bed, the front moves slowly and a kind of parabolic shape of the reaction front establishes. The exact shape is not tracked by the experiment, as only the temperatures at location T1, T3, and T7 are measured. The temperature distribution in the vapor vessel is described by the parameters k–k. Via the temperature profiles at the locations T1, T3 and T7, it is thus inferred how much heat is transferred to the HTF channel or lost to the vapor vessel.
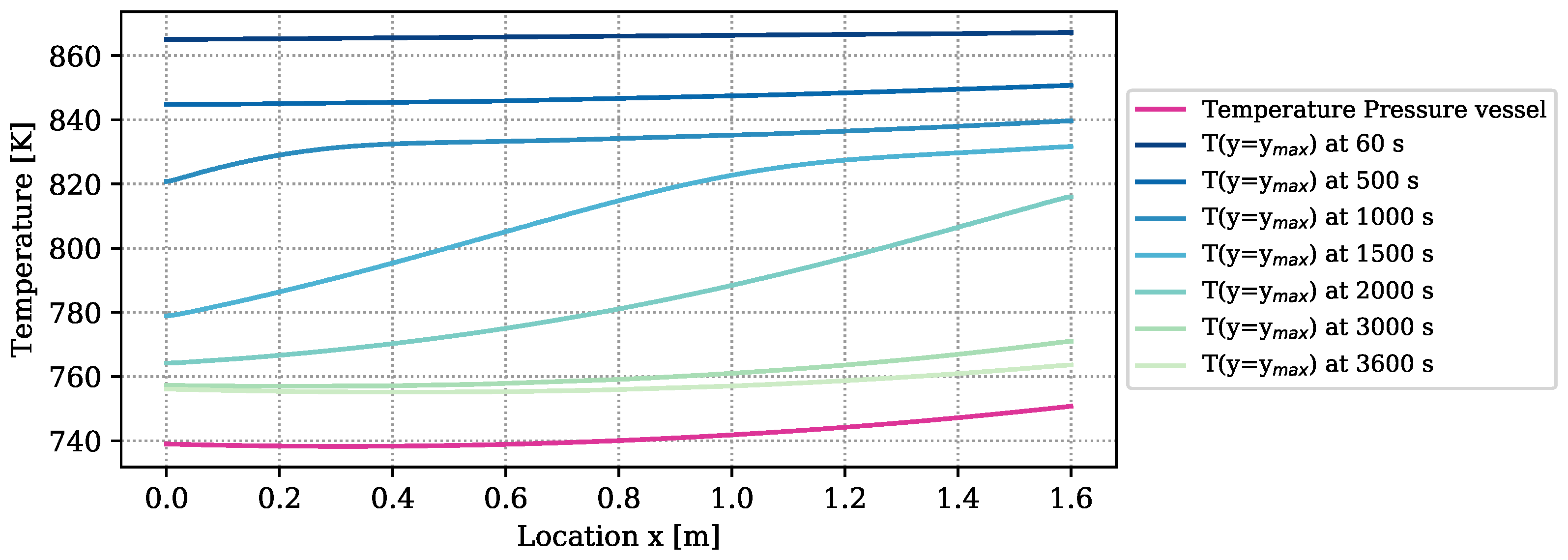
The amount of heat loss is determined by the temperature difference between the boundary of the reactive bed and the vapor vessel, and by the heat loss coefficient. The temperature distribution of the outer vessel is plotted in purple in
Figure 4. It furthermore contains the temperatures at the boundary of the reactive bed,
), determined by a simulation with the numrical model at optimized parameters. The temperature differences between bed and vessel amount to more than 100 K at early times of reaction. At the end of the experiment, they still amount to 20 K. Due to the big temperature differences,
of the overall released energy of reaction (
) is lost through the reactor surface and only
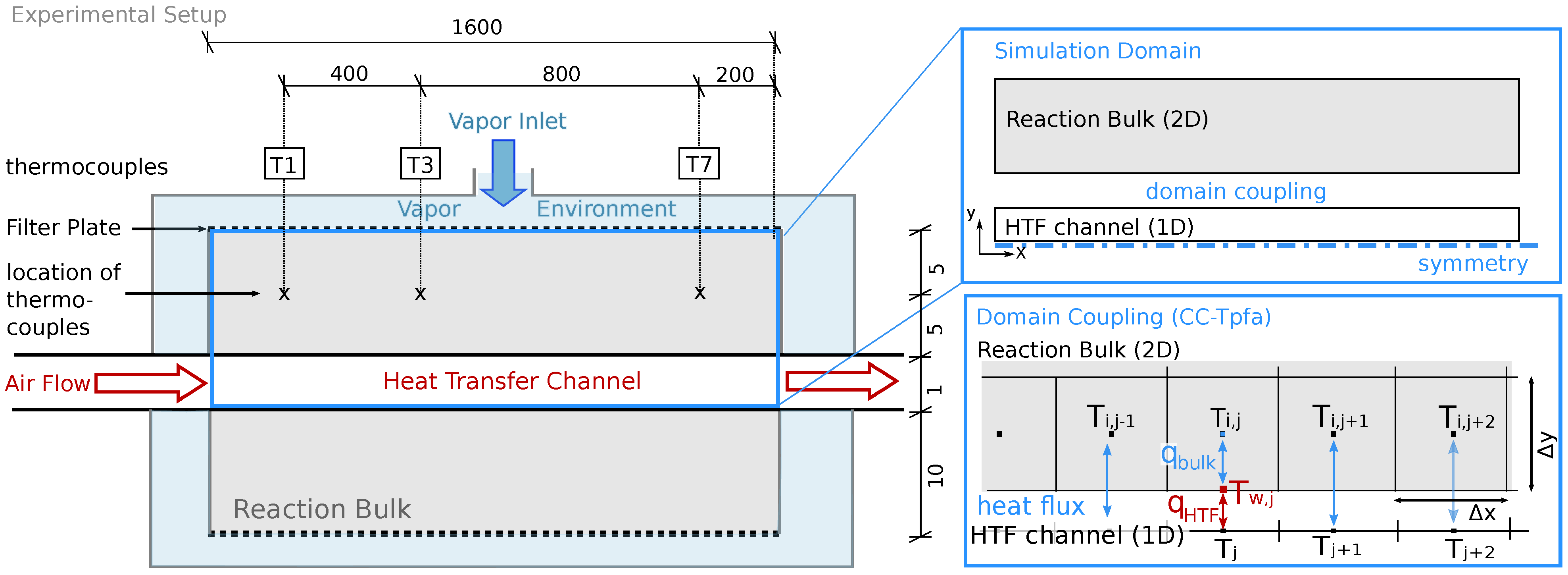
is transferred to the HTF channel. Temperature measurements in the HTF channel to verify these results are not available. The heat-transport mechanisms in form of heat loss, free convection, conduction, and radiation overlap. Free convection, however, appears only at the upper boundary of the symmetric reactor setup, as outlined in
Section 2.2.2. If this mechanism dominates the heat loss, the temperatures in the reactive bed below and above the HTF channel are different and the symmetry condition is not fulfilled. In the experiment, all the thermocouples are installed in the top part of the reactive bed. Thus, the experiment does not provide any information on whether or not the two parts behave symmetrically. The reduced simulation domain provides a considerable simulation speed-up.
The parameters k and k are linked via the reaction rate. Both a small value of k and a large value of k limit the reaction rate and lead to a flat slope in the temperature profiles. The optimal solution is found above the expected ranges for both parameters with k and k. Whereas k is only slightly larger than its upper value at 20, k is clearly above its range. At initial states of conversion, k hardly affects the reaction rate, as the term is close to one. Its impact increases with increasing conversion. At medium conversion, the dampening effect is compensated by the high value of k, but at final stages, it dominates the reaction rate. k in fact prevents complete conversion within the simulation time.
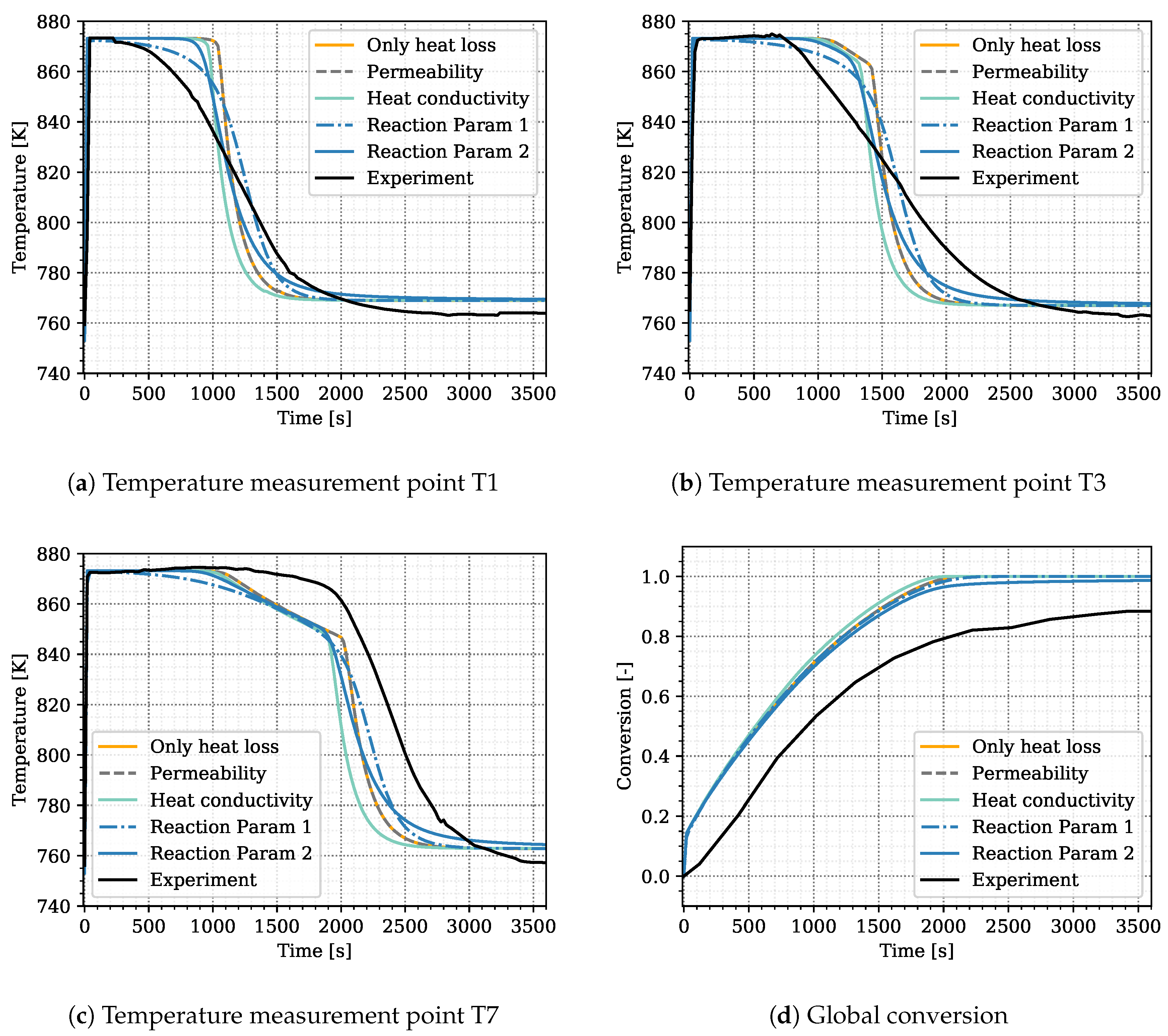
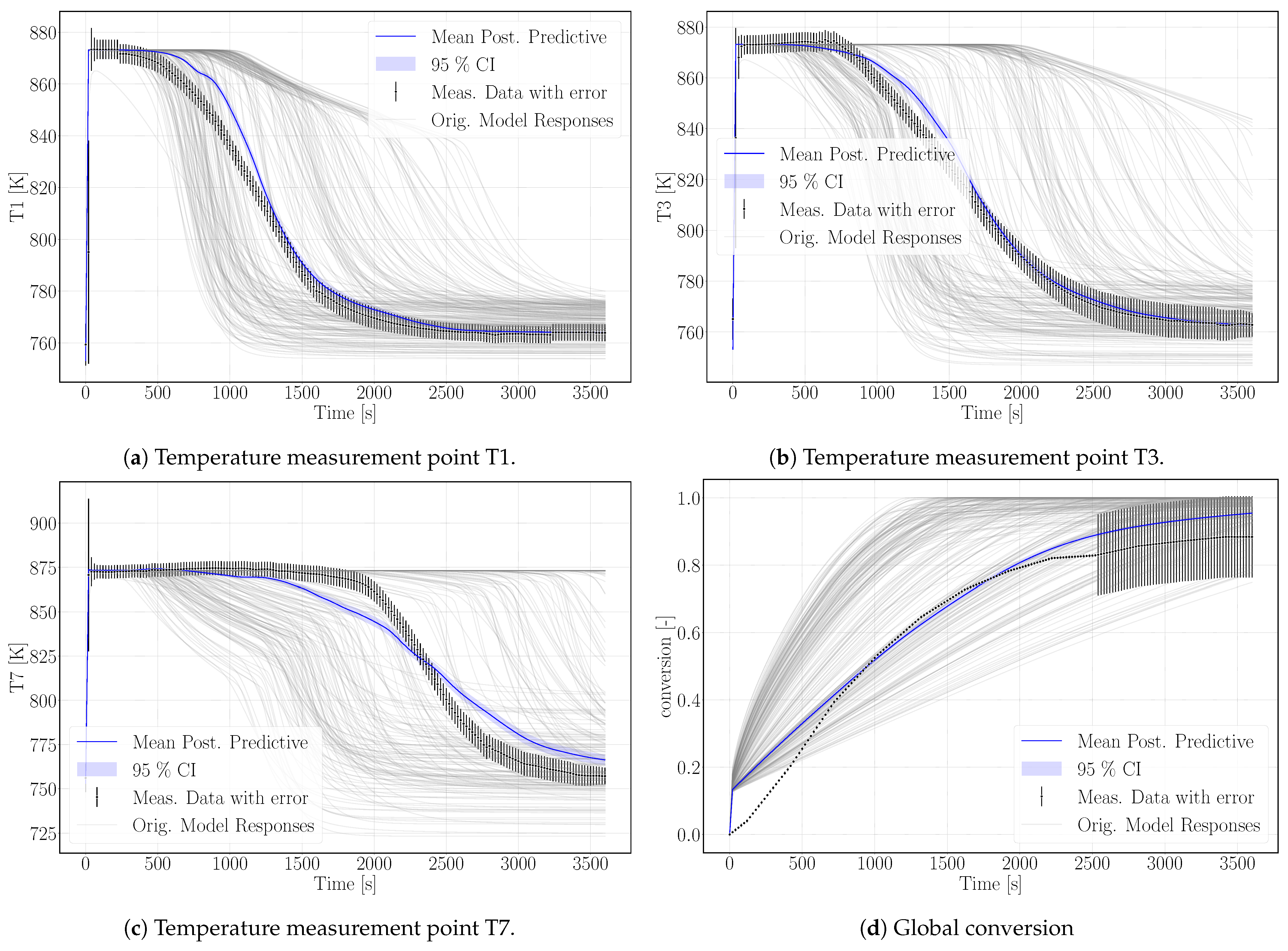
Experimental results and simulation results agree in this regard as shown in
Figure 5d. The conversion in the experiment stagnates at 88% and the maximum conversion of the simulation reaches 95% after 3600 s of reaction. A large error was assigned to the experimental values at final stages in order to not exclude complete conversion. Schmidt et al. [
32] performed 33 cycles of charging and discharging with the same reactor filling. They reach maximal values of conversion between 90–95% for the duration of the experiments and state that the final 5–10% need significanty more time [
31]. Additionally, they detect the formation of agglomerates. Rosskopf et al. [
57] show, that the surrounding of the agglomerates form fracture-like preferential flow paths with higher permeability compared to the agglomerates. Schaube et al. [
23] state for a directly operated fixed-bed reactor with CaO/Ca(OH)
, the last 20% of solid bulk get converted slower as soon as agglomerates have been formed. In the reactive bed of the indirectly operated reactor concept, pressure gradients are the result of water consumption due to the chemical reaction. Differences in permeability in the agglomerates and their surroundings result in inhomogeneous pressure gradients. The reactive material close to the preferential flow paths is well supplied with reaction fluid and reacts fast. Less water reaches the solid material within the agglomerates. Here, in a self-enhancing mechanism, a smaller pressure gradient deteriorates the supply of water vapor even further and the reactive solid material reacts slowly. This retardation effect of the agglomerates becomes noticeable with increasing conversion, when the material close to the preferential flow paths has already reacted. The reduced heat production due to the lower reaction rate is overlapped by heat conduction and the slope of the temporal temperature profile is flattened. It is thus deduced that agglomerates retard the reaction rate at progressed conversion also in the indirectly operated reactor concept. The term
represents the retardation at progressed conversion and describes the effect of the agglomerates phenomenologically. Thus, there is no easy physical interpretation of the parameter k
; primarily, it fulfilled the purpose of identifying a relevant phenomenon, so it may only be interpreted qualitatively. As its inferred value is large (k
= 5.58), we conclude that the effect of agglomerates is important. If it was not important, k
would have a value close to zero.
The surrogate model represents the conversion profile satisfactorily, see
Figure 5d. At the beginning, the simulation overestimates the conversion, as the model does not represent the experimental procedure exactly. The pressure in the vapor vessel was used as initial condition in the reactive bed, whereas in the experiment, the reactor had been evacuated beforehand. However, the initial pressure of the experiment is unknown. The initial water pressure in the simulation setup leads to increased conversion at early simulation stages until the additional water vapor caused by the initial condition is consumed by the reaction. At later times, experimental and simulation results match well, also with respect to incomplete conversion.
Figure 5 shows the simulation results of the surrogate model together with the experimental results for the temperature distributions at T1, T3, T7 and the conversion. The results of the calibrated model indicate a good agreement with the experimental data. In particular, the temperature curves T1 and T3 reflect the temperature profile well, including the slope of decreasing temperature at final conversion and the final temperature after conversion. The discrepancy in T7 is larger. As the reaction front moves from left to right, this measurement point is less determined by initial and boundary conditions. The surrogate model is built based on the 500 DuMu
-simulations. Thus, the model uncertainties accumulate at this point. This explains furthermore the wavy shape of the surrogate model results for T7. The shape of T1 and T3 is smoother and features a smaller confidence interval especially at later simulation times compared to T7.
5.2. Validation
The calibrated surrogate model was used for simulating the experiment Case R20, see
Table 3, with a similar setup but different water vapor pressure (
Pa) and air volume flux in the HTF channel (47.22
). The lower water pressure results in a lower equilibrium temperature and, despite a larger heat-transfer flux, in a slower conversion. The experimental data exceed 100% conversion against the statement of Reference [
31] that conversions of maximum 95% were reached. We attribute this to measurement uncertainty.
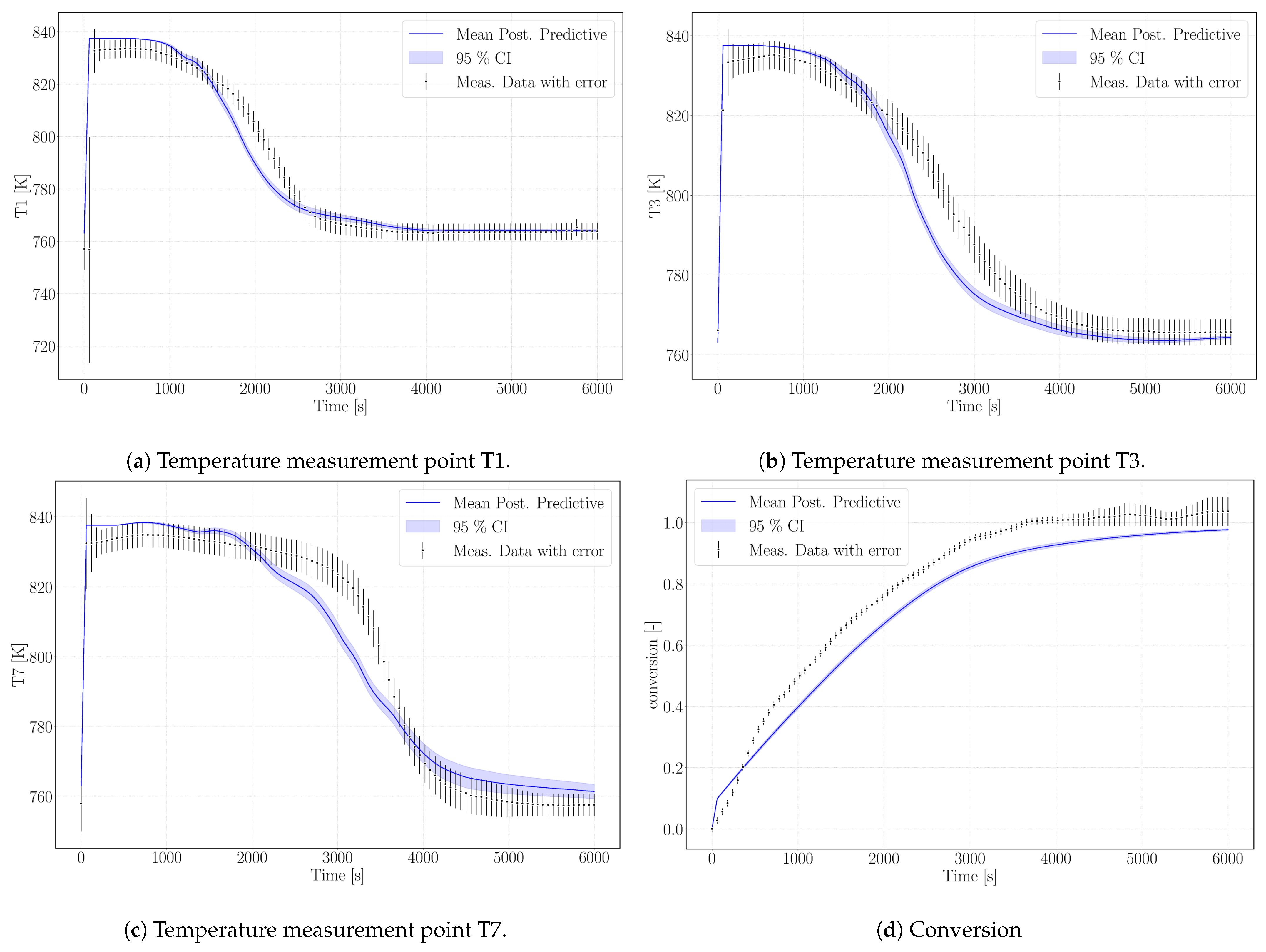
Figure 6 shows the simulation results of the surrogate model.
As outlined in the previous section, the simulation does not reach complete conversion due to the high value of the parameter k
that phenomenologically represents the changed reaction dynamics once agglomerates have formed. As the experiment reaches 100% in 6000 s, possibly no agglomerates are present yet. This would be the case, if this experimental run was one of the first in a row of the altogether 33 experiments performed with the same reactor filling [
32]. The chronological order of the experiments is not mentioned in References [
31,
32] or Reference [
20]. The parameter k
limits the reaction rate at progressed conversion and the temperature profiles unfold accordingly. Experimental data and simulation results of the temperatures T1, T3, and T7 are shown in
Figure 6a–c. The profiles show a good agreement with the experimental temperature curves. Thus, we tend to attribute this to a measurement bias in the experimental data regarding conversion.
The model results overestimate the equilibrium temperature of the experiment. The equilibrium condition for pressure and temperature of Reference [
14], which was used for the calibration case, is not adapted to the pressure conditions of the reaction conditions. The simulated temperatures, however, are still in the range of measurement uncertainty. Despite that, the temperature profiles of this experimental setup are reproduced with an accuracy comparable to the calibration case. The decrease in temperature is slightly steeper in the model results, but the velocity of the reaction front matches the model results. The final temperatures for each measurement lay within the range of measurement uncertainty.