Comparative Analysis of DFT+U, ACBN0, and Hybrid Functionals on the Spin Density of YTiO3 and SrRuO3
Abstract
1. Introduction
2. Computational Methods
3. Results
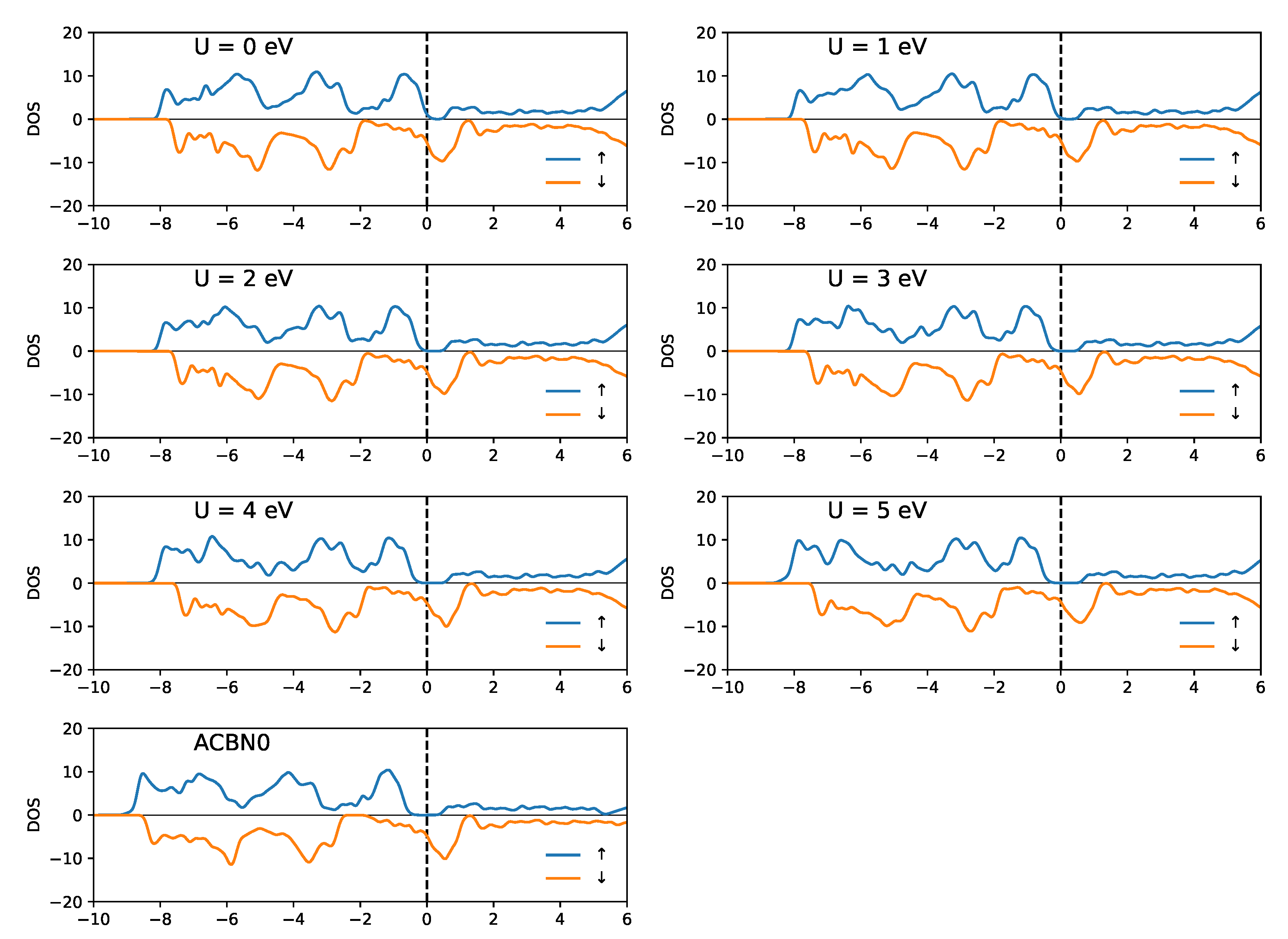
3.1. YTiO
3.2. SrRuO
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Tsuneda, T.; Hirao, K. Self-interaction corrections in density functional theory. J. Chem. Phys. 2014, 140, 18A513. [Google Scholar] [CrossRef] [PubMed]
- Petukhov, A.G.; Mazin, I.I.; Chioncel, L.; Lichtenstein, A.I. Correlated metals and the LDA+U method. Phys. Rev. B 2003, 67, 153106. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Georges, A.; Kotliar, G.; Krauth, W.; Rozenberg, M.J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 1996, 68, 13–125. [Google Scholar] [CrossRef]
- Hedin, L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796–A823. [Google Scholar] [CrossRef]
- Aryasetiawan, F.; Gunnarsson, O. The GW method. Rep. Prog. Phys. 1998, 61, 237–312. [Google Scholar] [CrossRef]
- Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef]
- Mezei, P.D.; Csonka, G.I.; Kállay, M. Electron Density Errors and Density-Driven Exchange-Correlation Energy Errors in Approximate Density Functional Calculations. J. Chem. Theory Comput. 2017, 13, 4753–4764. [Google Scholar] [CrossRef]
- Sang, X.; Kulovits, A.; Wang, G.; Wiezorek, J. Validation of density functionals for transition metals and intermetallics using data from quantitative electron diffraction. J. Chem. Phys. 2013, 138, 084504. [Google Scholar] [CrossRef] [PubMed]
- Choudhuri, I.; Truhlar, D.G. Calculating and Characterizing the Charge Distributions in Solids. J. Chem. Theory Comput. 2020, 16, 5884–5892. [Google Scholar] [CrossRef]
- Peng, D.; Nakashima, P.N.H. Measuring Density Functional Parameters from Electron Diffraction Patterns. arXiv 2020, arXiv:2010.09379. [Google Scholar]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Cococcioni, M.; de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 2005, 71, 035105. [Google Scholar] [CrossRef]
- Agapito, L.A.; Curtarolo, S.; Nardelli, M.B. Reformulation of DFT+U as a Pseudohybrid Hubbard Density Functional for Accelerated Materials Discovery. Phys. Rev. X 2015, 5. [Google Scholar] [CrossRef]
- Gopal, P.; Fornari, M.; Curtarolo, S.; Agapito, L.A.; Liyanage, L.S.I.; Nardelli, M.B. Improved predictions of the physical properties of Zn- and Cd-based wide band-gap semiconductors: A validation of the ACBN0 functional. Phys. Rev. B 2015, 91. [Google Scholar] [CrossRef]
- Gopal, P.; Gennaro, R.D.; dos Santos Gusmao, M.S.; Orabi, R.A.R.A.; Wang, H.; Curtarolo, S.; Fornari, M.; Nardelli, M.B. Improved electronic structure and magnetic exchange interactions in transition metal oxides. J. Phys. Condens. Matter 2017, 29, 444003. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Kibalin, I.A.; Yan, Z.; Voufack, A.B.; Gueddida, S.; Gillon, B.; Gukasov, A.; Porcher, F.; Bataille, A.M.; Morini, F.; Claiser, N.; et al. Spin density in YTiO3: I. Joint refinement of polarized neutron diffraction and magnetic x-ray diffraction data leading to insights into orbital ordering. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Masys, Š.; Jonauskas, V. On the crystalline structure of orthorhombic SrRuO3: A benchmark study of DFT functionals. Comput. Mater. Sci. 2016, 124, 78–86. [Google Scholar] [CrossRef][Green Version]
- Kunkemöller, S.; Jenni, K.; Gorkov, D.; Stunault, A.; Streltsov, S.; Braden, M. Magnetization density distribution in the metallic ferromagnet SrRuO3 determined by polarized neutron diffraction. Phys. Rev. B 2019, 100, 054413. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Schlipf, M.; Gygi, F. Optimization algorithm for the generation of ONCV pseudopotentials. Comput. Phys. Commun. 2015, 196, 36–44. [Google Scholar] [CrossRef]
- De-la Roza, A.O.; Johnson, E.R.; Luaña, V. Critic2: A program for real-space analysis of quantum chemical interactions in solids. Comput. Phys. Commun. 2014, 185, 1007–1018. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef]
- Ruiz, E.; Cirera, J.; Alvarez, S. Spin density distribution in transition metal complexes. Coord. Chem. Rev. 2005, 249, 2649–2660. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Agapito, L.A.; Fornari, M.; Ceresoli, D.; Ferretti, A.; Curtarolo, S.; Nardelli, M.B. Accurate tight-binding Hamiltonians for two-dimensional and layered materials. Phys. Rev. B 2016, 93, 125137. [Google Scholar] [CrossRef]
- Nardelli, M.B.; Cerasoli, F.T.; Costa, M.; Curtarolo, S.; Gennaro, R.D.; Fornari, M.; Liyanage, L.; Supka, A.R.; Wang, H. PAOFLOW: A utility to construct and operate on ab initio Hamiltonians from the projections of electronic wavefunctions on atomic orbital bases, including characterization of topological materials. Comput. Mater. Sci. 2018, 143, 462–472. [Google Scholar] [CrossRef]
- Lin, L. Adaptively Compressed Exchange Operator. J. Chem. Theory Comput. 2016, 12, 2242–2249. [Google Scholar] [CrossRef] [PubMed]
- Dovesi, R.; Orlando, R.; Erba, A.; Zicovich-Wilson, C.M.; Civalleri, B.; Casassa, S.; Maschio, L.; Ferrabone, M.; Pierre, M.D.L.; D’Arco, P.; et al. CRYSTAL14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. [Google Scholar] [CrossRef]
- Gatti, C.; Saunders, V.R.; Roetti, C. Crystal field effects on the topological properties of the electron density in molecular crystals: The case of urea. J. Chem. Phys. 1994, 101, 10686–10696. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Janotti, A.; Bjaalie, L.; de Walle, C.G.V. Interband and polaronic excitations in YTiO3 from first principles. Phys. Rev. B 2014, 90. [Google Scholar] [CrossRef]
- Varignon, J.; Bibes, M.; Zunger, A. Origin of band gaps in 3d perovskite oxides. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef]
- Jeng, H.T.; Lin, S.H.; Hsue, C.S. Orbital Ordering and Jahn-Teller Distortion in Perovskite Ruthenate SrRuO3. Phys. Rev. Lett. 2006, 97, 067002. [Google Scholar] [CrossRef]
- Ryee, S.; Jang, S.W.; Kino, H.; Kotani, T.; Han, M.J. Quasiparticle self-consistent GW calculation of Sr2RuO4 and SrRuO3. Phys. Rev. B 2016, 93, 075125. [Google Scholar] [CrossRef]
- Yan, Z.; Kibalin, I.A.; Claiser, N.; Gueddida, S.; Gillon, B.; Gukasov, A.; Voufack, A.B.; Morini, F.; Sakurai, Y.; Brancewicz, M.; et al. Spin density in YTiO3: II. Momentum-space representation of electron spin density supported by position-space results. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Hansen, N.K.; Coppens, P. Testing aspherical atom refinements on small-molecule data sets. Acta Crystallogr. Sect. A 1978, 34, 909–921. [Google Scholar] [CrossRef]
- Gilmore, C.J.; Shankland, K.; Bricogne, G. Applications of the Maximum Entropy Method to Powder Diffraction and Electron Crystallography. Proc. Math. Phys. Sci. 1993, 442, 97–111. [Google Scholar]
- Volkov, A.; Gatti, C.; Abramov, Y.; Coppens, P. Evaluation of net atomic charges and atomic and molecular electrostatic moments through topological analysis of the experimental charge density. Acta Crystallogr. Sect. A Found. Crystallogr. 2000, 56, 252–258. [Google Scholar] [CrossRef] [PubMed]
- Gatti, C.; Saleh, G.; Presti, L.L. Source Function applied to experimental densities reveals subtle electron-delocalization effects and appraises their transferability properties in crystals. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 180–193. [Google Scholar] [CrossRef]
- May, K.J.; Kolpak, A.M. Improved description of perovskite oxide crystal structure and electronic properties using self-consistent Hubbard U corrections from ACBN0. Phys. Rev. B 2020, 101. [Google Scholar] [CrossRef]
- Ceresoli, D.; Tosatti, E. Pressure-induced insulator-metal and structural transitions of BaBiO3 from first principles LDA+U. In Proceedings of the APS March Meeting Abstact L40.00008, New Orleans, LA, USA, 10–14 March 2008. [Google Scholar]
- Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Yuk, S.F.; Pitike, K.C.; Nakhmanson, S.M.; Eisenbach, M.; Li, Y.W.; Cooper, V.R. Towards an accurate description of perovskite ferroelectrics: Exchange and correlation effects. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, J.; Perdew, J.P.; Wu, X. Comparative first-principles studies of prototypical ferroelectric materials by LDA, GGA, and SCAN meta-GGA. Phys. Rev. B 2017, 96. [Google Scholar] [CrossRef]
- Gautam, G.S.; Carter, E.A. Evaluating transition metal oxides within DFT-SCAN and SCAN+U frameworks for solar thermochemical applications. Phys. Rev. Mater. 2018, 2. [Google Scholar] [CrossRef]
- Jr, V.L.C.; Cococcioni, M. Extended DFT+U+V method with on-site and inter-site electronic interactions. J. Phys. Condens. Matter 2010, 22, 055602. [Google Scholar] [CrossRef]
- Lee, S.H.; Son, Y.W. Efficient First-Principles Approach with a Pseudohybrid Density Functional for Extended Hubbard Interactions. arXiv 2019, arXiv:1911.05967. [Google Scholar]
- Tancogne-Dejean, N.; Rubio, A. Parameter-free hybridlike functional based on an extended Hubbard model: DFT+U+V. Phys. Rev. B 2020, 102. [Google Scholar] [CrossRef]
- James, A.D.N.; Harris-Lee, E.I.; Hampel, A.; Aichhorn, M.; Dugdale, S.B. Wavefunctions, electronic localization and bonding properties for correlated materials beyond the Kohn-Sham formalism. arXiv 2020, arXiv:2010.04694. [Google Scholar]
- Bruno, G.; Macetti, G.; Presti, L.L.; Gatti, C. Spin Density Topology. Molecules 2020, 25, 3537. [Google Scholar] [CrossRef]
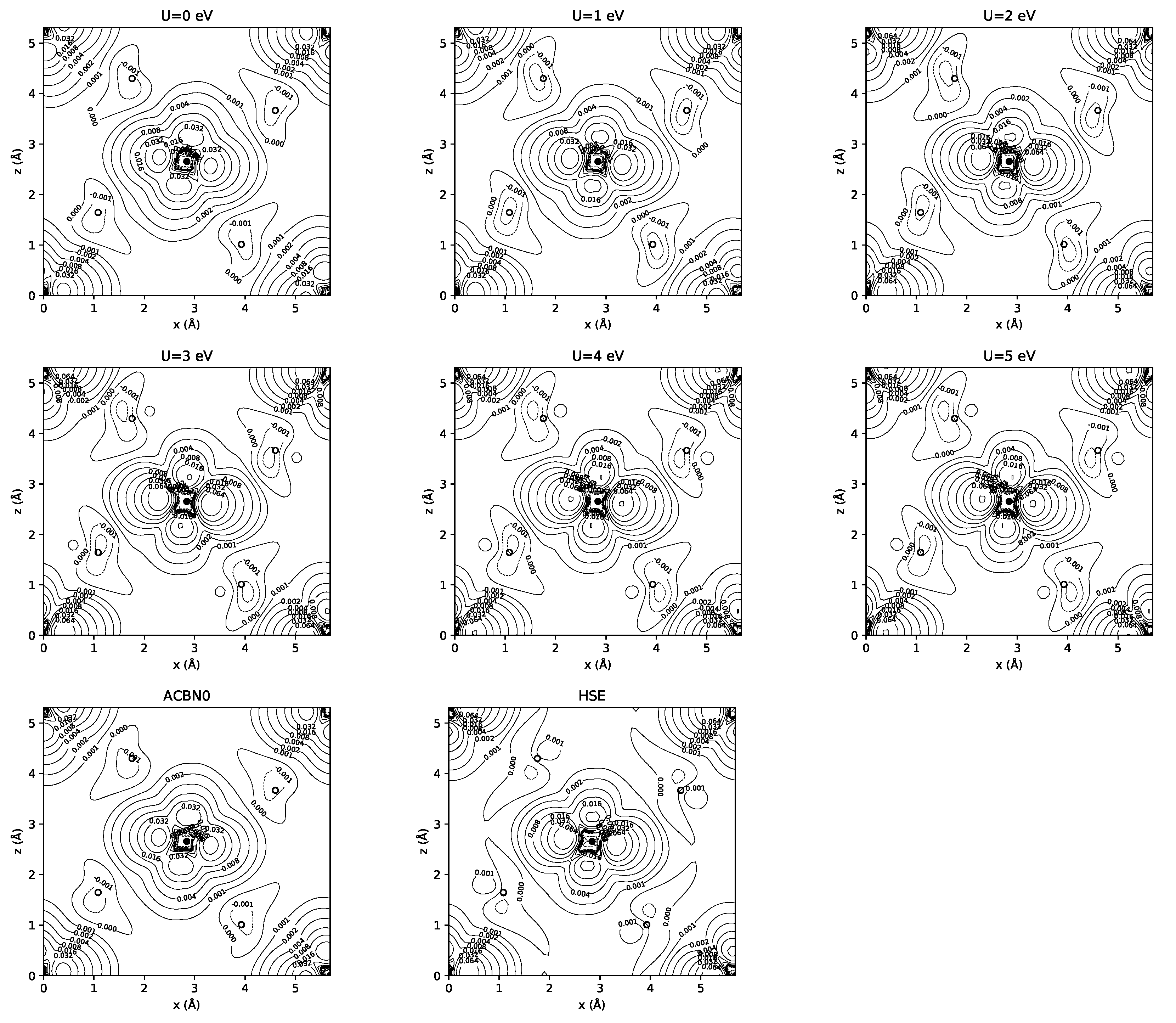
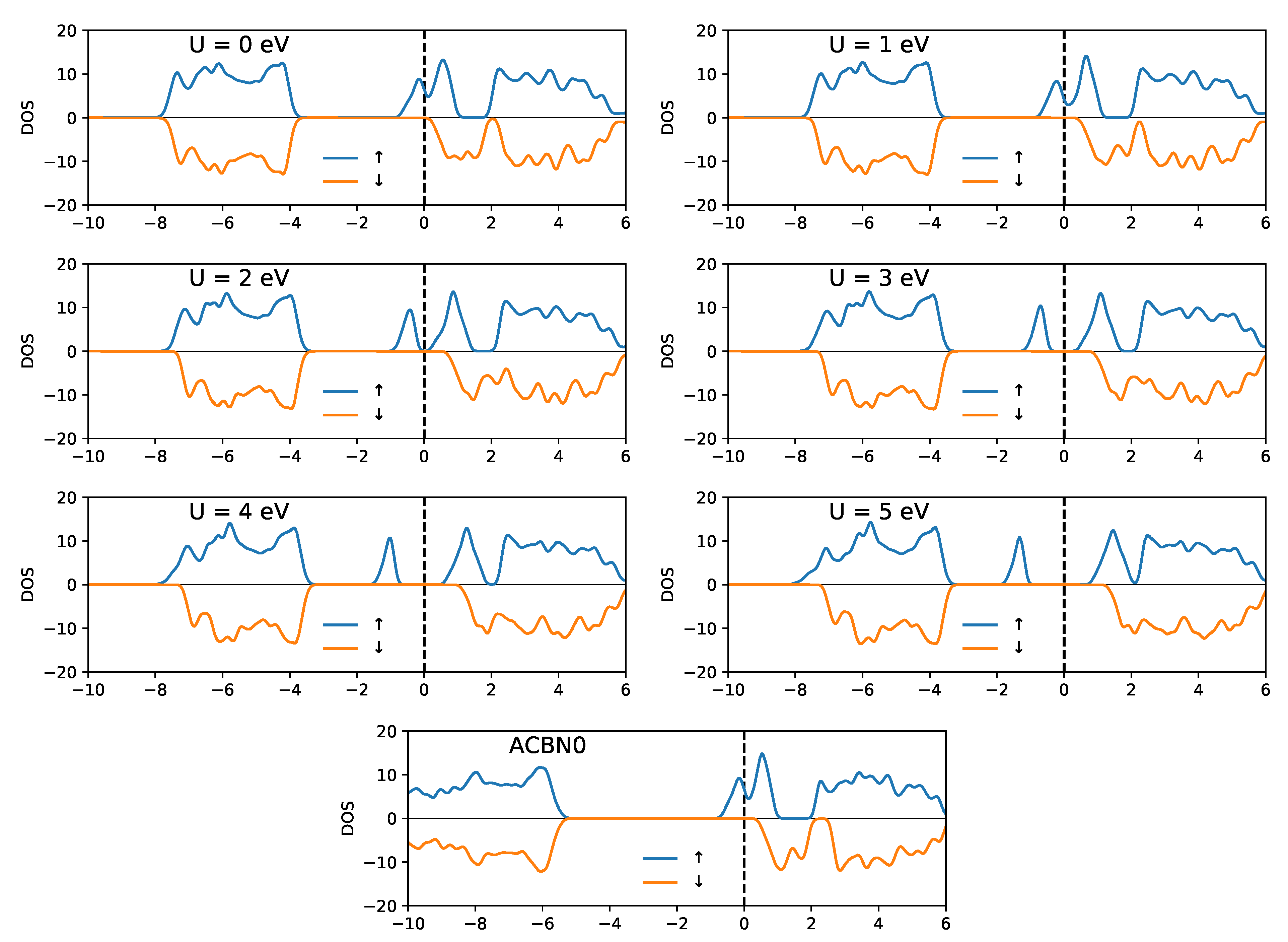
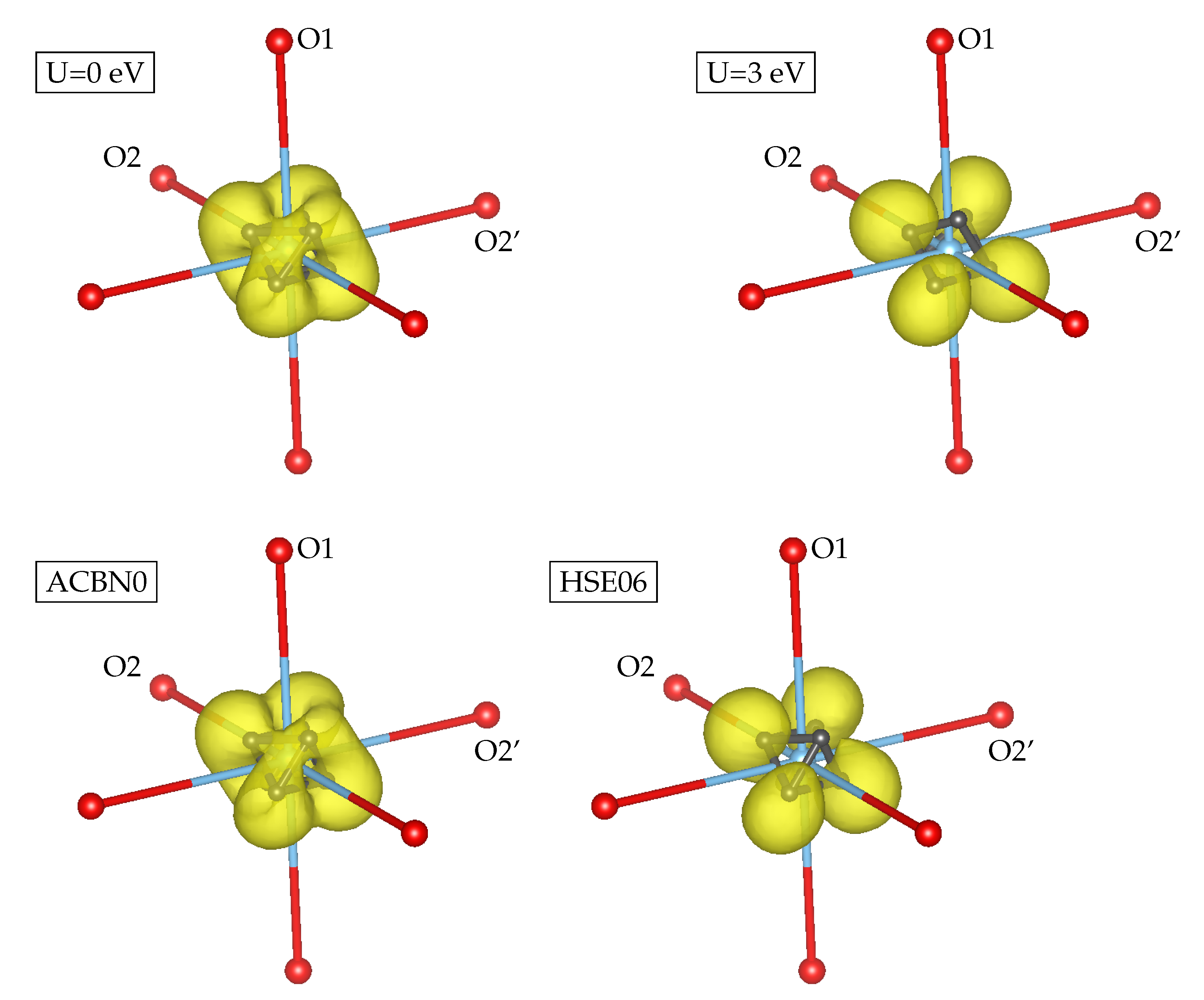
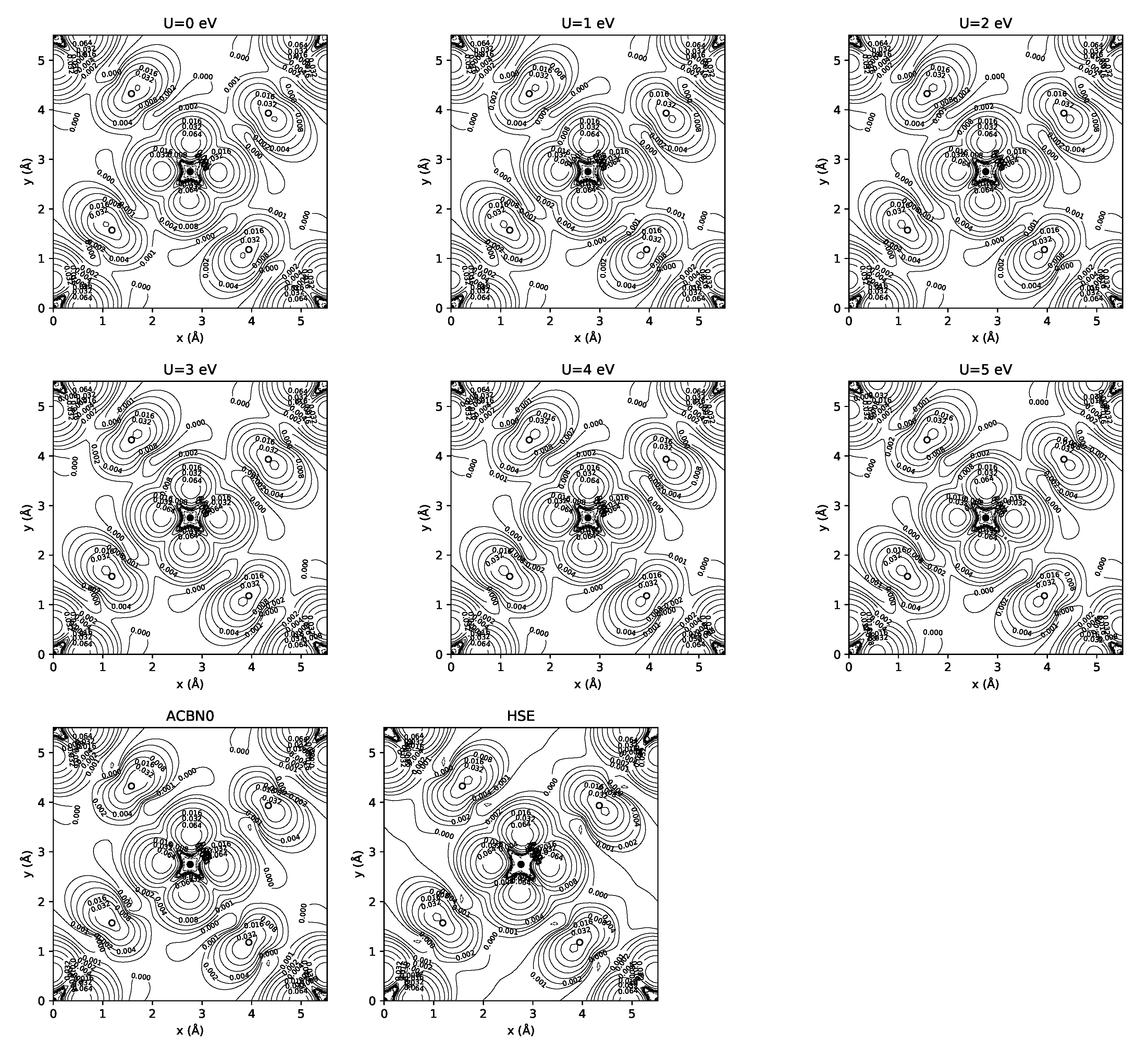


| Method | q(Y) | q(Ti) | q(O1) | q(O2) | m(Y) | m(Ti) | m(O1) | m(O2) | Tot. Magn. |
|---|---|---|---|---|---|---|---|---|---|
| U = 0 eV | 2.1101 | 1.9066 | −1.3325 | −1.3423 | 0.0594 | 0.7974 | 0.0521 | 0.0456 | 1.0000 |
| U = 1 eV | 2.1131 | 1.9198 | −1.3387 | −1.3474 | 0.0549 | 0.8161 | 0.0461 | 0.0414 | 1.0000 |
| U = 2 eV | 2.1182 | 1.9336 | −1.3448 | −1.3537 | 0.0457 | 0.8348 | 0.0396 | 0.0399 | 1.0000 |
| U = 3 eV | 2.1220 | 1.9496 | −1.3510 | −1.3605 | 0.0376 | 0.8511 | 0.0342 | 0.0386 | 1.0000 |
| U = 4 eV | 2.1243 | 1.9671 | −1.3574 | −1.3673 | 0.0316 | 0.8647 | 0.0299 | 0.0369 | 1.0000 |
| U = 5 eV | 2.1255 | 1.9854 | −1.3636 | −1.3739 | 0.0272 | 0.8764 | 0.0264 | 0.0350 | 1.0000 |
| ACBN0 | 2.2678 | 2.0992 | −1.4481 | −1.4597 | 0.0450 | 0.8208 | 0.0458 | 0.0442 | 1.0000 |
| HSE06 | 2.2343 | 2.0259 | −1.4127 | −1.4239 | 0.0273 | 0.8513 | 0.0369 | 0.0422 | 1.0000 |
| expt. PND | N/A | N/A | N/A | N/A | -0.047 | 0.715 | 0.016 | 0.004 | 0.704 |
| PBE0 | N/A | N/A | N/A | N/A | 0.015 | 0.852 | 0.036 | 0.049 | 0.998 |
| Method | q(Sr) | q(Ru) | q(O1) | q(O2) | m(Sr) | m(Ru) | m(O1) | m(O2) | Tot. Magn. |
|---|---|---|---|---|---|---|---|---|---|
| U = 0 eV | 1.5745 | 1.6715 | −1.0795 | −1.0872 | 0.0136 | 1.3898 | 0.1942 | 0.1853 | 1.9772 |
| U = 1 eV | 1.5754 | 1.6576 | −1.0750 | −1.0832 | 0.0136 | 1.3967 | 0.1988 | 0.1909 | 1.9989 |
| U = 2 eV | 1.5763 | 1.6423 | −1.0703 | −1.0784 | 0.0134 | 1.3869 | 0.2025 | 0.1946 | 2.0000 |
| U = 3 eV | 1.5773 | 1.6263 | −1.0653 | −1.0733 | 0.0134 | 1.3740 | 0.2068 | 0.1990 | 2.0000 |
| U = 4 eV | 1.5783 | 1.6098 | −1.0601 | −1.0682 | 0.0134 | 1.3597 | 0.2115 | 0.2040 | 2.0000 |
| U = 5 eV | 1.5793 | 1.5927 | −1.0555 | −1.0612 | 0.0136 | 1.3436 | 0.2163 | 0.2102 | 2.0000 |
| ACBN0 | 1.6214 | 1.8594 | −1.1581 | −1.1649 | 0.0086 | 1.5103 | 0.1623 | 0.1565 | 2.0000 |
| HSE06 | 1.6608 | 2.1080 | −1.2576 | −1.2539 | −0.0023 | 1.4989 | 0.1801 | 0.1432 | 2.0000 |
| expt. 2 K S + L | N/A | N/A | N/A | N/A | N/A | 1.35 | 0.20 | 0.20 | 1.95 |
| expt. 2 K S | N/A | N/A | N/A | N/A | N/A | 1.42 | 0.20 | 0.20 | 2.02 |
| other DFT (PBE) | N/A | N/A | N/A | N/A | N/A | 1.34 | 0.16 | 0.13 | 1.79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Menescardi, F.; Ceresoli, D. Comparative Analysis of DFT+U, ACBN0, and Hybrid Functionals on the Spin Density of YTiO3 and SrRuO3. Appl. Sci. 2021, 11, 616. https://doi.org/10.3390/app11020616
Menescardi F, Ceresoli D. Comparative Analysis of DFT+U, ACBN0, and Hybrid Functionals on the Spin Density of YTiO3 and SrRuO3. Applied Sciences. 2021; 11(2):616. https://doi.org/10.3390/app11020616
Chicago/Turabian StyleMenescardi, Francesca, and Davide Ceresoli. 2021. "Comparative Analysis of DFT+U, ACBN0, and Hybrid Functionals on the Spin Density of YTiO3 and SrRuO3" Applied Sciences 11, no. 2: 616. https://doi.org/10.3390/app11020616
APA StyleMenescardi, F., & Ceresoli, D. (2021). Comparative Analysis of DFT+U, ACBN0, and Hybrid Functionals on the Spin Density of YTiO3 and SrRuO3. Applied Sciences, 11(2), 616. https://doi.org/10.3390/app11020616






