Leveraging the Generalization Ability of Deep Convolutional Neural Networks for Improving Classifiers for Color Fundus Photographs
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
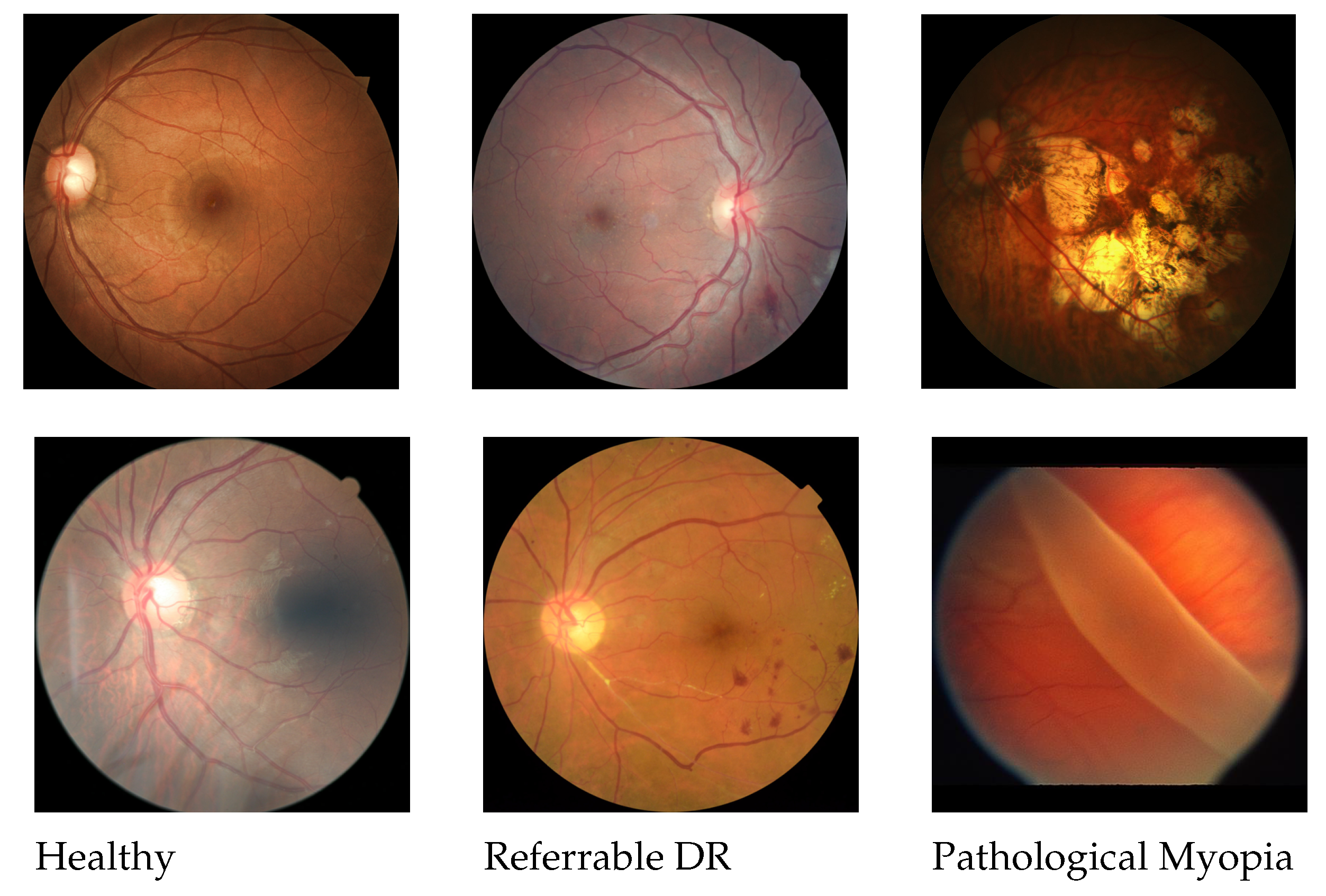
2.1. Classification of Referable Diabetic Retinopathy
2.1.1. Dataset
2.1.2. Filtering Suspicious Data
2.2. Classification of Pathological Myopia
2.2.1. Dataset
2.2.2. Reducing Annotation Cost with Active Learning
2.2.3. Collection of Scarce Data
2.2.4. Final Submission
2.3. Image Preprocessing
2.4. Training Details
3. Results
3.1. Classification of Referable Diabetic Retinopathy
3.2. Classification of Pathological Myopia
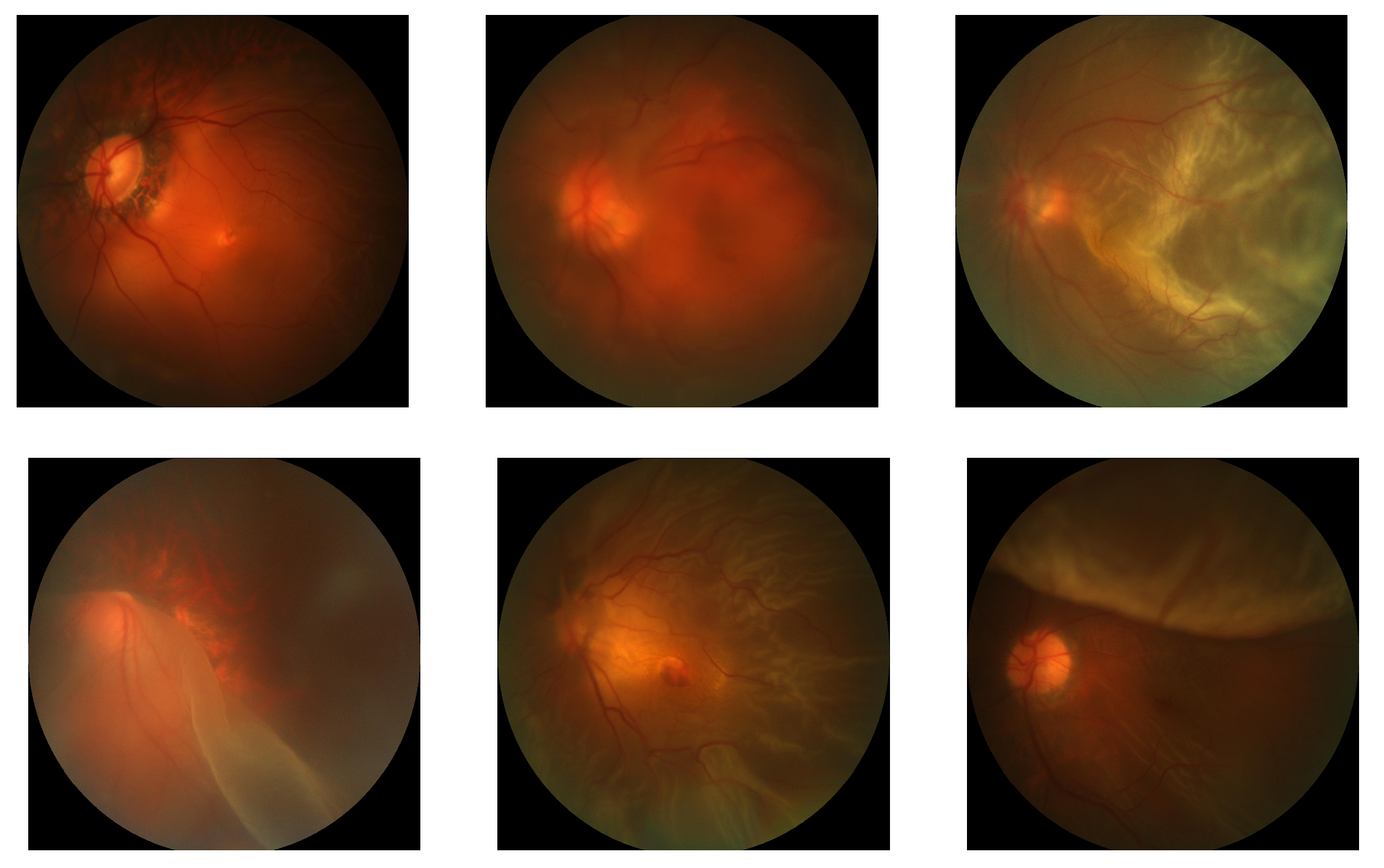
3.2.1. Positive Case Mining
3.2.2. Model Trained with Mined Labels and Supplemented Data
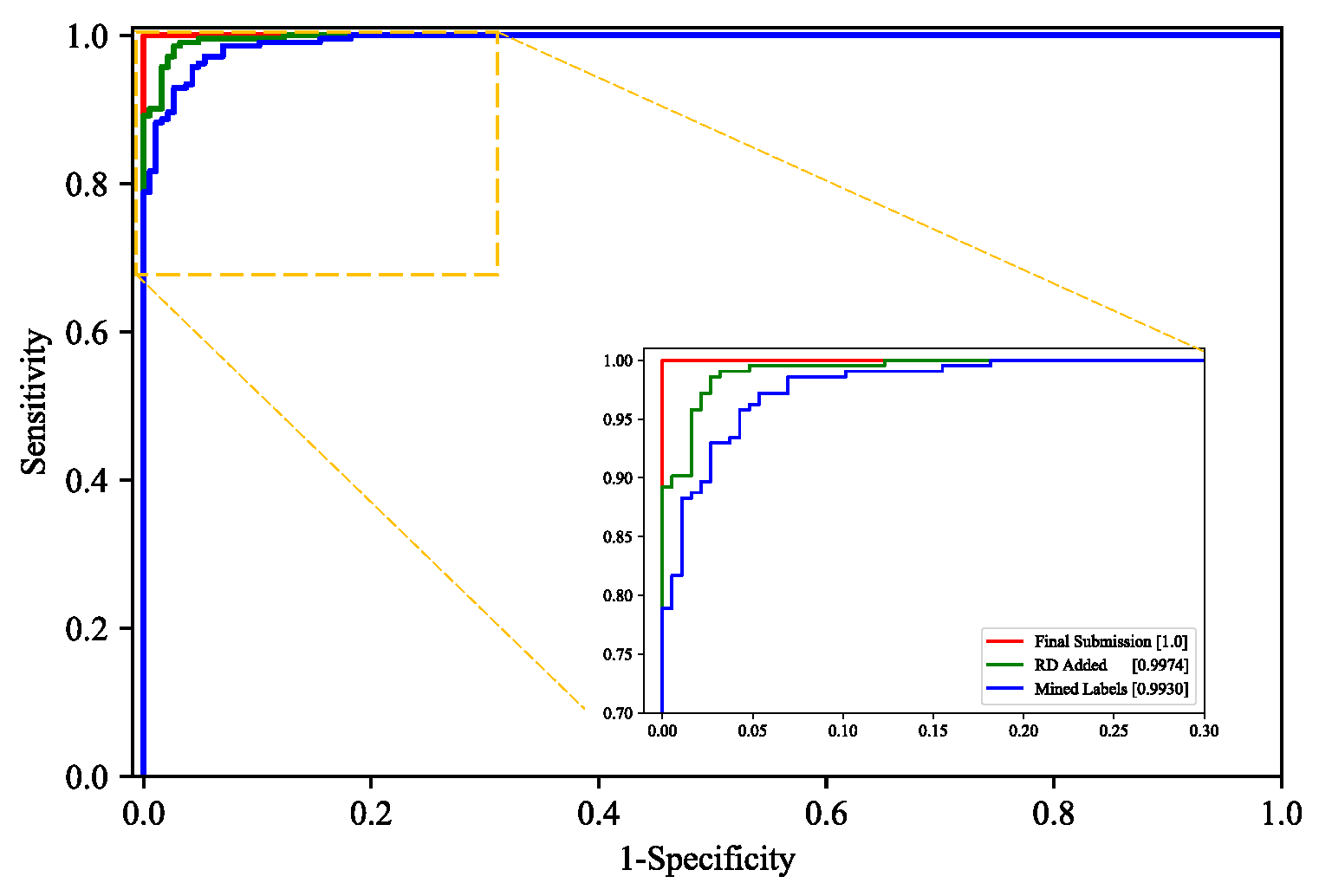
3.2.3. Model Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNN | Convolutional Neural Network |
| DR | Diabetic Retinopathy |
| PM | Pathologic Myopia |
| ROC | Receiver Operating Characteristics |
| AUROC | Area Under the Receiver Operating Characteristics curve |
References
- Chou, P.B.; Rao, A.R.; Sturzenbecker, M.C.; Wu, F.Y.; Brecher, V.H. Automatic defect classification for semiconductor manufacturing. Mach. Vis. Appl. 1997, 9, 201–214. [Google Scholar] [CrossRef]
- Wang, G.; Liao, T.W. Automatic identification of different types of welding defects in radiographic images. Ndt E Int. 2002, 35, 519–528. [Google Scholar] [CrossRef]
- Javed, O.; Shah, M. Tracking and object classification for automated surveillance. In Proceedings of the European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002; pp. 343–357. [Google Scholar]
- Hsieh, J.W.; Yu, S.H.; Chen, Y.S.; Hu, W.F. Automatic traffic surveillance system for vehicle tracking and classification. IEEE Trans. Intell. Transp. Syst. 2006, 7, 175–187. [Google Scholar] [CrossRef]
- Gulshan, V.; Peng, L.; Coram, M.; Stumpe, M.C.; Wu, D.; Narayanaswamy, A.; Venugopalan, S.; Widner, K.; Madams, T.; Cuadros, J.; et al. Development and validation of a deep learning algorithm for detection of diabetic retinopathy in retinal fundus photographs. JAMA 2016, 316, 2402–2410. [Google Scholar] [CrossRef] [PubMed]
- Son, J.; Bae, W.; Kim, S.; Park, S.J.; Jung, K.H. Classification of Findings with Localized Lesions in Fundoscopic Images Using a Regionally Guided CNN. In Computational Pathology and Ophthalmic Medical Image Analysis; Springer: Berlin/Heidelberg, Germany, 2018; pp. 176–184. [Google Scholar]
- Jung, K.H.; Park, H.; Hwang, W. Deep learning for medical image analysis: Applications to computed tomography and magnetic resonance imaging. Hanyang Med. Rev. 2017, 37, 61–70. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C. MNIST Handwritten Digit (Database). Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 30 November 2020).
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Li, H.; Yu, B.; Zhou, D. Error rate analysis of labeling by crowdsourcing. In ICML Workshop: Machine Learning Meets Crowdsourcing; Citeseer: Atalanta, GA, USA, 2013. [Google Scholar]
- Fiorino, C.; Reni, M.; Bolognesi, A.; Cattaneo, G.M.; Calandrino, R. Intra-and inter-observer variability in contouring prostate and seminal vesicles: Implications for conformal treatment planning. Radiother. Oncol. 1998, 47, 285–292. [Google Scholar] [CrossRef]
- Nielsen, P.; Stigsby, B.; Nickelsen, C.; Nim, J. Intra-and inter-observer variability in the assessment of intrapartum cardiotocograms. Acta Obstet. Gynecol. Scand. 1987, 66, 421–424. [Google Scholar] [CrossRef]
- Park, S.J.; Shin, J.Y.; Kim, S.; Son, J.; Jung, K.H.; Park, K.H. A Novel Fundus Image Reading Tool for Efficient Generation of a Multi-dimensional Categorical Image Database for Machine Learning Algorithm Training. J. Korean Med. Sci. 2018, 33, e239. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436. [Google Scholar] [CrossRef]
- Patrini, G.; Rozza, A.; Krishna Menon, A.; Nock, R.; Qu, L. Making deep neural networks robust to label noise: A loss correction approach. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1944–1952. [Google Scholar]
- Sukhbaatar, S.; Bruna, J.; Paluri, M.; Bourdev, L.; Fergus, R. Training convolutional networks with noisy labels. arXiv 2014, arXiv:1406.2080. [Google Scholar]
- Bekker, A.J.; Goldberger, J. Training deep neural-networks based on unreliable labels. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2682–2686. [Google Scholar]
- Goldberger, J.; Ben-Reuven, E. Training deep neural-networks using a noise adaptation layer. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; pp. 41–48. [Google Scholar]
- Jiang, L.; Zhou, Z.; Leung, T.; Li, L.J.; Fei-Fei, L. Mentornet: Learning data-driven curriculum for very deep neural networks on corrupted labels. arXiv 2017, arXiv:1712.05055. [Google Scholar]
- Dehghani, M.; Mehrjou, A.; Gouws, S.; Kamps, J.; Schölkopf, B. Fidelity-weighted learning. arXiv 2017, arXiv:1711.02799. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the knowledge in a neural network. arXiv 2015, arXiv:1503.02531. [Google Scholar]
- Ren, M.; Zeng, W.; Yang, B.; Urtasun, R. Learning to Reweight Examples for Robust Deep Learning. arXiv 2018, arXiv:1803.09050. [Google Scholar]
- Arpit, D.; Jastrzębski, S.; Ballas, N.; Krueger, D.; Bengio, E.; Kanwal, M.S.; Maharaj, T.; Fischer, A.; Courville, A.; Bengio, Y.; et al. A closer look at memorization in deep networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; JMLR.org. Volume 70, pp. 233–242. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning requires rethinking generalization. arXiv 2016, arXiv:1611.03530. [Google Scholar]
- Han, B.; Yao, Q.; Yu, X.; Niu, G.; Xu, M.; Hu, W.; Tsang, I.; Sugiyama, M. Co-teaching: Robust training of deep neural networks with extremely noisy labels. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 2–8 December 2018; pp. 8536–8546. [Google Scholar]
- Song, H.; Kim, M.; Lee, J.G. Selfie: Refurbishing unclean samples for robust deep learning. In Proceedings of the International Conference on Machine Learning, Long beach, CA, USA, 9–15 June 2019; pp. 5907–5915. [Google Scholar]
- Tanaka, D.; Ikami, D.; Yamasaki, T.; Aizawa, K. Joint optimization framework for learning with noisy labels. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5552–5560. [Google Scholar]
- Pathologic Myopia Challenge. Available online: http://palm.grand-challenge.org (accessed on 20 May 2019).
- Early Treatment Diabetic Retinopathy Study Research Group. Grading diabetic retinopathy from stereoscopic color fundus photographs—an extension of the modified Airlie House classification: ETDRS report number 10. Ophthalmology 1991, 98, 786–806. [Google Scholar] [CrossRef]
- Morgan, I.G.; Ohno-Matsui, K.; Saw, S.M. Myopia. Lancet 2012, 379, 1739–1748. [Google Scholar] [CrossRef]
- Kaggle Diabetic Retinopathy Detection Competition Report. 2015. Available online: https://www.kaggle.com/c/diabetic-retinopathy-detection (accessed on 20 May 2019).
- Decencière, E.; Zhang, X.; Cazuguel, G.; Lay, B.; Cochener, B.; Trone, C.; Gain, P.; Ordonez, R.; Massin, P.; Erginay, A.; et al. Feedback on a publicly distributed database: The Messidor database. Image Anal. Stereol. 2014, 33, 231–234. [Google Scholar] [CrossRef]
- Porwal, P.; Pachade, S.; Kamble, R.; Kokare, M.; Deshmukh, G.; Sahasrabuddhe, V.; Meriaudeau, F. Indian Diabetic Retinopathy Image Dataset (IDRiD): A Database for Diabetic Retinopathy Screening Research. Data 2018, 3, 25. [Google Scholar] [CrossRef]
- Retinal Fundus Glaucoma Challenge. Available online: http://refuge.grand-challenge.org (accessed on 20 May 2019).
- Almazroa, A.; Alodhayb, S.; Osman, E.; Ramadan, E.; Hummadi, M.; Dlaim, M.; Alkatee, M.; Raahemifar, K.; Lakshminarayanan, V. Retinal fundus images for glaucoma analysis: The RIGA dataset. In Proceedings of the Medical Imaging 2018: Imaging Informatics for Healthcare, Research, and Applications. International Society for Optics and Photonics, Houston, TX, USA, 10–15 February 2018; Volume 10579, p. 105790B. [Google Scholar]
- Ohno-Matsui, K.; Lai, T.Y.; Lai, C.C.; Cheung, C.M.G. Updates of pathologic myopia. Prog. Retin. Eye Res. 2016, 52, 156–187. [Google Scholar] [CrossRef]
- Retinal Image Bank. Available online: https://imagebank.asrs.org (accessed on 20 May 2019).
- Krause, J.; Gulshan, V.; Rahimy, E.; Karth, P.; Widner, K.; Corrado, G.S.; Peng, L.; Webster, D.R. Grader variability and the importance of reference standards for evaluating machine learning models for diabetic retinopathy. Ophthalmology 2018, 125, 1264–1272. [Google Scholar] [CrossRef] [PubMed]
- Reed, S.; Lee, H.; Anguelov, D.; Szegedy, C.; Erhan, D.; Rabinovich, A. Training deep neural networks on noisy labels with bootstrapping. arXiv 2014, arXiv:1412.6596. [Google Scholar]

| Noise Level p | 0 | 0.2 | 0.4 | 0.6 | 0.8 |
|---|---|---|---|---|---|
| Baseline | 0.9659 | 0.9489 | 0.6602 | 0.6345 | 0.6034 |
| Baseline (val) | 0.6060 | ||||
| S-model [18] | - | 0.9524 | 0.8892 | 0.6403 | 0.5953 |
| Bootstrap [40] | - | 0.9482 | 0.6515 | 0.6297 | 0.6115 |
| Joint-learning [28] | - | 0.9482 | 0.6521 | 0.6301 | 0.6113 |
| Ours | - | 0.9654 | 0.9221 | 0.6357 | 0.6113 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Son, J.; Kim, J.; Kong, S.T.; Jung, K.-H. Leveraging the Generalization Ability of Deep Convolutional Neural Networks for Improving Classifiers for Color Fundus Photographs. Appl. Sci. 2021, 11, 591. https://doi.org/10.3390/app11020591
Son J, Kim J, Kong ST, Jung K-H. Leveraging the Generalization Ability of Deep Convolutional Neural Networks for Improving Classifiers for Color Fundus Photographs. Applied Sciences. 2021; 11(2):591. https://doi.org/10.3390/app11020591
Chicago/Turabian StyleSon, Jaemin, Jaeyoung Kim, Seo Taek Kong, and Kyu-Hwan Jung. 2021. "Leveraging the Generalization Ability of Deep Convolutional Neural Networks for Improving Classifiers for Color Fundus Photographs" Applied Sciences 11, no. 2: 591. https://doi.org/10.3390/app11020591
APA StyleSon, J., Kim, J., Kong, S. T., & Jung, K.-H. (2021). Leveraging the Generalization Ability of Deep Convolutional Neural Networks for Improving Classifiers for Color Fundus Photographs. Applied Sciences, 11(2), 591. https://doi.org/10.3390/app11020591





