Abstract
The main purpose of this study was to develop and validate a 3D model for calculating knee joint loads during seated cycling. A 3D inverse dynamics approach was used to calculate knee and ankle joint loads using kinematics and kinetics data. For such a model, four kinematics clusters and three pedal markers were used, integrated with a 6-component force/torque pedal dynamometer. Seven subjects performed one five-minute trial on 75% of their maximum power at fixed cadence of 85 rpms. Data from two consecutive samples of the same cycling trial (first and last minute) were used to validate the model with the mean difference between two samples, Cronbach’s alpha, intraclass correlation coefficient (ICC), and p-value. Results showed high ICC (>0.735) and internal consistency (>0.700) with no statistically significant values (p > 0.050) except for crank angle of peak anterior force and peak axial forces at the knee and minimum normal force (p = 0.010) and minimum crank angle (p = 0.010) on the pedal. Further analyses are required to validate the model between days and to test the sensitivity to mechanical constraints.
1. Introduction
Cycling is becoming an increasingly popular activity with subsequent increase in overuse injury occurrence [1]. This has resulted in a higher number of physiotherapy and sport science specialists working in the field to prevent and treat the injured cyclists using advanced diagnostic approaches in a process of adjusting body position (i.e., bike fitting), off-the-bike assessment, and equipment optimization [2]. Cycling is also frequently used during rehabilitation in a clinical setting [3].
Most overuse injuries in cycling occur due to repetitive high loads applied to the joints. These loads normally excel when riding in low gear, long uphill riding, or with incorrect body position [4,5]. Along the entire kinetic chain, the knee is the most affected joint [6], with varus/valgus and internal/external torques as the primary mechanisms for the overuse injury occurrence [7]. To reduce the loads on the lower extremity and test the efficacy of specific constraints, a comprehensive three-dimensional (3D) model of the lower extremity loading needs to be used.
The driving power during cycling comes from the hip and knee extension in the downstroke [8]. For that reason, the knee is also the most common site of an overuse injury [9]. Even though pedaling is constraint to a constant path in a sagittal plane defined by the crank trajectory, a recent study [10] showed that varus/valgus moments can reach values of up to 16 Nm at relatively low workloads (~150 W at 60 rpm).
To understand the interaction between the injury occurrence and knee loading during cycling, a valid diagnostical approach needs to be developed. To the best of our knowledge, only two studies have attempted to develop such a model. The first one, presented by Ruby, Hull, and Hawkins (1992) used two two-dimensional (2D) models with one defined in the sagittal and the other in the frontal plane. The model calculated all six loads relative to the three axes at the knee joint. They assumed that both the knee and pedal local medial-lateral axis is perpendicular to the sagittal plane, which can cause an error in the calculations [11]. The second model presented by Gregersen and Hull (2003) was calculated using a 3D inverse dynamic approach, but only non-driving (varus/valgus and internal/external) torques at the knee joint were presented. The virtual point on the pedal was used as a foot marker, which can be done only when zero-float clipless pedals are used. Their main purpose was to compare a complete spherical joint model with a simplified spherical and revolution joint model [12].
Therefore, the main objective of this study was to develop a complete 3D model of the lower extremity to evaluate joint loading during seated cycling with a specific emphasis given to the knee joint by calculating the net joint forces and torques [13]. Moreover, the secondary aim was to test the measured and calculated variables for intra-session reliability. We hypothesized that all variables would exhibit high reliability without statistically significant differences between two trials.
2. Materials and Methods
2.1. Analytic Model
The inverse dynamic approach was used to calculate 3D joint loads in lower extremity during seated cycling. From a simplicity point of view, the following model is explained on a single side only, but can be directly transferred to the contralateral side. The segments were modeled as rigid bodies. On each segment at least three coplanar markers were defined. All coordinate systems were right-handed Cartesian coordinate systems. Calculations were based on Winter, while mass, dimensions, center of mass (CoM), and moments of inertia of lower limb segments have been deduced for extensive anthropometric studies [14]. Cardan x, y’, z’’ rotation was used. For simplicity, calculations were divided in two-phase, static calibration, and trial measurements. During static calibration, first the anatomical coordinate system (ACS) and local marker coordinate system (LCS) were defined, while the global coordinate system (GCS) was defined during the motion-capturing system calibration procedure. Next, during trial measurements, kinematics and kinetics parameters were calculated.
2.1.1. Static Calibration
In the first phase, constant ACS and LCS were defined during the static calibration. Kinematic clusters in conjunction with a digitizing probe were used to define all virtual markers on the segments’ anatomical points except for the pedal, where three physical markers were used. Markers, visually shown in Figure 1, were defined on the left and right anterior superior iliac spine (p1 and p2, respectively), sacrum (p3), greater trochanter (p4), medial and lateral condyle (p5 and p5, respectively), tibial tuberosity (p7), medial and lateral malleolus (p8 and p9, respectively), heel (p10), metatarsal I and V (p11 and p12, respectively), and three pedal markers (p13, p14, and p15). The hip joint center was defined using three pelvis markers based on the work from Vaughan, Davis, and O’Connor [15], while the knee and ankle joint centers were defined at mid-point between the medial and lateral condyle and malleolus, respectively. Body mass, segment center of mass, and segment mass were based on Winter (2009), while segments’ length and inertial parameters of segment were based on the work from Yeadon and Morlock [16].
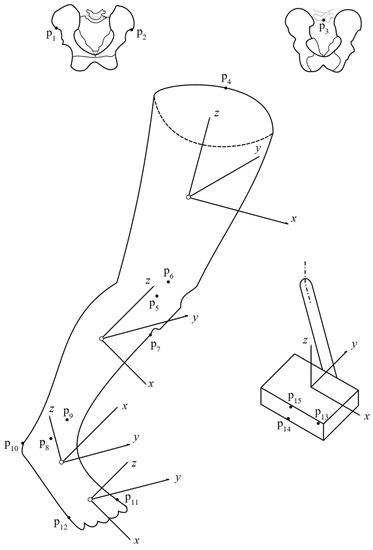
Figure 1.
Segments’ local coordinate systems with origin in CoM are shown on leg and pedal, while marker placements are shown on pelvis (p1–p3), leg (p4–p12), and pedal (p13–p15).
The pedal system was defined to express all measured loads in a local pedal system using three markers such that the x-axis was positive forward, the y-axis was positive medial, and the z-axis was positive vertical upwards. The foot anatomical z-axis was defined between the underneath metatarsal II and ankle joint (positive proximal), the x-axis was perpendicular to line between metatarsal I and V, and the z-axis (positive anterior) and y-axis were perpendicular to the z- and x-axis (positive medial). Similarly, the calf z-axis was defined between the ankle and knee joint center (positive proximal), the x-axis was perpendicular to the line between medial and lateral malleolus and z-axis (positive anterior), while the y-axis was perpendicular to the z- and x-axis (positive medial). Lastly, the thigh z-axis was the line between the knee and hip joint center (positive proximal), the x-axis was perpendicular to the line between medial and lateral condyle and z-axis (positive anterior), while the y-axis was perpendicular to the z- and x-axis (positive medial). All orientations and marker placements are illustrated in Figure 1.
All ACS including the local pedal system were transformed to the unit length and written in a matrix notation as shown in Equation (1):
where GAa is the transformation matrix between the GCS and ACS, while X, Y, and Z are the unit length vectors of the x-, y-, and z-axes of the ACS. Next, markers coordinates were expressed in the ACS as shown in Equation (2):
where MA is the marker coordinate expressed in the ACS, GAa is as defined in Equation (1), M is the marker coordinate in the GCS, and CoM is the coordinate of the segment CoM expressed in the GCS.
The LCS was defined using markers’ coordinates expressed in the ACS (Equation (2)) to find the relation between the LCS and ACS. The foot LCS was established with metatarsal I and V markers and with the origin in the heel marker. On the same assumption, the LCS was established for calf and thigh, with the origin point in the lateral malleolus and lateral condyle, respectively. The LCS was established in conjunction with the medial malleolus and tibial tuberosity for the calf, and medial condyle and greater trochanter for thigh. The pedal LCS was defined with three pedal markers. Segment LCS were normalized and written in matrix as shown in Equation (3):
where MA is the segment constant transformation matrix between LCS and GCS, while X, Y, and Z are unit length vectors of the x-, y-, and z-axes of LCS.
2.1.2. Trial Measurements
In the second phase, data from one trial were analyzed. The segment marker coordinate system on the i-th sample was established using the same procedure used for calculating the LCS in the calibration phase, with a difference that markers coordinates were in the GCS. The unit vector of the coordinate system was written in matrix (GMi) using the same notation as in Equation (3).
The transformation matrix (GAi) between the GCS and ACS were defined from the angles θ1, θ2, and θ3 calculated based on Winter [14]. Matrix MA and GMi were multiplied to define the GAi matrix as shown in Equation (4):
where GAi is the transformation matrix between the GCS and ACS on the i-th sample, MA is the segment constant transformation matrix between the LCS and ACS expressed in the ACS, and GMi is transformation matrix between the GCS and LCS on the i-th sample expressed in the GCS. CoM coordinates were defined as shown in Equation (5):
where Vc are coordinates of the CoM on the i-th sample, p are coordinates of the segment’s LCS origin marker expressed in the GCS on i-th sample, GAi is defined in Equation (4), and co is a constant vector between the origin marker of the segment’s LCS and CoM expressed in the ACS and calculated using Equation (2).
At this point linear acceleration and angular velocity and acceleration of segment could be calculated using the finite-difference technique. The linear acceleration in GCS was calculated as shown in Equation (6):
where ai is the linear acceleration on i-th sample, xi+1, xi, and xi−1 are coordinates in x, y, or z directions on the i + 1, i and i − 1 samples, and Δt is a change in time. The linear acceleration in the GCS was needed because all the forces were calculated in GCS and then were expressed in segment ACS.
Angular velocity in the ACS was calculated as shown in Equation (7):
where ωx, ωy, and ωz are angular velocity in the x, y, and z directions, θ1, θ2, and θ3 are Cardan rotational angles, and , and are first derivates of Cardan angles. The angular accelerations αx, αy, and αz were calculated using the finite-difference technique as shown in Equation (8):
where αi is linear acceleration on the i-th sample, ωi−1 and ωi+1 are angular velocities in the x, y, or z directions on the i + 1 and i − 1 sample, and Δt is a change in time.
The last phase was the calculation of joint loads. Newton–Euler 3D equations of motion for segments were used to calculate these loads. The solution for one segment is presented in Figure 2.
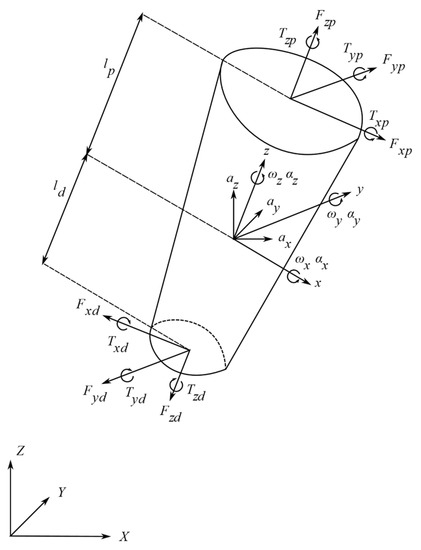
Figure 2.
Solution of 3D inverse dynamics. lp and ld represent proximal and distal lengths of the segment, respectively. Fxd, Fyd, Fzd, Txd, Tyd, and Tzd represent distal forces and torques of the segment, respectively. Variables ax, ay, az, ωx, ωy, ωz, αx, αx, and αx represent linear acceleration, angular velocity, and angular acceleration, respectively, while, x, y, and z are local segment coordinates. Fxp, Fyp, Fzp, Txp, Typ, and Tzp are proximal forces and torques of segments, respectively.
All forces were calculated in the GCS, while torques were calculated in ACS. Algorithms used for calculating proximal forces in the GCS are shown in Equations (9a), (9b), and (9c):
where FXP, FYP, FZP and FXD, FYD, FZD are segments’ proximal and distal forces in the x, y, and z directions on the i-th sample expressed in GCS, respectively, g is the gravitational acceleration, m is the segment mass, and ax, ay, and az are segment CoM linear accelerations on the i-th sample expressed in GCS, respectively.
Forces were transformed to the ACS to describe loads in the joint as shown in Equation (10):
where Fxp, Fyp, and Fzp are segment proximal forces in the x, y, and z directions on the i-th sample expressed in the ACS, respectively.
Torques were calculated in the ACS as shown in Equations (11a), (11b), and (11c):
where Ix, Iy, and Iz are the constant segment moments of inertia in the x, y, and z directions expressed in ACS, respectively, αx, αy, and αz are angular accelerations in the x, y, and z directions on the i-th sample expressed in ACS, respectively, Fxd, Fyd, and Fzd are segment distal forces in the x, y, and z directions on the i-th sample expressed in ACS, respectively, Txp, Typ, Tzp and Txd, Tyd, Tzd are proximal and distal torques in the x, y, and z directions on the i-th sample expressed in ACS, respectively, and lp and ld are proximal and distal moment arms from the CoM to the joint center.
It is worth noting that the torque around the z-axis does not involve forces because they have zero lever arms around the corresponding axis. Before calculating next joint loads, torques were transformed to GCS as shown in Equation (12):
where TXP, TYP, and TZP are the proximal torques in the x, y, and z directions on i-th sample expressed in GCS.
Then, torques were transformed back in ACS of the next segment to express distal torques (Txd, Tyd, Tzd) in the ACS of the next segment. Joint ACS with forces’ and torques’ orientation expressed with respect to lower segment ACS are shown in Figure 3.
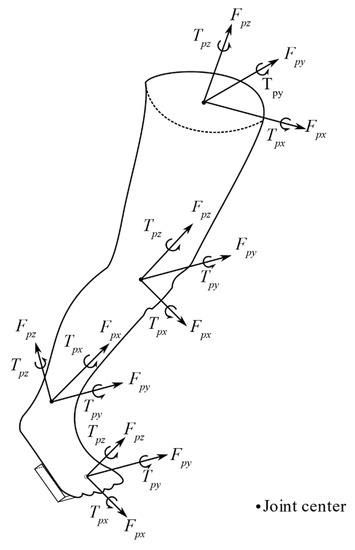
Figure 3.
Joint coordinate system with forces and torques orientation in each segment’s local coordinate system.
2.2. Protocol
Seven highly trained recreational male cyclists and triathletes voluntarily participated in the study. Cyclists verbally confirmed that they cycle on average 15,000 km per year. The subjects’ mean age was 31.4 ± 3.7 years, body height 178.1 ± 1.1 cm, and body mass 73.5 ± 4.5 kg. They used their own bike, so no bike setup was needed. The bike was mounted on a direct drive ergo-trainer (Elite Drivo, Treviso, Italy) which allowed it to set up a constant workload, and which has been proven reliable [17]. The subjects used a clipless shoe-pedal system, while the pedal float (only left–right) was not defined as it did not affect the calculations.
The right leg was analyzed. The kinematics data were collected using a 3D high-speed motion-capturing system with active LED markers (NDI Certus, Waterloo, ON, Canada). The system was calibrated at the start of the experiment, while the digitizing probe was calibrated for each subject separately. Forces and torques were collected with a six-component force–torque pedal system (Forped, Cycling Science, d.o.o., Ljubljana, Slovenia), and a customized software (ARS Free Measurement, S2P, d.o.o., Ljubljana, Slovenia) was used. Pedal dynamometer offset was corrected prior to each trial. All data were further processed with a bespoke script written in MATLAB (MathWorks R2018a, Inc., Natick, MA, USA, 2018).
First, the marker setup was established and markers were digitized. After the warm-up, static calibration was performed. The subjects sat still on the bicycle for ten seconds with the right leg clipped to the pedal semi-extended in a way that the pedal was in the lowest position. The fourth to sixth seconds of the raw data from the static calibration were averaged to minimize the error. Following the static calibration, subjects rode for five minutes at a workload of 75% of their maximal power with a cadence of 85 rpm, while the gear ratio was not defined. Data from the first and the last minute were analyzed and compared. Data were presented as an ensemble average of the whole minute recorded, from which the joint/pedal forces and torques were calculated. The sampling rate of kinematics data was 128 Hz, while kinetics data had a sampling rate of 1000 Hz and were down-sampled in the post-analysis. A +3 V trigger was used to synchronize kinematics and kinetics data. The kinematics and kinetics data were smoothed with a fourth-order, zero phase shift low-pass Butterworth filter with a cut-off frequency of 12 and 8 Hz, respectively.
The minimum (min) and maximum (max) joint force and torque were calculated from the average values of one crank cycle (which is specified by z-coordination of the pedal marker 360° degree clockwise from top dead center) using mean top decile as shown in Equations (13a) and (13b):
The intra-class coefficients of the correlation (ICC), Cronbach’s alpha, and t-test without a statistically significant difference were used to assess the intra-session reliability between two trials of the measured parameters. Statistical analyses were performed using SPSS V.24 for Windows (IBM Corporation, Somers, NY, USA, 2018) with levels of significance set to p < 0.050.
3. Results
Results of the reliability analysis for pedal and knee loading are presented in Table 1 and Table 2, respectively. The tables show the max and min loading and corresponding crank angle, which is defined as the duration of max and min loading (in degrees). Knee loads are expressed in respect to calf ACS. Peak medial knee force and peak medial pedal force exhibited negative ICC and Cronbach’s alpha values. This occurred due to relatively small between-subject variation compared to within-subject variation. All other variables exhibited Cronbach’s alpha >0.7, indicating high internal consistency. Furthermore, high ICC values were also recorded (>0.735) on all peak loads and crank angles. There were no significant p-values from ANOVA except for minimum normal force and a crank angle of minimum tangential force.

Table 1.
Reliability results for pedal forces and torques.

Table 2.
Reliability results for knee forces and torques.
All loads and corresponding crank angles had high internal consistency with Cronbach’s alpha exceeding >0.714. Furthermore, high ICC values were also recorded (>0.740) on all loads and corresponding crank angles. There were no significant p-values from the t-test except for a crank angle of anterior force and axial loads (minimum and maximum).
Figure 4 illustrates average pedal forces (A) and torques (B) of all seven participants. The solid line (Figure 4A) shows tangential backward and forward pedal force with its peak approximately at the crank angle of 45 and 180°, respectively. The dashed line (Figure 4A) shows transverse pedal force which reaches its minimums approximately at the crank angle of 100°, while the maximum is at 270°. The dotted line (Figure 4A) shows normal pedal force, which reaches its minimum at the crank angle of 110°, while the maximum is at 350°.
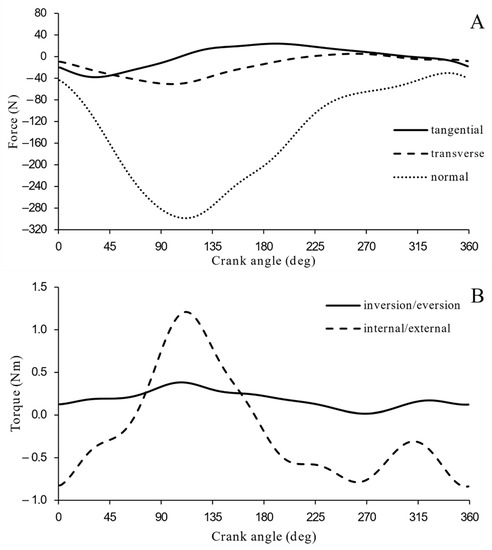
Figure 4.
Pedal forces (A) and torques (B). Positive pedal torque values represent eversion and internal rotation torques, while negative values represent inversion and external rotation torques. Positive knee forces values represent tangential forward, transverse maximum, and normal maximum forces, while negative values represent tangential backward, transverse minimum, and normal minimum axial forces.
The solid line (Figure 4B) shows pedal inversion/eversion torque, which is almost constant during all crank cycles with a small positive (eversion) peak at the crank angle of 100° and negative (inversion) peak at 280°. The dashed line (Figure 4B) shows an internal rotation torque which reached its peak at crank angle of 110°, while the external rotation torque reached its peak at 360°.
Figure 5 illustrates average knee forces (A) and torques (B) of all seven participants. The solid line (Figure 5A) shows knee posterior force with its peaks approximately at the crank angle of 45°, while peak anterior force was at 110°. The dashed line (Figure 5B) shows medial/lateral knee force which reached its minimums approximately at a crank angle of 100°, while the maximum was at 270°. The dotted line (Figure 5B) shows axial knee force which reached its minimum peak at a crank angle of 100°, while the maximum knee axial force reached its peaks at 350°.
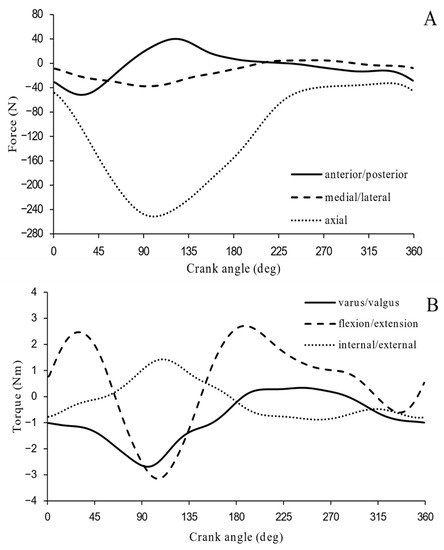
Figure 5.
Knee forces (A) and torques (B). Positive knee torque values represent varus, flexion, and internal rotation torques, while negative values represent varus, extension, and external rotation torques. Positive knee forces values represent posterior, medial, and maximum axial forces, while negative values represent anterior, lateral, and minimum axial forces.
The solid line (Figure 5B) shows knee varus/valgus torque. The varus peak occurred at the crank angle of 100°, while the peak valgus moment was at 200°. The dashed (Figure 5B) line shows knee flexion torque which reached its peaks at crank angles of 35 and 180°, while the peak knee extension torque reached its peak at 110°. The dotted line (Figure 5B) shows internal rotation torque which reached its peak at a crank angle of 110°, while the external rotation torque reached its peak at 260°. The first peak of the knee flexion torque was at crank angle of 40° due to the posterior knee force increasing, while the anterior/posterior knee force was primarily responsible for flexion/extension torque.
The forces on the pedal and in the knee had identical orientation and similar amplitude through all crank cycles, which can be noted in Figure 4A and Figure 5A. Furthermore, the amplitude of the knee anterior/posterior force was greater than the pedal tangential force, while the amplitude of the knee medial–lateral force was similar to the pedal transverse force. The amplitude of the varus/valgus torque in the knee was higher than the inversion/eversion torque on the pedal due to the contribution of the medial–lateral force (Figure 4B and Figure 5B).
4. Discussion
To understand complete knee loading during cycling, a comprehensive 3D model of the leg including ankle, knee, and hip joint was developed. To validate such a model, the first step had to be reliability analysis using data from the same trial. Reliability analysis showed high internal consistency as well as good ICC for the vast majority of parameters. Differences between two consecutive samples of the same cycling trial for each subject were within acceptable limits. Overall, the results showed that the model presented in this study can be used in further biomechanical research to understand overuse injuries.
To the authors’ best knowledge, previous studies performed only one trial and calculated average values and their variability merely for descriptive purposes, whilst reliability analysis remained unaccounted [11,12]. To date, the model made by Gregersen and Hull [12] is the closest to the presented model, but a different protocol was used to calculate the actual loads. They used seven reflective markers mounted on anatomical points and three pedal markers from which two of them were mounted only during static calibration to evaluate foot and calf kinematics parameters [12]. The model presented in this paper used four kinematics clusters plus three pedal markers to evaluate foot, calf, and thigh kinematics parameters. The presented study is not comparable with Gregersen and Hull [12] because different calculation protocols were used. The study presented by Manal, McClay, Richards, Galinat, and Stanhope [18] showed that the coordinate reference system of the segment calculated using markers mounted on an anatomical point or kinematic cluster affected the calculated parameters due to soft tissue movement [18]. Another source of error in kinematics data could be during the calibration and markers’ digitization.
Some knee force and torque parameters had lower ICC and statistically significant differences between the two trials. These were closely related to the parallel differences in the recorded forces and torques at the pedal. We can only hypothesize that this could be due to the change in pedaling technique whilst sustaining the same power output. It has been previously demonstrated that forces and torques increase at the onset of fatigue [19]. Cyclists in this study rode at a steady-state pace for five minutes from which the two one-minute trials were recorded. Because ICC and Cronbach’s alpha were negative for peak medial force at the knee and on the pedal, it was not possible to interpret these results. This meant that the scale was not reliable [20].
Gregersen and Hull (2003) compared the simplified spherical joint and revolute joint models [11]. The main difference was that the spherical joint model assumed that inertial properties around the x- and z-axes and shank medial/lateral acceleration were equal to zero. Furthermore, the revolution joint model assumed all simplified spherical model assumptions with the additional assumption that the knee y-axis had the same orientation as the laboratory coordinate system (GCS). The results showed differences between the two models. The main reasons for the differences between the models were the assumptions described above. They concluded that joint loads were best described using the spherical joint model. Such a model contributed to a better understanding of the overuse injuries [11,12].
The anatomy of lower limb and foot/pedal platform degrees of freedom could affect joint loads [11,21]. Furthermore, the marker setup was simple, while only kinematics clusters needed to be fixed on segment and visible to cameras.
It is important to emphasize that the model presented in this paper was a step-by-step model by which the net joint forces and torques determined could not discriminate the individual contributions of the muscle forces and the passive joint reaction force (bone-to-bone contact force and force). In order to achieve this, more in-depth muscle modeling and adequate optimization techniques are needed. Joint reaction forces are of interest in cycling, since they can describe force applied at the patellofemoral cartilage which can influence the incidence of overuse injuries. Despite the limitations of the presented model, it plays an important role in clinical settings due to its simplicity and demonstrated reliability. A more recent study made by Bini and Hume (2013) focused on tibiofemoral compressive and shear force and patellofemoral compressive force. However, only a 2D pedal dynamometer was used, which limited the interpretation of knee loading only to these compressive and shear forces [22]. For better understanding of the knee loading, varus/valgus torque needs to be considered [7].
In recent years, musculoskeletal models using the OpenSim modeling tool have been used in biomechanical research [23]. Such models can give meaningful information about a wide range of variables which can be computed. Furthermore, these models have big potential in certain pathologies such as osteoarthritis and in biomechanical research since they can be used to better understand how muscles act during movement and their impact on forces and moments across all joints. However, many assumptions have been made in the development of a musculoskeletal model, such as limited experimental evidence, size, age, etc. [24,25].
The model presented in this paper can therefore provide important information for applied scientists, clinicians, and practitioners in relation to: (1) Prevention and occurrence of overuse injury in cycling and (2) use of stationary cycling in knee rehabilitation. From a practical point of view, the model was described in detail, which makes it easy for the reader to implement it and use in further studies or practical settings. Its practical value is in its simple design and quick setup which can be used on daily bases in, e.g., clinical work.
The 3D model evaluated knee joint loads during seated cycling. Such a model may be needed for adjusting bike position to an individual with the intention to optimize knee joint loads, which can be key to preventing overuse injuries. Furthermore, knee loads can be minimized using different pedaling techniques. In rehabilitation purposes, such a model can be used to prevent a patient from producing high load in a certain direction. The model was developed to describe 3D loads using a simple and straightforward marker setup, which is the key for daily use. The duration of pedaling was also one of the limitations of this study that potentially resulted in higher inter-subject variability.
5. Conclusions
In summary, this paper showed a repeatable step-by-step model to calculate knee joint loading that can be used in everyday practice. Reliability analysis showed high internal consistency and good ICC for the vast majority of the observed parameters. Results of the experimental part of this study have practical implications to study knee loading in rehabilitation and research setups. Further studies are required to validate between-day reliability in a larger number of participants all riding at a identical workload. Further research should also focus on mechanical constraints and aim to relate the recorded absolute values to injury occurrence.
Author Contributions
Conceptualization, P.K. and B.F.; methodology, N.Š. and B.F.; software, P.K.; validation, P.K., N.Š., and B.F.; formal analysis, B.F.; investigation, P.K.; resources, N.Š.; data curation, P.K.; writing—original draft preparation, B.F.; writing—review and editing, N.Š.; visualization, N.Š.; supervision, B.F.; project administration, B.F.; funding acquisition, N.Š. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the National Medical Ethics Committee Republic of Slovenia (code: 0120-313/2017-3; date: 13 September 2017).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors would like to thank all participants. N.Š. would like to acknowledge financial support of the Slovenian Research Agency in the framework of (1) research project L5-1845: Body asymmetries as a risk factor in musculoskeletal injury development: Studying etiological mechanisms and designing corrective interventions for primary and tertiary preventive care; and (2) research program P5-0147 kinesiology of monostructural, polystructural, and conventional sports.
Conflicts of Interest
Two authors of the manuscript were at the time of data collection employed by the institution that manufactured part of the equipment used in the study. Regardless, they both have no conflict of interest.
References
- De Bernardo, N.; Barrios, C.; Vera, P.; Laíz, C.; Hadala, M. Incidence and risk for traumatic and overuse injuries in top-level road cyclists. J. Sports Sci. 2012, 30, 1047–1053. [Google Scholar] [CrossRef] [PubMed]
- Swart, J.; Holliday, W. Cycling Biomechanics Optimization—The (R) Evolution of Bicycle Fitting. Curr. Sports Med. Rep. 2019. [Google Scholar] [CrossRef] [PubMed]
- Salacinski, A.J.; Krohn, K.; Sco, F.L.; Megan, L.H.; Ireland, K.; Marchei, G. The effects of group cycling on gait and pain-related disability in individuals with mild-to-moderate knee osteoarthritis: A randomized controlled trial. J. Orthop. Sports Phys. Ther. 2012. [Google Scholar] [CrossRef]
- Bertucci, W.; Grappe, F.; Girard, A.; Betik, A.; Rouillon, J.D. Effects on the crank torque profile when changing pedalling cadence in level ground and uphill road cycling. J. Biomech. 2005, 38, 1003–1010. [Google Scholar] [CrossRef] [PubMed]
- Fonda, B.; Sarabon, N. Biomechanics of Cycling (Literature review). Sport Sci. Rev. 2010, 19, 187–210. [Google Scholar] [CrossRef]
- Callaghan, M.J. Lower body problems and injury in cycling. J. Bodyw. Mov. Ther. 2005, 9, 226–236. [Google Scholar] [CrossRef]
- Bini, R.; Flores-Bini, A. Potential factors associated with knee pain in cyclists: A systematic review. Open Access J. Sports Med. 2018. [Google Scholar] [CrossRef]
- Faria, E.W.; Parker, D.L.; Faria, I.E. The science of cycling: Factors affecting performance—Part 2. Sports Med. 2005, 35, 313–337. [Google Scholar] [CrossRef]
- Asplund, C.; St Pierre, P. Knee pain and bicycling: Fitting concepts for clinicians. Phys. Sportsmed. 2004. [Google Scholar] [CrossRef]
- Fang, Y.; Fitzhugh, E.C.; Crouter, S.E.; Gardner, J.K.; Zhang, S. Effects of workloads and cadences on frontal plane knee biomechanics in cycling. Med. Sci. Sports Exerc. 2016, 48, 260–266. [Google Scholar] [CrossRef]
- Ruby, P.; Hull, M.L.; Hawkins, D. Three-dimensional knee joint loading during seated cycling. J. Biomech. 1992, 25, 41–53. [Google Scholar] [CrossRef]
- Gregersen, C.S.; Hull, M.L. Non-driving intersegmental knee moments in cycling computed using a model that includes three-dimensional kinematics of the shank/foot and the effect of simplifying assumptions. J. Biomech. 2003, 36, 803–813. [Google Scholar] [CrossRef]
- Vigotsky, A.D.; Zelik, K.E.; Lake, J.; Hinrichs, R.N. Mechanical misconceptions: Have we lost the “mechanics” in “sports biomechanics”? J. Biomech. 2019, 93, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 9780470549148. [Google Scholar]
- Vaughan, C.L.; Davis, B.L.; O’Connor, J.C. DYNAMICS OF HUMAN GAIT; Kiboho Publishers: Cape Town, South Africa, 1999; ISBN 0-620-23558-6. [Google Scholar]
- Yeadon, M.R.; Morlock, M. The appropriate use of regression equations for the estimation of segmental inertia parameters. J. Biomech. 1989. [Google Scholar] [CrossRef]
- Vaeck, J.; Bouillid, A.; Bouzigon, R.; Pinot, J.; Grappe, F. Accuracy of the new Elite Drivo ergometer. In Proceedings of the Science & Cycling Congress, Düsseldorf, Germany, 28–29 June 2017. [Google Scholar]
- Manal, K.; McClay, I.; Richards, J.; Galinat, B.; Stanhope, S. Knee moment profiles during walking: Errors due to soft tissue movement of the shank and the influence of the reference coordinate system. Gait Posture 2002, 15, 10–17. [Google Scholar] [CrossRef]
- Bini, R.R.; Diefenthaeler, F.; Mota, C.B. Fatigue effects on the coordinative pattern during cycling: Kinetics and kinematics evaluation. J. Electromyogr. Kinesiol. 2010. [Google Scholar] [CrossRef]
- Costa-Santos, C.; Bernardes, J.; Ayres-De-Campos, D.; Costa, A.; Costa, C. The limits of agreement and the intraclass correlation coefficient may be inconsistent in the interpretation of agreement. J. Clin. Epidemiol. 2011, 64, 264–269. [Google Scholar] [CrossRef]
- Ruby, P.; Hull, M.L. Response of intersegmental knee loads to foot/pedal platform degrees of freedom in cycling. J. Biomech. 1993, 26, 1327–1340. [Google Scholar] [CrossRef]
- Bini, R.R.; Hume, P.A. Effects of workload and pedalling cadence on knee forces in competitive cyclists. Sports Biomech. 2013, 12, 93–107. [Google Scholar] [CrossRef]
- Thompson, R.L.; Gardner, J.K.; Zhang, S.; Reinbolt, J.A. Lower-limb joint reaction forces and moments during modified cycling in healthy controls and individuals with knee osteoarthritis. Clin. Biomech. 2020. [Google Scholar] [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.; Sherman, M.; Reinbolt, J.A.; Delp, S.L. OpenSim: A musculoskeletal modeling and simulation framework for in silico investigations and exchange. Procedia Iutam 2011, 2, 212–232. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).