Abstract
The continuous development of computer technology has made it applicable in many scientific fields, including research into a wide range of processes in agricultural machines. It allows the simulation of very complex physical phenomena, including grain motion. A recently discovered discrete element method (DEM) is used for this purpose. It involves direct integration of equations of grain system motion under the action of various forces, the most important of which are contact forces. The method’s accuracy depends mainly on precisely developed mathematical models of contacts. The creation of such models requires empirical validation, an experiment that investigates the course of contact forces at the moment of the impact of the grains. To achieve this, specialised test stations equipped with force and speed sensors were developed. The correct selection of testing equipment and interpretation of results play a decisive role in this type of research. This paper focuses on the evaluation of the force sensor dynamic properties’ influence on the measurement accuracy of the course of the plant grain impact forces against a stiff surface. The issue was examined using the computer simulation method. A proprietary computer software with the main calculation module and data input procedures, which presents results in a graphic form, was used for calculations. From the simulation, graphs of the contact force and force signal from the sensor were obtained. This helped to clearly indicate the essence of the correct selection of parameters used in the tests of sensors, which should be characterised by high resonance frequency.
1. Introduction
The computer simulation used by the discrete element method (DEM) has been applied more frequently in studies of processes in agricultural machines, which describes the motion of the grain related to sowing, fertilising, drying, sorting, pneumatic transport, etc. [1,2,3]. This method includes direct equation integration of grain system motion under the action of various forces—aerodynamic, electrostatic, and, most importantly, the contact forces that arise between the grains and the surfaces limiting the space of their motion [4]. To make correct calculations, mathematical models of grain contact with motion surfaces are necessary [5,6]. The creation of such models requires their empirical validation by measuring the course of contact forces at the impact of grains with stiff surfaces, which may be movable or immovable [7]. The investigation into force measurement, the reduction of measurement errors, and the development of possibly the smallest sensors have been described in other works [8,9]. A rapid increase in researchers’ interest in the DEM has led to its application in various types of calculations [10]. Kustermann [11] was one of the first researchers to measure the impact forces of maize grain against a steel plate. The test was carried out in a laboratory station where a steel plate driven by a crank mechanism hit the motionless grain through a piezoelectric force sensor. This helped to control precisely the impact velocity and place of the grain impact. The literature has also shown research results from the influence of the grain elasticity model on the development of individual signals, where the energy decline was shown to be slower for glass balls than wolfram balls [12]. Research into the sensor response to crop waste in a combine-harvester has also been conducted, but the possibility of reducing sensor measuring errors has not been analysed here [13,14]. In Poland, such research into the needs of the computer simulation of threshing and sowing processes was undertaken for the first time at the Poznan University of Technology by Professor Kęska [15]. A spring-arm thrower was used to give the grain velocity, which allowed velocities of grain impact with the sensor to reach values of up to 10 . The grain velocity was measured with photoelectric sensors before and after the impact. A piezoelectric PCB companies impact force sensor of 70 kHz natural vibration frequency was used to measure the force. Figure 1 shows a typical course of the impact force recorded in these tests.
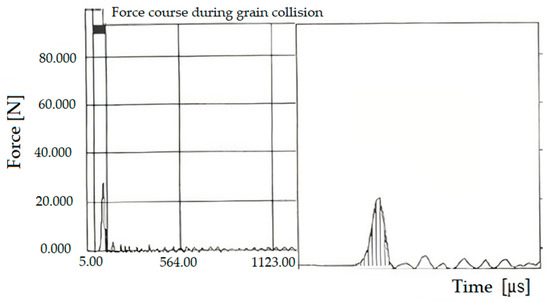
Figure 1.
The measuring signal course of the impact force of rye grain of 14% moisture at the speed of 8 in a force sensor with a 70 kHz resonance frequency [15].
In the studies by Professor Kęska [15], regression relations of the impact force and the impact duration maximum value to moisture and velocity were determined for several selected cultivated seed species. Some interpretation difficulties of the recorded signals from the force sensor were observed while measuring hard, small grains (of rye) with low moisture. The grain, after having bounced off of the surface of the force transducer, had an oscillating fading motion for a significant time after bouncing off. These oscillations resulted from the sensor’s own vibrations excited by a sufficiently short force pulse. Similar studies on rapeseed were later performed in the Institute of Agrophysics in Lublin, Poland [16]. In the tests, rapeseed was dropped freely on a piezoelectric force sensor from a height of 0.2 m, which caused an impact velocity of approximately 2 . Figure 2 shows the results; a clear course of the measuring signal in the form of fading vibrations of approximately 40 kHz, which is characteristic of many piezoelectric force sensors.
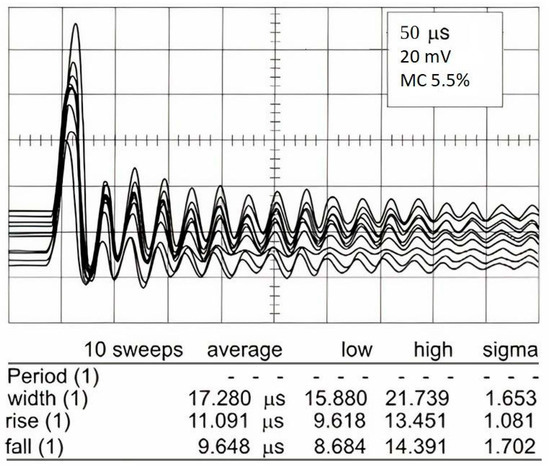
Figure 2.
Courses of the signal measuring the impact force of rapeseed about moisture content (MC) 5.5% falling from a height of 0.2 m into a piezoelectric force sensor, [17].
This type of testing assumes that an impact occurs with a perfectly stiff surface. In fact, such a material does not exist, so grain hitting a sensor material induces parasitic vibrations, which usually take the form of a high fading sound. A quartz crystal, stimulated to vibrate, generates a voltage measurement signal that reproduces these vibrations. Thus, it is difficult to assess to what extent the course of the first main cycle of the measurement signal from the sensor could be considered as a course of a contact force, as apparently further cycles no longer correspond to this force. After the grain impact, the force is zero by definition. It is assumed for piezoelectric vibration sensors that their useful band should lie below the resonance frequency because resonance leads to inaccurate measurement results, similar to force measurements. This issue was investigated in this work with the computer simulation method. The main aim of the work, however, was to validate the method using the discrete element method (DEM).
2. Materials and Methods
2.1. Computer Simulation
In the computer simulation of the grain impact with the surface of the force sensor, a simple dual mass model of the force-grain sensor system was used (Figure 3). Mass refers to the investigated grain, and mass describes the reduced masses of the sensor being subject to shifting during the impact. Spring describes the sensor elastic susceptibility, and the spring shows the value of the contact stiffness between the grain and the sensor surface [18,19]. The mass and elasticity values of the sensor were selected so that its resonance frequency corresponded to an assumed value 40 kHz. The grain contact with the sensor was modelled using various mathematical relationships [20]. In the simplest case, the contact was modelled as a linear elastic one-sided bond, using the relationships described in [21]. The contact model can be programmed freely, in a particular case as perfectly plastic, elastic–plastic, or viscoelastic [22,23,24,25]. A linear, viscoelastic model with linear damping was adopted for modelling the stiffness of the sensor.
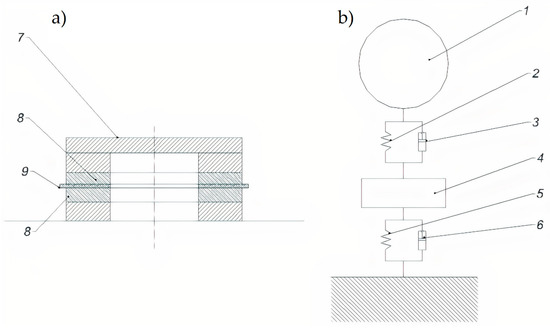
Figure 3.
Diagram of a piezoelectric force sensor (a) and physical model of the grain sensor system at the moment of impact (b): (1) grain mass m2, (2) grain contact stiffness k2, (3) grain damping parameter c2, ( 4) parasitic force sensor mass m1, (5) stiffness of the measuring element of the force transducer k1, (6) damping of the measuring element of the force transducer c1, (7) sensor dial, (8) piezoelectric crystals, and (9) electrode.
2.2. Mathematical Contact Model
The mass motion equations in this model can be recorded using the force equilibrium condition and the second law of motion as two ordinary second-order equations, which can be presented in the form of four first order equations suitable for numerical calculations (Equations (1)–(4)):
where:
- m1, m2—particle mass (kg);
- S1, S2—contact force (N);
- t—time (s);
- v1, v2—velocity (m s−1).
Forces S1 and S2 for the viscoelastic model result from the relationship of (5) and (6):
where:
- c1, c2—damping parameter (kg s−1);
- k1, k2—contact stiffness (N m−1);
- x1, x2—overlap (m).
For the perfectly plastic impact model, it was assumed that the contact force had a constant value selected so that the velocity of the grain fell to zero during the impact (zero value of the velocity restitution parameter [18,26,27]). This condition was met when the momentum of this force was equal to the momentum of the grain during the impact. This force value can be calculated from this condition assuming the contact time tk in (7) and (8):
where:
- tk—contact time (s).
To best develop a model that reflects reality, in the calculation, a trapezoidal course was introduced instead of a rectangular one, which is physically impossible to develop, with short sections of this force rising and falling. Any relationships with the contact force can be introduced to the model, given, among others, in [20]; but only the two presented above as the extreme cases were used in the calculations.
The system of nonlinear ordinary equations described above was integrated with a simple Euler algorithm, using a very short integration step. The calculations were performed using the proprietary computer software, coded in the Rad Delphi Embarcadelo 2010 system, with the working name GKWK. The software included the main calculation module and procedures for data input, as well as for graphical presentation of results. The software also contained a procedure for automatic analysis of the resultant oscillograms of S1 and S2 forces. By changing the value of the integration step by one row, it was possible to check whether the solution was subject to the length of this step. The repeated results indicated that the adopted integration step dt = 1 × 10−10 s was sufficiently short. Figure 4 shows the proprietary software interface.
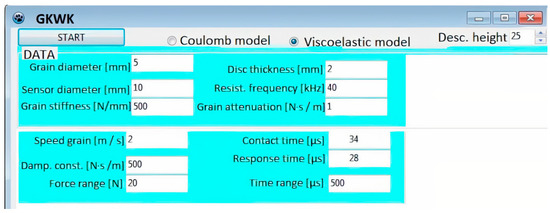
Figure 4.
GKWK, Poznan, Poland, 2017, software interface view.
The grains used in the simulation were standard spherical grains with the following constant parameters:
- − Poisson parameter—0.2 (-);
- − Kirchhoff’s module—9.0 (MPa);
- − Particle friction parameter—0.25 (-);
- − Damping parameter—1.0 (Ns·m−1);
- − Grain diameter—5.0 (mm);
- − Grain velocity—2.0 (m·s−1);
- − Grain density—765 (kg·m−3).
It was also assumed that the force sensor had the following constant parameters:
- − Sensor diameter—10.0 (mm);
- − Disc thickness—2.0 (mm).
For the purpose of this research, the effects of two parameters were investigated for a time scope of 200 (µs):
- − Constant contact stiffness—k1 = 1 × 104 (N·m−1), k2 = 1 × 105 (N·m−1),
- − Force sensor resonance frequency—f = 20, 40, and 200 kHz.
On the basis of earlier computer research results, it was concluded that the most crucial factors influencing the accuracy of measuring the forces’ course of cereal grain impact were the dimensions of a grain’s diameter and the resonance frequency of the force sensor freq. To determine the effect of those two factors on the accuracy of measuring the forces’ impact course, extended simulation research was conducted with the varied values of the assumed grain diameter and the resonance frequency of the sensor freq. Two parameters were assumed to check the measuring accuracy: the error of impact time (red line—Figures 10–12), showing the percentage standard deviation of the measured time of grain exposure to the sensor from the actual time, and the force error (green line—Figures 10–12) describing the percentage standard deviation of the maximum force indicated by the sensor from its actual value.
3. Results
As a result of the simulation, if the measurement was correct, the graphs should have shown an overlap between the contact force and force signal from the sensor.
Figure 5 shows the course of the contact force (the thick line) and the response of the sensor (the thin line) for an elastic impact of a 5 mm diameter grain assuming a contact stiffness of 1 × 104 Nm−1, which corresponds to a soft material, i.e., a grain with a high moisture content. The resonance frequency of the force sensor was f = 40 kHz. In this case, the contact was approximately 100 μs, and the course of the measurement signal corresponded to the course of the contact force.
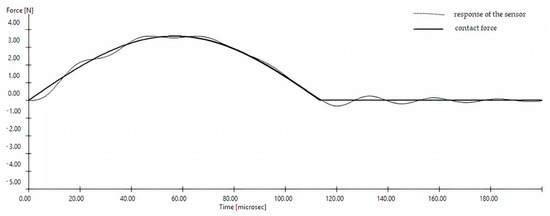
Figure 5.
The course of the impact force and measurement signal from the sensor for a large moist grain. Contact stiffness k1 = 1 × 104 Nm−1, frez = 40 kHz.
Figure 6 shows similar courses for a hard grain, i.e., with equivalent contact stiffness increased tenfold to 1 × 105 Nm−1. In this case, the course of the contact force differed significantly from the course of the measurement signal from the sensor. The time of the first half-period of sensor oscillation, which is often considered in tests as the contact duration, was significantly longer than the actual contact time.
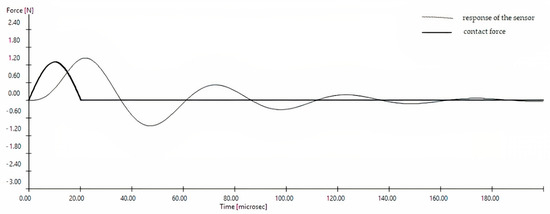
Figure 6.
The course of the impact force and measurement signal from the sensor for a small dry grain. Contact stiffness k2 = 1 × 105 Nm−1, frez = 20 kHz.
Figure 7 shows that the sensor resonance frequency in the simulation increased to 200 kHz. At this point, the course of the measurement signal from the sensor was closer to the course of the contact force.
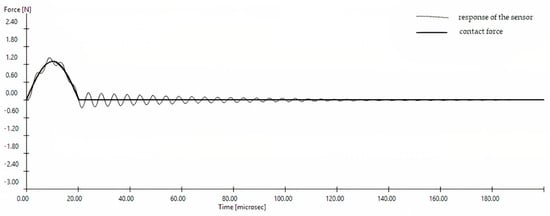
Figure 7.
The course of the impact force and measurement signal from the sensor for a large dry grain. Contact stiffness k2 = 1 × 105 Nm−1, frez = 200 kHz.
Similar experiments were performed for the second extreme case of the contact force model, i.e., using a perfectly plastic impact model, with a constant value of the contact force (Figure 8 and Figure 9).
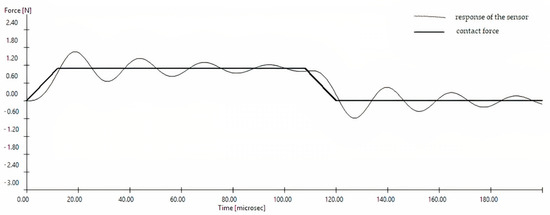
Figure 8.
The course of the impact force and measurement signal from the sensor for the perfectly plastic model and large soft grains. The contact force value was k1 = 1 × 104 Nm−1, frez = 20 kHz.
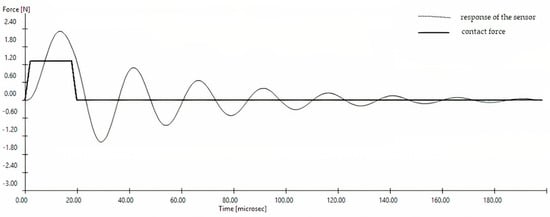
Figure 9.
The course of the impact force and measurement signal from the sensor for small hard grains and the perfectly plastic model. Contact stiffness k2 = 1 × 105 Nm−1, frez = 40 kHz.
The validity of the considerations may be confirmed by numerous research works concerning the measurement of the mechanical characteristics of machines and devices, in which the problem of the proper selection of force sensor properties has been repeatedly addressed [28,29,30,31,32,33]. However, such considerations have not been undertaken regarding the aspect of the correct assessment of measuring plant material mechanical characteristics, where the diversity of morphological structure poses many problems. The graphs above show the risk of obtaining false measurements of the course of plant grain impact forces against a flat surface. In the majority of the widely available scientific publications on measuring the course of impact forces for vegetable grain, it is not possible to find analyses that take into account the influence of sensor mechanical characteristics. The authors have focused on direct analyses of the obtained courses, in which components after the main input period have been rejected as measuring noise. Figure 5 and Figure 8 show that this may have been significantly false and could have led to a wrong conclusion about the course of the input function. According to the characteristics obtained, the size and moisture content of the investigated samples (caryopsis) had a significant influence on the discrepancies in the results obtained at low resonance frequencies of the sensor. Therefore, conducting research on larger legume seeds such as soya, beans, and peas has enabled the use of simple sensors with a relatively low resonance frequency, confirmed in numerous publications by authors such as Kuwabar, Kono, Alizadeh, and Hu [34,35,36,37,38,39], who presented courses of the impact force according to the calculations from this paper (Figure 6). In contrast, it has been more difficult to identify the course of forces for small grains with a low moisture content, forcing the use of specially designed sensors with a high resonance frequency whose exemplary application for wheat grain research is presented in a study by Kęska (1996) [15].
Figure 10 and Figure 11 show the course of two errors as frequency functions (the red line is the error of the impact time, while the green line is the error of the force). The simulations were repeated 10 times, with the random coefficient value of grain stiffness changing in uniform distribution in the range of 50% of the mean value. Figure 10 shows a grain diameter of 5.0 mm, while Figure 11 shows a grain diameter of 2.5 mm. The research showed that both errors decreased rapidly as the sensor resonance frequency increased, and that their irregular courses resulted from various overlaps of the sensor vibrations and the impact force impulse.
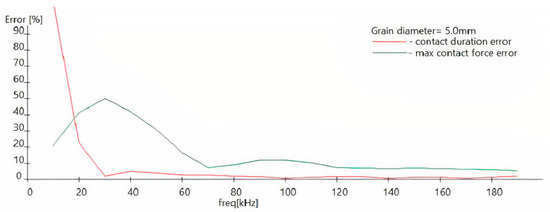
Figure 10.
The error course of the contact time (red line) and the maximum impact force (green line) for grains of 5.0 mm diameter depending on the sensor resonance frequency function.
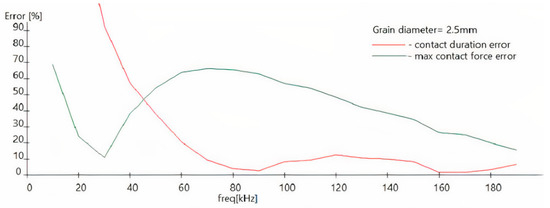
Figure 11.
The error course of the contact time (red line) and the maximum impact force (green line) for grains of 2.5 mm diameter depending on the sensor resonance frequency function.
Figure 12 shows the influence of grain diameter on the indicated measurement (the red line is the error of the impact time, while the green line is the error of the force). This clearly demonstrates that, for the sensor resonance frequencies that can be obtained at the level of 40 kHz, the measuring errors of the impact force are only practically ignored when the diameter of the grain is greater than 5.0 mm, such as pea or maize.
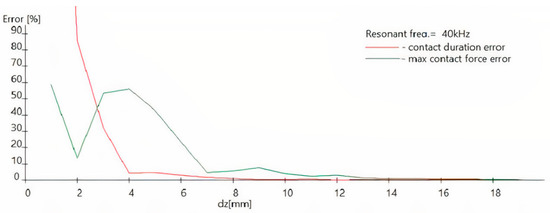
Figure 12.
The error course of the contact time (red line) and the maximum impact force (green line) depending on grain diameter.
4. Conclusions
- The key influence on the precision of impact force course modelling was the frequency of the free vibrations (resonance frequency) of the force sensor and the grain size.
- If the duration of the contact force pulse was longer than half of the sensor’s own vibration period, the measurement signal coincided significantly with the contact force course. This occurred for large and soft grains with a higher moisture content.
- If the duration of the contact force pulse was shorter than half of the sensor’s own vibration period, the results of the contact force measurement were not reliable because the first cycle of the measurement signal lasted longer than the actual contact time. Moreover, with hard fine grain, the signal itself was always close to half a sinusoid of a period corresponding to the resonance vibration period of the force sensor, regardless of the shape of the contact force pulse resulting from the shape of the grain mechanical properties.
- For large grains (e.g., maize, pea, and Pisum arvense) with a diameter greater than 5.0 mm, the modelling of the impact force by the sensor response signal with free vibrations of approximately 40 kHz could be considered adequate.
- For fine grains (e.g., rape) with a diameter of less than 2.0 mm, the exact modelling could only be obtained by a sensor with a free vibration frequency exceeding 200 kHz. Piezoelectric force sensors available for sale have a free vibration frequency of 70 kHz, which does not allow the credible impact force value to be measured for fine grain e.g., rape and mustard.
- To reliably measure the course of the impact force, impact force sensors of a special design with high resonance frequency should be used. The technological capabilities of manufacturers of such sensors allow resonance frequencies of up to 200 kHz.
- The most crucial factors influencing the measurement accuracy of the grain impact force course were the grain dimensions (diameter) and the force sensor resonance frequency.
- In DEM calculations, where the contact force course is of key importance, the empirical research results of the force courses for fine grain should be approached carefully, by only relying on theoretical models (rheological) of the force courses.
Author Contributions
Conceptualization, W.K. and J.M.; methodology, W.K.; software, W.K.; validation, J.M., J.S., Ł.G., and K.K.; formal analysis, J.S. and Ż.S.; resources, J.M. and J.S.; writing—original draft preparation, J.M., W.K., and Ł.G.; writing—review and editing, Ż.S., Ł.G., and K.K.; visualization, J.M.; project administration, Ł.G. and K.K., supervision, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by SBAD, grant number 0613/SBAD/4677.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anand, A.; Curtis, J.S.; Wassgren, C.R.; Hancock, B.C.; Ketterhagen, W.R. Predicting discharge dynamics of wet cohesive particles from a rectangular hopper using the discrete element method (DEM). Chem. Eng. Sci. 2009, 64, 5268–5275. [Google Scholar] [CrossRef]
- Raji, A.O.; Favier, J.F. Model for deformation in agricultural and food particulate materials under bulk compressive loading using discrete element method. II: Compression of oilseeds. J. Food Eng. 2004, 64, 373–380. [Google Scholar] [CrossRef]
- Sakaguchi, E.; Kawakami, S.; Tobita, F. Simulation of Flowing Phenomena of Grains by Distinct Element Method; Report No. 94-G-025; Ageng’ 94: Milano, Italy, 1994; pp. 1–8. [Google Scholar]
- Cundall, P.A.; Strack, O.D. A discrete element model for granular assemblies. Geotehnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Malone, K.F.; Xu, B.H. Determination of contact parameters for discrete element method simulations of granular systems. Particuology 2008, 6, 521–528. [Google Scholar] [CrossRef]
- Tijskens, E.; Ramon, H.; Baerdemaeker, J. Discrete element modelling for process simulation in agriculture. J. Sound Vib. 2003, 266, 493–514. [Google Scholar] [CrossRef]
- Mishra, B.; Murty, C. On the determination of contact parameters for realistic DEM simulations of ball mills. Powder Technol. 2001, 115, 290–297. [Google Scholar] [CrossRef]
- Fraczek, J. Method of measuring the force of internal friction of biological bulk materials. Zesz. Probl. Adv. Agric. Sci. 1998, 423, 93–101. (In Polish) [Google Scholar]
- Youngdahl, C.J.; Sanders, P.G.; Eastman, J.; Weertman, J.R. Compressive yield strengths of nanocrystalline Cu and Pd. Scr. Mater. 1997, 37, 809–813. [Google Scholar] [CrossRef]
- Jaeger, H.M.; Shinbrot, T.; Umbanhowar, P.B. Does the granular matter? Proc. Natl. Acad. Sci. USA 2000, 97, 12959–12960. [Google Scholar] [CrossRef]
- Kustermann, M. Stossartige Belastung von Maiskörner. Grundl. Landtech. 1987, 37, 121–131. [Google Scholar]
- Musson, R.W.; Carlson, W. Finite element study of the effect of material properties on reaction forces produced by solitary wave propagation in granular chains. Granul. Matter 2019, 18, 22. [Google Scholar] [CrossRef]
- Arslan, S. A Grain Flow Model to Simulate Grain Yield Sensor Response. Sensors 2008, 8, 952–962. [Google Scholar] [CrossRef] [PubMed]
- Reinke, R.; Dankowicz, H.; Phelan, J.; Kang, W. A dynamic grain flow model for a mass flow yield sensor on a combine. Precis. Agric. 2011, 12, 732–749. [Google Scholar] [CrossRef]
- Kęska, W. Research on the course of forces at the collision of seeds of some cultivated plants with the working surfaces of agricultural machines. Work. Ind. Inst. Agric. Mach. 1996, 41, 17–21. (In Polish) [Google Scholar]
- Horabik, J.; Molenda, M. Parameters and contact models for DEM simulations of agricultural granular materials: A review. Biosyst. Eng. 2016, 147, 206–225. [Google Scholar] [CrossRef]
- Wojtkowski, M.; Pecen, J.; Horabik, J.; Molenda, M. Rapeseed impact against a flat surface: Physical testing and DEM simulation with two contact models. Powder Technol. 2010, 198, 61–68. [Google Scholar] [CrossRef]
- Feder, S. Examination of the coefficient of grain velocity restitution in the separation process. Work. Ind. Inst. Agric. Mach. 1996, 41, 27–33. (In Polish) [Google Scholar]
- Michalak, D. Examination of mechanical properties of cereal grains. Work. Ind. Inst. Agric. Mach. 1996, 41, 22–26. (In Polish) [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Munjiza, A. The Combined Finite-Discrete Element Method; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Kruggel-Emden, H.; Simsek, E.; Rickelt, S.; Wirtz, S.; Scherer, V. Review and extension of normal force models for the Discrete Element Method. Powder Technol. 2007, 171, 157–173. [Google Scholar] [CrossRef]
- Thornton, C.; Ning, Z. A theoretical model for the stick/ bounce behaviour of adhesive, elasticeplastic spheres. Powder Technol. 1998, 99, 154–162. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Weir, G.; Tallon, S. The coefficient of restitution for normal incident, low velocity particle impacts. Chem. Eng. Sci. 2005, 60, 3637–3647. [Google Scholar] [CrossRef]
- Chen, Z.; Wassgren, C.; Veikle, E.; Ambrose, R.K. Determination of material and interaction properties of maize and wheat kernels for DEM simulation. Biosyst. Eng. 2020, 195, 208–226. [Google Scholar] [CrossRef]
- Marinack, M.C., Jr.; Jasti, V.K.; Choi, Y.E.; Higgs, C.F.; Higgs, C.F. Couette grain flow experiments: The effects of the coefficient of restitution, global solid fraction, and materials. Powder Technol. 2011, 211, 144–155. [Google Scholar] [CrossRef]
- Chwaleba, A.; Ponięski, M.; Siedlecki, A. Electrical Metrology; WNT: Warszawa, Poland, 1998. (In Polish) [Google Scholar]
- Miłek, M. Measurements of Non-Electrical Quantities by Electrical Methods; Academic textbook ed.; Zielona Góra University of Technology: Zielona Góra, Poland, 1998. (In Polish) [Google Scholar]
- Romer, E. Industrial Measurement; PWN: Warszawa, Poland, 1978. (In Polish) [Google Scholar]
- Altintas, Y.; Eynian, M.; Onozuka, H. Identification of dynamic cutting force coefficients and chatter stability with process damping. CIRP Ann. Manuf. Technol. 2008, 57, 371–374. [Google Scholar] [CrossRef]
- Hagel, R.; Zakrzewski, J. Dynamic Measuremen; WNT: Warszawa, Poland, 1984. (In Polish) [Google Scholar]
- Szumielewicz, B.; Słomski, B.; Styburski, W. Electronic Measurements in Technolog; WNT: Warszawa, Poland, 1982. (In Polish) [Google Scholar]
- Kuwabara, G.; Kono, K. Restitution Coefficient in a Collision between Two Spheres. Jpn J. Appl. Phys. 1987, 26, 1230–1233. [Google Scholar] [CrossRef]
- Alizadeh, E.; Bertrand, F.; Chaouki, J. Development of a granular normal contact force model based on a non-Newtonian liquid filled dashpot. Powder Technol. 2013, 237, 202–212. [Google Scholar] [CrossRef]
- Hu, S.; Xinglin, G. A dissipative contact force model for impact analysis in multibody dynamics. Multibody Syst. Dyn. 2015, 35, 131–151. [Google Scholar] [CrossRef]
- Hu, Z.-Y.; Hua, W.; Zhang, L.; Deng, L.-B.; Wang, X.-F.; Liu, G.-H.; Hao, W.J.; Wang, H.Z. Seed struc-ture characteristics to form ultrahigh oil content in rapeseed. PLoS ONE 2013, 8, e62099. [Google Scholar]
- Hu, G.; Hu, Z.; Jian, B.; Liu, L.; Wan, H. On the determination of the damping coef-ficient of non-linear springdashpot system to model Hertz contact for simulation by discrete ele-ment method. J. Comput. 2011, 6, 984–988. [Google Scholar] [CrossRef]
- Van Zeebroeck, M.; Tijskens, E.; Van Liedekerke, P.; Deli, V.; De Baerdemaeker, J.; Ramon, H. Determination of the dynamical behaviour of biologicalmaterials during impact using apendulumdevice. J. Soundandvibration 2003, 266, 456–480. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).