Keyboard Model of Seismic Cycle of Great Earthquakes in Subduction Zones: Simulation Results and Further Generalization
Abstract
1. Introduction
2. Materials and Methods
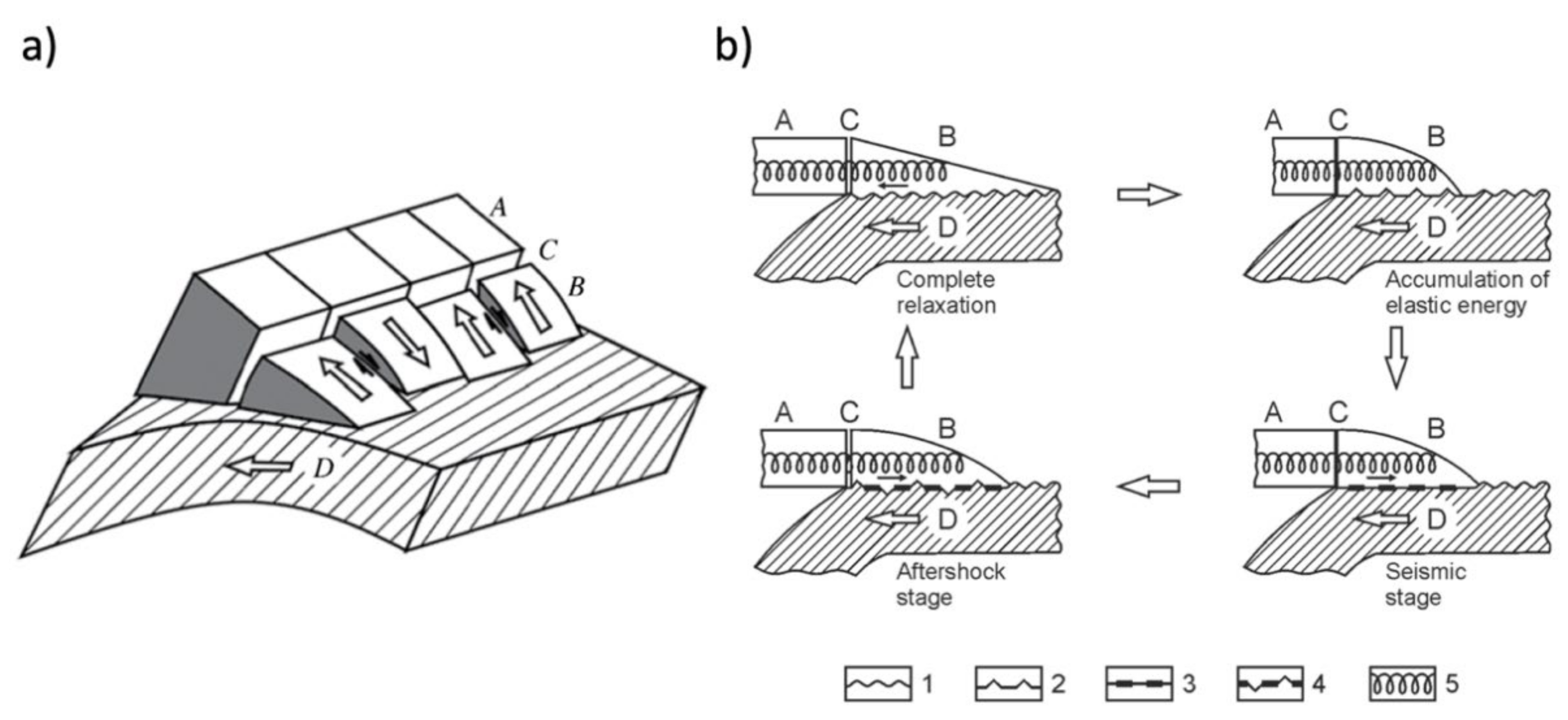
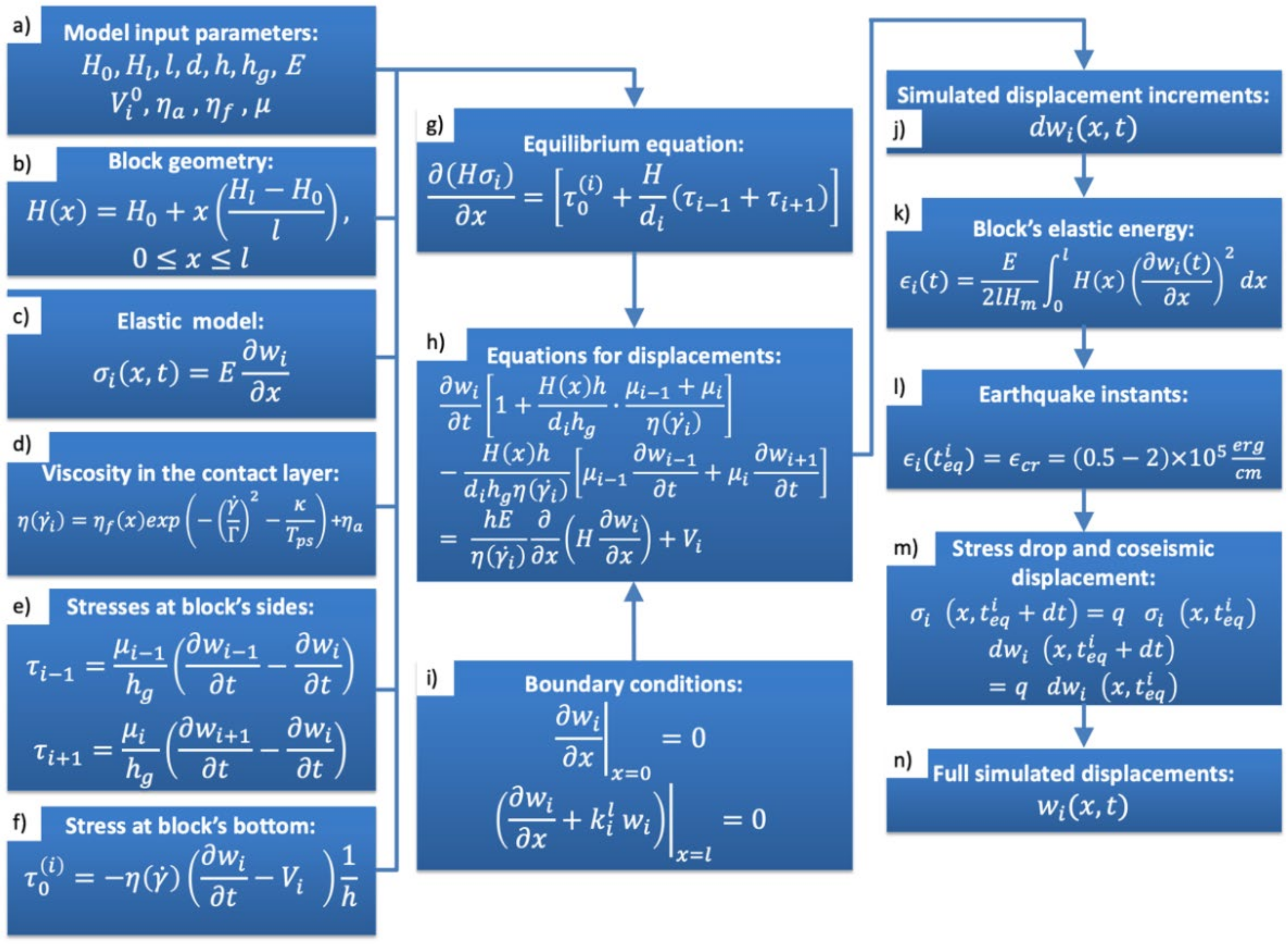
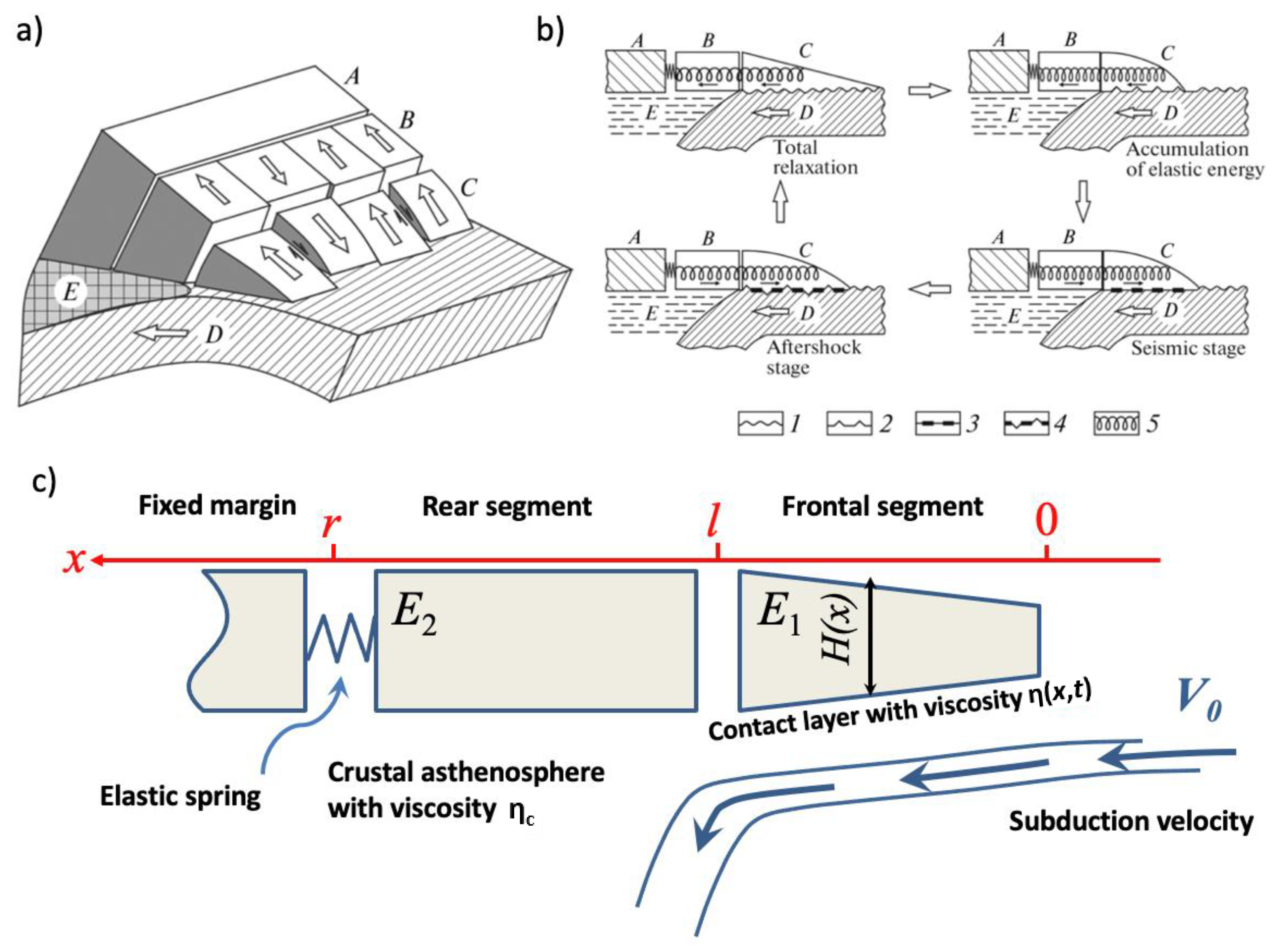
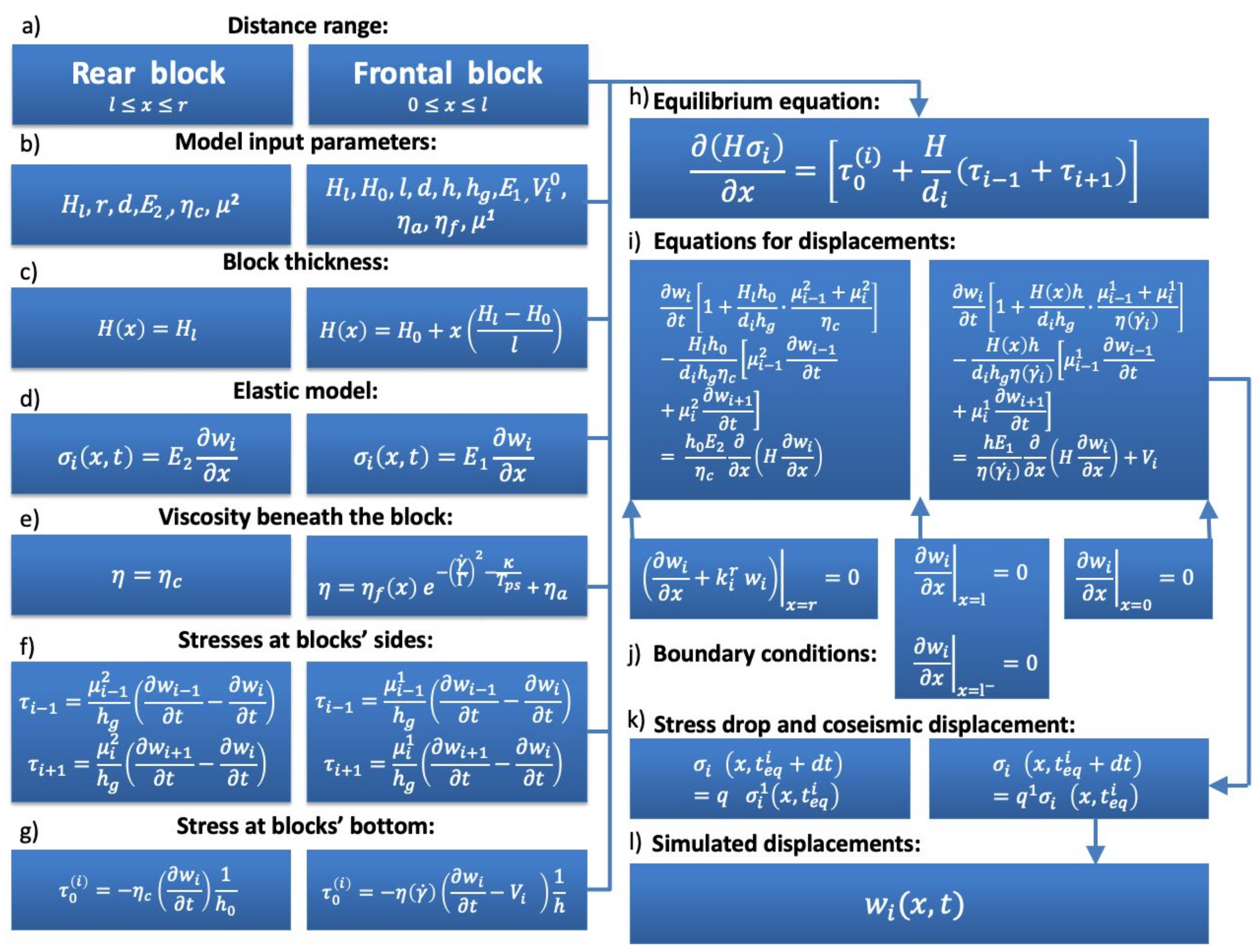
2.1. Keyboard Model of Seismic Cycles of Great Subduction-Associated Earthquakes
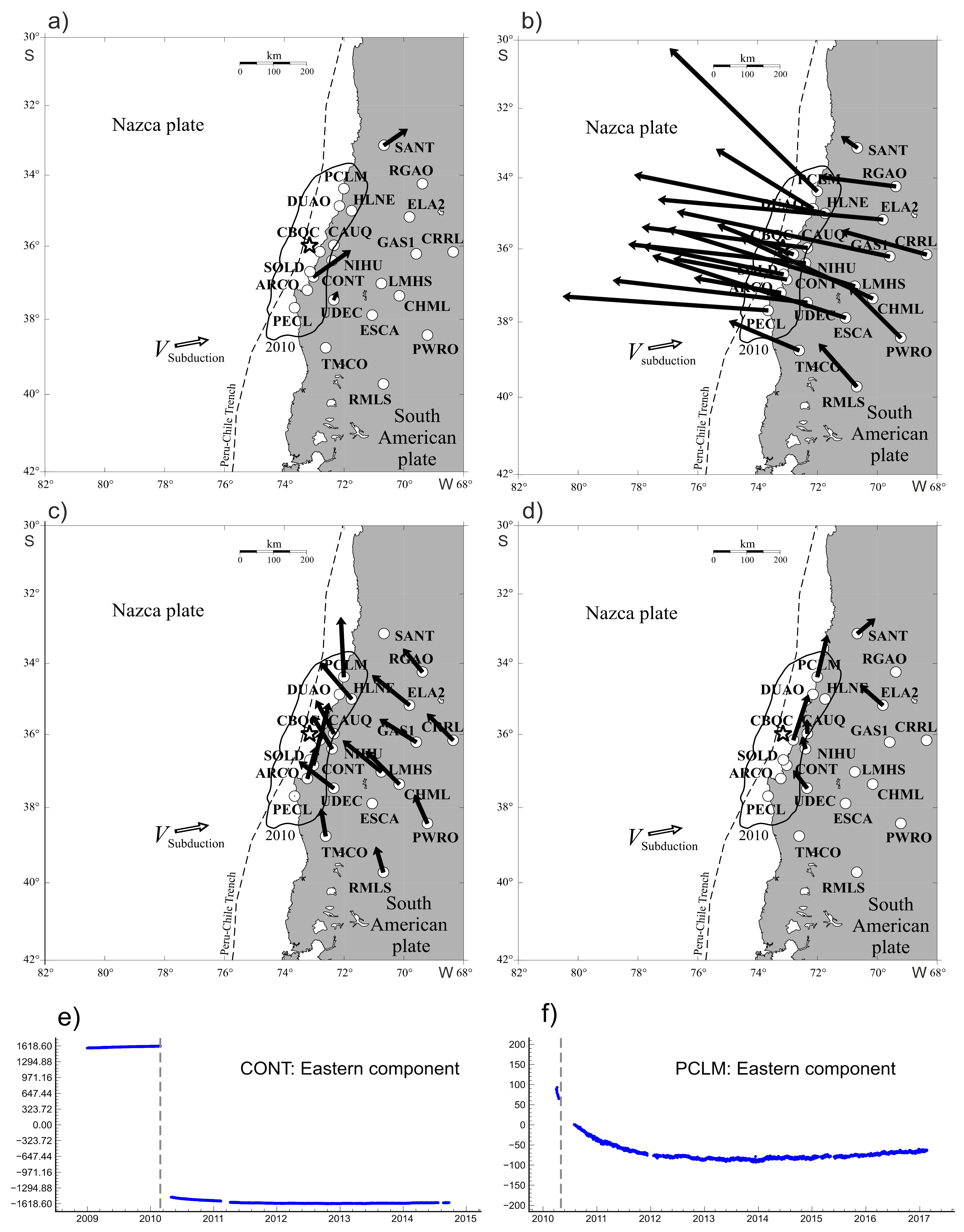
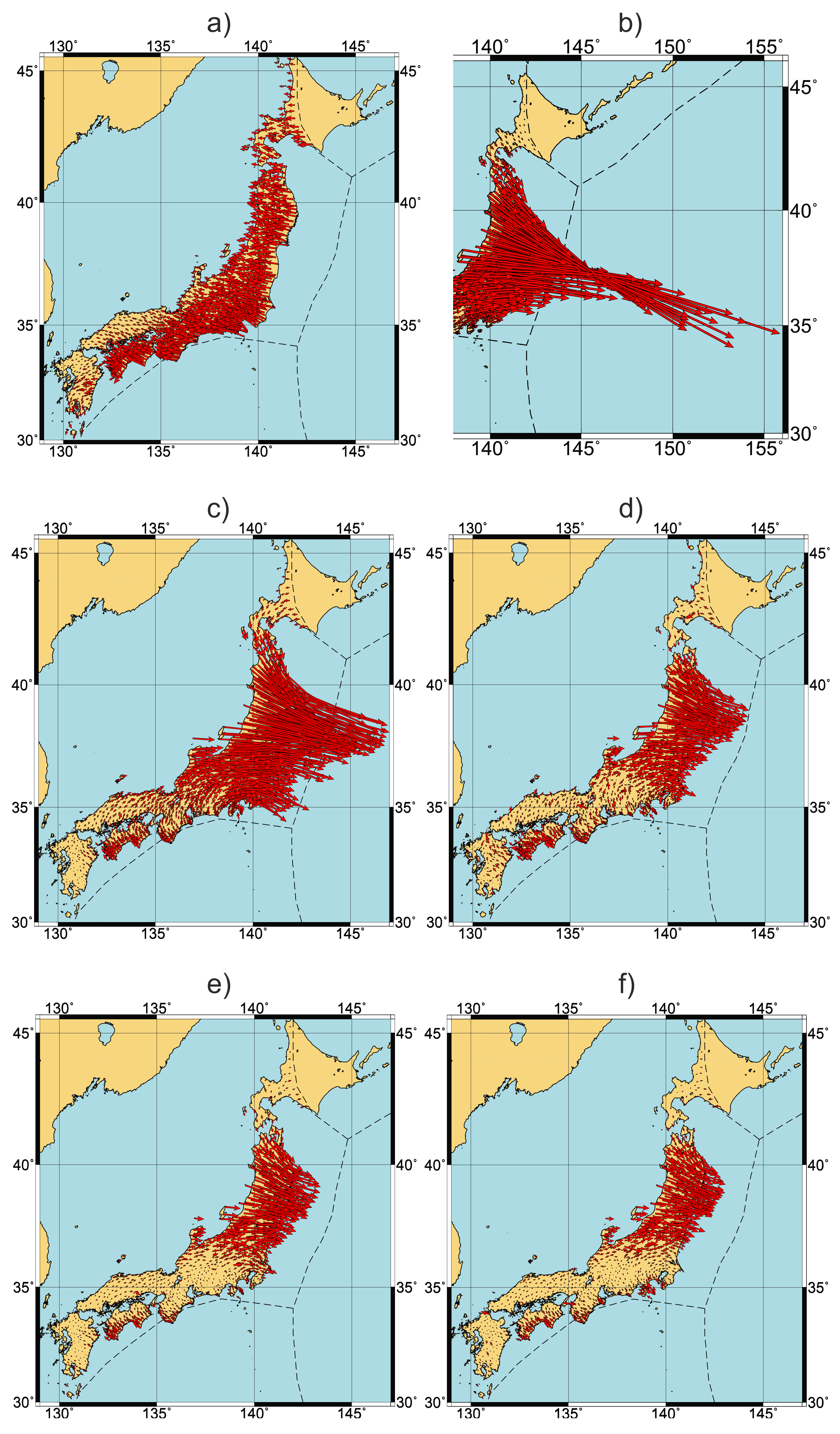
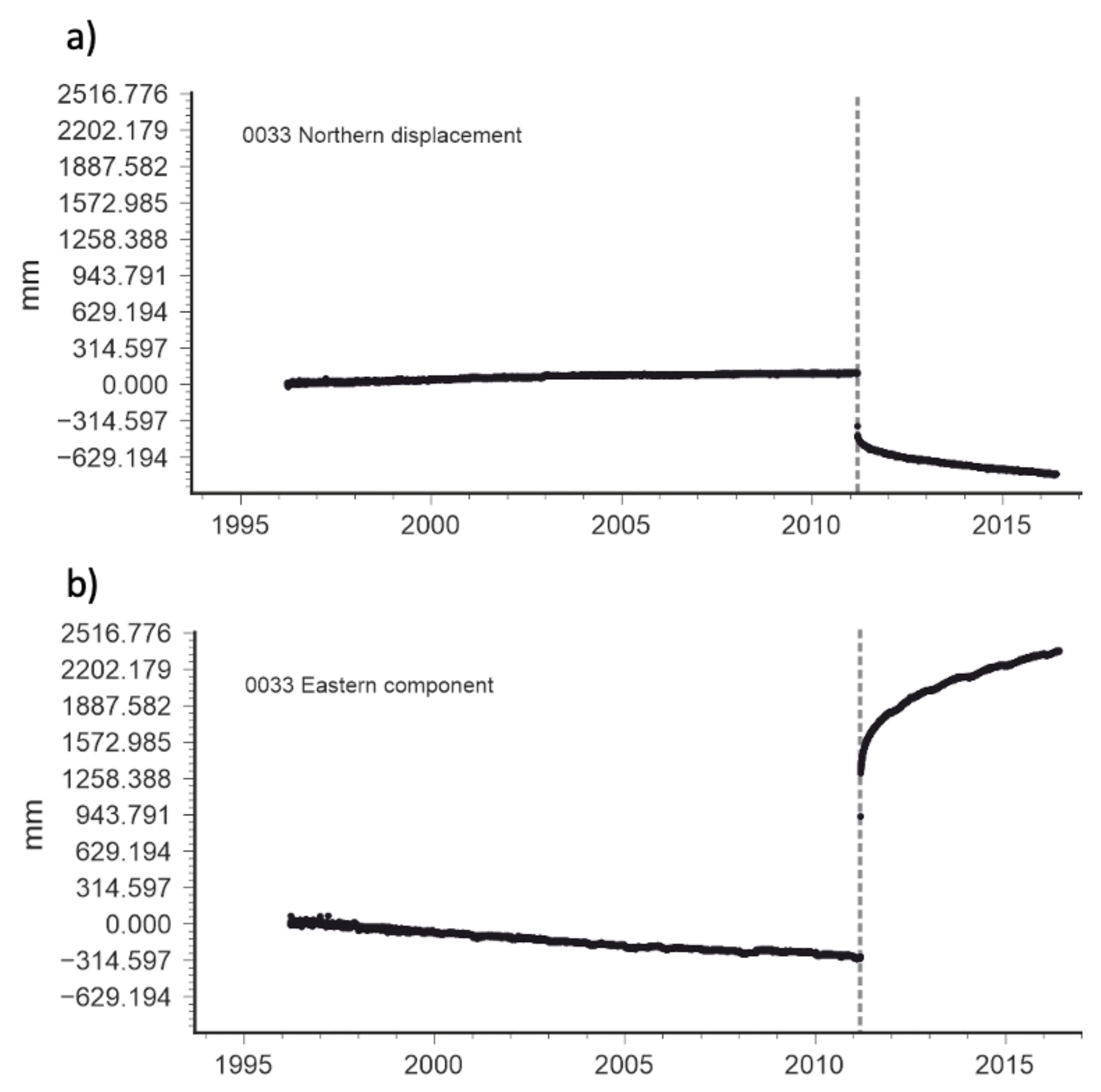
2.2. GNSS-Measured Motions and Stress-Deformation Cycle in Subduction Regions
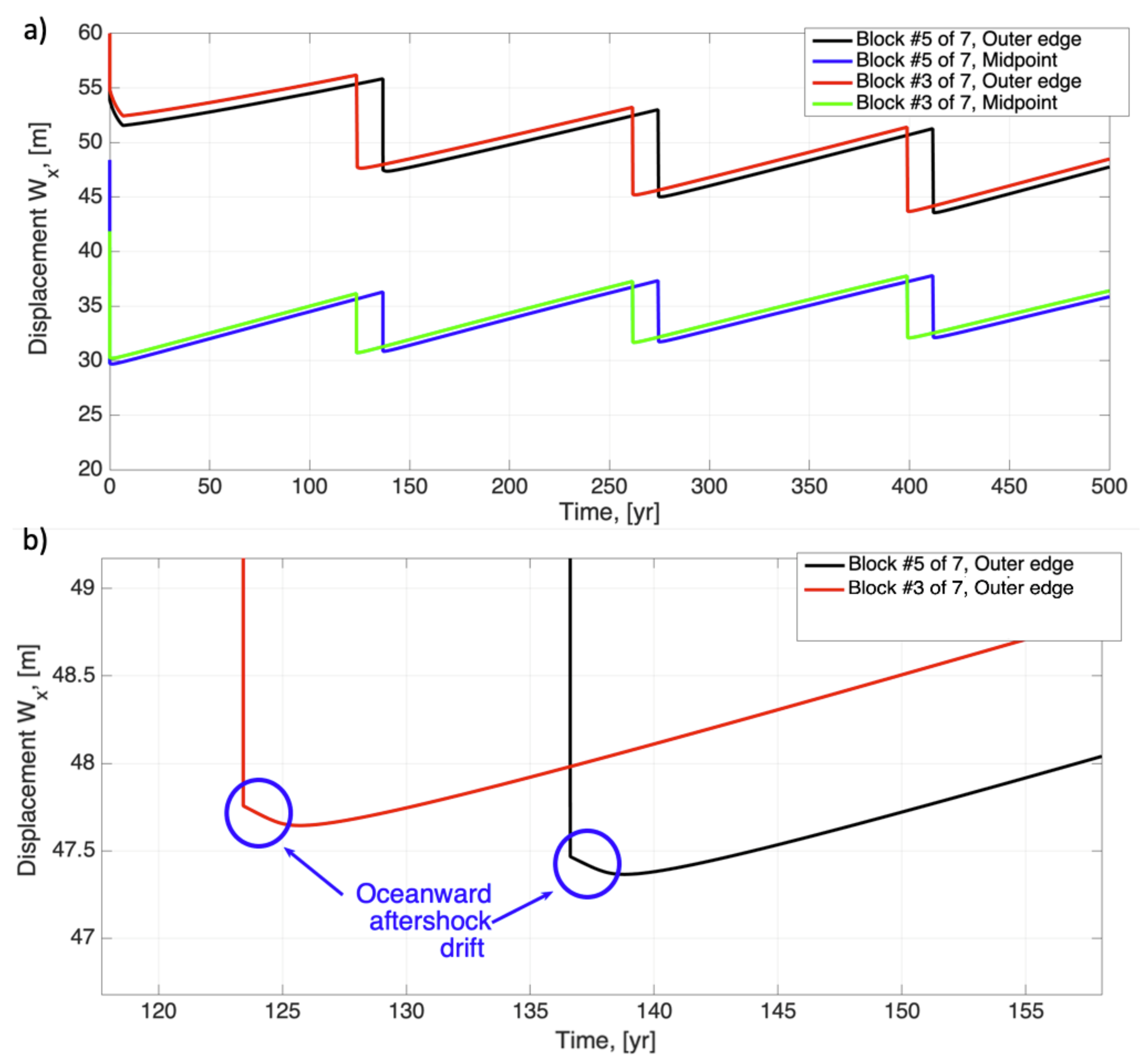
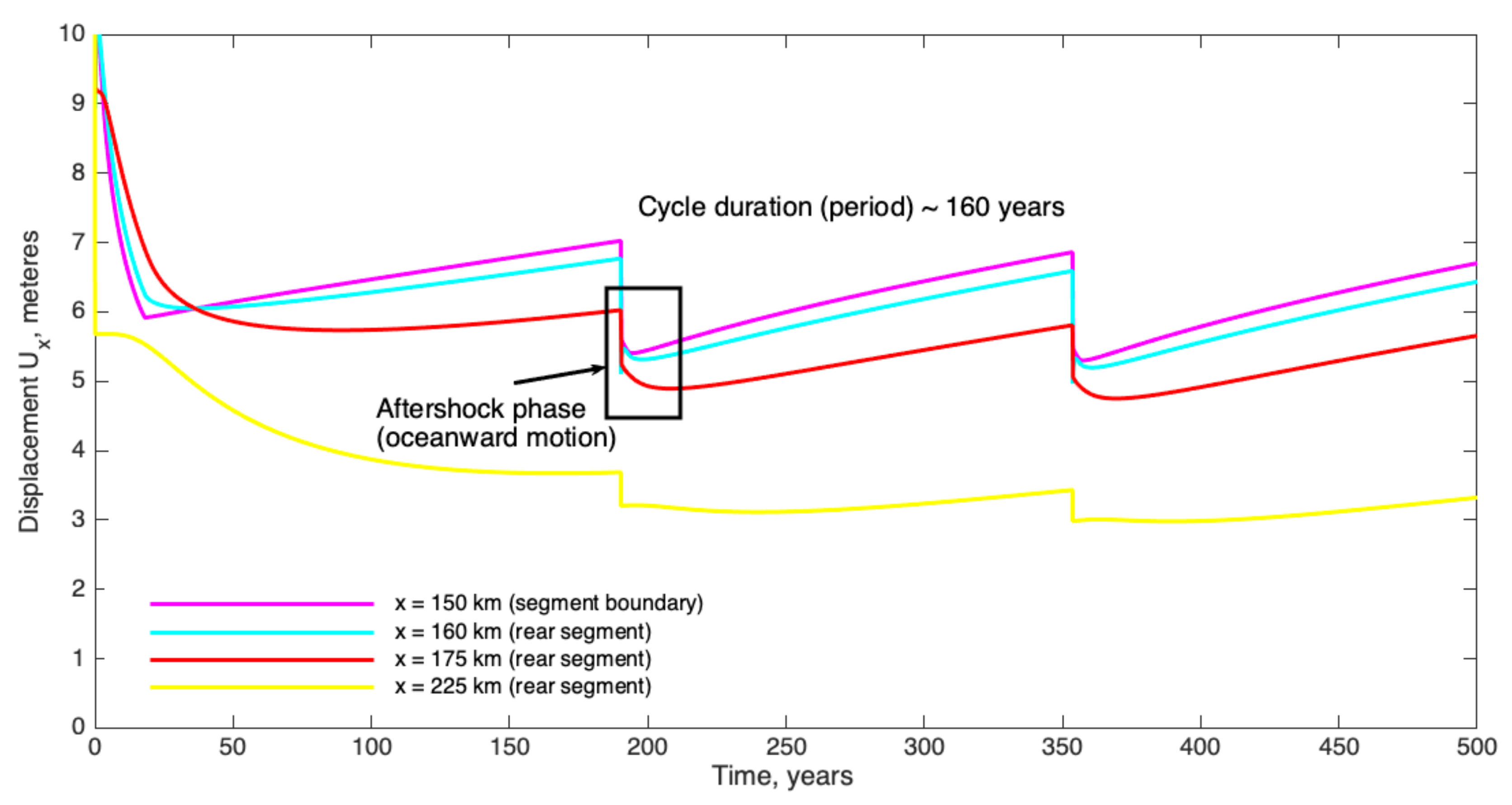
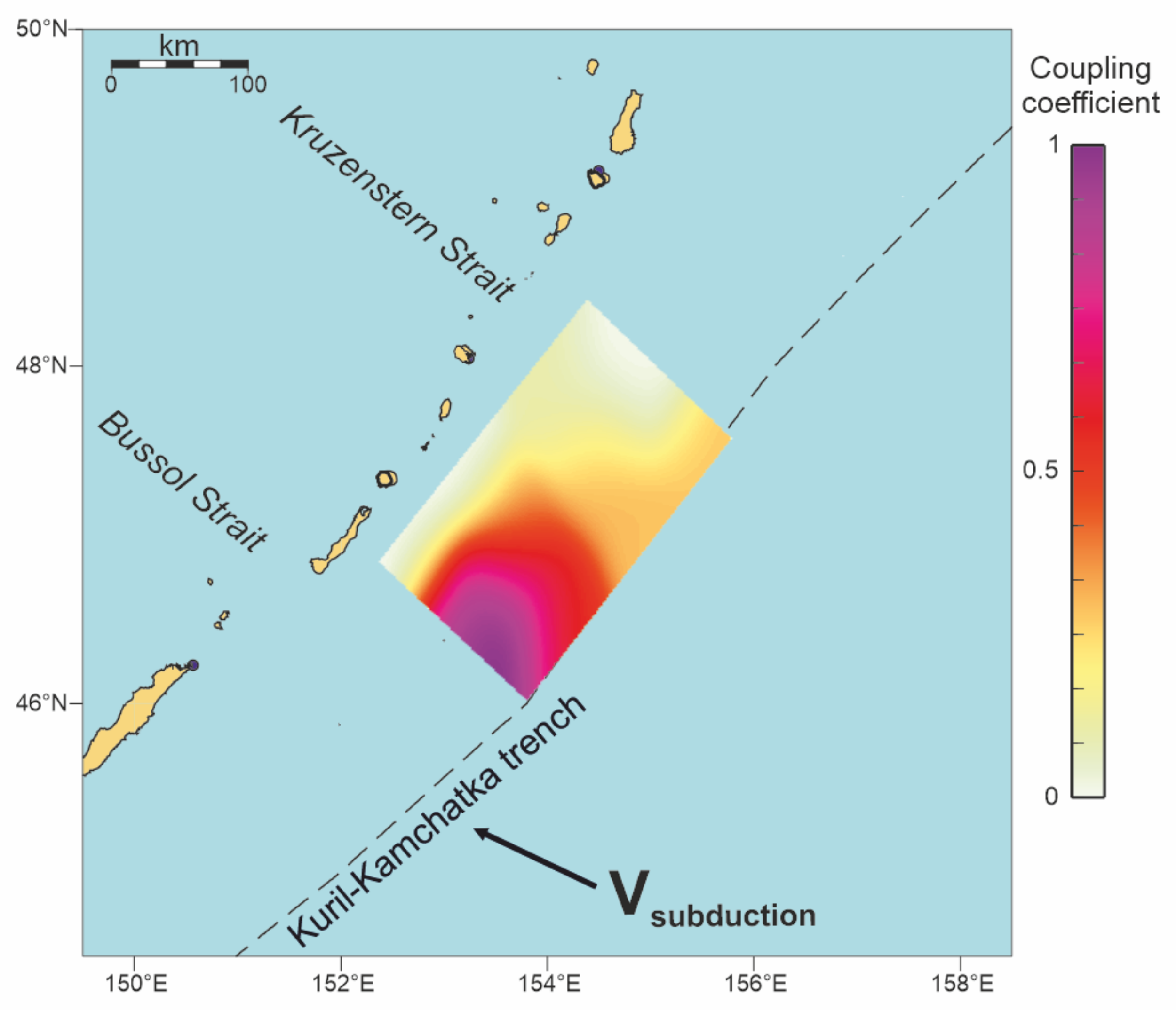
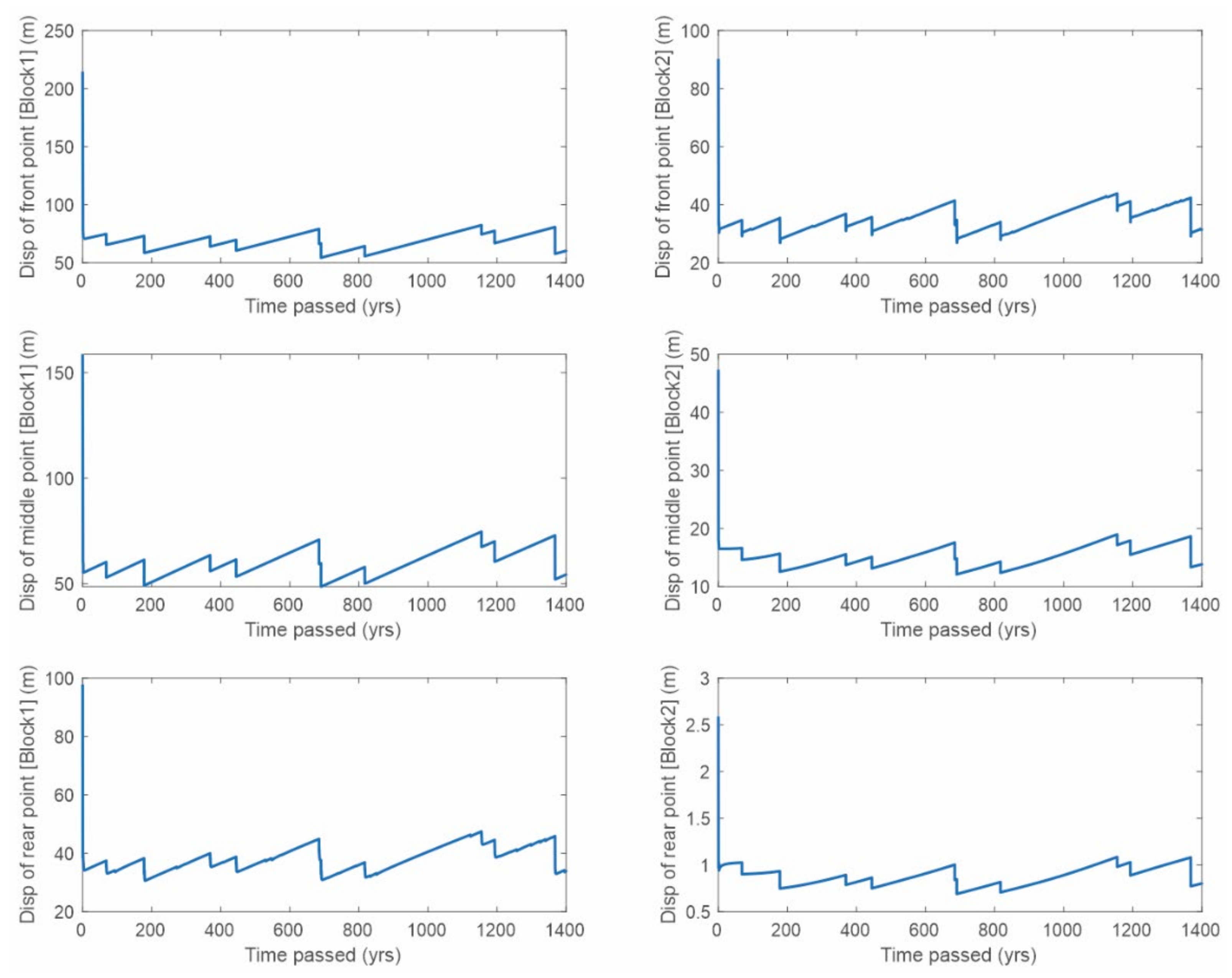
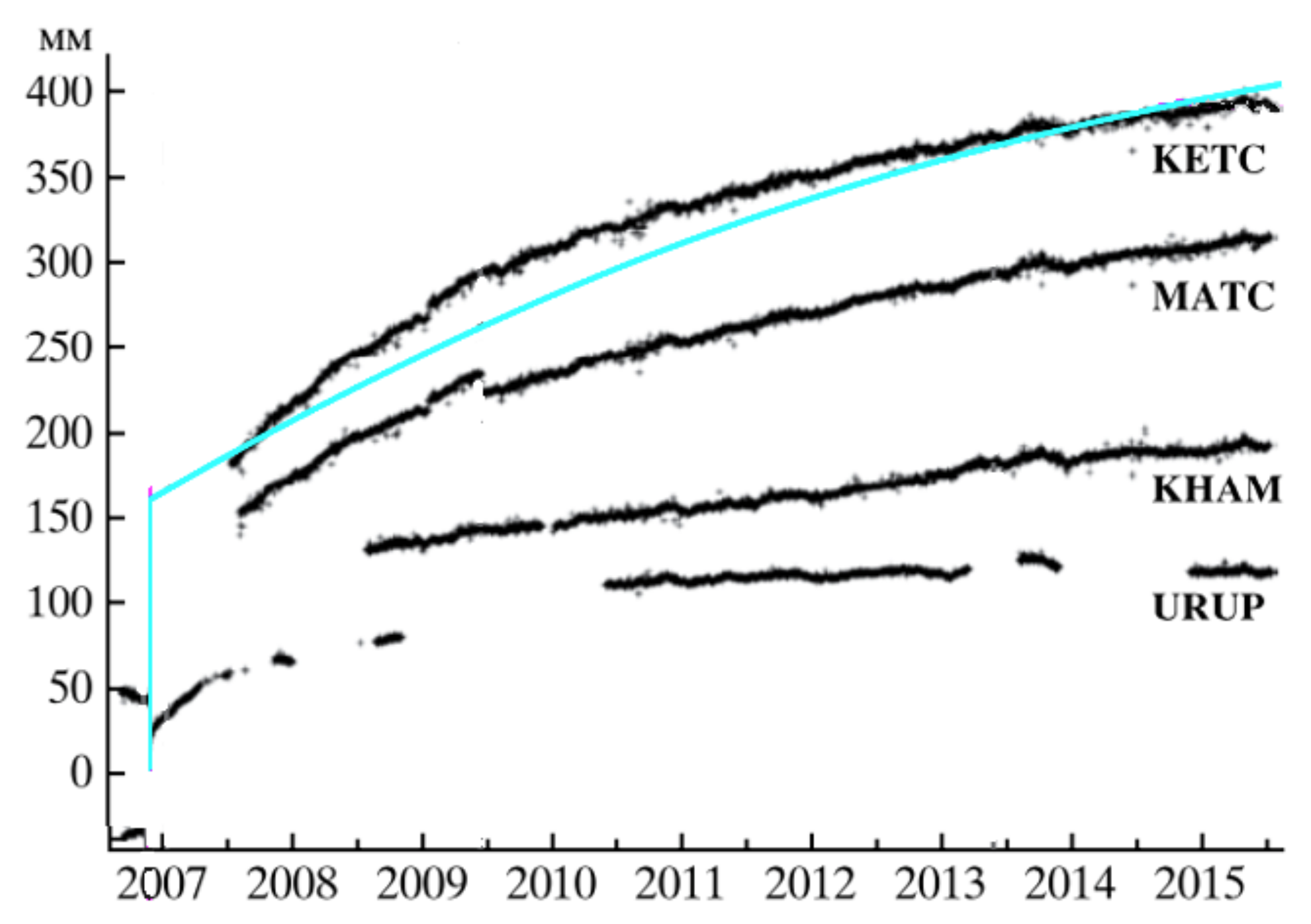
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shebalin, N.V. Selected Publications. Great Earthquakes; Mining Academy Publishing House: Moscow, Russia, 1997; 542p. (In Russian) [Google Scholar]
- Keilis-Borok, V. Earthquake Prediction: State-of-the-Art and Emerging Possibilities. Annu. Rev. Earth Planet. Sci. 2002, 30, 1–33. [Google Scholar] [CrossRef]
- Ruff, L.J. Asperity distributions and large earthquake occurrence in subduction zones. Tectonophysics 1992, 211, 61–83. [Google Scholar] [CrossRef][Green Version]
- Kaneko, Y.; Avouac, J.P.; Lapusta, N. Towards inferring earthquake patterns from 513 geodetic observations of interseismic coupling. Nat. Geosci. 2010, 3, 363–369. [Google Scholar] [CrossRef]
- Rosenau, M.; Horenko, I.; Corbi, F.; Rudolf, M.; Kornhuber, R.; Oncken, O. Synchronization of great subduction megathrust earthquakes: Insights from scale model analysis. J. Geophys. Res. 2019, 124, 3646–3661. [Google Scholar] [CrossRef]
- Kossobokov, V.G.; Keilis-Borok, V.I.; Smith, S.W. Localization of intermediate-term earthquake prediction. J. Geophys. Res. 1990, 95, 12763–12772. [Google Scholar] [CrossRef]
- Soloviev, A.A.; Gvishiani, A.D.; Gorshkov, A.I.; Dobrovolsky, M.N.; Novikova, O.V. Recognition of Earthquake-Prone Areas: Methodology and Analysis of the Results. Izv. Phys. Solid Earth 2014, 50, 151–168. [Google Scholar] [CrossRef]
- Sykes, L.R.; Menke, W. Repeat times of large earthquakes: Implications for earthquake mechanics and long-term prediction. BSSA 2016, 96, 1569–1596. [Google Scholar] [CrossRef]
- Banna, M.H.A.; Taher, K.A.; Kaiser, M.S.; Mahmud, M.; Rahman, M.S.; Hosen, A.S.M.S.; Cho, G.H. Application of Artificial Intelligence in Predicting Earthquakes: State-of-the-Art and Future Challenges. IEEE Access 2020, 8, 192880–192923. [Google Scholar] [CrossRef]
- Battaglia, M.; Cervelli, P.F.; Murray, J.R. Modeling crustal deformation near active faults and volcanic centers—A catalog of deformation models. In Techniques and Methods; U.S. Geological Survey: Menlo Park, CA, USA, 2013; Book 13, Chapter B1; 96p. [Google Scholar]
- Madariaga, R. Seismic Source Theory. In Treatise on Geophysics; Elsevier: Amsterdam, The Netherlands, 2015; pp. 51–71. [Google Scholar]
- Lay, T.; Kanamori, H. An asperity model of large earthquake sequences. In Earthquake Prediction: An International Review; American Geophysical Union: Washington, DC, USA, 1981; pp. 579–592. [Google Scholar]
- Senatorski, P. Effect of slip-weakening distance on seismic–aseismic slip patterns. Pure Appl. Geophys. 2019, 176, 3975–3992. [Google Scholar]
- Lobkovsky, L.I.; Mazova, R.K.; Garagash, I.A.; Kataeva, L.Y.; Nardin, I. To analysis of source mechanism of the 26 December 2004 Indian Ocean tsunami. Russ. J. Earth. Sci. 2006, 8, ES5001. [Google Scholar]
- Baranov, B.V.; Ivanchenko, A.I.; Dozorova, K.A. The Great 2006 and 2007 Kuril Earthquakes, Forearc Segmentation and Seismic Activity of the Central Kuril Islands Region. Pure Appl. Geophys. 2015, 172, 3509–3535. [Google Scholar] [CrossRef]
- Lobkovsky, L.I.; Baranov, B.V.; Vladimirova, I.S.; Gabsatarov, V.V.; Steblov, G.M.; Garagash, I.A. Post-seismic motions after the 2006–2007 Simushir earthquakes at different stages of the seismic cycle. Dokl. Earth Sci. 2017, 473, 375–379. [Google Scholar] [CrossRef]
- Lobkovsky, L.I.; Vladimirova, I.S.; Gabsatarov, Y.V.; Baranov, B.V.; Garagash, I.A.; Steblov, G.M. Seismotectonic deformations associated with the 2010 Maule earthquake at different stages of the seismic cycle according to satellite geodetic observations. Dokl. Earth Sci. 2017, 477, 716–721. [Google Scholar]
- Lobkovsky, L.I.; Vladimirova, I.S.; Gabsatarov, Y.V.; Steblov, G.M. Seismotectonic Deformations Related to the 2011 Tohoku Earthquake at Different Stages of the Seismic Cycle, Based on Satellite Geodetic Observations. Dokl. Earth Sci. 2018, 481, 1060–1065. [Google Scholar] [CrossRef]
- Vladimirova, I.S.; Lobkovsky, L.I.; Gabsatarov, Y.V.; Steblov, G.M.; Vasilenko, N.F.; Frolov, D.I.; Prytkov, A.S. Patterns of the Seismic Cycle in the Kuril Island Arc from GPS Observations. Pure Appl. Geophys. 2020, 177, 3599–3617. [Google Scholar]
- Lobkovsky, L.I.; Kerchman, V.I.; Baranov, B.V.; Pristavakina, E.I. Analysis of seismotectonic processes in subduction zones from the standpoint of a keyboard model of great earthquakes. Tectonophysics 1991, 199, 211–236. [Google Scholar] [CrossRef]
- Ozawa, S.; Nishimura, T.; Suito, H.; Kobayashi, T.; Tobita, M.; Imakiire, T. Coseismic and postseismic slip of the 2011 magnitude-9 Tohoku-Oki earthquake. Nature 2011, 475, 373–377. [Google Scholar] [CrossRef]
- Lobkovsky, L.I.; Vladimirova, I.S.; Alekseev, D.A.; Gabsatarov, Y.V. Two-element keyboard model of strongest subduction earthquakes generation. Dokl. Earth Sci. 2021, 496, 72–75. [Google Scholar] [CrossRef]
- Fedotov, S.A. Regularities of distribution of large earthquakes of Kamchatka, Kuril Islands and North-Eastern Japan. Tr. Inst. Fiz. Zemli Akad. Nauk SSSR 1965, 36, 66–93. (In Russian) [Google Scholar]
- Loveless, J.P.; Brendan, J.M. Geodetic imaging of plate motions, slip rates, and partitioning of deformation in Japan. J. Geophys. Res. 2010, 115, 1–35. [Google Scholar] [CrossRef]
- Panayotopoulos, Y.; Hirata, N.; Sato, H.; Kato, A.; Imanishi, K.; Kuwahara, Y.; Cho, I.; Takeda, T.; Asano, Y. Investigating the role of the Itoigawa-Shizuoka tectonic line towards the evolution of the Northern Fossa Magnarift basin. Tectonophysics 2014, 615–616, 12–26. [Google Scholar] [CrossRef]
- Minoura, K.; Imamura, F.; Sugawara, D.; Kono, Y.; Iwashita, T. The 869 Jogan tsunami deposit and recurrence interval of large-scale tsunami on the Pacific coast of northeast Japan. J. Nat. Disaster Sci. 2001, 23, 83–88. [Google Scholar]
- Melnick, D.; Echtler, H.P. Morphotectonic and geologic digital map compilations of the south-central Andes (36°–42° S). In The Andes—Active Subduction Orogeny; Frontiers in Earth Science; Oncken, O., Chong, G., Franz, G., Giese, P., Götze, H.-J., Ramos, V.A., Strecker, M., Wigger, P., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006; Volume 1, pp. 565–568. [Google Scholar]
- Geersen, J.; Behrmann, J.H.; Völker, D.; Krastel, S.; Ranero, C.R.; Diaz-Naveas, J.; Weinrebe, W. Active tectonics of the South Chilean marine fore arc (35° S–40° S). Tectonics 2011, 30, 1–16. [Google Scholar] [CrossRef]
- Moreno, M.; Melnick, D.; Rosenau, M.; Baez, J.; Klotz, J.; Oncken, O.; Tassara, A.; Chen, J.; Bataille, K.; Bevis, M.; et al. Toward understanding tectonic control on the Mw 8.8 2010 Maule Chile earthquake. Earth Planet. Sci. Lett. 2012, 321–322, 152–165. [Google Scholar] [CrossRef]
- Jara-Muñoz, J.; Melnick, D.; Brill, D.; Strecker, M.R. Segmentation of the 2010 Maule Chile earthquake rupture from a joint analysis of uplifted marine terraces and seismic-cycle deformation patterns. Quat. Sci. Rev. 2015, 113, 171–192. [Google Scholar] [CrossRef]
- Metois, M.; Vigny, C.; Socquet, A. Interseismic Coupling, Megathrust Earthquakes and Seismic Swarms Along the Chilean Subduction Zone (38°–18° S). Pure Appl. Geophys. 2016, 173, 1431–1449. [Google Scholar]
- Fedotov, S.A. The seismic cycle, possibility of the quantitative seismic zoning, and long-term seismic forecasting. In Seismic Zoning in the USSR; Medvedev, S.V., Ed.; Nauka: Moscow, Russia, 1968. (In Russian) [Google Scholar]
- DeMets, C. Oblique convergence and deformation along the Kuril and Japan trenches. J. Geophys. Res. 1992, 97, 17615–17625. [Google Scholar] [CrossRef]
- Cross, R.S.; Freymueller, J.T. Evidence for and implications of a Bering plate based on geodetic measurements from the Aleutians and western Alaska. J. Geophys. Res. 2008, 113, B07405. [Google Scholar]
- Piersanti, A. Postseismic deformation in Chile: Constraints on the asthenospheric viscosity. Geophys. Res. Lett. 1999, 26, 3157–3160. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, K.; He, J.; Klotz, J.; Khazaradze, G. Three-dimensional viscoelastic finite element model for post-seismic deformation of the great 1960 Chile earthquake. J. Geophys. Res. 2004, 109, B12403. [Google Scholar] [CrossRef]
- Wang, K. Elastic and viscoelastic models of crustal deformation in subduction zone cycles. In The Seismogenic Zone of Subduction Thrust Faults; Dixon, T.H., Moore, J.C., Eds.; Columbia University Press: New York, NY, 2007; pp. 540–577. [Google Scholar]
- Bürgmann, R.; Dresen, G. Rheology of the Lower Crust and Upper Mantle: Evidence from Rock Mechanics, Geodesy and Field Observations. Annu. Rev. Earth Planet. Sci. 2008, 36, 531–567. [Google Scholar] [CrossRef]
- Suito, H.; Freymueller, J.T. A viscoelastic and afterslip postseismic deformation model for the 1964 Alaska earthquake. J. Geophys. Res. 2009, 114, B11404. [Google Scholar] [CrossRef]
- Sato, T.; Larsen, C.F.; Miura, S.; Ohta, Y.; Fujimoto, H.; Sun, W.; Motyka, R.J.; Freymuller, J.T. Reevaluation of the viscosity of upper mantle beneath southeast Alaska. Tectonophysics 2011, 511, 79–88. [Google Scholar] [CrossRef]
- Kogan, M.G.; Steblov, G.M. Current global plate kinematics from GPS (1995–2007) with the plate-consistent reference frame. J. Geophys. Res. 2008, 113, B04416. [Google Scholar] [CrossRef]
- Ekström, G.; Nettles, M.; Dziewonski, A.M. The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 2012, 200–201, 1–9. [Google Scholar] [CrossRef]
- Rogozhin, E.A. Application of tectonophysical approaches to the solution of seismotectonic problems by the example of the Simushir earthquakes of November 15, 2006 and January 13, 2007 in Central Kuriles. Izv. Phys. Solid Earth 2013, 49, 643–652. [Google Scholar] [CrossRef]

| Subduction Zone | Block Width/Length, km | Block Length (Frontal/Rear Segment), km | Cycle Period, yrs | Horizontal Coseismic/Aftershock Displacement at Rear Segment, cm |
|---|---|---|---|---|
| Kuril-Kamchatka | 30–100 [15] | 100/100 [15] | 140 ± 60 [23] | 50/50 [19] |
| Japan | 100–150 [24,25] | 200/300 [24,25] | 100–1000 [21,26] | 50–200/10–50 [18] |
| Chile | 100–200 [27,28,29,30] | 100/300 [27,28,29,30] | 63–176 [31] | 5–50/50–80 [17] |
| Contact Layer Thickness, | Stationary Viscosity of the Contact Layer, | Postseismic Viscosity of the Contact Layer, | Interblock Fault Thickness, | Interblock Viscosity, |
|---|---|---|---|---|
| ~0.5 km | ~1019 Pa·s | ~1018 Pa·s | ~1 km | ~4 × 1018 Pa·s |
| Geological+ Geophysical Data [32] | Continuous Medium Model [19] | Mechanical Keyboard Model | Generalized Mechanical Keyboard Model | |
|---|---|---|---|---|
| Seismic cycle duration | 14060 years | 159 years | 60–267 years (av. 136 years) | 40–338 years (av. 162 years) |
| Postseismic stage duration | Up to 35–50 years | 0.5 years (afterslip) up to 10 years (viscoe-lastic relaxation) | 2–7 years | 1–5 years |
| Coseismic horizontal surface displacements | ─ | 55 × 10−2 m (GNSS observations) | 10 × 10−2–1.8 m (depends on distance from trench and magnitude) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobkovsky, L.I.; Vladimirova, I.S.; Gabsatarov, Y.V.; Alekseev, D.A. Keyboard Model of Seismic Cycle of Great Earthquakes in Subduction Zones: Simulation Results and Further Generalization. Appl. Sci. 2021, 11, 9350. https://doi.org/10.3390/app11199350
Lobkovsky LI, Vladimirova IS, Gabsatarov YV, Alekseev DA. Keyboard Model of Seismic Cycle of Great Earthquakes in Subduction Zones: Simulation Results and Further Generalization. Applied Sciences. 2021; 11(19):9350. https://doi.org/10.3390/app11199350
Chicago/Turabian StyleLobkovsky, Leopold I., Irina S. Vladimirova, Yurii V. Gabsatarov, and Dmitry A. Alekseev. 2021. "Keyboard Model of Seismic Cycle of Great Earthquakes in Subduction Zones: Simulation Results and Further Generalization" Applied Sciences 11, no. 19: 9350. https://doi.org/10.3390/app11199350
APA StyleLobkovsky, L. I., Vladimirova, I. S., Gabsatarov, Y. V., & Alekseev, D. A. (2021). Keyboard Model of Seismic Cycle of Great Earthquakes in Subduction Zones: Simulation Results and Further Generalization. Applied Sciences, 11(19), 9350. https://doi.org/10.3390/app11199350






