Abstract
A finite element thermal analysis was conducted in this study with the aim of evaluating the influence of the geometrical parameters of steel sections on their thermal response under solar radiation. Four W12 and W24 standard steel beams were investigated under the solar irradiation conditions of a sunny summer day. The finite element analysis was carried out using COMSOL Multiphysics considering the Sun’s movement from sunrise to sunset, reflected radiation from the ground, surface convection of air and long wave radiation as the main boundary thermal loads. The temperature-time variation at different locations in the sections, vertical temperature distributions, temperature gradient distributions and thermal stress distributions were investigated. The results showed that the daily maximum temperatures, temperature variation, temperature and temperature gradient distributions and thermal stresses are influenced by the geometry of the steel section. The flange width and flange thickness were found to be the controlling parameters during the noon hours, while these parameters in addition to web depth control the shading effect during the afternoon. On the other hand, web thickness affects the temperature of webs at sunrise and sunset times. Geometrical ratios like Wf/H, Wf/tf2 and 2Wf/Htf were the most influential parameters on temperatures, temperature gradients and thermal stresses of steel beams subjected to solar radiation. The investigated section with the maximum Wf/tf2 value of 0.96 (W12 × 58) recorded the highest top-surface noon temperature, while section W24 × 84 with the lowest Wf/tf2 value of 0.60 exhibited the lowest temperature.
1. Introduction
Climate change is becoming more noticeable with time and has been the focus of hundreds of research works during the last few years. It is agreed that climate change and global warming can impact all aspects of human life, including the construction industry [1,2]. Short-duration cold waves were also reported to impose undesirable temperature-induced stresses, especially for large bridge structures [3]. Some types of structures, like bridges, are under the direct influence of climate variations due to their outside exposure [4,5,6]. Wide differences in temperature between seasons could induce larger end displacements for simply-supported superstructures or higher end-restraint moments for continuous spans [7,8,9]. On the other hand, wider daily temperature differences lead to higher vertical and lateral (if any) temperature gradients in the sections, which may induce unfavorable sectional flexural stresses [10,11,12,13,14,15]. Self-equilibrating stresses are the type of stresses that are induced to equilibrate the nonlinear sectional deformations due to nonlinear temperature gradients along the depth or width of a bridge’s superstructure [16]. Previous studies showed that self-equilibrating stresses can be high enough to initiate surface cracking of bridge girders, which impacts the long-term serviceability and results in unplanned rehabilitation costs [10,17]. A recent study [18] on a large span steel space dome showed that seasonal changes of environmental thermal loads can lead to an axial stress of up to 20 MPa.
The geometry and configuration of the bridge superstructure play a major role in the distribution of sectional temperature gradients in both directions or across the thickness of these sections, where lateral gradients are significant in the case of concrete box-girders, while these gradients are noticeably small compared to vertical gradients in precast I-girders. Wider temperature gradients would be imposed in thick sections, while the gradient across the thickness of steel sections is almost zero. Several recent field, experimental and numerical studies aiming to investigate the possible impacts of temperature changes on concrete [19,20,21,22,23,24,25,26] and composite [6,12,27,28,29] girders have been published. However, only a few focused on the influence of geometrical aspects and girder superstructure configuration. Hagedorn et al. [30] constructed three experimental concrete I-girders. The three girders were AASHTO Type-I girders, but with different top flange configurations. Thermocouples were placed in the sections vertically along the webs and horizontally along the flanges. The authors showed that significant temperature gradients were recorded during the pre-deck placement. They concluded that the current design gradient model differs from the recorded gradient distribution, and there is a lack of a model to capture the flanges’ significant lateral gradients. Song et al. [31] constructed an experimental concrete box-girder segment with an unconventional configuration where the bottom flange was noticeably larger and wider than the top flange. The section was instrumented with thermocouples at different locations to evaluate the changes of temperature gradient shape with time. The authors concluded that the design temperature gradient models of most of current bridge codes are not suitable for the tested unconventional configuration. Moreover, their results revealed large lateral temperature gradients that affect the stress distribution in the section. A previous study on concrete I-girders [32] compared the thermal gradients of I-girders during construction (before deck slab placement) and after the placement of deck slab on a parallel series of I-girders. The research revealed that the lateral bottom-flange’s gradient was reduced by 3 °C after slab placement due to the shading effect from the overhanging slab.
The available literature on the influence of the daily and seasonally variation of atmospheric thermal loads on steel sections and girders is limited. A few experimental studies [33,34,35,36,37] have tried to give clearer picture about the behavior of steel sections under direct environmental exposure, while some field works on steel sections and girders were also published during the last years [38,39,40]. However, most of these studies did not pay attention to the effect of sectional properties. Wang et al. [41] showed that steel truss girders exhibited larger transverse temperature gradients compared to vertical ones. Chen et al. [42] instrumented three steel sections of different sectional shapes with thermocouples and left them exposed to solar radiation changes. Rectangular box-section, circular tube section and I-section forms were adopted in their study. Their records showed that there are almost no temperature changes across the sectional plate thickness and along the span of the beams, which a typical result due to the high thermal conductivity and thin walls of steel sections. The authors also concluded that section size is one of the most influential factors affecting the non-uniformity of temperature gradients in such sections, where larger steel sections were predicted to suffer higher temperature changes. Lee et al. [43] showed numerically for steel I-sections that the sectional strength against buckling can be improved by using a larger flange width and thickness. A very recent study [44] on I-steel beams was directed experimentally and numerically to evaluate the influence of the several sectional aspects under environment exposure. The investigated parameters were the section’s shape and its depth, the thickness of section member’s (flange and web), the width of the flanges in addition to size comparisons. The author concluded that larger beams suffer higher temperature gradients by approximately 8 °C. Similarly, for sections with equal flange width and flange thickness, temperature gradients in deep sections are higher than in shallow ones by approximately 7 °C. The author also concluded that the thickness of the flange is an influential factor on the vertical temperature variation.
2. Study Objective
The hourly, diurnal and seasonal variation of air temperature are controlled by the amount of warming from sunrays, which is controlled mainly by the variation of solar radiation intensity. Exposed objects on the Earth’s surface, including bridges, are subjected to time-dependent temperature alterations due to air temperature changes and the radiation from the Sun. Many influential factors can affect the degree of heating or cooling of the different parts of bridges. Among these factors is the sectional configuration of the superstructure. For I-steel girders and members, the depth of the web and width of flanges control the amount of targeting solar radiations on the web by controlling the length of the shaded area, while the thickness of members controls the temperature conductivity from exposed to shaded areas. Figure 1 shows that shading area of the web side facing the Sun (from the top flange) increases as the Sun moves higher in the sky during the morning hours, while the other side is completely shaded. This movement is reversed after mid-day, where the shaded area of the facing side decreases as the Sun moves down towards sunset. Figure 2 shows that for two beams with the same depth and at the same time, increasing top flange width leads to deeper shaded web areas. Shading reduces the heating of the target area as the direct heating from solar radiation is obstructed by the top flange, while the top surface is being heated at a faster rate. Thus, high temperature differences would be induced between the flanges and the web, which as discussed in the previous section, would induce unfavorable thermal stresses. Figure 2 highlights the importance of geometry of the adopted members for steel bridge superstructures, which spots the light on the need of detailed studies on the different candidate sections in such constructions. Standard sections including I-sections, channels, angles and tubes are the most used sections in bridges’ steel and composite superstructures.
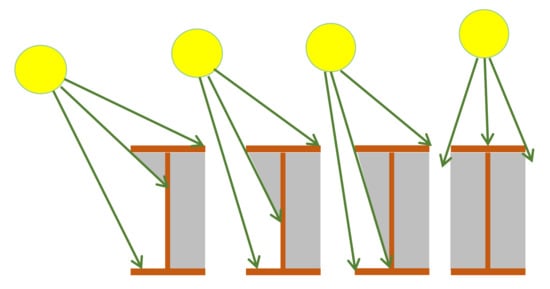
Figure 1.
Web shadowing from top flange.
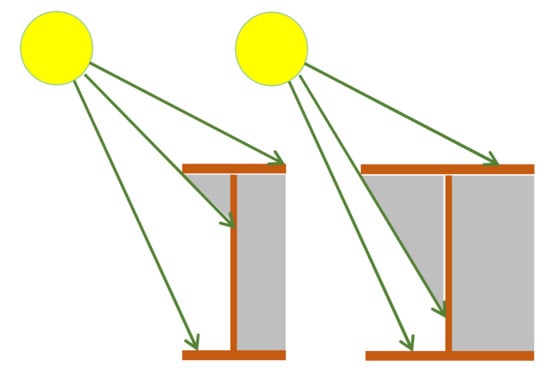
Figure 2.
Effect of flange width on web shadowing.
The literature survey conducted in the Introduction showed that several studies were carried out at the aim of better evaluation of bridge girder thermal response due to climate time-dependent variation, although, the number of experimental and numerical studies on steel girders still lags far behind those on concrete sections. Moreover, despite the importance of geometrical parameters like member depth, width and thickness on temperature sectional variation, very few studies have focused on these parameters. Aiming to fill the knowledge gap in this area, an I-steel beam equipped with temperature sensors was installed in the field and a finite element study was conducted. The main focus of this research is to better understand the combined influence of geometrical parameters as functions of the effective main parameters like depth, width and thickness of sections.
In the steel construction industry, the work may be interrupted for many reasons and for long times, which leaves the structural sections exposed to the changing environmental thermal loads. In the case of extreme thermal conditions, like high summer solar radiation intensity or high daily temperature fluctuation, effective thermal stresses, deformations or movements may be induced in the sections, which require a structural evaluation. This research focuses on the most important geometrical parameters controlling the thermal response of steel members under such conditions. Therefore, the outputs of this research are useful to understand the time-dependent variation of temperatures and stresses in steel sections during the construction period where the whole structure is exposed to open environments.
3. The Experimental Steel Beam
Figure 3 illustrates the sectional and longitudinal dimensions of the steel beam used in this research. As shown, the beam was made from 8 mm thickness steel plates to form an I-shape with 200 mm width flanges and a depth of 500 mm. After instrumentation, the beam was installed in an open field where shadings from all buildings around the field were calculated and found ineffective. A compact weather station composed of three sensors was installed beside the beam as shown in Figure 4a. The first sensor was a temperature probe to measure the shade air temperature (covered by a solar shield), the second was a pyranometer to measure the total solar radiation received by a horizontal surface, while the third was a three-cup anemometer to measure the speed of the wind in the field. The three environmental sensors were provided by Campbell Scientific (Logan, UT , USA) to assure their compatibility of the used data acquisition system that uses a Campbell CR1000 system as the core data logger. The 108-air temperature probe use a thermistor that can accurately measure a temperature range of −5 to +95 °C with an error of approximately ±0.2 to ±0.3 °C. The dome-shaped CS300 silicon type pyranometer was the adopted solar radiation sensor. This sensor can measure a high range of global Sun plus sky radiation reaching 2000 W/m2 with a maximum error of 5%. The three–cup NRG#40 anemometers from NRG system will be used to measure wind speed as shown in Figure 4a. This type of device recommended by Campbell Scientific. The sensor is able to read the wind speed ranging from 0 to 96 m/s (0 to 215 mph). The NRG#40 was the three conical-cups wind sensor used. It measures wind speeds up to 10 m/s with an estimated error of ±0.14 m/s. The three sensors are clearly visible next to the steel beam in Figure 4a.
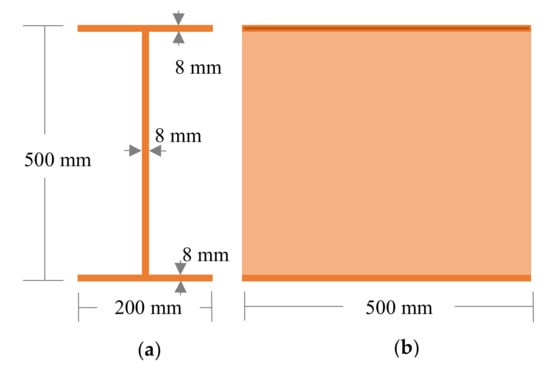
Figure 3.
The steel beam dimensions: (a) Section; (b) Side view.

Figure 4.
The experimental steel beam: (a) Southern view and thermal loads sensors; (b) Northern view and thermocouple locations.
To study the distribution of temperatures in the steel beam, seven type-T thermocouples were installed on the top flange, bottom flange and the northern surface of the web as shown in Figure 4b. The thermocouples are made of copper and constantan, have a measurement range of −200 to 370 °C with an accuracy of ±0.5 °C. Two thermocouples were installed on the top surface (TS) and bottom surface (BS) of the beam, while two thermocouples (TF and BF) were installed on the opposite surfaces of the top and bottom flanges. The rest three thermocouples were installed along the vertical centerline of the beam’s web, which are W1, W2 and W3. The locations of these thermocouples are shown in Figure 4b, while their exact coordinates are listed in Table 1. The coordinates were calculated considering the origin (0, 0) is located at the bottom surface of the bottom flange along the vertical centerline of the web, while all thermocouples were installed at the mid-span section.

Table 1.
Sectional locations of virtual thermocouples.
4. Finite Element Modeling
4.1. Heat Conduction and Thermal Boundary Conditions
As disclosed in Section 2, the main cause of temperature rising is solar radiation which also heats up the air temperature. The warming occurs within light hours, in which the intensity of solar radiation and the temperature of air are functions of time. The radiation from the Sun reaches the exposed surfaces directly as beam rays or indirectly as reflected radiations from the ground and other close surfaces. During the dark night times, the air becomes colder due to the absence of the warming source (Sun), which cools faster than concrete surfaces and works as a cooling load via surface convection. Another cooling load is the heat dissipation from warm surfaces to atmosphere via long-wave radiations. The abovementioned heating and cooling loads summarize the thermal boundary loads that should be simulated in the finite element analysis of externally exposed structures and members, which were all successfully modeled in the current finite element thermal analysis as detailed in previous studies [32,44]. On the other hand, the heat conduction from surfaces to body core during warming time or vice versa during cooling time is the main process, for modeling which the Fourier heat conduction equation (Equation (1)) was utilized. This equation solves for the temperature as a function of time and position (coordinates) and is dependent of material’s density (ρ), specific heat (Cp) and the thermal conductivity (k) [16]:
The convection cooling (qc) between the beam external surfaces and the moving air in the field environment is represented in Equation (2), where Ts represents the temperature of the beam’s surface and Ta represents the air temperature, while h is the convection coefficient, which is represented as a function of wind speed (v). It is important to address the used formula (Equation (3)) for the convection coefficient as there are several empirical formulas in the literature for I-beam sections. This formula was adopted from previous studies where it was used successfully to model the convection between air and beam surfaces:
4.2. Finite Element Thermal Analysis
COMSOL Multiphysics [45] was used in this research to carry out the three-dimensional finite element thermal analysis of the steel beams and modeling of all the boundary conditions, including solar radiation, convection, long-wave radiation, reflected radiation and convection. The volume of the identical geometry of the experimental steel beam was meshed using second order tetrahedral elements with a fine mesh that included 18,730 elements. To apply the radiation boundary conditions, including the built-in solar model, long wave radiation and surface-to-surface radiation, COMSOL automatically generates triangular surface elements. The triangular surface elements are automatically created by the COMSOL surface-to-surface radiation module and are used to apply the radiation boundary conditions including the built-in solar radiation model that account for solar radiation angles and quantities along the day hours, the surface-to-surface radiations and the reflected radiations. The number of generated triangular elements to cover the surfaces of the meshed steel beam was 12,700. As the analysis was conducted by coupling the heat transfer module with the mechanical module, the essential material parameters of both modules should be defined. In the current research, the typical material properties of constructional steel were adopted. The heat capacity, thermal conductivity and density were 475 J/kg·K, 44.5 W/m·K and 7850 kg/m3, respectively, while the elastic modulus and coefficient of thermal expansion were 200 GPa and 12.3 × 10−6 1/K, respectively. The input data (experimental records) of the environmental thermal loads were tabulated for each 30 min along the target day and the preceding two days then loaded into the model. On the other hand, the coordinates of the experimental field, the daily maximum solar radiation intensity and time were fed to the model as required solar model inputs. All runs were started 48 h before the target day to stabilize any possible effects due to the applied initial temperature. To further reduce the effect of the initial temperature, the analysis was started at midnight where the temperature of the beam is almost uniform.
The analysis was conducted in two steps. In the first, the experimental beam was modeled with the exact geometry and orientation of the beam (Figure 5), where the measured solar radiation, air temperature and wind speed data of a selected sunny day from the test period, which was 14 June, were applied. The purpose of this analysis was to verify the conducted thermal analysis with the recorded surface temperatures. In the second step, the verified model was used to analyze two W12 and two W24 standard steel beams using the same conditions (boundary conditions, initial conditions, temperature and radiation loads, materials and so on). However, to evaluate the required geometrical parameters, only the geometry was different between the four beams as detailed in Table 2. Using the comparisons between the distributions and timely variations of temperatures and thermal stresses of the investigated beams, the effective geometrical parameters were investigated. These beams were selected because the beams of each pair have the same depth and different flange widths, which allows to study the shadowing effect on standard sections.
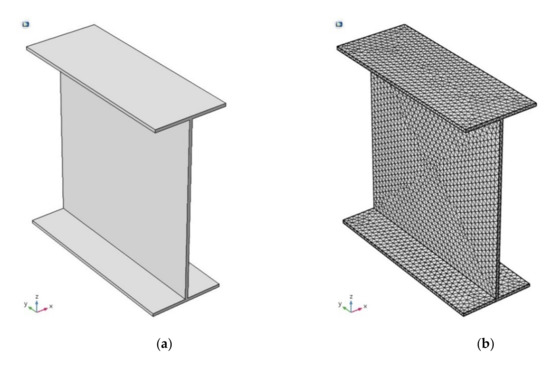
Figure 5.
The finite element model of the experimental beam: (a) Geometry; (b) Mesh.

Table 2.
Dimensions of the analyzed standard steel beams.
4.3. Verification with Experimental Records
As disclosed in the previous sections, the experimental temperature records of the seven thermocouples were used to verify the finite element thermal analysis. Comparisons were made between the predicted temperatures from the finite element analysis at the same locations of the fielded test thermocouples with the recorded test temperatures of these thermocouples. The comparisons were made at 48 time steps, each of 30 min, along the full hours of the selected sunny day, which was 14 June. The test recoding of temperature at time intervals of 30 min allowed for more accurate temperature comparisons with 48 points/day. Figure 6 shows the comparisons of four selected thermocouples, which are the top and bottom surfaces (TS and BS), the top web thermocouples (W1) and the bottom flange one (BF). Figure 6a shows that the behavior of temperature with time of both TS and BS is similar to the experimental behavior with slight differences. The temperature rises during the day hours reaching a maximum range between 11:00 and 14:00, and then drops with time until the temperature is almost equalized at midnight. The differences between the predicted and recorded temperatures of TS and BS were in the range of 0.06 to 4.01 °C within the 48 time steps, which were mostly the highest among the seven thermocouples. Figure 6b shows the comparisons at the web thermocouples W1 (30 mm below the top flange) and BF (top surface of bottom flange). The same above addressed notes can be adopted here, where minor differences can be noticed between the time-dependent variations of predicted and recorded temperatures. The temperature differences at W1 were in the range of 0.07 to 3.81 °C, while those at BF were in the range of 0.06 and 3.93 °C. It should be noticed that the highest differences were occurred at similar time intervals for all thermocouples as shown in Figure 6, which means that differences between temperature gradients are much less. Along the 48 time steps of the selected days, the differences between the recorded and predicted vertical temperature gradients ranged between zero during cold hours and 1.2 °C during shiny hours. The same analysis procedure was also followed and verified recently for different configurations of steel-concrete composite girders and concrete girders [46,47,48,49].
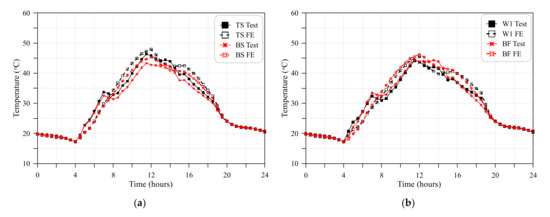
Figure 6.
Verification of predicted finite element temperatures with test records: (a) TS and BS; (b) W1 and BF.
5. Results and Discussion
5.1. Temperature-Time Relations
The hourly temperature-time relations for the investigated day are shown in Figure 7, Figure 8 and Figure 9 for the top surface, bottom surface and web mid-depth for the four ASTM standard sections.
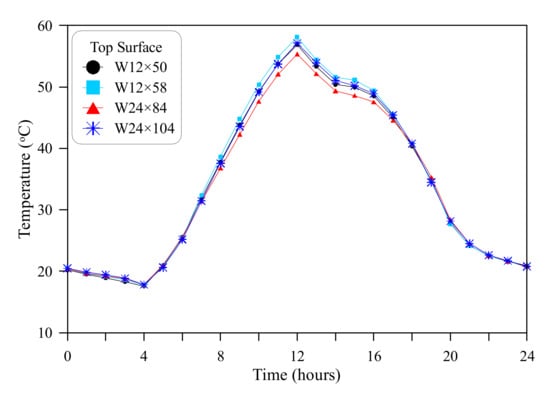
Figure 7.
Temperature-time relations for the top surface of the steel sections.
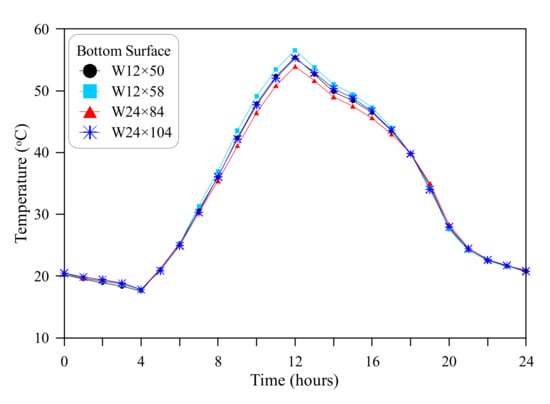
Figure 8.
Temperature-time relations for the bottom surface of the steel sections.
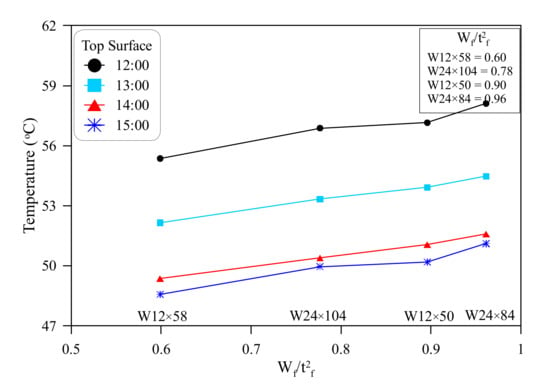
Figure 9.
Relationship between top surface temperature and Wf/tf2 at noon hours.
Figure 7 shows that the top-surface temperatures of the four sections are almost the same during the cold (night) time, which is also obvious for the bottom-surface temperatures as shown in Figure 8. This is mainly attributed to the high thermal conductivity of steel that accelerates heat expulsion from the section core through surfaces. Adding the influence of the small thickness of web and flanges compared to concrete sections, which reduces the heat transfer path resulting in faster cooling. The cooling during the night hours is attributed to the exchange with air via surface convection and the heat dissipation via surface long-wave radiation. Owing to the large surface area to volume ratio of the steel sections, quick surface cooling takes place. After receiving a significant amount of solar radiation beyond 8:00, the top surface gets warmer and differences between the four sections become clearer, especially at the noon hour as shown in Figure 7. However, the differences at this time are not so significant. The W12 sections exhibit the highest temperatures due to the thinner flanges, while W24 × 84 exhibited the lowest temperature owing to its thickest flange among the four sections. The thickness of the top flange of the W12 sections is 16.25 mm, while those of W24 × 104 and W24 × 84 are 19.05 and 19.56 mm, respectively. Thicker section means longer heat transfer time from the heated surface to the section’s core, which means slower gain of temperature. The same observations are applicable for the bottom flange as shown in Figure 8. The bottom flange receives the heating solar radiation from the top surfaces of the flange and the reflected component from the bottom surface of the flange.
The above discussion comparing between the two groups of specimens relies on the sole effect of flange thickness. For better understanding, there should be a physical quantity that can by a good comparison tools between the four sections. The heating of the top surface is not solely affected by flange thickness, where the increase of flange width (Wf) leads to higher accumulated absorbed energy. Thus, both flange width and flange thickness are effective. When the temperature variation behavior at the peak temperature hours (12:00 to 15:00) was compared with the ratio of flange width to flange thickness (Wf/tf), no specific trend was clear, which is mainly due to giving equal weights for both flange width and flange thickness. The flange thickness should be given a higher influence weight as it is the main controller of temperature at this time of day. Therefore, the temperature variations were investigated with the ratio of flange width to the square of flange thickness (Wf/tf2) as shown in Figure 9. It is obvious in the figure that the top surface temperature increases with the increase of the quantity Wf/tf2. The section W12 × 58 with the highest Wf/tf2 value of 0.96 exhibited the highest top surface temperature at noon hours, while the section W24 × 84 with the lowest Wf/tf2 value of 0.60 showed the lowest temperatures at the same time. This means that the top surface temperature increases with the increase of top flange width and the decrease of its thickness but is more affected by flange thickness than flange width.
The temperature variation of the top and bottom surfaces (Figure 7 and Figure 8) is obvious to be uniform with time. Oppositely, Figure 10 shows that the temperature distributions of the mid-depth of the web exhibit some sharp edges that reveal local drop or rise of temperatures. This is attributed to the location of the measured temperature, where the web (especially the upper part) receives solar radiation intensities with different amounts from those received by the top surface. This fluctuation in the received amount of solar radiation, and hence the fluctuation of web temperature is directly attributed to the shading effect from the top flange, where shaded areas receive a much smaller fraction of solar radiation than exposed areas.
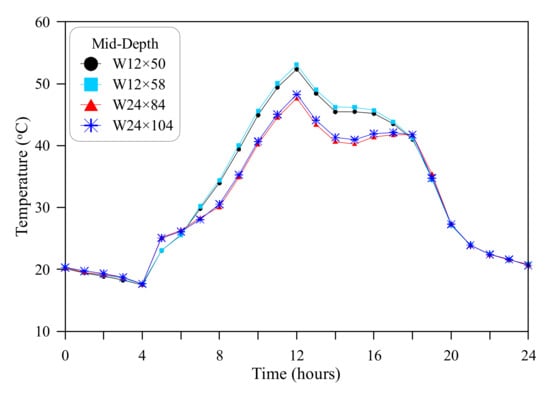
Figure 10.
Temperature-time relations for the mid-depth of the steel sections.
The mid-depth temperature at noon hour is a function of the previously received solar energy during the late morning hours, in addition to the amount of energy transferred from the top surface through web during noon hour. As shown in Figure 10, the noon temperatures is significantly affected by the received solar energy (and hence web temperature) from 8:00 to 12:00. This temperature is also affected by the heat absorbed by the totally exposed top surface, which heats up the web owing to the high thermal conductivity of steel. The amount of received heat by the top surface, as discussed in Figure 7, Figure 8 and Figure 9 is controlled by the top flange width and thickness, while the bath of the mid-depth is half the section’s depth (H/2). Thus, the ration of flange width to the product of flange thickness and H/2, which is Wf/tf × H/2 or more simply 2Wf/Htf, is a key geometrical parameter that shares the heating of this region at noon hour. Figure 11 shows that the temperature of the mid-depth section around noon hour increases with the increase of the quantity 2Wf/Htf. The increasing of flange width and decreasing of flange thickness leads to hooter flange, while shorter path (H/2) leads to faster heating of the mid-depth of the section via top surface. As shown in the figure, although W24 sections have wider flanges, their temperatures were the lowest at noon hours due to their significantly higher depth (H), while the compact depths of W12 sections make the path shorter to heat up their mid-depth.
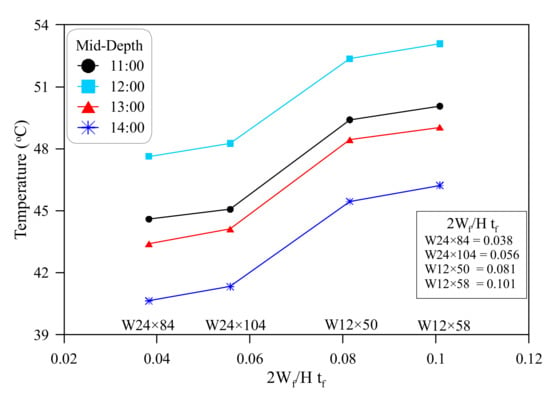
Figure 11.
Relationship between mid-depth temperature 2Wf/Htf at noon hours.
The shading from the top flange plays a controlling role in the variation of web temperature during the afternoon period. In this time, the sun moved from its highest location towards sunset with decreasing solar inclination angles. Therefore, one of the web sides is totally shaded, while the other one is partially shaded under the length effect of the top flange’s overhanging portion. Thus, the increasing of the flange width at a specific time leads to deeper shading effect on the web. However, longer webs are less affected by this shading. Therefore, the temperature variation at this time is controlled by the ratio of flange width to section depth (Wf/H). As shown in Figure 10, the slope of temperature variation after 15:00 is positive for the deep W24 sections, which means that the mid-depth is receiving direct solar radiation at this period. On contrary, the slope of the shallow W12 sections is negative at the same period reflecting a continuous cooling process, which means that the mid-depth is shaded at this time by the top flange. Figure 12 translate this behavior in terms of temperature variation with the geometrical quantity Wf/H. the vertical axis of this figure represents the temperature difference between the subsequent hourly records from 15:00 to 18:00. It is shown in the figure that the slope of temperature variation is positive for the sections with lower shading effect (lower Wf/H), which are the W24 sections, from 15:00 to 17:00 which reflects their heating process at this time. On the other hand, the slopes of the sections with higher shading effect (higher Wf/H) is obviously negative, which refers to a cooling phase at this time due to the shading effect. The temperature variation slope is obvious to decrease with the increase of shading effect (Wf/H) from section W24 × 84 with Wf/H = 0.37 to section W12 × 58 with Wf/H = 0.82.
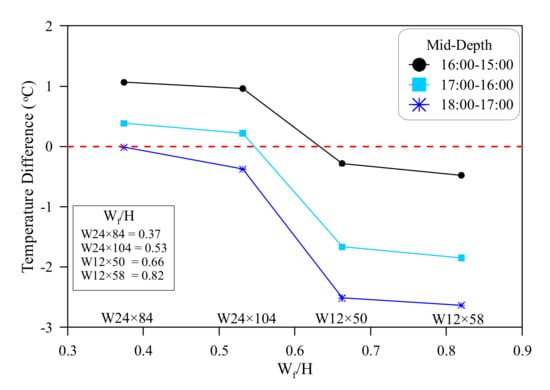
Figure 12.
Relationship between mid-depth temperature and Wf/H at afternoon hours.
5.2. Vertical Temperature Distributions and Gradients
The distributions of temperature along the depth of the four steel sections are presented at sunrise, noon and sunset times in Figure 13a, Figure 14a, Figure 15a, respectively, while their corresponding gradient distributions are shown in Figure 13b, Figure 14b, Figure 15b, respectively. The three figures show that the W12 sections are colder than W24 sections at sunrise and sunset hours, while hotter than W24 sections at noon hour. This is attributed to the thinner web and flanges of W12 sections compared to W24 sections, which facilitates their faster cooling and faster heating.
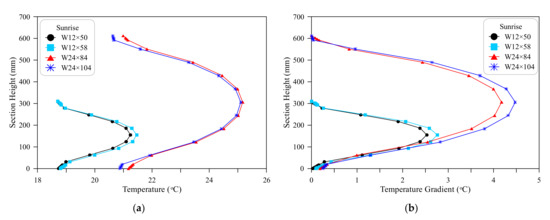
Figure 13.
Vertical temperature distributions and temperature gradients at sunrise: (a) Temperature distributions; (b) Temperature gradients.
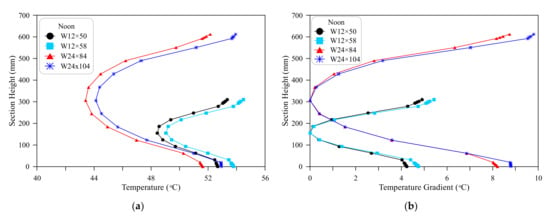
Figure 14.
Vertical temperature distributions and temperature gradients at noon: (a) Temperature distributions; (b) Temperature gradients.
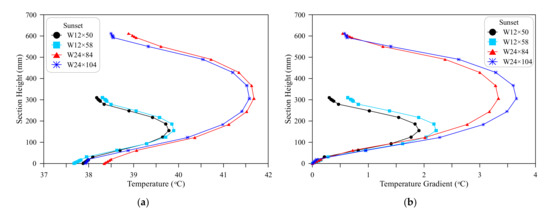
Figure 15.
Vertical temperature distributions and temperature gradients at sunset: (a) Temperature distributions; (b) Temperature gradients.
The effect of shadowing from the top flange is not clear at sunrise and sunset times due to the low inclination angle of sunrays, which reduces or eliminates any influence of overhanging flange portions on web radiation. The slight differences in temperatures and temperature gradients between the beams of each pair of sections shown Figure 13 are attributed to the effects of other geometrical aspects like the thickness of the web and to the already preserved temperatures along the night hours. On the other hand, the effect of shadowing from the flanges overhanging portions becomes more significant after 8:00 morning up to before midday and from approximately 14:00 to 17:00. In summer, the sun moves up in the sky within the early morning hours after sunrise with the angle between sunrays and the horizon increases as time passes until noon. With the increase of solar inclination angle, the amount of crossed radiation by the top flange increases leading to deeper shadow depth down along the web as discussed in Figure 1. At these hours, the top surface is being fully heated by solar radiation, while one side of the web is totally shaded and the other one is mostly shaded, which results in slow heating of the web. The different heating conditions between flanges and web lead to a higher temperature gradient, which increases with the accumulation of this process until midday. For beams with wider flanges compared to depth (flange width/section depth ratio), the effect of shadowing from the top flange becomes more pronounced as shown in Figure 2.
Figure 14a shows that the temperature of W12 × 58 is higher than that of W12 × 50, which is attributed to the larger surface area of the former, where the surface area equals approximately 10,970 mm2 for W12 × 58 and 9420 mm2 for W12 × 50. Similarly, the temperature of W24 × 104 is higher than that of W24 × 84 for the same reason. The surface areas of W24 × 84 and W24 × 104 are approximately 15,940 and 19,740 mm2, respectively. As all thermal loads are surface loads, then larger surface area leads to the absorbing of larger total amount of solar radiation and hence more heat. Figure 14b shows that section W12 × 58 recorded higher temperature gradient than that of W12 × 50, which can be attributed to the wider flange width and smaller thickness as discussed in Figure 9. The larger surface area leads to the increase of the whole body temperature, yet, the wider flange slowed down the heating of the web leading to higher difference with the top surface, which is recorded as larger temperature gradient. The flange widths of sections W12 × 50 and W12 × 58 are 205 and 254 mm, respectively. Since both sections have the same depth of 310 mm, then the flange width/section depth ratios of the two sections equal 0.66 and 0.82, respectively. Thus, increasing this ratio for the same depth increases the vertical temperature gradients at noon hours, and thus increasing the daily maximum positive temperature gradient. This conclusion is confirmed by the results of the larger W24 sections. As it is clear in Figure 14b, the temperature gradient of W24 × 104 is higher than that of W24 × 84. The flange width/section depth ratios of the two sections are 0.53 and 0.37, respectively. It should be noticed that as discussed in the previous section, the noon temperature is affected by the shadowing effect during the preceding late morning hours (after 8:00) and the Wf/tf2 ratio during the noon hours.
After noon, the Sun moves from the highest point in the sky towards its setting position in the horizon. Hence, the solar radiation inclination angle keeps decreasing until sunset. Most of the heating budget of the day hours before sunset comes from low inclination solar radiations that affect majorly on the web. Thus, the temperature of the section during this period relies mainly on the geometrical properties of the web and less on the shading effect of the flange. Therefore, and as shown in Figure 15a, the temperature of the sections with thinner webs are higher than those with thicker webs. It is clear in the figure that the temperature of W12 × 58 (web thickness = 9.14 mm) is higher than that of W12 × 50 with the web thickness of 9.4 mm. Similarly, the temperature of W24 × 84 with web thickness of 11.94 mm is higher than that of W24 × 104 with web thickness of 12.7 mm. On the other hand, the temperature gradient of W24 × 104 is obviously higher than that of W24 × 84 as shown in Figure 15b, which can be attributed to the wider flanges that led to faster long-wave radiation and convection cooling, where these surfaces are not exposed to solar heating during these hours. Consequently, the temperature gradient with the heated web becomes higher. The same result is obvious for the W12 sections, where the W12 × 58 section with wider flange exhibited larger temperature gradient than W12 × 50. Referring to the effect of Wf/H ratio discussed in Figure 12, it is obvious in Figure 15b that W24 sections with lower Wf/H ratio exhibited higher temperature gradients than W12 sections that are of higher Wf/H ratio.
5.3. Thermal Stresses
The nonlinear temperature gradient distributions shown in Figure 13b, Figure 14b, Figure 15b result in the nonlinear stress distributions shown in Figure 16a–c. The uniform temperature change at the centroid of the beam leads to an axial deformation, which is translated into an axial force if restricted. On the other hand, the nonlinear temperature distribution along the depth of the section tends to deform the section nonlinearly, but it is restricted by the adjacent fibers that keep this deformation linear. The difference between the nonlinear free thermal strains, uniform thermal strains and restricted linear strains results in residual nonlinear distribution of what is called as self-equilibrating stresses. Figure 16 shows the distribution of self-equilibrating thermal stresses induced from the temperature gradients of the four investigated sections at sunrise, noon and sunset times. It is obvious that thermal stresses follow approximately similar trend of variation with depth as that of temperature gradients, but with reversed signs because the heated portions (hotter portions) try to elongate, therefore, compression thermal self-equilibrating stresses are induced to arrest this elongation. Oppositely, the tendency of shrinkage at colder portions is restricted by tensile equilibrating stresses. Figure 13b and Figure 15b show that at sunrise and sunset, the webs are hotter than the top and bottom surfaces (negative gradient). Consequently, compression stresses arise in the web while the top and bottom surfaces are under tensile stresses as shown in Figure 16a,c. On the other hand, the opposite occurs for noon thermal stresses, where the hotter top and bottom surfaces exhibit compression stresses, while the maximum tensile stress occurs in the colder web as shown in Figure 16b.
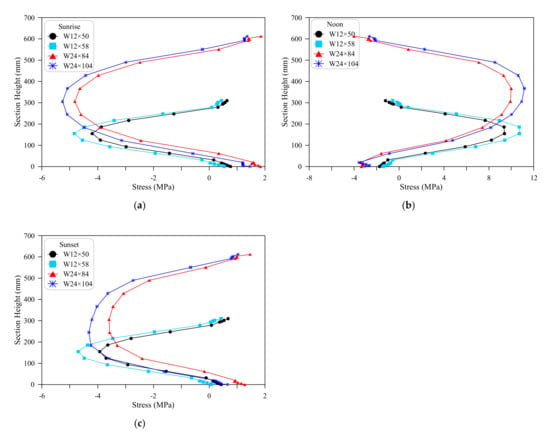
Figure 16.
Thermal stresses of the four sections: (a) At sunrise; (b) At noon; (c) At sunset.
The distributions of stresses shown in Figure 16 confirm the discussed results and the conclusions obtained in the previous sections about the effect of geometrical aspects and shading from top flange. It is shown in Figure 16a that at sunrise, W12 sections are subjected to lower thermal stresses than W24 sections, and sections with larger surface area exhibited lower thermal stresses than those of smaller surface area. Thinner web also leads to faster heating and hence higher stresses at this time. The maximum thermal stress at sunrise in section W12 × 50 equals 4.19 MPa, while that of W12 × 58 equals 4.84 MPa. Similarly, the maximum sunrise thermal stresses of sections W24 × 84 and W24 × 104 are 4.82 and 5.26 MPa, respectively. The maximum stresses at sunrise are compression stresses that are located close to the mid-depth due to the negative temperature gradient at this time. The stress distribution at sunset (Figure 16c) has a similar variation trend to that at sunrise with maximum compression stresses in the web and smaller tensile stresses at top and bottom surfaces. The stresses are noticed to be influenced by the combined effect of the pre-heating of web through top flange during the hot hours before sunset period (as discussed in Figure 11) and the web thickness.
Figure 16b shows the noon stress distribution which differs from those at sunrise and sunset, where it is the result of a positive temperature gradient. Thus, compression stresses are composed at the hotter top and bottom surfaces, while tensile stresses arise in the web. The effect of the flange width to thickness ratio is obvious in the figure, where sections with wider and thinner flanges exhibited larger stresses. It was discussed in Figure 9 that at noon hour, the geometrical ratio Wf/tf2 is the key parameter controlling the heating of the top surface. Hotter surfaces mean larger gradients with the colder webs resulting in higher self-equilibrating stresses. Section W12 × 58 with the wider top flange (Wf/tf = 15.6) exhibited a maximum stress of 10.72 MPa, which is higher that of W12 × 50 (9.39 MPa) that has Wf/tf ratio of 12.62. Similarly, the Wf/tf ratios of sections W24 × 104 and W24 × 84 are 17.07 and 11.71, respectively, and their maximum noon stresses are 11.16 and 9.99 MPa, respectively.
6. Conclusions
During the construction of steel frames of buildings, bridges or industrial structures, the frame might be left exposed to open-field conditions for a long time. With the presence of permanent fluctuating thermal loads like solar radiation and air temperature, unfavorable stresses would be induced, which might be not adequately considered in the design of the structure. The finite element analysis conducted in this study was directed to investigate the influence of geometrical parameters and shadowing effect on temperature gradients and thermal stresses induced from solar radiation in steel beams. Four ASTM standard sections were used to evaluate the effect of the investigated parameters. The results were presented at three distinguished times of solar radiation effect, which are sunrise, noon and sunset. The most important conclusions obtained from this investigation are as follows:
- (1)
- The smaller W12 sections are obviously colder than the bigger W24 sections at sunrise and sunset and hotter than W24 sections at noon hour. This is due to the thinner web and flanges of W12 sections compared to W24 sections, which allows for faster cooling and heating. The temperature gradient along the section depth is controlled by the time-dependent temperature variation, which is strongly affected by the geometrical properties of the steel sections.
- (2)
- The maximum temperature of the top surface at noon hour is mostly affected by the geometrical parameters of the top flange. The maximum temperature increases as the top flange width increases and its thickness decreases. However, this variation is more sensitive to flange thickness than flange width, where the maximum temperature of the top surface was found to be positively correlated to the ratio of flange width to the square of flange thickness (Wf/tf2). Section W12 × 58 with the maximum Wf/tf2 value among the four steel sections (0.96) recorded the highest top surface temperature at noon hour, while the temperature of W24 × 84, which has the lowest Wf/tf2 value of 0.60, was the lowest.
- (3)
- The temperature of the web’s mid-depth at noon hour is mainly due to the huge amount of solar radiation received by the top surface during this period. The influential geometrical parameters are the area and thickness of the heated part, which is the top flange, and the path to the target point, which is the mid-depth of the web. The temperature of the centroid of the web at noon hours increases with the increase of the quantity 2Wf/Htf. The wider and thinner flange results in faster heating, while the shorter path (H/2) leads to faster heat conduction to the web’s centroid from the top surface
- (4)
- The shading from the top flange on the web’s temperature becomes effective during afternoon hours. Wider flanges impose deeper shadows that reduce the temperature of the web, while deeper sections are less influenced by flange’s shading. The variation of temperature during afternoon hours affects that at sunset and is affected by the geometrical ratio of flange width to flange thickness (Wf/H).
- (5)
- The vertical thermal stress distributions are directly influenced by the nonlinear temperature gradients at the same times. In addition, their maximum values are also related to the geometrical parameters that affect the heat transfer and temperature variation during the heating and cooling phases. The thicknesses of web and flange and the ratio of flange width to flange thickness are the most influential parameters.
Author Contributions
Conceptualization, S.R.A.; Data curation, J.X. and J.L.; Formal analysis, J.X. and Y.L.; Funding acquisition, B.B.; Investigation, S.R.A. and T.S.A.-G.; Methodology, S.R.A. and T.S.A.-G.; Project administration, Y.L. and B.B.; Resources, S.R.A. and B.B.; Software, S.R.A.; Supervision, S.R.A. and B.B.; Validation, Y.L., J.L. and B.B.; Visualization, S.R.A. and J.X.; Writing—original draft, S.R.A. and Y.L.; Writing—review & editing, J.X., Y.L. and B.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (51778148) and the National Natural Science Foundation of China (51508103).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would also thank Mustafa Özakça for his support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Nasr, A.; Kjellstrom, E.; Bjornsson, I.; Honfi, D.; Ivanov, O.L.; Johansson, J. Bridges in a changing climate: A study of the potential impacts of climate change on bridges and their adaptations. Struct. Infrastruct. Eng. 2020, 16, 738–749. [Google Scholar] [CrossRef]
- Khotbehsara, M.M.; Manalo, A.; Aravinthan, T.; Turner, J.; Ferdous, W.; Hota, G. Effects of ultraviolet solar radiation on the properties of particulate-filled epoxy based polymer coating. Polym. Degrad. Stab. 2020, 181, 109352. [Google Scholar] [CrossRef]
- Gu, B.; Chen, Z.; Chen, X. Temperature gradients in concrete box girder bridge under effect of cold wave. J. Cent. South Univ. 2014, 21, 1227–1241. [Google Scholar] [CrossRef]
- Giussani, F. The effects of temperature variations on the long-term behaviour of composite steel-concrete beams. Eng. Struct. 2009, 31, 2392–2406. [Google Scholar] [CrossRef]
- Abid, S.R.; Tayşi, N.; Özakça, M. Experimental analysis of temperature gradients in concrete box girders. Constr. Build. Mater. 2016, 106, 523–532. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Jiang, L.; Zhang, N. Long-term field test of temperature gradients on the composite girder of a long-span cable-style bridge. Adv. Struct. Eng. 2019, 22, 2785–2798. [Google Scholar] [CrossRef]
- Zhou, G.D.; Yi, T.H. Thermal loads in large-scale bridges: A state-of-the-art review. Int. J. Distrib. Sens. Netw. 2013, 9, 217983. [Google Scholar] [CrossRef]
- Abid, S.R.; Mussa, F.; Tayşi, N.; Özakça, M. Experimental and finite element investigation of temperature distributions in concrete-encased steel girders. Struct. Control Health Monit. 2018, 25, 1–23. [Google Scholar] [CrossRef]
- Lin, J.H.; Briseghella, B.; Xue, J.Q.; Tabatabai, H.; Huang, F.Y.; Chen, B.C. Temperature monitoring and response of deck-extension side-by-side box-girder bridges. J. Perform. Constr. Facil. 2020, 34, 04019122. [Google Scholar] [CrossRef]
- Elbadry, M.; Ghali, A. Thermal stresses and cracking of concrete bridges. ACI J. 1986, 83, 1001–1009. [Google Scholar]
- Wang, H.; Zhang, Y.M.; Mao, J.X.; Wan, H.P.; Tao, T.Y.; Zhu, Q.X. Modeling and forecasting of temperature-induced strain of long-span bridge using an improved Bayesian dynamic linear model. Eng. Struct. 2019, 192, 220–232. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.J.; Zhang, G.J.; Jiang, L.; Yan, X.K. Prediction formula for temperature gradient of concrete-filled steel tubular member with an arbitrary inclination. J. Bridge Eng. 2020, 25, 0402007. [Google Scholar] [CrossRef]
- Lucas, J.M.; Berred, A.; Louis, A. Thermal actions on a steel box girder bridge. Struct. Build. ICE Proc. 2003, 156, 175–182. [Google Scholar] [CrossRef]
- Nandan, H.; Singh, M. Effects of thermal environment on structural frequencies: Part 1-A simulation study. Eng. Struc. 2014, 81, 480–490. [Google Scholar] [CrossRef]
- Kong, B.; Cai, C.S.; Pan, F. Thermal field distributions of girder bridges with GFRP panel deck versus concrete deck. J. Bridge Eng. 2014, 19, 04014046. [Google Scholar] [CrossRef]
- Ghali, A.; Favre, R.; Elbadry, M. Concrete Structures: Stresses and Deformation, 3rd ed.; E & FN Spon: London, UK, 2002. [Google Scholar]
- Tayşi, N.; Abid, S.R. Temperature distributions and variations in concrete box-girder bridges: Experimental and finite element parametric studies. Adv. Struct. Eng. 2015, 18, 469–486. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, H.; Chen, Z. Thermal behavior of large-span reticulated domes covered by ETFE membrane roofs under solar radiation. Thin Wall. Struct. 2017, 115, 1–11. [Google Scholar] [CrossRef]
- Kulprapha, N.; Warnitchai, P. Structural health monitoring of continuous prestressed concrete bridges using ambient thermal responses. Eng. Struct. 2012, 40, 20–38. [Google Scholar] [CrossRef]
- Lee, J.H. Investigation of extreme environmental conditions and design thermal gradients during construction for prestressed concrete bridge girders. J. Bridge Eng. 2012, 17, 547–556. [Google Scholar] [CrossRef]
- Zhao, L.; Zhou, L.Y.; Zhang, G.C.; Wei, T.Y.; Mahunon, A.D.; Jiang, L.Q.; Zhang, Y.Y. Experimental study of the temperature distribution in CRTS-II ballastless tracks on a high-speed railway bridge. Appl. Sci. 2020, 10, 1980. [Google Scholar] [CrossRef] [Green Version]
- Abid, S.R.; Tayşi, N.; Özakça, M. Temperature Records in Concrete Box-Girder Segment Subjected to Solar Radiation and Air Temperature Changes. IOP Conf. Ser. Mater. Sci. Eng. 2020, 870, 012074. [Google Scholar] [CrossRef]
- Lin, J.H.; Xue, J.Q.; Huang, F.Y.; Chen, B.C. Research on the thermal boundary conditions of concrete closed girder cross-sections under historically extreme temperature conditions. Appl. Sci. 2020, 10, 1274. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.Q.; Briseghella, B.; Lin, J.H.; Huang, F.Y.; Chen, B.C. Design and field tests of a deck-extension bridge with small box-girder. J. Traffic Transp. Eng. 2018, 5, 467–479. [Google Scholar] [CrossRef]
- Gottsater, E.; Ivanov, L. Spatial temperature differences in portal frame bridges. Struct. Eng. Int. 2019, 30, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Xue, J.Q.; Lin, J.H.; Briseghella, B.; Tabatabai, H.; Chen, B.C. Solar radiation parameters for assessing temperature distributions on bridge cross-sections. Appl. Sci. 2020, 8, 627. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.Y.; Liu, Y.J.; Liu, J.; Yuan, Z.Y.; Zhang, G.J.; Ma, Z.Y. Validation of long-term temperature simulations in a steel-concrete composite girder. Structures 2020, 27, 1962–1976. [Google Scholar] [CrossRef]
- Mussa, F.; Abid, S.R.; Tayşi, N. Winter Temperature Measurements in a composite girder segment. IOP Conf. Ser. Mater. Sci. Eng. 2020, 888, 012074. [Google Scholar] [CrossRef]
- Lu, H.L.; Hao, J.; Zhong, J.W.; Wang, Y.F.; Yang, H.Y. Analysis of sunshine temperature field of steel box-girder based on monitoring data. Adv. Civ. Eng. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Hagedorn, R.; Marti-Vargas, J.R.; Dang, C.N.; Hale, W.M.; Floyd, R.W. Temperature gradients in bridge concrete I-girders under heat wave. J. Bridge Eng. 2019, 24, 04019077. [Google Scholar] [CrossRef]
- Song, Z.W.; Xiao, J.Z.; Shen, L.M. On temperature gradients in high-performance concrete box girder under solar radiation. Adv. Struct. Eng. 2012, 15, 399–415. [Google Scholar] [CrossRef]
- Abid, S.R. Three-dimensional finite element temperature gradient analysis in concrete bridge girders subjected to environmental thermal loads. Cogent Eng. 2018, 5, 1–15. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Y.; Lin, C. Experimental study on the temperature of steel members in sunshine. J. Build. Struct. 2010, 31, 140–147. [Google Scholar]
- Liu, H.; Chen, Z.; Zhou, T. Numerical and experimental investigation on the temperature distribution of steel tubes under solar radiation. Struct. Eng. Mech. 2012, 43, 725–737. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Z.; Zhou, T. Theoretical and experimental study on the temperature distribution of H-shaped steel members under solar radiation. Appl. Therm. Eng. 2012, 37, 329–335. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Z.; Zhou, T. Investigation on temperature distribution and thermal behavior of large span steel structures considering solar radiation. Adv. Steel Construct. 2013, 9, 41–58. [Google Scholar]
- Chen, D.; Wang, H.; Qian, H.; Li, X.; Fan, F.; Shen, S. Experimental and numerical investigation of temperature effects on steel members due to solar radiation. Appl. Therm. Eng. 2017, 127, 696–704. [Google Scholar] [CrossRef]
- Kim, S.H.; Park, S.J.; Wu, J.; Won, J.H. Temperature variation in steel box girders of cable-stayed bridges during construction. J. Construct. Steel Res. 2015, 112, 80–92. [Google Scholar] [CrossRef]
- Arabi, S.; Shafei, B.; Phares, B.M. Investigation of fatigue in steel sign-support structures under diurnal temperature changes. J. Construct. Steel Res. 2019, 153, 286–297. [Google Scholar] [CrossRef]
- Zhao, H.W.; Ding, Y.L.; Nagarajaiah, S.; Li, A.Q. Behavior analysis and early age warning of girder deflections of a steel-truss arch railway bridge under the effects of temperature and trains: Case study. J. Bridge Eng. 2019, 24, 05018013. [Google Scholar] [CrossRef]
- Wang, G.; Ding, Y. Reliability estimation of horizontal rotation at beam end of long-span continuous truss bridge affected by temperature gradients. J. Perform. Constr. Facil. 2019, 33, 04019061. [Google Scholar] [CrossRef]
- Chen, D.; Qian, H.; Wang, H.; Chen, Y.; Fan, F.; Shen, S. Experimental and numerical investigation on the non-uniform temperature distribution of thin-walled steel members under solar radiation. Thin Wall. Struct. 2018, 122, 242–251. [Google Scholar] [CrossRef]
- Lee, J.; Jeong, Y.; Kim, W. Buckling behavior of steel girder in integral abutment bridges under thermal loadings in summer season during deck replacement. Int. J. Steel Struct. 2016, 16, 1071–1082. [Google Scholar] [CrossRef]
- Abid, S.R. Temperature variation in steel beams subjected to thermal loads. Steel Compos. Struct. 2020, 34, 819–835. [Google Scholar]
- COMSOL. COMSOL Multiphysics User’s Guide; COMSOL Multiphysics v 4.3; COMSOL: Stockholm, Sweden, 2012. [Google Scholar]
- Mussa, F.; Abid, S.R. Investigation of temperature gradients in composite girders in the southern region of the black sea. IOP Conf. Ser. J. Phys. 2021, 1895, 012069. [Google Scholar] [CrossRef]
- Abid, S.R.; Tayşi, N.; Özakça, M.; Xue, J.; Briseghella, B. Finite element thermo-mechanical analysis of concrete box-girders. Structures 2021, 33, 2424–2444. [Google Scholar] [CrossRef]
- Mussa, F.; Abid, S.R.; Tayşi, N. Design temperatures for composite concrete-steel girders: A-verification of the finite element model. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1090. [Google Scholar] [CrossRef]
- Mussa, F.; Abid, S.R.; Tayşi, N. Design temperatures for composite concrete-steel girders: B-case study. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1090, 012109. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).