A Dynamic Methodology for Setting Up Inspection Time Intervals in Conditional Preventive Maintenance
Abstract
:1. Introduction
2. Materials and Methods
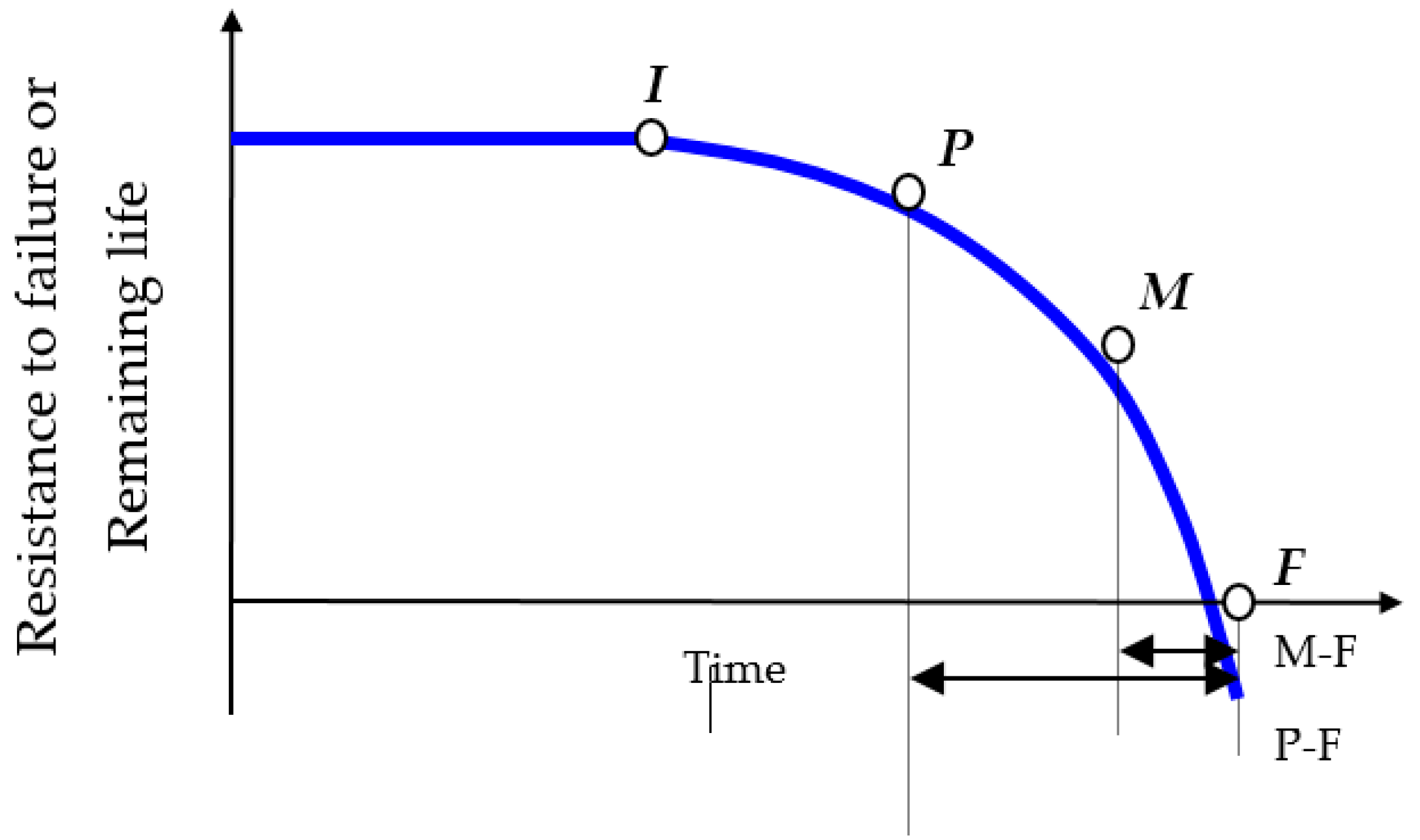
2.1. Determination of an Optimal Inspection Calendar
- ⯀
- when α < 1, (tn+1 − tn) < (tn+2 − tn+1), and the risk function h(t) decreases;
- ⯀
- when α = 1, (tn+1 − tn) = (tn+2 − tn+1), and the risk function h(t) is constant; and
- ⯀
- when α > 1, (tn+1 − tn) > (tn+2 − tn+1), and the risk function h(t) increases.
2.2. Equating All Pertinent Costs
- ⯀
- , the cost of each inspection;
- ⯀
- , the cost of repairing or replacing a potential failure at any time or at moment Tp;
- ⯀
- , the cost of a functional failure due to repair or replace and lost production; and
- ⯀
- , the cost of degradation incurred over time.
- ⯀
- Inspections cost supposed to be performed at moments Mn;
- ⯀
- Opportunity cost due to the built up of production degradation;
- ⯀
- Repair cost of a potential failure, which may or may not happen;
- ⯀
- Consequence cost of a functional failure (repair and loss of production), which may or may not happen.
2.3. Expected Cost of a Functional Failure
2.4. Expected Repair Cost of a Potential Failure
2.5. Expected Cost of Inspections
2.6. Expected Cost of Lost Production
2.7. Expected Cost Per Time Unit
3. Results
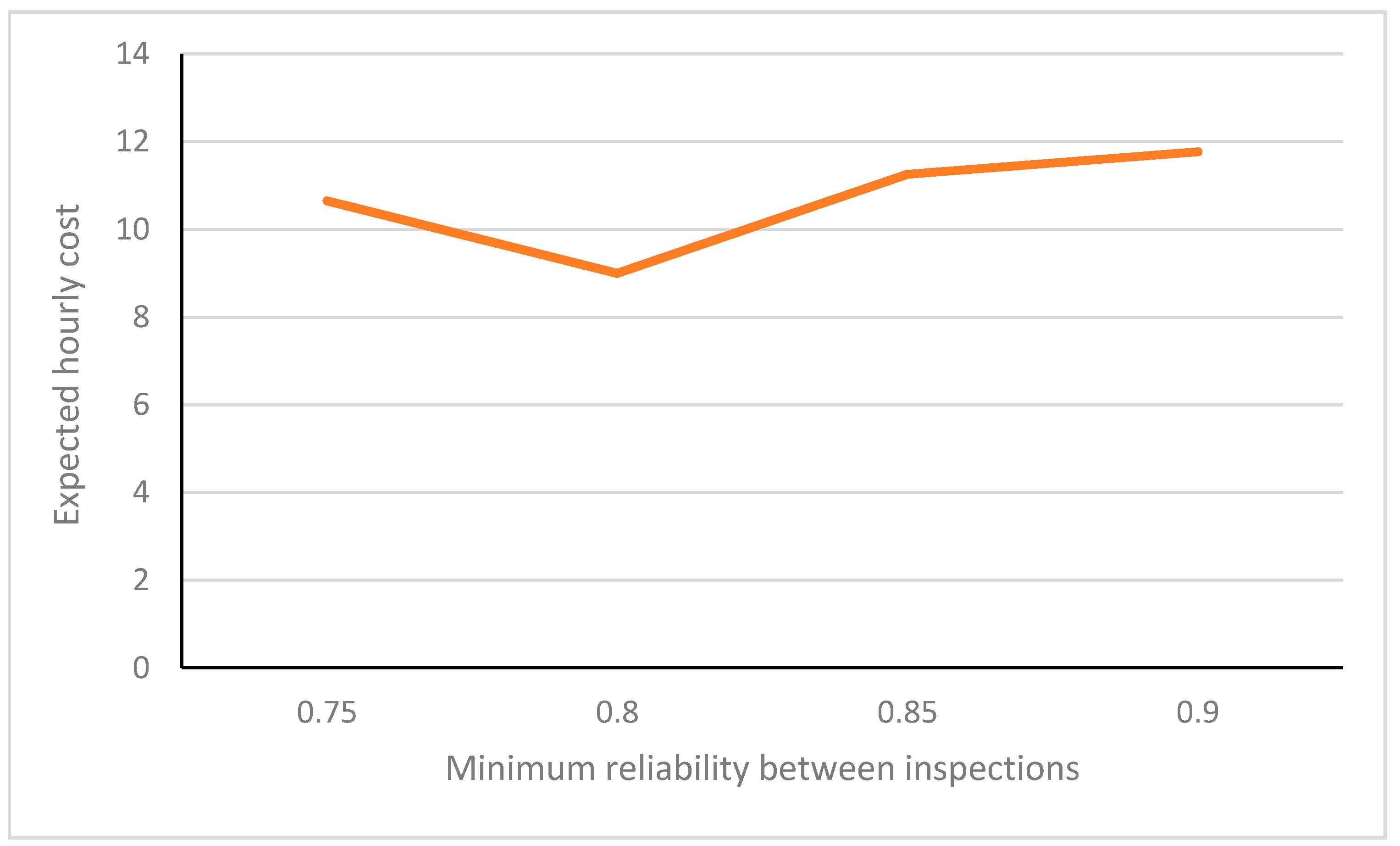
The Search for Optimality
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | |
| ITR | Interest Tax Rate |
| MTTF | Mean Time To Failure |
| MTTR | Mean Time To Repair (or Replace) |
| STW | Safe Time Window |
| TTF | Time To Failure |
| TTR | Time To Repair (Replace or Recover) |
| UTW | Unsafe Time Window |
| Notation | |
| α | Weibull shape parameter |
| β | Weibull scale parameter |
| Total expected cost | |
| Failure expected cost | |
| Repair expected cost | |
| Inspections expected cost | |
| Degraded production expected cost | |
| f(t) | Failure density function |
| F | Moment of a functional failure |
| F(t) | Probability of failure |
| F(tn-t|t) | Conditional probability of failure in the interval (tn − t) given age t has been attained |
| F′(t) | Prior probability of a failure being in progress despite the test has been negative |
| F″(t) | Subsequent probability of a failure being in progress despite the test has been negative with a confidence level of Pc |
| h(t) | Hazard function |
| H | Today |
| M-F | Minimum time span to prevent a functional failure after a potential failure has been detected |
| Mn | Moments of inspection or start of an unsafe time window |
| n* | Order number of the STW from which a potential failure will be surely noticed |
| N | Number of inspections that took place until moment Tp |
| P | Moment of detection of a potential failure |
| P-F | Time span between a potential failure and a functional failure |
| Pn | Start of a safe time window |
| Pt | Accuracy of the test |
| Pt(T−|Fs) | Likelihood of a false negative in a test |
| Pt(T+|Fn) | Likelihood of a false positive in a test |
| R(t) | Reliability to the moment t |
| R(Δt|t) | Conditional reliability in the time interval Δt, given age t is accumulated |
| t0 | Weibull location parameter |
| Tp | Scheduled moment for overhauling |
| Expected life until the occurrence of the functional failure | |
| Expected life until the occurrence of the potential failure | |
| Expected life until moment Tp | |
| Total expected life | |
References
- Dieulle, L.; Berenguer, C.; Grall, A.; Roussignol, M. Continuous time predictive maintenance scheduling for a deteriorating system. In Proceedings of the Annual Reliability and Maintainability Symposium, Philadelphia, PA, USA, 22–25 January 2001; pp. 150–155. [Google Scholar]
- Jamali, M.A.; Ait-Kadi, D.; Cléroux, R.; Artiba, A. Joint optimal periodic and conditional maintenance strategy. J. Qual. Maint. Eng. 2005, 11, 107–114. [Google Scholar] [CrossRef]
- Garg, A.; Deshmukh, S.G. Maintenance management: Literature review and directions. J. Qual. Maint. Eng. 2006, 12, 205–238. [Google Scholar] [CrossRef]
- Greenough, R.M.; Grubic, T. Modelling Condition-Based Maintenance to Deliver a Service to Machine Tool Users. Int. J. Adv. Manuf. Technol. 2011, 52, 1117–1132. [Google Scholar] [CrossRef]
- Rosmaini, A.; Kamaruddin, S. An overview of time-based and condition-based maintenance in industrial application. Comput. Ind. Eng. 2012, 63, 135–149. [Google Scholar]
- Elsayed, A. Reliability Engineering; Addison Wesley Longman: New York, NY, USA, 1996. [Google Scholar]
- Moubray, J. Reliability-Centered Maintenance, 2nd ed.; Industrial Press: New York, NY, USA, 1997. [Google Scholar]
- Wang, W. An inspection model for a process with two types of inspections and repairs. Reliab. Eng. Syst. Saf. 2009, 94, 526–533. [Google Scholar] [CrossRef]
- Barker, C.T.; Newby, M.J. Optimal non-periodic inspection for a multivariate degradation model. Reliab. Eng. Syst. Saf. 2009, 94, 33–43. [Google Scholar] [CrossRef]
- Li, W.; Pham, H. Reliability modeling of multi-state degraded systems with multi-competing failures and random shocks. IEEE Trans. Reliab. 2005, 54, 297–303. [Google Scholar] [CrossRef]
- Mathew, S. Optimal inspection frequency—A tool for maintenance planning/forecasting. Int. J. Qual. Reliab. Manag. 2004, 21, 763–771. [Google Scholar] [CrossRef]
- Rouhan, A.; Schoefs, F. Probabilistic modeling of inspection results for offshore structures. Struct. Saf. 2003, 25, 379–399. [Google Scholar] [CrossRef] [Green Version]
- Badía, F.G.; Berrade, M.; Campos, C.A. Optimal inspection and preventive maintenance of units with revealed and unrevealed failures. Reliab. Eng. Syst. Saf. 2002, 78, 157–163. [Google Scholar] [CrossRef]
- Baohe, S. An optimal inspection and diagnosis policy for a multi-mode system. Reliab. Eng. Syst. Saf. 2020, 76, 181–188. [Google Scholar] [CrossRef]
- Kuntz, P.A.; Christie, R.D.; Venkata, S.S. A reliability centered optimal visual inspection model for distribution feeders. IEEE Trans. Power Deliv. 2001, 16, 718–723. [Google Scholar] [CrossRef]
- Bahrami-Ghasrchami, K.; Price, J.W.H.; Mathew, J. Optimum inspection frequency for manufacturing systems. Int. J. Qual. Reliab. Manag. 1998, 15, 250–258. [Google Scholar] [CrossRef]
- Wang, W.; Christer, A.H. Towards a general condition-based maintenance model for a stochastic dynamic system. J. Oper. Res. Soc. 2000, 51, 145–155. [Google Scholar] [CrossRef]
- Wang, W. Modelling condition monitoring intervals: A hybrid of simulation and analytical approaches. J. Oper. Res. Soc. 2003, 54, 273–282. [Google Scholar] [CrossRef]
- De Jonge, B.; Scarf, P.A. A review on maintenance optimization. Eur. J. Oper. Res. 2020, 285, 805–824. [Google Scholar] [CrossRef]


| Order of Inspection (n) | Moments of Inspection (Mn) | Time Intervals between Inspections | Moments (Pn−1) | Probability of a Functional Failure (Pn − Mn-1) | Failure Expected Cost | Inspection Expected Cost | Repair Expected Cost | Degraded Production Expected Cost |
|---|---|---|---|---|---|---|---|---|
| 1 | 2597 | 2597 | 2147 | 0.009462 | 969 | 165 | 1127 | 0 |
| 2 | 3672 | 1076 | 3222 | 0.052975 | 5176 | 745 | 1445 | 60 |
| 3 | 4498 | 825 | 4048 | 0.038167 | 3640 | 994 | 1587 | 82 |
| 4 | 5193 | 696 | 4743 | 0.027059 | 2531 | 1181 | 1640 | 102 |
| 5 | 5806 | 613 | 5356 | 0.018516 | 1703 | 1316 | 1640 | 120 |
| 6 | 6361 | 554 | 5911 | 0.011877 | 1077 | 1409 | 1606 | 136 |
| 7 | 6870 | 510 | 6420 | 0.006699 | 599 | 1468 | 1551 | 149 |
| 8 | 7345 | 474 | 6895 | 0.002660 | 235 | 1499 | 1482 | 161 |
| 9 | 7795 | 450 | 7345 | 0 | 0 | 1522 | 1405 | 172 |
| 10 | 8245 | 450 | 7795 | 0 | 0 | 1595 | 1319 | 191 |
| 11 | 8695 | 450 | 8245 | 0 | 0 | 1640 | 1227 | 208 |
| 12 | 9145 | 450 | 8695 | 0 | 0 | 1657 | 1130 | 224 |
| 13 | 9595 | 450 | 9145 | 0 | 0 | 1648 | 1032 | 237 |
| 14 | 10,045 | 450 | 9595 | 0 | 0 | 1615 | 934 | 248 |
| 15 | 10,495 | 450 | 10,045 | 0 | 0 | 1562 | 839 | 256 |
| 16 | 10,945 | 450 | 10,495 | 0 | 0 | 10,864 | 5439 | 1894 |
| 0.167418 | EUR 15931 | EUR 30881 | EUR 25404 | EUR 4238 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Assis, R.; Marques, P.C. A Dynamic Methodology for Setting Up Inspection Time Intervals in Conditional Preventive Maintenance. Appl. Sci. 2021, 11, 8715. https://doi.org/10.3390/app11188715
Assis R, Marques PC. A Dynamic Methodology for Setting Up Inspection Time Intervals in Conditional Preventive Maintenance. Applied Sciences. 2021; 11(18):8715. https://doi.org/10.3390/app11188715
Chicago/Turabian StyleAssis, Rui, and Pedro Carmona Marques. 2021. "A Dynamic Methodology for Setting Up Inspection Time Intervals in Conditional Preventive Maintenance" Applied Sciences 11, no. 18: 8715. https://doi.org/10.3390/app11188715
APA StyleAssis, R., & Marques, P. C. (2021). A Dynamic Methodology for Setting Up Inspection Time Intervals in Conditional Preventive Maintenance. Applied Sciences, 11(18), 8715. https://doi.org/10.3390/app11188715







