Abstract
In periodic condition monitoring, the main problem lies in determining the inspection time intervals. This paper presents a new method for setting an optimum calendar to inspect a critical component that fails due to wear and tear as described by a Weibull probability function. By considering a set of inspection intervals, such that reliability between every two inspections is kept equal or below a pre-set threshold while keeping the total costs of inspection, degraded production, consequences of failure, and repair to a minimum. The resulting calendar may be adjusted dynamically over time as inspections take place and test results are found to be negative, by considering the inspector’s confidence in the test and the likelihood of the method’s yielding false negatives. Consequently, the method becomes self-adjustable as it returns a new calendar after the observations of each test are known and properly interpreted. There are several studies that deal with this issue, but none addresses the concept of safe and unsafe time windows which results from merging two other concepts: descendant inspection time intervals and the time delay between a potential failure and a functional failure (the P-F period).
1. Introduction
A critical component of an equipment unit under preventive maintenance (PM) is periodically replaced or repaired, either alone or with other critical components to take advantage of equipment stoppage for that purpose. This PM policy has been replaced over the past few years by a predictive (condition-based) maintenance (PdM) policy, which has proven to be more cost-effective. In the processing industry, PdM is much preferred due to the severe consequences of shutdowns [1,2,3]. PdM can be performed on-line and off-line, the latter consisting mainly of periodic inspections and deciding whether to stop or proceed until the next inspection based on the results. This conclusion is often doubtful as a false negative may result, depending on the accuracy of the test and the inspector’s confidence in it [4,5].
In many cases the onset of a failure is not immediately noticed. Instead, the inspection reveals some signal that a failure is about to occur (potential failure). If nothing is done, it will evolve and give rise to a functional failure after some time. This issue is often addressed as the P-F time interval. The more accurate the measuring method, the longer the P-F time interval might be. On the other hand, inspections must be carried out at times when a minimum reliability threshold is observed between successive inspections. This gives rise to decreasing time intervals when a degradation failure mode is addressed to prevent a failure in progress from going unnoticed. If these two concepts (P-F period and decreasing time intervals) are merged, a series of safe and unsafe time windows is obtained. Inspections might represent a high cost, particularly when production must be interrupted, but the voluntary shutdown of an equipment unit for preventive replacement of a critical component might also incur a high cost, which leads to the event’s being postponement as much as possible. If this is the case, the likelihood of a failure increases progressively as does the degraded production cost. This suggests that all these costs must be properly equated and balanced in accordance with all safe and unsafe time windows. A particular reliability threshold might exist such that a global minimum cost might be achieved [6,7].
In this paper, a numerical method to determine an optimum set of dates (“calendar”) for inspections is demonstrated. The method assumes that the failure mode behavior under consideration is described by a Weibull probability function. The method also takes into consideration the loss of monetary value over time. The method is suitable for a first phase where a preliminary calendar is based on prior probabilities of failure and the cost is evaluated for budgetary or bidding purposes. A second phase will take place if the result of an inspection is negative at which time the calendar will be reformulated in view of the accuracy of the test and the inspector’s confidence in the prevailing test conditions. In other words, the calendar must be adjusted to consider the subsequent probabilities of failure, given the results of the test observations. The recalculation of the calendar after each inspection is definitively a dynamic attribute of the proposed method.
In the literature, several researchers have addressed this issue. Cost optimization is often the main approach for determining time inspection intervals. Wang [8] developed an optimization model for a process with two types of inspections and repairs to minimize the expected cost from a time delay. Barker and Newby (2009) [9] aimed at optimizing a non-periodic inspection policy by evaluating the expected lifetime costs with the use of a multivariate stochastic process. Li and Pham [10] proposed a model to estimate the optimum policy for minimizing the average long-run maintenance cost rate for systems with multiple competing processes. Mathew [11] assumed that for the frequency of inspections to be optimal, it had to exactly match the failure rate of the equipment, so he proposed an optimal inspection frequency model to be used as a tool for planning and forecasting maintenance costs that uses a cost rate factor. Rouhan and Shoefs [12] evaluated the global cost of inspection planning for offshore structures based on decision and detection theories and included both the probability of false alarms and detection. Revealed and unrevealed failures were tackled by Badía et al. [13] whose objective was to minimize the cost per unit time over an infinite time span by selecting a unique interval for both inspection and maintenance. Bahoe [14] formulated an optimal inspection and diagnosis policy for a multimode system through the optimization of expected total profit and proposed reliability indices. Kuntz et al. [15] presented a Markov model for visual inspections of distribution feeders in electric power distribution systems, where the objective was to minimize the total cost of inspection, repair, and reliability. Bahrami-Ghasrchami, Price and Mathew [16] derived an optimal inspection frequency model that minimizes downtime cost based on a three-layered structure for decreasing, constant or increasing hazard rates. Wang and Christer [17] suggested cost, downtime, or reliability as optimization criteria to determine the optimal critical level and inspection interval, based on a random coefficient growth model where coefficients follow known distributions functions. Wang [18] presented five cost criteria functions in a model for optimal inspection intervals based on failure delay time and conditional residual time concepts. None addressed an method equivalent to the one proposed in this paper [19], which is organized as follows: Section 1 presents a basic introduction and a brief literature review. Section 2 describes how to build a decision model to establish inspection time intervals such that the sum of all pertinent costs is minimized. Section 3 illustrates how the decision model can be applied. Section 4 provides a conclusion of the main results.
2. Materials and Methods
2.1. Determination of an Optimal Inspection Calendar
Consider an equipment unit scheduled for overhauling within a certain period, where an evident critical failure mode exists for which a P-F time interval is known and monitored off-line over time. Contrary to the case of PM, where a component is regularly repaired or replaced, in PdM, the interval between inspections might not be constant. More appropriately, it will vary with the course of the failure mechanism. When, for instance, the hazard rate h(t) increases with time, the adoption of shorter and shorter time intervals seems to make common sense. A calendar may thus assume a minimum threshold of reliability between inspections. If optimization is envisaged, then all costs have to be taken into consideration [2,18]. According to Elsayed [6], the reliability between inspections is a conditional probability; that is, the probability R that a failure will not happen within a period Δt (time until next inspection) is given by R(Δt|t) = . From this expression, one can determine R(t + Δt) = R(Δt|t)·R(t). Because reliability must be kept constant between successive inspections, the condition R(Δt|t) = R(t) = Ri must apply. Therefore, considering n as the nth inspection, one can determine (1):
R(t + Δt) = Rn
This expression can now be combined with any distribution that might describe the specific failure behavior. If it is combined with the Weibull distribution, the time intervals between every two inspections are determined by the expression [6,19]:
Keeping R(t) constant between successive inspections and giving α the values described below, one can conclude
- ⯀
- when α < 1, (tn+1 − tn) < (tn+2 − tn+1), and the risk function h(t) decreases;
- ⯀
- when α = 1, (tn+1 − tn) = (tn+2 − tn+1), and the risk function h(t) is constant; and
- ⯀
- when α > 1, (tn+1 − tn) > (tn+2 − tn+1), and the risk function h(t) increases.
As the risk function decreases, the time interval between inspections increases and vice-versa. The value α = 1 plays the role of a “division line” between infant and wear-out failures. The model described so far has not considered the existence of a P-F time interval (see Figure 1). According to Moubray [7], when a failure commences it deteriorates to the point at which it can be detected (point P). If it happens not to be detected and corrected, the deterioration process proceeds—usually at an increasing rate—until the point of functional failure (point F) is reached. Sometimes an intermediate point M is defined as the minimum time interval (M-F) available for an action to be carried out to prevent functional failure. If expression (2) is merged with the P-F time interval and all related costs, a mathematically optimized calendar of inspections can be obtained.
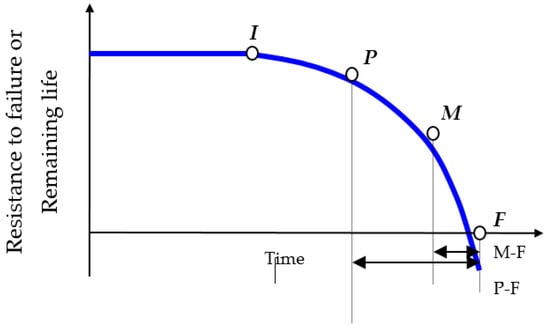
Figure 1.
P-F curve (authors’ figure).
2.2. Equating All Pertinent Costs
A critical component after H working hours presents a predominant failure mode described by a Weibull probability distribution of three parameters t0, α, and β. The equipment unit to which this component belongs is scheduled to be overhauled at moment Tp (Tp > H). To assess the condition of this component, expensive means of diagnosis are necessary. Each inspection n = 1, 2, 3, … costs Ci and will take place at moments ti1, ti2, … tin. The last inspection detected no sign of a failure in progress. Periods P-F and M-F are known. If a potential failure is not noticed or there is insufficient time to do anything if it is, functional failure will occur, and the equipment will come to a halt. The estimated opportunity cost is Cop, which is obtained multiplying the standard production rate by the contribution margin. The contribution margin is the difference between the unit sale price of the product and its standard variable cost. If a potential failure is detected and there is enough time to prevent functional failure, the equipment unit is scheduled to stop as soon as possible, and the component will be repaired or replaced at a cost Crp; meanwhile, the production degradation cost Cd builds up slowly. R(tn|tn−1) is the conditional reliability between inspections and the annual ITR is the company’s current interest tax rate, which must be adjusted to conform to the base period of the analysis. If m represents the number of base periods in a year, the adjusted tax rate can then be derived from j = (1 + ITR)1/m − 1.
Once these four costs are known, they are multiplied twice: first, by the probability of each of them occurring at certain times up to moment Tp and second, by a conversion factor that allows calculating its value from moment H for each of the points mentioned above.
After each of these four categories of costs is obtained, the corresponding expected costs are calculated. These are referred to in subsequent sections as:
- ⯀
- , the cost of each inspection;
- ⯀
- , the cost of repairing or replacing a potential failure at any time or at moment Tp;
- ⯀
- , the cost of a functional failure due to repair or replace and lost production; and
- ⯀
- , the cost of degradation incurred over time.
The sum of these four costs is “the expected global cost (Cg)” Next, the expected life of component is calculated to allow the transformation of into a uniform series of payments spread over the period H–Tp. This capital recovery, , is the variable that can now be minimized by trial and error. Varying R(tn|tn−1) progressively and maintaining Tp constant, a value of R(tn|tn−1) exists which will turn into a minimum, the optimal value for R(tn|tn−1). The same reasoning can be applied to keeping R(tn|tn−1) constant and making Tp vary, a value of which exists that will turn into a minimum, the optimal value for Tp. Each inspection n must then be performed at moments tn from (2) until the period where the condition (tn+1 − tn) < P–M (see Figure 1) is verified.
After entering this period, inspections must be performed with P-M periodicity (see Figure 1). A sequence of safe time windows (STW) was given by (Mn − Pn) and unsafe time windows (UTW) by (Pn − Mn−1) (See Figure 2). The probability of a failure in progress not being detected is given by the sum of probabilities that point P will fall within any UTW. Because it is assumed that all inspections will occur at moments Mn ≡ tn, STW will hence extend backwards in time by (Mn − Pn). If a potential failure is noticed to be in progress within a STW, the equipment unit will be scheduled to stop, the component will be promptly removed or repaired, and the incurred cost will be only Crp. If, on the contrary, a potential failure occurs within a UTW and is not noticed, a functional failure will happen with all the undesired consequences Cop. If no potential failure occurs until moment Tp, then the component will be replaced or recovered at this very moment at a cost Crp.

Figure 2.
Safe time windows Pn–Mn (grey), moment H (today), moment Tp (overhauling). Arrows represent inspection moments (authors’ figure).
This stochastic economic assessment model consists of four different costs spread over the period H–Tp:
- ⯀
- Inspections cost supposed to be performed at moments Mn;
- ⯀
- Opportunity cost due to the built up of production degradation;
- ⯀
- Repair cost of a potential failure, which may or may not happen;
- ⯀
- Consequence cost of a functional failure (repair and loss of production), which may or may not happen.
An optimal solution can be found after a few trials (scenarios) making R(tn|tn−1) vary and keeping Tp constant, or vice-versa, if interest exists. The best scenario is found when is a minimum.
2.3. Expected Cost of a Functional Failure
Let n* be the order number of the STW from which a potential failure will be surely noticed; that is, since the moment the condition (Pn − Mn−1) < (P-F − M-F) was observed. The probability of a functional or undetected potential failure is given by the sum of the probabilities of a potential failure occurrence within any UTW (Pn − Mn−1) over the period H–Tp. Similarly, the expected cost of a functional failure will result from the sum of the present worth of the opportunity cost Cop weighted with probabilities of time intervals (Pn − Mn−1).
In this formula represents the average worth of the opportunity cost Cop if a functional failure happens within any of the time intervals (Pn − Mn−1).
This expression can be solved to yield (5):
2.4. Expected Repair Cost of a Potential Failure
The moments at which a repair might take place are inside an STW (Mn − Pn), where (Pn − Mn−1) ≥ (P-F − M-F); inside an STW (Mn − Mn−1), where (Pn − Mn−1) < (P-F – M-F) applies, and the onset of a failure is certain to be detected; and at Tp if no failure is detected during the whole period H–Tp.
Let N be the total number of inspections performed at moments Mn. Like the previous section, the expected cost of a repair may be expressed as (6).
where and represent the average present worth of the repair cost Crp if a failure ever happens, and represents the present current worth of the repair cost Crp performed at moment Tp. The term represents the conditional reliability until moment Tp; that is, the probability that no failure will occur from H to Tp.
2.5. Expected Cost of Inspections
While a failure may be revealed randomly at any moment inside an STW or UTW, inspections only take place at moments Mn. Consequently, the expected cost of inspections may be expressed as
The first term of (7) is determined by summing the present worth of inspection costs Ci weighted by the probability increments of potential failure inside time intervals (Mn − Mn−1). The second term is obtained multiplying the present worth of inspection costs Ci by the conditional reliability until moment Tp.
2.6. Expected Cost of Lost Production
Whether or not a failure may be developing, the efficiency of the system to which the component under surveillance belongs may be diminishing with time. From an economic perspective, this fact will favor the anticipation of a halt. Let be the expected cost of degradation. The accumulated degraded production d(%) until any moment Mn can typically be equated by a third-order polynomial d(%) = K1 + K2.Mn + K3.Mn2 + K4.Mn3. The average production loss occurred in the time interval (Mn − Mn−1), assuming linearity if the interval is sufficiently short, can be given by Δd(%)/2.(Mn – Mn−1). Once converted to product units, this loss can be expressed by [Δd(%)/2.(Mn − Mn−1)].1/100.P, where P represents the nominal capacity of the system, e.g., kWh or Ton/hour).
Let m be the contribution margin (the difference between selling price and variable cost), of units produced in the equipment. The opportunity cost increment originating at time interval (Mn – Mn−1) will then be given by P.m.[Δd(%)/200.(Mn – Mn−1)]. The expected degraded production cost can now be determined by (8).
The first term is determined by summing the present worth of the opportunity costs Cd weighted by the probability increments of potential failure inside time intervals (Mn − Mn−1). The second term is obtained multiplying the present worth of the opportunity costs Cd by the conditional reliability until moment Tp
2.7. Expected Cost Per Time Unit
To determine the expected cost per unit time, the expected global cost (sum of the four costs in the previous sections) has to be divided by the expected life of the component, which can be achieved by adding up three different expected lives: (1) , life until the functional failure occurs; (2) , life until a potential failure is detected; and (3) , life until the moment Tp when no failure has occurred.
The expected life until the functional failure is given by adding up the products of the various UTW average lives with the correspondent probabilities (9).
The expected life until detection of a potential failure can be found by adding up the products of the various STW average lives with the corresponding probabilities (1 ≤ n ≤ n* in the case of alternate STW and UTW and n* + 1 ≤ n ≤ N when only STW are left).
Life until the moment Tp if no failure has occurred, , is given by the product of Tp and the conditional reliability until moment Tp.
Finally, the expected life of the component , which might undergo a failure (noticed in time to avoiding functional failure) or a functional failure, or on the contrary survive until moment Tp can now be obtained by adding up those three expected lives (12).
The expected cost per unit time is finally given by a uniform series of payments (13).
3. Results
In this section, a decision model application was presented through which results were shown to check the consistency of the model proposed for the selection of inspection intervals. This application was based on a confidential case study in a sanitary ceramics company. Although the figures were not the real data, they were conveniently changed to represent a realistic and consistent context.
In this company, a component that comprised part of the natural gas burning system of a tunnel oven was subjected to erosion and fatigue and failed according to a Weibull distribution with two parameters α = 2 and β = 8000 h. This component had accumulated 3000 h of running time. The equipment worked round the clock (365 days per year × 24 h a day = 8760 h per year) and was presently scheduled to be overhauled by 9000 h. The nominal production rate was 350 units/hour, and the contribution margin was EUR 100/unit. Based on historical data, as symptoms were aggravated, the throughput had to be lowered and the cumulated production loss was estimated over time from new as being described by a third order polynomial d(%) = −4.8983 + 0.0032Mn − 6.10−7Mn2 + 7.10−11Mn3. If a potential failure is noticed in due time, the repair will take place immediately and its cost is estimated to be EUR 35,000. If a functional failure arises, the equipment will have to stop unexpectedly costing EUR 100,000 due to repair and lost production mainly. Inspections will be performed for EUR 4000 each. The interest tax rate currently used in the company is 25% per year. Periods P-F and M-F are approximately 500 and 50 h, respectively. The component has already accumulated 2.000 h of work (H = 2000).
If the company sets a minimum reliability between inspections of 0.9, what will the hourly cost of this course of action be?
The limit time interval during which an inspection must take place after point P has been noticed is (P–M) = (P-F) − (M-F) = 500 − 50 = 450 h. If inspections are accomplished at moments M, each STW will therefore extend 450 h backwards in time. The interest tax rate must be adjusted for the hour as time is measured in hours in this example.
j = (1 + ITR)1/m – 1 = (1 + 0.25)1/8760 − 1 = 0.002547%.hour.
Expected costs until 9000 h from now will have to be computed. Excel enabled all the calculations in a tabular form. Table 1 and Figure 3 show the results. In Table 1, one can see that 17 inspections were necessary to accomplish a minimum reliability of 0.9 between every two inspections until 9000 h from the present moment. From the ninth inspection onwards, inspections were performed with a periodicity of (P–M) = 450 h because only STW remained. The expected costs obtained were: Failure: EUR 15,931; Inspections: EUR 30,881; Repair: EUR 25,404; Degraded production: EUR 4238, the sum of which yielded a total of EUR 76,454 over almost 11,000 h.

Table 1.
Expected costs.

Figure 3.
Moments Mn and Pn (authors’ figure).
A failure inside a UTW takes place at 665 h on average (9). A failure inside a STW takes place every 4594 h on average (10). When no failures occur, the expected life from until 9000 h from now is 0.1674 × 9000 = 1841 h (11). The total expected life is therefore (1841 + 665 + 4594) = 7100 h (12).
Finally, the expected hourly cost can be found (13):
The Search for Optimality
The hourly maintenance cost given by equation (13) can be set to a minimum by finding a suitable value of the conditional probability R(tn|tn−1). As matter of fact, this is the right variable to be considered as it is set arbitrarily; there are no strong arguments for it to assume any value in advance. Given the discrete nature of equations seen previously, an iterative method is appropriate. For instance, considering the previous example and letting the minimum reliability between inspections vary by increments of, say, R(tn|tn−1) = 0.05, gives results that are depicted in Figure 4.
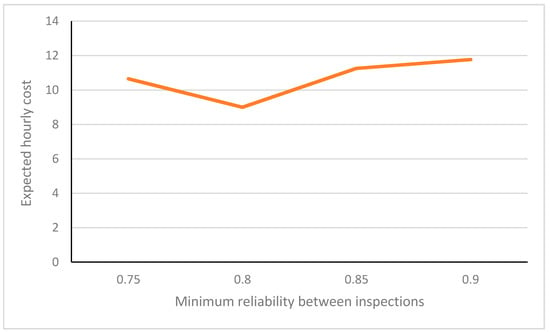
Figure 4.
Variation of with R(tn|tn−1) (authors’ figure).
Figure 4 shows that for R(tn|tn−1) ≅ 0.8, is approximately a minimum equal to EUR 9/hour. In practice, it would be of no use to adopt more accuracy.
4. Conclusions
This study demonstrated how to determine an optimal inspection calendar to monitor the status of any critical component of a piece of production equipment. It was delivered as a combination of foreseeable failure, the time interval between the onset of a failure and functional failure, and all associated costs (inspections, production degradation, failure consequences and repair). The resultant inspection calendar was composed of increasingly shorter time intervals. A sensitivity analysis allowed the search for a particular value of the decision variable “reliability between inspections”, which returned a minimum global maintenance cost per running hour. Similarly, it was shown that the calendar might be automatically updated each time an inspection turned out negative. For this purpose, the probability of false negatives that might occur, as well as the inspector’s confidence in the test, were taken into consideration. As a result, the method proved to be dynamic and self-adjusting.
Author Contributions
Conceptualization, R.A.; methodology, R.A.; validation, R.A., and P.C.M.; formal analysis, R.A.; investigation, R.A., and P.C.M.; data curation, R.A.; writing—original draft preparation, R.A.; writing—review and editing, R.A., and P.C.M.; visualization, R.A.; supervision, R.A.; project administration, R.A.; funding acquisition, P.C.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowvska-Curie grant agreement 871284 project SSHARE.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Acronyms | |
| ITR | Interest Tax Rate |
| MTTF | Mean Time To Failure |
| MTTR | Mean Time To Repair (or Replace) |
| STW | Safe Time Window |
| TTF | Time To Failure |
| TTR | Time To Repair (Replace or Recover) |
| UTW | Unsafe Time Window |
| Notation | |
| α | Weibull shape parameter |
| β | Weibull scale parameter |
| Total expected cost | |
| Failure expected cost | |
| Repair expected cost | |
| Inspections expected cost | |
| Degraded production expected cost | |
| f(t) | Failure density function |
| F | Moment of a functional failure |
| F(t) | Probability of failure |
| F(tn-t|t) | Conditional probability of failure in the interval (tn − t) given age t has been attained |
| F′(t) | Prior probability of a failure being in progress despite the test has been negative |
| F″(t) | Subsequent probability of a failure being in progress despite the test has been negative with a confidence level of Pc |
| h(t) | Hazard function |
| H | Today |
| M-F | Minimum time span to prevent a functional failure after a potential failure has been detected |
| Mn | Moments of inspection or start of an unsafe time window |
| n* | Order number of the STW from which a potential failure will be surely noticed |
| N | Number of inspections that took place until moment Tp |
| P | Moment of detection of a potential failure |
| P-F | Time span between a potential failure and a functional failure |
| Pn | Start of a safe time window |
| Pt | Accuracy of the test |
| Pt(T−|Fs) | Likelihood of a false negative in a test |
| Pt(T+|Fn) | Likelihood of a false positive in a test |
| R(t) | Reliability to the moment t |
| R(Δt|t) | Conditional reliability in the time interval Δt, given age t is accumulated |
| t0 | Weibull location parameter |
| Tp | Scheduled moment for overhauling |
| Expected life until the occurrence of the functional failure | |
| Expected life until the occurrence of the potential failure | |
| Expected life until moment Tp | |
| Total expected life | |
References
- Dieulle, L.; Berenguer, C.; Grall, A.; Roussignol, M. Continuous time predictive maintenance scheduling for a deteriorating system. In Proceedings of the Annual Reliability and Maintainability Symposium, Philadelphia, PA, USA, 22–25 January 2001; pp. 150–155. [Google Scholar]
- Jamali, M.A.; Ait-Kadi, D.; Cléroux, R.; Artiba, A. Joint optimal periodic and conditional maintenance strategy. J. Qual. Maint. Eng. 2005, 11, 107–114. [Google Scholar] [CrossRef]
- Garg, A.; Deshmukh, S.G. Maintenance management: Literature review and directions. J. Qual. Maint. Eng. 2006, 12, 205–238. [Google Scholar] [CrossRef]
- Greenough, R.M.; Grubic, T. Modelling Condition-Based Maintenance to Deliver a Service to Machine Tool Users. Int. J. Adv. Manuf. Technol. 2011, 52, 1117–1132. [Google Scholar] [CrossRef]
- Rosmaini, A.; Kamaruddin, S. An overview of time-based and condition-based maintenance in industrial application. Comput. Ind. Eng. 2012, 63, 135–149. [Google Scholar]
- Elsayed, A. Reliability Engineering; Addison Wesley Longman: New York, NY, USA, 1996. [Google Scholar]
- Moubray, J. Reliability-Centered Maintenance, 2nd ed.; Industrial Press: New York, NY, USA, 1997. [Google Scholar]
- Wang, W. An inspection model for a process with two types of inspections and repairs. Reliab. Eng. Syst. Saf. 2009, 94, 526–533. [Google Scholar] [CrossRef]
- Barker, C.T.; Newby, M.J. Optimal non-periodic inspection for a multivariate degradation model. Reliab. Eng. Syst. Saf. 2009, 94, 33–43. [Google Scholar] [CrossRef]
- Li, W.; Pham, H. Reliability modeling of multi-state degraded systems with multi-competing failures and random shocks. IEEE Trans. Reliab. 2005, 54, 297–303. [Google Scholar] [CrossRef]
- Mathew, S. Optimal inspection frequency—A tool for maintenance planning/forecasting. Int. J. Qual. Reliab. Manag. 2004, 21, 763–771. [Google Scholar] [CrossRef]
- Rouhan, A.; Schoefs, F. Probabilistic modeling of inspection results for offshore structures. Struct. Saf. 2003, 25, 379–399. [Google Scholar] [CrossRef] [Green Version]
- Badía, F.G.; Berrade, M.; Campos, C.A. Optimal inspection and preventive maintenance of units with revealed and unrevealed failures. Reliab. Eng. Syst. Saf. 2002, 78, 157–163. [Google Scholar] [CrossRef]
- Baohe, S. An optimal inspection and diagnosis policy for a multi-mode system. Reliab. Eng. Syst. Saf. 2020, 76, 181–188. [Google Scholar] [CrossRef]
- Kuntz, P.A.; Christie, R.D.; Venkata, S.S. A reliability centered optimal visual inspection model for distribution feeders. IEEE Trans. Power Deliv. 2001, 16, 718–723. [Google Scholar] [CrossRef]
- Bahrami-Ghasrchami, K.; Price, J.W.H.; Mathew, J. Optimum inspection frequency for manufacturing systems. Int. J. Qual. Reliab. Manag. 1998, 15, 250–258. [Google Scholar] [CrossRef]
- Wang, W.; Christer, A.H. Towards a general condition-based maintenance model for a stochastic dynamic system. J. Oper. Res. Soc. 2000, 51, 145–155. [Google Scholar] [CrossRef]
- Wang, W. Modelling condition monitoring intervals: A hybrid of simulation and analytical approaches. J. Oper. Res. Soc. 2003, 54, 273–282. [Google Scholar] [CrossRef]
- De Jonge, B.; Scarf, P.A. A review on maintenance optimization. Eur. J. Oper. Res. 2020, 285, 805–824. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).