Featured Application
The proposed application could be exploited for the design of a desalination device at various scales, depending on the desired flow rate of clean water.
Abstract
An array of ion separation cells is presented in this work, to propose a novel desalination device. Molecular Dynamics simulations have been incorporated to establish the theoretical background and calculate all parameters that could lead the manufacturing step. The main system component is an ion separation cell, in which water/NaCl solution flows due to an external pressure difference and ions are directed towards the non-permeable walls under the effect of an electric field, with direction perpendicular to the flow. Clean water is gathered from the output, while the remaining, high-concentration water/ion solution is re-cycled in the cells. The strength of the electric field, cell dimensions, and wall/fluid interactions are investigated over a wide range, and shear viscosity and the volumetric flow rate are calculated for each case.
1. Introduction
Water flow at the nanoscale has gained increased research interest in nanofluidics, due to its key role in environmental, biological, and chemical processes that can lead the development of novel devices in the neighboring fields of physics, chemistry, and materials science [1]. As the classical Navier theory of slip at the macroscale breaks down, predicting fluid behavior at the nanoscale and understanding the link between molecular structure and macroscopic behavior requires deep investigation over a number of parameters that can affect its flow and transport properties [2]. Only after having established deep understanding at these scales, we will be able to design devices with desired properties for practical applications [3].
The experimental investigation of devices at the nanoscale is uniquely important, as it would not only unravel phenomena taking place there, but also, would offer fabrication guidelines for commercial use. Nevertheless, the whole experimental processes are complex and challenging. Going down to less than 10 nm in pore sizes has only recently been accessible experimentally [4], and the best way to overcome these barriers emerges from numerical approaches [5]. Molecular dynamics (MD) simulations have given a boost in establishing water properties at the nanoscale through numerical calculations, bridging fluid mechanics, statistical mechanics, and condensed matter physics and setting the basis for the design and fabrication of nanofluidic devices [6]. Among these, novel desalination and water purification techniques have been proposed, covering membrane-based applications, reverse osmosis, Capacitive De-Ionization (CDI) and flow-electrode CDI [7,8,9].
Similar to the CDI philosophy, the recently proposed electric ion drift (EID) method does not use membranes or special electrodes [10,11]. The EID method is of the same energy consumption as the capacitive deionization method. This method is approached by the Poisson–Nerst–Planck (PNP) theory, which can be less computationally demanding than MD but, on the other hand, it succeeds only at the bulk and cannot incorporate wall effects in regions near the channel walls. At the macroscale, the PNP scheme is a popular choice to explain the relation between the electrostatic problem and the mass transport [12,13].
System design, either in real applications or simulation models, has the main role in achieving an efficient desalination process. First, the choice of materials is primarily important. Towards minimization of energy consumption during the desalination process, novel materials have been employed, although sometimes they have been found to have only a slight impact on increasing energy efficiency [14]. On the other hand, carbon-based materials, such as graphene, are among the most popular choices and have been incorporated for the construction of permeable membranes due to their porous structure and wetting characteristics [15]. Recently, synthetic nano-conduits have been introduced, such as artificial water channels (AWCs), to develop highly selective membranes for water desalination [16]. In a neighboring research field with biological interest, bacterial membrane potential dynamics have been investigated for exploitation in microfluidic-based platforms [17].
Another significant parameter that should be borne in mind is the choice of the driving method that removes unwanted substances from the solution. The application of an external electric field, , parallel or perpendicular to the walls, is common choice. Care has to be taken as the presence of the electric field may alter the hydrogen bond network structure, relaxation times, and rotational dynamics of water [18]. Depending on direction and strength, water molecules could be subject to phase change [19] but, in general, higher value leads to higher ion rejection rate [20]. In salt solutions, the electric field along with ion concentration have also a considerable impact on the mutual diffusion coefficients [21,22,23]. In contrast, the water flux is insensitive to the applied voltage and depends on pore size, pressure, thickness, ion concentration, water salinity, and pore geometry [24,25]. Hydrophobic/hydrophilic behavior of the walls is also a matter of investigation, since it could diminish the high flow resistance owing to surface and confinement effects [26]. It has been shown that cotton beads acting as pseudo-superhydrophilic surfaces could enhance clean water flow in a novel, condensation-based desalination system [27,28].
In this work, an array of desalination cells has been incorporated to suggest a novel desalination device. Each cell lies in the order of some nanometers, which is also the typical size-scale for membrane separation techniques for nanofiltration [29], and when the cells are connected in parallel, they comprise a device that could even reach at the macroscale. It is of importance to highlight water/ion behavior in each cell to guide possible fabrication. Towards this direction, in the next sections we present the structure of the proposed model, calculate the volumetric flow rate, and the shear viscosity (in direction parallel and perpendicular to the flow) versus the cell size, wettability, and the strength of the applied electric field.
2. Materials and Methods
2.1. System Model
Figure 1 presents the architecture of the proposed desalination device, built by an array of N cells. Each cell resembles a nanochannel, where water molecules and Na+ and Cl− ions flow between two planar, periodic, carbon surfaces, theoretically analogous to Poiseuille flow (see the inset of Figure 1). In a previous work, we have investigated the effect of the electric field strength, E, and the distance between the two wall surfaces, h, on desalination performance in a stand-alone nanochannel [30]. In this work, we consider a parallel network of such nanochannels and extend the investigation over the whole network.
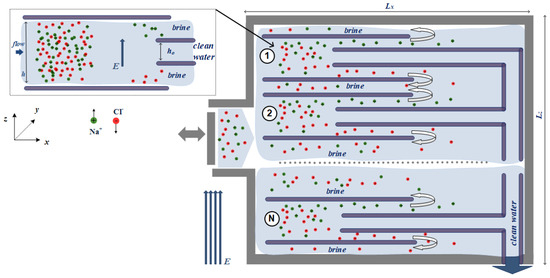
Figure 1.
Τhe proposed desalination device, consisted by an array of N cells. The inset figure presents a detailed view of each cell. Green and red circles are Na+ and Cl− ions, respectively. The external electric field Ez is applied perpendicular to the piston-driven flow. Clean water is gathered from each cell to the common outlet, while the remaining water/ion solution (brine) is recirculated to further separate water from ions.
In each cell, water/ion solution is inserted on the left, while water and ions are separated at the outlet, as the solution flows from left to right, driven by a piston. This is achieved by the application of an external electric field, E, acting perpendicular to the walls, which is expected to lead Na+ near the upper wall, Cl− ions near the lower wall, and clean water in the region around the cell centerline. During the simulations, the solution density is constant, ρ = 1078 kg/m3, and temperature remains constant at T = 300 K with the application of Nose–Hoover thermostats.
Cells of various heights (i.e., the distance between the walls) are simulated and, along with the number of cells, N, inside the device, the flow rate of clean water is estimated in Section 3.
Simulation parameters for all atoms in the system are described by the Lennard–Jones (LJ) potential. For two i and j species, the potential is given by [31]
where parameters ε and σ are the energy and size parameters, respectively, and rc = 9 Å is the cut-off radius. Moreover, coulombic interaction between hydrogen, oxygen, and ions is given by , where C the energy conversion constant, qi and qj the charges of interacting atoms, and ε0 is the dielectric constant. For two different species i and j we consider , . When i and j correspond to wall (w) and fluid (f) atoms, the ratio represents whether the wall is treated as hydrophobic ( = 0.1 and 0.2) or hydrophilic ( = 0.5 and 1.0). Water molecules comply to the SPC/E (extended simple point charge) pair potential, which has been found to reproduce adequately the structural and dynamic properties of water [32], especially under confinement [33].
Molecular Dynamics is a common method for interpretation and investigation of nanoscale phenomena. This does not exclude investigation with Navier–Stokes equations or quasi-continuum approaches, provided that one considers the appropriate scale factors and coefficients [34]. For example, shear viscosity across a nanochannel is not constant and this has to be addressed when applying the classical N-S theory [35]. The breakdown of the continuum hypothesis of the no-slip condition is believed as the main reason that continuum relations have to alter. Moreover, the occurrence of EDLs and specific adsorption effects are to be expected, while possible wall roughness would have a pronounced effect on transport properties [36].
2.2. Mathematical Formulation
Shear viscosity, μ, is given by the Stokes–Einstein’s relation [37,38] as
where constant α = 1.7 Å is the effective hydrodynamic diameter of the water molecule, and the Boltzmann constant.
The channel diffusion coefficient, Dch, is obtained from the time-averaging of the mean square displacement of N fluid particles [39] as
and
where is the position vector of the jth atom. The brackets indicate time average. We distinguish a parallel, DP, and a perpendicular to the wall direction, DT, component, as
where, is the position vector in x- and y-dimensions, and the position vector in z-dimension of the jth atom.
To calculate shear viscosity in direction parallel to the cell walls, μP, or perpendicular, μT, we, respectively, substitute in Equation (2) the diffusion coefficients DP and DT.
Diffusion coefficient calculations from the above equations, characterizing the mechanism of mass transfer at the lower scales, improve our understanding on the microscopic effects taking place at these scales. This would be of interest for problems that have to do with electric fields, since the system behavior is investigated at the lower possible level and all hidden effects are revealed [40]. Equation (2) provides calculations on shear viscosity, bypassing a significant amount of time-dependent statistical mechanics simulations needed to extract shear viscosity by other methods, such as the Green–Kubo formalism, and has been widely considered in nanoscale systems [37,38]. It shows that the size effect of Dch is directly influenced by the size effect of the shear viscosity μ. As Dch is decreasing with the channel width, μ is increasing. Shear viscosity is connected to friction, i.e., a macroscopic property, and it becomes clear that it also affects the ion and clean water flow rate for the proposed device.
In order to argue on the achievable performance of the proposed desalination method, the volumetric flow rate in every channel is calculated, as
where A is the cross-sectional channel area, the outlet height, the average fluid velocity and Ly is the channel y-dimension. To disjoin calculations from Ly, since the simulation system is periodic in the y-direction, we consider the more general volumetric flow rate per unit length to be
3. Results and Discussion
3.1. Shear Viscosity Calculations
Shear viscosity is extracted from the diffusion coefficients according to Equation (2). By separating the calculations in a parallel and a perpendicular direction, μP and μT, respectively, we obtain a close-up view of the internal mechanism that affects ion movement inside each cell. For the narrowest cell under investigation (h = 3 nm), in Figure 2a, we observe that there exists increased shear viscosity perpendicular to the wall, μT, significantly higher that the parallel component, μP. As the strength of E increases from E = 0.0 to 1.0 V/Å, μT decreases monotonically. In contrast, μP remains unaffected by the electric field value. The channel shear viscosity is, though, unaffected, remaining around the water bulk value for the range of E investigated here. In a weaker E range, the viscosity component parallel to the electric field has been found to increase monotonically with the electric field strength, while the perpendicular component first decreases and then increases with E [41]. We also note that experimental results do not always adhere to simulation, and this is attributed to the lower E strength applied, compared to simulated nanoscale systems [42].
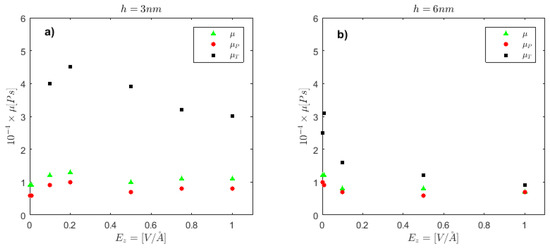
Figure 2.
Shear viscosity, μ, in parallel and perpendicular to the wall direction, and as total channel value vs. the strength of the electric field, E, for (a) h = 3 nm and (b) h = 6 nm.
For the h = 6 nm cell, where the effect of wall confinement is weaker on the transport properties of fluids [43], we observe that shear viscosity anisotropy is smaller compared to h = 3 nm, and its behavior is almost isotropic at E = 1.0 V/Å.
Shear viscosity is also examined on its dependence on wall/fluid interaction in Figure 3, for cells of height h = 3–15 nm. For h = 3 nm (Figure 3a), all shear viscosity components acquire their maximum value for the strongly hydrophilic wall ( However, this effect is weak and does not have a strong impact on μ values, and this is also the case for h = 6, 9 and 15 nm in Figure 3b–d, respectively.
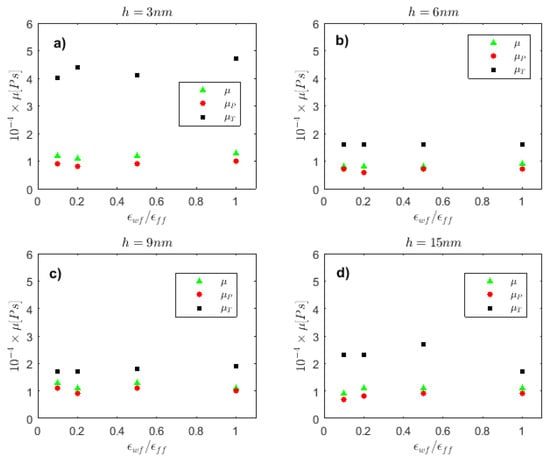
Figure 3.
Shear viscosity vs. the wall wettability strength, , for (a) h = 3 nm, (b) h = 6 nm, (c) h = 9 nm, and (d) h = 15 nm. E = 0.1 V/Å.
From a macroscopic point of view, studied under the Poisson–Boltzmann (PB) theory, it has been shown that the response of an electrolyte to an applied voltage leads to sharp ion concentration near a surface [21,22]. This has major implications for the system dynamics, as changes in diffusion and viscosity have been observed. In fact, the viscosity, which increases in high-concentration solutions, dominates the concentration dependence of D for some systems. Nevertheless, PB theory has many shortcomings because it neglects ion–ion interactions and steric effects and it is proposed that the electrolyte dynamics are better described by a modified form of the PNP equations [12,23].
3.2. Volumetric Flow Rate
The volumetric flow rate per unit length, q, for each cell is shown in Figure 4, calculated over the range . For the h = 3 nm cell, q presents a monotonic, decreasing behavior as the walls vary from being strongly hydrophobic () to strongly hydrophilic (). Moreover, for and for all cell heights investigated here, q obtains its maximum value. This is attributed to the existence of slip near the solid boundaries, which facilitates flow and, in the case of narrower channels, is more pronounced [26]. As the cell height increases, e.g., for h = 21 nm, the flow rate is stabilized to a constant value within statistical accuracy, without being further affected by the wall/fluid interaction.
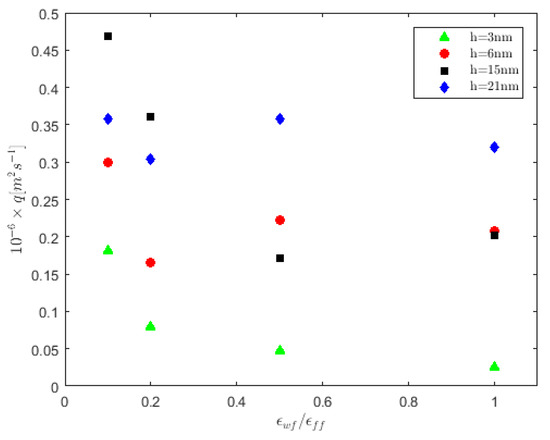
Figure 4.
Volumetric flow rate per unit length calculations for various cell heights vs. the wall wettability strength. E = 0.1 V/Å.
3.3. Configuration Issues
We now turn our attention to configuration issues and how the previous theoretical analysis can be transformed to real applications, such as the ion separation device presented in Figure 1. Apart from piston and water/ion feeding issues, which are not examined in this work, characteristics of the cell array have to be pointed out, such as the cell dimensions, the number of cells, and, consequently, the device dimensions, to be assessed over the induced flow rate of pure water from the output channel. All these parameters are presented in Table 1.

Table 1.
Calculated volumetric flow rate per unit length, for various cases of cell heights and number of cells incorporated in a device.
At first, the minimum channel length Lx for a cell of height h that could yield satisfying ion separation results has been estimated in a previous work and is given by [30]. For the device dimension on z-direction equal to , the number of cells, N, in the array can be calculated, as well as the resulting volumetric flow rate q (per unit length). Depending on the configuration capability, one may choose to construct an array of 395,257 cells in a (, ) = (1 cm, 7.3310−4 cm) where = 1.5410−7 lt/day or an array of only 80 cells with macroscale dimensions (, ) = (1 cm, 3.64 cm) where .
The proposed ion separation device could be incorporated to construct small/medium-sized systems and cannot be considered as a replacement for well-established, industrial water desalination plants. However, this approach seems to have advantages over classical methods, and further manufacturing issues are to be explored in the future.
4. Conclusions
A novel desalination procedure has been presented in this work, consisting of an array of cells that can function in parallel, based on simulation data derived frοm molecular dynamics simulations. The investigation has been based on nanoscale simulations to extract each cell property and project the findings on a wider scale.
Each cell comprises a nanochannel filled with water/ion solution. A perpendicular to the walls electric field is applied to drive ions towards the walls, while an external force with direction parallel to the walls is applied to induce flow. Clean water is gathered at the outlet. Nanoscale surface effects are expected to affect water/ion properties inside the cell. In terms of shear viscosity, calculations have shown that there exists increased shear viscosity perpendicular to the wall, which decreases monotonically as the strength of the external electric field E increases from E = 0.0 to 1.0 V/Å. On the other hand, the shear viscosity component parallel to the flow direction remains unaffected. Wall hydrophobicity/hydrophilicity does not seem to affect shear viscosity significantly, at least at the range investigated here.
Moreover, calculations on the volumetric flow rate per unit length for each cell has revealed a monotonic, decreasing effect behavior as the walls turn from hydrophobic to hydrophilic. This effect is more pronounced in the smaller cell dimensions studied, for h = 3 nm. However, for every cell dimension shown here, the flow rate obtains its maximum value for the strongly hydrophobic channel.
By establishing a parallel array of cells investigated in this work, it is possible to achieve practical water desalination rates, without the need to experiment on expensive membrane materials and/or electrodes. Some indicative cases have been tabulated and we believe that this will assist on establishing a practical desalination device in the future.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting the findings of this study are available within the article.
Acknowledgments
This work was partially supported by computational time granted from the National Infrastructures for Research and Technology S.A. (GRNET S.A.) in the National HPC facility—ARIS—under project ID PR011044/ULTRAS_ML.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, J.H.; Gao, L.; Hou, D.; Wang, P.; Zhou, Y.; Ding, Q.; Xiong, C. Insights on the ion migration throughout the nano-channel of ettringite under an external electric field: Structure, dynamics, and mechanisms. Constr. Build. Mater. 2020, 262, 120074. [Google Scholar] [CrossRef]
- Wen, Q.; Jia, P.; Cao, L.; Li, J.; Quan, D.; Wang, L.; Zhang, Y.; Lu, D.; Jiang, L.; Guo, W. Electric-Field-Induced Ionic Sieving at Planar Graphene Oxide Heterojunctions for Miniaturized Water Desalination. Adv. Mater. 2020, 32, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Alibakhshi, M.A.; Jiao, S.; Xu, Z.; Hempel, M.; Kong, J.; Park, H.G.; Duan, C. Fast water transport in graphene nanofluidic channels. Nat. Nanotechnol. 2018, 13, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Faucher, S.; Aluru, N.; Bazant, M.Z.; Blankschtein, D.; Brozena, A.H.; Cumings, J.; Pedro De Souza, J.; Elimelech, M.; Epsztein, R.; Fourkas, J.T.; et al. Critical Knowledge Gaps in Mass Transport through Single-Digit Nanopores: A Review and Perspective. J. Phys. Chem. C 2019, 123, 21309–21326. [Google Scholar] [CrossRef]
- Zhong, J.; Alibakhshi, M.A.; Xie, Q.; Riordon, J.; Xu, Y.; Duan, C.; Sinton, D. Exploring Anomalous Fluid Behavior at the Nanoscale: Direct Visualization and Quantification via Nanofluidic Devices. Acc. Chem. Res. 2020, 53, 347–357. [Google Scholar] [CrossRef]
- Shahbabaei, M.; Kim, D. Advances in nanofluidics for water purification and filtration: Molecular dynamics (MD) perspective. Environ. Sci. Nano 2021, 8, 2120–2151. [Google Scholar] [CrossRef]
- Liu, P.Y.; Yan, T.T.; Shi, L.Y.; Park, H.S.; Chen, X.S.; Zhao, Z.G.; Zhang, D.S. Graphene-based materials for capacitive deionization. J. Mater. Chem. A. 2017, 5, 13907–13943. [Google Scholar] [CrossRef]
- Zunita, M. Graphene Oxide-Based Nanofiltration for Hg Removal from Wastewater: A Mini Review. Membranes 2021, 11, 269. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; He, Y.; Rosentsvit, L.; Suss, M.E.; Zhang, X.; Gao, T.; Liang, P. Flow-Electrode Capacitive Deionization: A Review and New Perspectives. Water Res. 2021, 200, 117222. [Google Scholar] [CrossRef]
- Bartzis, V.; Sarris, I.E. Time Evolution Study of the Electric Field Distribution and Charge Density Due to Ion Movement in Salty Water. Water 2021, 13, 2185. [Google Scholar] [CrossRef]
- Bartzis, V.; Sarris, I.E. A Theoretical Model for Salt Ion Drift Due to Electric Field Suitable to Seawater Desalination. Desalination 2020, 473, 114163. [Google Scholar] [CrossRef]
- Lodi, M.B.; Fanari, F.; Fanti, A.; Desogus, F.; Getaneh, W.; Mazzarella, G.; Valera, P. Preliminary Study and Numerical Investigation of an Electrostatic Unit for the Removal of Fluoride from Thermal Water of Ethiopian Rift Valley. IEEE J. Multiscale Multiphys. Comput. Tech. 2020, 5, 72–82. [Google Scholar] [CrossRef]
- Li, J.; Chen, D.; Ye, J.; Zhang, L.; Zhou, T.; Zhou, Y. Direct Numerical Simulation of Seawater Desalination Based on Ion Concentration Polarization. Micromachines 2019, 10, 562. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Patel, S.K.; Patel, S.K.; Ritt, C.L.; Deshmukh, A.; Wang, Z.; Qin, M.; Qin, M.; Epsztein, R.; Elimelech, M.; Elimelech, M. The relative insignificance of advanced materials in enhancing the energy efficiency of desalination technologies. Energy Environ. Sci. 2020, 13, 1694–1710. [Google Scholar] [CrossRef] [Green Version]
- Le, V.T.; Almomani, F.; Vasseghian, Y.; Vilas–Boas, J.A.; Dragoi, E.N. Graphene-based nanomaterial for desalination of water: A systematic review and meta-analysis. Food Chem. Toxicol. 2021, 148, 1–8. [Google Scholar] [CrossRef]
- Hardiagon, A.; Murail, S.; Huang, L.B.; Van Der Lee, A.; Sterpone, F.; Barboiu, M.; Baaden, M. Molecular dynamics simulations reveal statistics and microscopic mechanisms of water permeation in membrane-embedded artificial water channel nanoconstructs. J. Chem. Phys. 2021, 154, 184102. [Google Scholar] [CrossRef]
- Jofre, M.; Jofre, L.; Jofre-Roca, L. On the Wireless Microwave Sensing of Bacterial Membrane Potential in Microfluidic-Actuated Platforms. Sensors 2021, 21, 3420. [Google Scholar] [CrossRef]
- Murail, S.; Vasiliu, T.; Neamtu, A.; Barboiu, M.; Sterpone, F.; Baaden, M. Water permeation across artificial I-quartet membrane channels: From structure to disorder. Faraday Discuss. 2018, 209, 125–148. [Google Scholar] [CrossRef]
- Qiu, H.; Guo, W. Electromelting of confined monolayer ice. Phys. Rev. Lett. 2013, 110. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E.; Spetsiotis, D. Molecular dynamics simulations of ion separation in nano-channel water flows using an electric field. Mol. Simul. 2019, 45, 1395–1402. [Google Scholar] [CrossRef]
- Lu, R.; Leaist, D.G. Mutual Diffusion in Solutions of Alkali Metal Halides. J. Chem. Soc. Faraday Trans. 1998, 94, 111–114. [Google Scholar] [CrossRef]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric Effects in the Dynamics of Electrolytes at Large Applied Voltages. I. Double-Layer Charging. Phys. Rev. E 2007, 75, 021502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric Effects in the Dynamics of Electrolytes at Large Applied Voltages. II. Modified Poisson-Nernst-Planck Equations. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 75, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Ali Abdol, M.; Sadeghzadeh, S.; Jalaly, M.; Mahdi Khatibi, M. On the desalination performance of multi-layer graphene membranes; A molecular dynamics study. Comput. Mater. Sci. 2021, 191, 110335. [Google Scholar] [CrossRef]
- Golchoobi, A.; Tasharrofi, S.; Taghdisian, H. Functionalized nanoporous graphene membrane for water desalination; Effect of feed salinity on permeability and salt rejection, a molecular dynamics study. Comput. Mater. Sci. 2020, 172, 109399. [Google Scholar] [CrossRef]
- Hu, H.; Bao, L.; Priezjev, N.V.; Luo, K. Identifying two regimes of slip of simple fluids over smooth surfaces with weak and strong wall-fluid interaction energies. J. Chem. Phys. 2017, 146, 34701. [Google Scholar] [CrossRef] [PubMed]
- Sadeghpour, A.; Zeng, Z.; Ji, H.; Ebrahimi, N.D.; Bertozzi, A.L.; Ju, Y.S. Water vapor capturing using an array of traveling liquid beads for desalination and water treatment. Sci. Adv. 2019, 5, eaav7662. [Google Scholar] [CrossRef] [Green Version]
- Ruan, Y.; Nadim, A.; Duvvoori, L.; Chugunova, M. Liquid Films Falling Down a Vertical Fiber: Modeling, Simulations and Experiments. Fluids 2021, 6, 281. [Google Scholar] [CrossRef]
- Mohammad, A.W.; Teow, Y.H.; Ang, W.L.; Chung, Y.T.; Oatley-Radcliffe, D.L.; Hilal, N. Nanofiltration membranes review: Recent advances and future prospects. Desalination 2015, 356, 226–254. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.; Sarris, I.E. Molecular dynamics simulations of ion drift in nanochannel water flow. Nanomaterials 2020, 10, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017; ISBN 9780198803195. [Google Scholar]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Prasad, V.; Kannam, S.K.; Hartkamp, R.; Sathian, S.P. Water desalination using graphene nanopores: Influence of the water models used in simulations. Phys. Chem. Chem. Phys. 2018, 20, 16005–16011. [Google Scholar] [CrossRef] [Green Version]
- Giannakopoulos, A.E.; Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. Unified Description of Size Effects of Transport Properties of Liquids Flowing in Nanochannels. Int. J. Heat Mass Transf. 2012, 55, 5087–5092. [Google Scholar] [CrossRef]
- Liakopoulos, A.; Sofos, F.; Karakasidis, T.E. Friction Factor in Nanochannel Flows. Microfluid. Nanofluidics 2016, 20, 1–7. [Google Scholar] [CrossRef]
- Sparreboom, W.; van Den Berg, A.; Eijkel, J.C.T. Transport in Nanofluidic Systems: A Review of Theory and Applications. New J. Phys. 2010, 12, 015004. [Google Scholar] [CrossRef]
- Ritos, K.; Mattia, D.; Calabrò, F.; Reese, J.M. Flow enhancement in nanotubes of different materials and lengths. J. Chem. Phys. 2014, 140, 014702. [Google Scholar] [CrossRef] [Green Version]
- Thomas, J.A.; Mcgaughey, A.J.H. Reassessing Fast Water Transport in CNT.pdf. Nano Lett. 2008, 8, 2788–2793. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. How wall properties control diffusion in grooved nanochannels: A molecular dynamics study. Heat Mass Transf. und Stoffuebertragung 2013, 49, 1081–1088. [Google Scholar] [CrossRef]
- Banerjee, P.; Bagchi, B. Ions’ Motion in Water. J. Chem. Phys. 2019, 150, 190901. [Google Scholar] [CrossRef]
- Zong, D.; Hu, H.; Duan, Y.; Sun, Y. Viscosity of Water under Electric Field: Anisotropy Induced by Redistribution of Hydrogen Bonds. J. Phys. Chem. B 2016, 120, 4818–4827. [Google Scholar] [CrossRef] [PubMed]
- Kimura, H.; Sugiyama, T.; Takahashi, S.; Tsuchida, A. Viscosity change in aqueous hectorite suspension activated by DC electric field. Rheol. Acta 2013, 52, 139–144. [Google Scholar] [CrossRef]
- Sofos, F.; Karakasidis, T.E.; Liakopoulos, A. Fluid flow at the nanoscale: How fluid properties deviate from the bulk. Nanosci. Nanotechnol. Lett. 2013, 5, 457–460. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).