Development of a Coordinate Measuring Machine—Based Inspection Planning System for Industry 4.0
Abstract
1. Introduction
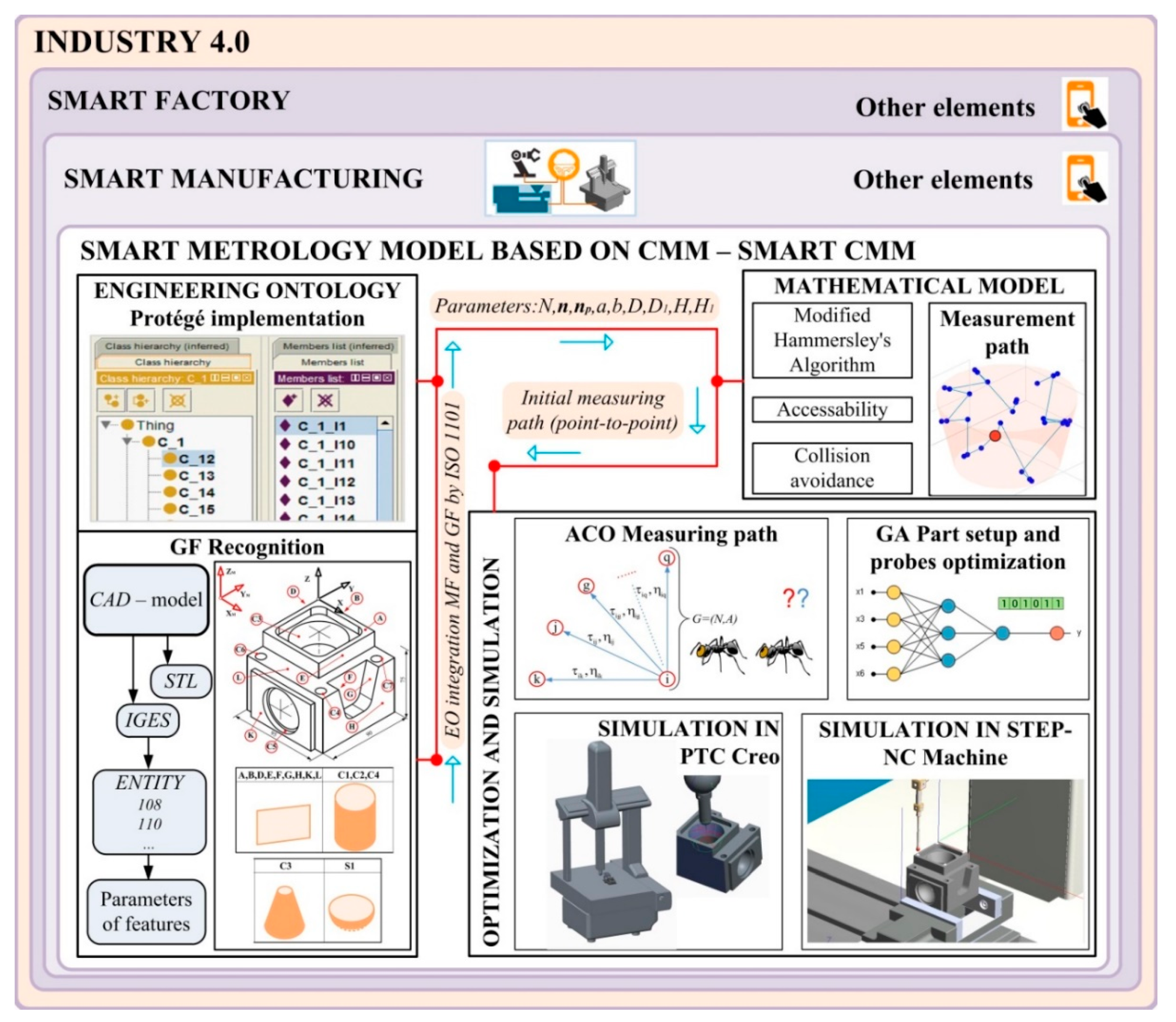
2. Outline of the Concept
- EO model for extraction of geometric features from IGES and STL file and define GD&T of metrological feature of the PWs and integration by ontology knowledge base;
- ACO model for design of MP optimization as a first main part of IP2SM4.0;
- GA model for optimal part setup and probes optimization, as a second main part of IP2SM4.0;
- Mathematical model integrates distribution of the measurement points, accessibility and collision avoidance analysis;
- Simulation in MatLab (shown as a measurement path on Figure 1), PTC Creo and STEP-NC Machine and generation of an appropriate output file.
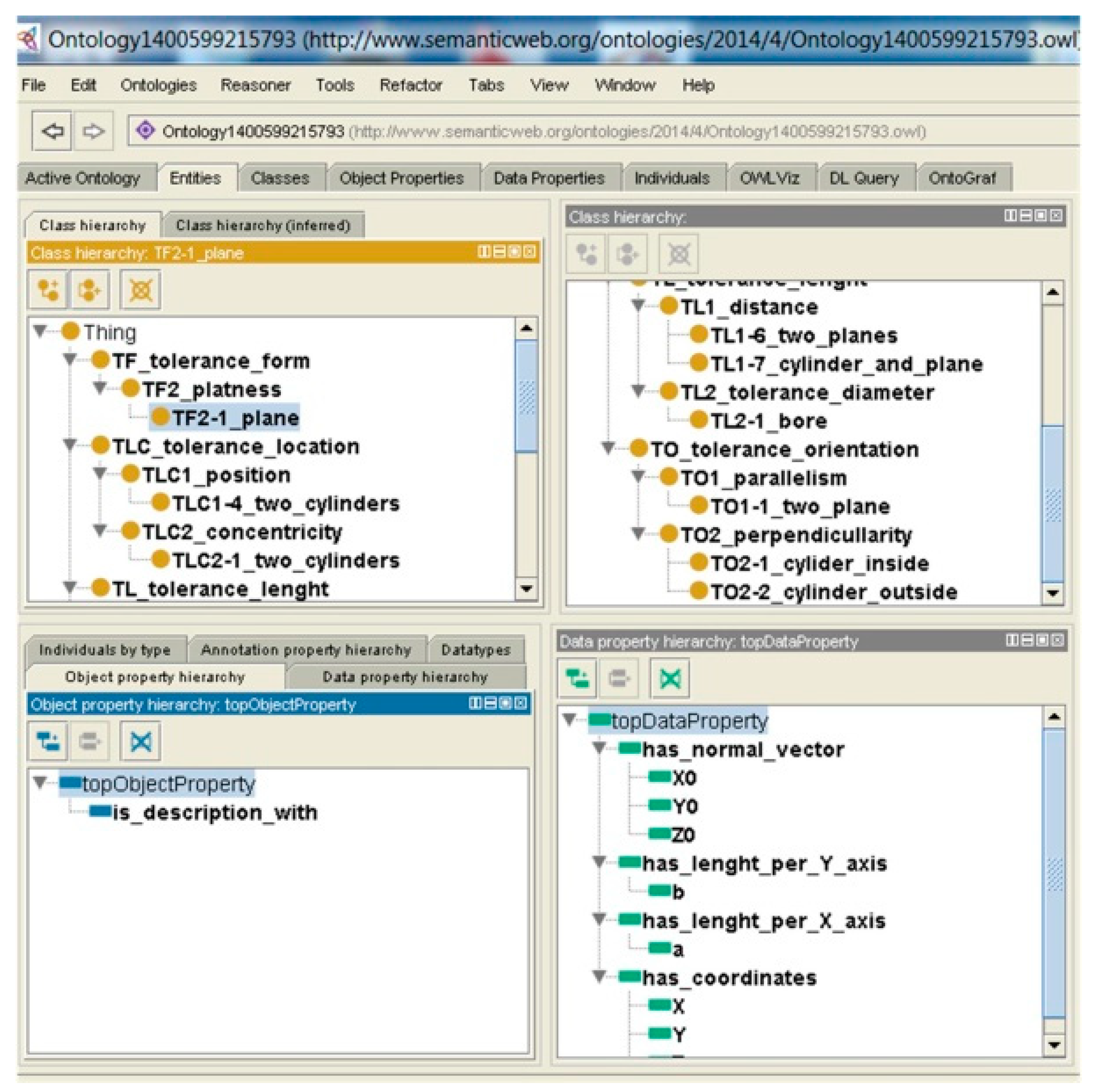
3. Inspection Features and Engineering Ontology
3.1. Inspection Feature Modeling
3.2. Ontology Knowledge Base
- Classes: represent GFs such as: point C_1, line C_2, circle C_3, ellipse C_4, plane C_5, sphere C_6, cylinder C_7, cone C_8 and torus C_9.
- Subclasses: GFs that participate in creating other primitives are EO subclasses: C_11, C_12, C_13, …, C_19; C_52, C_53, C_54, C_57, C_58, C_59). e.g., C_52 represents the plane that participates in creating a line.
- Individuals: represent GFs defined by mentioned parameters. The example of individuals for class point is labeled as C_12_I1 and represents the point obtained as an intersection of straight lines.
- Properties: individual parameters represent EO properties as four types of properties: coordinates of points, normal vectors, diameter, and angle.
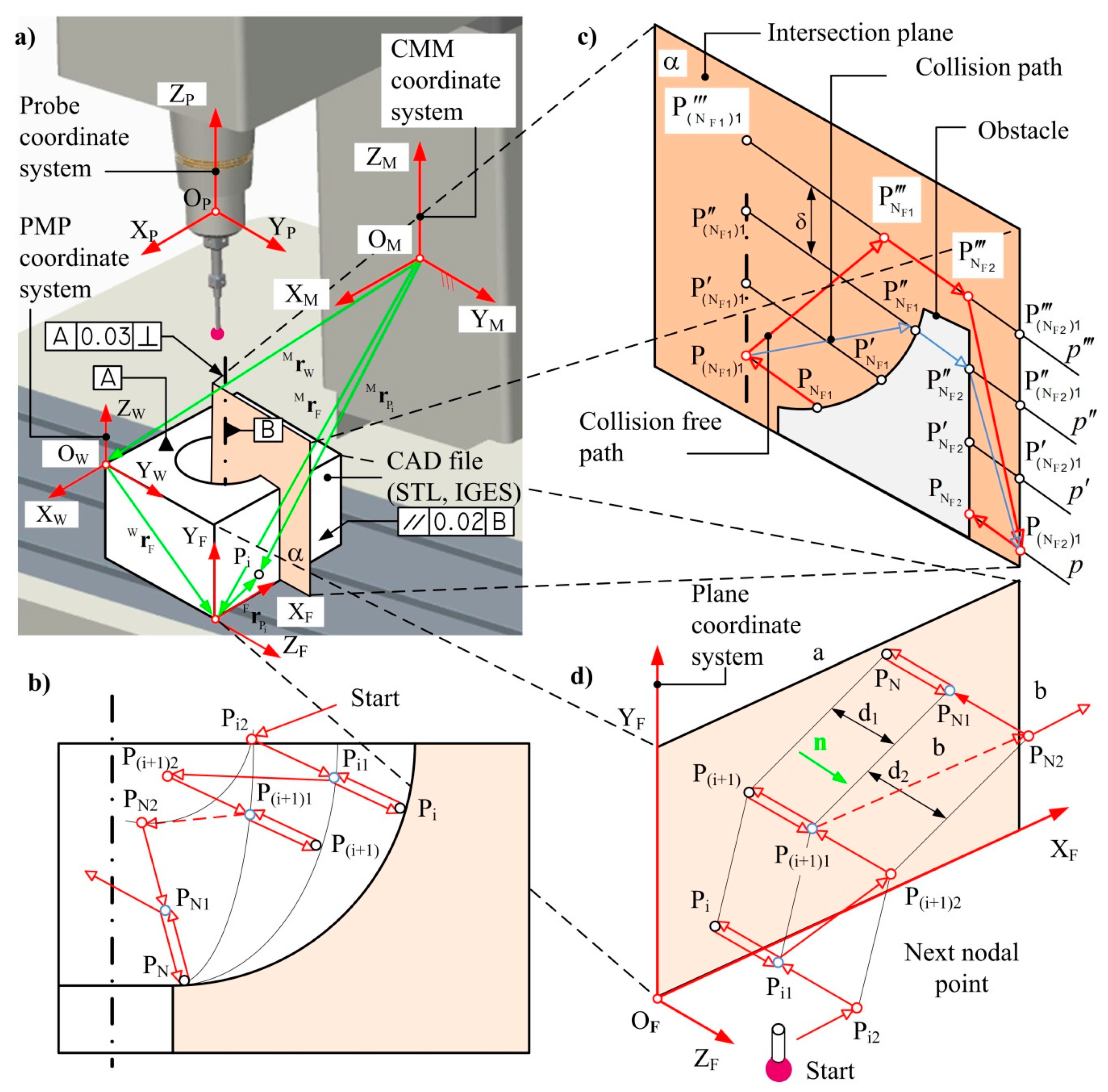
4. Inspection Planning Model
4.1. Initial Measuring Path Generating
4.2. Analysis of PW Setups and Configuration of Sensors
5. Optimization Models
5.1. Optimization of PW Setups and Probe Configuration
- initial population,
- fitness function,
- selection.
5.1.1. Initial Population
5.1.2. Fitness Function
5.1.3. Selection
5.2. Optimization of Initial Measuring Path
6. Simulation of Measuring Path
6.1. MatLab Simulation
- measuring points distribution,
- collision free pat generation, and
- measuring path planning.
6.2. PTC Creo Simulation
- CMM granite table (MACH_ZERO),
- PW (MACH_ZERO),
- probe holder (TOOL_POINT), and
- probe tip (TOOL).
6.3. STEP-NC Machine Simulation
6.4. Results of Comparison
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | artificial intelligence |
| ACO | ants colony optimization |
| AP | application protocols |
| BDA | big data analytics |
| CAI | computer aided inspection |
| CAD | computer aided design |
| CAM | computer aided manufacturing |
| CMM | coordinate measuring machine |
| CPS | cyber physical system |
| CP2M | cyber physical manufacturing metrology |
| CP3M | cyber physical manufacturing metrology model |
| CL | cutter location |
| CS | coordinate system |
| DMIS | dimensional measuring interface standard |
| DML | dimensional markup language |
| ERP | enterprise resource planning |
| EO | engineering ontology |
| FAD | feature approach direction |
| GA | genetic algorithm |
| GF | geometric feature |
| IoT | Internet of Things |
| IT | information technology |
| IIoT | industrial internet of things |
| IP2SM4.0 | inspection planning system as a support of manufacturing metrology 4.0 |
| IGES | initial graphics exchange specification |
| MES | manufacturing execution system |
| MM4.0 | manufacturing metrology |
| MP | measuring path |
| OWL | web ontology language |
| PAD | probe approach direction |
| PW | prismatic workpiece |
| STEP | standard for the exchange of product model data |
| STL | standard triangle language |
| SaaS | software as a service |
| SMEs | small and medium-sized enterprises |
| TSP | traveling salesman problem |
| TL | tolerances of length |
| TF | tolerances of form |
| TO | tolerances of orientation |
| TLC | tolerances of location |
| VCMM | virtual coordinate measuring machine |
References
- Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent manufacturing in the context of industry 4.0: A review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
- Lee, J.; Bagheri, B.; Kao, H.-A. A Cyber-Physical Systems architecture for Industry 4.0-based manufacturing systems. Manuf. Lett. 2015, 3, 18–23. [Google Scholar] [CrossRef]
- Stojadinovic, S.M.; Majstorovic, V.D.; Durakbasa, N.M. Toward a cyber-physical manufacturing metrology model for industry 4.0. Artif. Intell. Eng. Des. Anal. Manuf. 2021, 35, 20–36. [Google Scholar] [CrossRef]
- RWTH Aachen Campus. Available online: https://i40mc.de/en (accessed on 20 April 2020).
- Industry 4.0 and the Fourth Industrial Revolution Explained. Available online: https://www.i-scoop.eu/industry-4-0 (accessed on 20 April 2020).
- Majstorovic, V.D.; Durakbasa, N.; Takaya, Y.; Stojadinovic, S. Advanced Manufacturing Metrology in Context of Industry 4.0 Model. In Proceedings of the Recent Advances in Computational Mechanics and Simulations, Belgrade, Serbia, 4–7 June 2019; pp. 1–11. [Google Scholar]
- Majstorovic, D.V.; Stojadinovic, S. Cyber Physical Manufacturing Metrology NEWTECH 2020 IOP Conf. 2020 Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2020. [Google Scholar]
- Yong, Y.; Kathryn, E.S.; Dongni, L. The evolution of production systems from Industry 2.0 through Industry 4.0. Int. J. Prod. Res. 2018, 56, 848–861. [Google Scholar]
- Lu, Y.; Xu, X.; Wang, L. Smart manufacturing process and system automation–A critical review of the standards and envi-sioned scenarios. J. Manuf. Syst. 2020, 56, 312–325. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, H.; Liu, C.; Xu, X. Standards for Smart Manufacturing: A review. In Proceedings of the 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 73–78. [Google Scholar]
- Takaya, Y. Strategic Vision for Smart Machining Tool and Measuring Instrument. NTN Tech. Rev. 2018, 86, 20–41. [Google Scholar]
- Lee, C.-H.; Chen, C.-H.; Lin, C.; Li, F.; Zhao, X. Developing a Quick Response Product Configuration System under Industry 4.0 Based on Customer Requirement Modelling and Optimization Method. Appl. Sci. 2019, 9, 5004. [Google Scholar] [CrossRef]
- Lazzari, A.; Pou, J.-M.; Dubois, C.; Leblond, L. Smart metrology: The importance of metrology of decisions in the big data era. IEEE Instrum. Meas. Mag. 2017, 20, 22–29. [Google Scholar] [CrossRef]
- Ana, P.C.-M.; Horacio, A.-G.; Darío, G.-L.; Maria, F.M.-A.; Pedro, D.U.C.; Pedro, A.O.C.; Thomas, R.K.; Emilio, G.C. Connectivity as a Design Feature for Industry 4.0 Production Equipment: Application for the Development of an In-Line Metrology System. Appl. Sci. 2021, 11, 1312. [Google Scholar]
- Sander, L.; Norbert, G. A factory operating system for extending existing factories to Industry 4.0. Comput. Ind. 2020, 115, 103128. [Google Scholar]
- Tariq, M.; Paul, S. Industry 4.0: Adoption challenges and benefits for SMEs. Comput. Ind. 2020, 121, 103261. [Google Scholar]
- Alberto, C.; Miguel, A.S.; Cristina, G.G. Industry 4.0 HUB: A Collaborative Knowledge Transfer Platform for Small and Me-dium-Sized Enterprises. Appl. Sci. 2021, 11, 5548. [Google Scholar]
- Szilárd, J.; Adrienn, S.; Tibor, H.; Tibor, C.; János, A. Development of manufacturing execution systems in accordance with Industry 4.0 requirements: A review of standard- and ontology-based methodologies and tools. Comput. Ind. 2020, 123, 103300. [Google Scholar]
- Sameer, M.; Muztoba, K.; David, R.; Thorsten, W. A critical review of smart manufacturing & Industry 4.0 maturity models: Implications for small and medium-sized enterprises (SMEs). J. Manuf. Syst. 2019, 49, 194–214. [Google Scholar]
- Dan, L.; Asa, F.-B.; Dan, P. Current and future Industry 4.0 capabilities for information and knowledge sharing-Case of two Swedish SMEs. Int. J. Adv. Manuf. Technol. 2019, 105, 3951–3963. [Google Scholar]
- Majstorović, V.; Mačužić, J.; Šibalija, T.; Živković, S. Cyber-Physical Manufacturing Systems–Manufacturing Metrology Aspects. J. Proc. Manuf. Syst. 2015, 10, 9–14. [Google Scholar]
- Berthold, J.; Imkamp, D. Looking at the future of manufacturing metrology: Roadmap document of the German VDI/VDE Society for Measurement and Automatic Control. J. Sens. Sens. Syst. 2013, 2, 1–7. [Google Scholar] [CrossRef][Green Version]
- Majstorovic, V.D.; Stojadinovic, S.M.; Sibalija, T.V. Development of a knowledge base for the planning of prismatic parts inspection on CMM. Acta IMEKO 2015, 4, 10. [Google Scholar] [CrossRef]
- Stanford University, Protégé. Available online: http://protege.stanford.edu/ (accessed on 5 April 2012).
- Stojadinović, S.M.; Majstorovic, V. Developing engineering ontology for domain coordinate metrology. FME Trans. 2014, 42, 249–255. [Google Scholar] [CrossRef]
- Stojadinovic, S.; Majstorovic, V. Towards the Development of Feature–Based Ontology for Inspection Planning System on CMM. J. Mach. Eng. 2012, 12, 89–98. [Google Scholar]
- Stojadinović, S.M.; Majstorović, V.D. An Intelligent Inspection Planning System for Prismatic Parts on CMMs; Springer Science and Business Media LLC: Berlin, Germany, 2019. [Google Scholar]
- Stojadinovic, S.M.; Majstorovic, V.D.; Durakbasa, N.M.; Sibalija, T.V. Towards an intelligent approach for CMM inspection planning of prismatic parts. Measurement 2016, 92, 326–339. [Google Scholar] [CrossRef]
- Rice, O.; Nyman, R. Efficiently Vectorized Code for Population Based Optimization Algorithms; UCL Department of Computer Science: London, UK, 2013. [Google Scholar]
- Stojadinovic, S.; Majstorovic, V.; Durakbasa, N.; Sibalija, T. Ants Colony Optimization of the Measuring Path of Prismatic Parts on a CMM. Metrol. Meas. Syst. 2016, 23, 119–132. [Google Scholar] [CrossRef]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; The MIT Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Dorigo, M.; Blum, C. Ant colony optimization theory: A survey. Theor. Comput. Sci. 2005, 344, 243–278. [Google Scholar] [CrossRef]
- Stojadinovic, M.S.; Zivanovic, S.; Slavkovic, N. Verification of the CMM Measurement Path Based on the Modified Ham-mersly’s Algorithm. In Proceedings of the 12th International Conference on Measurement and Quality Control–Cyber Physical Issue, Belgrade, Serbia, 4–7 June 2019; pp. 25–38. [Google Scholar]
- Sładek, J.; Gąska, A.; Olszewska, M.; Kupiec, R.; Krawczyk, M. Virtual coordinate measuring machine built using Laser Tracer system and spherical standard. Metrol. Meas. Syst. 2013, 1, 77–86. [Google Scholar] [CrossRef]
- STEP Tools. Available online: https://www.steptools.com (accessed on 11 February 2021).



| Points and No. | Unit GF | ||||||
|---|---|---|---|---|---|---|---|
| Plane | Truncated Hemisphere | ||||||
| X | Y | Z | X | Y | Z | ||
| Pi | 1 | 0.0000 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 |
| 2 | 0.1000 | 0.6641 | 0.0000 | 0.6049 | 0.4395 | 0.6641 | |
| 3 | 0.2000 | 0.3281 | 0.0000 | 0.2919 | 0.8984 | 0.3281 | |
| 4 | 0.3000 | 0.9922 | 0.0000 | −0.0386 | 0.1186 | 0.9922 | |
| 5 | 0.4000 | 0.1563 | 0.0000 | −0.7991 | 0.5806 | 0.1563 | |
| 6 | 0.5000 | 0.8203 | 0.0000 | −0.5719 | 0.0000 | 0.8203 | |
| 7 | 0.6000 | 0.4844 | 0.0000 | −0.7078 | −0.5142 | 0.4844 | |
| 8 | 0.7000 | 0.1484 | 0.0000 | −0.3056 | −0.9405 | 0.1484 | |
| 9 | 0.8000 | 0.0625 | 0.0000 | 0.3084 | −0.9492 | 0.0625 | |
| 10 | 0.9000 | 0.7266 | 0.0000 | 0.5559 | −0.4039 | 0.7266 | |
| Pi1 | 1 | 0.0000 | 0.0000 | 0.3333 | 0.9200 | 0.0000 | 0.0000 |
| 2 | 0.1000 | 0.6641 | 0.3333 | 0.5565 | 0.4043 | 0.6641 | |
| 3 | 0.2000 | 0.3281 | 0.3333 | 0.2686 | 0.8265 | 0.3281 | |
| 4 | 0.3000 | 0.9922 | 0.3333 | −0.0355 | 0.1092 | 0.9922 | |
| 5 | 0.4000 | 0.1563 | 0.3333 | −0.7352 | 0.5341 | 0.1563 | |
| 6 | 0.5000 | 0.8203 | 0.3333 | −0.5262 | 0.0000 | 0.8203 | |
| 7 | 0.6000 | 0.4844 | 0.3333 | −0.6512 | −0.4731 | 0.4844 | |
| 8 | 0.7000 | 0.1484 | 0.3333 | −0.2811 | −0.8653 | 0.1484 | |
| 9 | 0.8000 | 0.0625 | 0.3333 | 0.2837 | −0.8733 | 0.0625 | |
| 10 | 0.9000 | 0.7266 | 0.3333 | 0.5114 | −0.3716 | 0.7266 | |
| Pi2 | 1 | 0.0000 | 0.0000 | 1.0000 | 0.6000 | 0.0000 | 0.0000 |
| 2 | 0.1000 | 0.6641 | 1.0000 | 0.3629 | 0.2637 | 0.6641 | |
| 3 | 0.2000 | 0.3281 | 1.0000 | 0.1751 | 0.5390 | 0.3281 | |
| 4 | 0.3000 | 0.9922 | 1.0000 | −0.0231 | 0.0712 | 0.9922 | |
| 5 | 0.4000 | 0.1563 | 1.0000 | −0.4794 | 0.3483 | 0.1563 | |
| 6 | 0.5000 | 0.8203 | 1.0000 | −0.3431 | 0.0000 | 0.8203 | |
| 7 | 0.6000 | 0.4844 | 1.0000 | −0.4247 | −0.3085 | 0.4844 | |
| 8 | 0.7000 | 0.1484 | 1.0000 | −0.1834 | −0.5643 | 0.1484 | |
| 9 | 0.8000 | 0.0625 | 1.0000 | 0.1850 | −0.5695 | 0.0625 | |
| 10 | 0.9000 | 0.7266 | 1.0000 | 0.3335 | −0.2423 | 0.7266 | |
| No. | Name of Path/Impact | Feature | ||||
|---|---|---|---|---|---|---|
| Plane | Trunscated Hemisphere | Circe | Cylinder | Trunscated Cone | ||
| 1 | PTC Creo (DC) [mm] | 202.6522 | 183.6755 | 126.4420 | 228.9870 | 440.1400 |
| 2 | STEP-NC (DS) [mm] | 172.4683 | 165.2395 | 116.2687 | 195.8100 | 362.5900 |
| 3 | Optimized by ACO (DO) [mm] | 159.4604 | 159.0962 | 110.2460 | 172.2140 | 307.6090 |
| 4 | IC = 100 − (DO/DC [%]) | 21.31 | 13.38 | 12,81 | 24.79 | 30.11 |
| 5 | IS = 100 − (DO/DS [%]) | 7.54 | 3.71 | 5.17 | 12.05 | 15.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stojadinovic, S.M.; Majstorovic, V.D.; Gąska, A.; Sładek, J.; Durakbasa, N.M. Development of a Coordinate Measuring Machine—Based Inspection Planning System for Industry 4.0. Appl. Sci. 2021, 11, 8411. https://doi.org/10.3390/app11188411
Stojadinovic SM, Majstorovic VD, Gąska A, Sładek J, Durakbasa NM. Development of a Coordinate Measuring Machine—Based Inspection Planning System for Industry 4.0. Applied Sciences. 2021; 11(18):8411. https://doi.org/10.3390/app11188411
Chicago/Turabian StyleStojadinovic, Slavenko M., Vidosav D. Majstorovic, Adam Gąska, Jerzy Sładek, and Numan M. Durakbasa. 2021. "Development of a Coordinate Measuring Machine—Based Inspection Planning System for Industry 4.0" Applied Sciences 11, no. 18: 8411. https://doi.org/10.3390/app11188411
APA StyleStojadinovic, S. M., Majstorovic, V. D., Gąska, A., Sładek, J., & Durakbasa, N. M. (2021). Development of a Coordinate Measuring Machine—Based Inspection Planning System for Industry 4.0. Applied Sciences, 11(18), 8411. https://doi.org/10.3390/app11188411









