A Coupled Multiscale Approach to Modeling Aortic Valve Mechanics in Health and Disease
Abstract
1. Introduction and Objective
2. Materials and Methods
2.1. Multiscale Modeling Framework
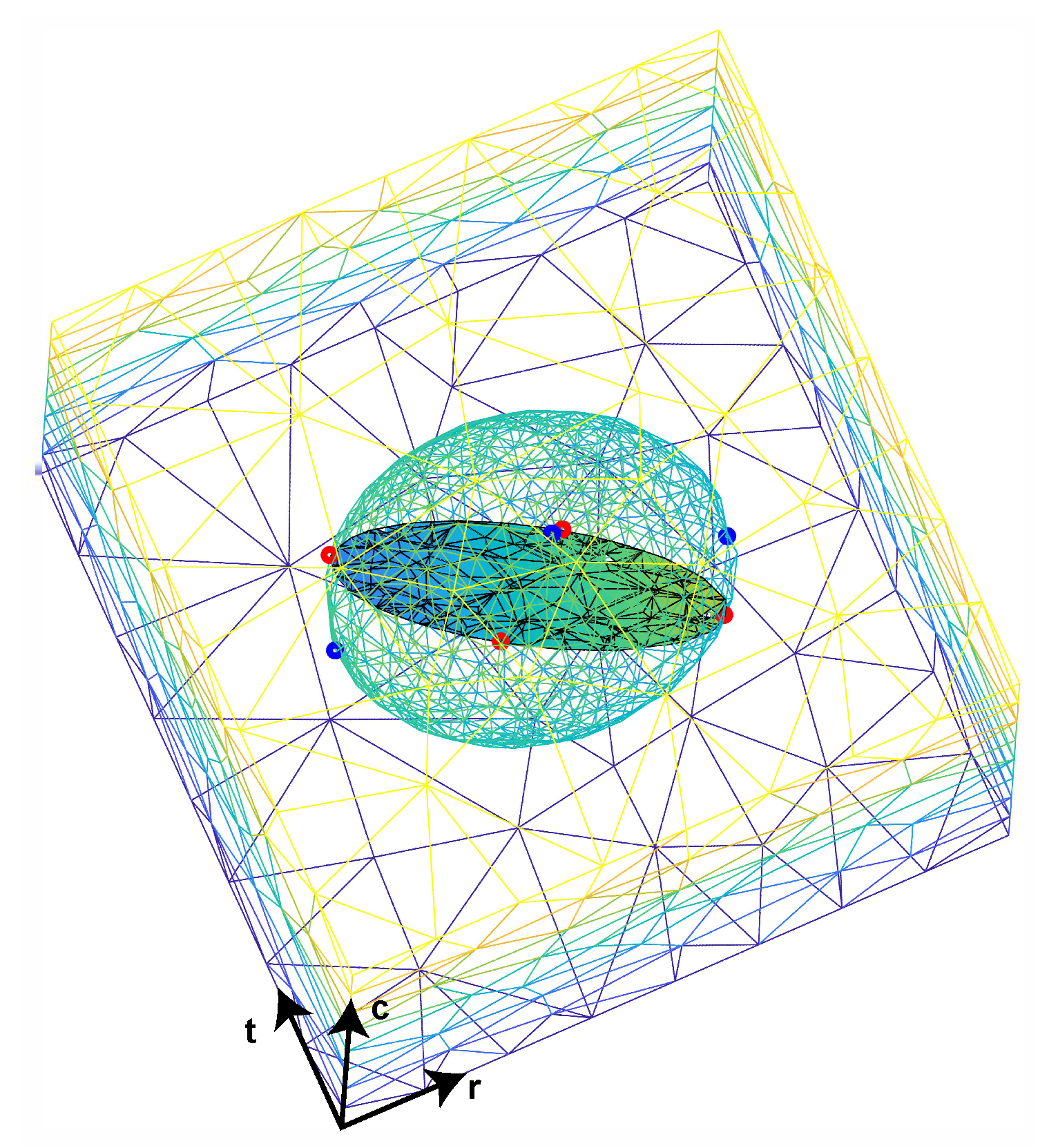
RVE Boundary Conditions
2.2. Implementation of FE Approach to Aortic Valve Leaflet Tissue
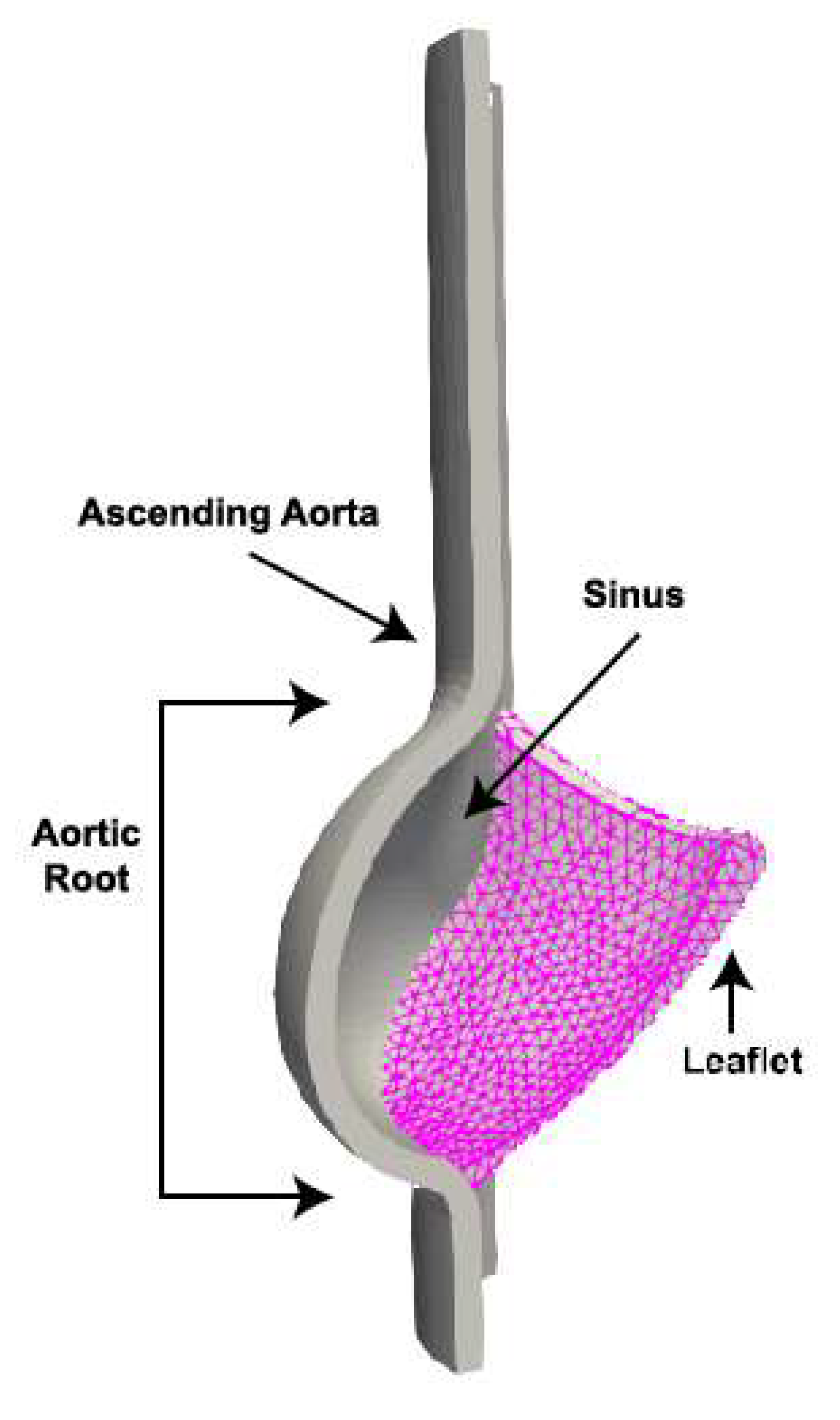
2.2.1. Macroscale Model
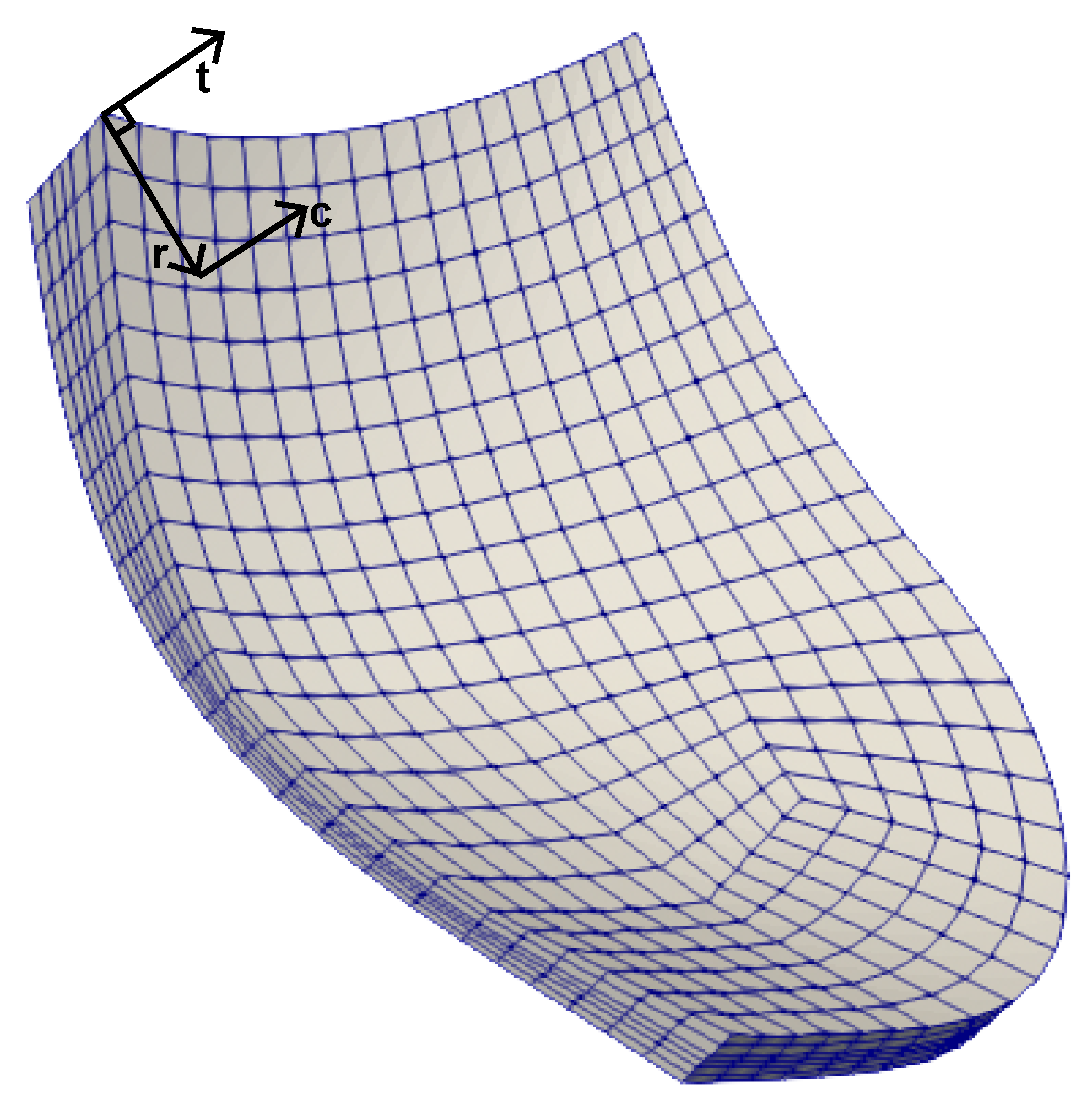
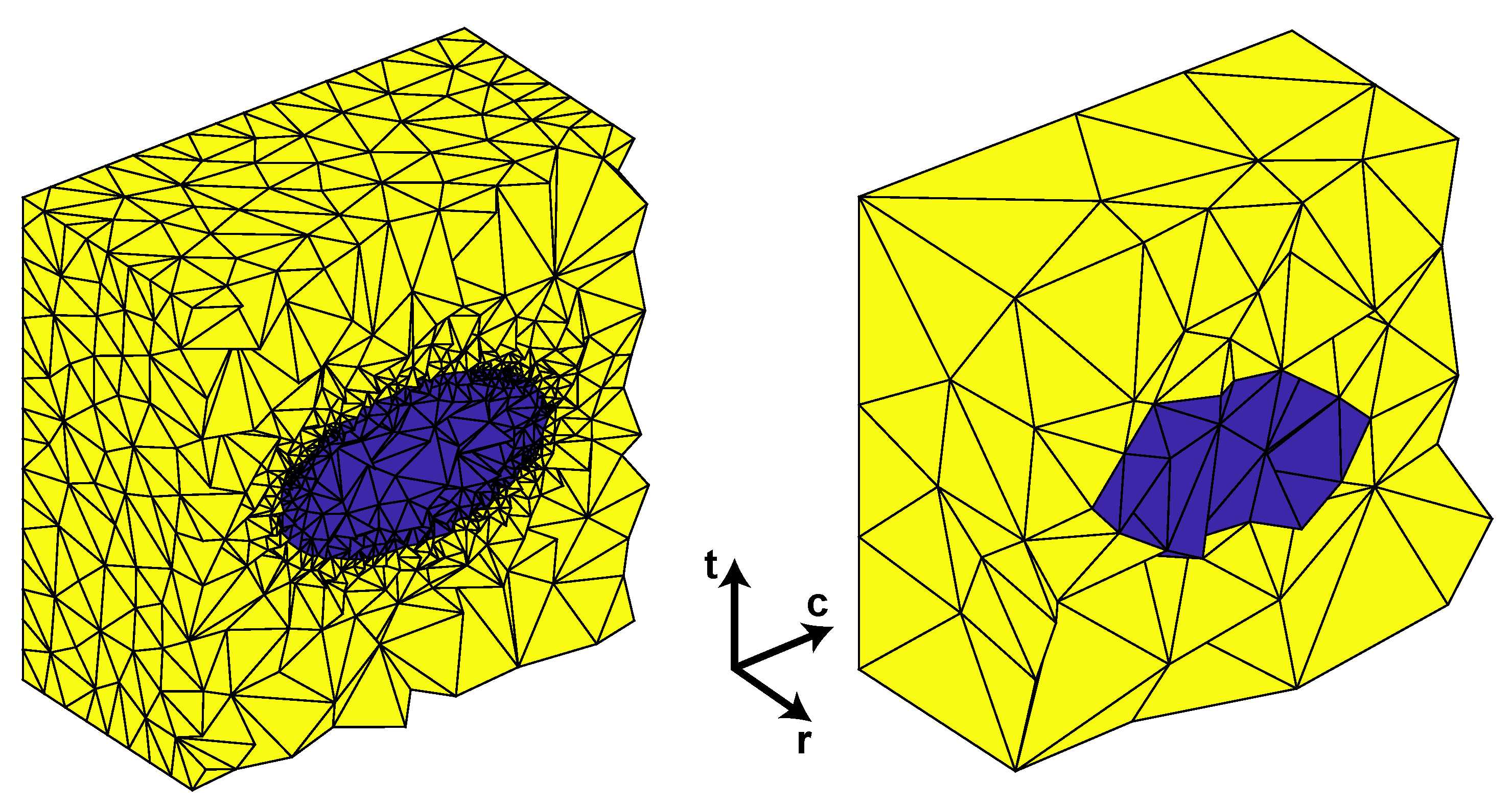
2.2.2. Microscale Model (RVE)
2.3. Application to Calcific Aortic Valve Leaflet Tissue
3. Results
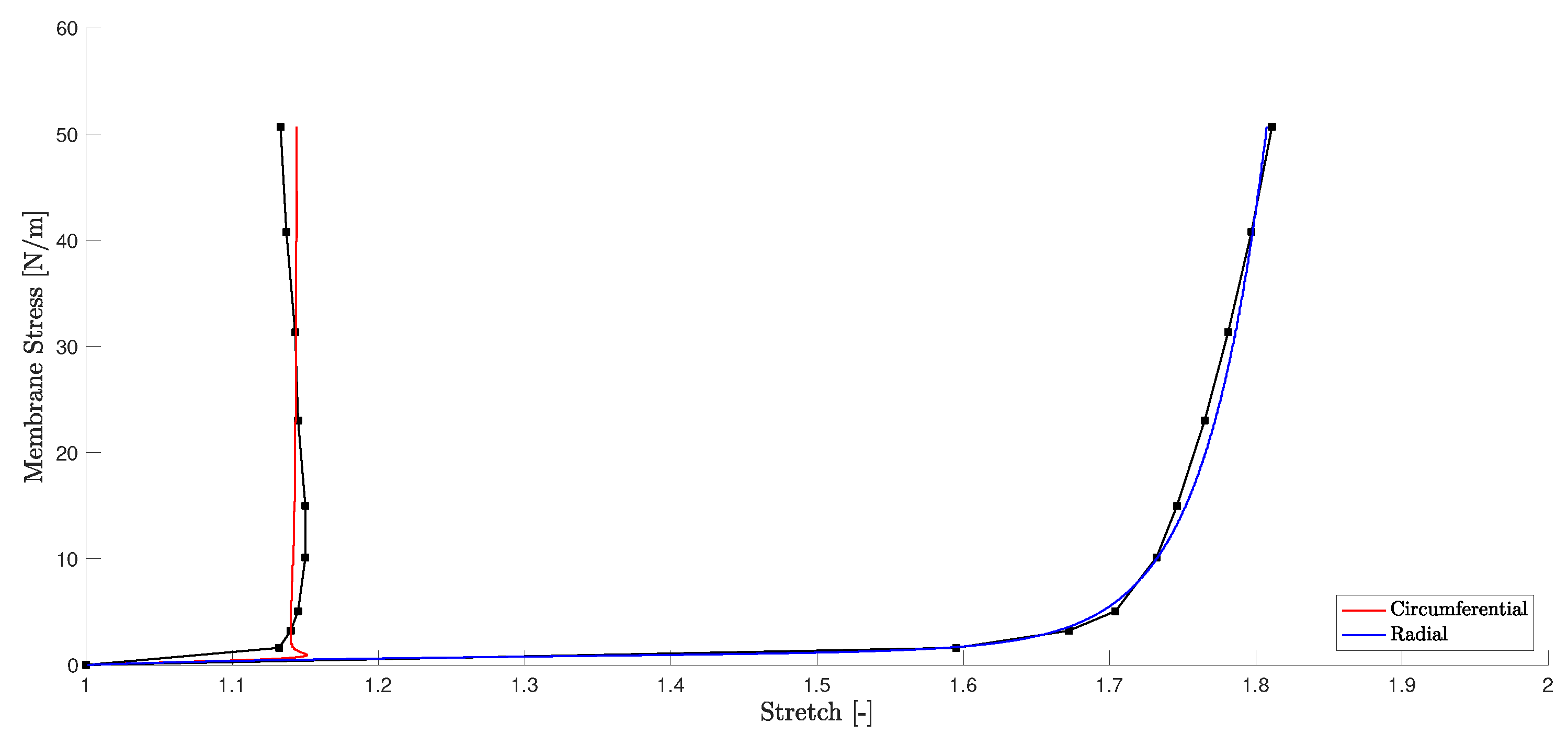
3.1. RVE Material Parameter Fitting
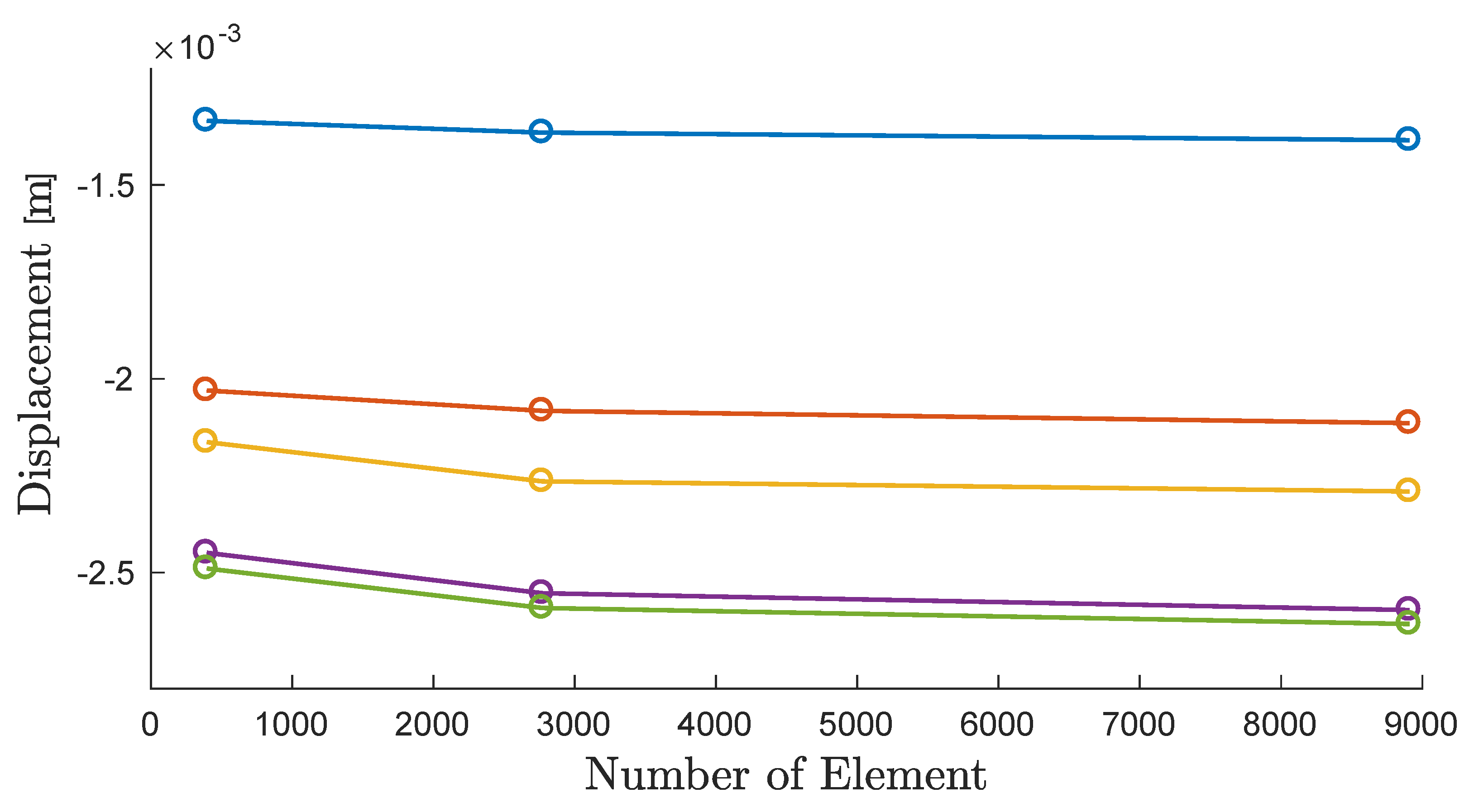
3.2. Mesh Convergence
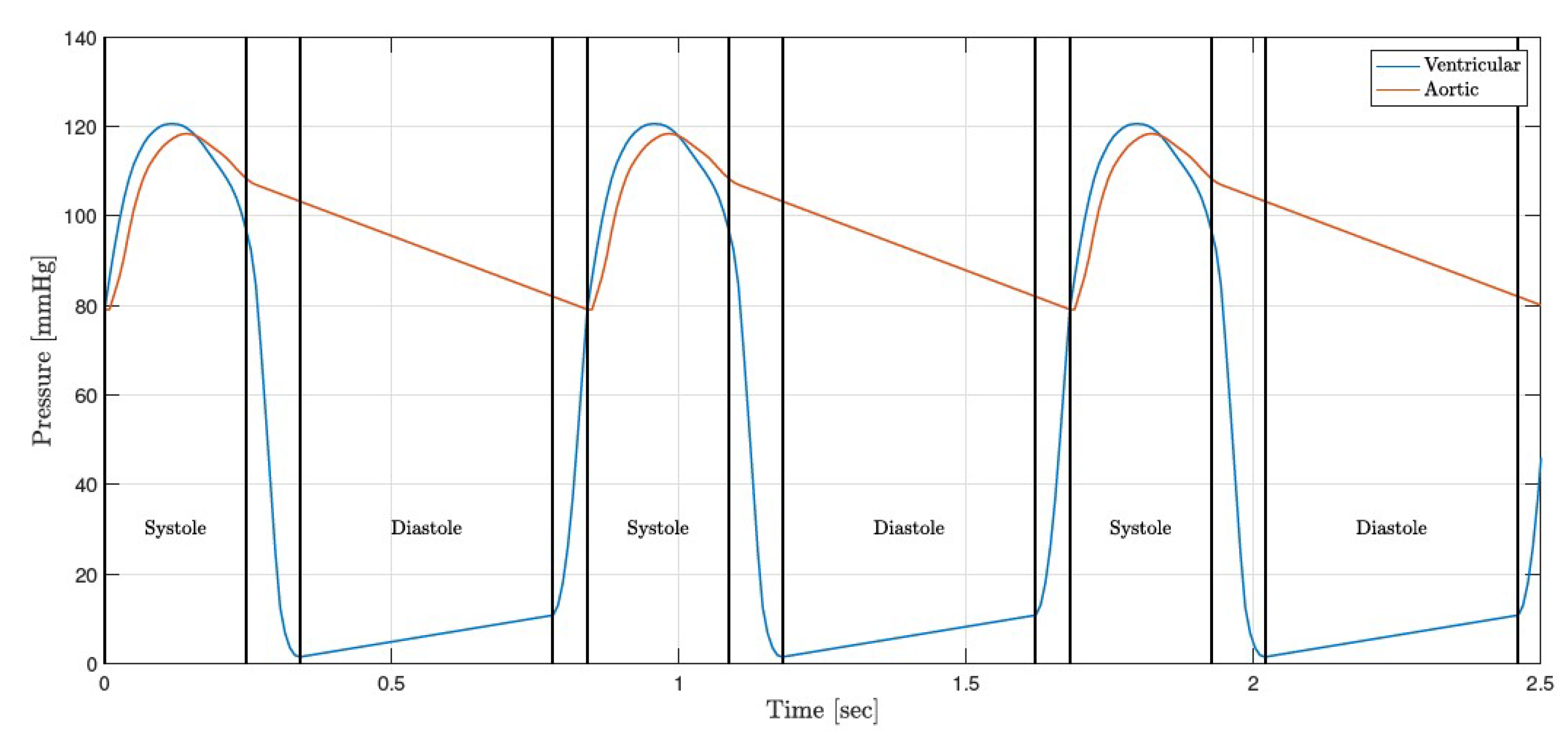
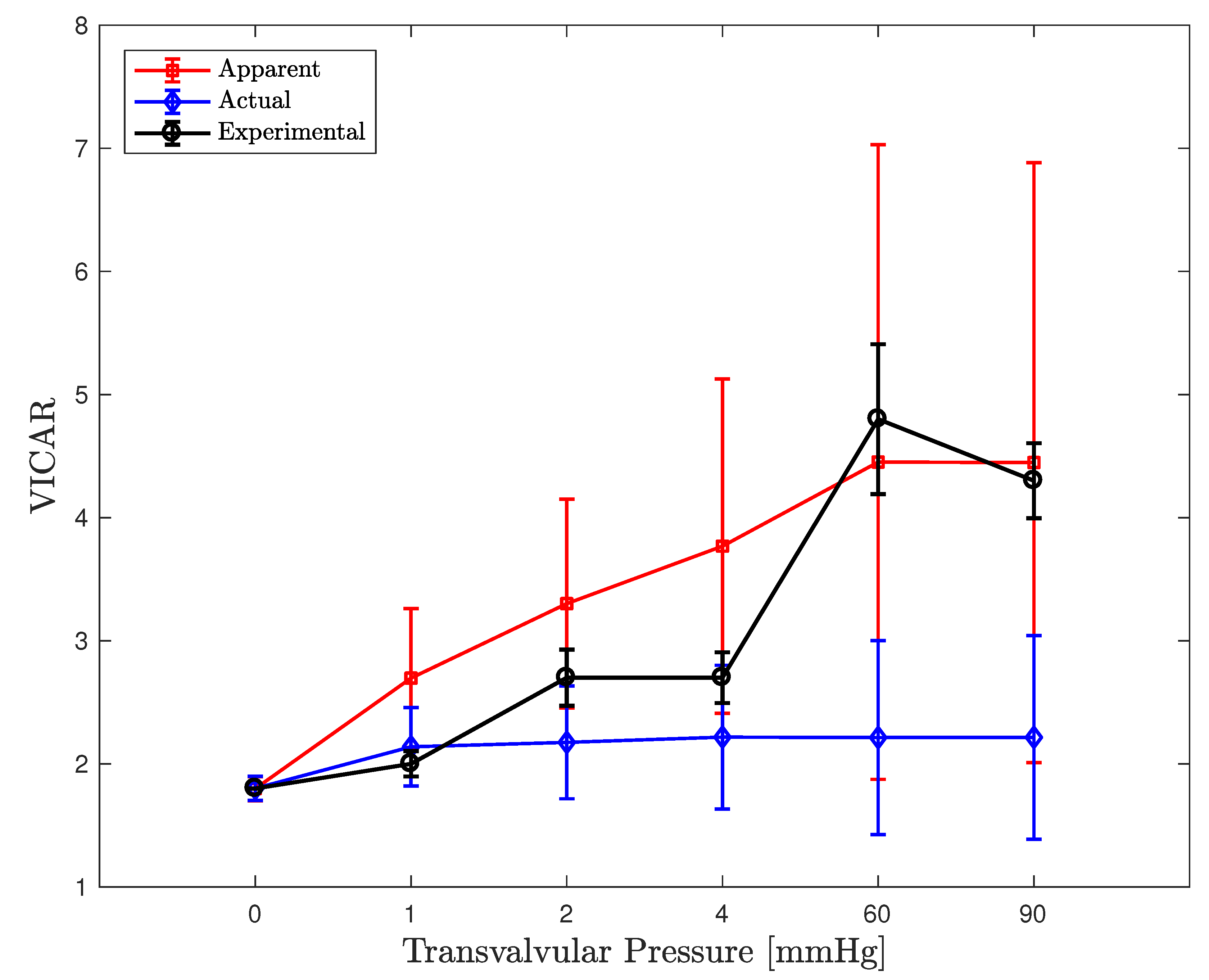
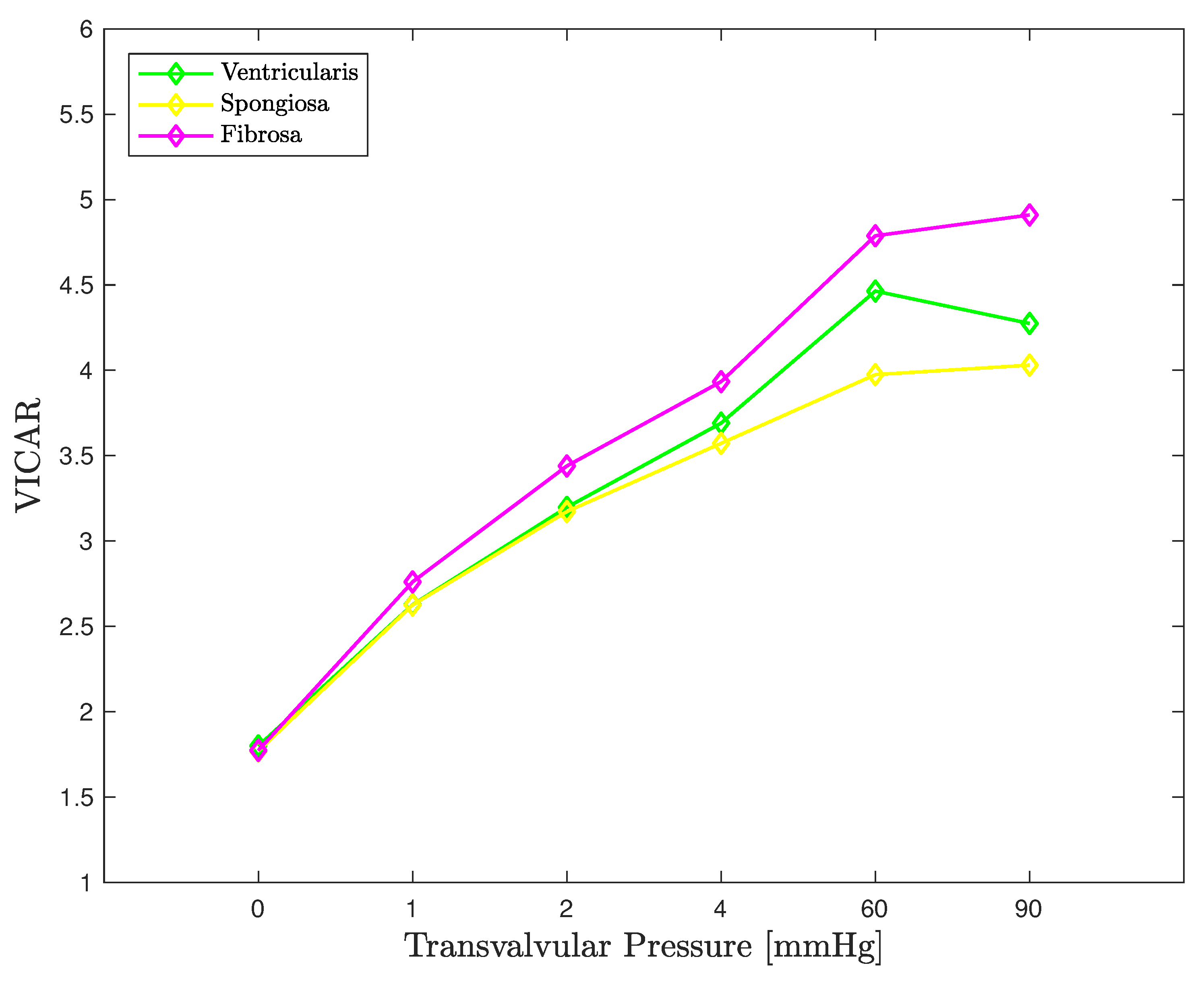
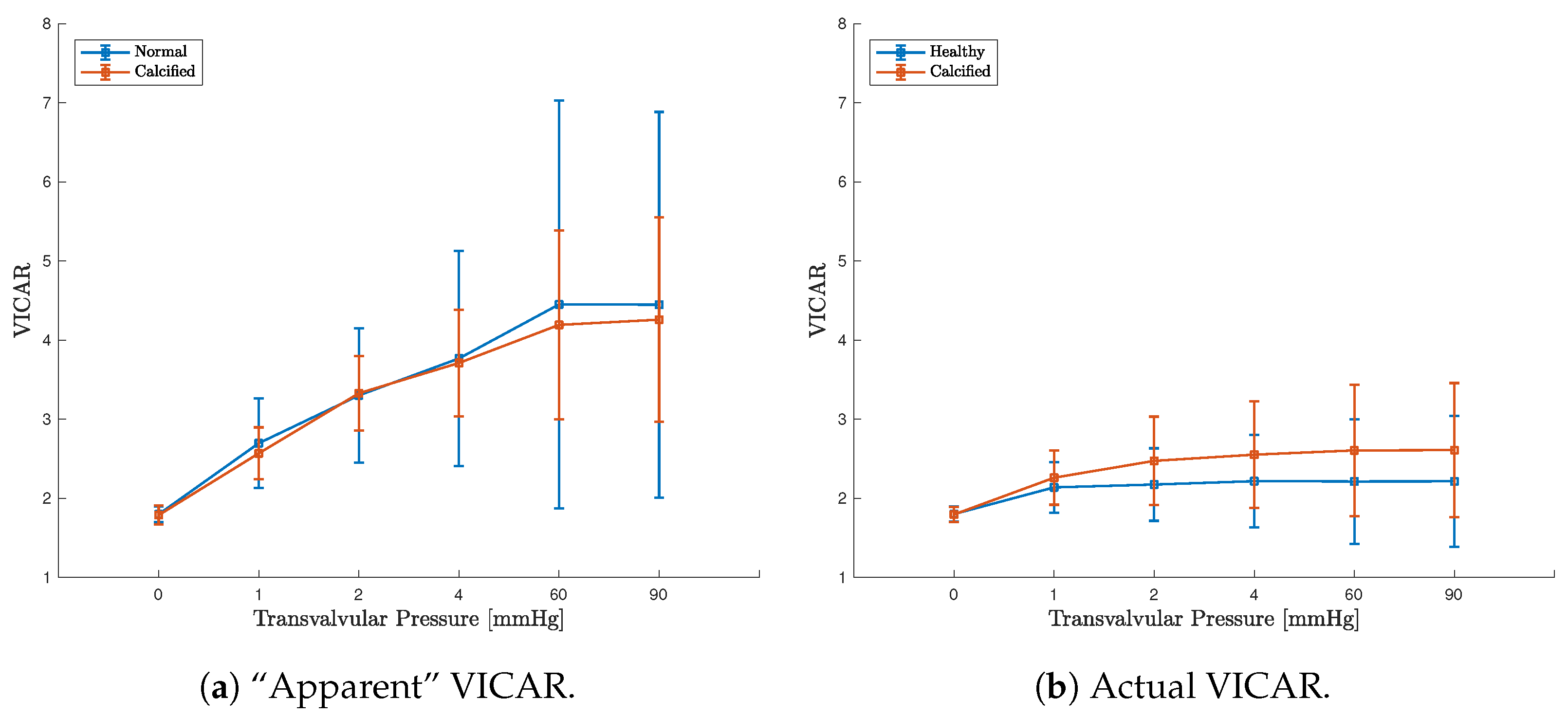
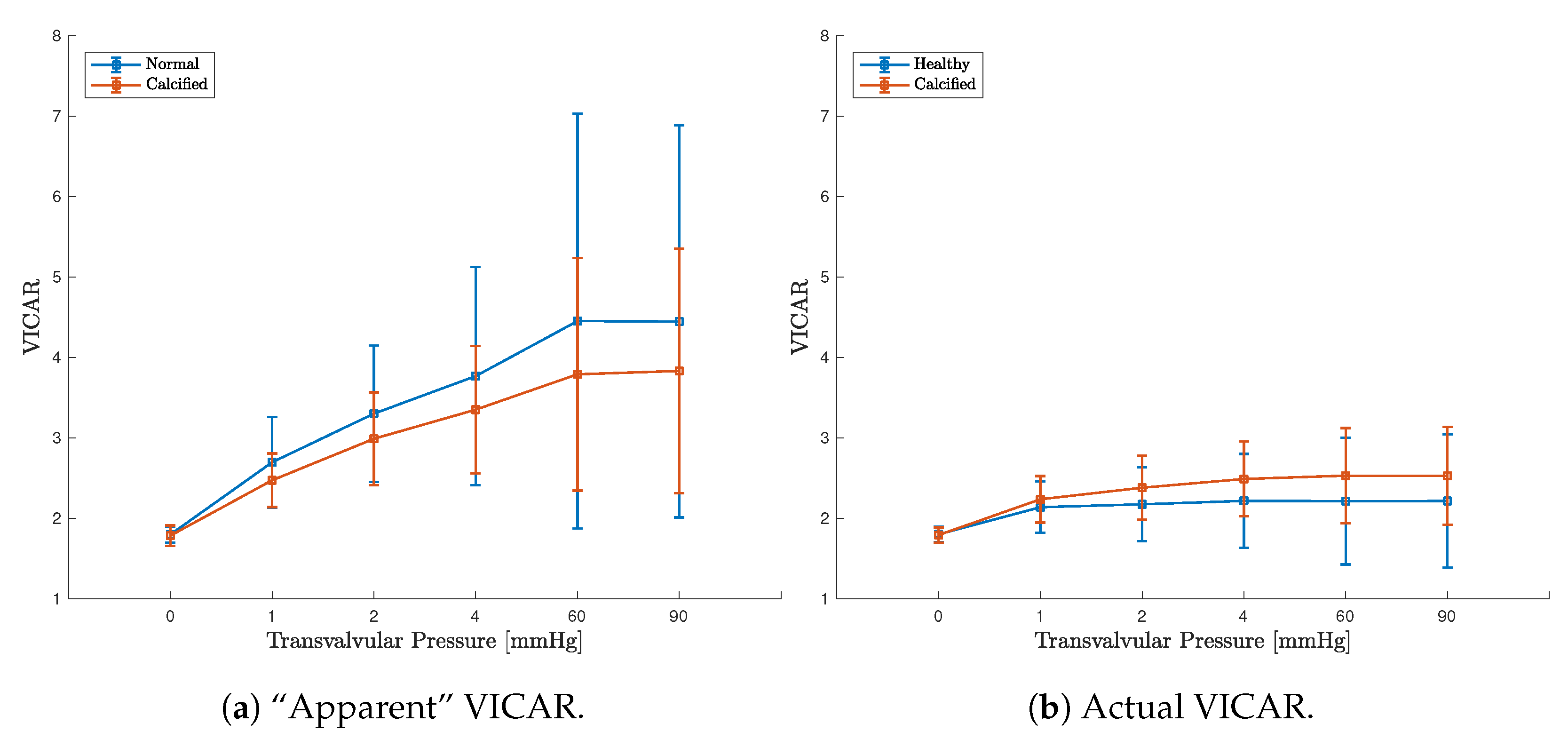
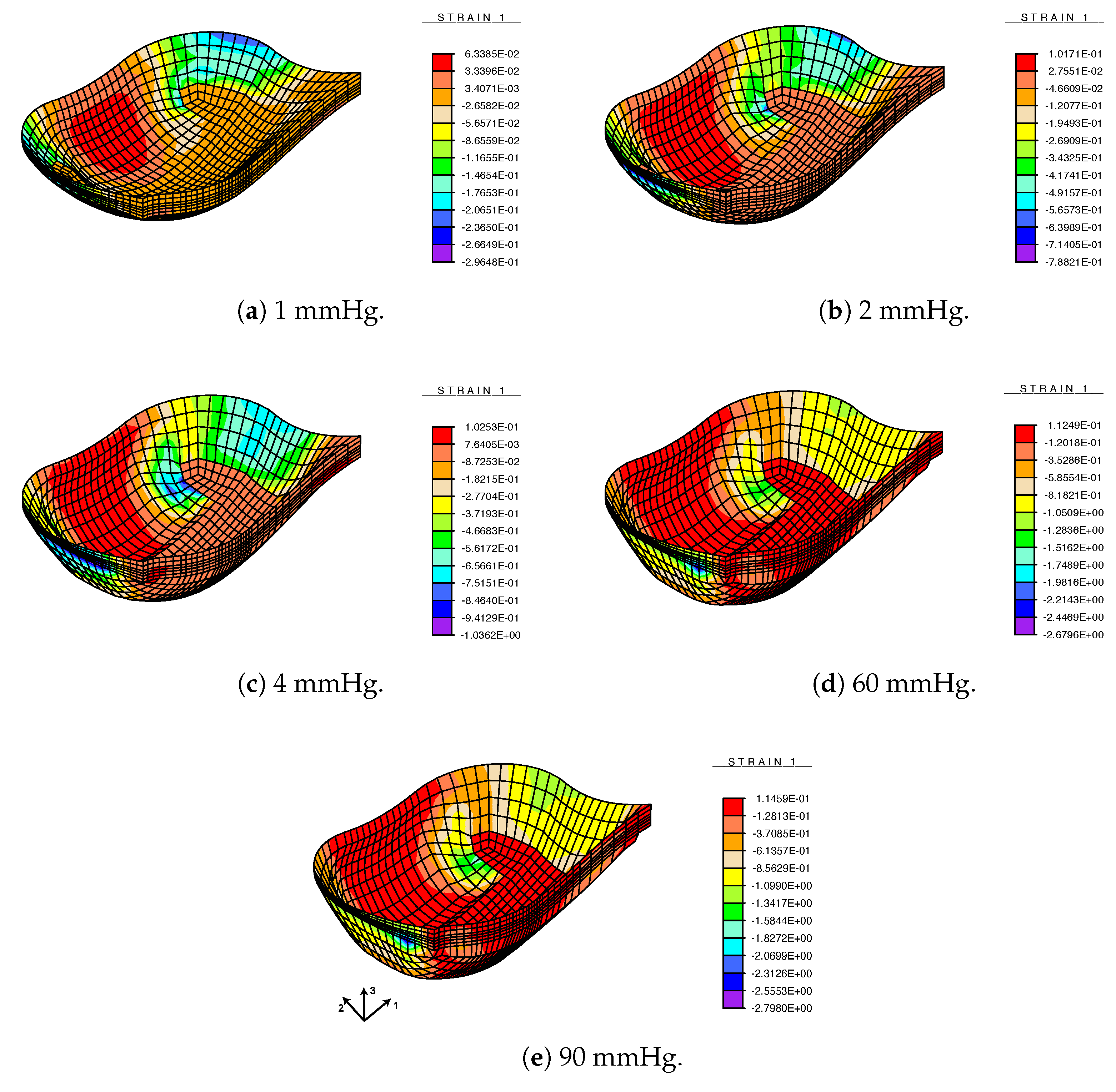
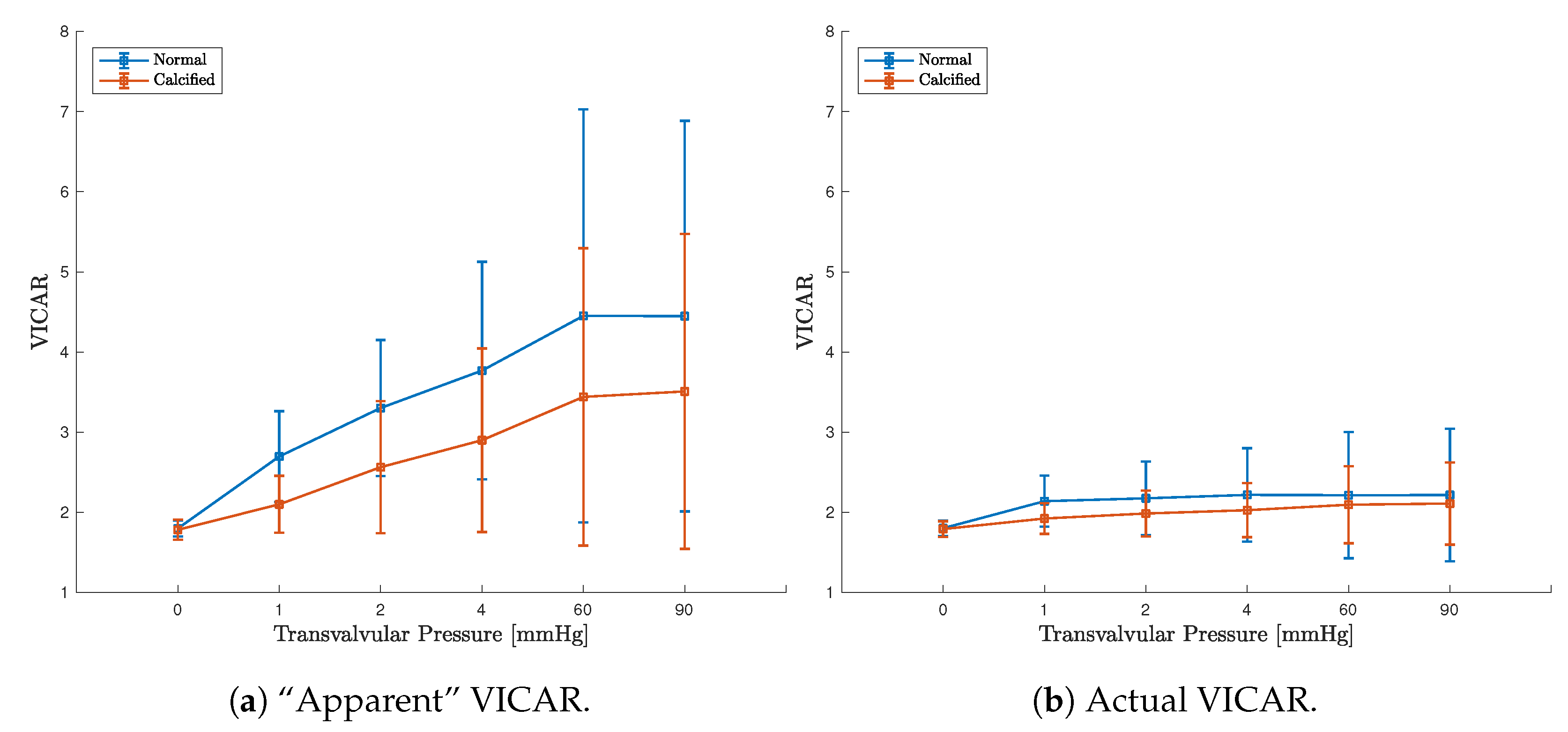
3.3. FE Result: Healthy Valve
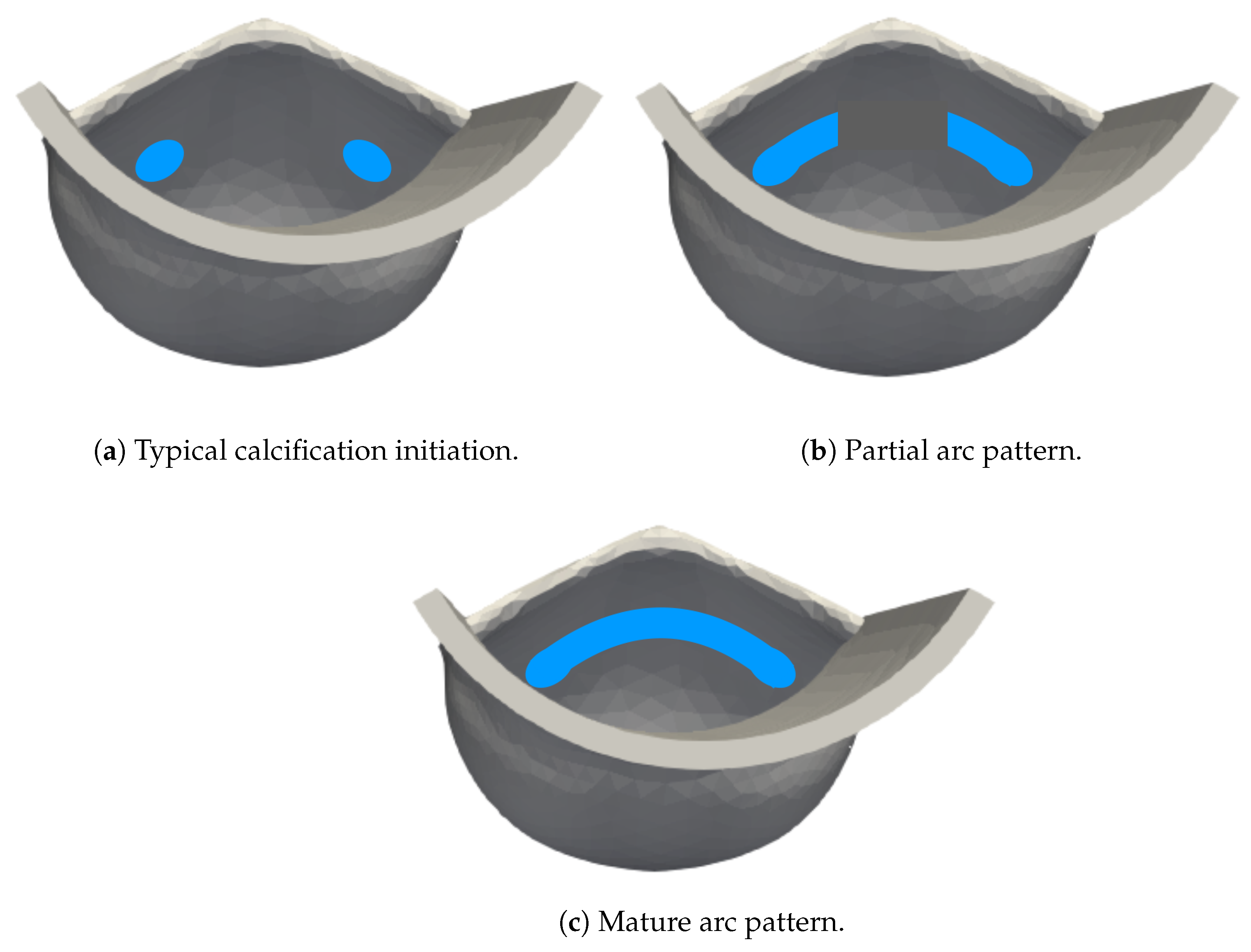
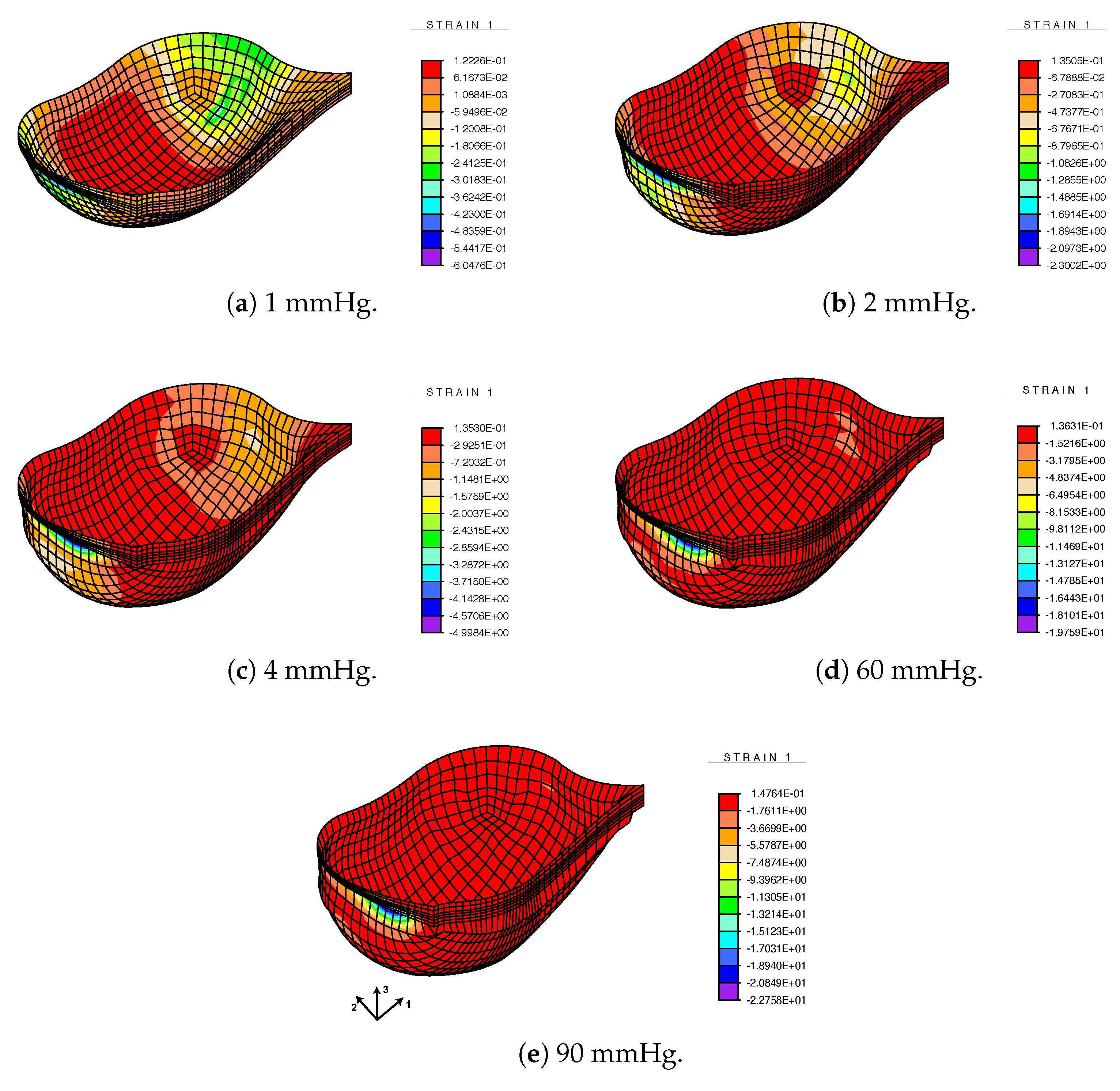
3.4. Calcified Valve: Early-Stage Nodules
3.5. Calcified Valve: Partial Arc Pattern
3.6. Calcified Valve: Mature Arc Pattern
4. Discussion
4.1. Healthy Valve
4.2. Calcified Valve
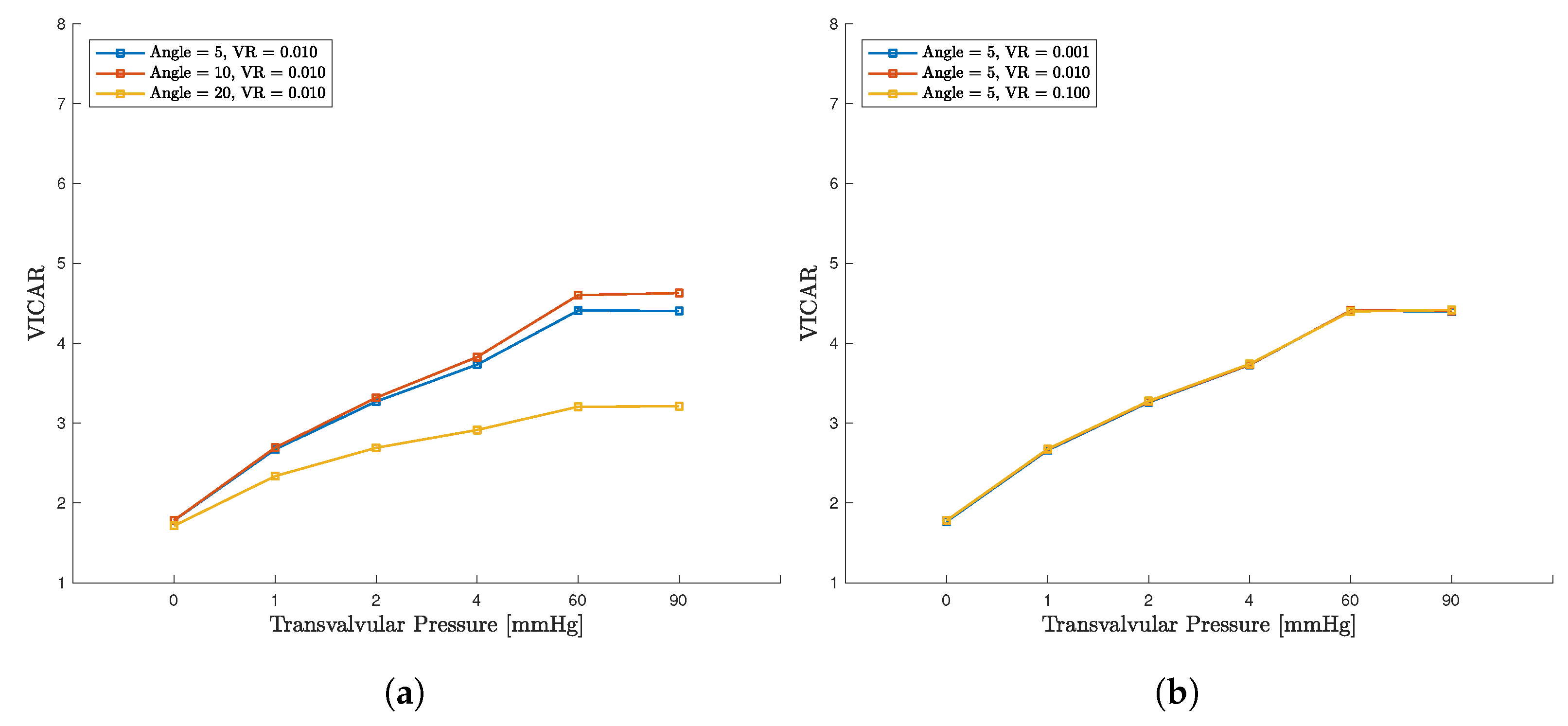
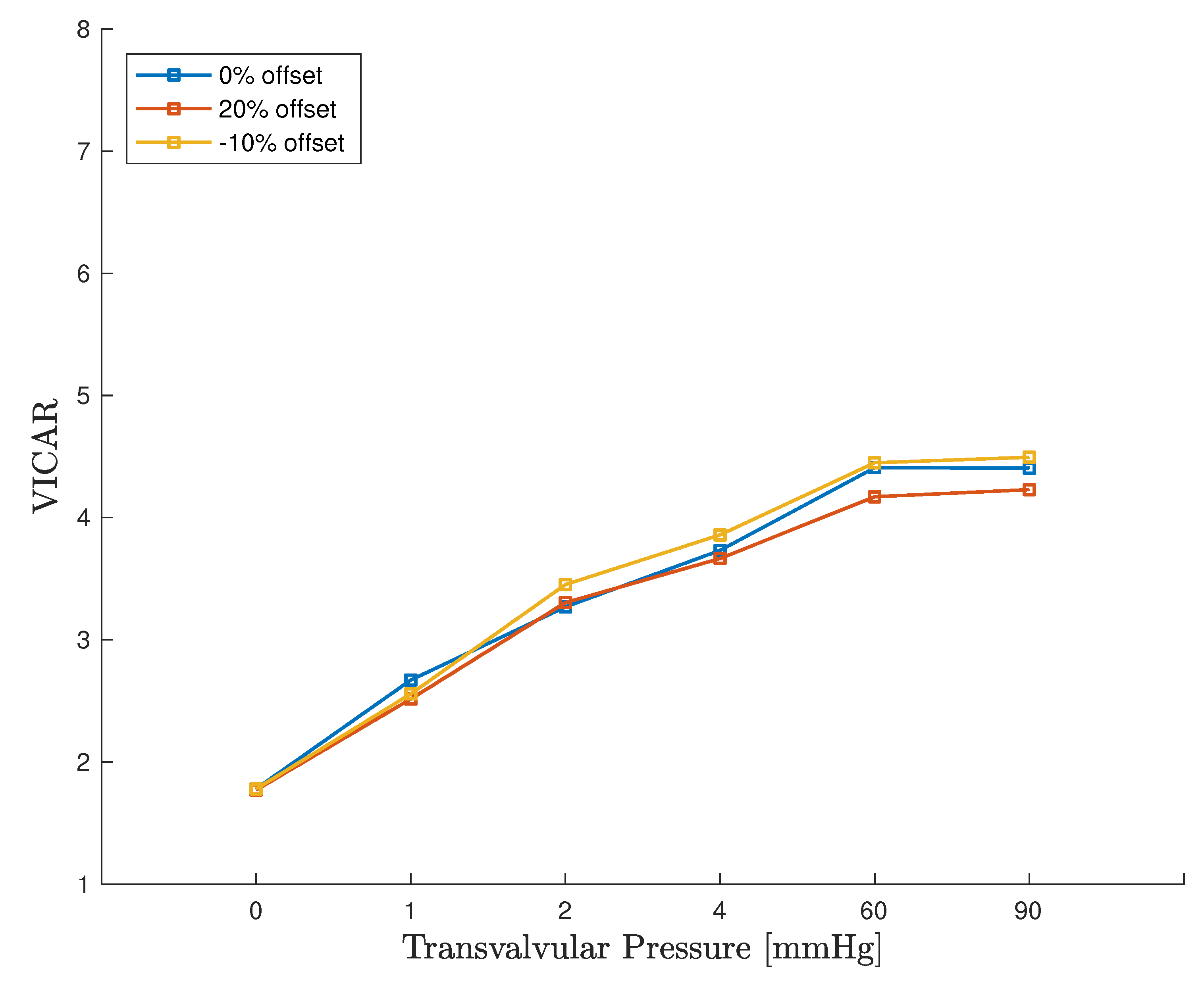
4.3. Computational Considerations
4.4. Summary and Outlook for Future Extensions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 2D | two dimension(s)(al) |
| 3D | three dimension(s)(al) |
| AV | aortic valve |
| CAS | calcified aortic stenosis |
| CRT | circumferential, radial, and transmural |
| CT | computed tomography |
| ECM | extracellular matrix |
| FE | finite element |
| FE | finite element method squared, computational homogenization |
| OOP | out-of-plane |
| RVE | representative volume element |
| VIC | valvular interstitial cells |
| VICAR | valvular interstitial cell aspect ratio |
| VR | volume ratio |
References
- Sacks, M.S.; Liao, J. (Eds.) Advances in Heart Valve Biomechanics: Valvular Physiology, Mechanobiology, and Bioengineering; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Taylor, P.M.; Batten, P.; Brand, N.J.; Thomas, P.S.; Yacoub, M.H. The Cardiac Valve Interstitial Cell. Int. J. Biochem. Cell Biol. 2003, 35, 113–118. [Google Scholar] [CrossRef]
- Arzani, A.; Mofrad, M.R.K. A Strain-based Finite Element Model for Calcification Progression In Aortic Valves. J. Biomech. 2017, 65, 216–220. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.Y.S. Micromechanical Simulations of Heart Valve Tissues. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2004. [Google Scholar]
- Huang, H.Y.S.; Liao, J.; Sacks, M.S. In-situ Deformation of the Aortic Valve Interstitial Cell Nucleus Under Diastolic Loading. J. Biomech. Eng. 2007, 129, 880–889. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, E.J.; Mofrad, M.R.K. Transient, Three-dimensional, Multiscale Simulations of the Human Aortic Valve. Cardiovasc. Eng. 2007, 7, 140–155. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Huang, H.Y.S. Virtual Experiments of Heart Valve Tissues. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; pp. 6645–6648. [Google Scholar]
- Weinberg, E.J.; Mofrad, M.R.K. A Multiscale Computational Comparison of the Bicuspid and Tricuspid Aortic Valves In Relation To Calcific Aortic Stenosis. J. Biomech. 2008, 41, 3482–3487. [Google Scholar] [CrossRef] [PubMed]
- Weinberg, E.J.; Schoen, F.J.; Mofrad, M.R.K. A Computational Model of Aging and Calcification In the Aortic Heart Valve. PLoS ONE 2009, 4, e5960. [Google Scholar] [CrossRef] [PubMed]
- Kouznetsova, V.G. Computational Homogenization for the Multi-Scale Analysis of Multi-Phase Materials. Ph.D. Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2002. [Google Scholar]
- Aikawa, E.; Hutcheson, J.D. Cardiovascular Calcification and Bone Mineralization; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Thubrikar, M.J. The Aortic Valve; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Ahrens, J.; Geveci, B.; Law, C. Paraview: An End-User Tool for Large-Data Visualization. In Visualization Handbook; Hansen, C.D., Johnson, C.R., Eds.; Butterworth-Heinemann: Burlington, MA, USA, 2005; pp. 717–731. [Google Scholar]
- Stewart, B.F.; Siscovick, D.; Lind, B.K.; Gardin, J.M.; Gottdiener, J.S.; Smith, V.E.; Kitzman, D.W.; Otto, C.M. Clinical Factors Associated With Calcific Aortic Valve Disease fn1. J. Am. Coll. Cardiol. 1997, 29, 630–634. [Google Scholar] [CrossRef]
- Mohler, E.R.; Gannon, F.; Reynolds, C.; Zimmerman, R.; Keane, M.G.; Kaplan, F.S. Bone Formation and Inflammation In Cardiac Valves. Circulation 2001, 103, 1522–1528. [Google Scholar] [CrossRef]
- Rajamannan, N.M.; Subramaniam, M.; Rickard, D.; Stock, S.R.; Donovan, J.; Springett, M.; Orszulak, T.; Fullerton, D.A.; Tajik, A.J.; Bonow, R.O. Human Aortic Valve Calcification Is Associated with an Osteoblast Phenotype. Circulation 2003, 107, 2181–2184. [Google Scholar] [CrossRef]
- Thubrikar, M.J.; Aouad, J.; Nolan, S.P. Patterns of Calcific Deposits In Operatively Excised Stenotic Or Purely Regurgitant Aortic Valves and Their Relation To Mechanical Stress. Am. J. Cardiol. 1986, 58, 304–308. [Google Scholar] [CrossRef]
- Halevi, R.; Hamdan, A.; Marom, G.; Mega, M.; Raanani, E.; Haj-Ali, R. Progressive Aortic Valve Calcification: Three-dimensional Visualization and Biomechanical Analysis. J. Biomech. 2015, 48, 489–497. [Google Scholar] [CrossRef]
- Otto, C.M.; Kuusisto, J.; Reichenbach, D.D.; Gown, A.M.; O’Brien, K.D. Characterization of the early lesion of `degenerative’ valvular aortic stenosis. Histological and immunohistochemical studies. Circulation 1994, 90, 844–853. [Google Scholar] [CrossRef]
- Weinberg, E.J.; Shahmirzadi, D.; Mofrad, M.R.K. On the Multiscale Modeling of Heart Valve Biomechanics In Health and Disease. Biomech. Model. Mechanobiol. 2010, 9, 373–387. [Google Scholar] [CrossRef] [PubMed]
- Yip, C.Y.Y.; Simmons, C.A. The Aortic Valve Microenvironment and Its Role In Calcific Aortic Valve Disease. Cardiovasc. Pathol. 2011, 20, 177–182. [Google Scholar] [CrossRef] [PubMed]
- Ge, L.; Sotiropoulos, F. Direction and Magnitude of Blood Flow Shear Stresses on the Leaflets of Aortic Valves: Is There a Link With Valve Calcification? J. Biomech. Eng. 2010, 132, 014505. [Google Scholar] [CrossRef] [PubMed]
- Balachandran, K.; Sucosky, P.; Jo, H.; Yoganathan, A.P. Elevated Cyclic Stretch Alters Matrix Remodeling In Aortic Valve Cusps: Implications for Degenerative Aortic Valve Disease. Am. J. Physiol.-Heart Circ. Physiol. 2009, 296, H756–H764. [Google Scholar] [CrossRef] [PubMed]
- Bouchareb, R.; Boulanger, M.C.; Fournier, D.; Pibarot, P.; Messaddeq, Y.; Mathieu, P. Mechanical Strain Induces the Production of Spheroid Mineralized Microparticles In the Aortic Valve Through a Rhoa/rock-dependent Mechanism. J. Mol. Cell. Cardiol. 2014, 67, 49–59. [Google Scholar] [CrossRef]
- Merryman, W.D. Mechano-Potential Etiologies of Aortic Valve Disease. J. Biomech. 2010, 43, 87–92. [Google Scholar] [CrossRef]
- Freeman, R.V.; Otto, C.M. Spectrum of Calcific Aortic Valve Disease: Pathogenesis, Disease Progression, and Treatment Strategies. Circulation 2005, 111, 3316–3326. [Google Scholar] [CrossRef] [PubMed]
- Yap, C.H.; Saikrishnan, N.; Tamilselvan, G.; Yoganathan, A.P. Experimental Measurement of Dynamic Fluid Shear Stress on the Aortic Surface of the Aortic Valve Leaflet. Biomech. Model. Mechanobiol. 2012, 11, 171–182. [Google Scholar] [CrossRef]
- Fisher, C.I.; Chen, J.; Merryman, W.D. Calcific Nodule Morphogenesis By Heart Valve Interstitial Cells Is Strain Dependent. Biomech. Model. Mechanobiol. 2013, 12, 5–17. [Google Scholar] [CrossRef] [PubMed]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; Wiley: Chichester, UK, 2000. [Google Scholar]
- Anand, L.; Govindjee, S. Continuum Mechanics of Solids; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Fung, Y.C. Biomechanical Aspects of Growth and Tissue Engineering. In Biomechanics: Motion, Flow, Stress, and Growth; Springer: New York, NY, USA, 1990; pp. 499–546. [Google Scholar]
- Ball, J.M. Convexity Conditions and Existence Theorems In Nonlinear Elasticity. Arch. Ration. Mech. Anal. 1976, 63, 337–403. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method: Solid Mechanics; Butterworth-Heinemann: Oxford, UK, 2000; Volume 2. [Google Scholar]
- Taylor, R.L.; Govindjee, S. FEAP—Finite Element Analysis Program; University of California: Berkeley, CA, USA, 2020. [Google Scholar]
- Haj-Ali, R.; Marom, G.; Zekry, S.B.; Rosenfeld, M.; Raanani, E. A General Three-dimensional Parametric Geometry of the Native Aortic Valve and Root for Biomechanical Modeling. J. Biomech. 2012, 45, 2392–2397. [Google Scholar] [CrossRef]
- Stella, J.A.; Sacks, M.S. On the Biaxial Mechanical Properties of the Layers of the Aortic Valve Leaflet. J. Biomech. Eng. 2007, 129, 757–766. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, R.M.; Sacks, M.S. Interlayer Micromechanics of the Aortic Heart Valve Leaflet. Biomech. Model. Mechanobiol. 2014, 13, 813–826. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sacks, M.S.; Yoganathan, A.P. Heart valve function: A Biomechanical Perspective. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1369–1391. [Google Scholar] [CrossRef] [PubMed]
- Bakhaty, A.A.; Govindjee, S.; Mofrad, M.R.K. Consistent trilayer biomechanical modeling of aortic valve leaflet tissue. J. Biomech. 2017, 61, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Fang, Q.; Boas, D. Tetrahedral mesh generation from volumetric binary and gray-scale images. In Proceedings of the 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Boston, MA, USA, 28 June–1 July 2009; pp. 1142–1145. [Google Scholar]
- Rho, J.Y.; Hobatho, M.C.; Ashman, R.B. Relations of Mechanical Properties To Density and CT Numbers In Human Bone. Med. Eng. Phys. 1995, 17, 347–355. [Google Scholar] [CrossRef]
- Weatherill, N.P.; Hassan, O. Efficient Three-dimensional Delaunay Triangulation With Automatic Point Creation and Imposed Boundary Constraints. Int. J. Numer. Methods Eng. 1994, 37, 2005–2039. [Google Scholar] [CrossRef]
- Miehe, C.; Schröder, J.; Schotte, J. Computational Homogenization Analysis In Finite Plasticity Simulation of Texture Development In Polycrystalline Materials. Comput. Methods Appl. Mech. Eng. 1999, 171, 387–418. [Google Scholar] [CrossRef]
- Li, S.; Wang, G. Introduction to Micromechanics and Nanomechanics; World Scientific Publishing Company: Singapore, 2008. [Google Scholar]
- Mofrad, M.R.K.; Kamm, R.D. Cellular Mechanotransduction: Diverse Perspectives from Molecules to Tissues; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]





| Load Step | 1 | 2 | 3 | 4 | 5 |
| Pressure | 1 | 2 | 4 | 60 | 90 |
| Model | (Pa) | (-) | (Pa) | (-) | () |
|---|---|---|---|---|---|
| Fibrosa | 6.7 | 16.31 | 43.19 | 0.64 | |
| Ventricularis | 0.25 | 0.39 | 1.51 | 3.63 | 9.71 |
| Spongiosa | 0 | 0 | 0 | 0 | 0 |
| Load (mmHg) | 1 | 2 | 4 | 60 | 90 |
| Circumferential Strain Ratio | 0.96 | 1.19 | 1.32 | 1.26 | 1.21 |
| Radial Strain Ratio | 0.14 | 0.31 | 0.42 | 0.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakhaty, A.A.; Govindjee, S.; Mofrad, M.R.K. A Coupled Multiscale Approach to Modeling Aortic Valve Mechanics in Health and Disease. Appl. Sci. 2021, 11, 8332. https://doi.org/10.3390/app11188332
Bakhaty AA, Govindjee S, Mofrad MRK. A Coupled Multiscale Approach to Modeling Aortic Valve Mechanics in Health and Disease. Applied Sciences. 2021; 11(18):8332. https://doi.org/10.3390/app11188332
Chicago/Turabian StyleBakhaty, Ahmed A., Sanjay Govindjee, and Mohammad R. K. Mofrad. 2021. "A Coupled Multiscale Approach to Modeling Aortic Valve Mechanics in Health and Disease" Applied Sciences 11, no. 18: 8332. https://doi.org/10.3390/app11188332
APA StyleBakhaty, A. A., Govindjee, S., & Mofrad, M. R. K. (2021). A Coupled Multiscale Approach to Modeling Aortic Valve Mechanics in Health and Disease. Applied Sciences, 11(18), 8332. https://doi.org/10.3390/app11188332






