Towards Autonomous Bridge Inspection: Sensor Mounting Using Aerial Manipulators
Featured Application
Abstract
1. Introduction
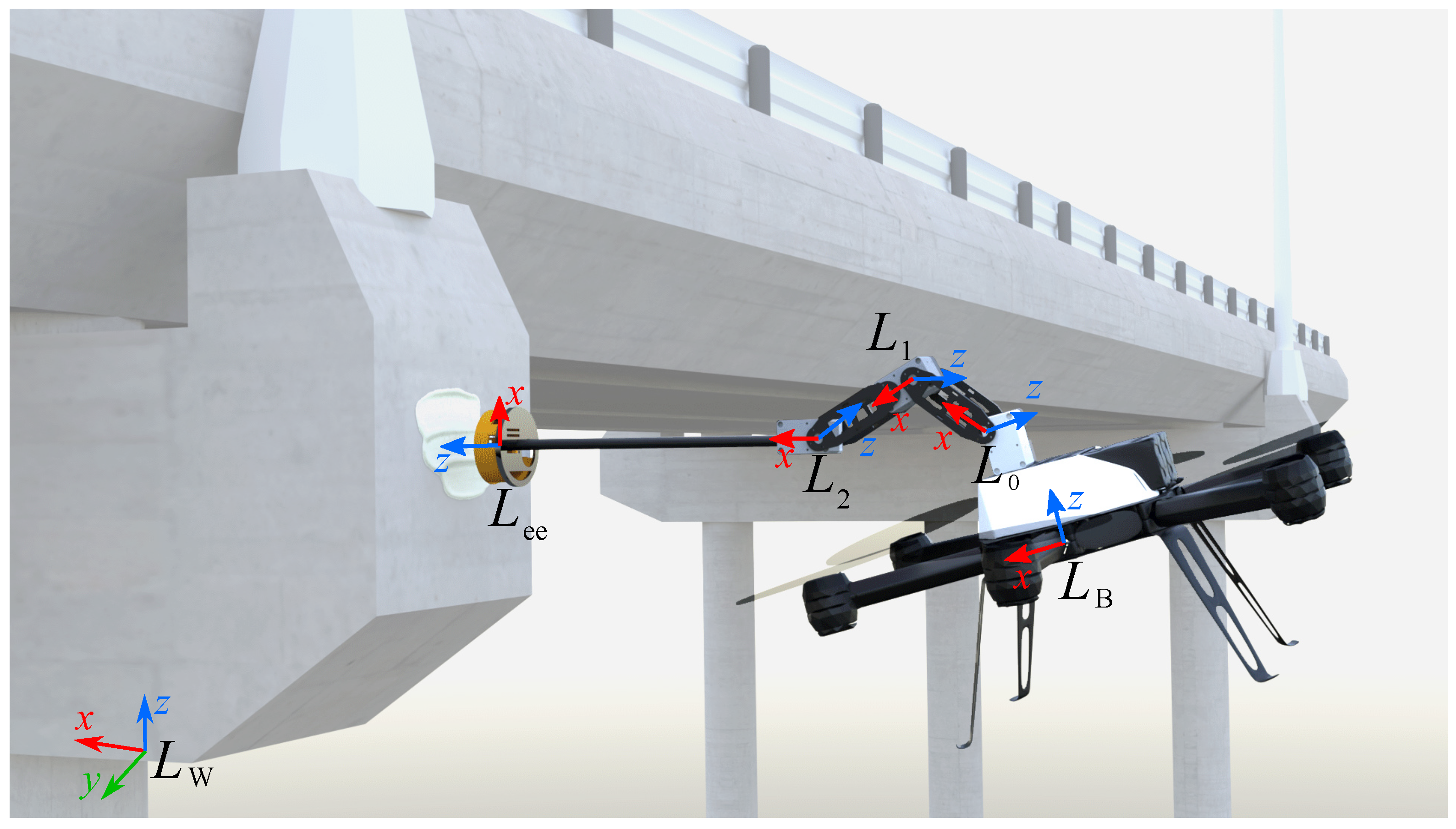
1.1. Concept
1.2. Contributions
2. Related Work
3. Mathematical Model
3.1. Kinematics
3.2. Dynamics
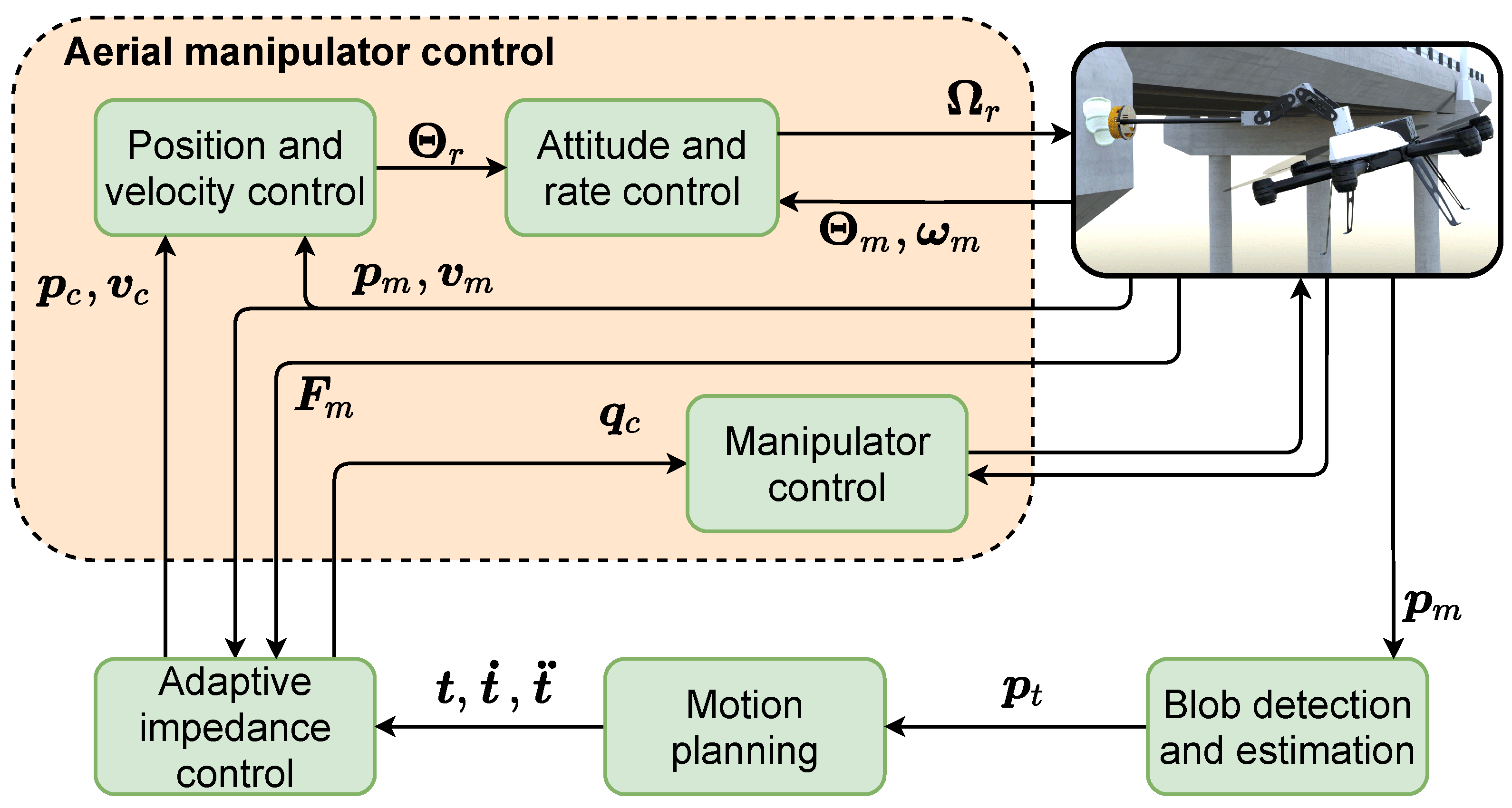
4. Control System
4.1. Aerial Manipulator Control
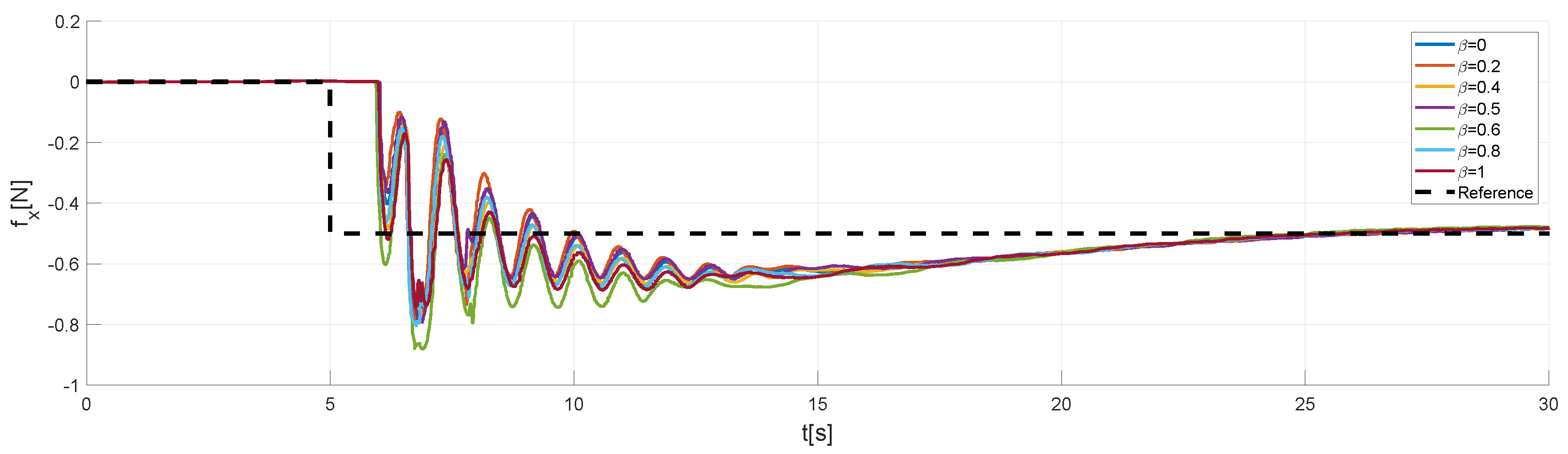
4.2. Adaptive Impedance Control
5. Motion Planning
5.1. Waypoint Configuration
5.2. Trajectory Planning
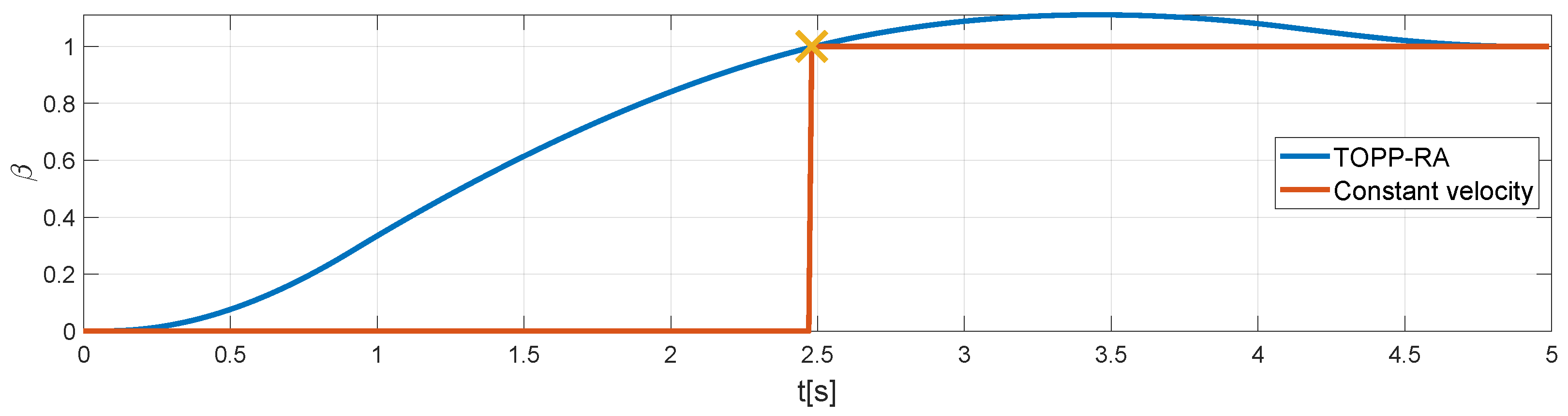
Initial Trajectory
5.3. Model-Based Corrections
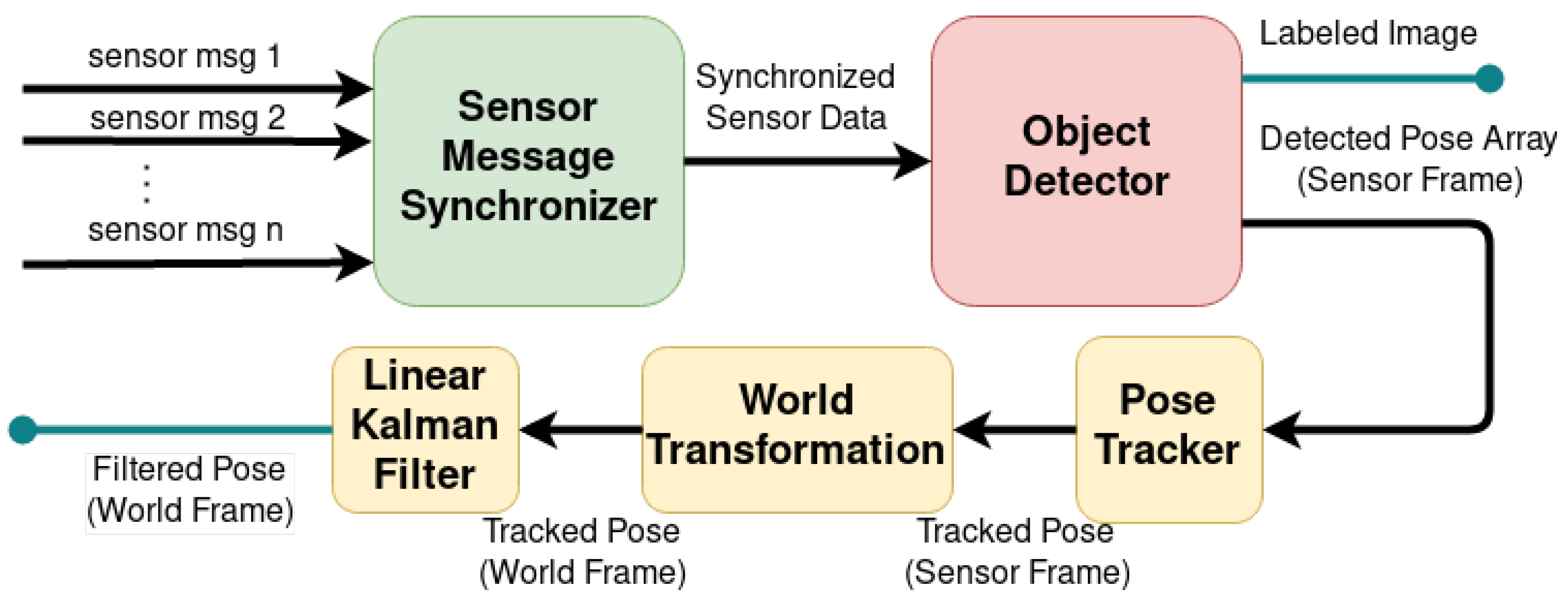
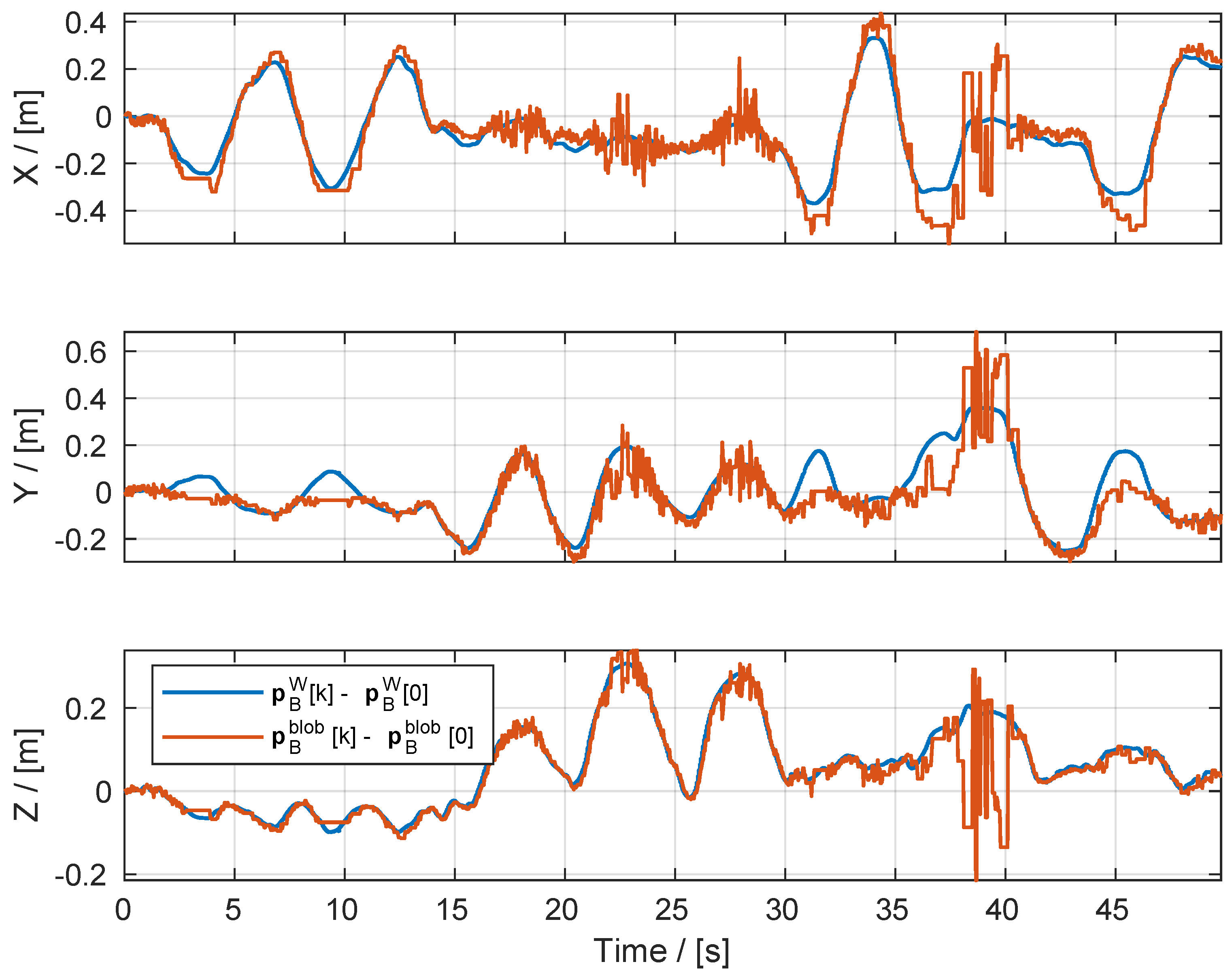
6. Blob Detection
7. Simulation
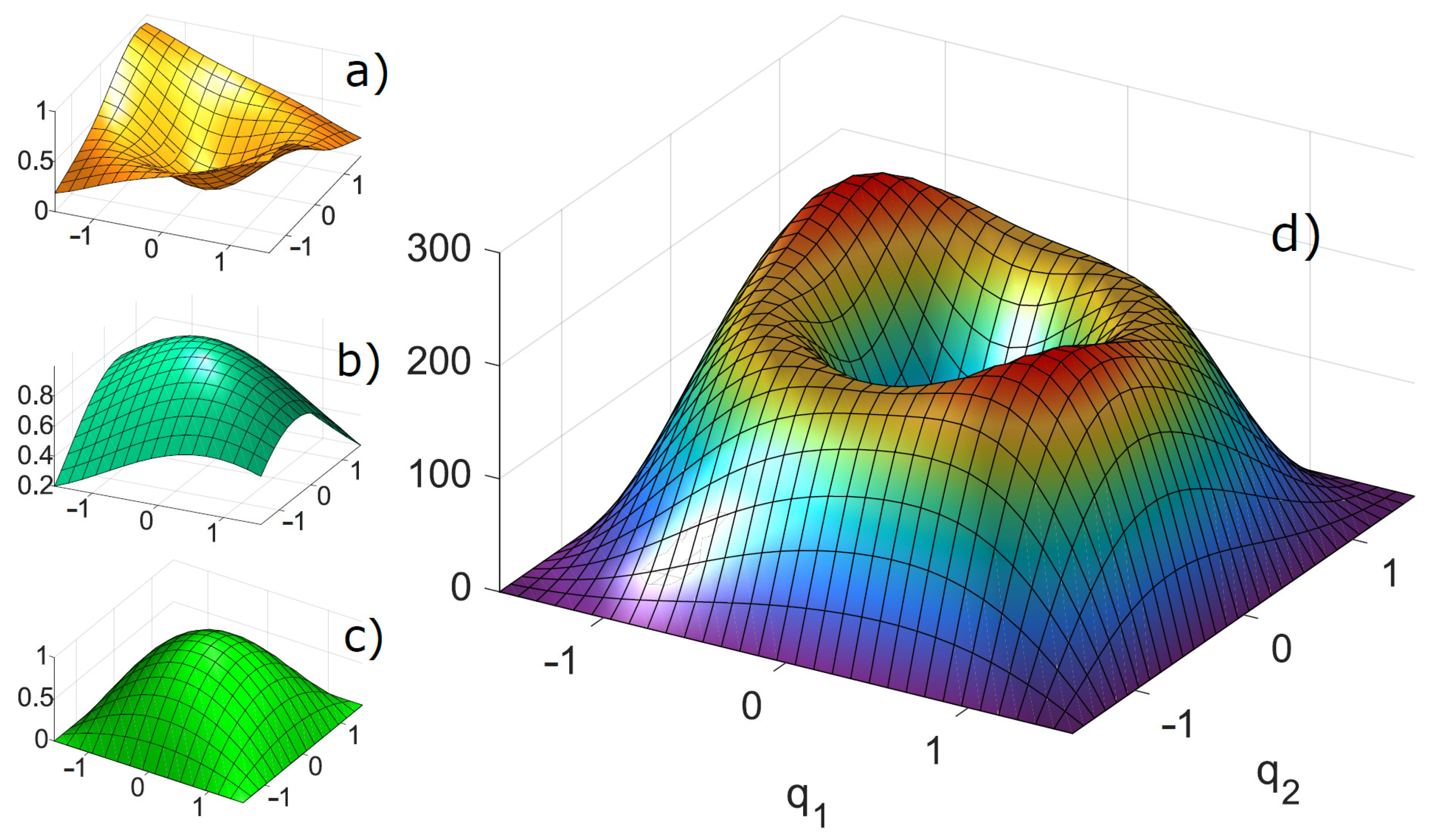
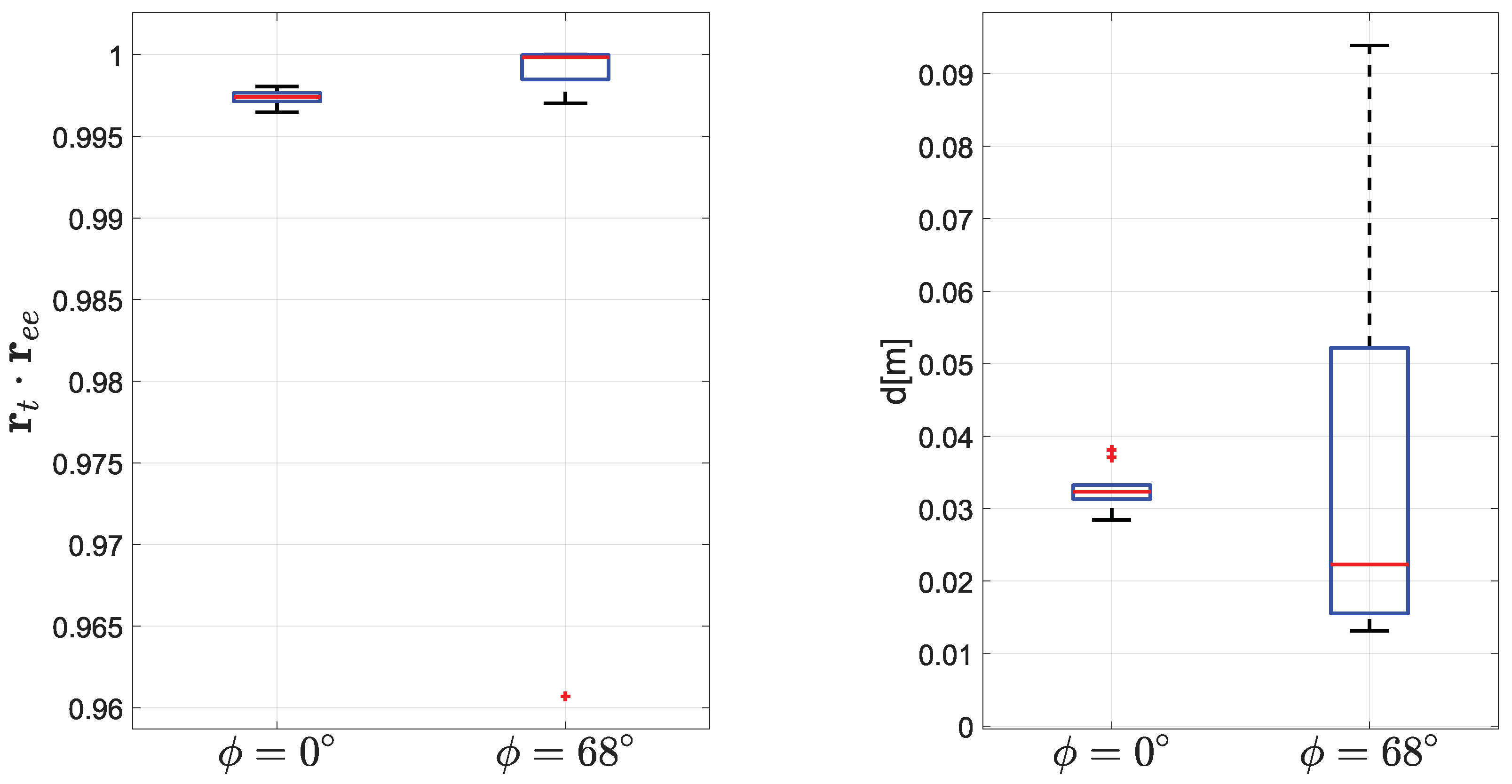
7.1. End-Effector Motion Distribution Analysis
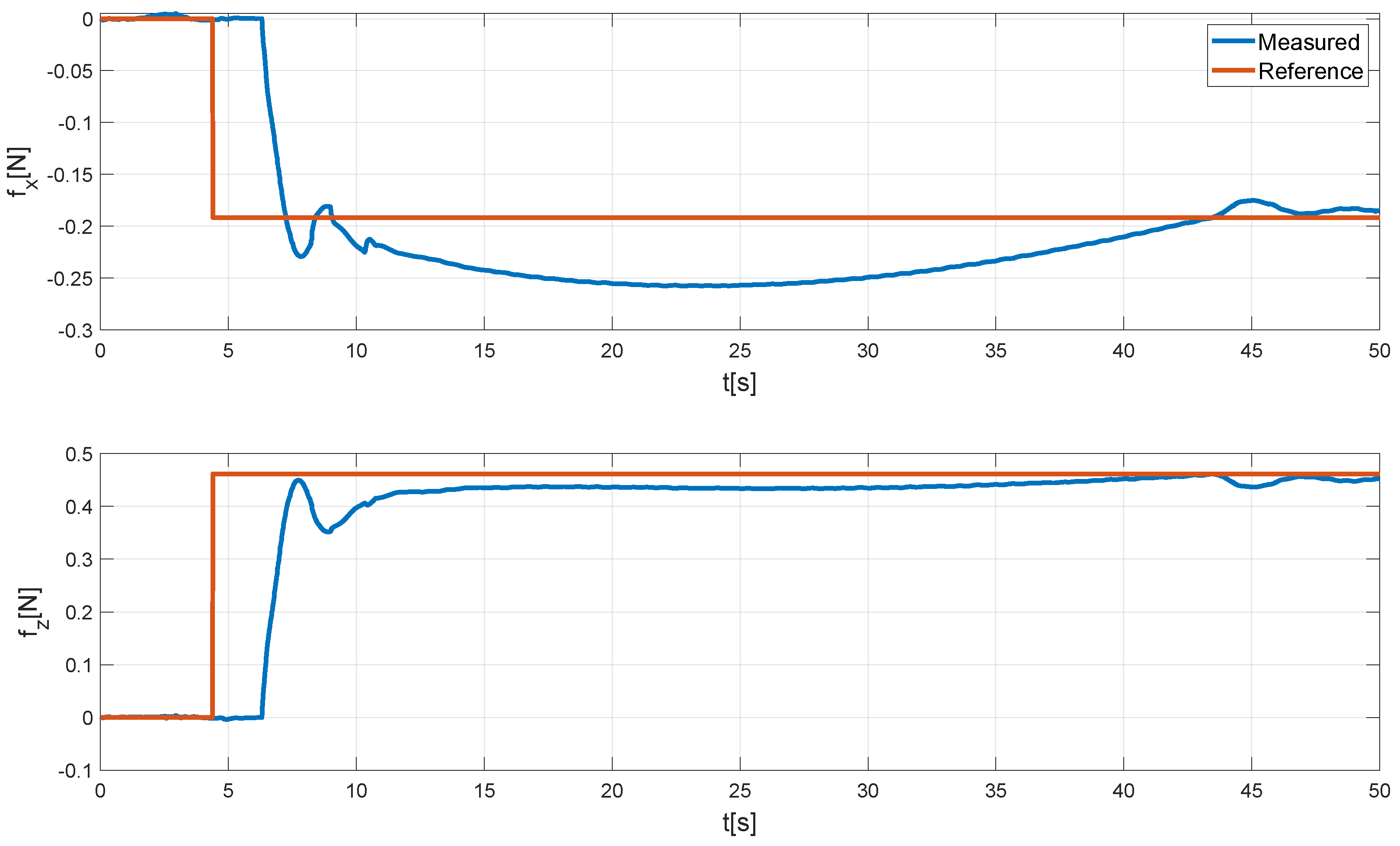
7.2. Bridge Sensor Mounting
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Kashif Ur Rehman, S.; Ibrahim, Z.; Memon, S.A.; Jameel, M. Nondestructive test methods for concrete bridges: A review. Constr. Build. Mater. 2016, 107, 58–86. [Google Scholar] [CrossRef]
- Hunt, G.; Mitzalis, F.; Alhinai, T.; Hooper, P.A.; Kovac, M. 3D printing with flying robots. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 4493–4499. [Google Scholar] [CrossRef]
- Vempati, A.S.; Kamel, M.; Stilinovic, N.; Zhang, Q.; Reusser, D.; Sa, I.; Nieto, J.; Siegwart, R.; Beardsley, P. PaintCopter: An Autonomous UAV for Spray Painting on Three-Dimensional Surfaces. IEEE Robot. Autom. Lett. 2018, 3, 2862–2869. [Google Scholar] [CrossRef]
- Jeong, E.; Seo, J.; Wacker, J. Literature Review and Technical Survey on Bridge Inspection Using Unmanned Aerial Vehicles. J. Perform. Constr. Facil. 2020, 34, 04020113. [Google Scholar] [CrossRef]
- Cacace, J.; Orozco-Soto, S.M.; Suarez, A.; Caballero, A.; Orsag, M.; Bogdan, S.; Vasiljevic, G.; Ebeid, E.; Rodriguez, J.A.A.; Ollero, A. Safe Local Aerial Manipulation for the Installation of Devices on Power Lines: AERIAL-CORE First Year Results and Designs. Appl. Sci. 2021, 11, 6220. [Google Scholar] [CrossRef]
- Zollini, S.; Alicandro, M.; Dominici, D.; Quaresima, R.; Giallonardo, M. UAV Photogrammetry for Concrete Bridge Inspection Using Object-Based Image Analysis (OBIA). Remote Sens. 2020, 12, 3180. [Google Scholar] [CrossRef]
- Bolourian, N.; Hammad, A. LiDAR-equipped UAV path planning considering potential locations of defects for bridge inspection. Autom. Constr. 2020, 117, 103250. [Google Scholar] [CrossRef]
- Reagan, D.; Sabato, A.; Niezrecki, C. Unmanned aerial vehicle acquisition of three-dimensional digital image correlation measurements for structural health monitoring of bridges. In Proceedings of the Nondestructive Characterization and Monitoring of Advanced Materials, Aerospace, and Civil Infrastructure, Portland, OR, USA, 25–29 March 2017; Wu, H.F., Gyekenyesi, A.L., Shull, P.J., Yu, T.Y., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, DC, USA, 2017; Volume 10169, pp. 68–77. [Google Scholar] [CrossRef]
- Chen, H.; Quan, F.; Fang, L.; Zhang, S. Aerial Grasping with a Lightweight Manipulator Based on Multi-Objective Optimization and Visual Compensation. Sensors 2019, 19, 4253. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; He, Y.; Dai, B.; Gu, F.; Yang, L.; Han, J.; Liu, G. Aerial Grasping of an Object in the Strong Wind: Robust Control of an Aerial Manipulator. Appl. Sci. 2019, 9, 2230. [Google Scholar] [CrossRef]
- Sanchez-Cuevas, P.J.; Gonzalez-Morgado, A.; Cortes, N.; Gayango, D.B.; Jimenez-Cano, A.E.; Ollero, A.; Heredia, G. Fully-Actuated Aerial Manipulator for Infrastructure Contact Inspection: Design, Modeling, Localization, and Control. Sensors 2020, 20, 4708. [Google Scholar] [CrossRef] [PubMed]
- Baca, T.; Penicka, R.; Stepan, P.; Petrlik, M.; Spurny, V.; Hert, D.; Saska, M. Autonomous Cooperative Wall Building by a Team of Unmanned Aerial Vehicles in the MBZIRC 2020 Competition. arXiv 2020, arXiv:2012.05946. [Google Scholar]
- Vatavuk, I.; Polic, M.; Hrabar, I.; Petric, F.; Orsag, M.; Bogdan, S. Autonomous, Mobile Manipulation in a Wall-building Scenario: Team LARICS at MBZIRC 2020. J. Field Robot. 2021. submitted for publication. [Google Scholar]
- Barišić, A.; Petric, F.; Bogdan, S. Brain over Brawn—Using a Stereo Camera to Detect, Track and Intercept a Faster UAV by Reconstructing Its Trajectory. arXiv 2021, arXiv:2107.00962. [Google Scholar]
- Markovic, L.; Car, M.; Orsag, M.; Bogdan, S. Adaptive stiffness estimation impedance control for achieving sustained contact in aerial manipulation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation, Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Cazzato, D.; Cimarelli, C.; Sanchez-Lopez, J.L.; Voos, H.; Leo, M. A Survey of Computer Vision Methods for 2D Object Detection from Unmanned Aerial Vehicles. J. Imaging 2020, 6, 78. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Fumagalli, M.; Naldi, R.; Macchelli, A.; Carloni, R.; Stramigioli, S.; Marconi, L. Modeling and control of a flying robot for contact inspection. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Algarve, Portugal, 7–12 October 2012; pp. 3532–3537. [Google Scholar] [CrossRef]
- Alexis, K.; Darivianakis, G.; Burri, M.; Siegwart, R. Aerial Robotic Contact-based Inspection: Planning and Control. Auton. Robot. 2016, 40, 631–655. [Google Scholar] [CrossRef]
- Jimenez-Cano, A.E.; Sanchez-Cuevas, P.J.; Grau, P.; Ollero, A.; Heredia, G. Contact-Based Bridge Inspection Multirotors: Design, Modeling, and Control Considering the Ceiling Effect. IEEE Robot. Autom. Lett. 2019, 4, 3561–3568. [Google Scholar] [CrossRef]
- Cataldi, E.; Muscio, G.; Trujillo, M.A.; Rodriguez, Y.; Pierri, F.; Antonelli, G.; Caccavale, F.; Viguria, A.; Chiaverini, S.; Ollero, A. Impedance Control of an aerial-manipulator: Preliminary results. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 3848–3853. [Google Scholar] [CrossRef]
- Nava, G.; Sablé, Q.; Tognon, M.; Pucci, D.; Franchi, A. Direct Force Feedback Control and Online Multi-Task Optimization for Aerial Manipulators. IEEE Robot. Autom. Lett. 2020, 5, 331–338. [Google Scholar] [CrossRef]
- Meng, X.; He, Y.; Li, Q.; Gu, F.; Yang, L.; Yan, T.; Han, J. Contact Force Control of an Aerial Manipulator in Pressing an Emergency Switch Process. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2107–2113. [Google Scholar] [CrossRef]
- Stilman, M. Global Manipulation Planning in Robot Joint Space With Task Constraints. IEEE Trans. Robot. 2010, 26, 576–584. [Google Scholar] [CrossRef]
- Cefalo, M.; Oriolo, G. Task-constrained motion planning for underactuated robots. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2965–2970. [Google Scholar] [CrossRef]
- Yu, Y.; Lippiello, V. 6D Pose Task Trajectory Tracking for a Class of 3D Aerial Manipulator From Differential Flatness. IEEE Access 2019, 7, 52257–52265. [Google Scholar] [CrossRef]
- Tognon, M.; Cataldi, E.; Chavez, H.A.T.; Antonelli, G.; Cortés, J.; Franchi, A. Control-Aware Motion Planning for Task-Constrained Aerial Manipulation. IEEE Robot. Autom. Lett. 2018, 3, 2478–2484. [Google Scholar] [CrossRef]
- Ivanovic, A.; Car, M.; Orsag, M.; Bogdan, S. Exploiting Null Space in Aerial Manipulation through Model-In-The-Loop Motion Planning. In Proceedings of the 2020 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 1–4 September 2020; pp. 686–693. [Google Scholar] [CrossRef]
- Zargarbashi, S.; Khan, W.; Angeles, J. The Jacobian condition number as a dexterity index in 6R machining robots. Robot. Comput.-Integr. Manuf. 2012, 28, 694–699. [Google Scholar] [CrossRef]
- Car, M.; Ivanovic, A.; Orsag, M.; Bogdan, S. Position-based adaptive impedance control for a UAV. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 957–963. [Google Scholar] [CrossRef]
- Pham, H.; Pham, Q. A New Approach to Time-Optimal Path Parameterization Based on Reachability Analysis. IEEE Trans. Robot. 2018, 34, 645–659. [Google Scholar] [CrossRef]
- Maric, B.; Polic, M.; Tabak, T.; Orsag, M. Unsupervised optimization approach to in situ calibration of collaborative human–robot interaction tools. In Proceedings of the 2020 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Karlsruhe, Germany, 14–16 September 2020; pp. 255–262. [Google Scholar] [CrossRef]
- Furrer, F.; Burri, M.; Achtelik, M.; Siegwart, R. Robot Operating System (ROS): The Complete Reference (Volume 1). In Studies in Computational Intelligence; Chapter RotorS—A Modular Gazebo MAV Simulator Framework; Springer International Publishing: Cham, Switzerland, 2016; pp. 595–625. [Google Scholar] [CrossRef]
- LARICS. Aerial Manipulation Approach for Autonomous Bridge Inspection. Available online: https://youtu.be/bBaxPMZEV04 (accessed on 23 July 2021).



| Joint | d | a | ||
|---|---|---|---|---|
| 0 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 0 | |||
| 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanovic, A.; Markovic, L.; Car, M.; Duvnjak, I.; Orsag, M. Towards Autonomous Bridge Inspection: Sensor Mounting Using Aerial Manipulators. Appl. Sci. 2021, 11, 8279. https://doi.org/10.3390/app11188279
Ivanovic A, Markovic L, Car M, Duvnjak I, Orsag M. Towards Autonomous Bridge Inspection: Sensor Mounting Using Aerial Manipulators. Applied Sciences. 2021; 11(18):8279. https://doi.org/10.3390/app11188279
Chicago/Turabian StyleIvanovic, Antun, Lovro Markovic, Marko Car, Ivan Duvnjak, and Matko Orsag. 2021. "Towards Autonomous Bridge Inspection: Sensor Mounting Using Aerial Manipulators" Applied Sciences 11, no. 18: 8279. https://doi.org/10.3390/app11188279
APA StyleIvanovic, A., Markovic, L., Car, M., Duvnjak, I., & Orsag, M. (2021). Towards Autonomous Bridge Inspection: Sensor Mounting Using Aerial Manipulators. Applied Sciences, 11(18), 8279. https://doi.org/10.3390/app11188279








