1. Introduction
Tall buildings in moderate and high seismicity regions extensively adopt reinforced concrete (RC) shear wall structures to resist lateral loads because of their remarkable seismic performance. Owing to the increased seismic risk, accurate computation of the seismic demand is crucial to the seismic design of RC shear wall structures. The most precise method in computing seismic demands of building structures is the nonlinear response time history analysis (NLRHA) method. Still, the reliability and reasonability of the NLRHA are limited by the representative input ground motions (IGMs) because of the extreme uncertainty and contingency of earthquake events [
1,
2,
3,
4,
5]. The available IGM selection procedures [
6,
7,
8,
9] firstly evaluate local geological features and basic properties of the IGMs [
10,
11,
12,
13,
14,
15] to ensure these features of IGMs fulfil the requirement of the site. Then, the selection procedures adopt various spectra matching techniques to modify IGMs to provide the response spectra IGMs that match closely with the target spectrum [
16].
In the past two decades, plenty of research efforts have been made in developing spectra-matching-based IGM selection procedures for selecting and scaling proper IGMs for the NLRHA of building structures [
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28]. However, the structural seismic demand is affected by the peak modal responses and the modal response combinations in the time domain, which is determined by the frequency contents combinations in the frequency domain (FCCFD) and time-domain (FCCTD) of IGMs, respectively [
29]. For high-rise buildings, the peak modal responses and modal response combinations in the time domain are of the same importance to the seismic demand of the building structure. The response spectrum of IGMs quantifies the effect of FCCFD of IGMs. Thus, most of the available IGMs selection procedures that employ spectra matching techniques can only consider the impact of FCCFD of IGMs. The research of Wang [
20] and Anajafi [
24] showed that even if the individual records are tightly matched to the target spectrum, the record to record variability in the inelastic structural responses might be still noticeable. Moreover, Anajafi and Medina [
24] also illustrated that the record-to-record variability in higher-mode dominated responses is very sensitive to the value of the target damping. These findings highlighted the shortcoming of the spectral matching technique.
Recently, a modal-based ground motion selection (MGMS) procedure was developed by Liu et al. [
30] to consider the effect of FCCTD of IGMs in IGM selection. In the MGMS procedure, the impact of FCCTD of IGMs on the seismic demand of structures is quantified with the interaction of the first three modes. The MGMS procedure’s capability to select more reasonable IGMs for the NLRHA of structures has been proved for frame structures. At the same time, the deflection profile of the wall and frame structures is flexural and shear profiles, respectively, when the structures are subjected to the action of lateral load. Different deflection profiles of the wall and frame structures indicate different structural behavior [
31,
32]. The contribution of the seismic response of dominated modes to the final seismic demand shall also be different. Therefore, the capability of the MGMS procedure in improving the reliability of the NLHRA of RC shear wall structures is not guaranteed.
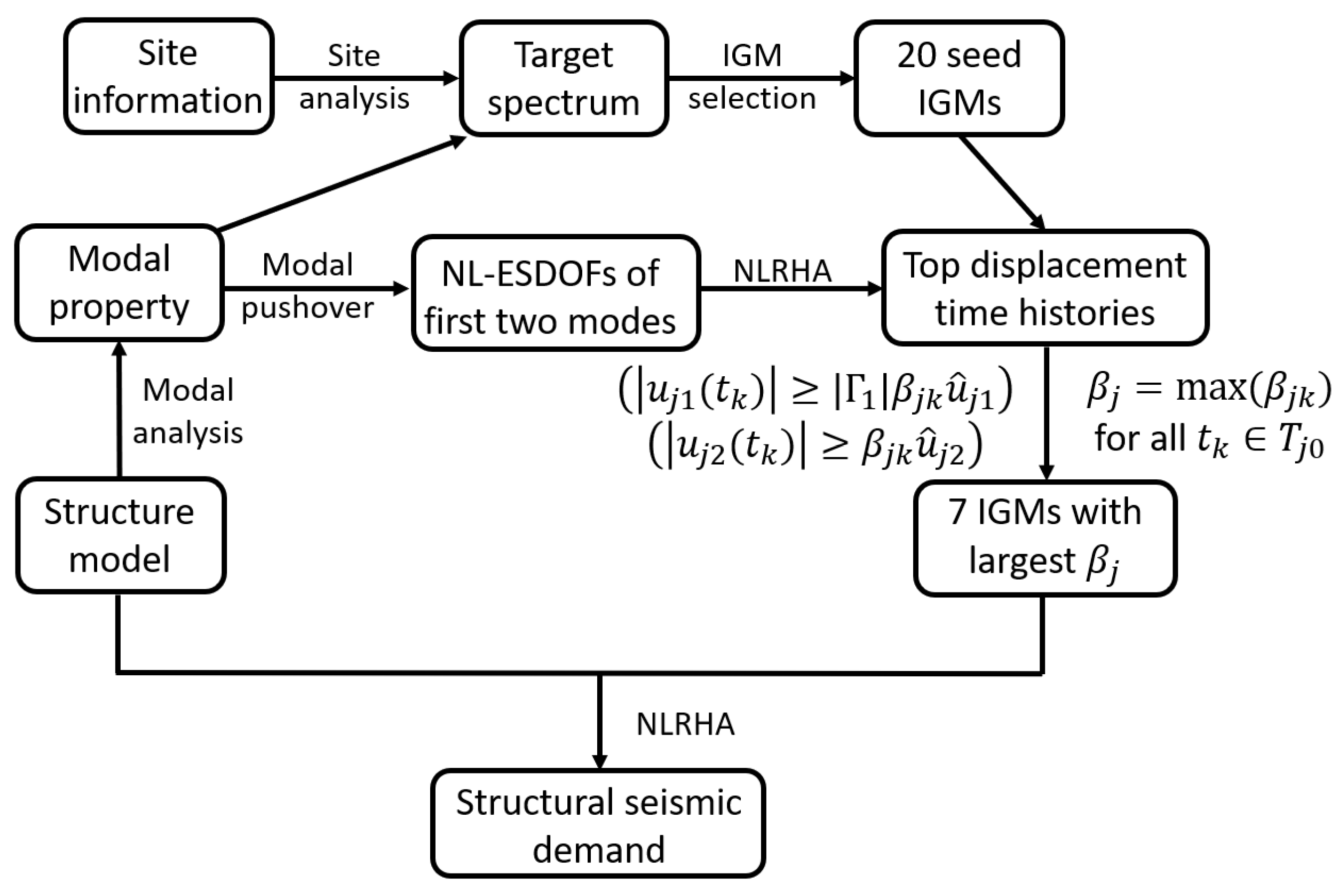
In this paper, the MGMS procedure is modified to take the modal response characteristics of RC shear wall structures into account in selecting IGMs for the NLRHA of the structure. In the MGMS procedure for wall structures, selected IGMs can induce the most significant interaction of the first two dominated modes, of which the modal mass coefficients are larger than the sum of modal mass coefficients of all the higher-order modes. A comprehensive case study was conducted on three RC shear wall structures with different heights. Seed IGMs were selected and scaled, with target spectra being conditional mean spectra [
33] and ASCE 7 design spectra [
6] to investigate the reliability and reasonability of the MGMS procedure when the target spectra vary. The results show that the MGMS procedure can effectively and consistently select suitable IGMs for the NLRHA of RC shear wall structures.
This paper has six sections, and the first section presents the background introduction, research significance and structure of the paper.
Section 2 first provides the basic information on the MGMS procedure and discusses why modifications should be made to the selection procedure to ensure a more reasonable selection of IGMs for the NLRHA of RC shear wall structures. Then,
Section 2 presents details about the proposed MGMS procedure for RC shear structures.
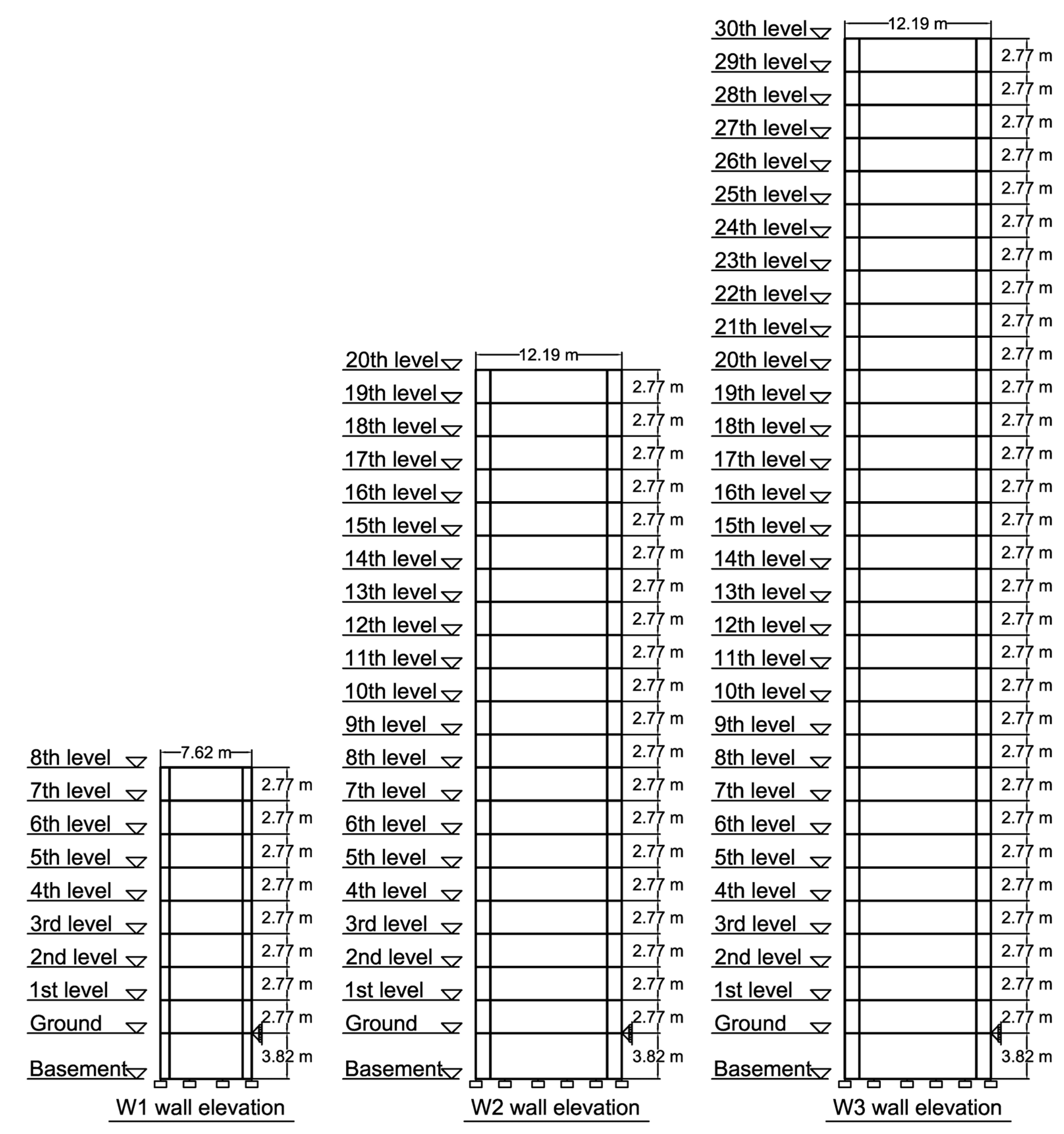
Section 3 shows detailed information on a comprehensive case study, including structural prototypes, seed IGMs and IGM selection for the NLRHA of RC shear wall structures.
Section 4 presents the NLRHA results adopting IGMs of different selection methods and discussions.
Section 5 summarizes the findings of the paper and draws conclusions based on the findings.
Appendix A provides details of the RC shear wall structures and seed IGMs.
4. Results and Discussions
4.1. Comparison of the Results of MGMS Procedures
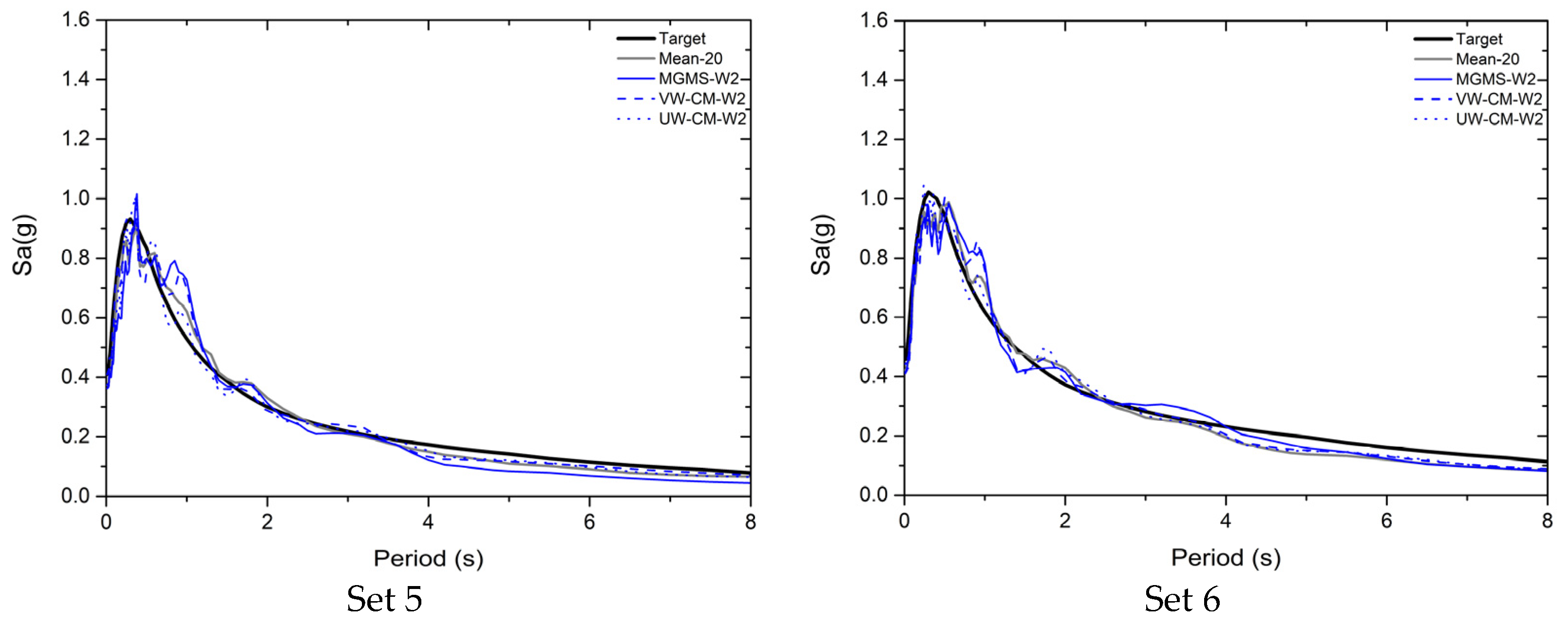
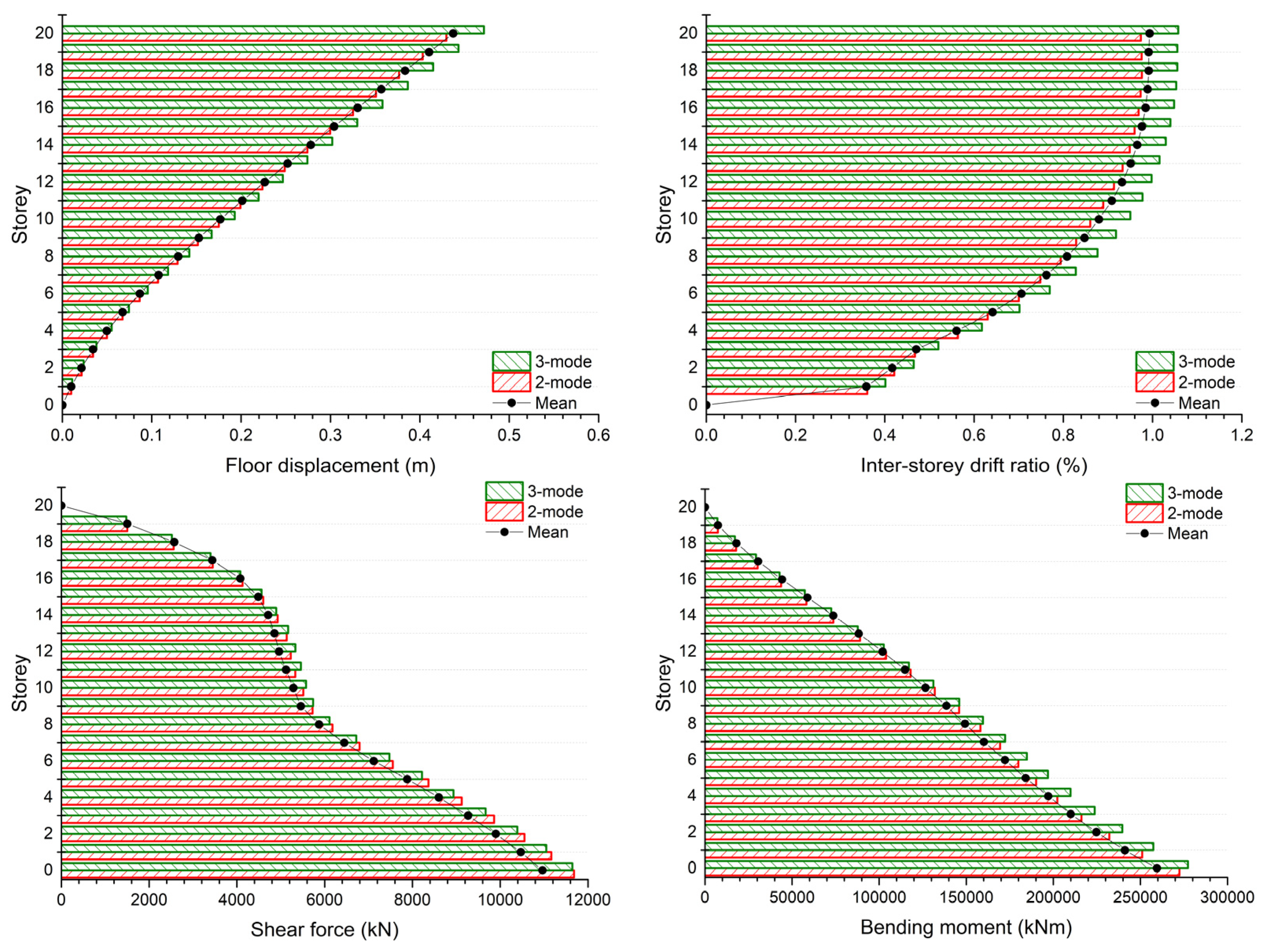
Figure 3 presents the seismic demands of wall structure W2 under motion set 6 adopting IGMs selected by MGMS procedures with and without considering the modal response characteristics of the RC shear wall structures, which is denoted as 2-mode and 3-mode, respectively. In
Figure 3, the mean demands of the NLRHA with the whole set of IGMs are plotted and marked as “Mean”. The presented MGMS procedure for RC shear wall structures, considering modal response characteristics of shear wall structures, selected seven IGMs that induced the most significant interaction of the first two modes from the seed IGMs set. The original MGMS procedure that does not take modal response characteristics of the RC shear wall structures into account selected seven IGMs that caused the most significant interaction of the first three modes for the NLRHA of the shear wall structures following the procedure in Reference [
30].
It is found that no matter whether the modal response characteristics of the shear walls were considered, the MGMS procedures can select proper IGMs for the NLRHA of the structure and seismic demands by both MGMS procedures are close to the benchmark demands. It is also noticed that IGMs selected by the MGMS procedure considers the modal response characteristics of the RC shear walls led to a more accurate computation of most of the seismic demands since the seismic demands approximated the benchmark demand better. The more reliable computed seismic demand shows the necessity and rationality of considering the modal response characteristics of shear wall structures in selecting IGMs with the MGMS procedure.
4.2. Comparison of Seismic Demands by Different IGM Selection Procedures
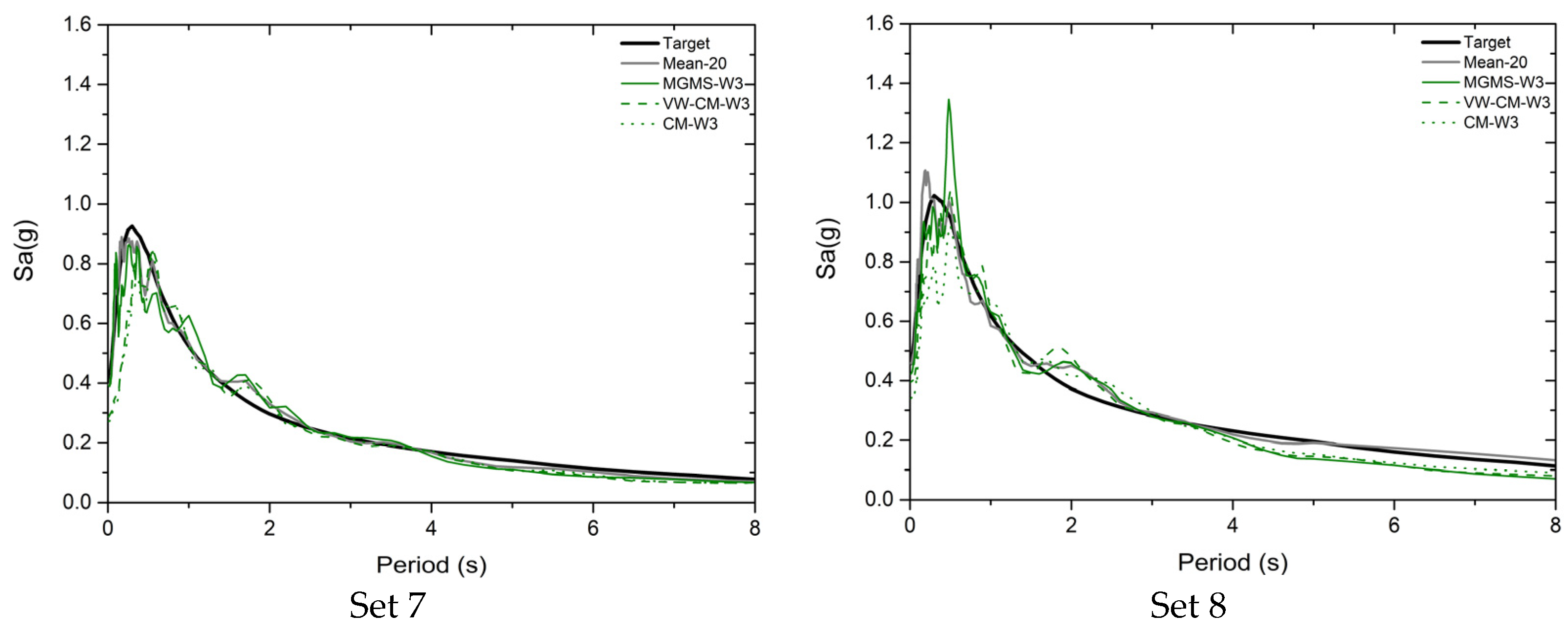
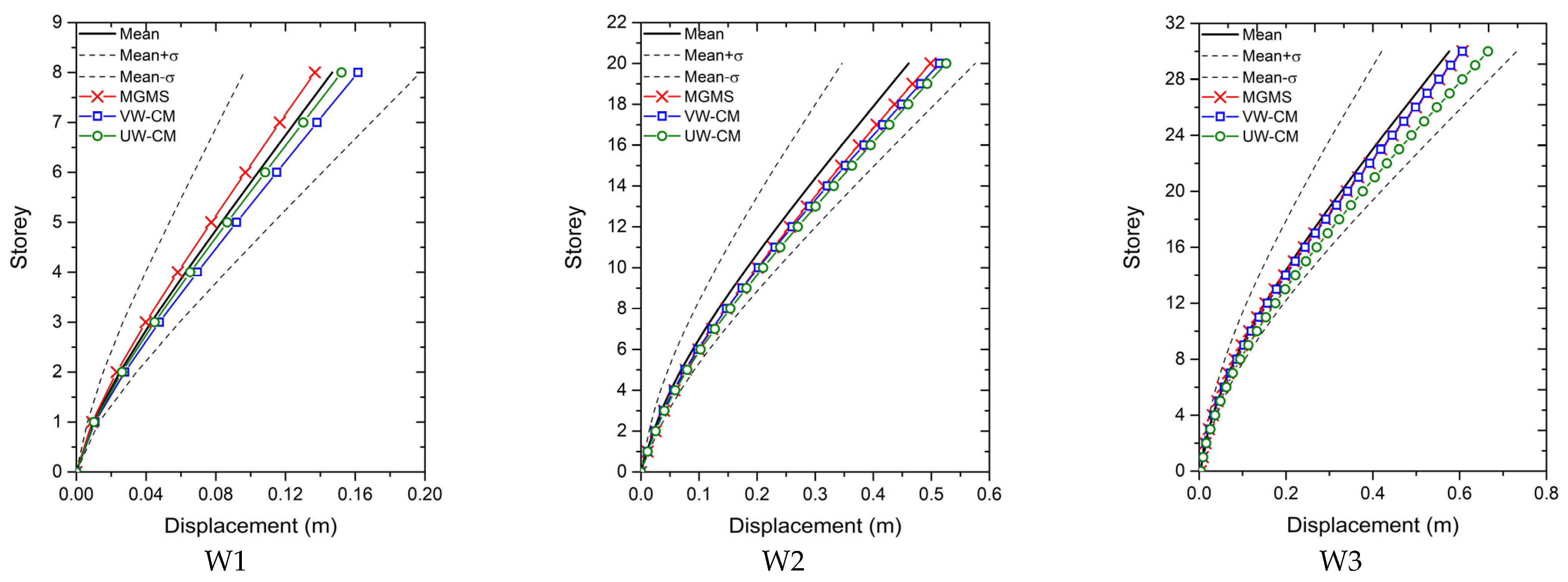
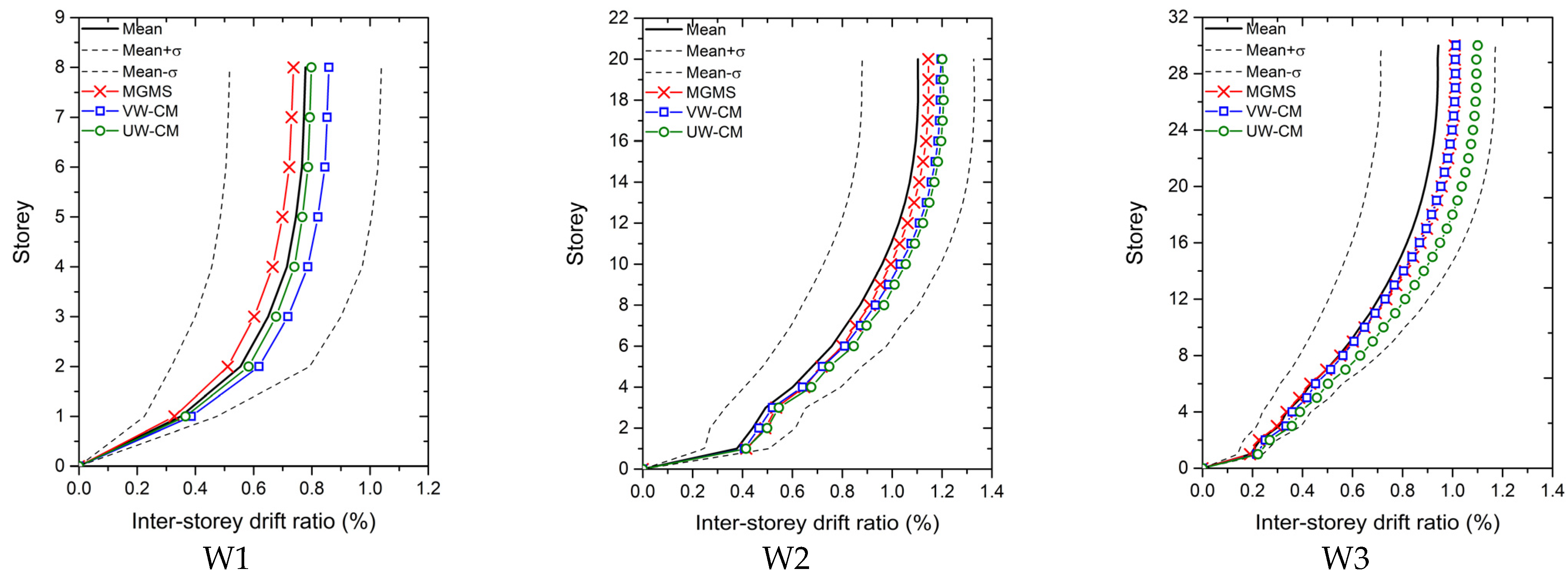
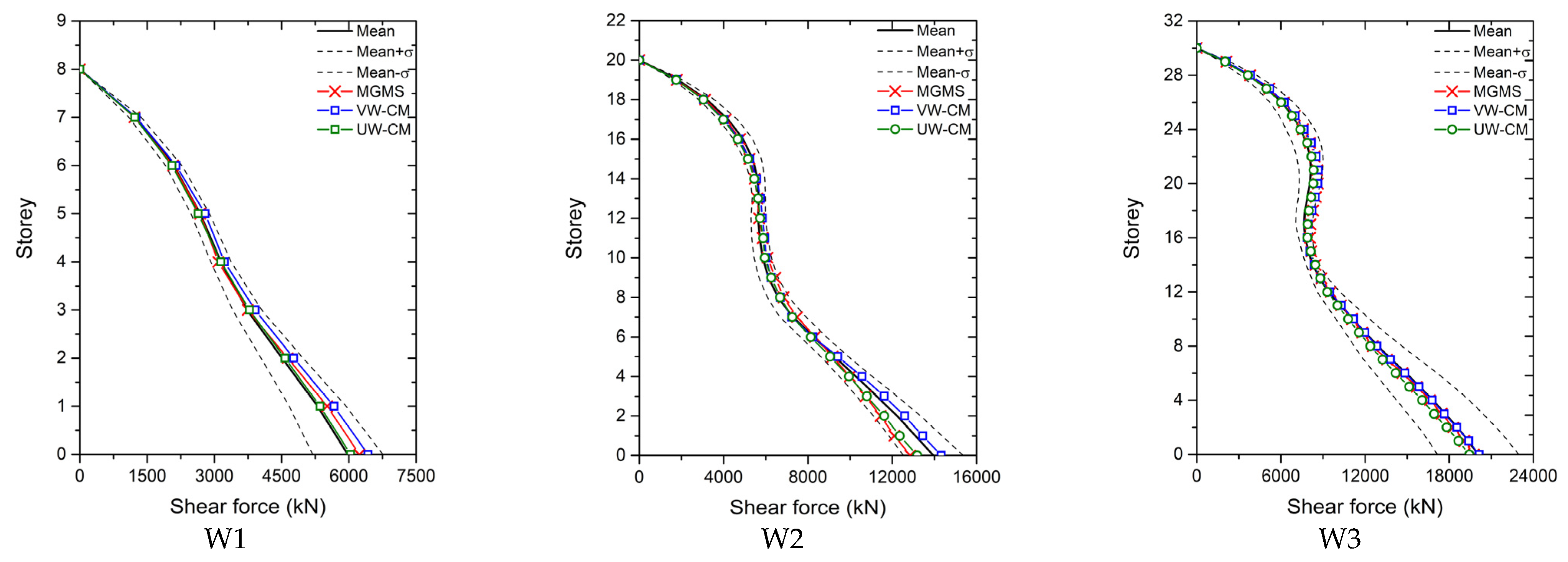
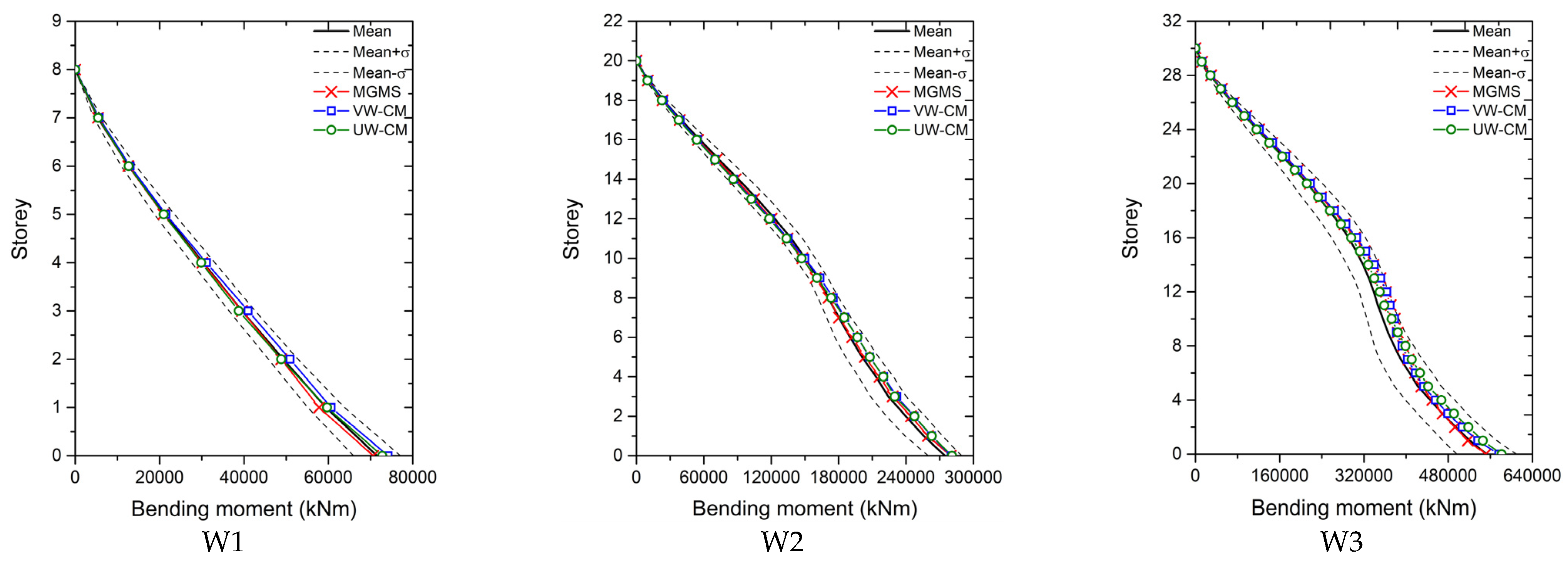
Figure 4,
Figure 5,
Figure 6 and
Figure 7 present the floor displacements, inter-story drift ratio, shear force, and bending moment computed by the IGMs from motion sets 2. The mean seismic demands of the set plus and minus one standard deviation of the demands, denoted as Mean + σ and Mean − σ, are also plotted. It is clear from
Figure 4,
Figure 5,
Figure 6 and
Figure 7 that the ratio of one standard deviation of seismic deformation to the mean deformation is much larger than that of seismically induced force. As a result, the seismic deformation is more sensitive to the variation of IGMs, compared with seismically induced force.
As shown in
Figure 4, the IGMs selected by the MGMS procedure and CM procedures caused a less and more conservative prediction of the floor displacement for all the stories of W1, respectively. Displacement calculated with UW-CM selected IGMs matched the best with the mean displacement of the set. When calculating the floor displacement of W2, NLRHA with IGMs chosen by all the selection methods led to an overestimated floor displacement. Still, the displacement by the MGMS-IGMs approximates the reference displacement the best. Floor displacement of W3 under motion set 2 calculated by IGMs selected by all the selection procedures is conservative. The displacements of MGMS-IGMs and VW-CM-IGMs are similar and close to the benchmark displacement.
Considering the inter-story drift ratio of W1, the UW-CM selected IGMs led to the most reliable computation of the drift ratio, although the drift ratio computed with UW-CM-IGMs is conservation. The MGMS selected IGMs and VW-CM selected IGMs induced an under- and overestimation of the inter-story drift ratio of W1, respectively. The results of the MGMS-IGMs are closer to the mean drift ratio of the set. As for W2 and W3, inter-story drift ratios were overestimated by IGMs selected by all the IGM selection methods, but those computed with the MGMS-IGMs matched the best with the reference drift ratio. Comparing the inter-story drift ratio of W2 and W3 calculated by the CM procedures, the results from NLRHA with VW-CM selected IGMs have better approximations to the benchmark drift ratio.
It can be found in
Figure 7 and
Figure 8 that IGMs of MGMS and both CM procedures could ensure shear force and bending moment of all the RC shear wall structures approximate the reference forces well in the upper floors. For shear force at lower stories, the UW-CM selected IGMs, VW-CM selected IGMs and MGMS-selected IGMs led to the most reliable computation of shear force of W1, W2 and W3, respectively. The bending moment of W1 at lower stories computed with UW-CM-IGMs is the closest to the reference bending moment, and the bending moment of W2 and W3 at lower floors from NLRHA with MGMS-IGMs has the best approximation to the mean moment of the set.
By comparing the seismically induced deformation and force of the wall structures under motion set 2, it is found that both MGMS procedure and CM procedures can select IGMs that ensure the seismic demands close to the mean demands of NLRHA with IGMs of the whole motion set. Additionally, MGMS-IGMs tend to provide a more reliable estimation of the seismic demands than CM procedures selected IGMs.
4.3. Comparison of the Deviation of the Computed Demands
The deviation between the seismic demands by different IGM selection procedures and the benchmark demands was calculated to quantitatively compare the reliability and reasonability of the seismic demands of NLRHA with a diverse selection of IGMs. The deviation
shows the relative difference between the benchmark demands of motion set
j and demands computed using IGMs from IGM selection method
N at the
ith story, respectively, which are calculated as:
where
N is the IGM selection methods, namely the MGMS method, UW-CM method and VW-CM method;
is the
i-th story’s seismic demands calculated using IGMs selected by method
N for motion set
j;
is the benchmark demands ith story for motion set j, which are the means demand of NLRHA with all IGMs of the set.
The statistics of the deviations are presented using box plots in
Figure 8. Deviations of MGMS procedure and CM procedures are compared for motion sets containing seed IGMs selected and scaled concerning design spectra and conditional mean spectra. For each plot, the highest and lowest edges of the cirrus stand for the largest and lowest deviation. The horizontal axial value of the line inside the box is the mean deviation. The horizontal axial values of the upper and lower box edges are the deviation value of 75th and 25th percentiles, respectively. The mean deviation value shows the reliability of the IGM selection procedure. Additionally, as the smaller the difference between the 75th percentile deviation and 25th percentile deviation (75th-25th deviation difference) is, the trend of distribution of computed seismic demands along the height of the structure is closer to that of the benchmark seismic demands. Therefore, the 75th-25th deviation difference reveals the reasonability of the IGMs selected by the different selection methods.
Comparing the mean deviation of the seismic demands, it is evident that the MGMS-IGMs and VW-CM-IGMs can achieve a much lower mean deviation than that of the UW-CM selected IGMs, except for computing shear forces with IGMs selected with DSs being the target spectra. Therefore, the reliability of NLRHA with UW-CM-IGMs is lower than that of NLRHA with IGMs chosen by the other two IGM selection methods. The mean deviation of seismic deformation, including inter-story drift ratio and floor displacement, by MGMS-IGMs and VW-CM-IGMs is similar when using the DS as the target spectra. Meanwhile, a more than 27% lower mean deviation of seismic deformation by IGMs selected by MGMS procedure is noticed when selecting and scaling IGMs referring to CMSs. Considering the seismically induced forces, the MGMS selected IGMs, and the VW-CM selected IGMs have a higher mean deviation of shear force and bending moment, respectively, but the difference is insignificant.
The 75th-25th deviation difference of most seismic demands of the UW-CM method is much higher than that of MGMS and VW-CM methods, indicating lower reasonability of the UW-CM selected IGMs. Comparing the 75th-25th deviation difference of seismic deformation of the VW-CM and MGMS methods, it is found that the deviation difference of the MGMS procedure is over 38% and 54% lower than that of the VW-CM method when the target spectrum is DSs and CMSs, respectively. Compared with the VW-CM method, the MGMS procedure tends to have a slightly lower and higher 75th-25th deviation difference of seismically induced forces, when the target spectra for selecting and scaling the IGMs are DSs and CMs, respectively.
Based on the comparison of deviation of the computed demands, it is clear that considering the modal contribution in the IGM selection procedure, the VW-CM procedure can select more reliable and reasonable IGMs, compared with the UW-CM procedure. Compared with the VW-CM procedure, the MGMS procedure for RC shear wall structures can achieve a noticeable lower mean deviation and 75th-25th deviation difference of the seismic deformation while having a similar mean deviation and deviation difference of the seismically induced forces. Meanwhile, it is seen in
Figure 8 that the seismically induced force is less sensitive to the variation of the IGMs and the seismic deformation is the control seismic demand in the seismic design and analysis of building structures. Therefore, selecting IGMs with MGMS procedure could considerably improve the reliability and reasonability of the NLRHA of RC shear wall structures.