The Influence of Permeability on the Propagation Characteristics of the Waves in Different Saturated Soils
Abstract
1. Introduction
2. Equations of Saturated Soils
2.1. u-w-p Formulation
- (1)
- Mass conservation equation of the pore fluid:
- (2)
- Dynamic equilibrium equations:
- (3)
- Effective stress principle:
2.2. u-p Formulation
3. Wave Equations and Theoretical Wave Velocities
3.1. Finite Permeability
3.1.1. Compressional Wave
3.1.2. Shear Wave
3.2. Infinite Permeability
3.3. Zero Permeability
4. Solutions of Wave Equations
4.1. Plane Wave
4.2. Cylindrical and Spherical Waves
5. Discussions of Wave Velocities, Dispersion and Attenuation Characteristics
5.1. Dispersion and Real Wave Velocity
5.2. Attenuation Coefficient
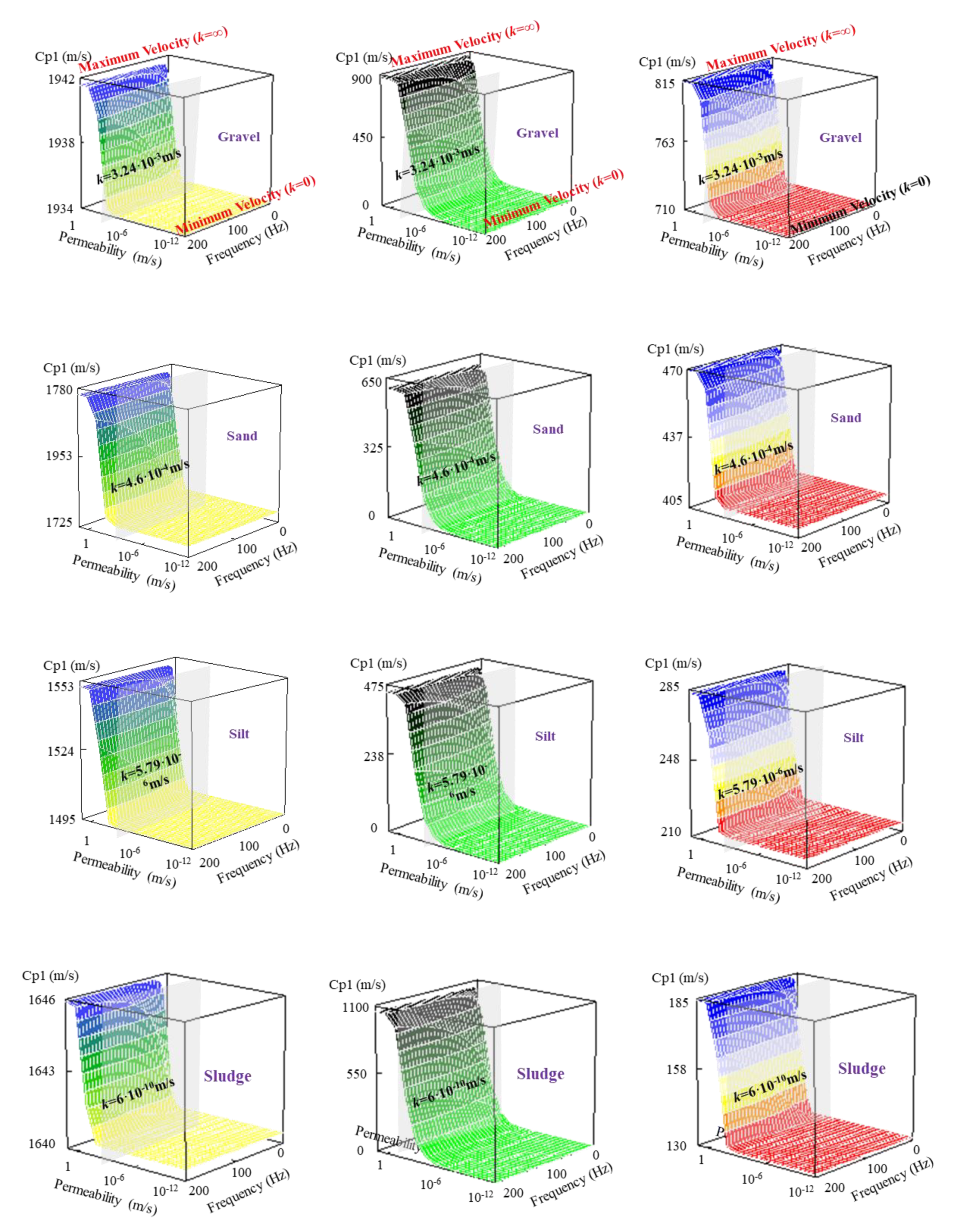
5.3. Comparison of Velocities and Frequency Dispersion in Different Saturated Soils
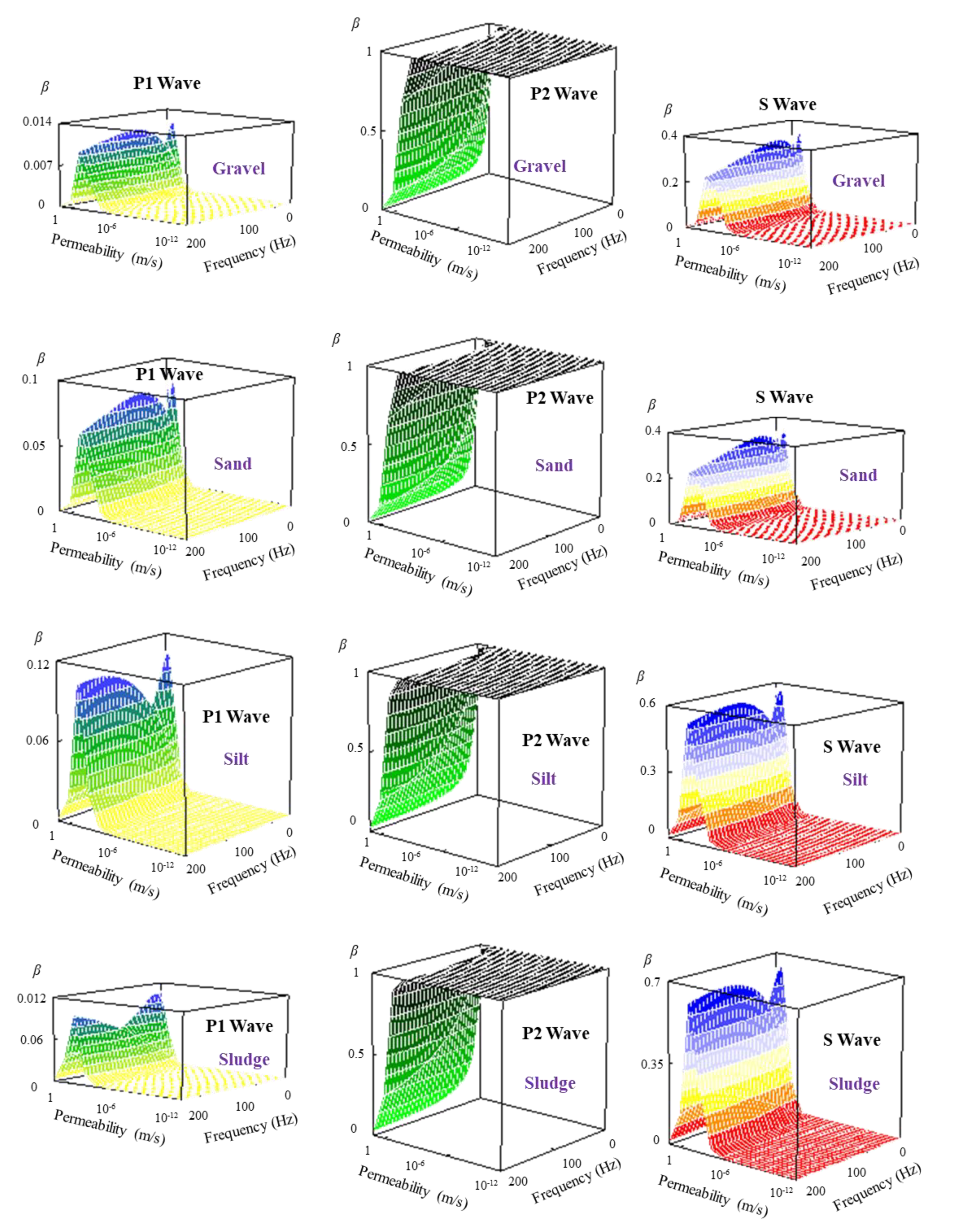
5.4. Comparison of Attenuation Coefficients in Different Saturated Soils
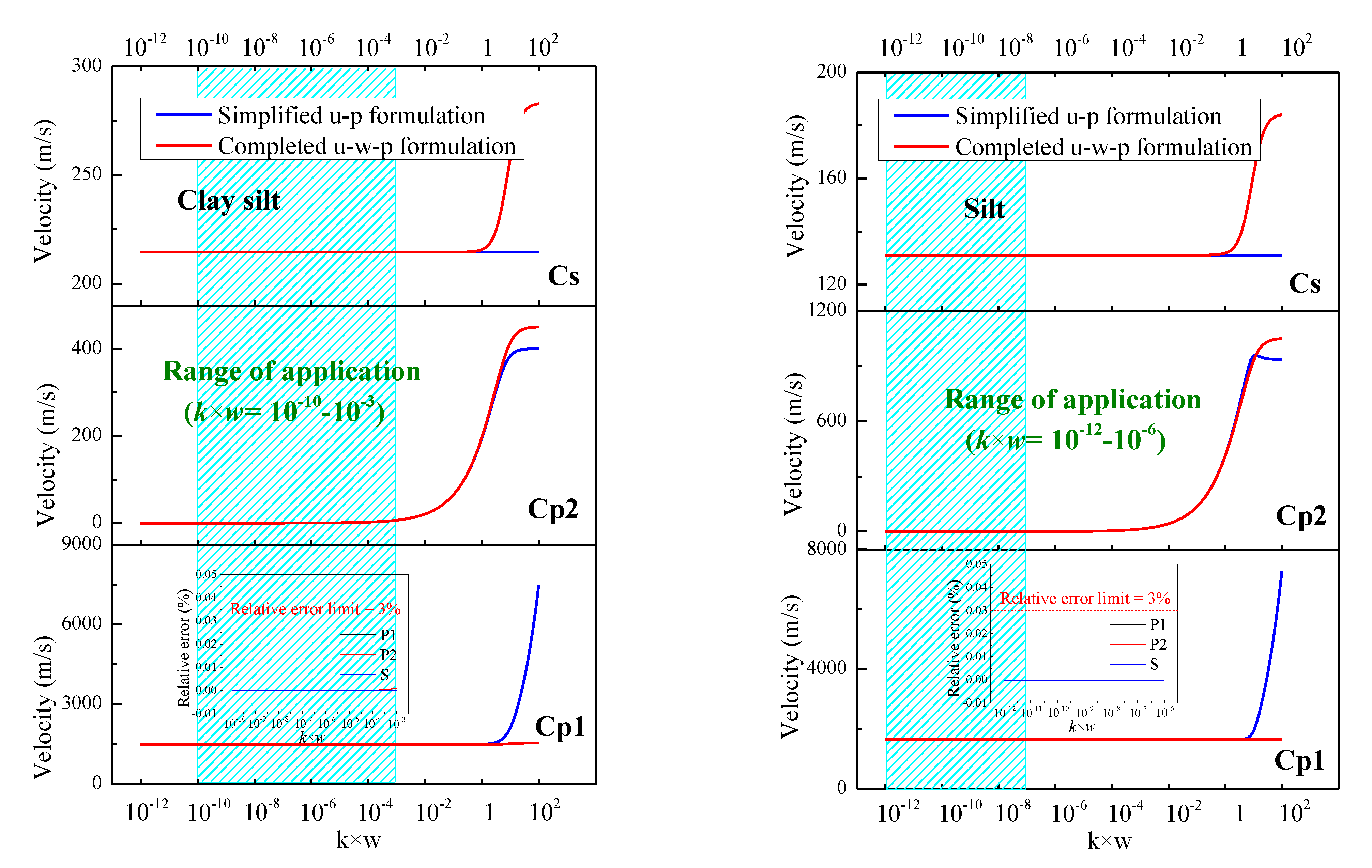
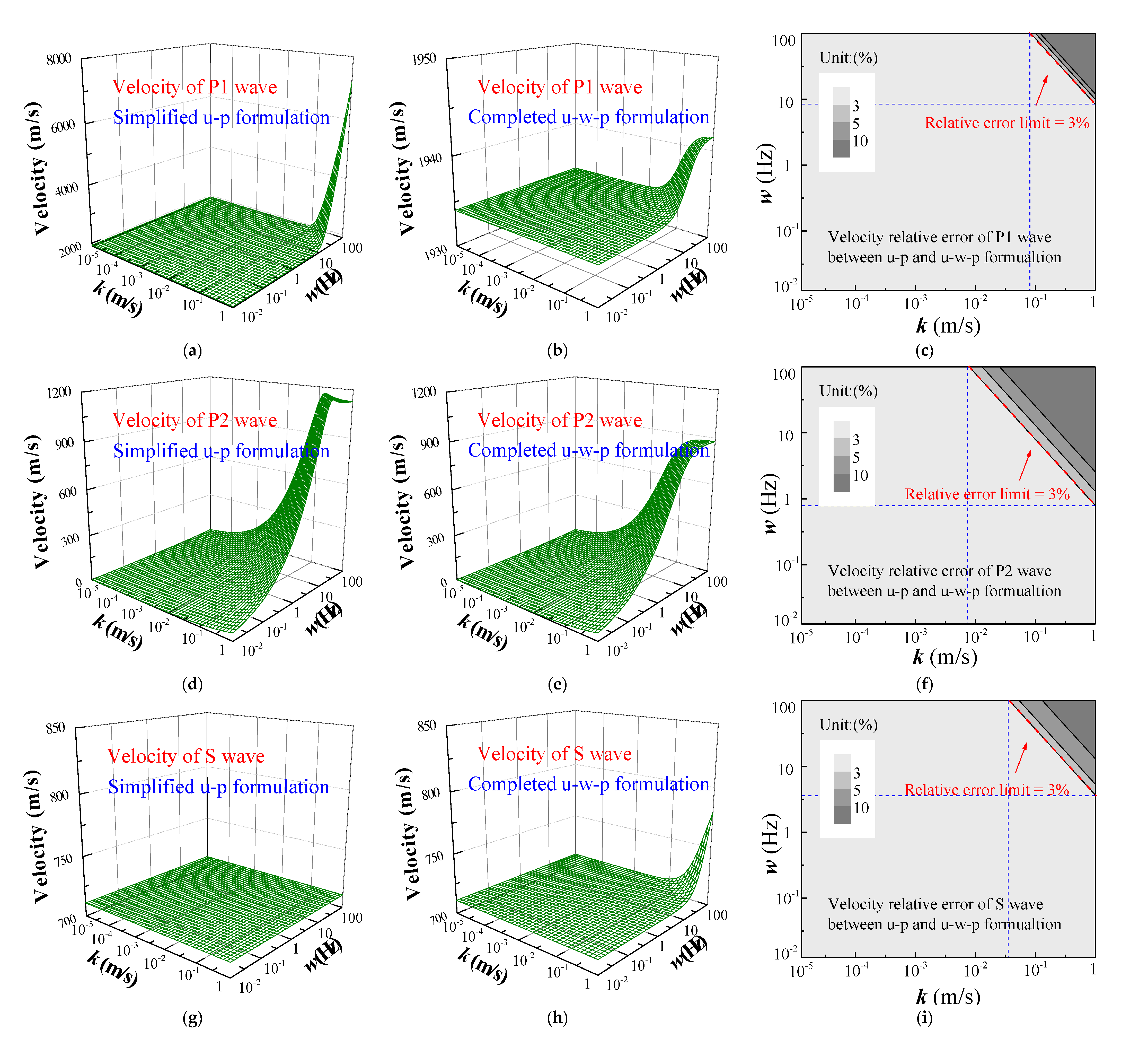
6. Analysis of the u-p Equation
7. Conclusions
- (1)
- Based on the u-w-p formulation of saturated porous medium, the wave equations and the corresponding velocities of P1, P2, and S waves are acquired under zero, finite, and infinite permeabilities, respectively.
- (2)
- The differences in the permeability and loading frequency of saturated soils have different influences on propagation properties, such as the velocities, dispersion and attenuation characteristics.
- (3)
- For zero and infinite permeabilities, P1, P2, and S waves are not dispersed and attenuated in the propagation process. Wave velocities keep constants.
- (4)
- For the finite permeability, the solutions of wave equations have real and imaginary parts, which represent the wave shape and attenuation during the propagation process, respectively. The actual velocities are the real parts of the velocities.
- (5)
- In different saturated soils, the variation tendency of wave velocities and attenuation coefficients are similar, but the amplitudes of velocities and attenuation coefficients have obvious discrepancies. The harder the soil, the faster the wave velocity. The softer the soil, the faster the attenuation wave is.
- (6)
- As a simplified formulation, the application scope of the u-p formulation is further discussed. The u-p formulation can be safely used as permeability k is less than 10−2 m/s and frequency ω is less than 1Hz.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coussy, O.; Bourbie, T. Propagation des ondes acoustiques dans les milieux poreux saturés. Rev. De L institut Français Du Pétrole 1984, 39, 47–66. [Google Scholar] [CrossRef]
- Snieder, R.; Hubbard, S.; Haney, M.; Bawden, G.; Hatchell, P.; Revil, A. DOE Geophysical Monitoring Working Group. Advanced noninvasive geophysical monitoring techniques. Annu. Rev. Earth Planet. Sci. 2007, 35, 653. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Lévy, T. Propagation of waves in a fluid-saturated porous elastic solid. Int. J. Eng. Sci. 1979, 17, 1005–1014. [Google Scholar] [CrossRef]
- Auriault, J.L. Dynamic behaviour of a porous medium saturated by a Newtonian fluid. Int. J. Eng. Sci. 1980, 18, 775–785. [Google Scholar] [CrossRef]
- Prevost, J.H. Nonlinear transient phenomena in saturated porous media. Comput. Methods Appl. Mech. Eng. 1982, 30, 3–18. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Shiomi, T. Dynamic behaviour of saturated porous media; the generalized Biot formulation and its numerical solution. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 71–96. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Chang, C.T.; Bettess, P. Drained, undrained, consolidating and dynamic behaviour assumptions in soils. Geotechnique 1980, 30, 385–395. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C. Basic formulation of static and dynamic behaviours of soil and other porous media. Appl. Math. Mech. 1982, 3, 457–468. [Google Scholar] [CrossRef]
- Gajo, A.; Mongiovi, L. An analytical solution for the transient response of saturated linear elastic porous media. Int. J. Numer. Anal. Methods Geomech. 1995, 19, 399–413. [Google Scholar] [CrossRef]
- Gajo, A. Influence of viscous coupling in propagation of elastic waves in saturated soil. J. Geotech. Eng. 1995, 121, 636–644. [Google Scholar] [CrossRef]
- Plona, T.J. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies. Appl. Phys. Lett. 1980, 36, 259–261. [Google Scholar] [CrossRef]
- Rasolofosaon, P.N.J. Importance of interface hydraulic condition on the generation of second bulk compressional wave in porous media. Appl. Phys. Lett. 1988, 52, 780–782. [Google Scholar] [CrossRef]
- Nagy, P.B.; Adler, L.; Bonner, B.P. Slow wave propagation in air-filled porous materials and natural rocks. Appl. Phys. Lett. 1990, 56, 2504–2506. [Google Scholar] [CrossRef]
- Berryman, J.G. Confirmation of Biot’s theory. Appl. Phys. Lett. 1980, 37, 382–384. [Google Scholar] [CrossRef]
- Kafaji, I.K.A. Formulation of a Dynamic Material Point Method (MPM) for Geomechanical Problems. Ph.D. Thesis, University of Stuttgart, Institut for Geotechnical Engineering, Stuttgart, Germany, 2013. [Google Scholar]
- Corapcioglu, M.Y.; Tuncay, K. Propagation of waves in porous media. Adv. Porous Media 1996, 3, 361–440. [Google Scholar]
- Berryman, J.G. Seismic wave attenuation in fluid-saturated porous media. Scatt. Attenuations Seism. Waves 1988, 128, 423–432. [Google Scholar]
- Schmitt, D.P. Acoustic multipole logging in transversely isotropic poroelastic formations. J. Acoust. Soc. Am. 1989, 86, 2397–2421. [Google Scholar] [CrossRef]
- Sharma, M.D.; Gogna, M.L. Wave propagation in anisotropic liquid-saturated porous solids. J. Acoust. Soc. Am. 1991, 90, 1068–1073. [Google Scholar] [CrossRef]
- Zhou, F.X.; Lai, Y.M. Propagation characteristics of elastic wave in saturated frozen soil. Rock Soil Mech. 2011, 32, 2669–2674. [Google Scholar]
- De Boer, I.R.; Liu, Z. One-dimensional transient wave propagation in fluid-saturated incompressible porous media. Arch. Appl. Mech. 1993, 63, 59–72. [Google Scholar] [CrossRef]
- Liu, Z.; de Boer, R. Dispersion and attenuation of surface waves in a fluid-saturated porous medium. Transp. Porous Media 1997, 29, 207–223. [Google Scholar] [CrossRef]
- Kumar, R.; Hundal, B.S. Symmetric wave propagation in a fluid-saturated incompressible porous medium. J. Sound Vib. 2005, 288, 361–373. [Google Scholar] [CrossRef]
- Kumar, R.; Hundal, B.S. Surface wave propagation in a fluid-saturated incompressible porous medium. Sadhana 2007, 32, 155–166. [Google Scholar] [CrossRef][Green Version]
- Dutta, N.C. Theoretical analysis of observed second bulk compressional wave in a fluid-saturated porous solid at ultrasonic frequencies. Appl. Phys. Lett. 1980, 37, 898–900. [Google Scholar] [CrossRef]
- Li, P.; Song, E.X. Compressional wave velocity and its physical nature in saturated soils with extreme permeability values. Rock Soil Mech. 2012, 33, 1979–1985. [Google Scholar]
- Kim, S.H.; Kim, K.J.; Blouin, S.E. Analysis of wave propagation in saturated porous media. I. Theoretical solution. Comput. Methods Appl. Mech. Eng. 2002, 191, 4061–4073. [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, K.J.; Blouin, S.E. Analysis of wave propagation in saturated porous media. II. Parametric studies. Comput. Methods Appl. Mech. Eng. 2002, 191, 4075–4091. [Google Scholar] [CrossRef]
- Yang, J.; Wu, S.M.; Cai, Y.Q. Characteristics of propagation of elastic waves in saturated soil. J. Vib. Eng. 1996, 9, 128–137. [Google Scholar]
- Steeb, H.; Kurzeja, P.S.; Frehner, M.; Schmalholz, S.M. Phase velocity dispersion and attenuation of seismic waves due to trapped fluids in residual saturated porous media. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Han, B.; Zdravkovic, L.; Kontoe, S. Numerical and analytical investigation of compressional wave propagation in saturated soils. Comput. Geotech. 2016, 75, 93–102. [Google Scholar] [CrossRef]
- Zheng, P.; Ding, B.; Zhao, S.-X.; Ding, D. Dynamic response of a multilayered poroelastic half-space to harmonic surface tractions. Transp. Porous Media 2013, 99, 229–249. [Google Scholar] [CrossRef]
- Liu, G.L.; Song, E.X. Visco-elastic transmitting boundary for numerical analysis of infinite saturated soil foundation. Chin. J. Geotech. Eng. 2006, 28, 2128–2133. [Google Scholar]
- Liao, Z.P. Introduction to Wave Motion Theories in Engineering; Science Press: Beijing, China, 2002. [Google Scholar]
- Deeks, A.J.; Randolph, M.F. Axisymmetric time-domain transmitting boundaries. J. Eng. Mech. 1994, 120, 25. [Google Scholar] [CrossRef]

| Symbols | Definitions | |
|---|---|---|
| u | Displacement of soil skeleton | |
| w | Displacement of pore fluid with respect to the soil skeleton | |
| p | Pore pressure | |
| Density of the solid–fluid mixture | ||
| Density of the fluid | ||
| n | Porosity | |
| b | Body force acceleration | |
| k | Permeability coefficient of pore fluid | |
| Dynamic permeability coefficient | ||
| Total stress of the two-phase media | Constitutive relationship: ; ; | |
| Effective stress of the soil skeleton | ||
| Compressibility coefficient of solid | KT = E/[3(1 − 2v)] = λ + 2G/3; where, KT, KS and Kf are the bulk modulus of soil skeleton, soil particles and pore fluid respectively. For the material of soil, soil particles are nearly incompressible relative to the soil skeleton, thus they have the relations of KS >> KD, α ≈ 1. | |
| Qb | Compressibility coefficient of fluid | |
| Parameter | Saturated Gravel Soil | Saturated Sand Soil | Saturated Clay Silt | Saturated Silt |
|---|---|---|---|---|
| Elastic modulus E (MPa) | 2000 | 700 | 166.8 | 64.7 |
| Shear modulus G (MPa) | 854.7 | 277.8 | 64.15 | 21.7 |
| Density of fluid (kg/m3) | 1000 | 1000 | 1000 | 1000 |
| Density of soil (kg/m3) | 2150 | 2100 | 1970 | 1700 |
| Poisson ratio | 0.17 | 0.26 | 0.3 | 0.49 |
| Bulk modulus of fluid Kf (GPa) | 1.85 | 1.85 | 1.85 | 1.85 |
| Bulk modulus of solid KS (GPa) | 45 | 30 | 20 | 12 |
| Porosity n | 0.4 | 0.4 | 0.594 | 0.625 |
| Permeability k (m/s) | 3.24 × 10−3 or 1 × 10−12 − 1 | 4.6 × 10−4 or 1 × 10−12 − 1 | 5.79 × 10−6 or 1 × 10−12 − 1 | 6 × 10−10 or 1 × 10−12 − 1 |
| Frequency (/s) | 0–200 | 0–200 | 0–200 | 0–200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Xu, C.; Li, L. The Influence of Permeability on the Propagation Characteristics of the Waves in Different Saturated Soils. Appl. Sci. 2021, 11, 8138. https://doi.org/10.3390/app11178138
Song J, Xu C, Li L. The Influence of Permeability on the Propagation Characteristics of the Waves in Different Saturated Soils. Applied Sciences. 2021; 11(17):8138. https://doi.org/10.3390/app11178138
Chicago/Turabian StyleSong, Jia, Chengshun Xu, and Liang Li. 2021. "The Influence of Permeability on the Propagation Characteristics of the Waves in Different Saturated Soils" Applied Sciences 11, no. 17: 8138. https://doi.org/10.3390/app11178138
APA StyleSong, J., Xu, C., & Li, L. (2021). The Influence of Permeability on the Propagation Characteristics of the Waves in Different Saturated Soils. Applied Sciences, 11(17), 8138. https://doi.org/10.3390/app11178138




