Abstract
The Zienkiewicz–Zhu (ZZ) super-convergent patch recovery technique based on a node neighborhood patch configuration is used most widely for recovery of the stress field of a finite element analysis. In this study, an improved ZZ recovery technique using element neighborhood patch configuration is proposed. The improved recovery procedure is based on recovery of the stress field in the least-squares sense over an element patch that consists of the union of the elements surrounding the element under consideration. The proposed patch configuration provides more sampling points and improves the performance of the standard ZZ recovery technique. The effectiveness and reliability of the improved ZZ recovery approach is demonstrated through plane elastic and plastic plate problems. The problem domain is discretized with triangular and quadrilateral elements of different sizes. A comparison of the quality of error estimation using the ZZ recovery of derivative field and recovery of the displacement field using similar element neighborhood patch configurations is also presented. The numerical results show that the ZZ recovery technique and the displacement recovery technique, using a modified patch configuration, yield better results, convergence rate, and effectivity as compared with the standard ZZ super-convergent patch recovery technique. It is concluded that the improved ZZ recovery technique-based adaptive finite element analysis is very effective for converging a predefined accuracy with a significantly smaller number of degrees of freedom, especially in an elastic problem. It is also concluded that the improved ZZ recovery technique captures the plastic deformation problem solution errors more reliably than the standard ZZ recovery technique.
1. Introduction
The finite element method is the most used numerical tool for solving industrial problems. Recently, there has been interest in overcoming the drawbacks of the finite element analysis method, and therefore improving the quality of finite element analysis results using a priori and a posteriori error estimators. A comprehensive review on the diverse applicability of the finite element approach is given by Cen et al. [1]. The different types of error estimation techniques have been reviewed by Gratsch and Bathe [2]. Ainsworth et al. [3] showed that the Zienkiewicz–Zhu error estimation was effective, convergent, and asymptotically exact when the exact stress boundary conditions were implemented. The classical super-convergent patch recovery (SPR) technique or ZZ recovery technique [4] has been proposed to recover the lost accuracy and continuity of the stress field by interpolating from a stress surface fitted to the super-convergent stress points in a node neighborhood patch. They emphasized that the error estimation would be asymptotically exact if the recovery of the finite element solution was super convergent. An in-depth discussion on improving the SPR technique was presented by R’odenas et al. [5]. Wiberg and Abdulwahab [6] proposed a recovery procedure (SPR-E technique) for improving the accuracy of the recovered stresses by imposing additional constraints on the equilibrium equations. Blacker and Belytschko [7] extended the ZZ recovery technique (SPR-EB technique) by including the squares of the residual of equilibrium equations and natural boundary conditions. A new conjoint polynomial for interpolation of the local patch stresses on the element was proposed which improved the derivative field within the element as compared with standard nodal interpolation. Li and Wiberg [8] presented a post-processing technique for determining more accurate solutions by fitting a higher order polynomial expansion to the computed solution at super-convergent points in the element patch that represented the union of the considered element and its neighbors. Wiberg et al. [9] proposed a patch recovery scheme for all stress components and coupling of the stress components was achieved through the equilibrium equations. Lee et al. [10] proposed a super-convergent stress recovery technique (LP technique) for obtaining stress interpolation polynomials over a patch of elements formed around a vertex node using the virtual work form of the equilibrium residual, while, employing a similar idea, Park et al. [11] proposed a recovery technique (SP technique) assuming stress field over a single element.
The Trefftz patch recovery (TPR) technique using Trefftz fields was proposed by Maunder [12] to obtain patch interpolation polynomials which satisfied the internal equilibrium and compatibility equations. R´odenas et al. [13] presented a modified SPR technique, the so-called SPR-C technique using the appropriate constraint equations, to produce stress interpolation polynomials that exactly satisfied the internal and boundary equilibrium equations. The explicit-type recovery error estimator in energy norm was proposed by Nadal et al. [14] for the linear elasticity problem using a smooth solution. Ulku et al. [15] developed a recovery-based error estimation technique for the Aifantis’ gradient elasticity theory to avoid the occurrence of singularities in the stress and strain fields. The super-convergent patch recovery (SPR) method was modified by Gu et al. [16] to improve the method accuracy and stability using an integration point as a sampling point, additional nodes, and weighted average procedure. Zhang and Naga [17] developed the polynomial preserving recovery (PPR) method to recover the accuracy in a finite element solution. A gradient recovery method, the so-called super-convergent cluster recovery method, was presented by Huang and Yi [18] in which a linear polynomial approximation was obtained by a least-squares fitting to the finite element solution at certain sample points. An error recovery procedure based on the least-squares fitting of the displacement field over an element neighborhood patch configuration was proposed by Ahmed et al. [19]. Boo et al. [20] proposed an error estimation procedure to accurately estimate the relative eigenvalue errors and to recover the solution error in an automated multilevel substructure method. Chen and Chen [21] presented a super convergence in the L2 norm using the patch recovery method to recover linear finite element solutions. Cai et al. [22] proposed a hybrid error recovery technique, consisting of the explicit residual and an enhanced Zienkiewicz–Zhu (ZZ) error recovery technique, for the conforming finite element method, and verified that the developed technique was accurate for all meshes. Sharma et al. [23] proposed a stress recovery procedure for low-order finite elements in three dimensions. Dong et al. [24] proposed an error estimation based on the element energy projection technique for adaptive finite element analysis. There has also been interest in developing support domain or mesh independent patch recovery techniques. Ahmed et al. [25] developed element-free Galerkin (EFG) approach-based error recovery techniques for finite element analysis employing mesh independent node patches.
From the literature review, it is clear that the quality of recovery-based error estimation depends on the approach for recovering the stress or displacement field that satisfies the equilibrium and boundary conditions. The ZZ recovery technique uses the least-squares fitting of stress field by the same order polynomial as that present in the basis function over a patch of neighborhood nodes. The number of polynomial terms in the basis function should be limited, in order that the number of unknown parameters in the interpolation equation does not exceed the number of independent equations for a particular patch configuration. The interpolation equation should be used with utmost care at boundaries where too few linear independent equations can be established within the patch. The improved ZZ method of error recovery, especially at a boundary, is proposed using a patch configuration (element neighborhood patch) larger than the standard patch (node neighborhood patch). The advantage of the proposed patch configuration is that it provides more sampling points near the boundary and improves the error recovery of boundary regions. The effectiveness and reliability of the improved ZZ recovery approach is assessed through plane elastic and plastic plate problems. The problem domains are discretized with triangular and quadrilateral (regular/irregular) elements with different sizes of regular and irregular subdivisions. We also carried out the least-squares fitting of the displacement field by a higher order polynomial to extract stress over a similar element neighborhood patch configuration. The quality of error estimation using the ZZ recovery of the derivative field was compared with that of error estimation using extracted stress from the recovery of a more accurate displacement field in terms of effectivity, rate of convergence, and adaptively refined meshes.
2. Node Patch Zienkiewicz–Zhu (ZZ) Stress Error Recovery Technique
The ZZ super-convergent patch recovery technique [4] for finite element solution errors recovery assumes that the node values of field variable derivatives (σ) belong to a polynomial expansion of the same complete order as that of the basis function and is valid over a patch of neighboring nodes of the vertex (Figure 1 and Figure 2). The following polynomial expansion may be used for each component of stress:
where P(x) is the basis function of the assumed polynomial, x = (xi, yi), are the coordinates of the sampling points, and a is the unknown parameters vector.
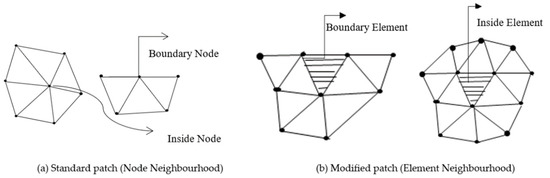
Figure 1.
Patch configuration in triangular mesh.
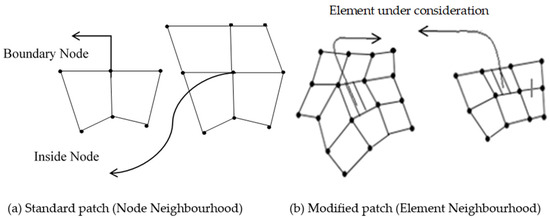
Figure 2.
Patch configuration in quadrilateral mesh.
A least-squares fit of σh values over the nodes patch, may be made by minimizing the following functional:
On simplification, it results into the following equation:
The matrices A and b are given as:
where np is the number of nodes in a patch.
3. Element Patch Displacement Error Recovery Technique
The recovery of the field variable (displacement) is obtained by the least-squares fit of the computed nodal field variable (u) using a higher order polynomial over an element neighborhood patch that consists of the union of the elements surrounding an element (Figure 1). To perform least-squares fitting, the following function is minimized:
where
where ui and vi are the nodal parameters of field variables in the x and y directions, respectively, and a is the vector of unknown parameters au and av.
where (xi, yi) are the sampling points (np) coordinates.
The minimization condition of πf (a) implies that a satisfies the following relation:
Solving for a, the following relation is obtained:
where and .
4. Error Estimator and Adaptive Mesh Improvement
The error in computing the state variable or state variable derivative, i.e., displacement (u) or stress (σ), eu* (or eσ*) is defined as the difference between the exact (or recovered) values of u (or σ) and respective numerical values, uh (or σh) as follows:
The finite element solution errors may be quantified in appropriate norms. The energy norm (E) giving integral measure of the error in energy may be defined as follows:
where Ω is problem domain and D is the elasticity matrix of linear isotropic materials.
The effectivity () of the evaluated error is defined as the ratio of evaluated error and true error. An error estimator is asymptotically exact for a particular problem if the problem global and local (element) effectivity () converge to one when the mesh size approaches zero [1]. The accuracy (η) of a finite element solution may be defined as follows:
The solution is acceptable if accuracy (η) is less than the predefined accuracy(ηallow). If the solution accuracy is more than the predefined accuracy, the mesh may be improved in an adaptive way in guidance of error estimator. The permissible global error is given as follows:
The allowable error in the ith element is calculated using the following relation:
The so-called element refinement parameter ξi given below, guides the refinement:
If ξi > 1, improvement of mesh is needed. The new element size (hnew) is found with the help of the following relation:
5. Elastic Plate Examples
The quality of recovery procedure, i.e., error convergence, effectivity, and adaptively improved meshes are obtained by adaptive finite element analysis of two plane elastic plate problems, for which an exact solution is available in [4], employing the ZZ stress recovery method with the standard (node neighborhood) and a modified (element neighborhood) patch configuration, and a modified patch-based displacement recovery method. The problem domains are discretized with triangular (linear/quadratic elements) and quadrilateral (linear elements) meshes. The analysis results are compared for the effect of patch configuration on the ZZ stress recovery of the finite element solution. The results are also compared for least squares-based recovery using an element neighborhood patch configuration to interpolate stresses and displacements. The standard or node neighborhood patch is the patch of nodes around a vertex node. The modified or element neighborhood patch configuration is the union of the elements surrounding the element under consideration. The standard and modified patches for triangular/quadrilateral elements are shown in Figure 1 and Figure 2.
5.1. Square Plate Example
The quality of the stress (ZZ) and displacement recovery is demonstrated through the finite element analysis of a plane square plate example. The example was used by Zienkiewicz and Zhu [4] to validate the effectiveness of the ZZ error estimation. The example was a 1 × 1 square domain subjected to the action of body forces (bx, by). The exact solution for displacement (u, v) and body forces in the form of polynomials, are given in Equations (20) to (22):
The constants α and β are given as:
where E and ν are the modulus of elasticity and Poisson’s ratio, respectively, with values of 1.0 N/mm2 and 0.3, respectively.
α = E ν/[(1−2ν) (1+ ν)]; β = E/[2(1 + ν)],
A two-dimensional computer software is developed, incorporating the adaptive finite element procedures explained above, to simulate the elastic and plastic plate problems. The square plate domain is discretized as regular and irregular meshes using triangular/quadrilateral elements. The triangular/quadrilateral element meshes for plate domain are shown in Figure 3. The error convergence with different orders of mesh in the finite element analysis and effectivity of error estimation using a standard/modified patch-based ZZ stress recovery and a modified patch-based displacement recovery, for triangular elements, are listed in Table 1, Table 2, Table 3 and Table 4. The analysis results for error convergence and effectivity using quadrilateral elements are shown in Table 5 and Table 6. The solution errors were measured in the energy norm. The convergence rate of error with regular subdivision for the linear/quadratic triangular elements and the linear quadrilateral element in the original solution, the recovered solution using a standard patch-based ZZ recovery, a modified patch-based ZZ recovery, and a modified patch-based displacement recovery are obtained, respectively, as (0.97875, 1.37313, 1.87252, and 1.88603), (1.97848, 2.50622, 3.19768, and 2.88449), and (1.00169, 1.65603, 2.35230, and 2.02723). The error convergence rates are obtained in finite element results as (0.58530, 0.848150, 0.95638, and 1.11017), (1.07415, 1.26349, 1.57042, and 1.61414), and (0.54163, 0.98011, 0.94495, and 0.98600), respectively, for linear/quadratic triangular elements and linear quadrilateral element considering irregular subdivisions.
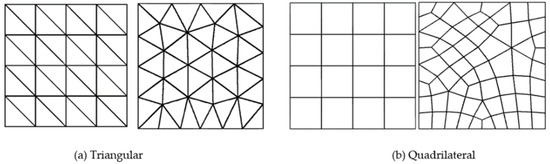
Figure 3.
Regular/irregular subdivided element meshes for square plate domain.

Table 1.
Solution error and global effectivity for the plate problem using stress/displacement recovery and patch configuration (regular linear triangular element).

Table 2.
Solution error and global effectivity (θ) for the plate problem using stress/displacement recovery and patch configuration (irregular linear triangular element).

Table 3.
Solution error and global effectivity for the plate problem using stress/displacement recovery and patch configuration (regular quadratic triangular element).

Table 4.
Solution error and global effectivity for the plate problem using stress/displacement recovery and patch configuration (irregular quadratic triangular element).

Table 5.
Solution error and global effectivity for the plate problem using stress/displacement recovery and patch configuration (regular linear quadrilateral element).

Table 6.
Solution error and global effectivity (θ) for the plate problem using stress/displacement recovery and patch configuration (irregular linear quadrilateral element).
5.2. Square Plate with a Circular Opening Example
The finite element analysis of the plate with an opening example, employing the improved ZZ recovery technique was also carried out to compare the analysis results obtained using the classical ZZ recovery and least-squares displacement recovery techniques in a stress concentration condition. Due to symmetry, only the upper left square quadrant of the plate is modeled. Along the symmetry line, the shear stress and the normal displacement component are zero. Equations (24) to (26) show the analytical solution for stresses in the plate with opening [4]:
where r2 = y2 + x2 and σ∞ is the uniaxial traction applied at infinity.
Figure 4 shows the holed plate domain discretized with three-node linear triangular, six-node quadratic triangular, and four-node linear quadrilateral elements. The computational results obtained from the analysis, related to error quality, i.e., errors and effectivity with decreasing element size, are tabulated in Table 7, Table 8 and Table 9.
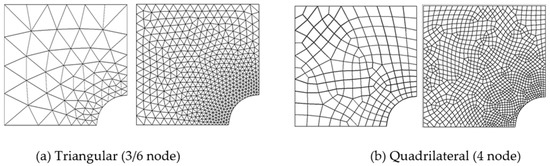
Figure 4.
Triangular/quadrilateral elements mesh for plate domain with opening.

Table 7.
Solution error and global effectivity for the plate with an opening problem using stress/displacement recovery and patch configuration (linear triangular element).

Table 8.
Solution error and global effectivity for the plate with an opening problem using stress/displacement recovery and patch configuration (quadratic triangular element).

Table 9.
Solution error and global effectivity for the plate with an opening problem using stress/displacement recovery and patch configuration (linear quadrilateral element).
5.3. Plastic Sheet under Stretching Process Problem
To demonstrate the quality of the improved ZZ stress recovery under large deformations, the problem of the axisymmetric sheet stretching process was analyzed using adaptive finite element analysis. The finite element formulation, error recovery, and adaptive procedures are followed, as explained in [26]. The sheet material is considered to be rigid plastic. The punch and die used in the process are assumed to be rigid. Friction is present at the punch-sheet and die-sheet interfaces. The downward displacement of the punch is modeled in incremental steps. The schematic diagram of the axisymmetric sheet forming process is shown in Figure 5. Due to symmetry, only one half of the sheet is modeled. The input parameters for the process are as follows:
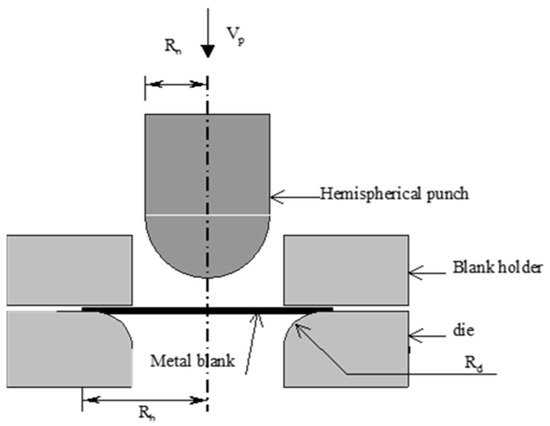
Figure 5.
Schematic diagram of sheet stretching process.
Radius of sheet, Rb = 66.0 mm and radius of the die corner, Rd = 6.35 mm;
Velocity of punch V = 1 mm/sec and sheet thickness (h) = 2 mm;
Blank to punch radius ratio (Rb/Rp) = 1.33 and the stress–strain relation is given as:
where
and are effective stress and effective strain, respectively.
The sheet is discretized using six nodded triangular elements. The number of elements of uniform mesh that have four layers of elements are 737 and the degrees of freedom are 3228 (Figure 6a). The target accuracy limit was taken as 14% of the global error. An adaptively modified mesh is generated during the analysis, based on the computed error by uniform distribution of the square of error in the elements of the domain, to attain the predefined solution accuracy. The meshes and deformed shapes at 2.0 mm punch displacements are shown in Figure 6 using the standard patch-based ZZ recovery, modified patch-based ZZ recovery, and modified patch-based displacement recovery techniques.

Figure 6.
Adaptively modified meshes in sheet stretching problem using stress/displacement recovery and patch configuration (triangular elements initial mesh = 737, with 14% target error).
6. Discussion
The accuracy of the recovery of stress field using the standard ZZ recovery technique has been improved through a larger patch configuration based on an element neighborhood pattern. In the so-called super-convergent patch recovery technique (ZZ technique), a nodal patch which represents the union of the element surrounding the node is defined and the recovery is made in the patch by least-squares fitting of polynomial expansion to the super-convergent stresses at some known points (usually gauss points) inside the elements. The improved recovery procedure is based on recovery of the stress field in the least-squares sense over an element patch that consists of the union of the elements surrounding the element under consideration. The proposed patch configuration provides more sampling points near the boundary and improves the performance of the ZZ recovery at boundary regions. The effectiveness and efficiency of the improved ZZ recovery approach is tested on benchmark plane elastic plate problems (given in [6]) involving four-node quadrilateral elements and three- and six-node triangular elements. The finite element analysis numerical results are also obtained using the same elemental patch for the extraction of more accurate displacement field. The computational results employing the recovery technique for plate problems are presented in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. The results obtained for the improved ZZ recovery technique and displacement recovery technique are compared with the ZZ super-convergent patch recovery technique.
The solution errors shown in the tables depict that the order of error obtained by employing recovery procedures is much lower than the FEM solution error and the error convergence is also higher as compared with the FEM solution error with a reduction in mesh size. The effect on error order, although with a reduced rate, is further improved taking higher order elements for domain discretization. It is clear from the tables that the ZZ recovery technique and displacement recovery technique using a modified patch configuration yield better results as compared with the standard ZZ super-convergent patch recovery technique when applied on two benchmark problems in elasticity. The rate of convergence and effectivity of the ZZ recovery technique using a modified patch configuration is higher than the displacement recovery technique using a modified patch configuration, indicating a higher efficiency and effectivity of the proposed modified ZZ recovery procedure. The optimal performance of the ZZ recovery technique using a modified patch is obtained with a four-node linear quadrilateral element.
The improved ZZ recovery technique-based error estimation for guiding the error controlling strategies of adaptive analysis is also demonstrated. Adaptively improved meshes of the elastic problem analyses are obtained for the ZZ super-convergent patch recovery, ZZ recovery technique, and displacement recovery technique using a modified patch configuration at a target error of 4%. Table 10 shows the global errors, the number of elements, and the DOF in refined meshes, obtained from the triangular and quadrilateral element meshes, to bring the solution accuracy to the target error level. The number of elements required to achieve the target error depends on the global error and distribution of error. The adaptively refined meshes with target error using different recovery-based error estimations are given in Figure 7, Figure 8 and Figure 9. The initial meshes are adaptively refined to bring the solution error within the target error limit. It is clear from the figures that the improved ZZ recovery technique-based finite element analysis is very effective for converging a predefined accuracy in a solution with a significantly smaller number of degrees of freedom for elastic plates.

Table 10.
Global errors (FEM and projected) and number of element (N) with DOF of adaptively refined meshes in a plate problem using stress/displacement recovery and patch configuration (4% target error).

Figure 7.
Adaptively modified mesh in benchmark plate problem using stress/displacement recovery and patch configuration (triangular elements initial mesh = 88.4% target error).

Figure 8.
Adaptively modified mesh in benchmark plate problem using stress/displacement recovery and patch configuration (triangular elements initial mesh = 395.4% target error).

Figure 9.
Adaptively modified mesh in benchmark plate problem using stress/displacement recovery and patch configuration (quadrilateral elements initial mesh = 99.4% target error).
The performance of the improved ZZ recovery technique is also assessed under large or plastic deformation using a sheet stretching process analysis. The adaptive analysis results considering the various stress/displacement recovery techniques are shown in Figure 6. From the adaptively modified meshes, it can be observed that the elements become finer in some parts of the sheet and coarsening in other parts. The meshes become finer in stress concentration zones of the problems. It is also clear from the large deformation problem analysis that the improved ZZ recovery technique-based finite element analysis recovers the errors more reliably, and a larger fine element zone across the full sheet thickness at the sheet-punch contact and at the sheet-die contact is created.
7. Conclusions
In this study, the classical ZZ recovery technique based on the standard node neighborhood patch configuration was improved using a larger element neighborhood patch configuration. The derivatives at any point in the element domain or node domain are calculated through better approximated stress/displacement fields through the least-squares fit of computed nodal stress/displacement using a higher order polynomial over an element patch that consists of the union of the elements surrounding the element under consideration. It is demonstrated through elastic and plastic plate examples involving four-node quadrilateral elements and three- and six-node triangular elements that the performance of the ZZ recovery technique is greatly improved using a modified patch configuration. It is observed that the relative error decreases and the convergence rate increases with mesh refinement. The quality of error estimation using the ZZ recovery of the derivative field, considering the standard and a modified patch configuration, was also compared with that of error estimation using extracted stress from recovery of a more accurate displacement field using the element neighborhood patch configuration in terms of effectivity, rate of convergence, and adaptively refined meshes. The quality of error estimation using the ZZ stress recovery technique employing an element neighborhood patch configuration is better as compared with the quality of error estimation using the displacement recovery technique. It is concluded that the improved ZZ recovery technique-based finite element analysis is very effective for converging a predefined accuracy in a solution with a significantly smaller number of degrees of freedom. The numerical results also show that the improved ZZ recovery technique using an element neighborhood patch configuration can effectively be incorporated into the adaptive computations, as performance is good with both coarser and finer element meshes. It is concluded that the improved ZZ recovery technique captures the large deformation errors more reliably than the standard ZZ recovery technique.
Author Contributions
Conceptualization, M.A. and D.S.; methodology, M.A.; software, D.S.; validation, S.A. and M.A.A.; formal analysis, M.A. and S.A.; investigation, M.A.; resources, S.A.; data curation, M.A.A.; writing—original draft preparation, M.A.; writing—review and editing, S.A. and M.A.A.; visualization, S.A.; supervision, D.S.; project administration, M.A.A.; funding acquisition, M.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the General Research Project under grant number (R.G.P2 /73/41). The authors acknowledge to the Dean of the Faculty of Engineering for his valuable support and help.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Exclude.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Cen, S.; Wu, C.J.; Li, Z.; Shang, Y.; Li, C. Some advances in high-performance finite element methods. Eng. Comput. 2019, 36, 2811–2834. [Google Scholar] [CrossRef]
- Gratsch, T.; Bathe, K. A posteriori error estimation technique in practical finite element analysis. Comput. Struct. 2005, 83, 75–90. [Google Scholar] [CrossRef] [Green Version]
- Ainsworth, M.; Zhu, J.Z.; Craig, A.W.; Zienkiewicz, O.C. Analysis of the Zienkiewicz–Zhu a-posteriori error estimator in the finite element method. Int. J. Num. Meth. Eng. 1989, 28, 2161–2174. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Zhu, J.Z. The super-convergent patch recovery and a-posteriori error estimates, part i, the error recovery technique. Int. J. Num. Meth. Eng. 1992, 33, 1331–1364. [Google Scholar] [CrossRef]
- Rodenas, J.J.; Tur, M.; Fuenmayor, F.J.; Vercher, A. Improvement of the super-convergent patch recovery technique by the use of constraint equations: The SPR-C technique. Int. J. Num. Meth. Eng. 2007, 70, 705–727. [Google Scholar] [CrossRef]
- Wiberg, N.E.; Abdulwahab, F. Patch recovery based on super-convergent derivatives and equilibrium. Int. J. Num. Meth. Eng. 1990, 36, 2703–2724. [Google Scholar] [CrossRef]
- Blacker, T.; Belytschko, T. Super-convergent patch recovery with equilibrium and conjoint interpolant enhancements. Int. J. Num. Meth. Eng. 1994, 37, 517–536. [Google Scholar] [CrossRef]
- Li, X.D.; Wiberg, N.E. A Posteriori error estimate by element patch post-processing, adaptive analysis in energy and l2 norms. Comput. Struct. 1994, 53, 907–919. [Google Scholar] [CrossRef]
- Wiberg, N.E.; Abdulwahab, F.; Ziukas, S. Enhanced superconvergent patch recovery incorporating equilibrium and boundary conditions. Int. J. Num. Meth. Eng. 1994, 37, 3417–3440. [Google Scholar] [CrossRef]
- Lee, T.; Park, H.C.; Lee, S.W. A super-convergent stress recovery technique with equilibrium constraint. Int. J. Num. Meth. Eng. 1997, 40, 1139–1160. [Google Scholar] [CrossRef]
- Park, H.C.; Shin, S.H.; Lee, S.W. A super-convergent stress recovery technique for accurate boundary stress extraction. Int. J. Num. Meth. Eng. 1999, 45, 1227–1242. [Google Scholar] [CrossRef]
- Maunder, E.A.W.; Trefftz, A. Patch recovery method for smooth stress resultants and applications to Reissner–Mindlin equilibrium plate models. Comput. Assist. Mech. Eng. Sci. 2001, 8, 409–424. [Google Scholar]
- Rodenas, J.J.; Estrada, G.; Andres, O.; Fuenmayor, F.J.; Chinesta, F. Enhanced error estimator based on a nearly equilibrated moving least squares recovery technique for FEM and XFEM. Comput. Mech. 2013, 52, 321–344. [Google Scholar] [CrossRef]
- Nadal, E.; D´ıez, P.; R´odenas, J.J.; Tur, M.; Fuenmayor, F.J. A recovery-explicit error estimator in energy norm for linear elasticity. Comput. Methods Appl. Mech. Eng. 2015, 287, 172–190. [Google Scholar] [CrossRef] [Green Version]
- Ülkü, H.; Karaköse, C.; Askes, H. A recovery-type a posteriori error estimator for gradient elasticity. Comput. Struct. 2015, 154, 204–209. [Google Scholar]
- Gu, H.; Zong, Z.; Hung, K.C. A modified super-convergent patch recovery method and its application to large deformation problems. Finite Elem. Anal. Des. 2004, 40, 665–687. [Google Scholar] [CrossRef]
- Zhang, Z.; Naga, A. A new finite element gradient recovery method: Superconvergence property. SIAM J. Sci. Comput. 2005, 26, 1192–1213. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Yi, N. The super-convergent cluster recovery method. J. Sci. Comput. 2010, 44, 301–322. [Google Scholar] [CrossRef]
- Ahmed, M.; Singh, D.; Islam, S. Effect of contact conditions on adaptive finite element simulation of sheet forming operations. Eur. J. Comput. Mech. 2015, 24, 1–15. [Google Scholar] [CrossRef]
- Boo, S.-H.; Kim, J.-G.; Lee, P.-S. Error estimation for the automated multi-level sub-structuring method. Int. J. Numer. Meth. Eng. 2016, 106, 927–950. [Google Scholar] [CrossRef]
- Chen, J.; Chen, Z. Three-dimensional super-convergent gradient recovery on tetrahedral meshes. Int. J. Numer. Meth. Eng. 2016, 108, 819–838. [Google Scholar] [CrossRef]
- Cai, D.; Cai, Z. A hybrid a posteriori error estimator for conforming finite element approximations. Comput. Methods Appl. Mech. Eng. 2018, 339, 320–340. [Google Scholar] [CrossRef]
- Sharma, R.; Zhang, J.; Langelaar, M.; van Keulen, F.; Aragón, A.M. An improved stress recovery technique for low-order 3D finite elements. Int. J. Numer. Methods Eng. 2018, 114, 88–103. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Yuan, S.; Xing, Q. Adaptive finite element analysis with local mesh refinement based on a posteriori error estimate of element energy projection technique. Eng. Comput. 2019, 36, 2010–2033. [Google Scholar] [CrossRef]
- Ahmed, M. A Comparative study of mesh-free radial point interpolation method and moving least squares method-based error estimation in elastic finite element analysis. Arab. J. Sci. Eng. 2020, 45, 3541–3557. [Google Scholar] [CrossRef]
- Ahmed, M.; Singh, D. An adaptive parametric study on mesh refinement during adaptive finite element simulation of sheet forming operations. Turk. J. Eng. Environ. Sci. 2008, 13, 1–13. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).