The Graphene Field Effect Transistor Modeling Based on an Optimized Ambipolar Virtual Source Model for DNA Detection
Abstract
:1. Introduction
2. Proposed Model
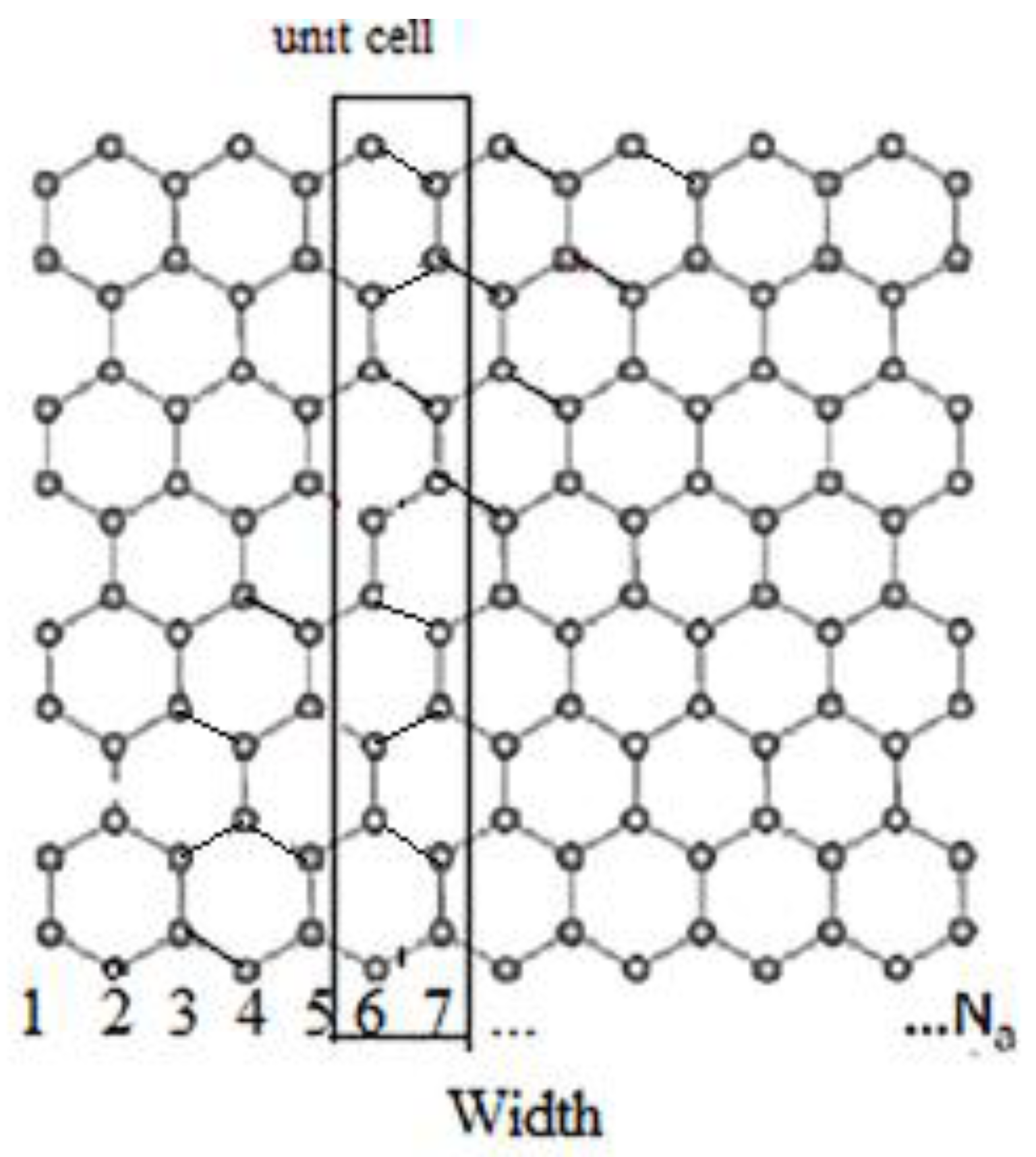
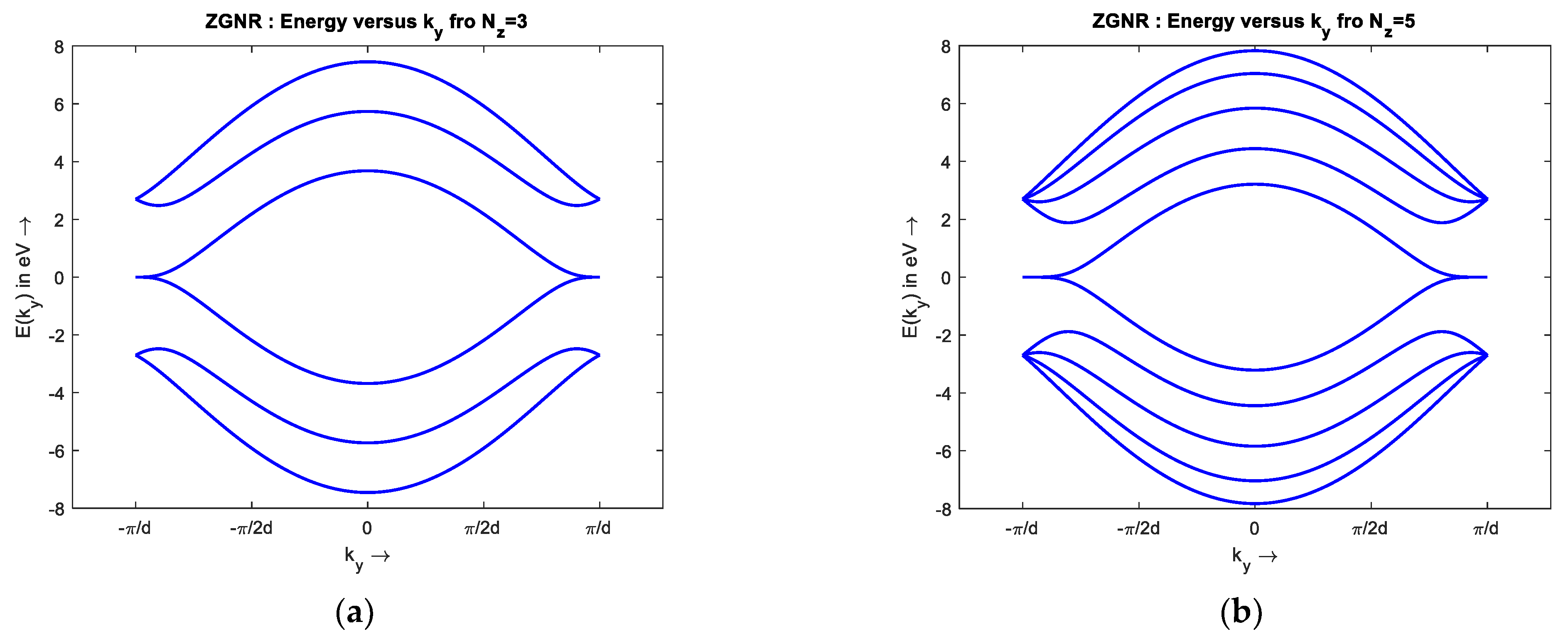
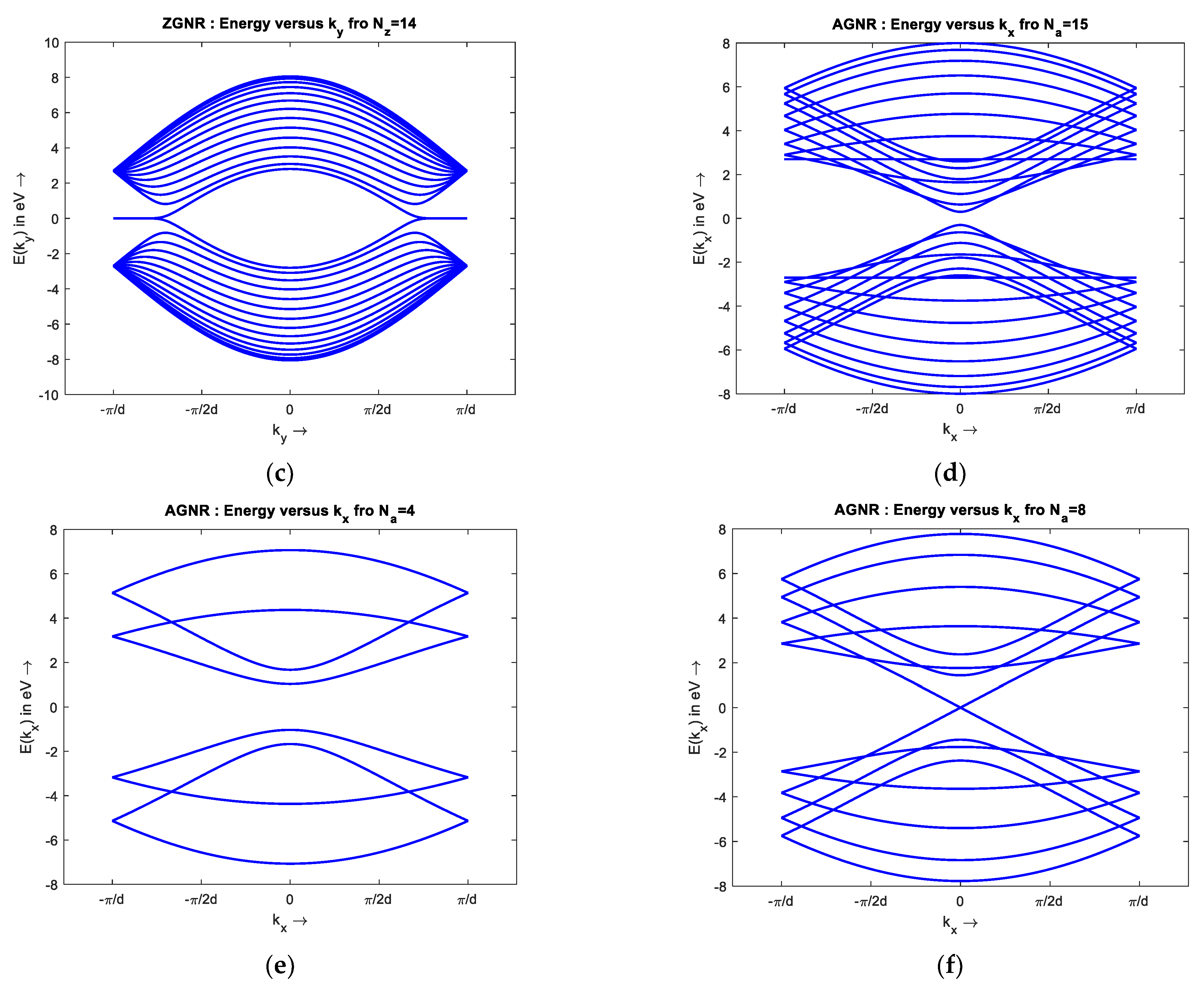
2.1. One-Dimensional Energy Band Structure of GNR
2.2. Green’s Function and Current–Voltage Derivation
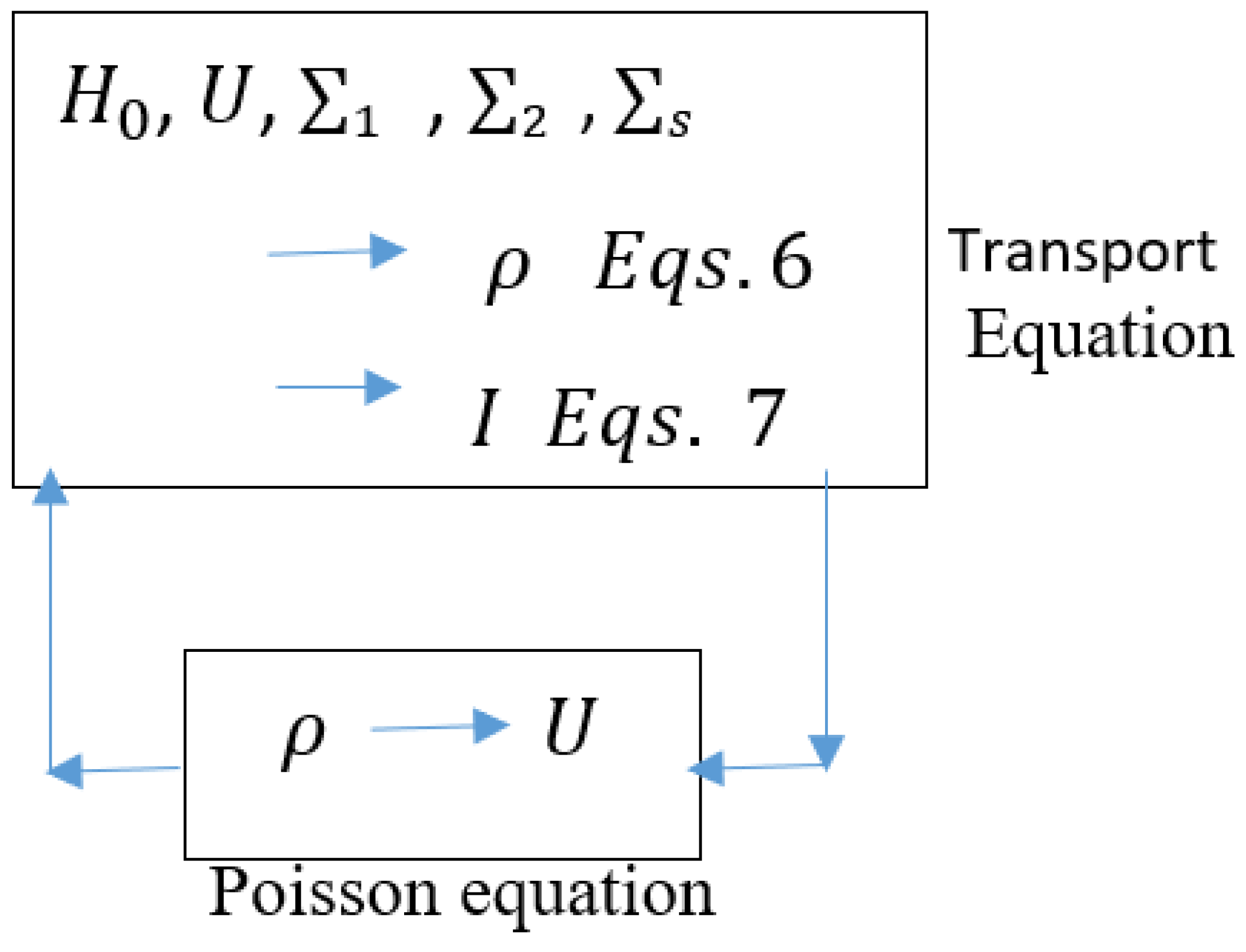
2.3. Electrostatics
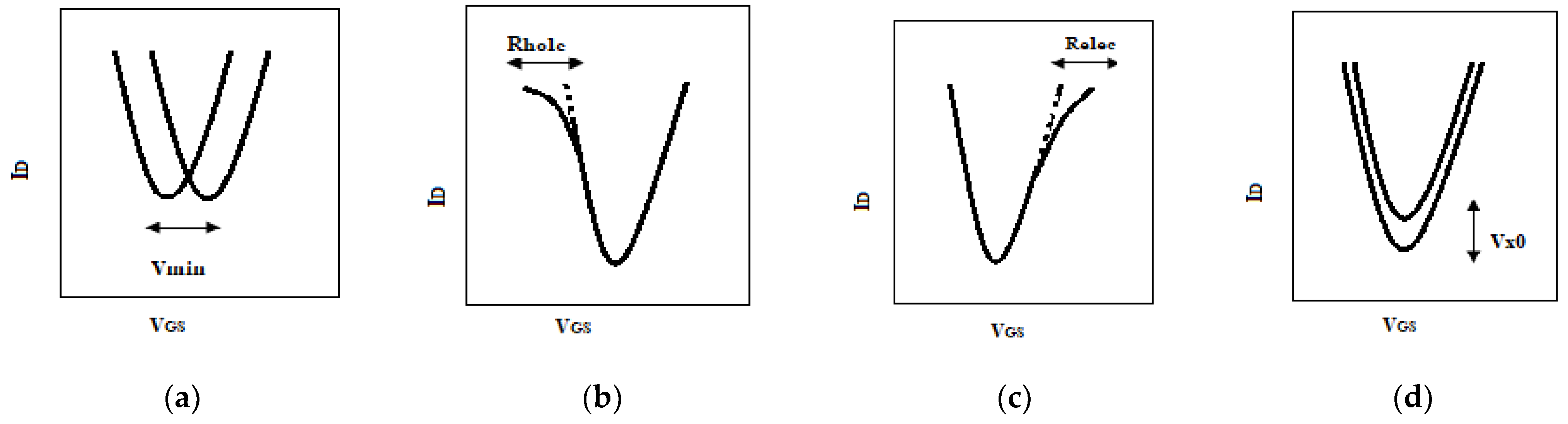
2.4. Physical-Based AVS Model
3. Results
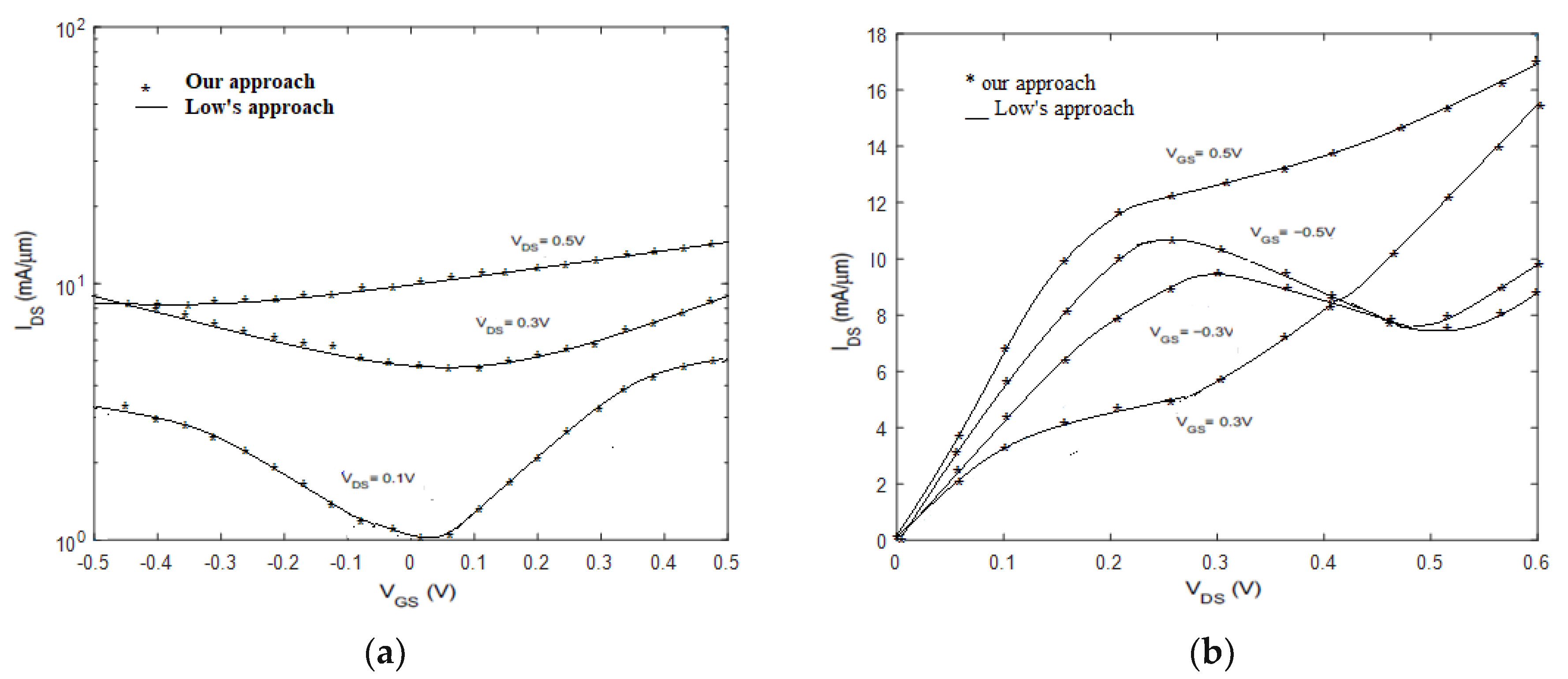
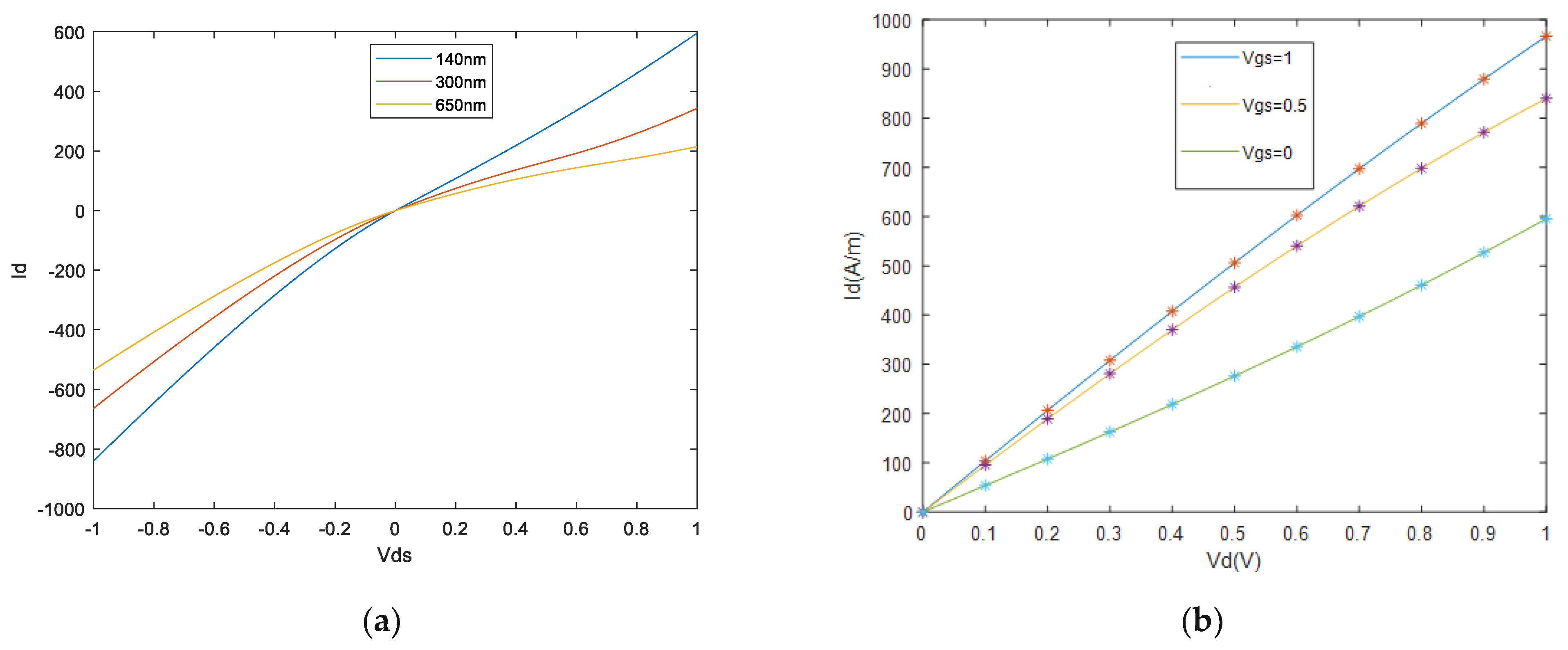
3.1. Simulation of GFET
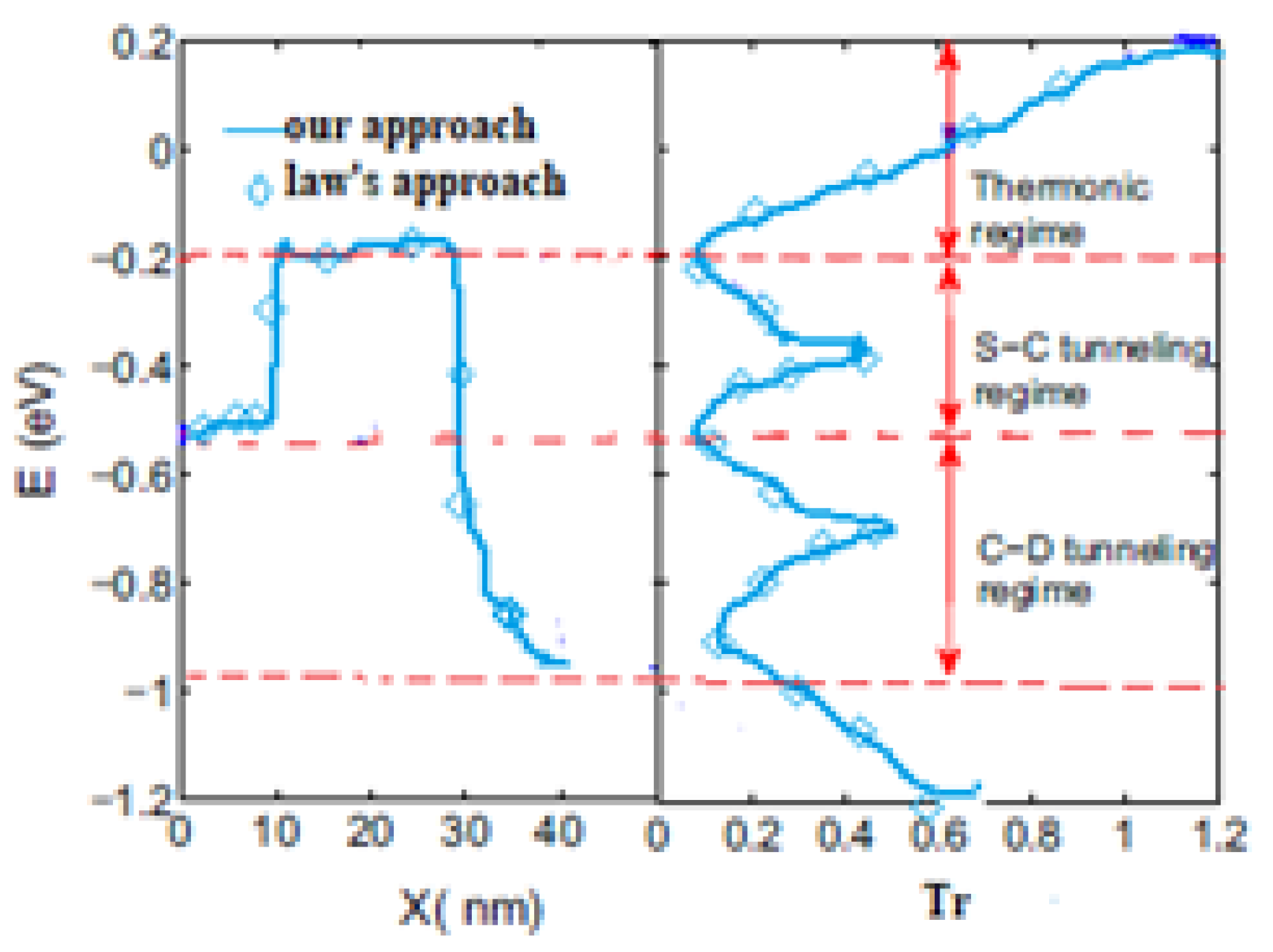
3.2. NEGF Modeling of GFET
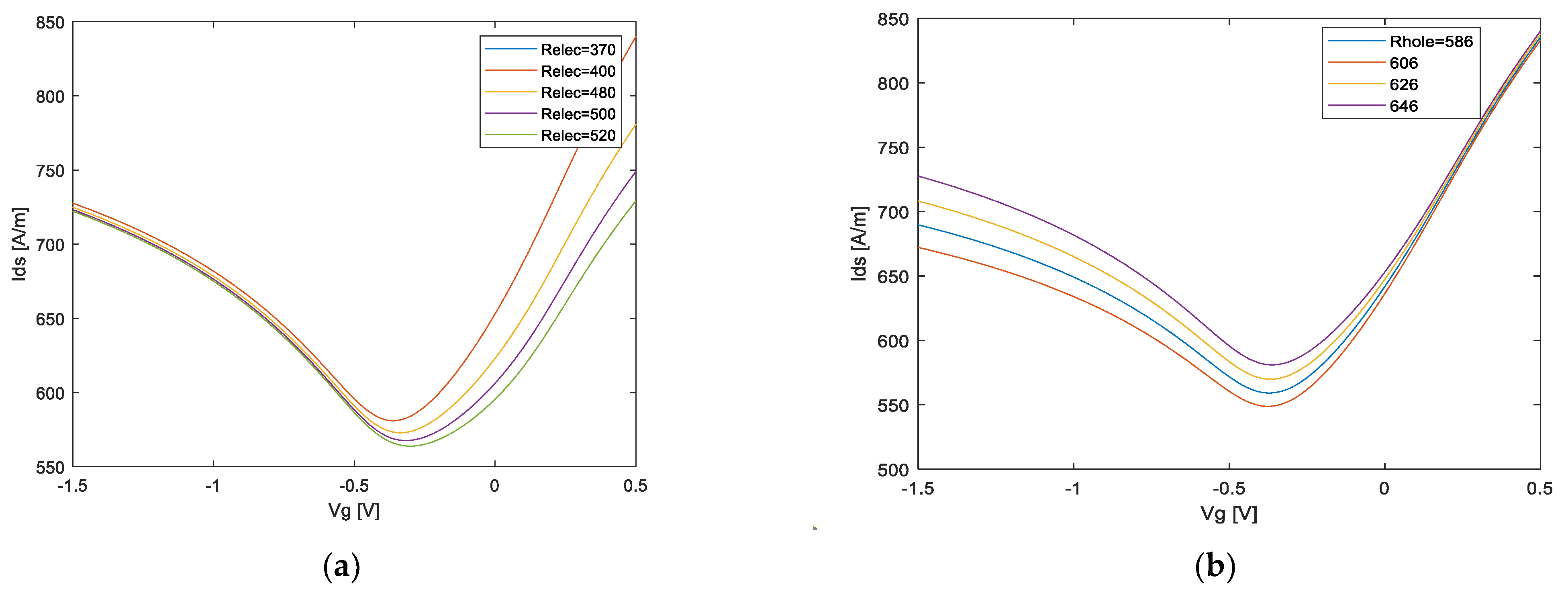
3.3. Physical-Based AVS Model Parameter Optimization
3.4. Biosensor Modelling by AVS Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Basic Concepts of Graphene
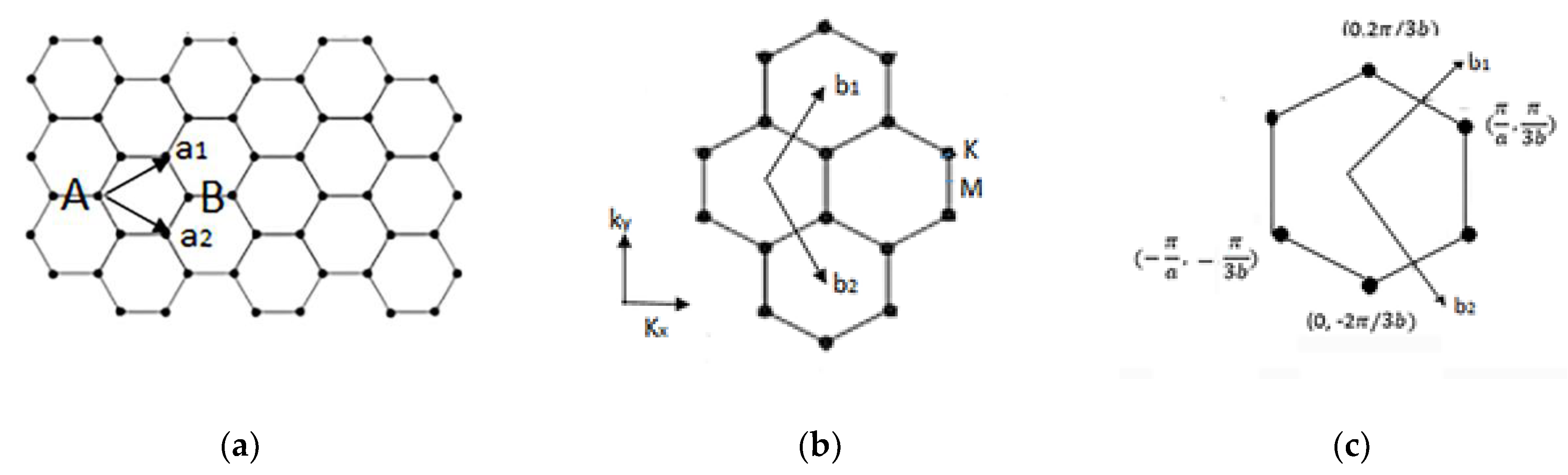
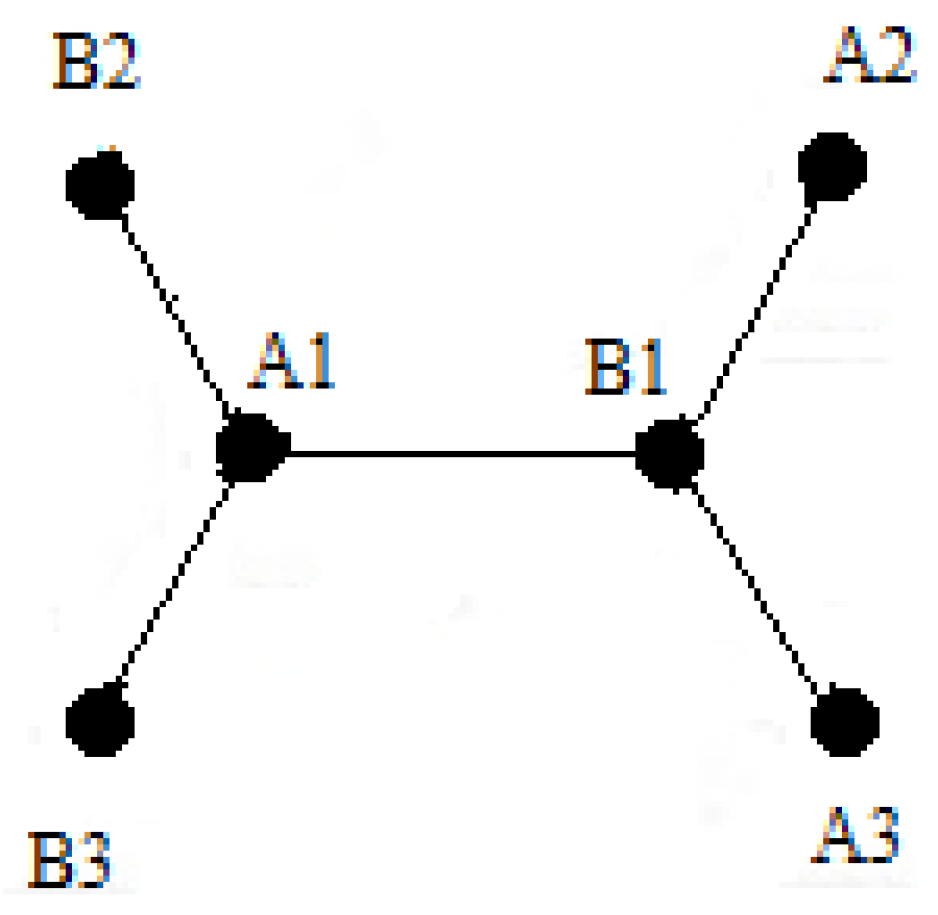
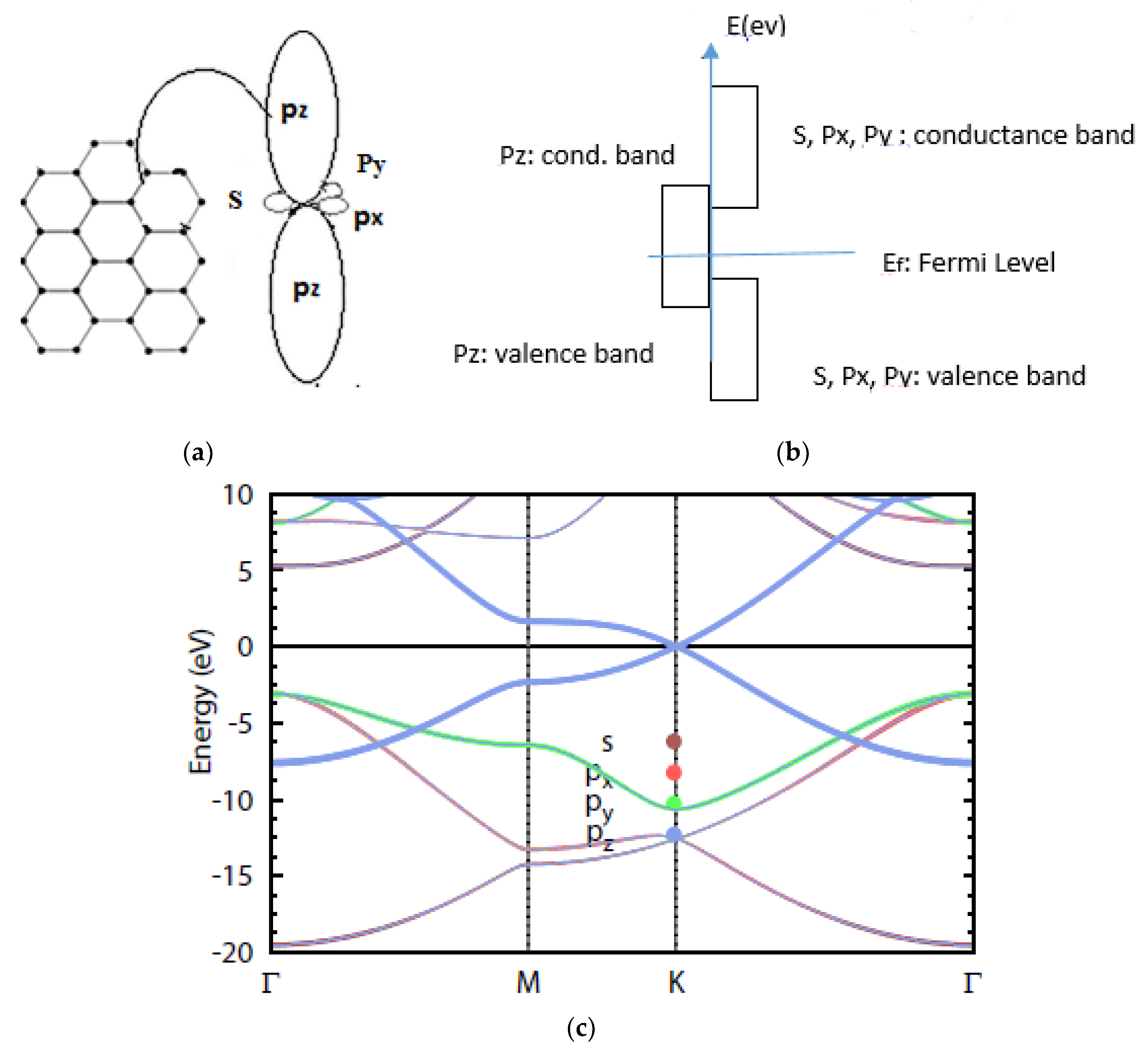
Appendix A.1. Basic Concepts of Graphene Band Structure
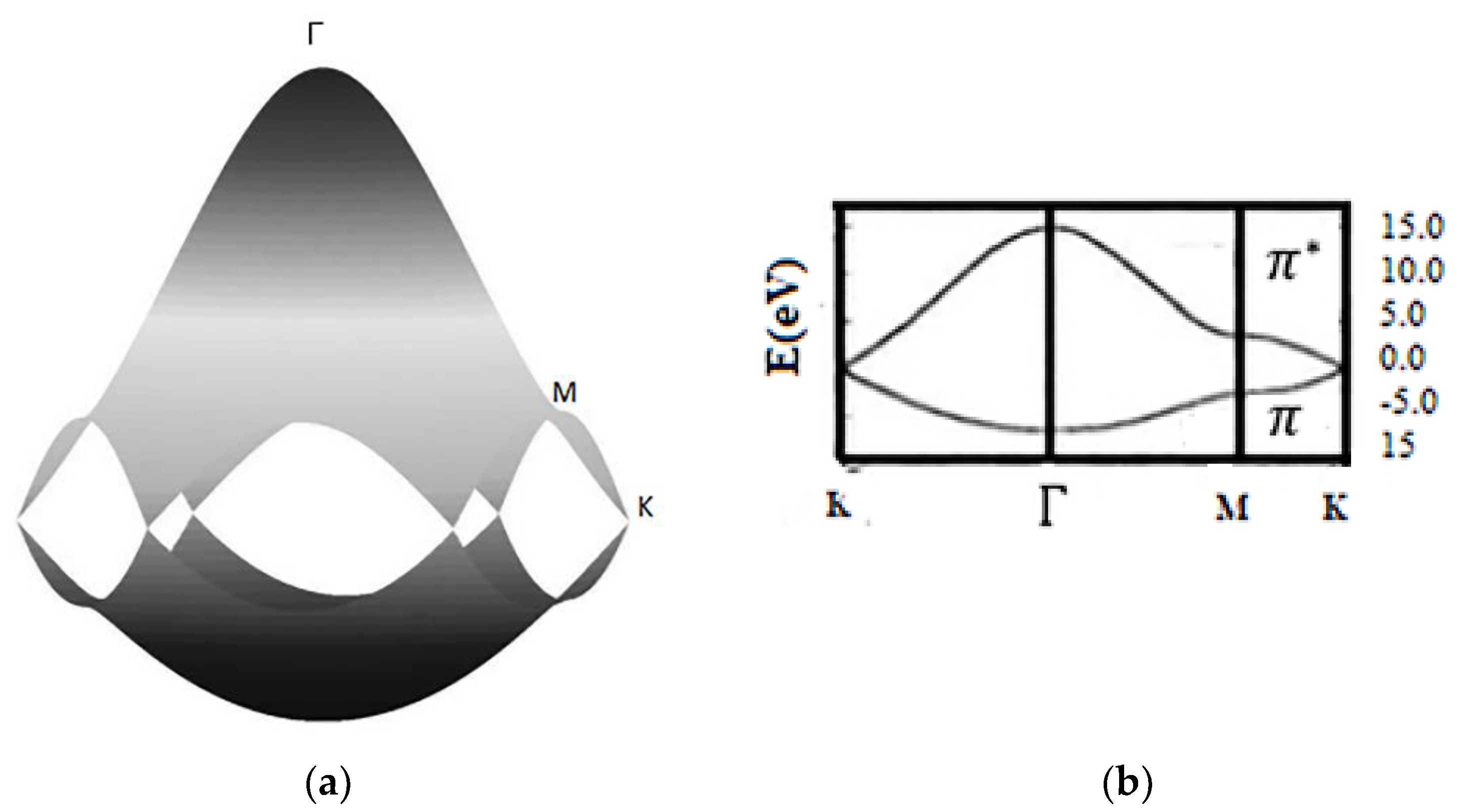
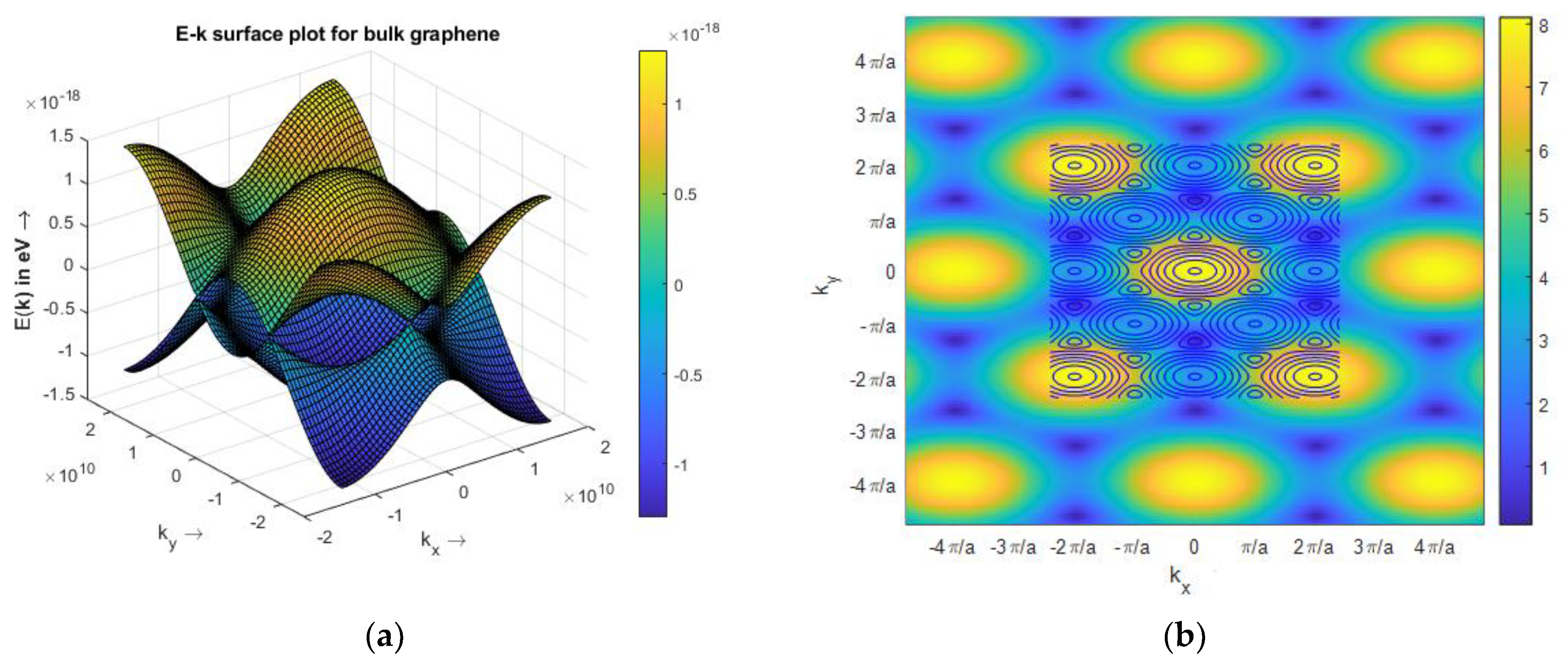
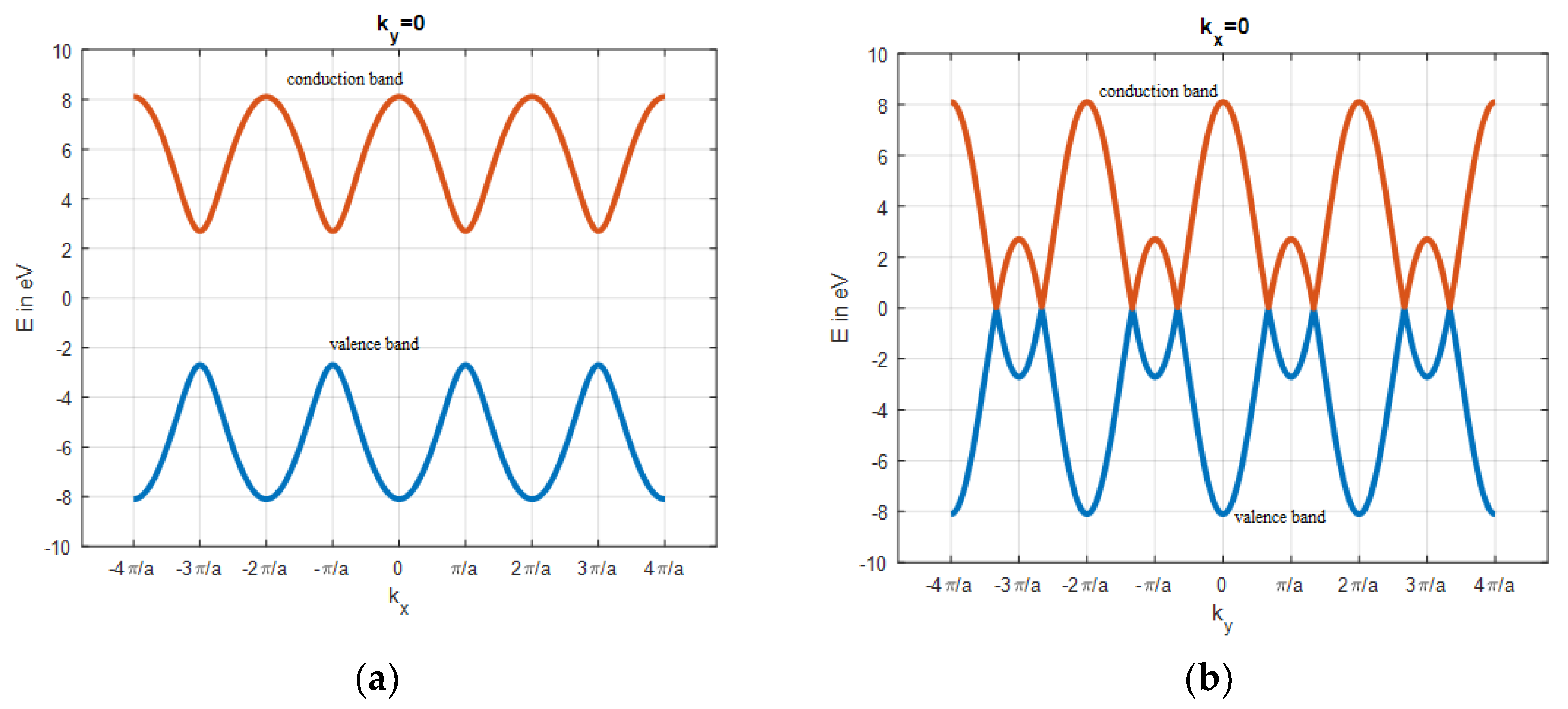
Appendix A.2. Two-Dimensional Energy Band Structure of Single-Layer Graphene


References
- Sheikhzadeh, E.; Eissa, S.; Ismail, A.; Zourob, M. Diagnostic techniques for COVID-19 and new developments. Talanta 2020, 220, 121392. [Google Scholar] [CrossRef]
- Singh, S.; Kumar, V.; Dhanjal, D.S.; Datta, S.; Prasad, R.; Singh, J. Biological Biosensors for Monitoring and Diagnosis. Microb. Biotechnol. Basic Res. Appl. 2020, 317–335. [Google Scholar] [CrossRef]
- Rawat, B. Royy Pally: Modeling of graphene-based field-effect transistors through a 1-D real-space approach. J. Comput. Electron. 2018, 17, 90–100. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Falko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192. [Google Scholar] [CrossRef]
- Wu, G.F.; Tang, X.; Meyyappan, M.; Lai, K.W.C. Doping effects of surface functionalization on graphene with aromatic molecule and organic solvents. Appl. Surf. Sci. 2017, 425, 713–721. [Google Scholar] [CrossRef]
- Akbari, E.; Buntat, Z.; Nilashi, M.; Afroozeh, A.; Farhange, Y.; Zeinalinezhad, A. ISVR modeling of an interferon gamma (IFN-) biosensor based on graphene. Anal. Methods 2016, 8, 7217–7224. [Google Scholar] [CrossRef]
- Karimi, H.; Rahmani, R.; Mashayekhi, R.; Ranjbari, L.; Shirdel, A.H.; Haghighian, N.; Movahedi, P.; Hadiyan, M.; Ismail, R. Analytical development and optimization of a graphene-solution interface capacitance model. Beilstein J. Nanotechnol. 2014, 5, 603–609. [Google Scholar] [CrossRef] [Green Version]
- Karimi, H.; Yusof, R.; Rahmani, R.; Hosseinpour, H.; Ahmadi, M.T. Development of solution-gated graphene transistor model for biosensors. Nano Res. Lett. 2014, 9, 71–78. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Logoteta, D.; Marconcini, P.; Bonati, C.; Fagotti, M.; Macucci, M. High-performance solution of the transport problem in a graphene armchair structure with a generic potential. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2014, 89, 063309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, G.F.; Tang, X.; Lin, Z.H.; Meyyappan, M.; Lai, K.W.C. The effect of ionic strength on the sensing performance of liquid-gated biosensors. In Proceedings of the IEEE 17th International Conference on Nanotechnology (IEEE-NANO), Pittsburgh, PA, USA, 25–28 July 2017; pp. 242–245. [Google Scholar]
- Wu, G.F.; Dai, Z.W.; Tang, X.; Lin, Z.H.; Lo, P.K.; Meyyappan, M.; Lai, K.W.C. Graphene field-effect transistors for the sensitive and selective detection of Escherichia coli using pyrene-tagged DNA aptamer. Adv. Healthc. Mater. 2017, 6, 1700736. [Google Scholar] [CrossRef]
- Pourasl, A.H.; Ahmadi, M.T.; Rahmani, M.; Ismail, R. Graphene Based Biosensor Model for Escherichia Coli Bacteria Detection. J. Nanosci. Nanotechnol. 2017, 17, 601–605. [Google Scholar] [CrossRef] [PubMed]
- Ushiba, S.; Okino, T.; Miyakawa, N.; Ono, T.; Shinagawa, A.; Kanai, Y.; Inoue, K.; Takahashi, K.; Kimura, M.; Matsumoto, K. State-space modeling for dynamic response of graphene FET biosensors. Jpn. J. Appl. Phys. 2020, 59, SGGH04. [Google Scholar] [CrossRef]
- Fiori, G.; Iannaccone, G. 3D Poisson/NEGF Solver for the Simulation of Graphene Nanoribbon, Carbon Nanotubes and Silicon Nanowire Transistors. NanoTCAD ViDES. 2016. Available online: https://nanohub.org/resources/vides (accessed on 30 April 2021).
- Low, T.; Hong, S.; Appenzeller, J.; Datta, S.; Lundstrom, M. Conductance asymmetry of graphene p-n junction. IEEE Trans. Electron. Dev. 2009, 56, 1292. [Google Scholar] [CrossRef] [Green Version]
- Datta, S. Nanoscale device modeling: The Green’s function method. Superlattices Microstruct. 2000, 28, 253. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport. In Mesoscopic System; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Coleman, T.; Li, Y. An interior trust region approach for nonlinear minimization subject to bounds. SIAM J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef] [Green Version]
- Zhao, P.; Guo, J. Modeling edge effects in graphene nanoribbon field-effect transistors with real and mode space methods. J. Appl. Phys. 2009, 105, 034503. [Google Scholar] [CrossRef] [Green Version]
- Wallace, P.R. The band theory of graphite. Phys. Rev. 1947, 71, 622–634. [Google Scholar] [CrossRef]
- Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Physical Properties of Carbon Nanotubes; Imperial College Press: London, UK, 1998. [Google Scholar]
- Brey, L.; Fertig, H.A. Electronic states of graphene nanoribbons studied with the Dirac equation. Phys. Rev. B Condens. Matter 2006, 73, 235–411. [Google Scholar] [CrossRef] [Green Version]
- Haug, H.; Jauho, A.P. Quantum Kinetics in Transport and Optics of Semiconductors; Springer Series in Solid State Sciences; Springer: New York, NY, USA, 1996; p. 123. [Google Scholar]
- Schomerus, H. Effective contact model for transport through weaklydoped graphene. Phys. Rev. B Condens. Matter 2007, 76, 45–433. [Google Scholar] [CrossRef] [Green Version]
- Mojarad, R.G.; Datta, S. Effect of Contact Induced States on Minimum Conductivity in Graphene. Phys. Rev. B 2009, 79, 085410. [Google Scholar] [CrossRef] [Green Version]
- Zheng, H.; Wang, Z.F.; Luo, T.; Shi, Q.W.; Chen, J. Analytical study of electronic structure in armchair graphene nanoribbons. Phys. Rev. B Condens. Matter 2007, 75, 165–414. [Google Scholar] [CrossRef] [Green Version]
- Lake, R.; Klimeck, G.; Brown, R.C.; Jovanovic, D. Single and multiband modeling of quantum electron transport through layered semiconductor devices. J. Appl. Phys. 1997, 81, 7845–7869. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Jenkins, K.A.; Valdes-Garcia, A.; Farmer, D.B.; Zhu, Y.; Bol, A.A.; Dimitrakopoulos, C.; Zhu, W.; Xia, F.; Avouris, P.; et al. State-ofthe-art graphene high-frequency electronics. Nano Lett. 2012, 12, 3062–3067. [Google Scholar] [CrossRef]
- Ganapathi, K.; Yoon, Y.; Lundstrom, M.; Salahuddin, S. Ballistic I-V characteristics of short-channel graphene field-effect transistors: Analysis and optimization for analog and RF applications. IEEE Trans. Electron. Dev. 2013, 60, 958. [Google Scholar] [CrossRef]
- Grassi, R.; Low, T.; Gnudi, A.; Baccarani, C. Contact-induced negative differential resistance in short-channel graphene FETs. IEEE Trans. Electron. Dev. 2013, 60, 140. [Google Scholar] [CrossRef] [Green Version]
- Grassi, R.; Gnudi, A.; Di Lecce, V.; Gnani, E.; Reggiani, S.; Baccarani, G. Exploiting negative differential resistance in monolayer graphene FETs for high voltage gains. IEEE Trans. Electron. Dev. 2014, 61, 617. [Google Scholar] [CrossRef] [Green Version]
- Meric, I.; Han, M.Y.; Young, A.F.; Ozyilmaz, B.; Kim, P.; Shepard, K.L. Current saturation in zero-bandgap, top-gated graphene fieldeffect transistors. Nat. Nanotechnol. 2008, 3, 654. [Google Scholar] [CrossRef]
- Han, S.J.; Reddy, D.; Carpenter, G.D.; Franklin, A.D.; Jenkins, K.A. Current saturation in submicrometer graphene transistors with thin gate dielectric: Experiment, simulation, and theory. ACS Nano 2012, 6, 5220. [Google Scholar] [CrossRef]
- Rakheja, S.; Antoniadis, D. Ambipolar Virtual Source Compact Model for Graphene FETs. Available online: https://nanohub.org/publications/10 (accessed on 23 October 2014).
- Dong, X.; Shi, Y.; Huang, W.; Chen, P.; Li, L.J. Electrical Detection of DNA Hybridization with Single-Base Specificity Using Transistors Based on CVD-Grown Graphene Sheets. Adv. Mater. 2010, 22, 1649–1653. [Google Scholar] [CrossRef]



| Variable | Meaning | Values |
|---|---|---|
| w | Device width (m) | 20 × 10−6 |
| Lg | Device Length | 140,300,650 × 10−9 |
| cg | Gate capacitance (F/) | 3.6 × 10−3 |
| Non-ideality factor (unit-less) | 2; | |
| alpha | Shift in threshold voltage (unit-less) | 6; |
| Tjun | Junction temperature | 298 |
| zeta | Channel ballisticity parameter (unit-less) | 0.2 |
| mc | Relative effective mass of carriers (kg) | 0.04 |
| cofs | Outer-fringing capacitance for the source—terminal (F/M) | 0 |
| cofd | Outer fringing capacitance for the drain—terminal (F/M) | 0 |
| Variable | Meaning | Lg = 140 nm | Lg = 3000 nm | Lg = 650 nm |
|---|---|---|---|---|
| Resistance due to electron concentrations (Ω-µm) | 373.8705 | 450.2130 | 486.7588 | |
| Resistance due to hole concentrations (Ω-µm) | 586.6873 | 760.9854 | 1092.3329 | |
| Saturation parameter (unit-less) | 1.8000 | 1.8000 | 1.8000 | |
| Minimum background doping (unit-less) | 3.0000 | 3.0000 | 1.0000 | |
| Carrier mobility () | 1130.7361 | 1721.3129 | 2220.9262 | |
| Injection velocity of carriers (m/s) | 5.4084 | 4.5471 | 3.0554 | |
| ΔV | Shift in threshold (v) | 0.0000 | 0.2363 | 0.2564 |
| Dirac-point voltage (v) | −0.6401 | −0.8731 | −1.0608 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akbari, M.; Shahbazzadeh, M.J.; La Spada, L.; Khajehzadeh, A. The Graphene Field Effect Transistor Modeling Based on an Optimized Ambipolar Virtual Source Model for DNA Detection. Appl. Sci. 2021, 11, 8114. https://doi.org/10.3390/app11178114
Akbari M, Shahbazzadeh MJ, La Spada L, Khajehzadeh A. The Graphene Field Effect Transistor Modeling Based on an Optimized Ambipolar Virtual Source Model for DNA Detection. Applied Sciences. 2021; 11(17):8114. https://doi.org/10.3390/app11178114
Chicago/Turabian StyleAkbari, Moaazameh, Mehdi Jafari Shahbazzadeh, Luigi La Spada, and Alimorad Khajehzadeh. 2021. "The Graphene Field Effect Transistor Modeling Based on an Optimized Ambipolar Virtual Source Model for DNA Detection" Applied Sciences 11, no. 17: 8114. https://doi.org/10.3390/app11178114
APA StyleAkbari, M., Shahbazzadeh, M. J., La Spada, L., & Khajehzadeh, A. (2021). The Graphene Field Effect Transistor Modeling Based on an Optimized Ambipolar Virtual Source Model for DNA Detection. Applied Sciences, 11(17), 8114. https://doi.org/10.3390/app11178114







