Noninteracting Control Design for 6-DoF Active Vibration Isolation Table with LMI Approach
Abstract
:1. Introduction
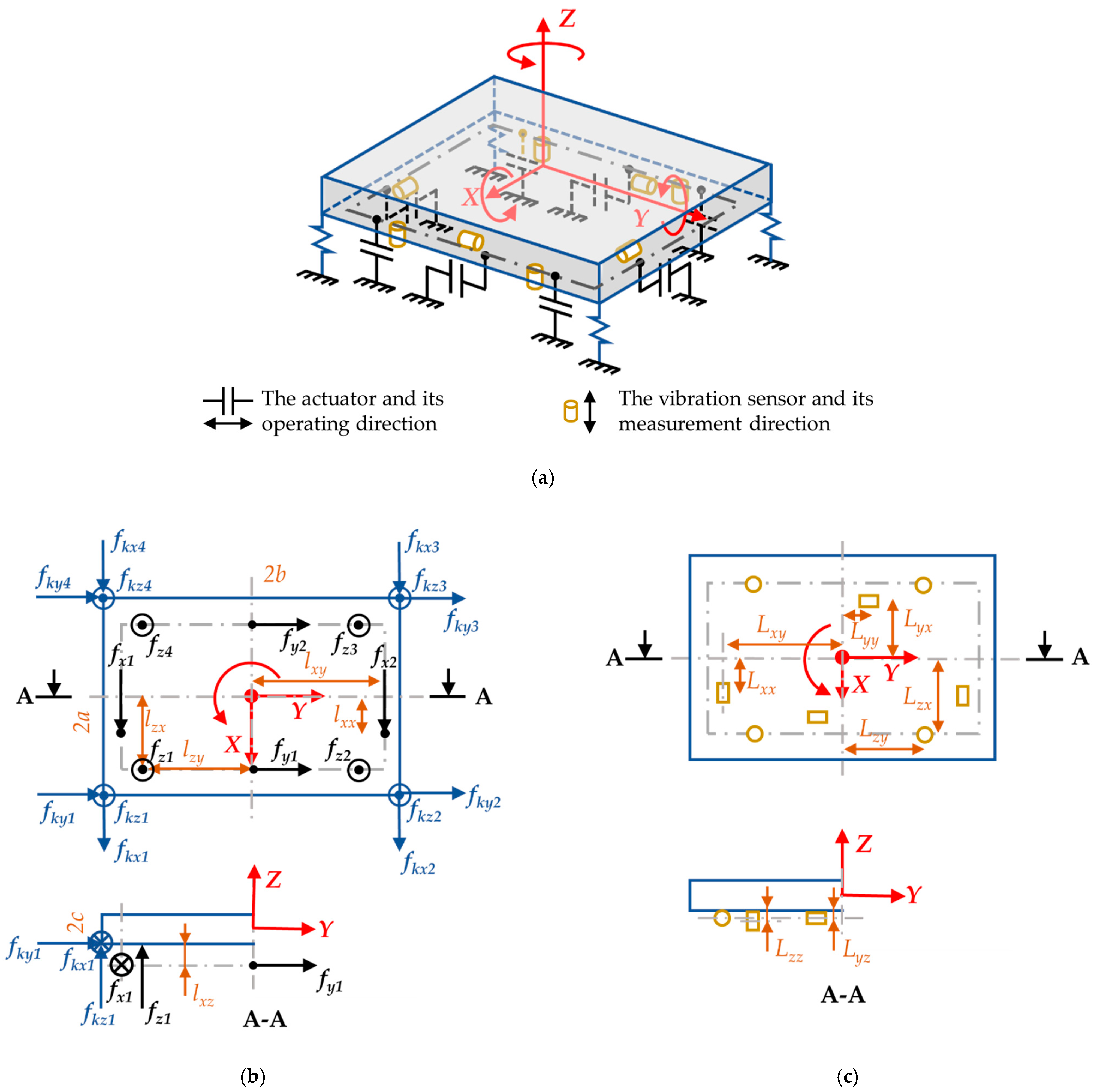
2. System Modeling
- The top plate fixed frame T is a right-handed coordinate system whose origin is at the mass center of the plate; the Z-axis points upward, the X-axis points forward, the counterclockwise is the positive rotation direction. This coordinate system is depicted by red-colored vectors in Figure 1.
- The bottom plate fixed frame B has its origin at the centroid of the bottom plate. Translation and rotation directions are similar to frame T.
- is the displacement of the origin O in the x-, y-, and z-directions;
- is the rotation about x-, y-, and z-axes of the upper plate;
- and are the displacement and the angular position of the bottom plate, respectively;
- m is the mass of the sprung weight;
- is the inertia tensor of the sprung mass;
- is the force in the j-axis direction generated by the ith actuator in the same direction;
- is the force in the j-axis direction generated by the four springs;
- is the distance in the j-axis direction from the center of mass to the sensor measuring the velocity in the i-axis direction (m);
- is the distance in the j-axis direction from the center of mass to the actuator that generates the force in the i-axis direction (m).
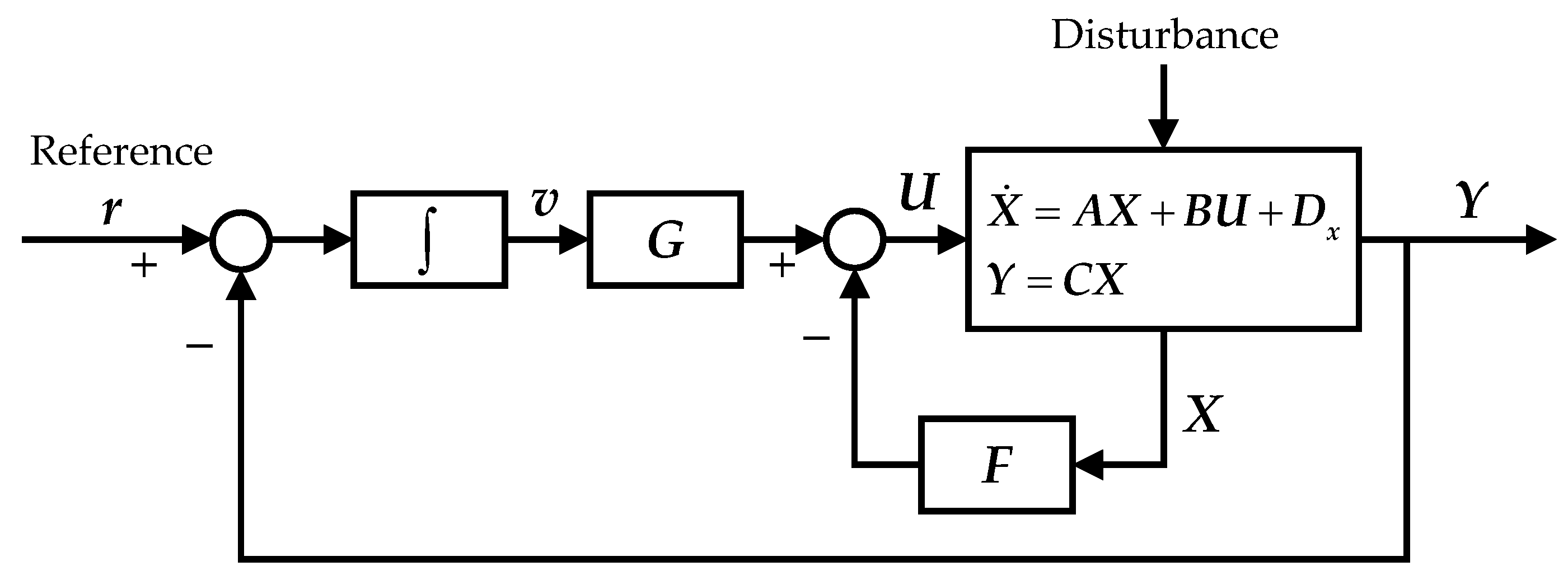
- is the state vector;
- is the system output vector;
- is the control signal vector;
- is the disturbance vector from the bottom plate.
3. Noninteracting Control Design
3.1. Conditions for a Decoupled Performance
3.2. Design of the State Feedback Matrix F
3.3. The LMI-Based Design of the Feedback Matrix G
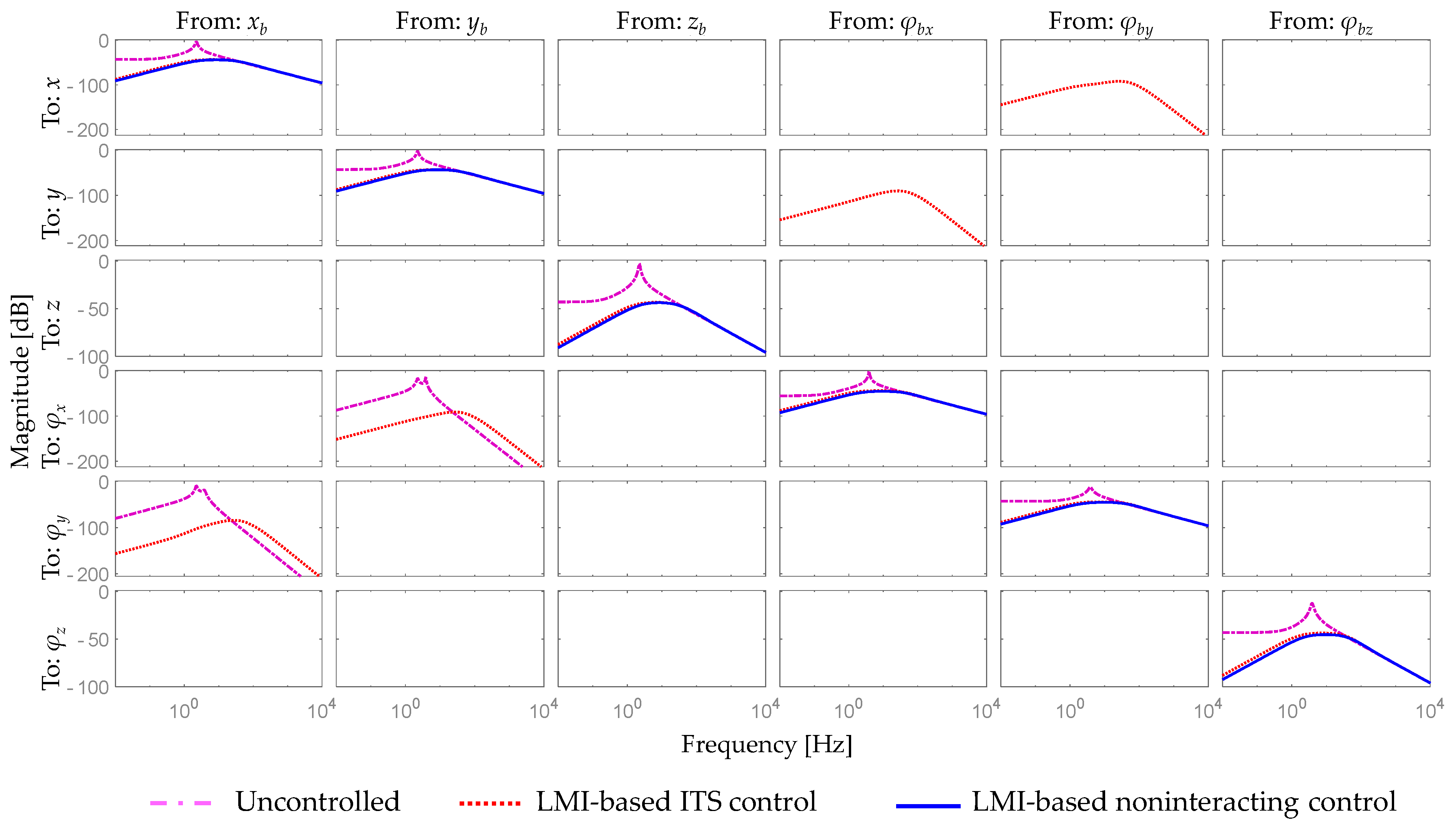
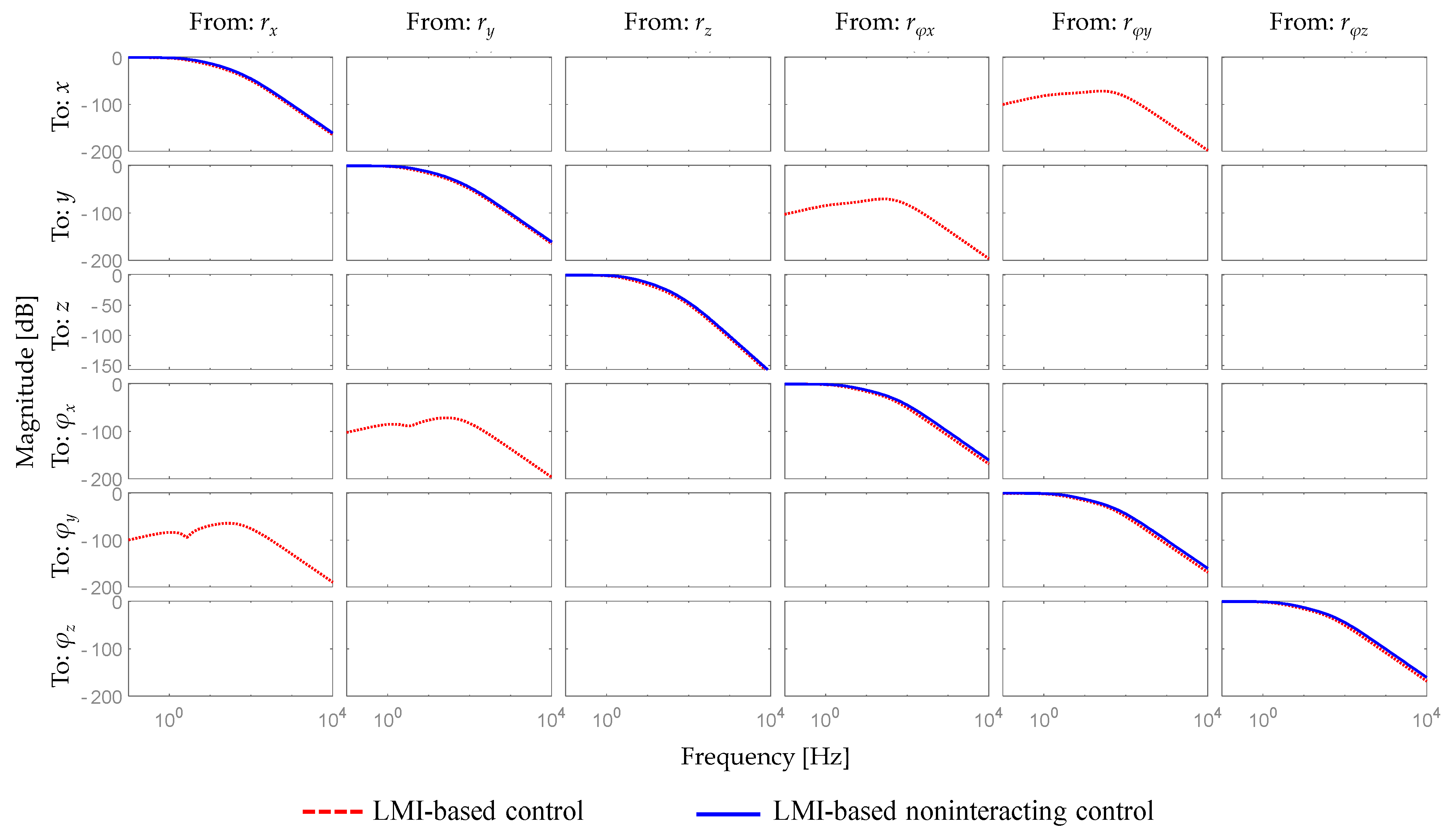
4. Simulation Studies
4.1. Implementation
4.2. Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Tuo, J.; Deng, Z.; Huang, W.; Zhang, H. A six degree of freedom passive vibration isolator with quasi-zero-stiffness-based supporting. J. Low Freq. Noise Vib. Act. Control 2018, 37, 279–294. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.O.; Kim, K.J. Six-degree of freedom active pneumatic table based on time delay control technique. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2012, 226, 622–637. [Google Scholar] [CrossRef]
- Nakamura, Y.; Nakayama, M.; Yasuda, M.; Fujita, T. Development of active six-degrees-of-freedom micro-vibration control system using hybrid actuators comprising air actuators and giant magnetostrictive actuators. Smart Mater. Struct. 2006, 15, 1133–1142. [Google Scholar] [CrossRef]
- Kang, S.; Wu, H.; Yang, X.; Li, Y.; Wang, Y. Fractional-order robust model reference adaptive control of piezo-actuated active vibration isolation systems using output feedback and multi-objective optimization algorithm. J. Vib. Control 2020, 26, 19–35. [Google Scholar] [CrossRef]
- Jiang, D.; Li, J.; Li, X.; Deng, C.; Liu, P. Modeling identification and control of a 6-DOF active vibration isolation system driving by voice coil motors with a Halbach array magnet. J. Mech. Sci. Technol. 2020, 34, 617–630. [Google Scholar] [CrossRef]
- Chen, Y.-D.; Fuh, C.C.; Tung, P.C. Application of voice coil motors in active dynamic vibration absorbers. IEEE Trans. Magn. 2005, 41, 1149–1154. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, D.H.; Park, H.C.; Kim, Y.B. Direct Disturbance Suppression System Design for High Precision Fabrication Tables. Trans. Korean Soc. Mech. Eng. A 2020, 44, 843–853. [Google Scholar] [CrossRef]
- Kim, M.H.; Kim, H.Y.; Kim, H.C.; Ahn, D.; Gweon, D.G. Design and Control of a 6-DOF active vibration isolation system using a halbach magnet array. IEEE/ASME Trans. Mechatron. 2016, 21, 2185–2196. [Google Scholar] [CrossRef]
- Kucera, V. Diagonal Decoupling of Linear Systems by Static-State Feedback. IEEE Trans. Autom. Control 2017, 62, 6250–6265. [Google Scholar] [CrossRef]
- Morse, A.; Wonham, W. Status of noninteracting control. IEEE Trans. Autom. Control 1971, 16, 568–581. [Google Scholar] [CrossRef]
- Bonilla, M.; Pallottino, L.; Bicchi, A. Noninteracting constrained motion planning and control for robot manipulators. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 4038–4043. [Google Scholar]
- Kim, Y.-B. An algorithm for robust noninteracting control of ship propulsion system. KSME Int. J. 2000, 14, 393–400. [Google Scholar] [CrossRef]
- Liu, H.; Duan, G. Input-output Energy Decoupling Control for Linear Neutral Time-delay Systems. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; Volume 1, pp. 2353–2357. [Google Scholar]
- Chu, D.; Tan, R.C.E. Numerically Reliable Computing for the Row by Row Decoupling Problem with Stability. SIAM J. Matrix Anal. Appl. 2002, 23, 1143–1170. [Google Scholar] [CrossRef]
- Jayawardhana, B. Noninteracting control of nonlinear systems based on relaxed control. In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 7087–7091. [Google Scholar]
- Freund, E. Design of time-variable multivariable systems by decoupling and by the inverse. IEEE Trans. Autom. Control 1971, 16, 183–185. [Google Scholar] [CrossRef]
- Porter, W. Decoupling of and inverses for time-varying linear systems. IEEE Trans. Autom. Control 1969, 14, 378–380. [Google Scholar] [CrossRef]
- Falb, P.; Wolovich, W. Decoupling in the design and synthesis of multivariable control systems. IEEE Trans. Autom. Control 1967, 12, 651–659. [Google Scholar] [CrossRef] [Green Version]
- Niku, S.B. Introduction to Robotics: Analysis, Control, Applications; John Wiley & Sons: New York, NY, USA, 2020. [Google Scholar]
- FUJISAKI, Y.; IKEDA, M. Synthesis of Two-Degree-of-Freedom Optimal Servosystems. Trans. Soc. Instrum. Control Eng. 1991, 27, 907–914. [Google Scholar] [CrossRef]
- Christodoulou, M.A. Decoupling in the design and synthesis of singular systems. Automatica 1986, 22, 245–249. [Google Scholar] [CrossRef]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994; ISBN 978-0-89871-485-2. [Google Scholar]

| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| a [m] | 0.4 | m [kg] | 288 | lzy [m] | 0.53 |
| b [m] | 0.6 | Jxx [kg.m2] | 34.8 | lxz [m] | 0.015 |
| c [m] | 0.2 | Jyy [kg.m2] | 15.6 | lzx [m] | 0.37 |
| kx, ky, kz [N/m] | 14,180 | Jzz [kg.m2] | 49.92 | lxy [m] | 0.53 |
| cx, cy, cz [Ns/m] | 100 | lxx [m] | 0.29 | lyz [m] | 0.015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.-H.; Kim, Y.-B.; Chakir, S.; Huynh, T.; Park, H.-C. Noninteracting Control Design for 6-DoF Active Vibration Isolation Table with LMI Approach. Appl. Sci. 2021, 11, 7693. https://doi.org/10.3390/app11167693
Lee D-H, Kim Y-B, Chakir S, Huynh T, Park H-C. Noninteracting Control Design for 6-DoF Active Vibration Isolation Table with LMI Approach. Applied Sciences. 2021; 11(16):7693. https://doi.org/10.3390/app11167693
Chicago/Turabian StyleLee, Dong-Hun, Young-Bok Kim, Soumayya Chakir, Thinh Huynh, and Hwan-Cheol Park. 2021. "Noninteracting Control Design for 6-DoF Active Vibration Isolation Table with LMI Approach" Applied Sciences 11, no. 16: 7693. https://doi.org/10.3390/app11167693
APA StyleLee, D.-H., Kim, Y.-B., Chakir, S., Huynh, T., & Park, H.-C. (2021). Noninteracting Control Design for 6-DoF Active Vibration Isolation Table with LMI Approach. Applied Sciences, 11(16), 7693. https://doi.org/10.3390/app11167693







