A Unified Approach for the Control of Power Electronics Converters. Part II: Tracking
Abstract
:1. Introduction
2. Preliminaries
3. Problem Statement
4. Main Result
5. Tracking with Perturbations
5.1. Rejection of Non-Measurable Perturbations
- (i)
- If , the tracking error is globally asymptotically stable, i.e.,
- (ii)
- If , for all , the tracking error is bounded and the perturbation is rejected with a gain lower than , i.e., we have, for ,
- (i)
- If , since for all , and because, at the instants of jumps , we have , .
- (ii)
- If , we have . Integrating between and , we deduce thatimplying that the error ) is bounded because . In addition, when , we have and if , then , concluding the proof.
5.2. Rejection of Measurable Perturbations
6. Numerical Examples
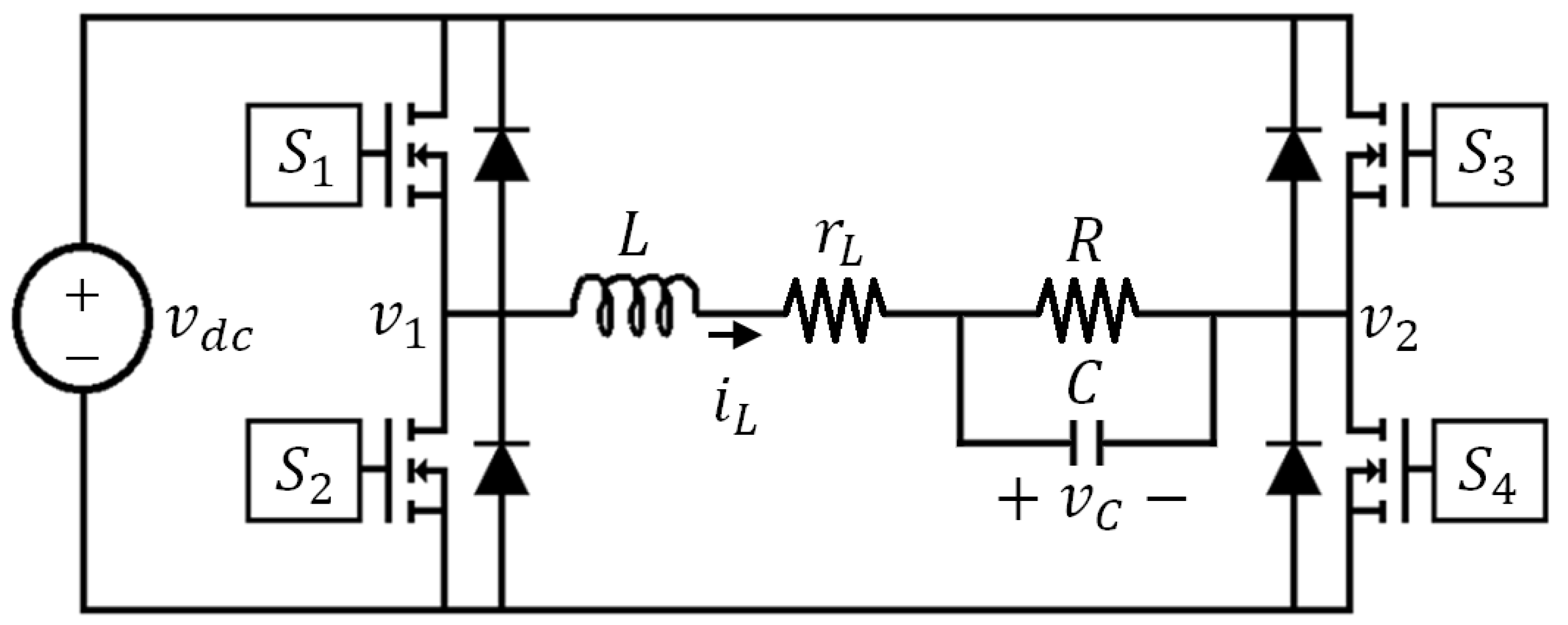
6.1. Full-Bridge Inverter for Stand-Alone Applications
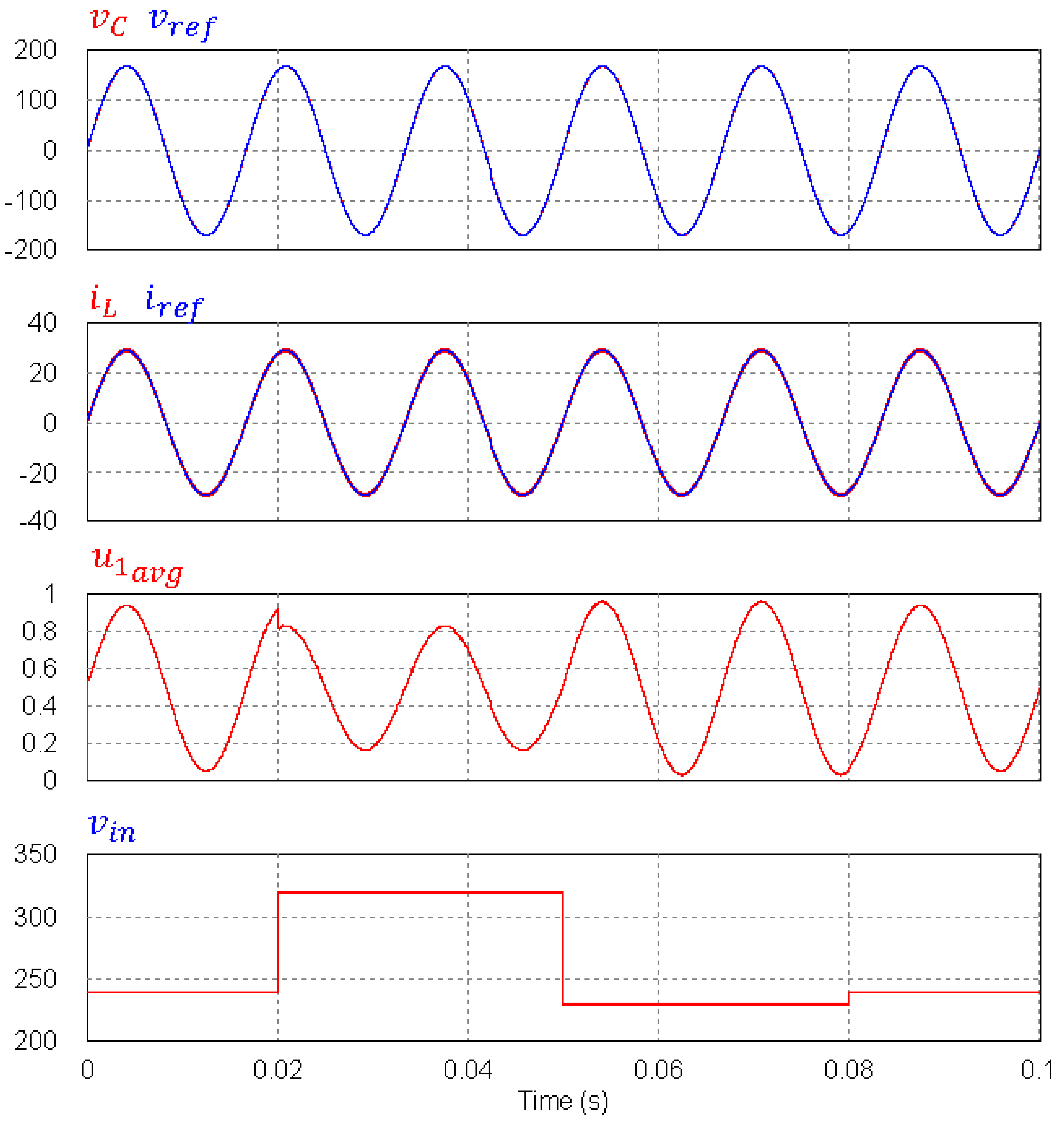
6.1.1. Sinusoidal Reference Tracking for a Resistive Load
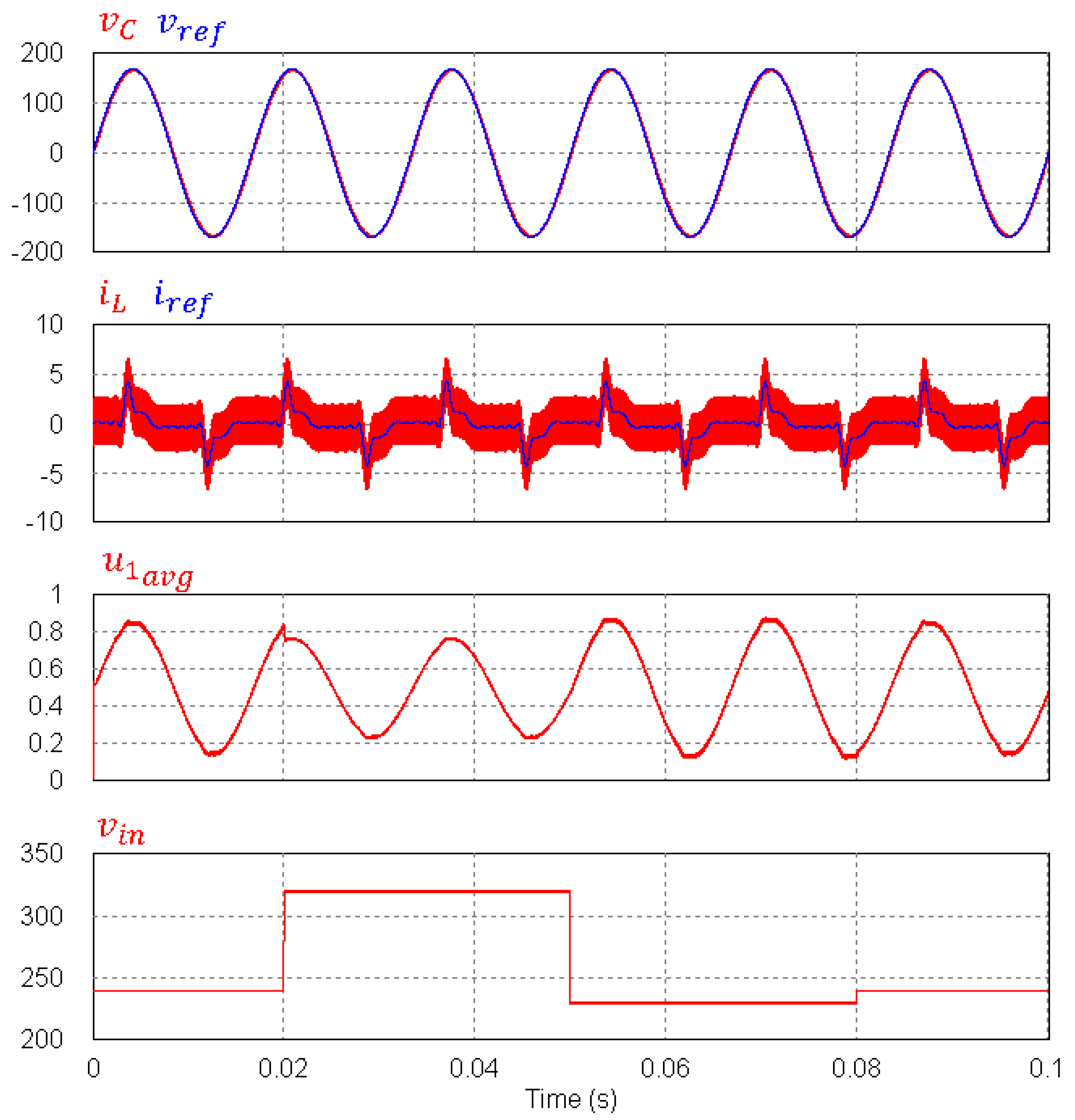
6.1.2. Sinusoidal Reference Tracking for Nonlinear Loads
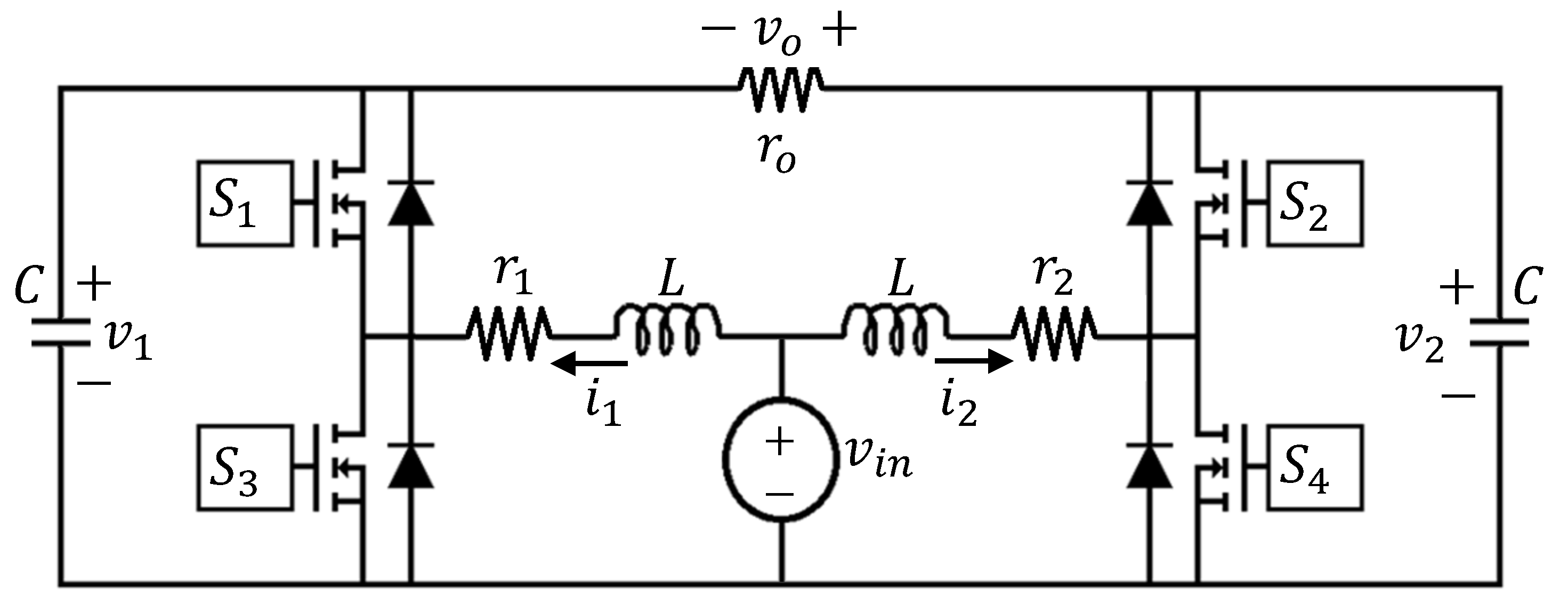
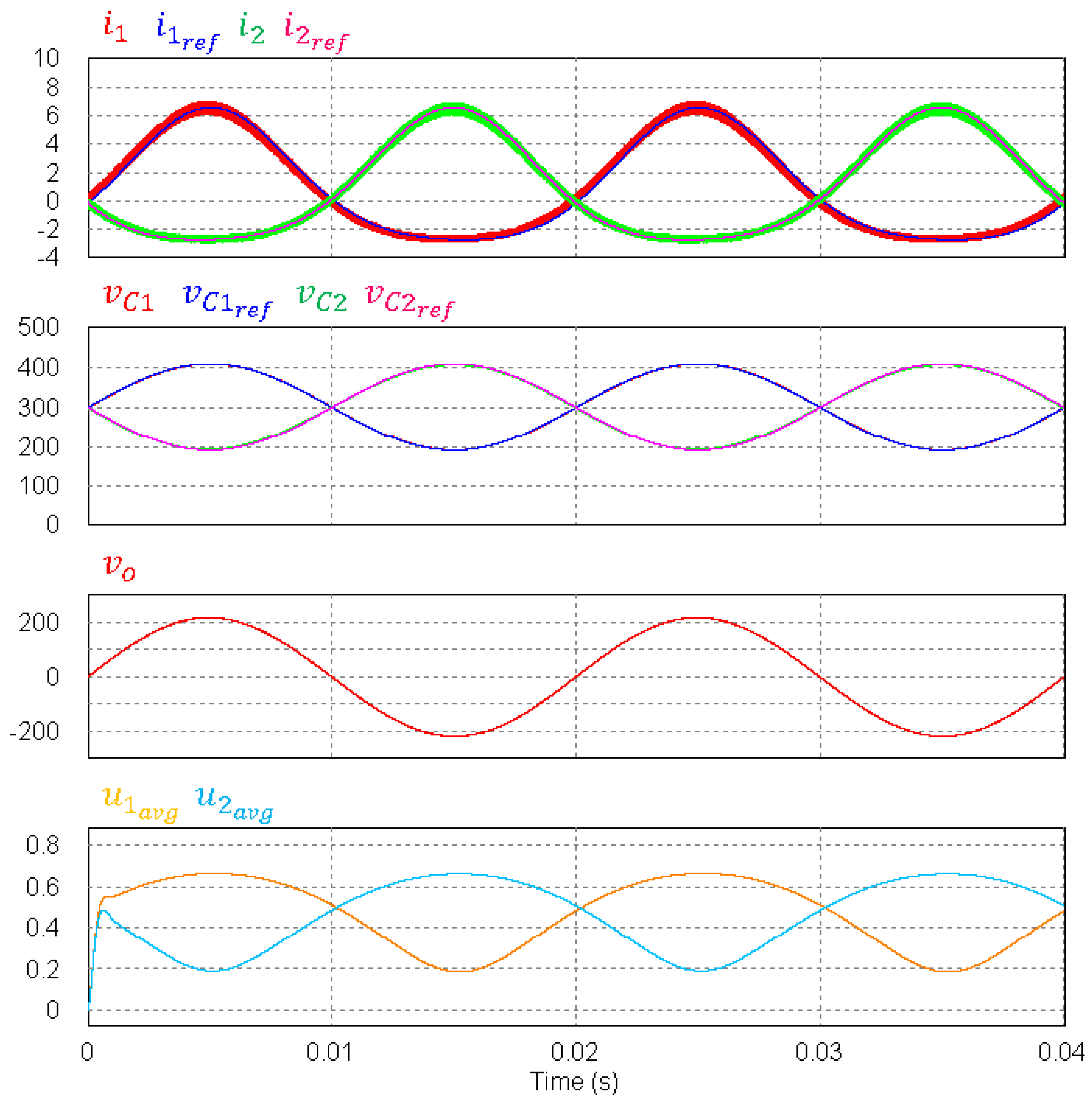
6.2. Boost Inverter for Stand-Alone Applications
7. Approximated State Reference Signal from a Periodic Output Reference Signal
7.1. Approximated State Reference Signal
- (i)
- From the given periodic output reference , and , we can compute ;
- (ii)
- From obtained in step i), we can compute , integrating the differential system (28), because , is an admissible reference.
7.2. Numerical Example
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Brockett, R.W.; Wood, J.R. Application of System Theory to Power Processing Problems; Contract NGR 22-007-172; National Aeronautics and Space Administration, NASA Lewis Research Center: Cleveland, OH, USA, 1974. [Google Scholar]
- Sanders, S.R. Nonlinear Control of Switching Power Converters. Ph.D. Thesis, MIT Department EECS, Cambridge, MA, USA, 1989. [Google Scholar]
- Sanders, S.R.; Verghese, G.C. Lyapunov-based control for switched power converters. IEEE Trans. Power Electron. 1992, 7, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Da Silva, W.D. Rethinking the World’s Energy. Cosmos Magazine, 1 April 2012. [Google Scholar]
- Smil, V. A skeptic Looks at alternative energy. IEEE Spectrum 2012, 49, 46–52. [Google Scholar] [CrossRef]
- Armstrong, R.C.; Wolfram, C.; Gross, R.; Lewis, N.S.; Boardman, B.; Ragauskas, A.J.; Ehrhardt-Martinez, K.; Crabtree, G.; Ramana, M.V. The frontiers of energy. Nat. Energy 2016, 1, 15020. [Google Scholar] [CrossRef] [Green Version]
- Kizilyalli, I.C.; Xu, Y.; Carlson, E.; Manser, J.; Cunningham, D.W. Current and Future Directions in Power Electronic Devices and Circuits based on Wide Band-Gap Semiconductors. In Proceedings of the IEEE 5th Workshop on Wide Bandgap Power Devices and Applications (WiPDA), Albuquerque, NM, USA, 30 October–1 November 2017; pp. 417–425. [Google Scholar]
- Cheng, X. Overview of Recent Progress of Semiconductor Power Devices Based on Wide Band Gap Materials. IOP Conf. Ser. Mater. Eng. 2018, 439, 022033. [Google Scholar] [CrossRef]
- Liberzon, D. Switching in Systems and Control; Volume in Series Systems and Control: Foundations and Applications; Birkhauser: Boston, MA, USA, 2003; ISBN 978-0-8176-4297-6. [Google Scholar]
- Goebel, R.; Sanfelice, R.G.; Teel, A.R. Hybrid Dynamical Systems: Modeling, Stability and Robustness; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Sira-Ramirez, H.J.; Silva-Ortigoza, R. Control Design Techniques in Power Electronic Devices; Springer: London, UK, 2006. [Google Scholar]
- Buso, S. Design of a robust voltage controller for a buck-boost converter using μ-synthesis. IEEE Trans. Control Technol 1999, 7, 222–229. [Google Scholar] [CrossRef] [Green Version]
- Olalla, C.; Leyva, R.; Aroudi, A.E.; Queinnec, I. Robust LQR control for PWM converters: An LMI Approach. IEEE Trans. Ind. Electron. 2009, 56, 2548–2558. [Google Scholar] [CrossRef]
- Santos, O.L.; Martinez-Salamero, L.; Garcia, G.; Valderrama-Blavi, H.; Polanco, T.S. Robust Sliding- Mode Control design for a voltage regulated quadratic boost converter. IEEE Trans. Power Electron. 2015, 30, 2313–2327. [Google Scholar] [CrossRef]
- Deaecto, G.; Geromel, J.C.; Garcia, F.; Pomilio, J. Switched affine systems control design with applications to DC-DC converters. IET Control Theory Appl. 2010, 4, 1201–1210. [Google Scholar] [CrossRef]
- Albea, C.; Garcia, G.; Zaccarian, L. Hybrid dynamic modeling and control of switched affine systems: Application to DC-DC converters. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japon, 15–18 December 2015. [Google Scholar]
- Hetel, L.; Fridman, E. Robust sampled-data control of switched affine systems. IEEE Trans. Autom. Control 2013, 58, 2922–2928. [Google Scholar] [CrossRef]
- Beneux, G.; Riedinger, P.; Daafouz, J.; Grimaux, L. Adaptive stabilization of switched affine systems with unknown equilibrium points: Application to power converters. Automtatica 2019, 99, 82–91. [Google Scholar] [CrossRef]
- Garcia, G.; Lopez-Santos, O. A unified approach for the control of power electronics converters. Part I Stabilization and Regulation. Appl. Sci. 2021, 11, 631. [Google Scholar] [CrossRef]
- Isidori, A.; Byrnes, C.I. Output regulation of nonlinear systems. IEEE Trans. Autom. Control 1990, 35, 131–140. [Google Scholar] [CrossRef]
- Francis, B.A. The Linear Multivariable Regulator Problem. SIAM J. Control Optim. 1977, 15, 873–878. [Google Scholar] [CrossRef]
- Biemond, J.J.B.; de Wouv, N.V.; Heemeels, W.P.M.H.; Nijmeyer, H. Tracking control for hybrid systems with state-triggered jumps. IEEE Trans. Autom. Control 2013, 58, 876–890. [Google Scholar] [CrossRef] [Green Version]
- Cox, N. Output Regulation for Linear Hybrid Systems with Periodic Jumps. Ph.D. Thesis, University of California, Santa Barbara, CA, USA, 2014. [Google Scholar]
- Carnevale, D.; Galeani, S.; Menini, L.; Sassane, M. Output regulation of linear hybrid systems with unpredictable jumps. In Proceedings of the 19th IFAC World Congress, Cape Town, South Africa, 24–29 August 2014; pp. 1531–1536. [Google Scholar]
- Loukianov, A.G.; Domínguez, J.R.; Castillo-Toledo, B. Robust sliding mode regulation of nonlinear systems. Automatica 2018, 89, 241–246. [Google Scholar] [CrossRef]
- Elmali, H.; Olgac, N. Robust output tracking control of nonlinar MIMO systems via sliding mode technique. Automatica 1992, 28, 145–151. [Google Scholar] [CrossRef]
- Lai, N.O.; Edwards, C.; Spurgeon, S.K. On output tracking using output feedback discrete-time sliding mode controllers. IEEE Trans. Autom. Control 2007, 52, 1975–1981. [Google Scholar] [CrossRef] [Green Version]
- Zheng, B.; Zhong, Y. Robust output regulation for a class of MIMO nonlinear systems with uncertain exo-systems. J. Frankl. Inst. 2013, 350, 1462–1475. [Google Scholar] [CrossRef]
- Govindaswamy, S.; Floquet, T.; Spurgeon, S.K. Discrete-time output feedback sliding mode tracking control for systems with uncertainties. Int. J. Robust Nonlinear Control 2014, 24, 2098–2118. [Google Scholar] [CrossRef]
- Jeong, H.S.; Utkin, V.I. Sliding mode tracking control of systems with unstable zero dynamics. In Variable Structure Systems, Sliding Mode and Nonlinear Control; Young, K.D., Azguner, U., Eds.; Springer: London, UK, 2014; pp. 303–327. [Google Scholar]
- Utkin, V.A.; Utkin, A.V. Problem of tracking in linear systems with parametric uncertainties under unstable zeros. Autom. Remote Control 2014, 75, 1577–1592. [Google Scholar] [CrossRef]
- Bonivento, C.; Marconi, L.; Zanasi, R. Output regulation of nonlinear systems by sliding mode. Automatica 2001, 37, 535–542. [Google Scholar] [CrossRef]
- Cáceres, R.O.; Barbi, I. Boost DC-AC Converter: Analysis, Design, and Experimentation. IEEE Trans. Power Electron. 1999, 14, 134–141. [Google Scholar] [CrossRef]
- Flores-Bahamonde, F.; Valderrama-Blavi, H.; Bosque-Moncusi, J.M.; Garcia, G.; Martinez-Salamero, L. Using the sliding mode approach for analysis and design of the boost inverter. IET Power Electron. 2016, 9, 1625–1634. [Google Scholar] [CrossRef]
- Shtessel, Y.B.; Zinober, A.S.; Shkolnikov, I.A. Sliding mode control, of boost and buck-boost power converters using the dynamic sliding manifold. Int. J. Robust Nonlinear Control 2003, 13, 1285–1298. [Google Scholar] [CrossRef]
- Fossas, E.; Olm, J.M. Galerkin method and approximate tracking in a non minimum phase bilinear system. Discret. Contin. Dyn. Syst. Ser. 2007, 7, 53–76. [Google Scholar] [CrossRef]
- Olm, J.M.; Ros, X. Approximate tracking of periodic references in a class of bilinear systems via stable inversion. Discret. Contin. Dyn. Syst. Ser. 2011, 15, 197–215. [Google Scholar]
- Almawlawe, M.; Mitìc, D.; Antìc, D.; Icìc, Z. An approach to microcontroller-based realization of boost converter with quasi-sliding mode control. J. Circ. Syst. Comp. 2017, 26, 1750106. [Google Scholar] [CrossRef]
- Repecho, V.; Biel, D.; Olm, J.M.; Fossas, E. Robust sliding mode control of a DC/DC boost converter with switching frequency regulation. J. Frank. Inst. 2018, 355, 5367–5383. [Google Scholar] [CrossRef]
- Pandey, S.K.; Patil, S.L.; Phadke, S.B. Regulation of non minimum phase DC-DC converters using integral sliding mode control combined with a disturbance observer. IEEE Trans. Circ. Syst. II Express Briefs 2018, 65, 1649–1653. [Google Scholar]
- Rivera, J.; Ortega-Cisneros, S.; Chavira, F. Sliding mode control output regulation for a boost power converter. Energies 2019, 12, 879. [Google Scholar] [CrossRef] [Green Version]
- Sanchez, C.A.; Lopez-Santos, O.; Zambrano-Prada, D.A.; Gordillo, F.; Garcia, G. Hybrid control scheme for a half- bridge inverter World IFAC Congress. IFAC-PapersOnLine 2017, 50, 9336–9341. [Google Scholar]
- Garcia, G.; Lopez-Santos, O. Unified modeling and control of the full-bridge inverter for stand alone applications. In Proceedings of the Seminario Anual de Automótica, Electrónica Industrial e Instrumentación (SAAEI’19), Córdoba, Spain, 3–5 July 2019. [Google Scholar]
- Albea-Sanchez, C.; Garcia, G.; Hadjeras, S.; Heemels, W.P.M.H.; Zaccarian, L. Practical stabilization of switched affine systems with dwell-time guarantees. IEEE Trans. Autom. Control 2019, 64, 4811–4817. [Google Scholar] [CrossRef] [Green Version]
- Gilmore, R.J.; Steer, M.B. Nonlinear circuit analysis using the method of harmonic balance: A review of the art. Part I. Introductory concepts. Int. J. Microw. Comput.-Aided Eng. 1991, 1, 22–37. [Google Scholar] [CrossRef]
- Ingalls, B.; Sontag, E. An infinite-time relaxation theorem for differential inclusions. Proc. Am. Math. (AMS) 2003, 131, 487–499. [Google Scholar] [CrossRef]
- Whitney, H. Differentiable Manifolds. Ann. Math. Second Ser. 1936, 37, 645–680. [Google Scholar] [CrossRef]
- CortÚs, J. Discontinuous Dynamical Systems. IEEE Control Syst. Mag. 2008, 28, 36–73. [Google Scholar]
- Boyd, S.; Ghaoui, L.E.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in Systems and Control; SIAM Studies in Applied Mathematics; SIMA: Philadelphia, PA, USA, 1994; Volume 15. [Google Scholar]
- Hasler, M.; Neirynck, J. Nonlinear Oscillations in Mechanical Engineering; Artech House: Boston, MA, USA, 2005; Volume 454, p. 1986. ISBN 9780890062081. [Google Scholar]
- Fidlin, A. Nonlinear Circuits; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; 358p, ISBN 9783540281160. [Google Scholar]
- Coddington, E.A.; Carlson, R. Linear Ordinary Differential Equations; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Jikuya, I.; Hodaka, I. Time Domain Analysis of Steady State Response in Linear Periodic Systems and Its Application to Switching Converters. IFAC Proc. Vol. 2011, 44, 1307–1312. [Google Scholar] [CrossRef] [Green Version]


| Parameter | Value | Unit |
|---|---|---|
| 240 | V | |
| V | ||
| L | 390 | H |
| C | F | |
| R | ||
| Rad/s |
| Frequency (Hz) | Amplitude (A) | Phase (Degrees) |
|---|---|---|
| 60 | 1.2864 | 0 |
| 180 | 0.8911 | 180 |
| 300 | 0.4690 | 26 |
| 420 | 0.4623 | −105 |
| 540 | 0.4623 | 90 |
| 660 | 0.3484 | −69 |
| 780 | 0.2613 | 143 |
| 900 | 0.2010 | −8 |
| 1020 | 0.1273 | −147 |
| Frequency (Hz) | Amplitude (A) | Phase (Degrees) |
|---|---|---|
| 60 | 1.524 | −30 |
| 180 | 0.8185 | 90 |
| 300 | 0.2878 | −90 |
| 420 | 0.2728 | 90 |
| 540 | 0.1636 | −90 |
| 660 | 0.1636 | 90 |
| 780 | 0.1168 | −90 |
| 900 | 0.1168 | 90 |
| Parameter | Value | Unit |
|---|---|---|
| 150 | V | |
| 220 | V | |
| 300 | V | |
| 100 | H | |
| 2 | F | |
| R | 100 | |
| 2 | ||
| rad/s |
| 4.5779 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia, G.; Lopez-Santos, O.; Martinez-Salamero, L. A Unified Approach for the Control of Power Electronics Converters. Part II: Tracking. Appl. Sci. 2021, 11, 7618. https://doi.org/10.3390/app11167618
Garcia G, Lopez-Santos O, Martinez-Salamero L. A Unified Approach for the Control of Power Electronics Converters. Part II: Tracking. Applied Sciences. 2021; 11(16):7618. https://doi.org/10.3390/app11167618
Chicago/Turabian StyleGarcia, Germain, Oswaldo Lopez-Santos, and Luis Martinez-Salamero. 2021. "A Unified Approach for the Control of Power Electronics Converters. Part II: Tracking" Applied Sciences 11, no. 16: 7618. https://doi.org/10.3390/app11167618
APA StyleGarcia, G., Lopez-Santos, O., & Martinez-Salamero, L. (2021). A Unified Approach for the Control of Power Electronics Converters. Part II: Tracking. Applied Sciences, 11(16), 7618. https://doi.org/10.3390/app11167618







