Multivariate Analysis Applied to Aquifer Hydrogeochemical Evaluation: A Case Study in the Coastal Significant Subterranean Water Body between “Cecina River and San Vincenzo”, Tuscany (Italy)
Abstract
:1. Introduction
2. Materials and Methods
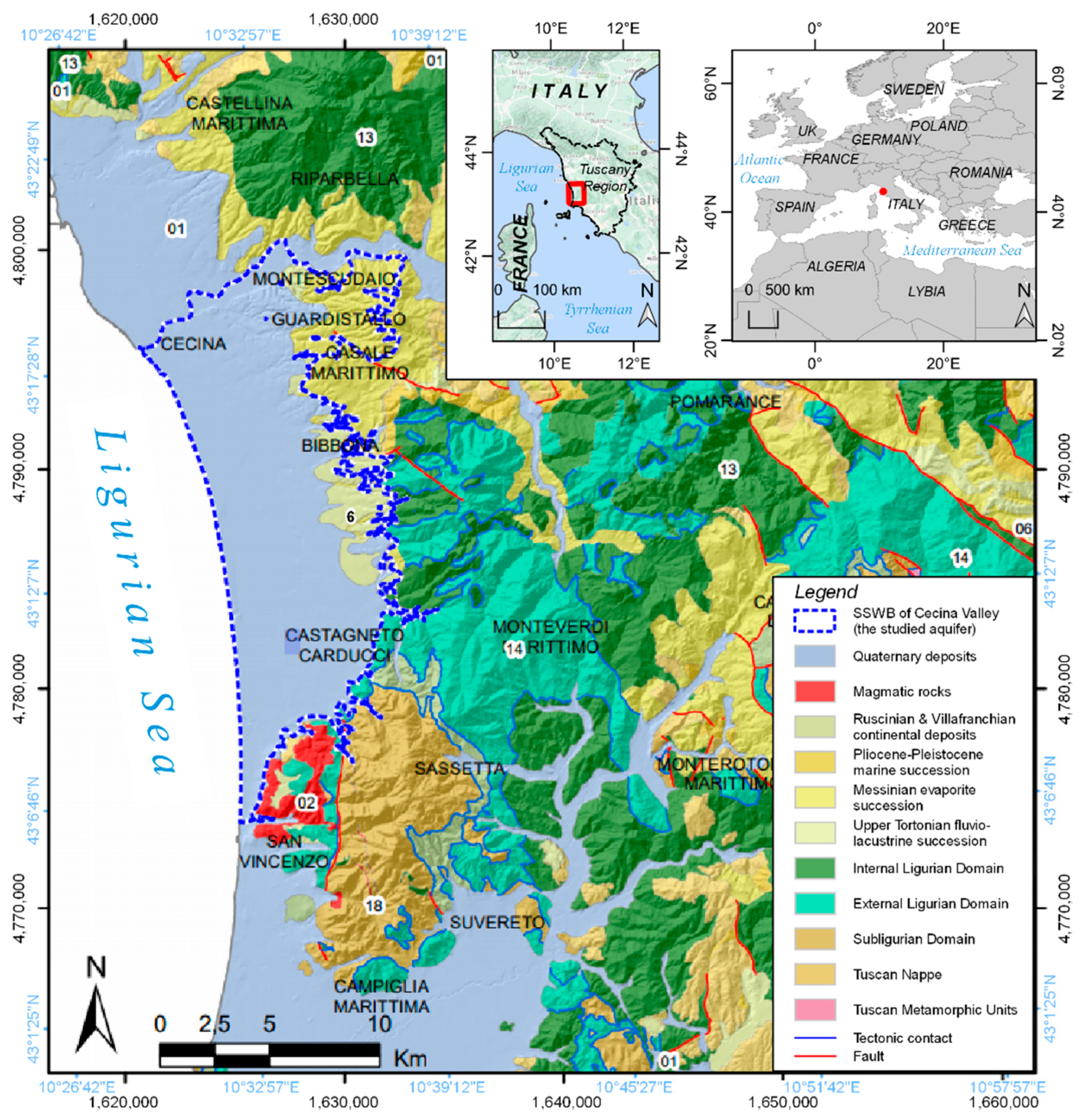
2.1. Geological and Hydrogeological Setting
2.2. Methodology
2.2.1. Selection of the Hydrogeochemical Data
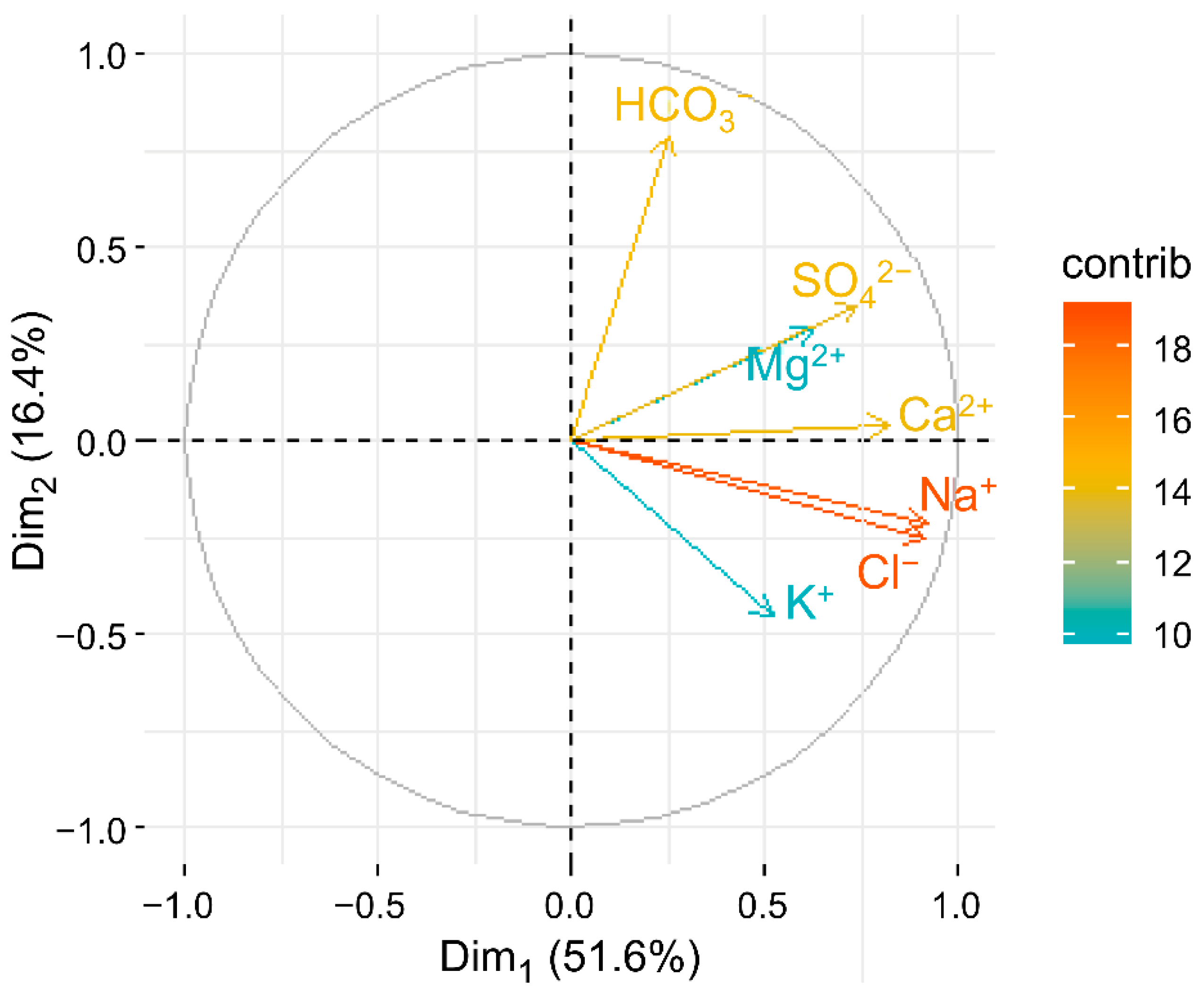
2.2.2. Principal Component Analysis
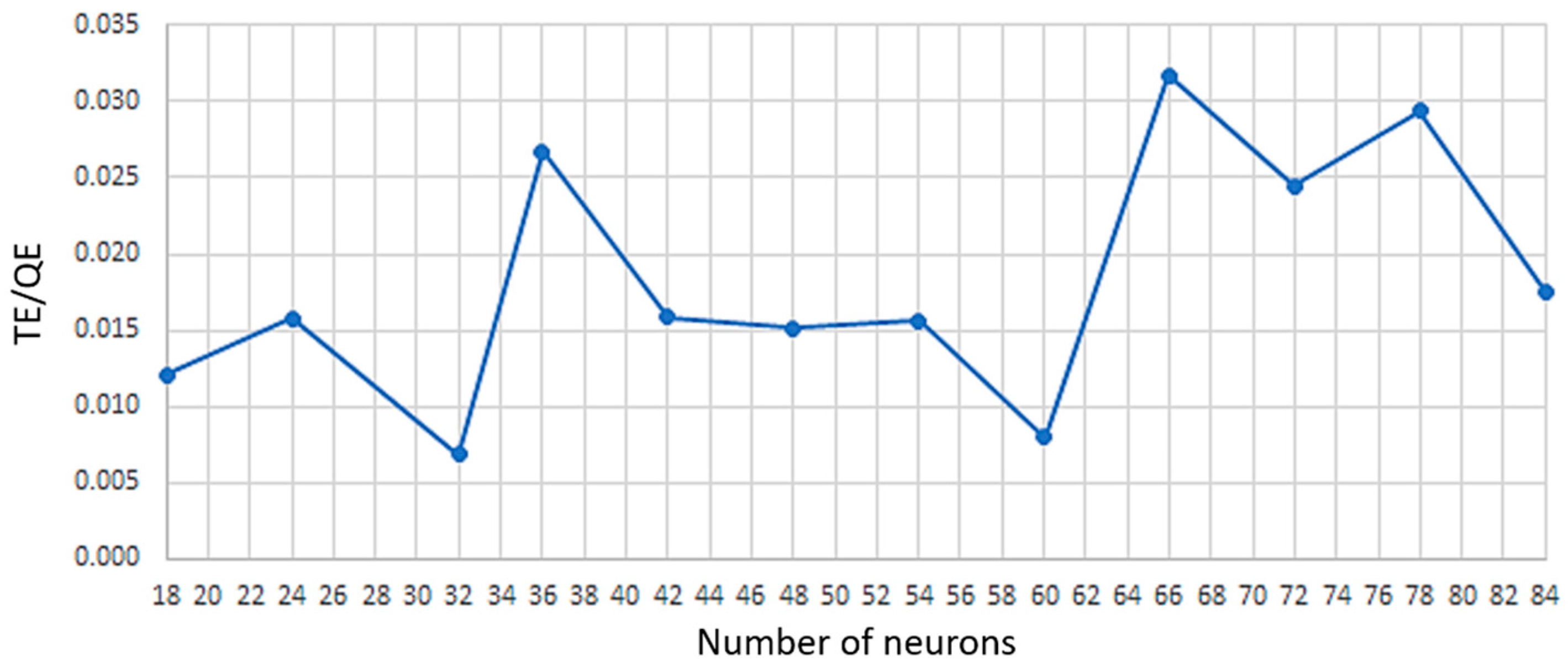
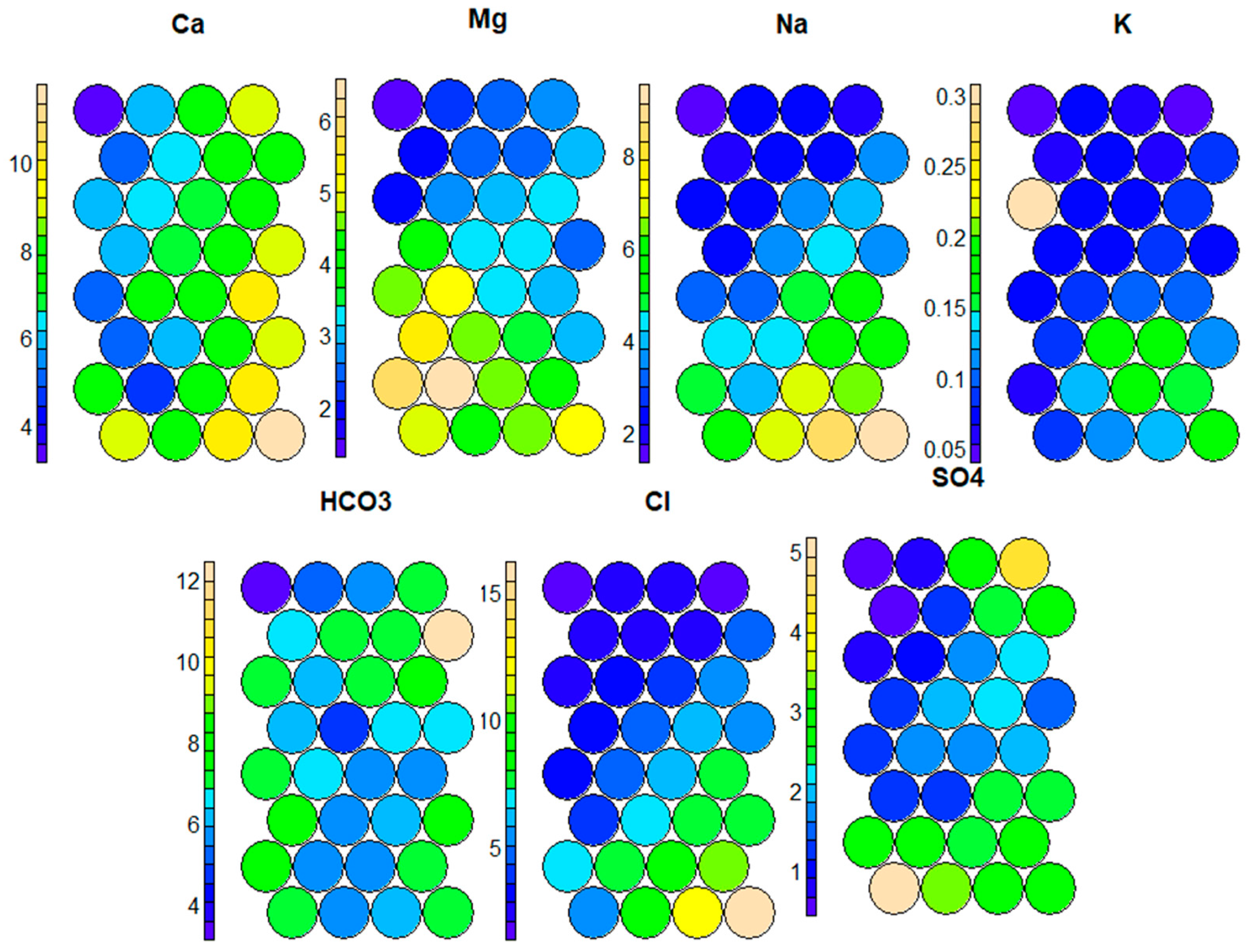
2.2.3. Self-Organizing Maps (SOMs)
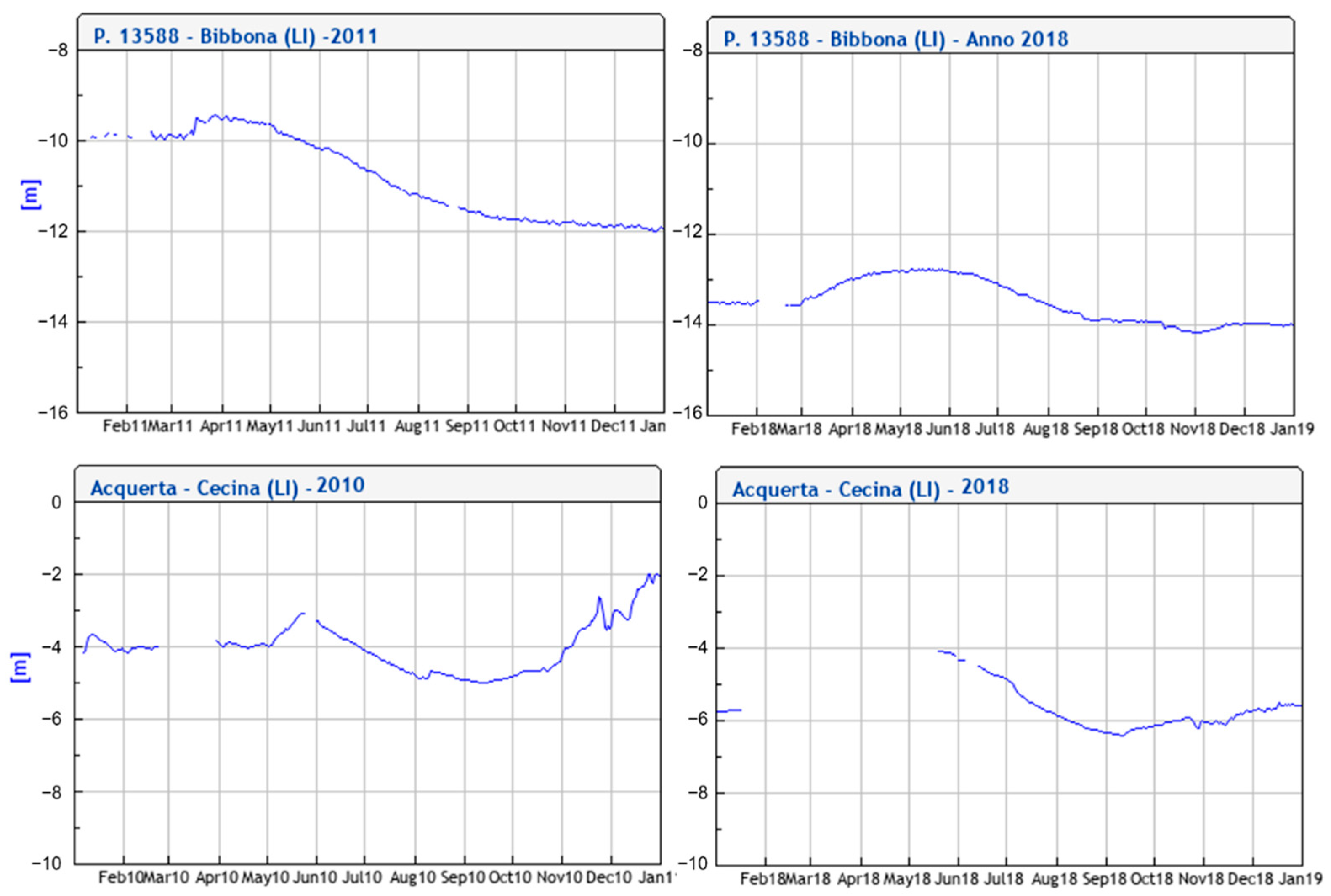
3. Results and Discussion
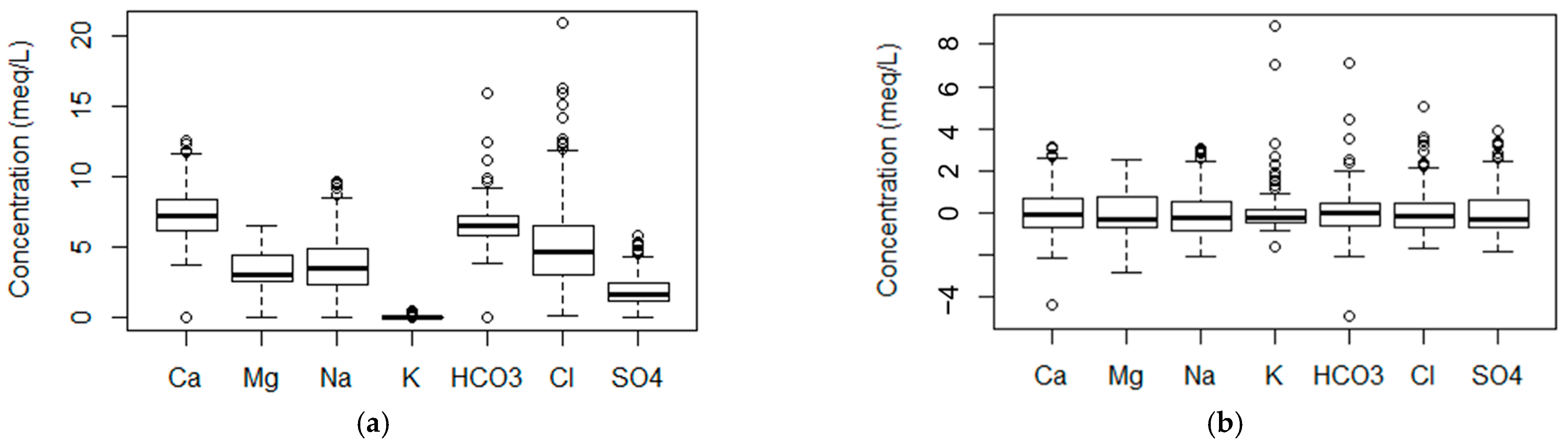
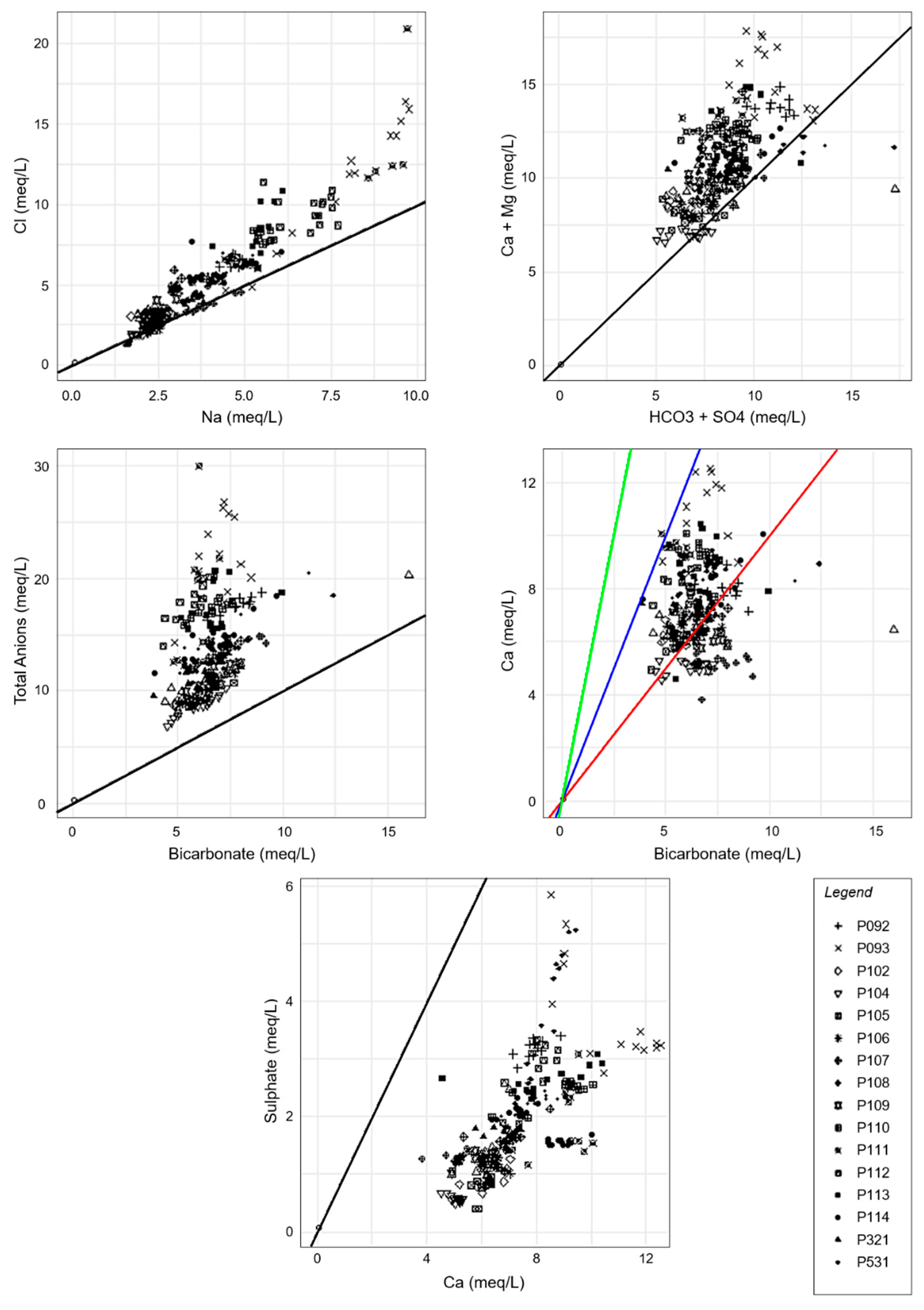
3.1. Hydrogeochemical Characteristics
3.2. Principal Component Analysis Applied to Identify the Main Sources of Variability in the Dataset
3.3. SOM and Hierarchical Clustering as a Tool for Identification of Groundwater Sources
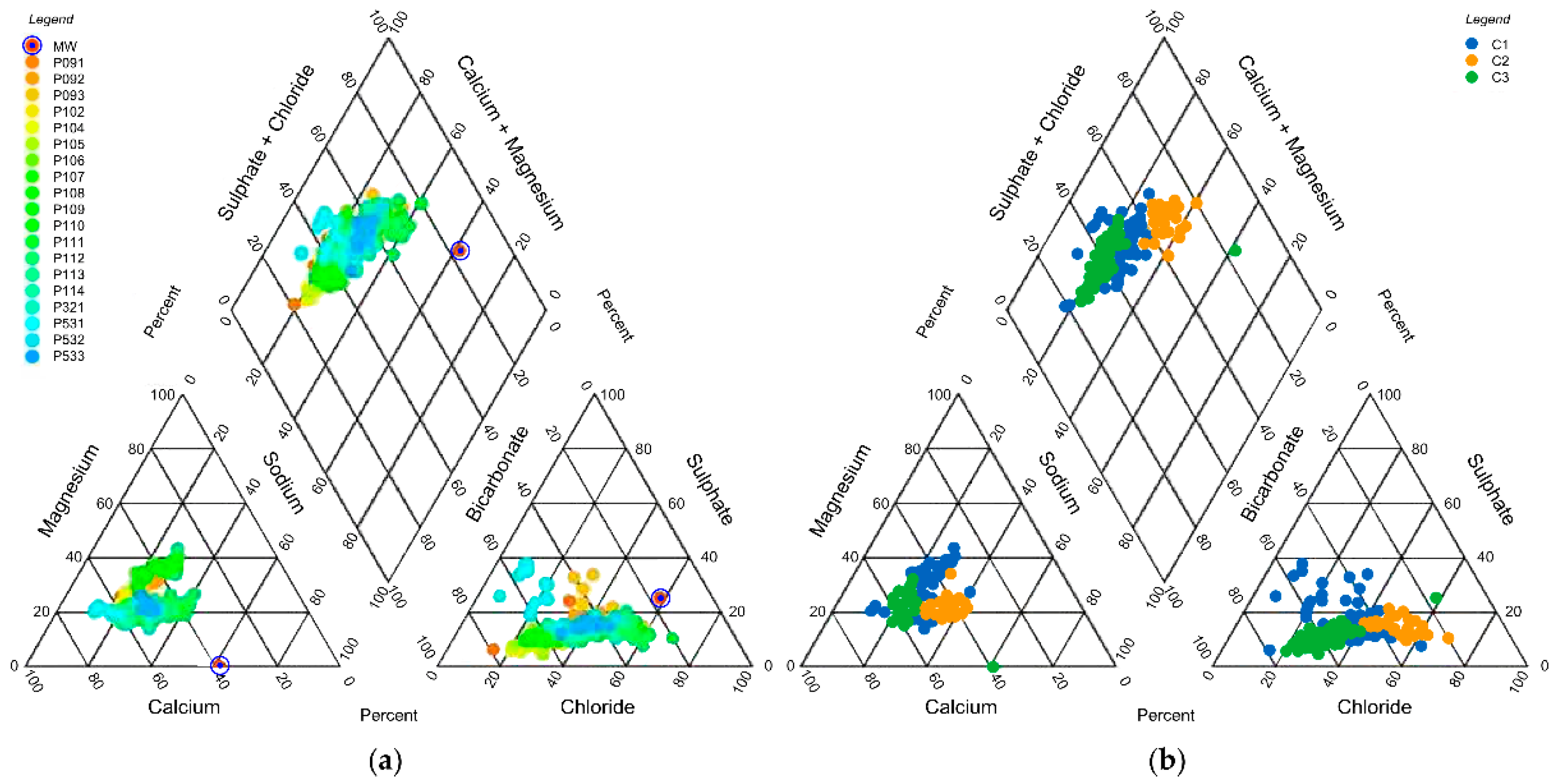
3.4. Insights from Piper Diagram and SOM Clustering Comparison
3.5. Seasonal Changes in the Distribution of the SOM Clusters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Well | Year | 2010 | 2010 | 2011 | 2011 | 2012 | 2012 | 2013 | 2013 | 2016 | 2016 | 2017 | 2017 | 2018 | 2018 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Season | Dry | Wet | Dry | Wet | Dry | Wet | Dry | Wet | Dry | Wet | Dry | Wet | Dry | Wet | |
| P091 | Neuron | 26 | 26 | 30 | 22 | 30 | 30 | 26 | 18 | 28 | 30 | 26 | 22 | 26 | 26 |
| Cluster | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C1 | C1 | C3 | C3 | C3 | C3 | C3 | |
| P092 | Neuron | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 | |
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | ||
| P093 | Neuron | 1 | 1 | 2 | 1 | 3 | 3 | 8 | 1 | 4 | 3 | 4 | 4 | 4 | 4 |
| Cluster | C1 | C1 | C2 | C1 | C2 | C2 | C2 | C1 | C2 | C2 | C2 | C2 | C2 | C2 | |
| P102 | Neuron | 22 | 22 | 22 | 30 | 30 | 30 | 30 | 25 | 22 | 26 | 22 | 22 | 26 | 22 |
| Cluster | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | |
| P104 | Neuron | 25 | 25 | 25 | 29 | 30 | 29 | 30 | 25 | 25 | 25 | 25 | 25 | 21 | 25 |
| Cluster | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | |
| P105 | Neuron | 30 | 21 | 25 | 30 | 30 | 30 | 30 | 26 | 26 | 30 | 30 | 30 | 30 | |
| Cluster | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | ||
| P106 | Neuron | 26 | 26 | 26 | 30 | 30 | 30 | 30 | 26 | 22 | 30 | 30 | 21 | 26 | |
| Cluster | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | C3 | ||
| P107 | Neuron | 14 | 10 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 13 | 14 | 14 | 14 | 14 |
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | |
| P108 | Neuron | 9 | 9 | 9 | 13 | 13 | 13 | 13 | 9 | 13 | 9 | 13 | 13 | 13 | 13 |
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | |
| P109 | Neuron | 13 | 14 | 17 | 17 | 17 | 17 | 17 | 17 | 17 | 13 | 25 | 17 | 13 | |
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C3 | C1 | C1 | ||
| P110 | Neuron | 12 | 24 | 12 | 16 | 16 | 15 | 16 | 12 | 12 | 12 | 12 | 12 | 12 | 12 |
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | |
| P111 | Neuron | 20 | 15 | 16 | 15 | 16 | 16 | 4 | 3 | 3 | 3 | 3 | |||
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C2 | C2 | C2 | C2 | C2 | ||||
| P112 | Neuron | 2 | 2 | 7 | 10 | 7 | 2 | 7 | 7 | 7 | 7 | 7 | 3 | 8 | 7 |
| Cluster | C2 | C2 | C2 | C1 | C2 | C2 | C2 | C2 | C2 | C2 | C2 | C2 | C2 | C2 | |
| P113 | Neuron | 8 | 8 | 8 | 11 | 6 | 11 | 11 | 11 | 11 | 12 | 11 | 12 | 28 | 12 |
| Cluster | C2 | C2 | C2 | C2 | C1 | C2 | C2 | C2 | C2 | C1 | C2 | C1 | C1 | C1 | |
| P114 | Neuron | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 20 | 24 | 12 | 12 |
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | |
| P321 | Neuron | 23 | 23 | 18 | 23 | 22 | 18 | 23 | 18 | 23 | 23 | 23 | 23 | 23 | 23 |
| Cluster | C1 | C1 | C1 | C1 | C3 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | |
| P531 | Neuron | 27 | 27 | 27 | 31 | 31 | 32 | 32 | 32 | 32 | 32 | 28 | 32 | 32 | |
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | ||
| P532 | Neuron | 19 | 18 | 19 | 18 | 24 | 18 | 24 | 19 | 19 | 19 | 24 | 11 | ||
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C2 | |||
| P533 | Neuron | 19 | 18 | 24 | 19 | 15 | 19 | 18 | 28 | 19 | 19 | 19 | 19 | 24 | |
| Cluster | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 | C1 |
References
- Cidu, R. Appunti al corso di Idrogeochimica. In Dipartimento di Scienze Chimiche e Geologiche; University of Cagliari: Cagliari, Italy, 2017. [Google Scholar]
- D’Angelis, R. Siccità 2016-2017: Il clima cambia e in Italia cresce il rischio idrico. Ecoscienza 2017, 4, 55–91. [Google Scholar]
- Piper, A. A graphic procedure in the geochemical interpretation of water-analyses. Trans. Am. Geophys. Union 1944, 25, 914–928. [Google Scholar] [CrossRef]
- Durov, S.A. Natural waters and graphic representation of their composition. Dokl. Akad. Nauk SSSR 1948, 59, 87–90. [Google Scholar]
- Nisi, B.; Buccianti, A.; Raco, B.; Battaglini, R. Analysis of complex regional databases and their support in the identification of background/baseline compositional facies in groundwater investigation: Developments and application examples. J. Geochem. Explor. 2015, 44, 3–17. [Google Scholar] [CrossRef]
- Haselbeck, V.; Kordilla, J.; Krause, F.; Sauter, M. Self-organizing maps for the identification of groundwater salinity sources based on hydrochemical data. J. Hydrogeol. 2019, 576, 610–619. [Google Scholar] [CrossRef]
- Astel, A.; Tsakovski, S.; Barbieri, P.; Simeonov, V. Comparison of self-organizing maps classification approach with cluster and principal components analysis for large environmental data sets. Water Res. 2007, 41, 4566–4578. [Google Scholar] [CrossRef]
- Choi, B.Y.; Yun, S.T.; Kim, K.H.; Kim, J.W.; Kim, H.M.; Koh, Y.K. Hydrogeochemical interpretation of south Korean groundwater monitoring data using self-organizing maps. J. Geochem. Explor. 2014, 137, 73–84. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Kawamura, A.; Tong, T.N.; Nakagawa, N.; Amaguchi, H.; Gilbuena, R. Clustering spatio-seasonal hydrogeochemical data using self-organizing maps for groundwater quality assessment in the red river delta, Vietnam. J. Hydrol. 2015, 522, 661–673. [Google Scholar] [CrossRef]
- Ledesma-Ruiz, R.; Pasten-Zapata, E.; Parra, R.; Harter, T.; Mahlknecht, J. Investigation of the geochemical evolution of groundwater under agricultural land: A case study in northeastern Mexico. J. Hydrogeol. 2015, 521, 410–423. [Google Scholar] [CrossRef] [Green Version]
- Jankowska, J.; Radzka, E.; Rymuza, K. Principal component analysis and cluster analysis in multivariate assessment of water quality. J. Ecol. Eng. 2017, 18, 92–96. [Google Scholar]
- Tsai, W.P.; Huang, S.T.; Cheng, S.P.; Shao, K.T.; Chang, F.J. A data-mining framework for exploring the multi-relation between fish species and water quality through self-organizing map. Sci. Total Environ. 2017, 579, 474–483. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Sun, Y.; Chupeng, G.; Liang, K.; Shengzhong, M.; Lei, H. Using self-organizing map for coastal water quality classification: Towards a better understanding of patterns and processes. Sci. Total Environ. 2018, 628-629, 1446–1459. [Google Scholar] [CrossRef] [PubMed]
- Cerrina Feroni, A.; Da Prato, S.; Doveri, M.; Ellero, A.; Lelli, M.; Masetti, G.; Nisi, B.; Raco, B. Caratterizzazione geologica, idrogeologica e idrogeochimica dei corpi idrici sotterranei significativi della regione toscana (CISS): 32CT010 Acquifero costiero tra Fiume Cecina e San Vincenzo, 32CT030 Acquifero costiero tra Fiume Fine e Fiume Cecina, 32CT050 Acquifero del Cecina. In Memorie Della Carta Geologica Italiana; Maretti, P., Ed.; Servizio Geologico d’Itali: Rome, Italy, 2010; pp. 5–80. [Google Scholar]
- Angeli, L.; Chiesi, M.; Ferrari, R.; Magno, R. Clima Che Cambia: Gli Impatti Sul Territorio Toscano; Consorzio LaMMA: Florence, Italy, 2012. [Google Scholar]
- Zirulia, A.; Brancale, M.; Barbagli, A.; Guastaldi, E.; Colonna, T. Hydrological changes: Are they present at local scales? Rend. Fis. Acc. Lincei 2021, 32, 295–309. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Le, S.; Josse, J.; Husson, F. Facto Mine R: An R Package for Multivariate Analysis. J. Stat. Softw. 2008, 25, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Kassambara, A.; Mundt, F. Factoextra R Package: Easy Multivariate Data Analyses and Elegant Visualization. 2017. Available online: http://www.sthda.com/english/wiki/factoextra-r-package-easy-multivariate-data-analyses-and-elegant-visualization (accessed on 17 August 2021).
- Wehrens, R.; Buydens, L.M.C. Self-and super-organizing maps in R: The Kohonen package. J. Stat. Softw. 2007, 21, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Boelaert, J.; Bendhaiba, L.; Olteanu, M.; Villa-Vialaneix, N. SOMbrero: An R package for numeric and non-numeric self-organizing maps. In Advances in Intelligent Systems and Computing; Villmann, T., Schleif, F.M., Kaden, M., Lange, M., Eds.; Springer: Berlin, Germany, 2014; Volume 295, pp. 5–80. [Google Scholar]
- Diekoff, A.L.; Lorenz, D. SMWR Graphs: An R Package for Graphing Hydrologic Data; United States Geological Survey: Reston, VA, USA, 2017.
- Wehrens, R. Chemometrics with R: Multivariate Data Analysis in the Natural Sciences and Life Sciences; Springer: Berlin, Germany, 2011. [Google Scholar]
- Kohonen, T. Essentials of the self-organizing map. Neural Netw. 2013, 37, 52–65. [Google Scholar] [CrossRef]
- Bernardinetti, S.; Bruno, P.P.G. The hydrothermal system of solfatara crater (Campi Flegrei, Italy) inferred from machine learning algorithms. Front. Earth Sci. 2019, 7, 286. [Google Scholar] [CrossRef] [Green Version]
- Vesanto, J.; Himberg, J.; Alhoniemi, E.; Parhankangas, J. Self-Organizing Map in Matlab: The SOM toolbox. J. Hydrogeol. 2015, 521, 410–423. [Google Scholar]
- Vialaneix, N.; Mariette, J.; Olteanu, M.; Rossi, F.; Bendhaiba, L.; Bolaert, J. SOMbrero: SOM Bound to Realize Euclidean and Relational Outputs. R package version 1.3-1. 2020. [Google Scholar]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. Nbclust: An R package for determining the relevant number of clusters in a data set. J. Stat. Softw. 2015, 61, 1–36. [Google Scholar] [CrossRef] [Green Version]
- Hounslow, A. Water Quality Data: Analysis and Interpretation; Research Gate: Berlin, Germany, 1995. [Google Scholar]
- Chiesa, G. Idrogeochimica; Edizioni GEO-GRAPH-Segrate: Milan, Italy, 2005. [Google Scholar]
- Appelo, C.A.J. Cation and proton exchange, pH variations, and carbonate reactions in a freshening aquifer. Water Resour. Res. 1994, 30, 2793–2805. [Google Scholar] [CrossRef]
- Ufficio Pianificazione del Territorio. Documento Programmatico Per L’avvio Del Procedimento Di Formazione Del Piano Strutturale; Comune di Castagneto Carducci (Provincia di Livorno): Castagneto Carducci, Italy, 2003. [Google Scholar]
- Krzanowski, W.J.; Lai, Y.T. A criterion for determining the number of groups in a data set using sum-of-squares clustering. Biometrics 1988, 44, 23–34. [Google Scholar] [CrossRef]
- Hartigan, J.A. Clustering Algorithms; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1975. [Google Scholar]
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Friedman, H.P.; Rubin, J. On some invariant criteria for grouping data. J. Am. Stat. Assoc. 1967, 62, 1159–1178. [Google Scholar] [CrossRef]
- Ratkowsky, D.A.; Lance, G.N. Criterion for determining the number of groups in a classification. Aust. Comput. J. 1978, 10, 115–117. [Google Scholar]
- Ball, G.H.; David, J.H. ISODATA, a Novel Method of Data Analysis and Pattern Classification; Stanford Research Inst: Menlo Park, CA, USA, 1965. [Google Scholar]
- Brizzio, M.C.; Kotzias, D.; Marchetto, A.; Rembges, D.; Tartari, G.; Mosello, R. The chemistry of atmospheric deposition in Italy in the framework of the national programme for forest ecosystems control (CONECOFOR). J. Limnol. 2002, 61 (Suppl. 1), 77–92. [Google Scholar]


| Unit | Ca2+ | Mg2+ | Na+ | K+ | HCO3− | Cl− | SO42− | |
|---|---|---|---|---|---|---|---|---|
| Mean | meq/L | 7.33 | 3.45 | 3.92 | 0.09 | 6.58 | 5.25 | 1.93 |
| Std. Dev. | meq/L | 1.66 | 1.22 | 1.89 | 0.05 | 1.33 | 3.10 | 1.01 |
| Minimum | meq/L | 0.05 | 0.00 | 0.08 | 0.01 | 0.04 | 0.14 | 0.06 |
| Maximum | meq/L | 12.53 | 6.56 | 9.74 | 0.54 | 16.01 | 20.90 | 5.85 |
| KL | Hart | TrCovW | TraceW | Rubin | Ratk | Ball | |
|---|---|---|---|---|---|---|---|
| Number of clusters | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Index value | 2.0 | 3.4 | 104.5 | 15.1 | 0.1 | 0.4 | 34.7 |
| Number of clusters | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| Index value | 2.0 | 3.4 | 104.5 | 15.1 | 0.1 | 0.4 | 34.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bastianoni, A.; Guastaldi, E.; Barbagli, A.; Bernardinetti, S.; Zirulia, A.; Brancale, M.; Colonna, T. Multivariate Analysis Applied to Aquifer Hydrogeochemical Evaluation: A Case Study in the Coastal Significant Subterranean Water Body between “Cecina River and San Vincenzo”, Tuscany (Italy). Appl. Sci. 2021, 11, 7595. https://doi.org/10.3390/app11167595
Bastianoni A, Guastaldi E, Barbagli A, Bernardinetti S, Zirulia A, Brancale M, Colonna T. Multivariate Analysis Applied to Aquifer Hydrogeochemical Evaluation: A Case Study in the Coastal Significant Subterranean Water Body between “Cecina River and San Vincenzo”, Tuscany (Italy). Applied Sciences. 2021; 11(16):7595. https://doi.org/10.3390/app11167595
Chicago/Turabian StyleBastianoni, Alessia, Enrico Guastaldi, Alessio Barbagli, Stefano Bernardinetti, Andrea Zirulia, Mariantonietta Brancale, and Tommaso Colonna. 2021. "Multivariate Analysis Applied to Aquifer Hydrogeochemical Evaluation: A Case Study in the Coastal Significant Subterranean Water Body between “Cecina River and San Vincenzo”, Tuscany (Italy)" Applied Sciences 11, no. 16: 7595. https://doi.org/10.3390/app11167595
APA StyleBastianoni, A., Guastaldi, E., Barbagli, A., Bernardinetti, S., Zirulia, A., Brancale, M., & Colonna, T. (2021). Multivariate Analysis Applied to Aquifer Hydrogeochemical Evaluation: A Case Study in the Coastal Significant Subterranean Water Body between “Cecina River and San Vincenzo”, Tuscany (Italy). Applied Sciences, 11(16), 7595. https://doi.org/10.3390/app11167595







