A Hybrid Approach Combining Fuzzy c-Means-Based Genetic Algorithm and Machine Learning for Predicting Job Cycle Times for Semiconductor Manufacturing
Abstract
:1. Introduction
2. Methodology
2.1. Notation
| Sets | |
| Dataset of job records for clustering and training, indexed by | |
| Dataset of job records for testing, indexed by | |
| Set of job attributes, indexed by | |
| Parameters | |
| Value of attribute of job record | |
| Cycle time of job record | |
| Weighted value of attribute | |
| Number of clusters, indexed by | |
| Number of attributes. | |
| Fuzziness exponent value | |
| Decisions variables | |
| -th cluster center of attribute | |
| -th K-dimensional cluster center | |
| Membership value of job record to -th cluster | |
| Expected job cycle time of cluster | |
| Cycle time prediction of new job record | |
2.2. Fuzzy c-Means Clustering
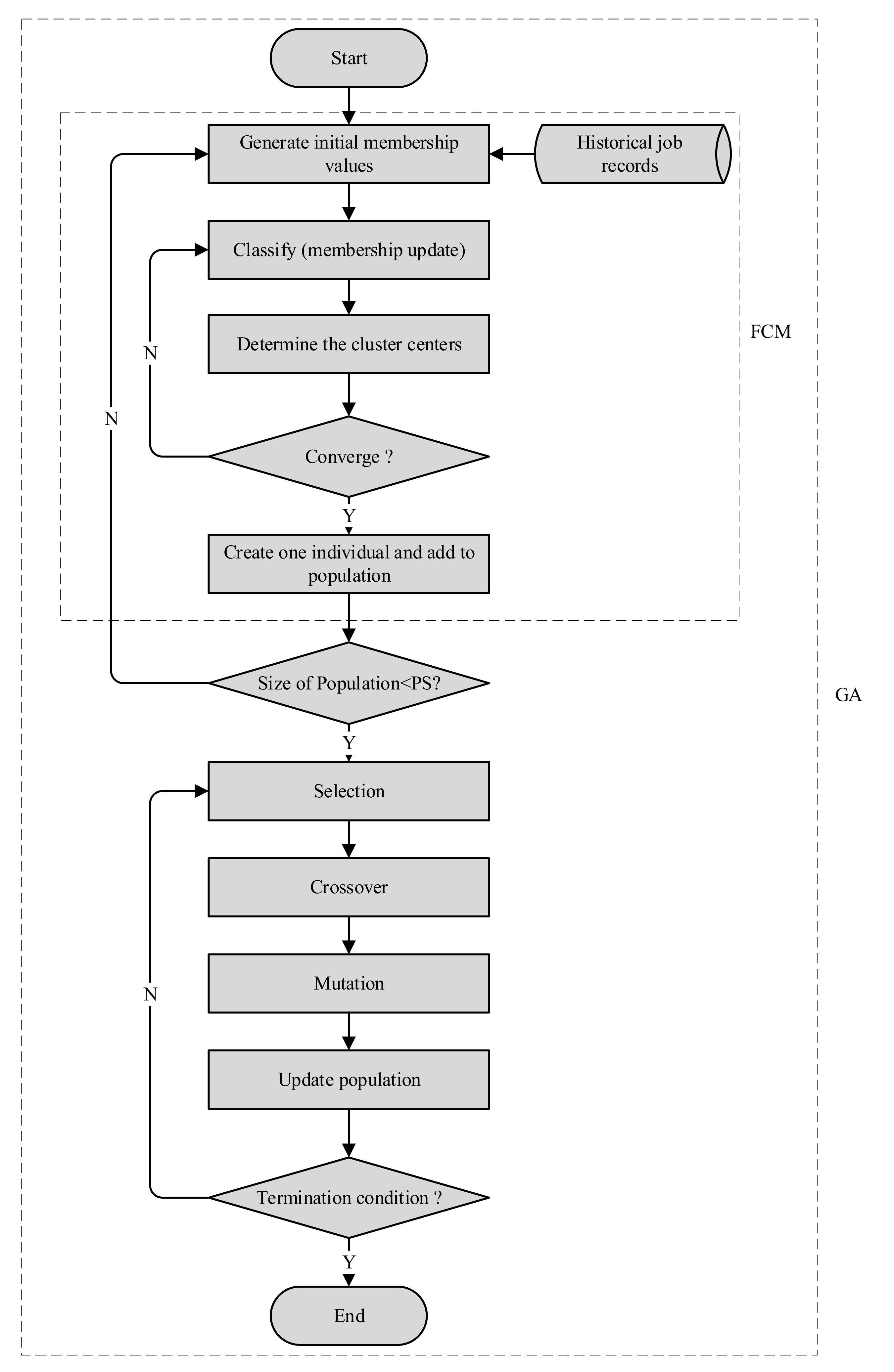
2.3. Design of FCM-Based GA
- (1)
- Chromosome structure
- (2)
- Fitness function
- (3)
- Genetic operators
- (1)
- Selection operator
- (2)
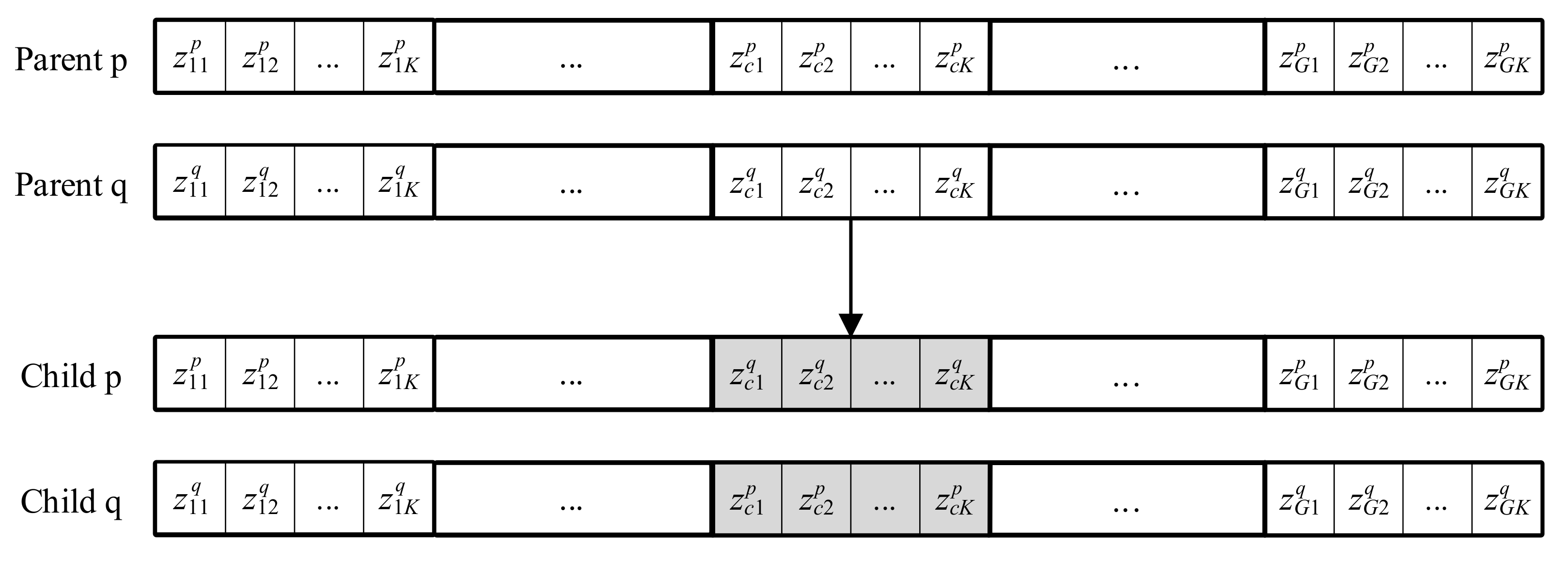
- Crossover operator
- (3)
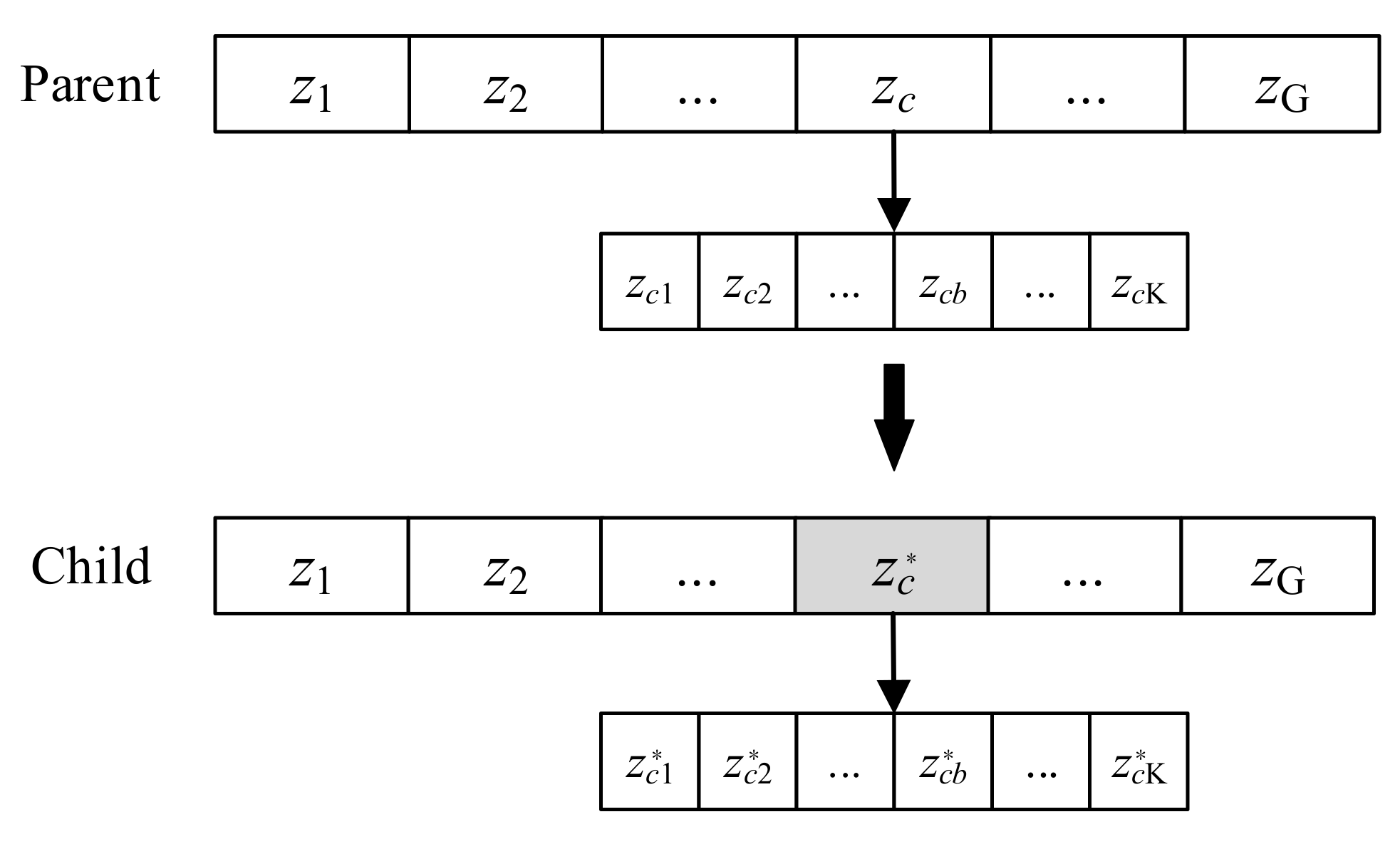
- Mutation operator
- (4)
- Steps of FCM-based GA
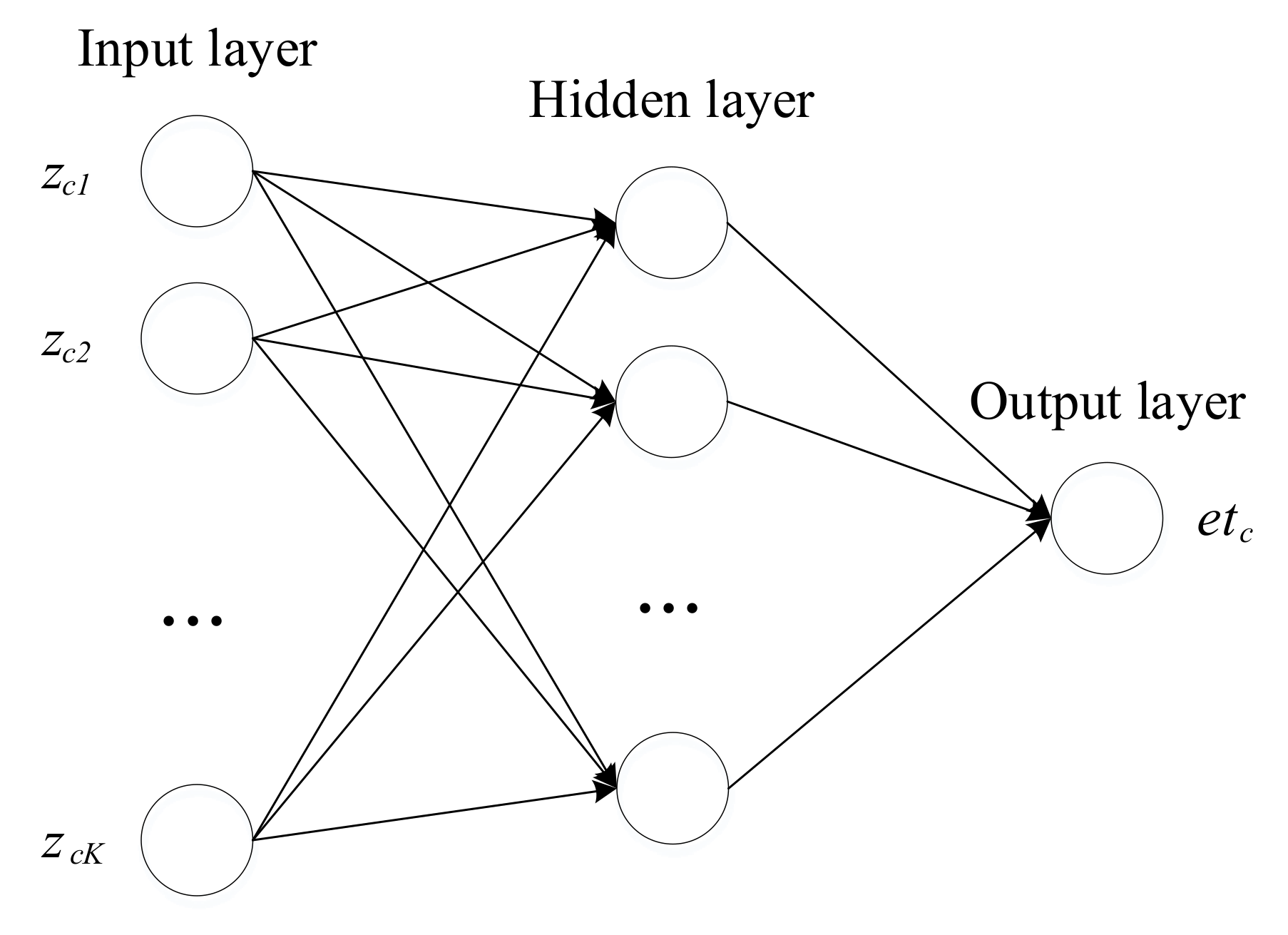
2.4. Backpropagation Network (BPN) Predictor
3. Computational Results
3.1. Data Description
3.2. Experimental Settings
3.3. Experimental Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chang, P.-C.; Hsieh, J.-C.; Liao, T.W. A case-based reasoning approach for due-date assignment in a wafer fabrication factory. In Proceedings of the International Conference on Case-Based Reasoning (ICCBR 2001), Vancouver, BC, Canada, 30 July–2 August 2001; pp. 648–659. [Google Scholar]
- Chen, T. A fuzzy back propagation network for output time prediction in a wafer fab. Appl. Soft Comput. 2003, 2, 211–222. [Google Scholar] [CrossRef]
- Kulkarni, V.; Nicola, V.; Smith, R.; Trivedi, K. Numerical Evaluation of Performability and Job Completion Time in Repairable Fault-tolerant Systems. In Proceedings of the 16th Intl. Symp. on Fault Tolerant Computing, Vienna, Austria, 1–4 July 1986. [Google Scholar]
- Mehrotra, K.; Chai, J.; Pillutla, S. A study of approximating the moments of the job completion time in PERT networks. J. Oper. Manag. 1996, 14, 277–289. [Google Scholar] [CrossRef]
- Chen, T. Job cycle time estimation in a wafer fabrication factory with a bi-directional classifying fuzzy-neural approach. Int. J. Adv. Manuf. Technol. 2011, 56, 1007–1018. [Google Scholar] [CrossRef]
- Chen, T.; Romanowski, R. Precise and accurate job cycle time forecasting in a wafer fabrication factory with a fuzzy data mining approach. Math. Probl. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- Glassey, C.R.; Resende, M.G. Closed-loop job release control for VLSI circuit manufacturing. IEEE Trans. Semicond. Manuf. 1988, 1, 36–46. [Google Scholar] [CrossRef]
- Pai, P.-F.; Lee, C.-E.; Su, T.-H. A daily production model for wafer fabrication. Int. J. Adv. Manuf. Technol. 2004, 23, 58–63. [Google Scholar] [CrossRef]
- Chen, T. A fuzzy-neural approach for estimating the monthly output of a semiconductor manufacturing factory. Int. J. Adv. Manuf. Technol. 2008, 39, 589–598. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J. Big data analytics for forecasting cycle time in semiconductor wafer fabrication system. Int. J. Prod. Res. 2016, 54, 7231–7244. [Google Scholar] [CrossRef]
- Chung, S.-H.; Huang, H.-W. Cycle time estimation for wafer fab with engineering lots. Iie Trans. 2002, 34, 105–118. [Google Scholar] [CrossRef]
- Raddon, A.; Grigsby, B. Throughput time forecasting model. In Proceedings of the 1997 IEEE/SEMI Advanced Semiconductor Manufacturing Conference and Workshop ASMC 97 Proceedings, Cambridge, MA, USA, 10–12 September 1997; pp. 430–433. [Google Scholar]
- Backus, P.; Janakiram, M.; Mowzoon, S.; Runger, C.; Bhargava, A. Factory cycle-time prediction with a data-mining approach. IEEE Trans. Semicond. Manuf. 2006, 19, 252–258. [Google Scholar] [CrossRef]
- Yang, F.; Ankenman, B.; Nelson, B.L. Efficient generation of cycle time-throughput curves through simulation and metamodeling. Nav. Res. Logist. (NRL) 2007, 54, 78–93. [Google Scholar] [CrossRef]
- Yang, F.; Ankenman, B.E.; Nelson, B.L. Estimating cycle time percentile curves for manufacturing systems via simulation. INFORMS J. Comput. 2008, 20, 628–643. [Google Scholar] [CrossRef]
- Pearn, W.; Chung, S.; Lai, C. Due-date assignment for wafer fabrication under demand variate environment. IEEE Trans. Semicond. Manuf. 2007, 20, 165–175. [Google Scholar] [CrossRef]
- Tai, Y.; Pearn, W.; Lee, J. Cycle time estimation for semiconductor final testing processes with Weibull-distributed waiting time. Int. J. Prod. Res. 2012, 50, 581–592. [Google Scholar] [CrossRef]
- Shanthikumar, J.G.; Ding, S.; Zhang, M.T. Queueing theory for semiconductor manufacturing systems: A survey and open problems. IEEE Trans. Autom. Sci. Eng. 2007, 4, 513–522. [Google Scholar] [CrossRef]
- Morrison, J.R.; Martin, D.P. Practical extensions to cycle time approximations for the G/G/m-queue with applications. IEEE Trans. Autom. Sci. Eng. 2007, 4, 523–532. [Google Scholar] [CrossRef]
- Singh, A.; Das, A.; Bera, U.K.; Lee, G.M. Prediction of transportation costs using trapezoidal neutrosophic fuzzy analytic hierarchy process and artificial neural networks. IEEE Access 2021, 9, 103497–103512. [Google Scholar] [CrossRef]
- Chang, P.C.; Hsieh, J.C. A neural networks approach for due-date assignment in a wafer fabrication factory. Int. J. Ind. Eng. 2003, 10, 55–61. [Google Scholar]
- Sha, D.Y.; Hsu, S.Y. Due-date assignment in wafer fabrication using artificial neural networks. Int. J. Adv. Manuf. Technol. 2004, 23, 768–775. [Google Scholar] [CrossRef]
- Chien, C.-F.; Hsu, C.-Y.; Hsiao, C.-W. Manufacturing intelligence to forecast and reduce semiconductor cycle time. J. Intell. Manuf. 2012, 23, 2281–2294. [Google Scholar] [CrossRef]
- Gazder, U.; Ratrout, N.T. A new logit—Artificial neural network ensemble for mode choice modeling: A case study for border transport. J. Adv. Transp. 2016, 49, 855–866. [Google Scholar] [CrossRef]
- Chiu, C.; Chang, P.-C.; Chiu, N.-H. A case-based expert support system for due-date assignment in a wafer fabrication factory. J. Intell. Manuf. 2003, 14, 287–296. [Google Scholar] [CrossRef]
- Chang, P.-C.; Fan, C.Y.; Wang, Y.-W. Evolving CBR and data segmentation by SOM for flow time prediction in semiconductor manufacturing factory. J. Intell. Manuf. 2009, 20, 421. [Google Scholar] [CrossRef]
- Liu, C.-H.; Chang, P.-C.; Kao, I.-W. Cluster based evolving FCBR for flow time prediction in semiconductor manufacturing factory. In Proceedings of the 8th WSEAS International Conference on Applied Computer Science (ACS’08), Venice, Italy, 21–23 November 2008; pp. 424–429. [Google Scholar]
- Vig, M.M.; Dooley, K.J. Dynamic rules for due-date assignment. Int. J. Prod. Res. 1991, 29, 1361–1377. [Google Scholar] [CrossRef]
- Veeger, C.; Etman, L.; Lefeber, E.; Adan, I.; Van Herk, J.; Rooda, J. Predicting cycle time distributions for integrated processing workstations: An aggregate modeling approach. IEEE Trans. Semicond. Manuf. 2011, 24, 223–236. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, L.Y.; Chang, K.-H.; Chien, C.-F. Efficient development of cycle time response surfaces using progressive simulation metamodeling. Int. J. Prod. Res. 2014, 52, 3097–3109. [Google Scholar] [CrossRef]
- Yang, D.; Hu, L.; Qian, Y. Due Date Assignment in a Dynamic Job Shop with the Orthogonal Kernel Least Squares Algorithm. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 212. [Google Scholar]
- Chang, P.-C.; Hieh, J.-C.; Liao, T.W. Evolving fuzzy rules for due-date assignment problem in semiconductor manufacturing factory. J. Intell. Manuf. 2005, 16, 549–557. [Google Scholar] [CrossRef]
- Chen, T. Fuzzy-neural-network-based fluctuation smoothing rule for reducing the cycle times of jobs with various priorities in a wafer fabrication plant: A simulation study. J. Eng. Manuf. 2009, 223, 1033–1043. [Google Scholar] [CrossRef]
- Gao, X.; Zhou, Y.; Amir, M.I.H.; Rosyidah, F.A.; Lee, G.M. A hybrid genetic algorithm for multi-emergency medical service center location-allocation problem in disaster response. Int. J. Ind. Eng. Theory Appl. Pract. 2017, 24, 663–679. [Google Scholar]
- Gao, X.; Lee, G.M. Moment-based Rental Prediction for Bicycle-sharing Transportation Systems Using a Hybrid Genetic Algorithm and Machine Learning. Comput. Ind. Eng. 2019, 128, 60–69. [Google Scholar] [CrossRef]
- Chen, T. An intelligent hybrid system for wafer lot output time prediction. Adv. Eng. Inform. 2007, 21, 55–65. [Google Scholar] [CrossRef]
- Chen, T.; Wu, H.-C.; Wang, Y.-C. Fuzzy-neural approaches with example post-classification for estimating job cycle time in a wafer fab. Appl. Soft Comput. 2009, 9, 1225–1231. [Google Scholar] [CrossRef]
- Tirkel, I. Cycle time prediction in wafer fabrication line by applying data mining methods. In Proceedings of the 2011 IEEE/SEMI Advanced Semiconductor Manufacturing Conference, Saratoga Springs, NY, USA, 16–18 May 2011; pp. 1–5. [Google Scholar]
- Chen, T.; Lin, Y.-C. A fuzzy back propagation network ensemble with example classification for lot output time prediction in a wafer fab. Appl. Soft Comput. 2009, 9, 658–666. [Google Scholar] [CrossRef]
- Chen, T. Asymmetric cycle time bounding in semiconductor manufacturing: An efficient and effective back-propagation-network-based method. Oper. Res. 2016, 16, 445–468. [Google Scholar] [CrossRef]
- Chen, T.; Wang, Y.-C. A nonlinearly normalized back propagation network and cloud computing approach for determining cycle time allowance during wafer fabrication. Robot. Comput. Integr. Manuf. 2017, 45, 144–156. [Google Scholar] [CrossRef]
- Yokota, T.; Gen, M.; Li, Y.-X. Genetic algorithm for non-linear mixed integer programming problems and its applications. Comput. Ind. Eng. 1996, 30, 905–917. [Google Scholar] [CrossRef]
- Yu, X.; Gen, M. Introduction to Evolutionary Algorithms; Springer: London, UK, 2010. [Google Scholar]
- Chen, T. Incorporating fuzzy c-means and a back-propagation network ensemble to job completion time prediction in a semiconductor fabrication factory. Fuzzy Sets Syst. 2007, 158, 2153–2168. [Google Scholar] [CrossRef]
- Chen, T. A job-classifying and data-mining approach for estimating job cycle time in a wafer fabrication factory. Int. J. Adv. Manuf. Technol. 2012, 62, 317–328. [Google Scholar] [CrossRef]
- Chen, T. A hybrid fuzzy-neural approach to job completion time prediction in a semiconductor fabrication factory. Neurocomputing 2008, 71, 3193–3201. [Google Scholar] [CrossRef]
- Sun, B.; Guo, H.; Karimi, H.R.; Ge, Y.; Xiong, S. Prediction of stock index futures prices based on fuzzy sets and multivariate fuzzy time series. Neurocomputing 2015, 151, 1528–1536. [Google Scholar] [CrossRef]
- Rezaee, M.J.; Jozmaleki, M.; Valipour, M. Integrating dynamic fuzzy C-means, data envelopment analysis and artificial neural network to online prediction performance of companies in stock exchange. Phys. A Stat. Mech. Its Appl. 2018, 489, 78–93. [Google Scholar] [CrossRef]
- Biju, V.; Mythili, P. A genetic algorithm based fuzzy C mean clustering model for segmenting microarray images. Int. J. Comput. Appl. 2012, 52, 42–48. [Google Scholar]
- Ding, Y.; Fu, X. Kernel-based fuzzy c-means clustering algorithm based on genetic algorithm. Neurocomputing 2016, 188, 233–238. [Google Scholar] [CrossRef]
- Chen, T.; Wu, H.-C. A new cloud computing method for establishing asymmetric cycle time intervals in a wafer fabrication factory. J. Intell. Manuf. 2017, 28, 1095–1107. [Google Scholar] [CrossRef] [Green Version]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Dunn, J.C. Optimal fuzzy partitions: A heuristic for estimating the parameters in a mixture of normal distributions. IEEE Trans. Comput. 1975, 100, 835–838. [Google Scholar] [CrossRef]
- Kenesei, T.; Balasko, B.; Abonyi, J. A MATLAB toolbox and its web based variant for fuzzy cluster analysis. In Proceedings of the 7th International Symposium on Hungarian Researchers on Computational Intelligence, Budapest, Hungary, 24–25 November 2006; pp. 24–25. [Google Scholar]
- Wikaisuksakul, S. A multi-objective genetic algorithm with fuzzy c-means for automatic data clustering. Appl. Soft Comput. 2014, 24, 679–691. [Google Scholar] [CrossRef]
- Ye, A.-X.; Jin, Y.-X. A fuzzy c-means clustering algorithm based on improved quantum genetic algorithm. Simulation 2016, 9, 227–236. [Google Scholar] [CrossRef]
- Chen, T. A systematic cycle time reduction procedure for enhancing the competitiveness and sustainability of a semiconductor manufacturer. Sustainability 2013, 5, 4637–4652. [Google Scholar] [CrossRef] [Green Version]
- Chen, T. Estimating job cycle time in a wafer fabrication factory: A novel and effective approach based on post-classification. Appl. Soft Comput. 2016, 40, 558–568. [Google Scholar] [CrossRef]
- Law, R. Back-propagation learning in improving the accuracy of neural network-based tourism demand forecasting. Tour. Manag. 2000, 21, 331–340. [Google Scholar] [CrossRef]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]


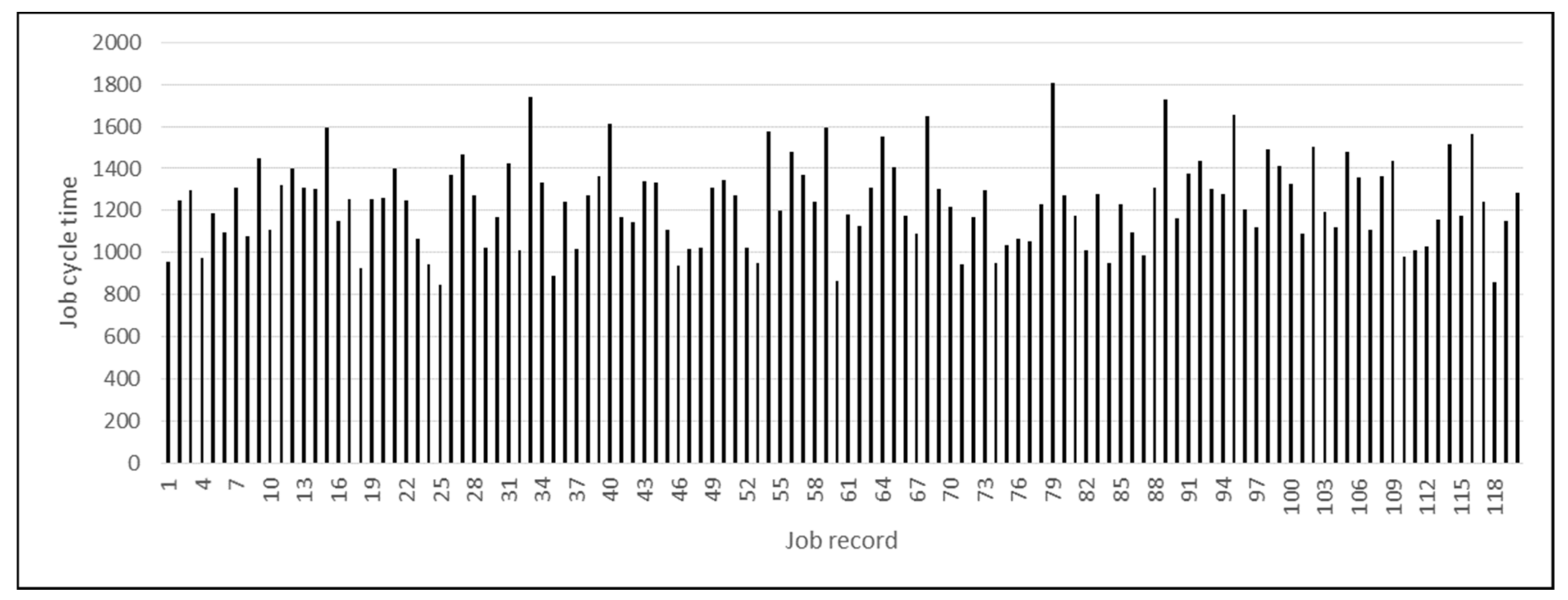
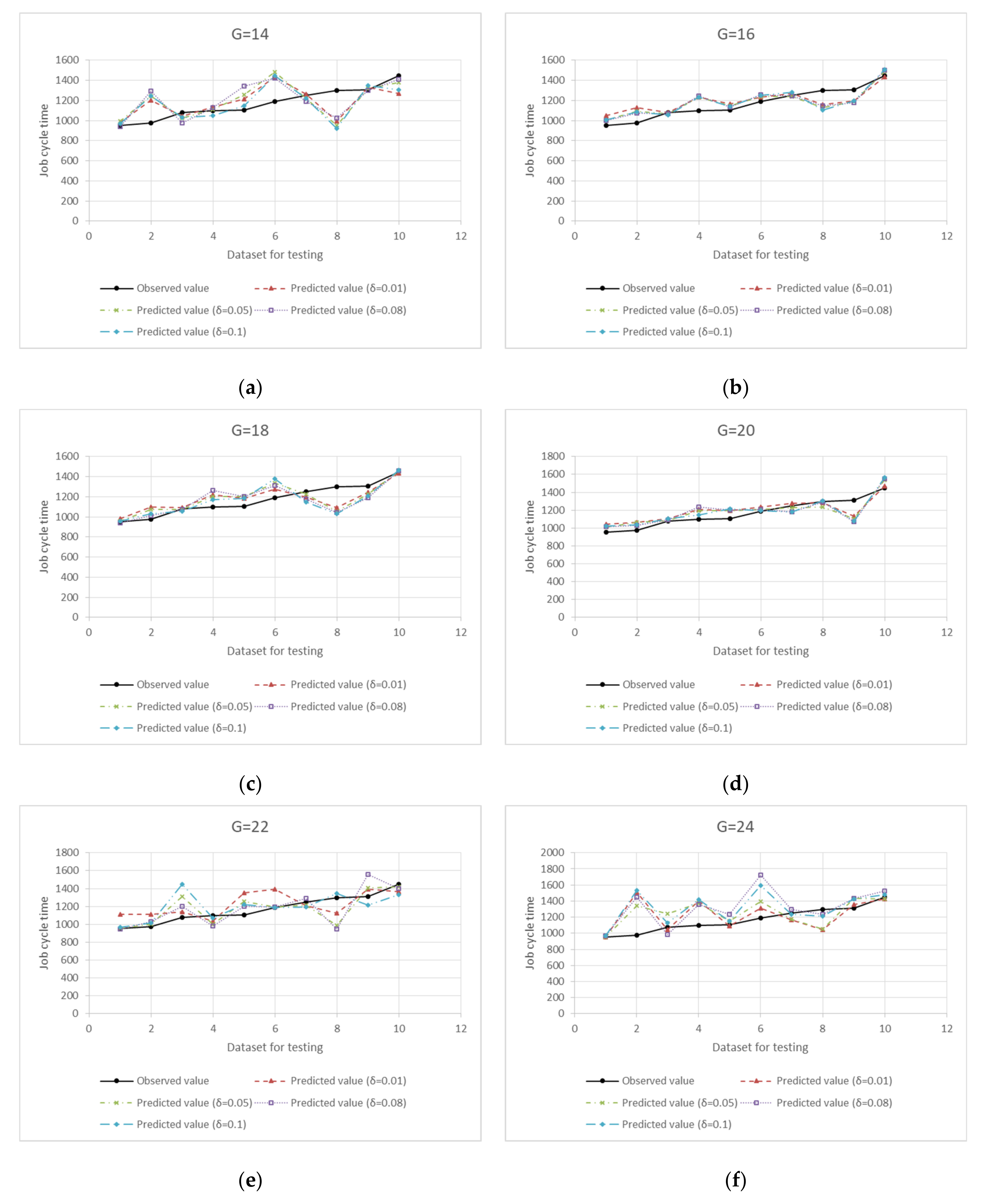

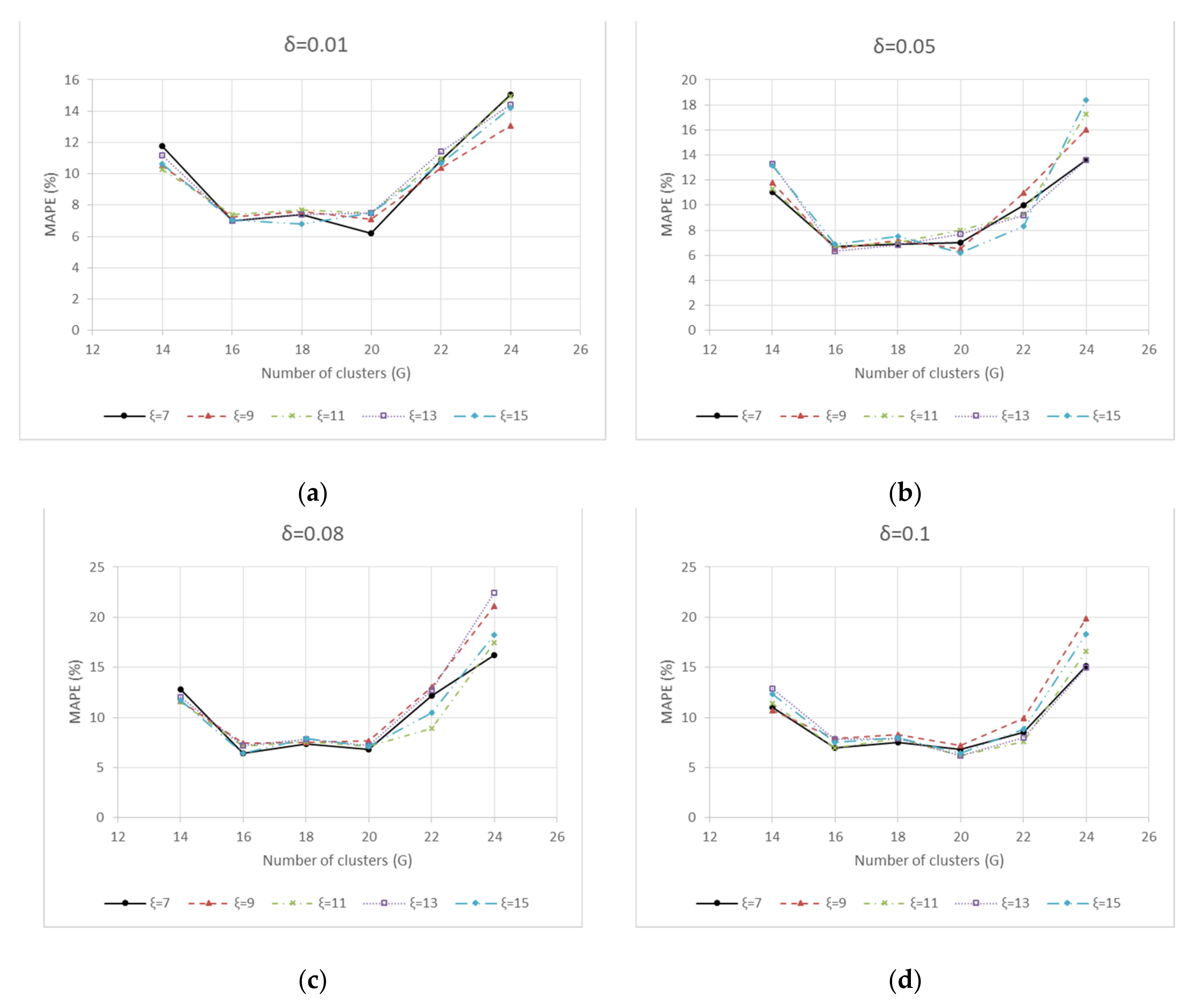
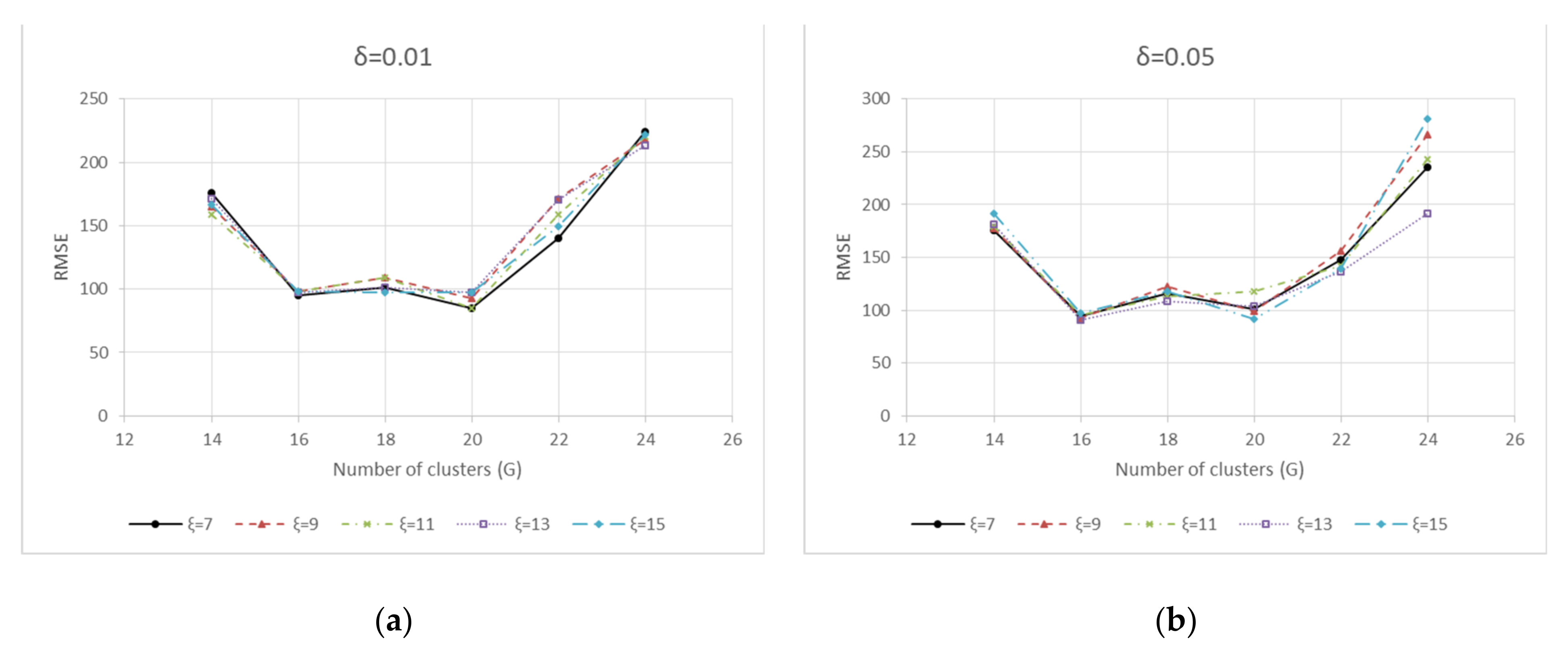
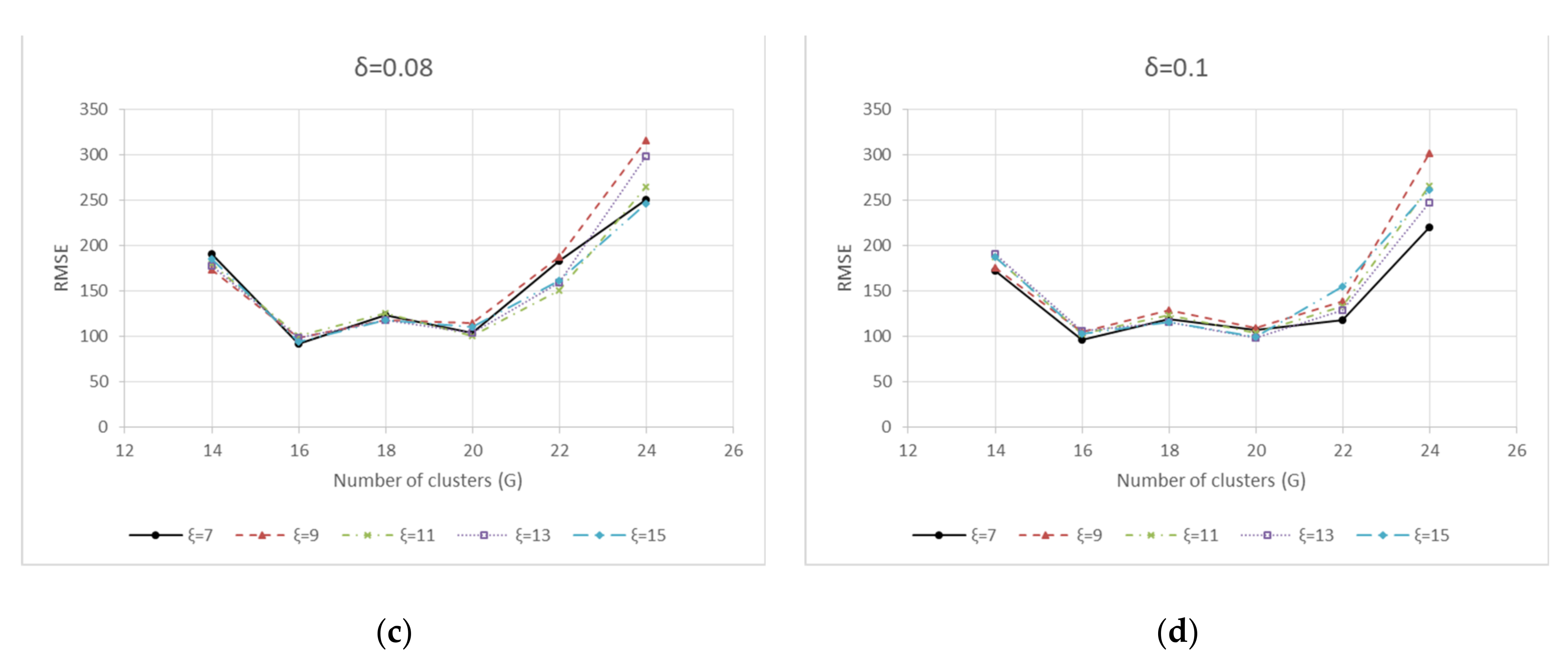
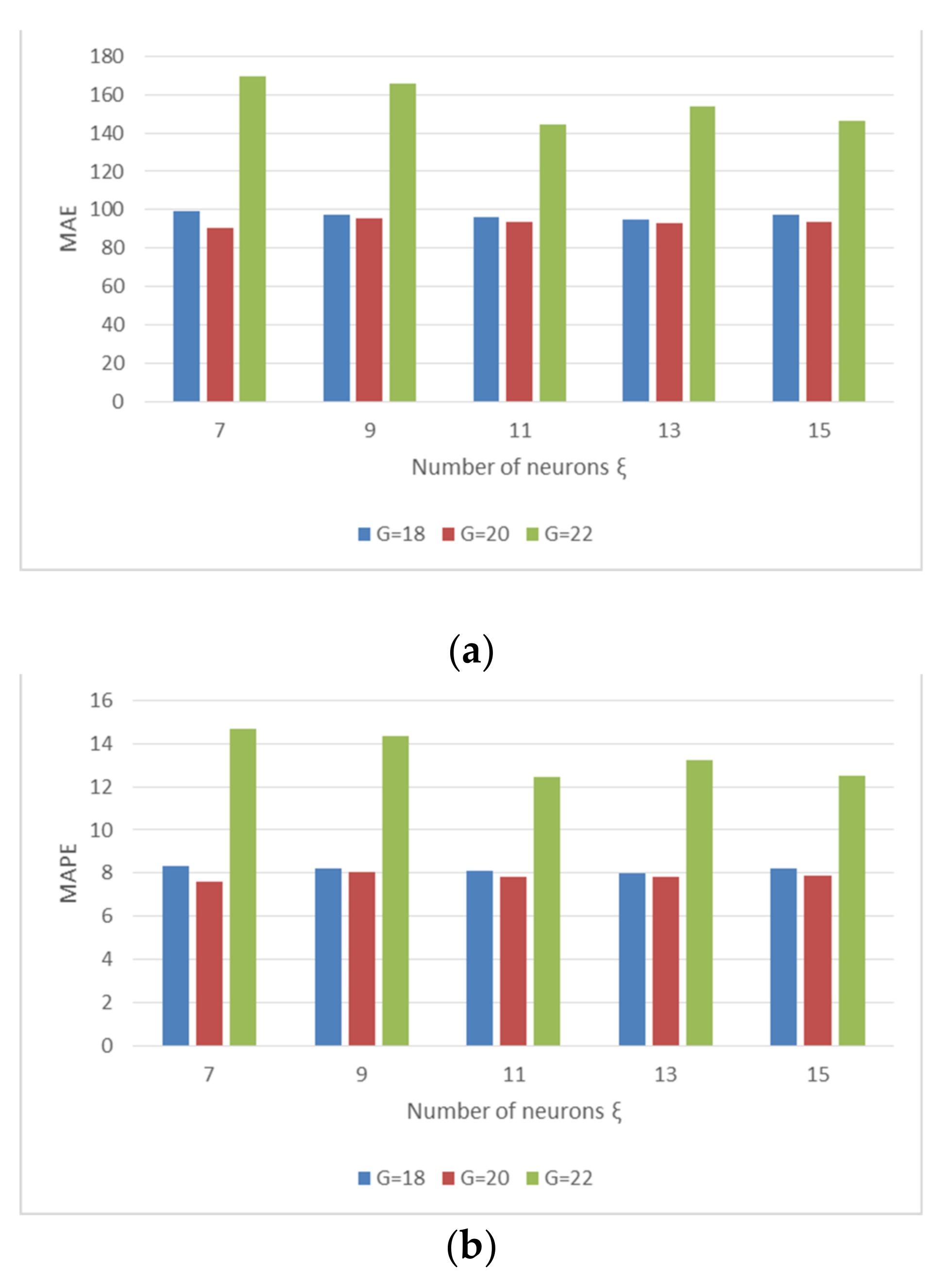
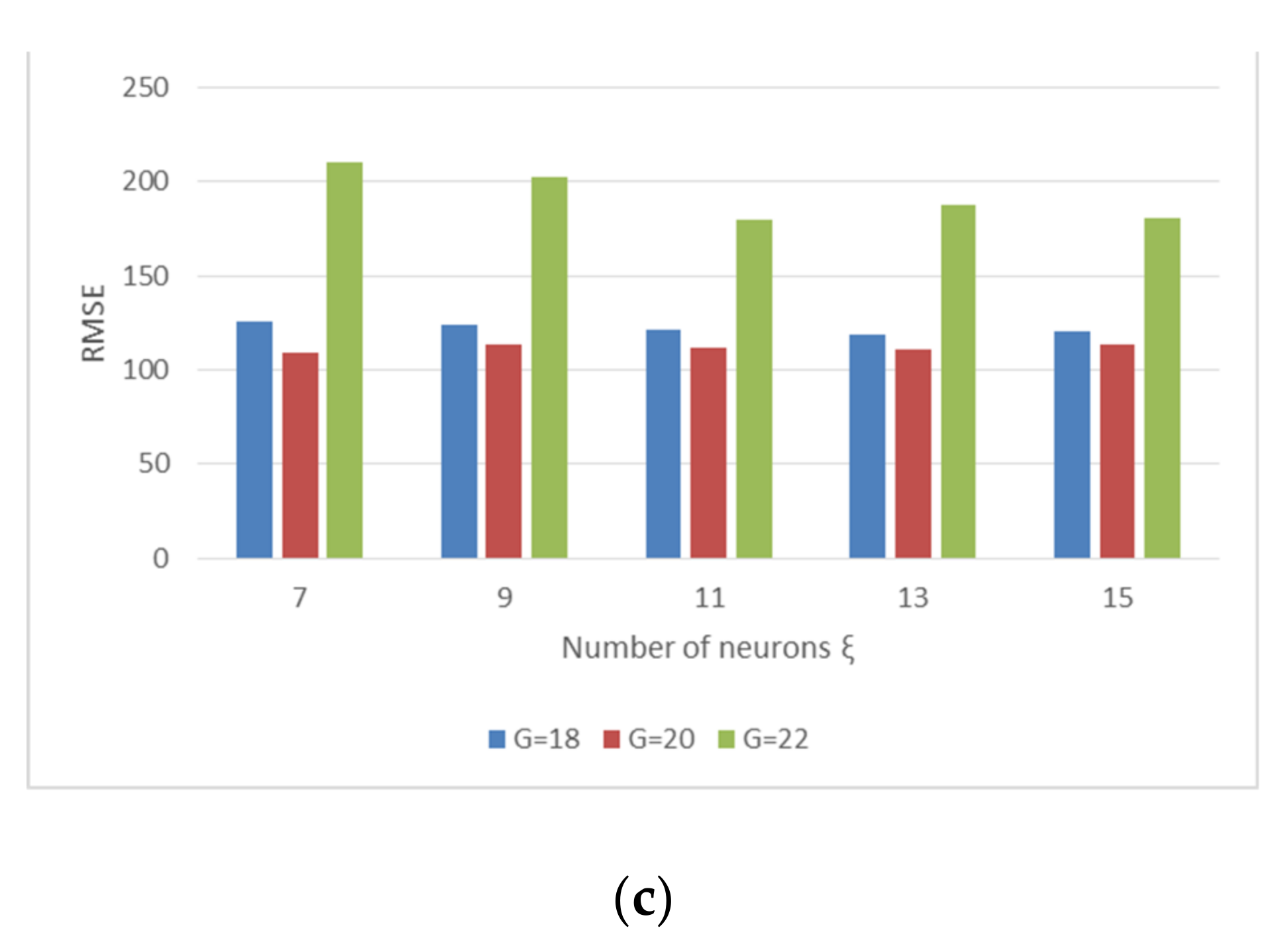
| Parameter | Value |
|---|---|
| Fuzziness exponent () | 2 |
| FCM termination tolerance () | |
| Number of clusters () | 14, 16, 18, 20, 22, and 24 |
| Population size () | 40 |
| Number of generations () | |
| Mutation probability () | 0.2 |
| Crossover probability () | 0.1 |
| Membership threshold value () | 0.01, 0.05, 0.08, and 0.1 |
| Fitness variance value () | |
| Learning rate () | 0.99 |
| Number of neurons in the input layer () | 6 |
| Number of neurons in the hidden layer () | 7, 9, 11, 13, and 15 |
| Best Value | Average Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 0.05 | 0.08 | 0.1 | 0.01 | 0.05 | 0.08 | 0.1 | |||
| 18 | 7 | MAE (h) | 86.04 | 82.33 | 89.51 | 89.99 | 92.14 | 105.53 | 98.87 | 100.27 |
| MAPE (%) | 7.40 | 6.90 | 7.40 | 7.50 | 7.90 | 8.80 | 8.20 | 8.30 | ||
| RMSE (h) | 101.67 | 115.76 | 123.37 | 118.79 | 111.55 | 135.14 | 129.99 | 125.45 | ||
| 9 | MAE (h) | 88.30 | 86.41 | 89.53 | 99.51 | 93.86 | 93.99 | 95.90 | 106.99 | |
| MAPE (%) | 7.60 | 7.20 | 7.50 | 8.30 | 8.20 | 7.80 | 8.00 | 8.90 | ||
| RMSE (h) | 108.87 | 122.07 | 117.35 | 128.34 | 112.11 | 124.32 | 127.07 | 132.91 | ||
| 11 | MAE (h) | 90.31 | 82.96 | 91.43 | 95.06 | 92.97 | 92.96 | 97.21 | 100.36 | |
| MAPE (%) | 7.70 | 7.00 | 7.60 | 7.90 | 8.00 | 7.80 | 8.10 | 8.40 | ||
| RMSE (h) | 109.41 | 112.97 | 125.36 | 123.62 | 109.81 | 119.69 | 130.09 | 125.51 | ||
| 13 | MAE (h) | 85.39 | 80.57 | 92.92 | 92.87 | 89.06 | 92.18 | 97.22 | 100.81 | |
| MAPE (%) | 7.40 | 6.80 | 7.80 | 7.90 | 7.70 | 7.70 | 8.10 | 8.40 | ||
| RMSE (h) | 101.04 | 108.55 | 117.95 | 116.12 | 105.12 | 116.75 | 126.01 | 127.03 | ||
| 15 | MAE (h) | 78.22 | 89.76 | 95.48 | 95.98 | 92.43 | 93.11 | 99.19 | 103.92 | |
| MAPE (%) | 6.80 | 7.50 | 7.90 | 8.00 | 8.00 | 7.80 | 8.30 | 8.70 | ||
| RMSE (h) | 97.27 | 118.15 | 117.98 | 115.53 | 110.32 | 120.37 | 125.70 | 127.18 | ||
| 20 | 7 | MAE (h) | 70.03 | 83.62 | 80.44 | 82.74 | 86.45 | 90.45 | 88.62 | 96.02 |
| MAPE (%) | 6.20 | 7.00 | 6.80 | 6.80 | 7.60 | 7.60 | 7.40 | 7.90 | ||
| RMSE (h) | 85.11 | 101.43 | 104.14 | 106.79 | 98.38 | 109.19 | 109.74 | 118.40 | ||
| 9 | MAE (h) | 80.54 | 78.40 | 92.96 | 88.35 | 88.39 | 97.85 | 98.12 | 98.65 | |
| MAPE (%) | 7.10 | 6.50 | 7.70 | 7.20 | 7.80 | 8.20 | 8.10 | 8.10 | ||
| RMSE (h) | 93.08 | 99.15 | 114.90 | 108.94 | 100.88 | 118.48 | 117.35 | 119.08 | ||
| 11 | MAE (h) | 86.36 | 96.98 | 83.55 | 76.77 | 90.25 | 100.74 | 97.36 | 85.25 | |
| MAPE (%) | 7.50 | 8.00 | 7.10 | 6.20 | 7.90 | 8.30 | 8.10 | 7.00 | ||
| RMSE (h) | 84.78 | 117.79 | 100.23 | 104.06 | 100.01 | 120.98 | 119.32 | 108.48 | ||
| 13 | MAE (h) | 86.17 | 91.82 | 85.09 | 74.43 | 88.82 | 94.47 | 97.58 | 90.25 | |
| MAPE (%) | 7.50 | 7.70 | 7.20 | 6.20 | 7.70 | 7.90 | 8.20 | 7.50 | ||
| RMSE (h) | 97.39 | 104.01 | 103.59 | 97.87 | 100.77 | 112.05 | 119.35 | 113.06 | ||
| 15 | MAE (h) | 84.97 | 73.20 | 87.94 | 78.02 | 91.31 | 94.05 | 96.38 | 93.12 | |
| MAPE (%) | 7.50 | 6.20 | 7.10 | 6.40 | 8.00 | 7.90 | 8.00 | 7.70 | ||
| RMSE (h) | 97.39 | 91.56 | 110.24 | 99.27 | 105.69 | 114.69 | 118.92 | 115.74 | ||
| 22 | 7 | MAE (h) | 123.99 | 116.03 | 144.75 | 96.68 | 144.20 | 190.13 | 187.16 | 156.08 |
| MAPE (%) | 10.90 | 10.00 | 12.20 | 8.50 | 12.60 | 16.70 | 16.30 | 13.20 | ||
| RMSE (h) | 140.28 | 147.88 | 182.79 | 117.55 | 181.68 | 238.56 | 232.60 | 186.85 | ||
| 9 | MAE (h) | 122.03 | 128.79 | 152.29 | 118.62 | 166.13 | 157.95 | 179.16 | 160.69 | |
| MAPE (%) | 10.40 | 11.00 | 13.00 | 9.90 | 14.40 | 13.70 | ` | 13.70 | ||
| RMSE (h) | 171.08 | 155.78 | 187.71 | 138.90 | 198.50 | 194.35 | 222.87 | 194.79 | ||
| 11 | MAE (h) | 128.49 | 111.02 | 107.62 | 87.14 | 145.13 | 141.60 | 149.09 | 142.26 | |
| MAPE (%) | 11.00 | 9.30 | 8.90 | 7.60 | 12.40 | 12.00 | 13.10 | 12.20 | ||
| RMSE (h) | 159.06 | 142.54 | 150.50 | 133.37 | 177.79 | 167.46 | 191.49 | 180.90 | ||
| 13 | MAE (h) | 131.87 | 107.62 | 143.40 | 90.92 | 148.16 | 156.34 | 158.13 | 153.17 | |
| MAPE (%) | 11.40 | 9.20 | 12.70 | 8.00 | 12.70 | 13.40 | 13.50 | 13.30 | ||
| RMSE (h) | 170.71 | 136.10 | 159.68 | 128.74 | 185.41 | 187.92 | 190.67 | 185.97 | ||
| 15 | MAE (h) | 123.17 | 97.93 | 124.83 | 106.08 | 144.37 | 133.21 | 153.99 | 152.81 | |
| MAPE (%) | 10.70 | 8.30 | 10.50 | 8.80 | 12.40 | 11.60 | 13.20 | 12.90 | ||
| RMSE (h) | 149.38 | 139.45 | 161.30 | 155.14 | 175.48 | 163.15 | 190.40 | 194.17 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, G.M.; Gao, X. A Hybrid Approach Combining Fuzzy c-Means-Based Genetic Algorithm and Machine Learning for Predicting Job Cycle Times for Semiconductor Manufacturing. Appl. Sci. 2021, 11, 7428. https://doi.org/10.3390/app11167428
Lee GM, Gao X. A Hybrid Approach Combining Fuzzy c-Means-Based Genetic Algorithm and Machine Learning for Predicting Job Cycle Times for Semiconductor Manufacturing. Applied Sciences. 2021; 11(16):7428. https://doi.org/10.3390/app11167428
Chicago/Turabian StyleLee, Gyu M., and Xuehong Gao. 2021. "A Hybrid Approach Combining Fuzzy c-Means-Based Genetic Algorithm and Machine Learning for Predicting Job Cycle Times for Semiconductor Manufacturing" Applied Sciences 11, no. 16: 7428. https://doi.org/10.3390/app11167428
APA StyleLee, G. M., & Gao, X. (2021). A Hybrid Approach Combining Fuzzy c-Means-Based Genetic Algorithm and Machine Learning for Predicting Job Cycle Times for Semiconductor Manufacturing. Applied Sciences, 11(16), 7428. https://doi.org/10.3390/app11167428







