A Topology Optimization Method for Reducing Communication Overhead in the Kalman Consensus Filter

Featured Application

This work can be used in network topology optimization for reducing communication overhead in the Kalman consensus filter.

Abstract

Distributed estimation and tracking of interested objects over wireless sensor networks (WSNs) is a hot research topic. Since network topology possesses distinctive structural parameters and plays an important role for the performance of distributed estimation, we first formulate the communication overhead reduction problem in distributed estimation algorithms as the network topology optimization in this paper. The effect of structural parameters on the algebraic connectivity of a network is overviewed. Moreover, aiming to reduce the communication overhead in Kalman consensus filter (KCF)-based distributed estimation algorithm, we propose a network topology optimization method by properly deleting and adding communication links according to nodes’ local structural parameters information, in which the constraint on the communication range of two nodes is incorporated. Simulation results show that the proposed network topology optimization method can effectively improve the convergence rate of KCF algorithm and achieve a good trade-off between the estimate error and communication overhead.

1. Introduction

Wireless sensor networks (WSNs), which are composed of a large number of stationary and/or mobile sensor nodes in a self-organizing and multi-hop manner, perceive, collect, process, and transmit collaboratively the information of interested objects in the geographical area covered by the network [1]. The performance of WSNs is directly affected by the network topology. For example, the planar network structure where all nodes are equivalent has better robustness, and the hierarchical network structure extended by the planar network structure has better expansibility [2]. Hence, in order to improve the performance, the problem of network topology optimization has become a hot research topic.

Distributed estimation over a network, one of the most fundamental information processing problems in WSNs, aims to estimate and track the state of interested objects in the noisy environment through the cooperation between sensor nodes [3,4]. Kalman filtering has been an effective algorithm for tracking dynamic processes for over four decades. In [5], the author introduced the Kalman consensus filter (KCF) algorithm, which relies on average consensus, and it is pointed out that this algorithm is applicable to sensor networks with variable topology. The KCF algorithm also has a lot of applications in other fields such as autonomous vehicles [6], indoor positioning systems (IPS) [7], wearable devices [8], visual tracking [9], underwater environment sensing [10], and trace applications [11,12]. Therefore, we focus on the KCF algorithm in this work, where each sensor node only communicates with its neighboring nodes in the network to generate an estimate, and the data exchanging constitutes the main reason of energy consumption. However, due to the limited energy of sensor nodes in WSNs, it is necessary to reduce communication overhead in distributed estimation algorithms.

In the past few years, there have been several methods [13,14,15,16,17] that reduced the communication overhead of distributed estimation algorithms, which can be classified, typically, into two categories. First, the sensor nodes probabilistically receive estimation information from neighbors. For example, in [13], sensor nodes choose to exchange a subset of intermediate estimation information with neighboring nodes. In [14], authors proposed a distributed estimation algorithm that relies on limited local information for average consensus where sensor nodes exchange messages with their neighboring nodes less frequently as nodes’ estimations approach to a stable value. Chen et al. provided a rule to build the optimal set of information neighbors for every node in [15]. Second, dimension reduction is also a method used to reduce communication overhead in distributed estimation algorithms. In [16], a distributed estimation algorithm based on compressed sensing is proposed, where sensor nodes only exchange their compressed estimation to reduce the communication overhead over the network. Obviously, all of these methods reduce the communication overhead at the cost of the precision of estimation.

It is pointed out in [5] that the structure of network topology plays an important role in distributed estimation algorithms, where the algebraic connectivity of network topology affects the upper bound of convergence rate. However, network topology optimization is a complex combinatorial optimization problem [18]. In recent years, many heuristic network topology optimization algorithms have been proposed. In [19], one finds that the convergence rate in random networks can be improved by redirecting a small portion of communication links. In [20], a method is presented to design a network topology for distributed estimation over a tree graph, where the convergence rate and security is the trade-off. In [21], a network topology optimization method based on the combination of a greedy algorithm and Tabu search is proposed, where the constraint on the distance of two nodes is incorporated. However, this method needs the global network information, and has high computational complexity.

In this paper, we solve the problem of communication overhead reduction for the distributed estimation, where the communication overhead problem is transformed into the network topology optimization problem. In order to optimize the network topology, we propose a method according to the local structure parameters of network nodes, in terms of node degree, average path length, and clustering coefficient. Since sensor nodes are power-limited, it is essential to constrain the communication range between sensor nodes.

The main contributions of this paper are as follows:

• The problem of communication overhead reduction in the KCF algorithm is converted into the optimization of network topology, which achieves a good trade-off between the mean square estimate error and network communication overhead.
• A network topology optimization method is proposed according to nodes’ local structural parameters information, in which the constraint on the communication range of two nodes is incorporated.

To the best of our knowledge, there are few works on reducing the communication overhead of the KCF algorithm from the perspective of network topology optimization. Moreover, due to the unstableness of WSNs, it is more desirable to adjust communication links for the performance improvement. In addition, the communication links are adjusted based on local structural parameters of the network, in terms of the degree of network nodes, average path length, and clustering coefficient. Compared with some existing heuristic search algorithms, the proposed method in this paper outperforms them in terms of the computational complexity and communication overhead.

The remainder of the paper is organized as follows. Section 2 introduces the system model and formulates the problem of network topology optimization. In Section 3, a network topology optimization method is proposed. Simulation results are given in Section 4. Finally, we conclude the paper in Section 5.

2. System Model and Problem Formulation

In this section, the system model is introduced, and the problem to be resolved is formulated.

2.1. Network Model

This work considers a WSN with topology $\mathcal{G}=\left(V,E\right)$, where $\mathcal{G}$ is undirected and connected, $V$ is the set of sensor nodes, $V=\left\{1,2,\cdots ,I\right\}$ and I is the number of sensor nodes in the network, $E$ is the set of communication links, and $|E|=K$ denotes the number of communication links in the network. The neighboring nodes set of node i is denoted as

$${\mathcal{N}}_i=\left\{j\in \mathcal{V}\prime :|\prime (i,j)\in ℰ\right\}$$

Adjacency matrix N denotes the neighborhood relationship of a network. If node i and node j are adjacent, the corresponding entry in N is $n_{ij}=1$; otherwise, $n_{ij}=0$. Let d_i be the degree of node i, and $d_i={\displaystyle \sum _{j=1}^I{n}_{ij}}$. Degree matrix D is a diagonal matrix, where the i-th entry is $d_i$. Laplacian matrix L is the symmetric and positive semi-definite matrix defined by $L=D-N$. The eigenvalues of L can be arranged as

$$0={\lambda }_1\left(\mathcal{G}\right)<{\lambda }_2\left(\mathcal{G}\right)\le \dots \le {\lambda }_I\left(\mathcal{G}\right)$$

where ${\lambda }_2\left(\mathcal{G}\right)$ is also called the algebraic connectivity of graph.

2.2. Kalman Consensus Filter Algorithm

Considering a dynamic process (or target) with a linear time-varying model as

$$x\left(k+1\right)=Ax\left(k\right)+Bw\left(k\right)$$

where $x\left(k\right)$ and $w\left(k\right)$ are the state and input noise of the process in time k, respectively, and A is the state transition matrix, and B is the control matrix.

The measurement model at node i in time k can be expressed as

$$z_i\left(k\right)=H_i\left(k\right)x\left(k\right)+v_i\left(k\right)$$

where $z_i\left(k\right)$ and $v_i\left(k\right)$ are the measurement vector and measurement noise vector at node i in time k, and $H_i\left(k\right)$ is the measurement matrix at node i in time k. In this work, we assume that $w\left(k\right)$ and $v_i\left(k\right)$ are mutually independent white Gaussian variables with zero-mean and covariance $Q\left(k\right)$ and $R_i\left(k\right)$.

Let ${\widehat{x}}_i\prime \left(k\right)$ and ${\overline{x}}_i\left(k\right)$ denote the estimate and predicted value of state $x\left(k\right)$, respectively. The estimate error and prediction error can be expressed as

$$\begin{array}{l}\eta \left(k\right)=\widehat{x}\left(k\right)-x\left(k\right)\\ \overline{\eta }\left(k\right)=\overline{x}\left(k\right)-x\left(k\right)\end{array}$$

The error covariance matrices are defined as

$$\begin{array}{l}M\left(k\right)={\rm E}\left[\eta \left(k\right){\eta }^{\mathrm{T}}\left(k\right)\right]\\ P\left(k\right)={\rm E}\left[\overline{\eta }\left(k\right){\overline{\eta }}^{\mathrm{T}}\left(k\right)\right]\end{array}$$

In the type-III KCF algorithm [22], node i in time k produces its local weighted measurement matrix $u_i\left(k\right)$ and local information matrix $U_i\left(k\right)$ as

$$\begin{array}{l}{u}_i\left(k\right)=H_i{}^{\mathrm{T}}\left(k\right)R_i{}^{-1}\left(k\right)z_i\left(k\right),y_i\left(k\right)={\displaystyle \sum _{j\in \left({\mathcal{N}}_i\cup i\right)}{u}_j}\left(k\right)\\ U_i\left(k\right)=H_i{}^{\mathrm{T}}\left(k\right)R_i{}^{-1}\left(k\right)H_i\left(k\right),S_i\left(k\right)={\displaystyle \sum _{j\in \left({\mathcal{N}}_i\cup i\right)}{U}_j}\left(k\right)\end{array}$$

The estimate value of node i in time k, ${\widehat{x}}_i\left(k\right)$, is obtained as

$$\begin{array}{l}{M}_i\left(k\right)={\left(P_i{}^{-1}\left(k\right)+S_i\left(k\right)\right)}^{-1}\\ {\widehat{x}}_i\left(k\right)={\overline{x}}_i\left(k\right)+M_i\left(k\right)\left(y_i\left(k\right)-S_i\left(k\right){\overline{x}}_i\left(k\right)\right)+\gamma M_i\left(k\right){\displaystyle \sum _{j\in {\mathcal{N}}_i}\left({\overline{x}}_j\left(k\right)-{\overline{x}}_i\left(k\right)\right)}\end{array}$$

The predicted value of node i in time k, ${\overline{x}}_i\left(k\right)$, is updated as

$$\begin{array}{l}{P}_i\left(k+1\right)=A{M}_i\left(k\right)A^{\mathrm{T}}+BQ\left(k\right)B^{\mathrm{T}}\\ {\overline{x}}_i\left(k+1\right)=A{\widehat{x}}_i\left(k\right)\end{array}$$

From the KCF algorithm mentioned above, one finds that node i should receive messages from its neighboring nodes

$$ms{g}_i\left(k\right)=\left\{\left(u_j\left(k\right),U_j\left(k\right),{\overline{x}}_j\left(k\right)\right)|j\in {\mathcal{N}}_i\right\}$$

i∈{1, 2, …, I}. Hence, the communication overhead in the KCF algorithm is relatively heavy.

2.3. Problem Formulation

To formulate the problem of communication overhead reduction in the KCF algorithm, we first make the following assumption.

Assumption 1.

The network topology keeps unchanged during the estimation processing.

Let $J_{i,\mathrm{overhead}}\left(k\right)$ denote the communication overhead of node i in time k, which equals the number of messages received by node i in time k under Assumption 1.

The total communication overhead is

$$J_{\mathrm{total},\mathrm{overhead}}\left(k\right)={\displaystyle \sum _{i=1}^I{J}_{i,\mathrm{overhead}}\left(k\right)}={\displaystyle \sum _{i=1}^I|{\mathrm{msg}}_i\left(k\right)|}$$

(1)

where $|{\mathrm{msg}}_i\left(k\right)|$ is the number of messages received by node i in time k.

Therefore, the problem of communication overhead reduction in the KCF algorithm can be denoted as

$$\min {\displaystyle \sum _{k=1}^n{J}_{\mathrm{total},\mathrm{overhead}}\left(k\right)}$$

(P1)

where n is the number of iterations.

When the number of sensor nodes and the state vector of interested object are given, only the number of iterations will affect the solution of (P1). Obviously, n is related to the convergence rate of KCF algorithm.

As described in [5,22], the estimate error dynamics of the KCF algorithm is a globally asymptotically stable system with a Lyapunov function

$$V\left(\eta \left(k\right)\right)={\eta }^{\mathrm{T}}\left(k\right)M\left(k\right)\eta \left(k\right)$$

and the convergence rate of $V\left(\eta \right)$ is expressed as

$$\delta V\left(\eta \left(k\right)\right)=V\left(\eta \left(k+1\right)\right)-V\left(\eta \left(k\right)\right)$$

which is related to the algebraic connectivity of network topology ${\lambda }_2\left(\mathcal{G}\right)$. That is,

$$\delta V\left(\eta \left(k\right)\right)\le -2\gamma {\lambda }_2\left(\mathcal{G}\right){\Vert \overline{\eta }\left(k\right)\Vert }^2$$

(2)

According to (2), we can optimize the network topology to improve the convergence rate of distributed estimation. However, since sensor nodes are power-limited, sensor nodes are not preferable to be communicated to nodes far away. In [23], the power relation between an idealized transmitting node and a receiving node behaves quadratically to the communication distance. Therefore, it is essential to constrain the communication range between sensor nodes.

Hence, the problem formulated in (P1) can be relaxed and converted into

$$\begin{array}{l}\max {\lambda }_2\left({\mathcal{G}}^{\prime }\right)\\ \mathrm{s}.\mathrm{t}.|{\mathcal{V}}^{\prime }|=I\\ |{ℰ}^{\prime }|=K\\ E\left(i,{\mathcal{N}}_i\right)\le D_i\end{array}$$

(P2)

where $E\left(i,j\right)$ is the Euclidean distance between nodes i and j, and $D_i$ is the communication range of node i. Therefore, the algebraic connectivity of network topology is maximized without changing the number of nodes and the number of communication links in the network, in which the constraint on the communication range of two neighboring nodes is incorporated. The optimized network topology is expressed as ${\mathcal{G}}^{\prime }=\left({\mathcal{V}}^{\prime },{ℰ}^{\prime }\right)$.

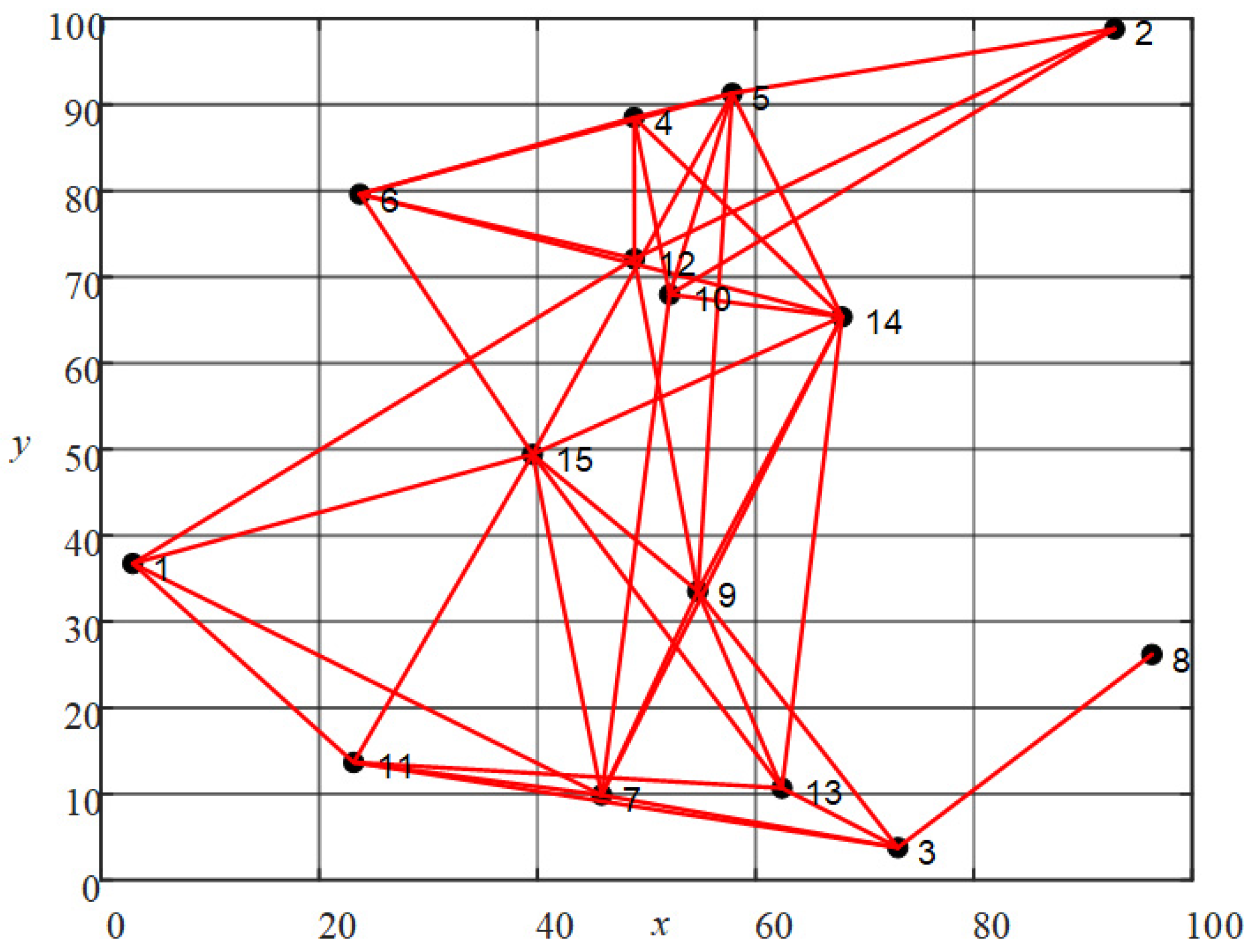
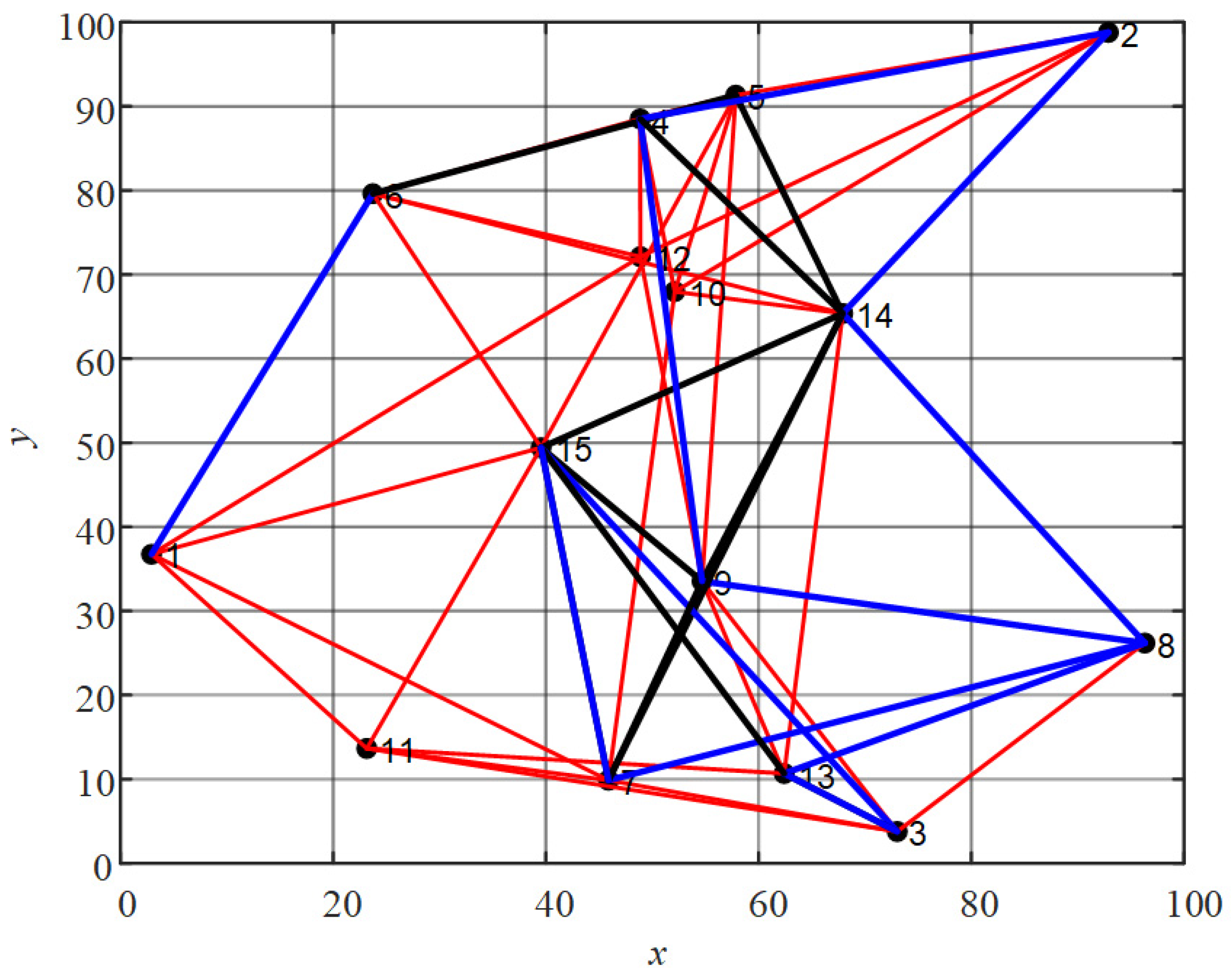
3. Network Topology Optimization Method

In this section, a network topology optimization method is presented to reduce the communication overhead in the KCF algorithm.

3.1. The Structural Parameters of Network Topology

It is indicated in [24] that the algebraic connectivity of network topology ${\lambda }_2\left(\mathcal{G}\right)$ is affected by structural parameters of network topology. Therefore, it is reasonable to take the structural parameters as the basis of a network topology optimization method.

The structural parameters of network topology, such as node’s degree (d), the average path length (l), and clustering coefficient (c), play a key role in the recent development of complex network theory.

The average value of the shortest path between any two sensor nodes in a network topology, l, determines the effective “size” of the network.

The clustering coefficient of node i, $c_i$, is defined as the ratio between the actual number of links, $E_i$, and the maximum number of links, $d_i\left(d_i-1\right)/2$, between neighboring nodes, and $c_i=\frac{2E_{{\mathcal{N}}_i}}{d_i\left(d_i-1\right)}$. The average of $c_i$ over all the sensor nodes, c, measures the extent to which a network is clustered.

Proposition 1.

In an undirected and connected topology,${\lambda }_2\left(\mathcal{G}\right)\le \frac{I{d}_{\min }}{I-1}$ and ${\lambda }_I\left(\mathcal{G}\right)\ge d_{\max }+1$, where $d_{\min }$ and $d_{\max }$ are the minimum and maximum degrees of topology $\mathcal{G}$, respectively.

Proof of Proposition 1.

See [25] (p. 300) and [26] (p. 224). □

Proposition 2.

The algebraic connectivity ${\lambda }_2\left(\mathcal{G}\right)$ is inversely proportional to the average path length l, and ${\lambda }_2\left(\mathcal{G}\right)\le \frac{1}{l}$ .

Proof of Proposition 2.

See [27] (p. 2141). □

Proposition 3.

The larger the clustering coefficient c, the more closely sensor nodes are connected.

Proof of Proposition 3.

See [28] (p. 50). □

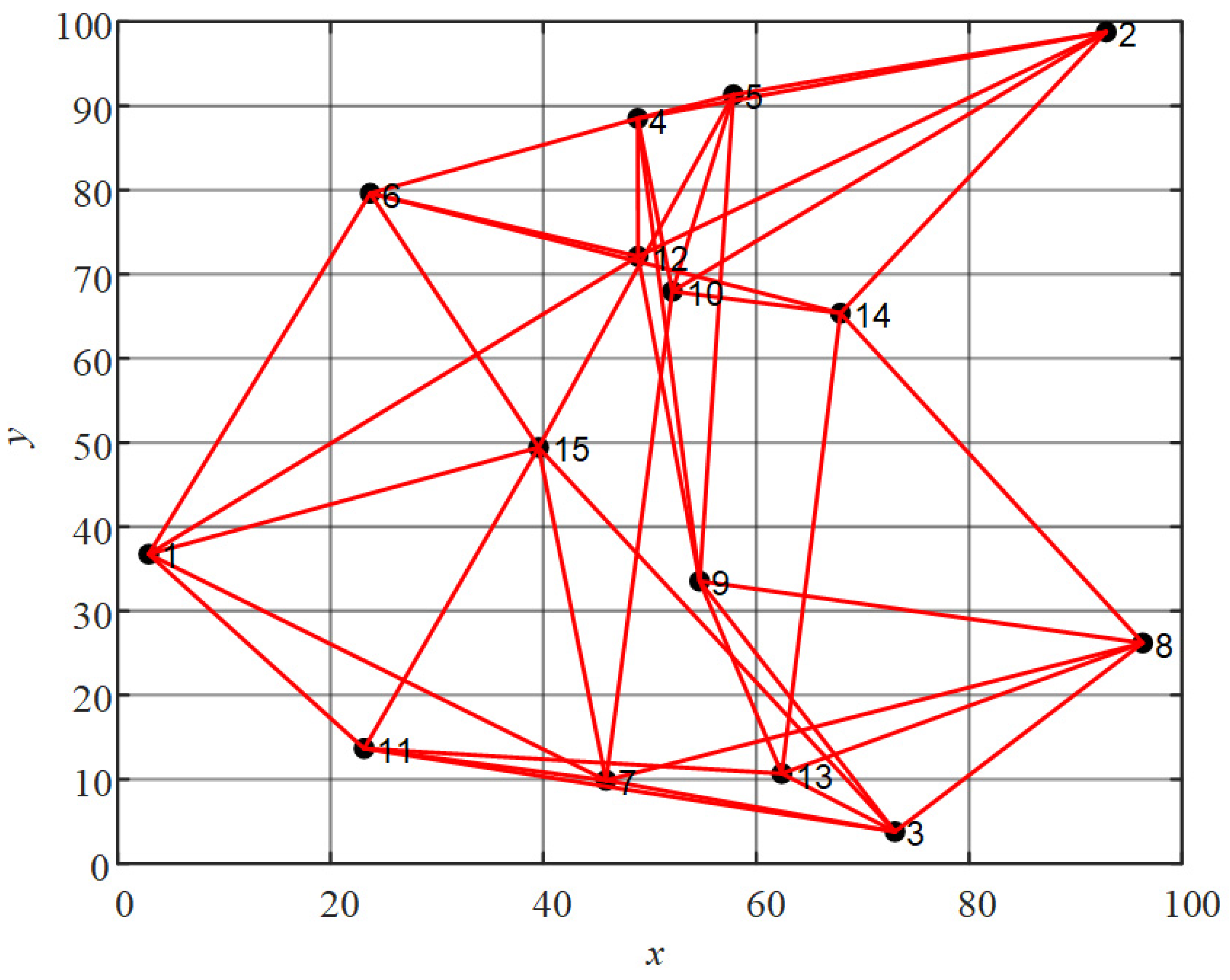
3.2. Network Topology Optimization Method

Combining with Propositions 1–3, we can properly delete and add communication links according to some rules to solve problem (P2).

The rules for deleting communication links are:

For any node i, i∈{1, 2, …, I},

Step 1: To determine the initial deleting communication link at node i:

(1-1) The links set ${ℰ}_{i,1}$ with local maximum sum of node degree d, is found, and

$${ℰ}_{i,1}=\left\{\left(i,j\right)|\underset{j\in {\mathcal{N}}_i}{\max }\left(d_i+d_j\right)\right\}$$

(3)

(1-2) The links set ${ℰ}_{i,2}$ with the average local maximum variation of average path length l is determined, and

$${ℰ}_{i,2}=\left\{\left(i,j\right)|\underset{(i,j)\in {ℰ}_{i,1}}{\max }\frac{\Delta l_i+{\displaystyle \sum _{k\in {\mathcal{N}}_i}\Delta l_k}}{d_i+1}\right\}$$

(4)

where $\Delta l_i$ denotes the variation of l at node i before and after deleting link (i, j).

(1-3) The links set ${ℰ}_{i,3}$ with the average local minimum variation of clustering coefficient c is determined, and

$${ℰ}_{i,3}=\left\{\left(i,j\right)|\underset{(i,j)\in {ℰ}_{i,2}}{\min }\frac{\Delta c_i+{\displaystyle \sum _{k\in {\mathcal{N}}_i}\Delta c_k}}{d_i+1}\right\}$$

(5)

where $\Delta c_i$ denotes the variation of c at node i before and after deleting link (i, j).

(1-4) The first link belonging to set ${ℰ}_{i,3}$ is taken as the initial deleting communication link at node i, and

$${{\mathrm{del}}^{\prime }}_i=\left\{\left(i,j\right),d_i+d_j,\frac{\Delta l_i+{\displaystyle \sum _{j\in {\mathcal{N}}_i}\Delta l_j}}{d_i+1},\frac{\Delta c_i+{\displaystyle \sum _{j\in {\mathcal{N}}_i}\Delta c_j}}{d_i+1}\right\}$$

(6)

Step 2: To determine the final deleting communication link at node i:

(2-1) The initial deleting communication link at node i is exchanged with its neighboring nodes, and ${{\mathrm{del}}^{\prime }}_{{}_{{\mathcal{N}}_i}}\triangleq {\left\{{{\mathrm{del}}^{\prime }}_j\right\}}_{j\in {\mathcal{N}}_i}$.

(2-2) The same operations in step 1 are used to determine the final deleting communication link at node i, and

$${\mathrm{del}}_i=\left\{\left(a,b\right),d_a+d_b,\frac{\Delta l_a+{\displaystyle \sum _{c\in {\mathcal{N}}_a}\Delta l_c}}{d_a+1},\frac{\Delta c_a+{\displaystyle \sum _{c\in {\mathcal{N}}_a}\Delta c_c}}{d_a+1}\right\}$$

(7)

The rules for adding communication links are:

For any node p, p∈{1, 2, …, I},

Step 1′: To determine the initial adding communication link at node p:

(1′-1) The links set ${ℒ}_{p,1}$ with local minimum sum of node degree d within the communication range of node p, $D_p$, is found, and

$${ℒ}_{p,1}=\left\{\left(p,s\right)|\underset{s:\left(s\notin {\mathcal{N}}_i\right)\cap E\left(p,s\right)\le D_p}{\min }\left(d_p+d_s\right)\right\}$$

(8)

(1′-2) The links set ${ℒ}_{p,2}$ with the average local maximum variation of average path length l is determined, and

$${ℒ}_{p,2}=\left\{\left(p,s\right)|\underset{(p,s)\in {ℒ}_{p,1}}{\max }\frac{\Delta l_p+{\displaystyle \sum _{q\in {\mathcal{N}}_p}\Delta l_q+\Delta l_s}}{d_p+2}\right\}$$

(9)

where $\Delta l_p$ denotes the variation of l at node p before and after adding link (p, s).

(1′-3) The links set ${ℒ}_{p,3}$ with the average local minimum variation of clustering coefficient c, is determined, and

$${ℒ}_{p,3}=\left\{\left(p,s\right)|\underset{(p,s)\in {ℒ}_{p,2}}{\min }\frac{\Delta c_p+{\displaystyle \sum _{q\in {\mathcal{N}}_p}\Delta c_q+\Delta c_s}}{d_p+2}\right\}$$

(10)

where $\Delta c_p$ denotes the variation of c at node p before and after adding link (p, s).

(1′-4) The first link belonging to ${ℒ}_{p,3}$ is taken as the initial adding communication link at node p, and

$${{\mathrm{add}}^{\prime }}_p=\left\{\left(p,s\right),d_p+d_s,\frac{\Delta l_p+{\displaystyle \sum _{q\in {\mathcal{N}}_p}\Delta l_q+\Delta l_s}}{d_p+2},\frac{\Delta c_p+{\displaystyle \sum _{q\in {\mathcal{N}}_p}\Delta c_q+\Delta c_s}}{d_p+2}\right\}$$

(11)

Step 2′: To determine the final adding communication link at node p:

(2′-1) The initial adding communication link at node p is exchanged with its neighboring nodes, and ${{\mathrm{add}}^{\prime }}_{{}_{{\mathcal{N}}_p}}\triangleq {\left\{{{\mathrm{add}}^{\prime }}_q\right\}}_{q\in {\mathcal{N}}_p}$.

(2′-2) The same operations in step 1′ are used to determine the final adding communication link at node p, and

$$ad{d}_p=\left\{\left(c,d\right),d_c+d_d,\frac{\Delta l_c+{\displaystyle \sum _{b\in {\mathcal{N}}_c}\Delta l_b+\Delta l_d}}{d_c+2},\frac{\Delta c_c+{\displaystyle \sum _{b\in {\mathcal{N}}_c}\Delta c_b+\Delta c_d}}{d_c+2}\right\}$$

(12)

According to the rules for deleting and communication links described above, we propose a network topology optimization method summarized in Algorithm 1 as follows, in which the communication range of each node is assumed to be the same.

Algorithm 1: A network topology optimization method according to local nodes’ topology parameter information.

Input: original network topology $\mathcal{G}$, the number of nodes I, the number of communication links K, the communication range of network D.  1: initialize the number of optimization adjustment, b = 0.  2: while $d_{\max }-d_{\min }>1$ && $b\le K$ do  3: select node i from set $\mathcal{V}$ randomly  4: determine ${\mathrm{del}}_i$ using operations (3)–(7)  5: delete link (a, b) determined in operation (7)  6: update $d_a$ and $d_b$  7: select node p from set $\mathcal{V}$ randomly  8: determine $ad{d}_p$ using operations (8)–(12)  9: add link (c, d) determined in operation (12)  10: update $d_c$ and $d_d$  11: b = b + 1  12: end while Output: optimized network topology ${\mathcal{G}}^{\prime }$.

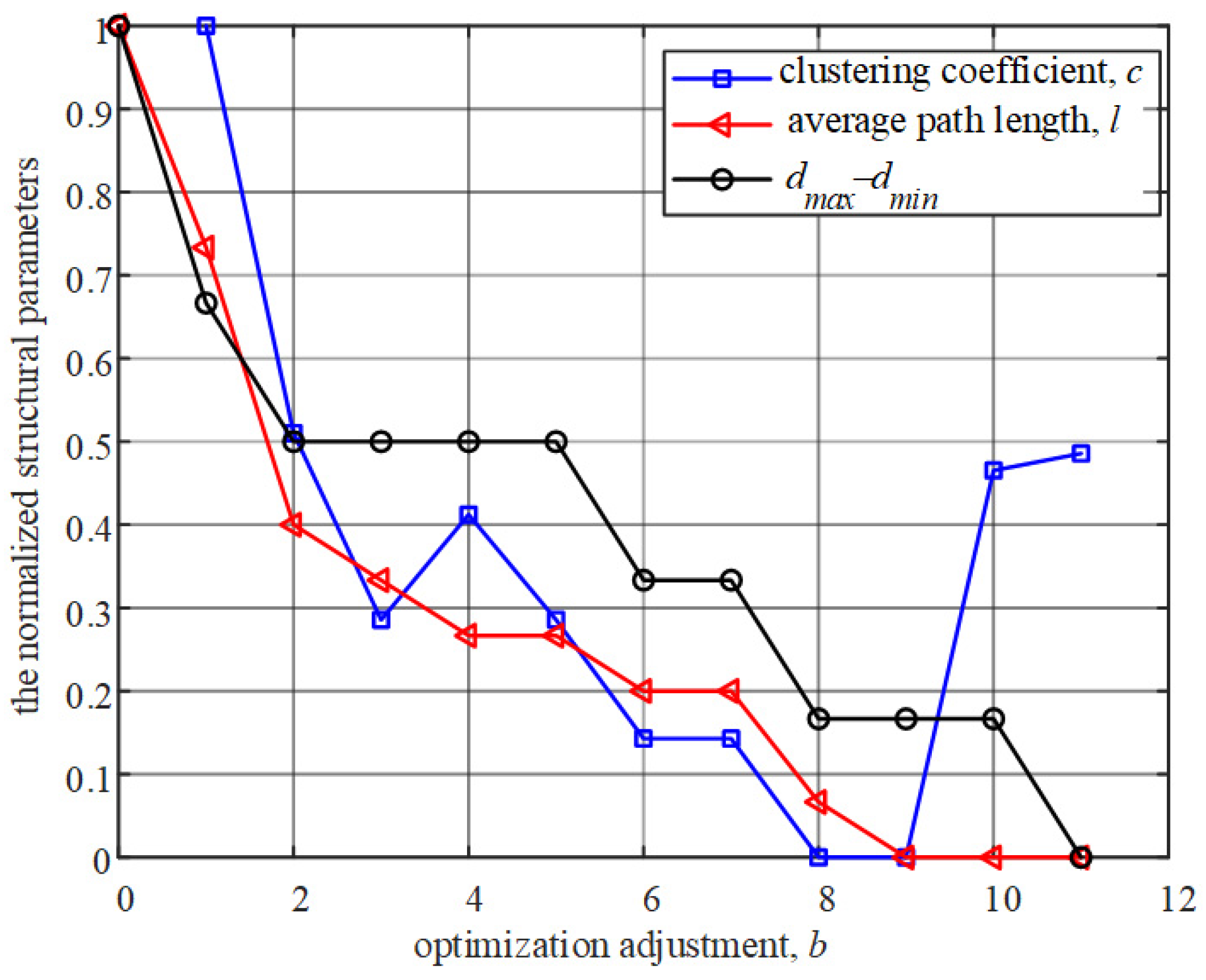
3.3. Performance Analysis

In Algorithm 1, the network topology is optimized according to nodes’ local structural parameters information. Hence, compared with other network topology optimization methods [21,29] based on global topology information, the communication overhead of the proposed method is smaller. Meanwhile, due to the structural parameters information, the computational complexity of the proposed method is lower than other heuristic search methods [21,29,30]. The concrete analysis is as follows.

In Algorithm 1, the maximum number of optimization adjustments is the communication links K. In the b-th adjustment, deleting links or adding links are determined by the rules described above. Taking deleting links as an example, where node i receives initial deleting links information from its neighboring nodes, i.e., ${{\mathrm{del}}^{\prime }}_{{}_{{\mathcal{N}}_i}}\triangleq {\left\{{{\mathrm{del}}^{\prime }}_j\right\}}_{j\in {\mathcal{N}}_i}$. Therefore, the communication overhead is ${\displaystyle \sum _{b=1}^K\left(|{{\mathrm{del}}^{\prime }}_{{}_{{\mathcal{N}}_i}}|+|{{\mathrm{add}}^{\prime }}_{{}_{{\mathcal{N}}_p}}|\right)}$, where node i (or node p) is the selected node in the b-th adjustment.

In the b-th adjustment, taking deleting links as an example, where node i should calculate its initial deleting links information, and combine with the initial deleting links information of neighboring nodes to determine the communication link to be deleted. Hence, the computational complexity for determining the communication link to be deleted at node i is $O\left(I^2\right)$. Therefore, the computational complexity of the proposed method is $O\left(K{I}^2\right)$.

The communication overhead and computational complexity of the proposed method in this paper and the WWKJ method proposed in [29] are given in

Table 1. The comparison of the communication overhead and computational complexity.

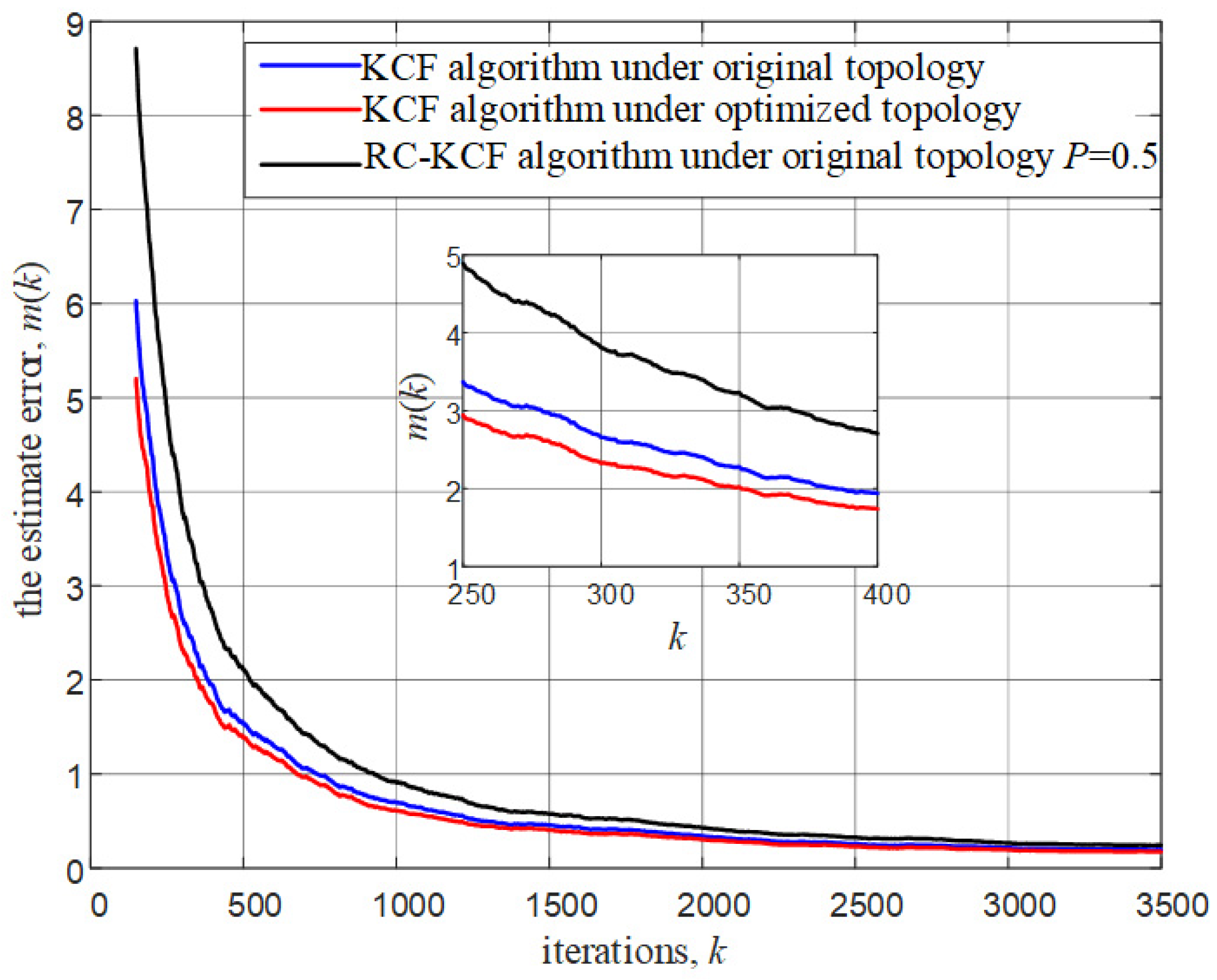
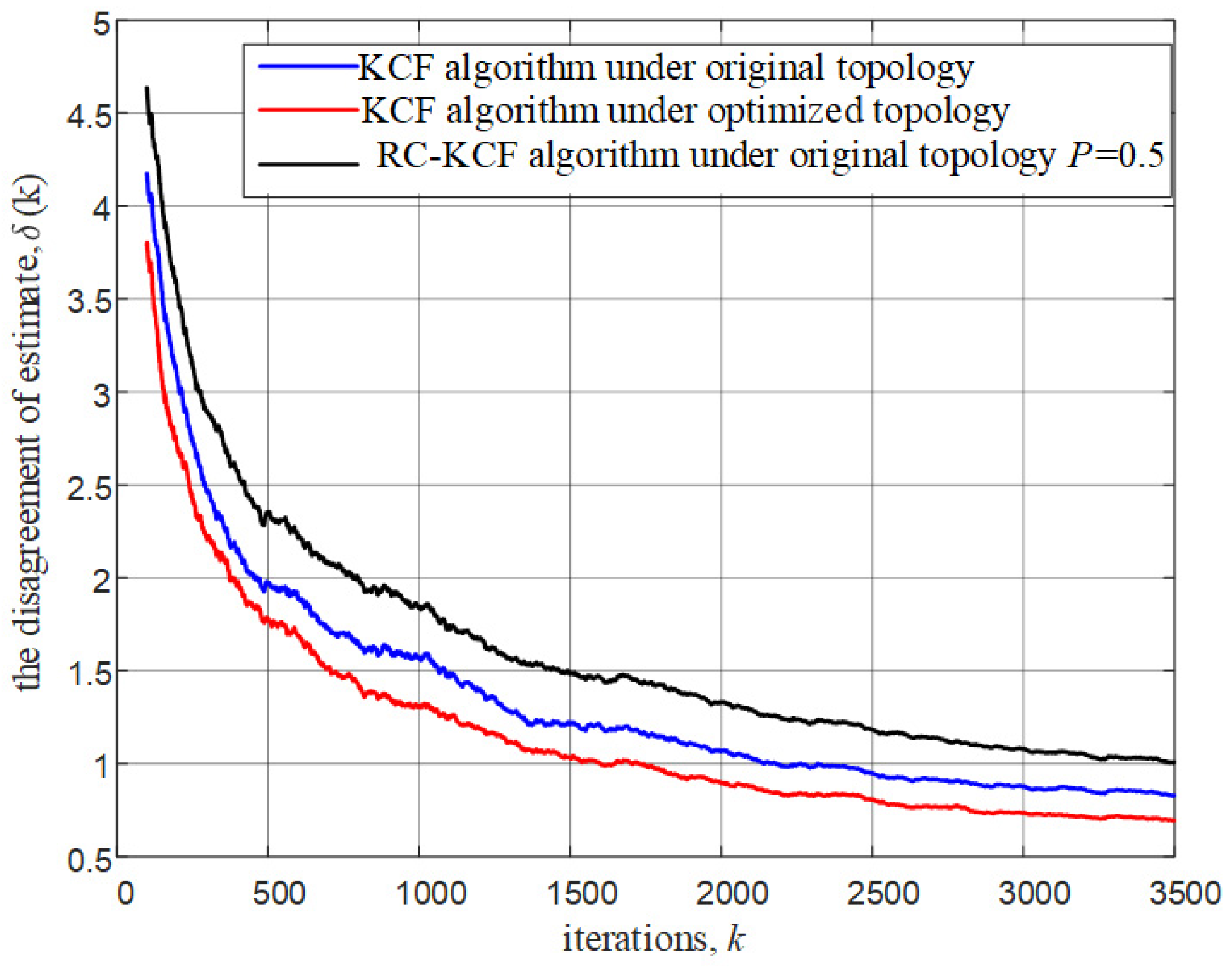
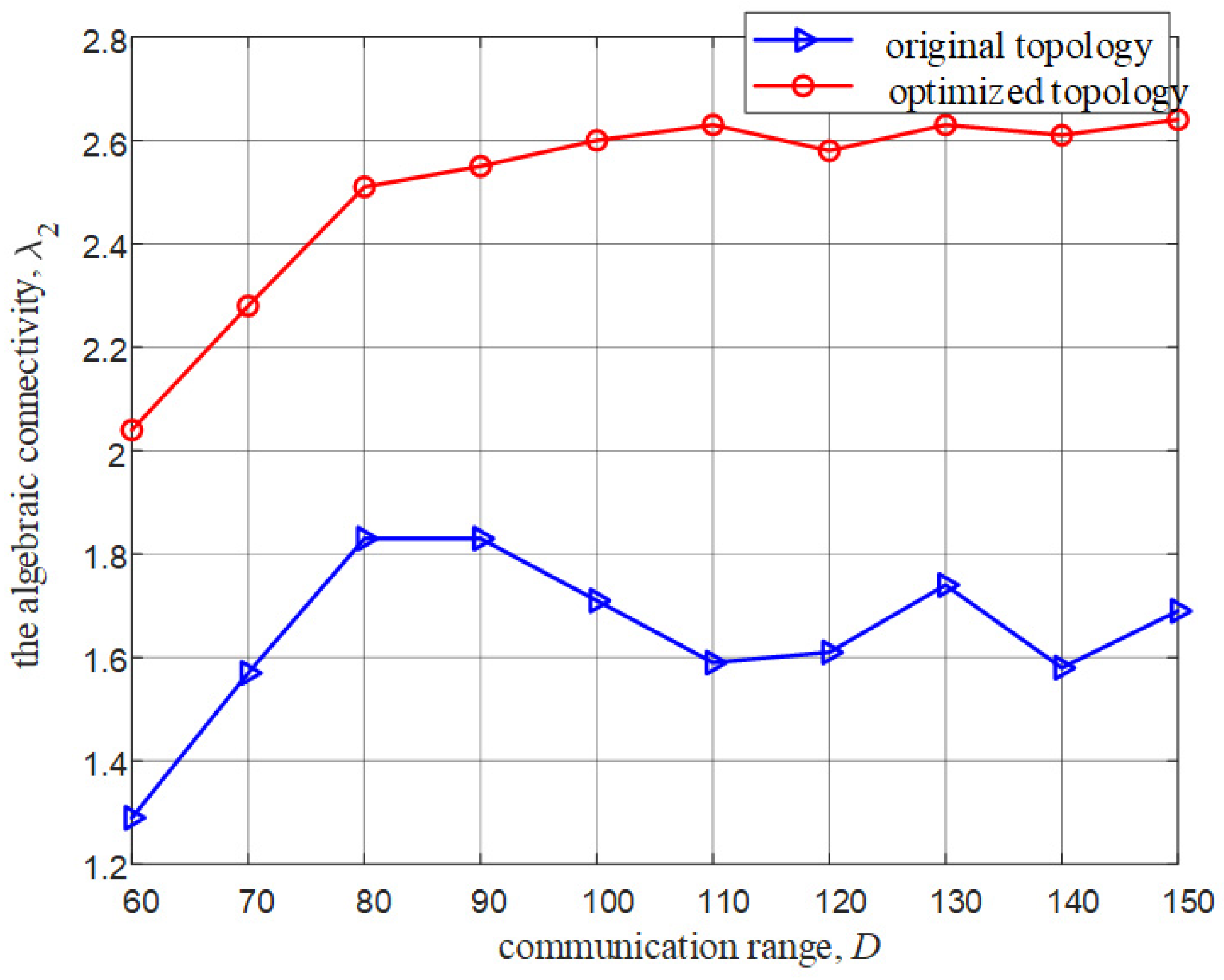
Methods	Communication Overhead	Computational Complexity
The proposed method	${\displaystyle \sum _{b=1}^K\left(|{{\mathrm{del}}^{\prime }}_{{}_{{\mathcal{N}}_i}}|+|{{\mathrm{add}}^{\prime }}_{{}_{{\mathcal{N}}_p}}|\right)}$	$O\left(K{I}^2\right)$
The WWKJ method [29]	$I^2{\displaystyle \sum _{b=1}^K\left(|{{\mathrm{del}}^{\prime }}_i|+|{{\mathrm{add}}^{\prime }}_{{}_p}|\right)}$	$O\left(T_m{I}^2\right)$

. The WWKJ method optimizes the network topology based on the global network information, and performs an iterative search for feasible solutions, where $T_m$ is the maximum number of iterations for each simulation m.

4. Performance Evaluation and Discussion

In this section, the performance of the proposed network topology optimization method is evaluated.

This section considers a WSN $\mathcal{G}=\left(\mathcal{V},ℰ\right)$ covering a region of $100\mathrm{m}\times 100\mathrm{m}$, I = 15, K = 40, and D = 60 m, as shown in Figure 1, where the algebraic connectivity ${\lambda }_2\left(\mathcal{G}\right)=0.78$.

Figure 2 shows the corresponding adjustments of the original network $\mathcal{G}$, where black lines and blue lines represent the deleted links and the added links, respectively. The normalized topology structural parameters as the corresponding adjustments of $\mathcal{G}$ are illustrated in Figure 3. From Figure 3, we observe that the degree distribution of nodes (d) becomes more uniform, and the average path length decreases (l), while clustering coefficient (c) decreases. Figure 4 shows the optimized topology ${\mathcal{G}}^{\prime }$, where ${\lambda }_2\left({\mathcal{G}}^{\prime }\right)=1.96$.

From Figure 1, Figure 2 and Figure 3, the proposed network topology optimization method is effective in that the algebraic connectivity of network topology is improved. Furthermore, the performance improved by d and l is larger than the performance decreased by c because of the locality of clustering coefficient (c).

In the tracking problem of a dynamic interested object, the state equation of the object is

$$x\left(k+1\right)=Ax\left(k\right)+Bw\left(k\right)$$

with parameters

$$A=I_3+\gamma A_0+\frac{{\gamma }^2}{2}{A}_0{}^2+\frac{{\gamma }^3}{6}{A}_0{}^3$$

where $A_0=\left[\begin{array}{ccc}0& 0& -1\\ 0& -1& 0\\ 1& 0& 0\end{array}\right]$, $\gamma ={10}^{-3}$, and $B=0.005{{\rm I}}_3$.

The initial position of the object is arbitrary. For example, $x\left(0\right)={\left(5,15,10\right)}^{\mathrm{T}}$. The initial covariance of the prediction error $P\left(0\right)=10I_3$ is adopted according to the parameters in [5]. The measurement equation of the object is

$$z_i\left(k\right)=H_{i}x\left(k\right)+v_i\left(k\right)$$

where $H_i$ has three forms, namely $H_i=\left[\begin{array}{ccc}1& 0& 0\end{array}\right]$, $H_i=\left[\begin{array}{ccc}0& 1& 0\end{array}\right]$ or $H_i=\left[\begin{array}{ccc}0& 0& 1\end{array}\right]$, $R_i=400\sqrt{i}$ at node i, and i∈{1, 2, …, I}.

To further evaluate the performance of the proposed network topology optimization method, three performance metrics, the total communication overhead $J_{\mathrm{total},\mathrm{overhead}}\left(k\right)$, the mean square estimate error m(k), and the mean square estimate disagreement $\delta \left(k\right)$ in the network are adopted, where

$$\begin{array}{l}m\left(k\right)={\displaystyle \sum _{i=1}^I{\Vert {\widehat{x}}_i\left(k\right)-x\left(k\right)\Vert }_2^2}\\ \delta \left(k\right)={{\displaystyle \sum _{i=1}^I\Vert {\widehat{x}}_i\left(k\right)-\frac{1}{N}{\displaystyle \sum _{j=1}^I{\widehat{x}}_j\left(k\right)}\Vert }}_2\end{array}$$

The performance of three cases, (1) the traditional KCF algorithm [5] under original topology $\mathcal{G}$, (2) the traditional KCF algorithm [5] under optimized topology ${\mathcal{G}}^{\prime }$, (3) the RC-KCF algorithm [14] under original topology $\mathcal{G}$, is evaluated, and P denotes the probability that each node receives messages from its neighboring nodes.

Figure 5 shows the total communication overhead at time k. From Figure 5, we observe that the number of iterations for three cases is 2425, 1556, and 3010, respectively, which means that the proposed method in this paper improves the convergence rate of the KCF algorithm effectively.

Figure 6 and Figure 7 show the mean square estimate error at time k and the mean square estimate disagreement at time k, respectively. From Figure 6 and Figure 7, one finds that the estimate converges to a stable value if

$$m\left(k\right)\le 0.05{\Vert x\left(k\right)\Vert }_2^2$$

and

$$\delta \left(k\right)\le 0.2\max \left(\delta \left(k\right)\right)$$

Therefore, from Figure 5, Figure 6 and Figure 7, we conclude that the proposed network topology optimization method achieves a good trade-off between the estimation error and communication overhead.

We also evaluated the performance of the proposed network topology optimization method using 20 WSNs with I = 15, K = 40, and D = 60 m, and the results are given in

Table 2. Comparison of the number of iterations, and P = 0.5.

$\mathbf{KCF}\mathbf{Algorithm}\mathbf{under}\mathcal{G}$	$\mathbf{KCF}\mathbf{Algorithm}\mathbf{under}{\mathcal{G}}^{\prime }$	$\mathbf{RC}-\mathbf{KCF}\mathbf{Algorithm}\mathbf{under}\mathcal{G}$ (P = 0.5)
1722	1427	2779
2818	2194	4020
1669	1467	2709
1884	1557	3112
1637	1360	2773
2119	1914	3539
2418	1601	3303
2647	1861	3671
2336	2099	3986
1823	1596	2906
1857	1607	3211
1826	1601	3044
1750	1183	2492
1974	1301	3129
1819	1373	2655
1620	1246	2497
1915	1279	2828
2156	1799	3238
2345	1583	3240
1527	1375	2636

. In these simulations, the number of iterations of the KCF algorithm under the optimized network topologies is reduced by 10–40% compared with that of the original network topologies. In the meantime, the proposed network topology optimization method achieves a trade-off between the estimate error and the communication overhead compared to other methods by probabilistic sending.

Figure 8 shows the impact of communication range over networks on the algebraic connectivity ${\lambda }_2$, the value given in the figure is averaged on 20 simulations. From Figure 8, we observe that the value of ${\lambda }_2$ is increased as the value of D increases. The reason is that sensor nodes can receive deleting or adding links information from more different nodes within a larger communication range, which is beneficial to the network topology optimization. As D = 110 m, sensor nodes receive enough information, and then the algebraic connectivity tends to be stable.

5. Conclusions

In this paper, we proposed a network topology optimization method. Firstly, we define the communication overhead of the KCF algorithm, which can be transformed into a network topology optimization problem. Secondly, the network topology optimization method is introduced, where the network topology is optimized by properly deleting and adding communication links, as well as considering the constraint on the communication range of two nodes. Simulation results show that the proposed optimization method can improve the algebraic connectivity of network topology and increase the convergence rate of the KCF algorithm under optimized network topologies. Moreover, the proposed network topology optimization method achieves a good trade-off between the estimate error and the communication overhead.

In the future, the network topology optimization method can be further combined with more structural parameters. Meanwhile, the network topology optimization method can also be considered to improve the stability of the topology.