Prognostic Validity of Statistical Prediction Methods Used for Talent Identification in Youth Tennis Players Based on Motor Abilities
Abstract
:1. Introduction
2. Materials and Methods
2.1. General Study Design
2.2. Participants
2.3. Tennis Success
2.4. Anthropometric Characteristics and Motor Abilities at U9
2.4.1. 20 m Sprint (SP)
2.4.2. Sideward Jumping (SJ)
2.4.3. Balancing Backwards (BB)
2.4.4. Standing Bend Forward (SBF)
2.4.5. Push-Ups (PU)
2.4.6. Sit-Ups (SU)
2.4.7. Standing Long Jump (SLJ)
2.4.8. Ball Throw (BT)
2.4.9. Six min Endurance Run (ER)
2.5. Statistical Analyses
2.5.1. Prediction Methods
2.5.2. Tennis-Specific Recommendation Score
2.5.3. Binary Logistic Regression Analysis
2.5.4. Discriminant Analysis
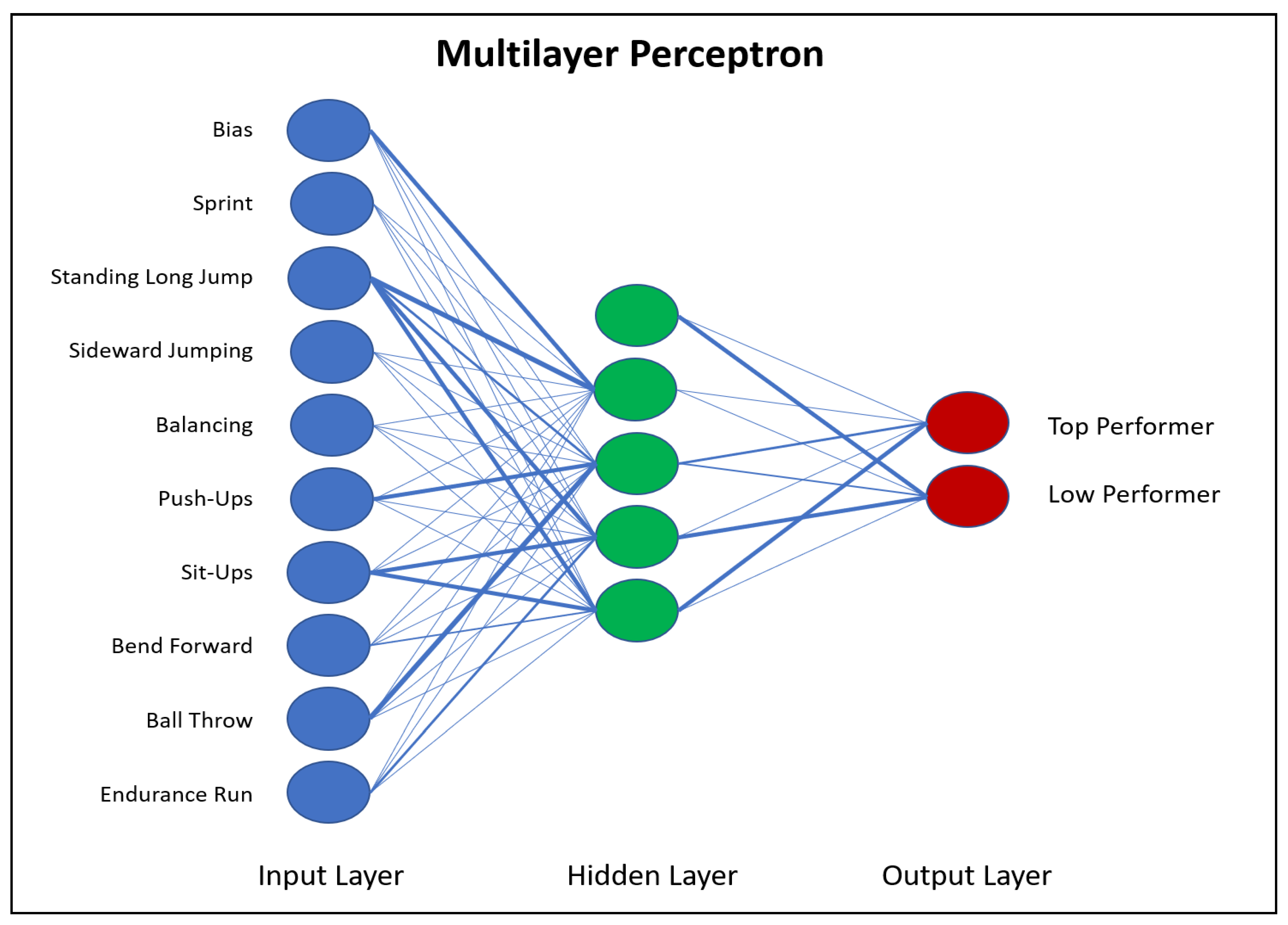
2.5.5. Neural Network Analysis
2.5.6. Prognostic Validity of the Analyses
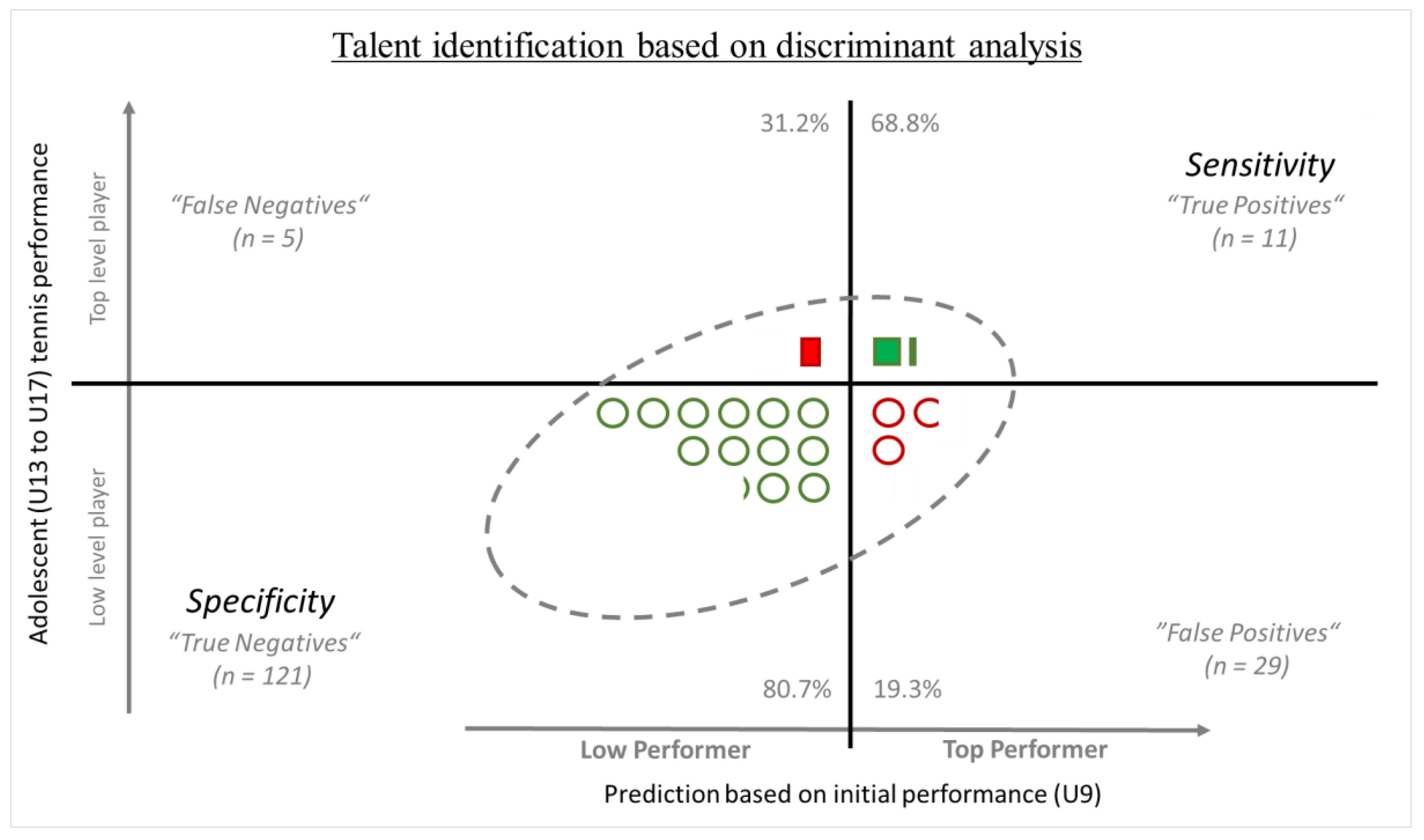
2.5.7. Classification of Individual Tennis Players
3. Results
3.1. Test Performance
3.2. Test Quality Parameters of the Prediction Methods
3.2.1. Tennis Recommendation Score
3.2.2. Logistic Regression
3.2.3. Discriminant Analysis
3.2.4. Neural Network Analysis
3.3. Prognostic Validity of the Prediction Methods
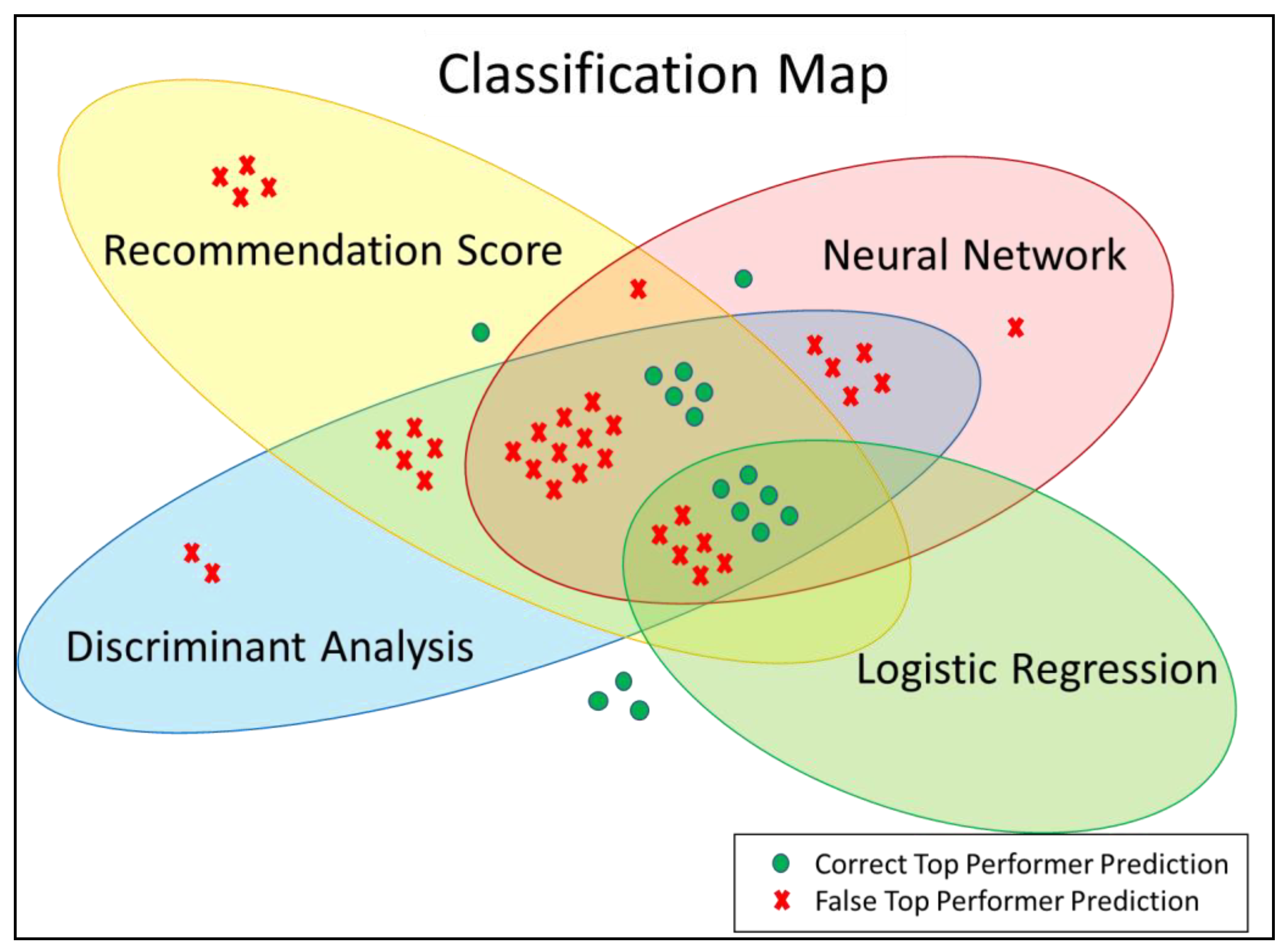
3.4. Classification of Individual Tennis Players
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reilly, T.; Williams, A.M.; Nevill, A.; Franks, A. A multidisciplinary approach to talent identification in soccer. J. Sports Sci. 2000, 18, 695–702. [Google Scholar] [CrossRef] [PubMed]
- De Bosscher, V.; de Knop, P.; van Bottenburg, M.; Shibli, S. A Conceptual Framework for Analysing Sports Policy Factors Leading to International Sporting Success. Eur. Sport Manag. Q. 2006, 6, 185–215. [Google Scholar] [CrossRef]
- De Bosscher, V.; de Knop, P.; van Bottenburg, M. Sports Policy Factors Leading to International Sporting Success; VUB Press: Brussels, Belgium, 2007. [Google Scholar]
- Baker, J.; Wilson, S.; Johnston, K.; Dehghansai, N.; Koenigsberg, A.; de Vegt, S.; Wattie, N. Talent Research in Sport 1990-2018: A Scoping Review. Front. Psychol. 2020, 11, 607710. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, M.D.; Colley, R.C.; Doyon, C.Y.; Wong, S.L.; Tomkinson, G.R.; Lang, J.J. Normative-referenced percentile values for physical fitness among Canadians. Health Rep. 2019, 30, 14–22. [Google Scholar] [CrossRef]
- Rowland, T. Counselling the young athlete: Where do we draw the line? Pediatric Exerc. Sci. 1997, 9, 197–201. [Google Scholar] [CrossRef]
- Wiersma, L.D. Risks and benefits of youth sport specialization: Perspectives and recommendations. Pediatric Exerc. Sci. 2000, 12, 13–22. [Google Scholar] [CrossRef]
- Faber, I.R.; Bustin, P.M.J.; Oosterveld, F.G.J.; Elferink-Gemser, M.T.; Nijhuis-van der Sanden, M.W. Assessing personal talent determinants in young racquet sport players: A systematic review. J. Sports Sci. 2016, 34, 395–410. [Google Scholar] [CrossRef]
- Fuchslocher, J.; Romann, M.; Rüdisüli, L.R.; Birrer, D.; Hollenstein, C. Das Talentselektionsinstrument PISTE: Wie die Schweiz Nachwuchsathleten auswählt. Leistungssport 2011, 41, 22–27. [Google Scholar]
- Golle, K.; Muehlbauer, T.; Wick, D.; Granacher, U. Physical Fitness Percentiles of German Children Aged 9–12 Years: Findings from a Longitudinal Study. PLoS ONE 2015, 10, e0142393. [Google Scholar] [CrossRef]
- Pion, J. The Flemish Sports Compass: From Sports Orientation to Elite Performance Prediction; University Press: Ghent, Belgium, 2015. [Google Scholar]
- Stemper, T.; Bachmann, C.; Diehlmann, K.; Kemper, B. Das Düsseldorfer Modell der Bewegungs-, Sport- und Talentförderung (DüMo). In Talentdiagnose und Talentprognose: 2. BISp-Symposium: Theorie trifft Praxis; Bundesinstitut für Sportwissenschaft, Ed.; Strauss: Kölln, Germany, 2009; pp. 139–142. [Google Scholar]
- Fernandez-Fernandez, J.; Sanz-Rivas, D.; Mendez-Villanueva, A. A review of the activity profile and physiological demands of tennis match play. Strength Cond. J. 2009, 31, 15–26. [Google Scholar] [CrossRef]
- Doherty, S.A.; Martinent, G.; Martindale, A.; Faber, I.R. Determinants for table tennis performance in elite Scottish youth players using a multidimensional approach: A pilot study. High Abil. Stud. 2018, 29, 241–254. [Google Scholar] [CrossRef]
- Balyi, I.; Hamilton, A. Long Term Athlete Development: Trainability in Childhood and Adolescence. Windows of Opportunity. Optimal Trainability; National Coaching Institute British Columbia & Advanced Training and Performance Ltd.: Victoria, BC, Canada, 2004. [Google Scholar]
- Knudsen, E.I. Sensitive periods in the development of the brain and behavior. J. Cogn. Neurosci. 2004, 16, 1412–1425. [Google Scholar] [CrossRef]
- Watanabe, D.; Savion-Lemieux, T.; Penhune, V.B. The effect of early musical training on adult motor performance: Evidemce for a sensitive perios in motor learning. Exp. Brain Res. 2007, 332–340. [Google Scholar] [CrossRef] [PubMed]
- Anderson, D.I.; Magill, R.A.; Thouvarecq, R. Critical periods, sensitive periods, and readiness for motor skill learning. In Skill Acquisition in Sport: Research, Theory, and Practice, 2nd ed.; Hodges, N., Williams, A.M., Eds.; Routledge: London, UK; New York, NY, USA, 2012; pp. 211–228. ISBN 9780203133712. [Google Scholar]
- De Bosscher, V.; Bingham, J.; Shibli, S.; van Bottenburg, M.; de Knop, P. The Global Sporting Arms Race. An International Comparative Study on Sports Policy Factors Leading to International Sporting Success; Meyer & Meyer: Aachen, Germany, 2008. [Google Scholar]
- Bloyce, D.; Smith, A. Sport, Policy and Development: An Introduction; Routledge: London, UK; New York, NY, USA, 2010; ISBN 041540407X. [Google Scholar]
- Houlihan, B.; Green, M. Comparative Elite Sport Development: Systems, Structures and Public Policy; Butterworth-Heineman: London, UK, 2008. [Google Scholar]
- Pion, J.; Hohmann, A.; Liu, T.; Lenoir, M.; Segers, V. Predictive models reduce talent development costs in female gymnastics. J. Sports Sci. 2016, 35, 806–811. [Google Scholar] [CrossRef] [PubMed]
- Roetert, E.P.; Garrett, G.E.; Brown, S.W.; Camaione, D.N. Performance Profiles of Nationally Ranked Junior Tennis Players. J. Appl. Sport Sci. Res. 1992, 6, 225–231. [Google Scholar] [CrossRef]
- Kovacs, M. Tennis physiology: Training the competitive athlete. Sports Med. 2007, 189–198. [Google Scholar] [CrossRef] [PubMed]
- Filipcic, A.; Filipcic, T. The influence of tennis motor abilities and anthropometric measures on the competition successfulness of 11 and 12 year-old female tennis players. Acta Univ. Palacki. Olomucensis. Gymnica 2005, 35, 35–41. [Google Scholar]
- Hohmann, A.; Siener, M.; He, R. Prognostic validity of talent orientation in soccer. Ger. J. Exerc. Sport Res. 2018, 48, 478–488. [Google Scholar] [CrossRef]
- Baker, J.; Schorer, J.; Wattie, N. Compromising Talent: Issues in Identifying and Selecting Talent in Sport. Quest 2018, 70, 48–63. [Google Scholar] [CrossRef]
- Höner, O.; Votteler, A. Prognostic relevance of motor talent predictors in early adolescence: A group- and individual-based evaluation considering different levels of achievement in youth football. J. Sports Sci. 2016, 34, 2269–2278. [Google Scholar] [CrossRef]
- Höner, O.; Leyhr, D.; Kelava, A. The influence of speed abilities and technical skills in early adolescence on adult success in soccer: A long-term prospective analysis using ANOVA and SEM approaches. PLoS ONE 2017, 12, e0182211. [Google Scholar] [CrossRef] [Green Version]
- Pion, J. Sustainable Investment in Sports Talent: The Path to the Podium Through the School and the Sports Club; HAN University of Applied Sciences Press: Arnhem, Germany, 2017. [Google Scholar]
- Zuber, C.; Zibung, M.; Conzelmann, A. Holistic patterns as an instrument for predicting the performance of promising young soccer players—A 3-years longitudinal study. Front. Psychol. 2016, 7, 1088. [Google Scholar] [CrossRef] [Green Version]
- Urbano, D.; Restivo, M.T.; Barbosa, M.R.; Fernandes, Â.; Abreu, P.; Chousal, M.d.F.; Coelho, T. Handgrip Strength Time Profile and Frailty: An Exploratory Study. Appl. Sci. 2021, 11, 5134. [Google Scholar] [CrossRef]
- Cairney, J.; Streiner, D.L. Using relative improvement over chance (RIOC) to examine agreement between tests: Three case examples using studies of developmental coordination disorder (DCD) in children. Res. Dev. Disabil. 2011, 32, 87–92. [Google Scholar] [CrossRef]
- Farrington, D.P.; Loeber, R. Relative improvement over chance (RIOC) and phi as measures of predictive efficiency and strength of association in 22 tables. J. Quant. Criminol. 1989, 5, 201–213. [Google Scholar] [CrossRef]
- Deutscher Tennis Bund. Jugendrangliste: Deutsche Ranglisten der Juniorinnen und Junioren. Available online: www.dtb-tennis.de/Tennis-National/Ranglisten/Jugend (accessed on 31 December 2020).
- Hohmann, A.; Seidel, I. Scientific aspects of talent development. Int. J. Phys. Educ. 2003, 40, 9–20. [Google Scholar]
- Bös, K.; Schlenker, L.; Albrecht, C.; Büsüch, D.; Lämmle, L.; Müller, H.; Oberger, J.; Seidel, I.; Tittlbach, S.; Woll, A. Deutscher Motorik-Test 6-18 (DMT 6-18); Feldhaus: Hamburg, Germany, 2009. [Google Scholar]
- Utesch, T.; Strauß, B.; Tietjens, M.; Büsch, D.; Ghanbari, M.-C.; Seidel, I. Die Überprüfung der Konstruktvalidität des Deutschen Motorik-Tests 6-18 für 9- bis 10-Jährige. Z. Für Sportpsychol. 2015, 22, 77–90. [Google Scholar] [CrossRef]
- Klein, M.; Fröhlich, M.; Emrich, E. Zur Testgenauigkeit ausgewählter Items des Deutschen Motorik-Tests DMT 6-18. Leipz. Sportwiss. Beiträge 2012, 53, 23–45. [Google Scholar]
- Bardid, F.; Utesch, T.; Lenoir, M. Investigating the construct of motor competence in middle childhood using the BOT-2 Short Form: An item response theory perspective. Scand. J. Med. Sci. Sports 2019, 29, 1980–1987. [Google Scholar] [CrossRef]
- Meylan, C.; Cronin, J.; Oliver, J.; Hughes, M. Reviews: Talent identification in soccer: The role of maturity status on physical. physiological and technical characteristics. Int. J. Sports Sci. Coach. 2010, 5, 571–592. [Google Scholar] [CrossRef]
- Carling, C.; Collins, D. Comment on “Football-Specific fitness testing: Adding value or confirming the evidence?”. J. Sports Sci. 2014, 32, 1206–1208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hohmann, A.; Fehr, U.; Siener, M.; Hochstein, S. Validity of early talent screening and talent orientation. In Sport Science in a Metropolitan Area; Platen, P., Ferrauti, A., Grimminger-Seidensticker, E., Jaitner, T., Eds.; University Press: Bochum, Germany, 2017; p. 590. [Google Scholar]
- Willimczik, K. Determinanten der sportmotorischen Leistungsfähigkeit im Kindesalter. In Kinder im Leistungssport.; Howald, H., Hahn, E., Eds.; Birkhäuser: Stuttgart, Germany, 1982; pp. 141–153. [Google Scholar]
- Siener, M.; Hohmann, A. Talent orientation: The impact of motor abilities on future success in table tennis. Ger. J. Exerc. Sport Res. 2019, 49, 232–243. [Google Scholar] [CrossRef]
- Kolias, P.; Stavropoulos, N.; Papadopoulou, A.; Kostakidis, T. Evaluating basketball player’s rotation line-ups performance via statistical markov chain modelling. Int. J. Sports Sci. Coach. 2021, 174795412110090. [Google Scholar] [CrossRef]
- Khasanshin, I. Application of an Artificial Neural Network to Automate the Measurement of Kinematic Characteristics of Punches in Boxing. Appl. Sci. 2021, 11, 1223. [Google Scholar] [CrossRef]
- Silva, A.J.; Costa, A.M.; Oliveira, P.M.; Reis, V.M.; Saavedra, J.; Perl, J.; Rouboa, A.; Marinho, D.A. The use of neural network technology to model swimming performance. J. Sports Sci. Med. 2007, 6, 117–125. [Google Scholar]
- Barron, D.; Ball, G.; Robins, M.; Sunderland, C. Artificial neural networks and player recruitment in professional soccer. PLoS ONE 2018, 13, e0205818. [Google Scholar] [CrossRef] [Green Version]
- Lancashire, L.J.; Rees, R.C.; Ball, G.R. Identification of gene transcript signatures predictive for estrogen receptor and lymph node status using a stepwise forward selection artificial neural network modelling approach. Artif. Intell. Med. 2008, 43, 99–111. [Google Scholar] [CrossRef]
- Musa, R.M.; Majeed, A.; Taha, Z.; Abdullah, M.R.; Maliki, A.B.H.M.; Kosni, N.A. The application of Artificial Neural Network and k-Nearest Neighbour classification models in the scouting of high-performance archers from a selected fitness and motor skill performance parameters. Sci. Sports 2019, 34, e241–e249. [Google Scholar] [CrossRef]
- Heazlewood, I.; Walsh, J.; Climstein, M.; Kettunen, J.; Adams, K.; DeBeliso, M. A Comparison of Classification Accuracy for Gender Using Neural Networks Multilayer Perceptron (MLP), Radial Basis Function (RBF) Procedures Compared to Discriminant Function Analysis and Logistic Regression Based on Nine Sports Psychological Constructs to Measure Motivations to Participate in Masters Sports Competing at the 2009 World Masters Games. In Proceedings of the 10th International Symposium on Computer Science in Sports (ISCSS); Chung, P., Soltoggio, A., Dawson, C.W., Meng, Q., Pain, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 93–101. ISBN 9783319245584. [Google Scholar]
- Marx, P.; Lenhard, W. Diagnostische Merkmale von Screeningverfahren. In Frühprognose Schulischer Kompetenzen; Hasselhorn, M., Schneider, W., Eds.; Hogrefe: Göttingen, Germany, 2010. [Google Scholar]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 32–35. [Google Scholar] [CrossRef]
- Kim, J.O.; Jeong, Y.-S.; Kim, J.H.; Lee, J.-W.; Park, D.; Kim, H.-S. Machine Learning-Based Cardiovascular Disease Prediction Model: A Cohort Study on the Korean National Health Insurance Service Health Screening Database. Diagnostics 2021, 11, 943. [Google Scholar] [CrossRef]
- Sieghartsleitner, R.; Zuber, C.; Zibung, M.; Conzelmann, A. Science or Coaches’ Eye?—Both! Beneficial Collaboration of Multidimensional Measurements and Coach Assessments for Efficient Talent Selection in Elite Youth Football. J. Sports Sci. Med. 2019, 18, 32–43. [Google Scholar]
- Beißert, H.; Hasselhorn, M.; Lösche, P. Möglichkeiten und Grenzen der Frühprognose von Hochbegabung (Possibilities and limits of the early prognosis of giftedness). In Handbuch Talententwicklung (Handbook of Talent Development); Stamm, M., Ed.; Hans-Huber: Bern, Germany, 2014; pp. 415–426. [Google Scholar]
- Giles, B.; Kovalchik, S.; Reid, M. A machine learning approach for automatic detection and classification of changes of direction from player tracking data in professional tennis. J. Sports Sci. 2020, 38, 106–113. [Google Scholar] [CrossRef]
- Ulbricht, A.; Fernandez-Fernández, J.; Mendez-Villanueva, A.; Ferrauti, A. Impact of fitness characteristics on tennis performance in elite junior tennis players. J. Strength Cond. Res. 2016, 30, 989–998. [Google Scholar] [CrossRef] [PubMed]
- Pion, J.; Segers, V.; Fransen, J.; Debuyck, G.; Deprez, D.; Haerens, L.; Vaeyens, R.; Philippaerts, R.; Lenoir, M. Generic anthropometric and performance characteristics among elite adolescent boys in nine different sports. Eur. J. Sport Sci. 2015, 15, 357–366. [Google Scholar] [CrossRef]
- Epuran, M.; Holdevici, I.; Tonita, F. Performance Sport Psychology. Theory and Practice; Fest: Bucharest, Romania, 2008. [Google Scholar]
- Mosoi, A.A. Skills and Motivation of Junior Tennis Players. Procedia Soc. Behav. Sci. 2013, 78, 215–219. [Google Scholar] [CrossRef] [Green Version]
- Zuber, C.; Zibung, M.; Conzelmann, A. Motivational patterns as an instrument for predicting success in promising young football players. J. Sports Sci. 2015, 33, 160–168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elferink-Gemser, M.T.; Jordet, G.; Coelho-E-Silva, M.J.; Visscher, C. The marvels of elite sports: How to get there? Br. J. Sports Med. 2011, 45, 683–684. [Google Scholar] [CrossRef] [Green Version]
- Phillips, E.; Davids, K.; Renshaw, I.; Portus, M. Expert performance in sport and the dynamics of talent development. Sports Med. 2010, 40, 271–283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kovacs, M. Applied physiology of tennis performance. Br. J. Sports Med. 2006, 40, 381–386. [Google Scholar] [CrossRef]
- Brouwers, J.; Bosscher, V.; de Sotiriadou, P. An examination of the importance of performances in youth and junior competition as an indicator of later success in tennis. Sport Manag. Rev. 2012, 15, 461–475. [Google Scholar] [CrossRef] [Green Version]
| Sex | Age | TP | Height | Weight | SP | SJ | BB | SBF | PU | SU | SLJ | BT | ER |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 97 | 1 | 132 | 27.3 | 4.21 | 33 | 38 | 4 | 17 | 23 | 153 | 19 | 1078 |
| 0 | 94 | 0 | 129 | 27.3 | 4.45 | 27 | 30 | –2 | 14 | 19 | 135 | 14 | 959 |
| Predicted/Recommended | ||||
|---|---|---|---|---|
| Low Performer | Top Performer | ∑ | ||
| Observed/Existing | Top Performer | C | A | A + C |
| Low Performer | D | B | B + D | |
| ∑ | C + D | A + B | A + B + C + D | |
| Variables | Groups | N | M | SD | SE | 95% CL | Min | Max | |
|---|---|---|---|---|---|---|---|---|---|
| LL | UL | ||||||||
| Calendar age * (month) (Time of testing; U9) | LP | 158 | 93.8 | 5.0 | 0.39 | 93.0 | 94.6 | 83 | 110 |
| TP | 16 | 97.5 | 6.4 | 1.60 | 94.1 | 100.9 | 88 | 112 | |
| Test results | |||||||||
| Body height * (cm) | LP | 158 | 129.1 | 5.7 | 0.45 | 128.2 | 130.0 | 117 | 145 |
| TP | 16 | 132.3 | 4.5 | 1.13 | 129.8 | 134.7 | 127 | 143 | |
| Body weight (kg) | LP | 158 | 27.2 | 4.1 | 0.33 | 26.6 | 27.9 | 20.0 | 39.3 |
| TP | 16 | 27.3 | 1.9 | 0.48 | 26.3 | 28.3 | 23.4 | 30.6 | |
| Sideward jumping ** (repeats) | LP | 157 | 27.3 | 6.1 | 0.49 | 26.3 | 28.2 | 6.5 | 40.5 |
| TP | 16 | 33.0 | 5.1 | 1.27 | 30.3 | 35.7 | 27.0 | 45.0 | |
| Balance backward ** (steps) | LP | 158 | 30.3 | 8.5 | 0.67 | 28.9 | 31.6 | 8 | 48 |
| TP | 16 | 38.3 | 5.7 | 1.42 | 35.2 | 41.3 | 28 | 48 | |
| Standing long jump ** (cm) | LP | 157 | 135.1 | 16.2 | 1.30 | 132.5 | 137.6 | 82 | 190 |
| TP | 16 | 153.0 | 17.2 | 4.30 | 143.8 | 162.2 | 125 | 178 | |
| 20 m sprint * (s) | LP | 158 | 4.45 | 0.36 | 0.03 | 4.39 | 4.51 | 3.10 | 5.32 |
| TP | 16 | 4.21 | 0.34 | 0.08 | 4.03 | 4.39 | 3.50 | 4.72 | |
| Push-ups * (repeats) | LP | 158 | 14.6 | 3.6 | 0.28 | 14.0 | 15.1 | 4 | 24 |
| TP | 16 | 17.1 | 5.2 | 1.30 | 14.3 | 19.9 | 9 | 25 | |
| Sit-ups * (repeats) | LP | 158 | 19.2 | 5.1 | 0.40 | 18.4 | 20.0 | 2 | 30 |
| TP | 16 | 23.4 | 4.1 | 1.02 | 21.3 | 25.6 | 15 | 29 | |
| Bend forward (cm) | LP | 158 | 1.98 | 5.94 | 0.47 | 1.05 | 2.92 | −11 | 18 |
| TP | 16 | 4.16 | 4.90 | 1.22 | 1.55 | 6.77 | −10 | 12 | |
| 6 min run ** (m) | LP | 154 | 959 | 130.8 | 10.5 | 938 | 979 | 545 | 1259 |
| TP | 16 | 1078 | 80.7 | 20.2 | 1035 | 1121 | 891 | 1200 | |
| Ball throw ** (m) | LP | 155 | 13.5 | 4.03 | 0.32 | 12.9 | 14.2 | 3.8 | 27.6 |
| TP | 16 | 18.8 | 5.35 | 1.34 | 15.9 | 21.6 | 9.2 | 28.3 | |
| Tennis Recommendation Score (zTRS = 1.3) | Predicted/Recommended | |||
|---|---|---|---|---|
| Low Performer | Top Performer | Percentage Correct | ||
| Top Performer | 4 | 12 | 75% | |
| Observed/Existing | Low Performer | 131 | 27 | 82.9% |
| Percentage (total) | 77.6% | 22.4% | 82.2% | |
| (Binary) Logistic Regression 1 | Predicted/Recommended | |||
|---|---|---|---|---|
| Low Performer | Top Performer | Percentage Correct | ||
| Top Performer | 10 | 6 | 37.5% | |
| Observed/Existing | Low Performer 2 | 144 | 6 | 96% |
| Percentage (total) | 92.8% | 7.2% | 90.4% | |
| Multilayer Perceptron 1 | Predicted/Recommended | |||
|---|---|---|---|---|
| Low Performer | Top Performer | Percentage Correct | ||
| Top Performer | 4 | 12 | 75% | |
| Observed/Existing | Low Performer 2 | 126 | 24 | 84% |
| Percentage (total) | 78.3% | 21.7% | 91% | |
| Recommendation Score | (Binary) Logistic Regression | Linear Discriminant Analysis | Multilayer Perceptron | |
|---|---|---|---|---|
| Sensitivity | 0.750 | 0.375 | 0.688 | 0.750 |
| Specificity | 0.829 | 0.960 | 0.807 | 0.840 |
| Selection Rate | 0.224 | 0.072 | 0.241 | 0.217 |
| Positive Predictive Value | 0.308 | 0.500 | 0.275 | 0.333 |
| Negative Predictive Value | 0.970 | 0.935 | 0.960 | 0.969 |
| Random Hit Rate | 0.725 | 0.845 | 0.709 | 0.729 |
| Hit Rate | 0.822 | 0.904 | 0.795 | 0.831 |
| Maximum Hit Rat | 0.868 | 0.976 | 0.855 | 0.880 |
| Youden’s J | 0.579 | 0.320 | 0.495 | 0.590 |
| F1 score | 0.437 | 0.429 | 0.393 | 0.462 |
| RIOC Value | 0.678 | 0.447 | 0.588 | 0.681 |
| Probability of Being a Top Performer (%) | ||||
|---|---|---|---|---|
| Recommendation Score | Logistic Regression | Discriminant Analysis | Multilayer Perceptron | |
| Top Performer 1 | 99 | 90 | 99 | 99 |
| Top Performer 2 | 97 | 86 | 98 | 97 |
| Top Performer 3 | 93 | 68 | 97 | 96 |
| Top Performer 4 | 96 | 71 | 96 | 90 |
| Top Performer 5 | 83 | 64 | 95 | 90 |
| Top Performer 6 | 89 | 68 | 90 | 95 |
| Top Performer 7 | 91 | 15 | 68 | 71 |
| Top Performer 8 | 79 | 33 | 85 | 88 |
| Top Performer 9 | 55 | 7 | 65 | 70 |
| Top Performer 10 | 66 | 18 | 63 | 68 |
| Top Performer 11 | 57 | 9 | 58 | 68 |
| Top Performer 12 | 67 | 16 | 41 | 32 |
| Top Performer 13 | 44 | 3 | 23 | 52 |
| Top Performer 14 | 40 | 5 | 24 | 37 |
| Top Performer 15 | 20 | 2 | 9 | 29 |
| Top Performer 16 | 33 | 1 | 1 | 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siener, M.; Faber, I.; Hohmann, A. Prognostic Validity of Statistical Prediction Methods Used for Talent Identification in Youth Tennis Players Based on Motor Abilities. Appl. Sci. 2021, 11, 7051. https://doi.org/10.3390/app11157051
Siener M, Faber I, Hohmann A. Prognostic Validity of Statistical Prediction Methods Used for Talent Identification in Youth Tennis Players Based on Motor Abilities. Applied Sciences. 2021; 11(15):7051. https://doi.org/10.3390/app11157051
Chicago/Turabian StyleSiener, Maximilian, Irene Faber, and Andreas Hohmann. 2021. "Prognostic Validity of Statistical Prediction Methods Used for Talent Identification in Youth Tennis Players Based on Motor Abilities" Applied Sciences 11, no. 15: 7051. https://doi.org/10.3390/app11157051
APA StyleSiener, M., Faber, I., & Hohmann, A. (2021). Prognostic Validity of Statistical Prediction Methods Used for Talent Identification in Youth Tennis Players Based on Motor Abilities. Applied Sciences, 11(15), 7051. https://doi.org/10.3390/app11157051







