Modeling Software Fault-Detection and Fault-Correction Processes by Considering the Dependencies between Fault Amounts

Abstract

Many NHPP software reliability growth models (SRGMs) have been proposed to assess software reliability during the past 40 years, but most of them have focused on modeling the fault detection process (FDP) in two ways: one is to ignore the fault correction process (FCP), i.e., faults are assumed to be instantaneously removed after the failure caused by the faults is detected. However, in real software development, it is not always reliable as fault removal usually needs time, i.e., the faults causing failures cannot always be removed at once and the detected failures will become more and more difficult to correct as testing progresses. Another way to model the fault correction process is to consider the time delay between the fault detection and fault correction. The time delay has been assumed to be constant and function dependent on time or random variables following some kind of distribution. In this paper, some useful approaches to the modeling of dual fault detection and correction processes are discussed. The dependencies between fault amounts of dual processes are considered instead of fault correction time-delay. A model aiming to integrate fault-detection processes and fault-correction processes, along with the incorporation of a fault introduction rate and testing coverage rate into the software reliability evaluation is proposed. The model parameters are estimated using the Least Squares Estimation (LSE) method. The descriptive and predictive performance of this proposed model and other existing NHPP SRGMs are investigated by using three real data-sets based on four criteria, respectively. The results show that the new model can be significantly effective in yielding better reliability estimation and prediction.

1. Introduction

Software reliability has been viewed as the most significant factor to improve the reliability of safety-critical software systems. Many time-dependent SRGMs have been studied to determine the reliability measures for software over the past four decades [1,2,3,4]. Researchers have developed different models upon different assumptions. Some models make an assumption that once a failure is detected, the errors which cause the failure are immediately corrected and no new errors are brought in simultaneously (i.e., perfect debugging) [5]. Other models take into account an imperfect debugging [6,7], i.e., faults are not always perfectly removed, and new ones can be introduced as a by-product of the fault repair process. However, most of the existing models assume that faults will be instantaneously repaired after being detected. However, it is not realistic and in fact detected faults will become more and more difficult to be corrected as testing progresses. Therefore, it is of great importance to build software reliability models from the viewpoint of the fault correction process, i.e., give the same priority to modeling the fault correction process as the fault detection process.

Schneidewind first modeled the software correction process along with the software detection process by proposing a fault-correction model using a constant time delay in the fault-detection process [8]. Then Xie and Zhao extended Schneidewind’s idea from a constant time delay to a time-dependent delay function [9]. Later, Schneidewind provided an extension of his original model by using a random variable for the time delay following an exponential distribution [10]. Xie et al. further proposed another distributed correction time model as to provide a more flexible modeling of correction processes [11,12] and Peng et al. incorporated a testing effort function and imperfect debugging into the time delay function [13]. Lo and Huang proposed a general framework for modeling software’s fault detection and correction processes and showed that many existing SRGMs based on NHPP could be covered by the proposed approaches [14]. Shu proposed a model from the viewpoint of the fault amount relationship between the two processes [15]. Additionally, some other attempts have been made to model these two processes from different viewpoints, such as Markov chain [16,17,18], finite and infinite server queuing models [19], and quasi-renewal time-delay fault removal model [20]. Researches also suggest that the estimation accuracy of SRGMs could be further improved by considering the influence of some real issues happening during the testing process [21,22], such as testing coverage. Testing coverage is a promising indicator for testing completeness and effectiveness, which can help developers evaluate how much test effort has been spent and help customers estimate the confidence of accepting the software product. Many time-dependent test coverage functions (TCFs) have been proposed by using different distributions, such as logarithmic-exponential [23], S-shaped [24], Rayleigh [25], Weibull and logistic [26] and lognormal [27]. Many TCFs based reliability models have been developed to formulate the relationship between the testing coverage and the number of detected faults, such as the Rayleigh model [25], logarithmic-exponential model [23], beta model, hyper-exponential model [22] and so on [22,24,26].

Therefore, it is of great importance to model dual fault detection and correction processes. In contrast to the existing research that considers the time dependency between fault detection and fault correction processes, in this paper, we will propose a new software reliability model considering both fault detection and correction processes from the viewpoint of fault content, that is, the quantitative dependence between the number of faults detected by the fault detection process and the number of faults corrected by the fault correction process. The fault introduction rate and test coverage are also considered to improve the accuracy of the final derived model.

The remainder of this paper is organized as follows. In Section 2, we first give a brief overview of the fault-detection models’ assumptions and fault-correction process, then build a relationship between the numbers of detected faults and corrected faults, after which we present the proposed model incorporating the fault introduction rate and testing coverage rate, and several existing SRGMs are also presented. In Section 3, we examine the fitting and prediction performance of this model on three sets of software failure data compared with other existing SRGMs. Finally, Section 4 gives the conclusions.

2. Modeling Fault Detection and Fault Correction Processes

2.1. Basic Assumptions of Existing NHPP SRGMs

NHPP is used to describe the failure phenomenon during the testing process. The counting process $\left\{N(t),t\ge 0\right\}$ of an NHPP process is given as follows.

$$\mathrm{Pr}\left\{N(t)=k\right\}=\frac{{[m(t)]}^k}{k!}{\mathrm{e}}^{-m(t)},k=0,1,2\dots$$

(1)

The mean value function (MVF) $m(t)$ can be expressed as follows.

$$m(t)={\displaystyle {\int }_0^t\lambda (s)}\mathrm{d}s$$

(2)

where $\lambda (s)$ is the fault intensity function.

Most existing SRGMs based on NHPP have the following basic assumptions concerning the software fault detection process:

• The software failures’ occurrence and faults’ removal follow NHPP;
• The software failure intensity at any time is proportional to the number of remaining faults presented at that time;
• The detected faults are immediately removed with certainty and correction of faults takes only negligible time.

According to the above assumptions, the general NHPP model can be proposed by solving the following equation:

$$\frac{\mathrm{d}m(t)}{\mathrm{d}t}=b(t)[a(t)-m(t)]$$

(3)

where $a(t)$ is the total fault content function, $m(t)$ is the mean number of detected faults and $b(t)$ represents the fault detection rate.

2.2. Considering the Fault-Detection Process and Fault-Correction Process Together

Most existing SRGMs only focus on describing the behavior of the fault detection process and assume that faults will be fixed instantaneously upon detection, but actually most latent software faults may remain uncorrected for a long time due to the complexity of software systems and incomplete comprehension of software by the testers and learning process even after they are detected.

Suppose $m_c(t)$ denotes the mean value of corrected faults by time $t$, and assume that the mean number of faults corrected in the time interval ($t$, $t+\Delta t$) is proportional to the mean number of detected but not yet corrected faults remaining in the software system. The MVF $m_c(t)$ can be expressed in terms of the following equations:

$$\frac{\mathrm{d}{m}_c(t)}{\mathrm{d}t}=\mu (t)[m(t)-m_c(t)]$$

(4)

where $\mu (t)$ is the fault correction rate, and $m(t)$ is shown in Equation (3).

2.3. The Relationship between $m(t)$ and $m_c(t)$

Here we use data collected from testing a software program (Data Set 1, DS-1) [28] to study the relationship between $m(t)$ and $m_c(t)$. Let $r(t)=\frac{m_c(t)}{m(t)}$, the cumulative detected faults and corrected faults are shown in Figure 1 and the value of $r(t)$ is shown in Figure 2. Apparently, at the beginning of the testing phase, lots of faults are detected and most of them are simple and easy to be removed, so the difference between the number of corrected faults and detected faults is small, then faults detected become more complicated and difficult to be removed, so the difference becomes larger, then the difference becomes less again. Thus, a concave or S-shaped function can be used to model the ratio of the number of corrected faults to the number of detected faults.

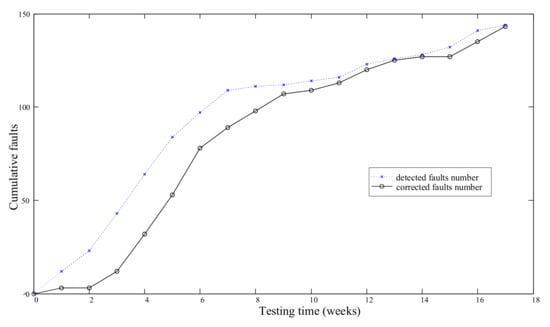
Figure 1. The number of cumulative detected faults and corrected faults for DS-1.

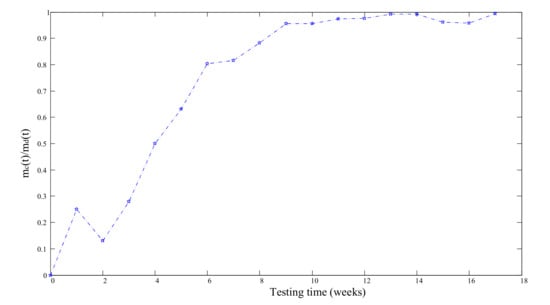
Figure 2. The ratio of the number of corrected faults to the number of detected faults for DS-1.

Here we use two S-shaped functions to model $r(t)$. From Table 1, we can see that $r(t)=\frac{1}{1+\beta {\mathrm{e}}^{-bt}}$ provides a better descriptive power.

Table 1. Comparison of two S-shaped functions as $r(t)$ for DS-1.

No.	$\mathit{r}(\mathit{t})$	MSE	${\mathit{R}}^2$	$\mathbf{Adjusted} {\mathit{R}}^2$
1	$\frac{1}{1+\beta e^{-bt}}$	0.0022	0.9765	0.9749
2	$1-(1+bt)e^{-bt}$	0.0038	0.9786	0.9756

Note: The definitions of MSE, $R^2$ and Adjusted $R^2$ are shown in Section 3.1.

2.4. A New Model with Imperfect Debugging and Testing Coverage

Here we incorporate testing coverage and fault introduction rate into software reliability model.

Suppose $c(t)$ denotes the proportion of the code covered by time $t$ against the whole code. Obviously, $c(t)$ increases with testing time $t$. Firstly, when testing starts, $c(t)$ grows at a quick rate as more test cases are executed to examine the software; after a certain point in time, the software becomes stable and less testing coverage take place to realize the residual fault detection, and function $c(t)$ becomes flat when the testing comes to the end. Thus, a concave or S-shaped function can be suitable to model the testing coverage function. Obviously, (1 − $c(t)$) is the percentage of the software code which has not yet been covered by test cases up to time $t$. The derivative of the testing coverage function, $c^{\prime }(t)$, represents the coverage rate. Therefore, $c^{\prime }(t)/(1-c(t))$ could be used to measure the fault detection rate $b(t)$, which is shown in Equation (3).

To build a model incorporating fault-detection process and fault-correction process as well as fault introduction rate and testing coverage, the following assumptions are proposed for this model:

• The software failures’ occurrence follows an NHPP process.
• The software failure rate at any time depends on both the fault detection rate and the number of remaining faults in the software at that time.
• The fault detection rate can be expressed by $\frac{c^{\prime }(t)}{1-c(t)}$; $c(t)$ is the percentage of the code that has been examined up to time $t$, $c^{\prime }(t)$ is the derivative of the testing coverage function and represents the coverage rate.
• Faults can be introduced during the debugging phase with a constant fault introduction rate and the overall fault content function is linear time-dependent.
• $m_c(t)$ denotes the mean value of corrected faults by time $t$, which is proportional to the mean number of detected but not yet corrected faults remaining in the software system, and $r(t)$ represents the relationship between $m(t)$ and $m_c(t)$ expressed by $r(t)=\frac{m_c(t)}{m(t)}$; $m(t)$ is the cumulative detected faults.

From Assumption 4, the total fault number function $a(t)$, is a linear function of the expected fault number detected up to time $t$. That is,

$$a(t)=a+\alpha m(t)$$

(5)

where $a$ denotes the initial fault number presented in the software system before testing starts and $\alpha >0$.

Substituting $a(t)$ from Equation (5) into Equation (3), and solving it in terms of the initial condition that at $t=0$, $m(t)=0$, we can obtain

$$m(t)=\frac{a}{p-\alpha }\left[1-{\left(\frac{1-c(0)}{1-c(t)}\right)}^{(\alpha -p)\beta }\right]$$

(6)

where $c(0)$ refers to the testing coverage function when $t=0$.

From Assumption 5, once $m(t)$ is determined, $m_c(t)$ can be achieved. That is,

$$m_c(t)=\frac{a}{p-\alpha }\left[1-{\left(\frac{1-c(0)}{1-c(t)}\right)}^{(\alpha -p)\beta }\right]·r(t)$$

(7)

Substituting different types of testing coverage functions for $c(t)$ and ratio functions of corrected faults number to detected faults number for $r(t)$ in Equation (7), we can obtain different MVFs corresponding to them. As mentioned above, the testing coverage function should be a non-negative and non-decreasing function of testing time $t$. So the following function can be used to model the testing coverage function, that is:

$$c(t)=\frac{A(1-e^{-rt})}{1+c{\mathrm{e}}^{-rt}}$$

(8)

where $A$ denotes the maximum percentage of testing coverage, $r$ is the shape parameter and $c$ is the scale parameter. Clearly, when $t=0$, $c(0)=0$.

According to the results of Section 2.3, here the following function is used to describe $r(t)$:

$$r(t)=\frac{1}{1+\beta {\mathrm{e}}^{-bt}}$$

(9)

Substituting Equations (8) and (9) into Equation (7), we can get the MVF of corrected faults correspondingly:

$$m_c(t)=\frac{a}{1-\alpha }\left\{1-{\left[1-\frac{A(1-e^{-rt})}{1+c{\mathrm{e}}^{-rt}}\right]}^{1-\alpha }\right\}\frac{1}{1+\beta {\mathrm{e}}^{-bt}}$$

(10)

It can be seen that fault detection process and correction process as well as fault introduction rate and testing coverage are all integrated into the proposed model.

Table 2 lists the existing NHPP models to depict the MVF of fault correction process [14] and fault detection process [24] as well as the proposed new model. All models together will be used for the following comparisons.

Table 2. Software reliability models and their MVFs.

No.	Model Name	Model Type	$\mathbf{MVF} (\mathit{m}(\mathit{t})$$\mathbf{or} {\mathit{m}}_{\mathit{c}}(\mathit{t}))$
1	G-O model(also called $m_1(t)$ [14])	Concave	$m(t)=a(1-e^{-bt})$
2	$m_2(t)$ [14]	Concave	$m_c(t)=a(1+\frac{c}{b-c}{e}^{-bt}-\frac{b}{b-c}{e}^{-ct})$
3	$m_3(t)$ [14]	S-shaped	$m_c(t)=a(1-(1+bt)e^{-bt})$
4	Inflection S-shaped [29]	Concave	$m(t)=\frac{a(1-e^{-bt})}{1+\beta {\mathrm{e}}^{-bt}}$
5	Yamada exponential [30]	Concave	$m(t)=a(1-e^{-\gamma \alpha (1-e^{-\beta t})})$
6	Yamada Rayleigh [30]	S-shaped	$m(t)=a(1-e^{-\gamma \alpha (1-e^{-\beta t^2/2})})$
7	Yamada Weibull [30]	Concave and S-shaped	$m(t)=a(1-e^{-\gamma \alpha (1-e^{-\beta t^r})})$
8	Delayed S-shaped [30]	S-shaped	$m(t)=a(1-(1+bt)e^{-bt})$
9	HD/G-O [31]	Concave	$m(t)=\log [(e^a-c)/(e^{a{\mathrm{e}}^{-bt}}-c)]$
10	Yamada imperfect (1) [32]	Concave	$m(t)=\frac{ab}{\alpha +b}(e^{\alpha t}-{\mathrm{e}}^{-bt})$
11	Yamada imperfect (2) [32]	Concave	$m(t)=a(1-e^{-bt})(1-\frac{\alpha }{b})+\alpha at$
12	P-Z(1997) model [33]	S-shaped and Concave	$m(t)=\frac{1}{(1+\beta e^{-bt})}\left((c+a)(1-e^{-bt})-\frac{ab}{b-\alpha }(e^{-\alpha t}-{\mathrm{e}}^{-bt})\right)$
13	Fault removal model (2003) [28]	S-shaped	$m(t)=\frac{a}{p-\beta }\left\{1-{\left(\frac{(1+\alpha ){\mathrm{e}}^{-bt}}{1+\alpha {\mathrm{e}}^{-bt}}\right)}^{\frac{c}{b}(p-\beta )}\right\}$
14	P-Z coverage model (2003) [24]	S-shaped and Concave	$m(t)=a(1+\alpha t-\frac{bt+1}{{\mathrm{e}}^{bt}})-\frac{a\alpha (1+bt)}{b{\mathrm{e}}^{bt+1}}\left[\ln (bt+1)+{\displaystyle \sum _{i=0}^{\infty }\frac{{(1+bt)}^{i+1}-1}{(i+1)!(i+1)}}\right]$
15	SRGM-3 model (2011) [34]	S-shaped	$m(t)=\frac{A}{1-\alpha }\left[1-{\left(\left(1+bt+\frac{b^2{t}^2}{2}\right){\mathrm{e}}^{-bt}\right)}^{p(1-\alpha )}\right]$
16	proposed model	S-shaped and Concave	$m_c(t)=\frac{a}{1-\alpha }\left\{1-{\left[1-\frac{A(1-e^{-rt})}{1+c{\mathrm{e}}^{-rt}}\right]}^{1-\alpha }\right\}\frac{1}{1+\beta {\mathrm{e}}^{-bt}}$

3. Model Comparisons

3.1. Comparison Criteria and Parameter Estimation Method

3.1.1. Criteria for Models’ Descriptive Power Comparison

Here we use three criteria to judge the performance of the models. The first criterion is the mean value of squared error (Mean Square Error, MSE), which can be calculated as follows:

$$\mathrm{MSE}=\frac{1}{n-N}{\displaystyle \sum _{i=1}^n{(y_i-\widehat{m}(t_i))}^2}$$

(11)

where $n$ represents the number of observations, $y_i$ represents the total number of faults observed by time $t_i$, $\widehat{m}(t_i)$ denotes the estimated cumulative number of faults up to time $t_i$, $N$ represents the number of parameters in the model. Therefore, the lower the value of MSE, the better the model performs.

The second criterion is correlation index of the regression curve equation ($R^2$), which can be expressed as follows:

$$R^2=1-\frac{{\displaystyle \sum _{i=1}^n{\left(y_i-\widehat{m}(t_i)\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

(12)

where $\overline{y}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{y}_i}$. Therefore, the larger $R^2$, the better the model explains the variation in the data.

The last criterion is adjusted $R^2$ (Adjusted $R^2$), which can be expressed as follows:

$$\mathrm{Adjusted} R^2=1-\frac{(1-R)(n-1)}{n-M-1}$$

(13)

where $R$ denotes the value of $R^2$ and $M$ represents the model’s predictor number. Therefore, the larger value of Adjusted $R^2$, the better is the model’s performance.

3.1.2. Criteria for Models’ Predictive Power Comparison

Here we use SSE criterion to examine the predictive power of SRGMs. SSE is the sum of squared error, which is expressed as follows:

$$\mathrm{SSE}={\displaystyle \sum _{i=m}^n{(y_i-\widehat{m}(t_i))}^2}$$

(14)

Assume that by the end of testing time $t_n$, totally $y_n$ faults have been detected. Firstly we use the data points up to time $t_{m-1}$($t_{m-1}$<$t_n$) to estimate the parameters of $m(t)$, then substituting the estimated parameters in the mean value function yields the prediction value of the cumulative fault number $\widehat{m}(t_m)$ by $t_m$($t_m$<$t_n$), $y_m$ is the actual number of faults detected by $t_m$. Then the procedure is repeated for several values of $t_i$ ($i=m+1,m+2,\dots ,n.$) until $t_n$.

Therefore, the less SSE, the better is the model’s performance.

3.1.3. Parameter Estimation Method

Once the analytical expression for $m(t)$ is derived, the parameters in $m(t)$ can be estimated by using the maximum likelihood estimation (MLE) method or the least square estimation (LSE) method. Though estimates from MLE are consistent and asymptotically normally distributed as the sample size increases, sometimes the estimations may not be obtained especially under conditions where $m(t)$ is too complex. Here we turn to LSE methods to estimate the models’ parameters.

The sum of the squared distance is given as follows:

$$L={\displaystyle \sum _{i=1}^n{(y_i-\widehat{m}(t_i))}^2}$$

(15)

where $y_i$ is the cumulative number of faults detected or corrected in time (0, $t_i$), and all failure data are denoted in the form of pairs ($t_i$,$y_i$) ($i=1,2,\dots ,n$;$0<t_1<t_2<\cdots <t_n$).

By taking derivatives of (15) with respect to each parameter, and setting the results equal to zero, we can obtain several equations for the proposed model as follows:

$$\frac{\partial L}{\partial a}=\frac{\partial L}{\partial \alpha }=\frac{\partial L}{\partial A}=\frac{\partial L}{\partial c}=\frac{\partial L}{\partial r}=\frac{\partial L}{\partial b}=\frac{\partial L}{\partial \beta }=0$$

(16)

After solving the above equations simultaneously, we can obtain the least square estimates of all parameters for the proposed model.

As noted, solutions of the above Equation (16) are extremely difficult and require either graphical or numerical methods. Under the help of MATLAB, the calculation of the parameters is not a critical problem, though adding additional parameters to make the software reliability model more complex makes the work of parameter estimation more difficult.

3.2. Data Analysis and Model Comparison with Real Application

3.2.1. A Middle-Size Software System Data

Here we examine the performance of the proposed model and compare it with several traditional models using data collected from testing a middle-size software system (Data Set 1, DS-1) [11]. The failure data are recorded by week and are shown in Table 3. In contrast to a traditional software reliability data set, this data set includes not only fault-detection data but also fault-correction data. We use all data points to fit the models and get the parameters estimation of all models. The model parameters, MSE values, $R^2$ values and Adjusted $R^2$ values are listed in Table 4.

Table 3. A middle-size software system data (DS-1).

Weeks	Cumulative Detected Faults	Cumulative Corrected Faults	Weeks	Cumulative Detected Faults	Cumulative Corrected Faults
1	12	3	10	114	109
2	23	3	11	116	113
3	43	12	12	123	120
4	64	32	13	126	125
5	84	53	14	128	127
6	97	78	15	132	127
7	109	89	16	141	135
8	111	98	17	144	143
9	112	107

Table 4. Comparison of goodness-of-fit power of SRGMs for $m_c(t)$ of DS-1.

Model No.	Model Name	Model Parameter Estimation Results	MSE	R2	Adjusted R2
1	$m_1(t)$	$\widehat{a}=231.6$, $\widehat{b}=0.05838$	148.3333	0.9396	0.9356
2	$m_2(t)$	$\widehat{a}=147.5$, $\widehat{b}=0.2627$, $\widehat{c}=0.263$	56.2357	0.9786	0.9756
3	$m_3(t)$	$\widehat{a}=147.5$, $\widehat{b}=0.2627$	52.4867	0.9786	0.9772
4	Inflection S-shaped	$\widehat{a}=129.9$, $\widehat{b}=0.5074$, $\widehat{c}=17.3$	48.1286	0.9817	0.9791
5	Yamada exponential	$\widehat{a}=235.8$, $\widehat{\beta }=0.001389$, $\widehat{\gamma }=6.448$, $\widehat{\alpha }=6.403$	171.4615	0.9395	0.9256
6	Yamada Rayleigh	$\widehat{a}=142.9$, $\widehat{\beta }=0.01177$, $\widehat{\gamma }=2.109$, $\widehat{\alpha }=1.638$	40.3308	0.9858	0.9825
7	Yamada Weibull	$\widehat{a}=141.9$, $\widehat{r}=2.315$, $\widehat{\alpha }=1.197$, $\widehat{\beta }=0.004362$	34.6385	0.9878	0.9850
8	Delayed S-shaped	$\widehat{a}=147.5$, $\widehat{b}=0.2627$	52.4867	0.9786	0.9772
9	HD/G-O	$\widehat{a}=231.6$, $\widehat{b}=0.05837$, $\widehat{c}=4.891$	158.9286	0.9396	0.9310
10	Yamada imperfect(1)	$\widehat{a}=231.6$, $\widehat{b}=0.05837$, $\widehat{\alpha }=1.436\times {10}^{-9}$	158.9286	0.9396	0.9356
11	Yamada imperfect(2)	$\widehat{a}=231.6$, $\widehat{b}=0.05837$, $\widehat{\alpha }=1.641\times {10}^{-9}$	158.9286	0.9396	0.9356
12	P-Z (1997) model	$\widehat{a}=0.9179$, $\widehat{b}=0.5102$, $\widehat{c}=129.3$, $\widehat{\alpha }=0.08294$, $\widehat{\beta }=17.49$	55.7917	0.9818	0.9758
13	Fault removal model (2003)	$\widehat{a}=99.8$, $\widehat{\alpha }=932.9$, $\widehat{b}=2.483$, $\widehat{p}=0.8698$, $\widehat{c}=0.3123$, $\widehat{\beta }=0.1595$	19.0364	0.9943	0.9917
14	P-Z coverage model (2003)	$\widehat{a}=147.5$, $\widehat{b}=0.2627$, $\widehat{\alpha }=4.776\times {10}^{-10}$	56.2357	0.9786	0.9772
15	SRGM-3 model (2011)	$\widehat{A}=126.7$, $\widehat{\alpha }=0.08195$, $\widehat{b}=2.569$, $\widehat{p}=0.1126$	34.0154	0.9880	0.9863
16	proposed model	$\widehat{a}=230.5$, $\widehat{A}=0.8538$, $\widehat{\alpha }=0.7528$, $\widehat{c}=73.78$ $\widehat{b}=3.794$, $\widehat{\beta }=0.05419$, $\widehat{r}=1.093$	5.9370	0.9984	0.9974

Notes: The bold number means the result of the best SRGM in this column.

All models’ fitting results for DS-1 are graphically illustrated in Figure 3. Figure 4 is three dimensional and the coordinates X, Y and Z illustrate the values of MSE, $R^2$ and Adjusted $R^2$ respectively. We can see that the proposed model has the best criteria values of MSE, $R^2$ and Adjusted $R^2$, i.e., the new model shows the best fitting power to the real data set than all other models.

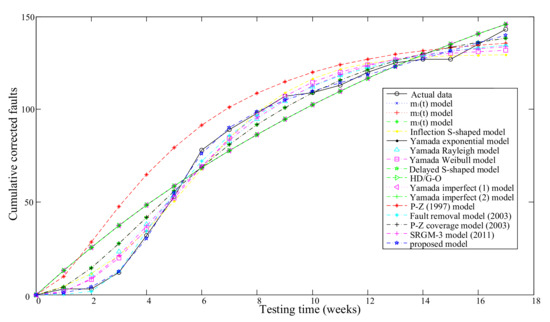
Figure 3. The comparison fitting results of SRGMs for DS-1.

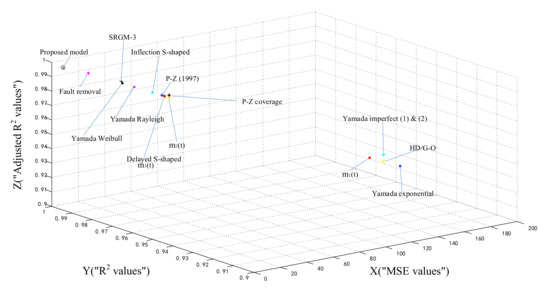
Figure 4. (X, Y, Z) represents (MSE, $R^2$, Adjusted $R^2$ ) values for DS-1.

3.2.2. Monitor and Control System Data

Here we examine models using another software’s testing data collected from testing a software program developed for a real-time monitor and control system (Data Set 2, DS-2) [35]. The failure data are recorded by day and are shown in Table 5. We use all data points to fit the models and estimate the parameters in the models. The fault data set has only detected fault number. The model parameters, MSE values, $R^2$ values and Adjusted $R^2$ values are listed in Table 6.

Table 5. Failures per day and cumulative failures for DS-2.

Days	Faults	Cumulative Faults	Days	Faults	Cumulative Faults
1	5	5	57	2	448
2	5	10	58	3	451
3	5	15	59	2	453
4	5	20	60	7	460
5	6	26	61	3	463
6	8	34	62	0	463
7	2	36	63	1	464
8	7	43	64	0	464
9	4	47	65	1	465
10	2	49	66	0	465
11	31	80	67	0	465
12	4	84	68	1	466
13	24	108	69	1	467
14	49	157	70	0	467
15	14	171	71	0	467
16	12	183	72	1	468
17	8	191	73	1	469
18	9	200	74	0	469
19	4	204	75	0	469
20	7	211	76	0	469
21	6	217	77	1	470
22	9	226	78	2	472
23	4	230	79	0	472
24	4	234	80	1	473
25	2	236	81	0	473
26	4	240	82	0	473
27	3	243	83	0	473
28	9	252	84	0	473
29	2	254	85	0	473
30	5	259	86	0	473
31	4	263	87	2	475
32	1	264	88	0	475
33	4	268	89	0	475
34	3	271	90	0	475
35	6	277	91	0	475
36	13	290	92	0	475
37	19	309	93	0	475
38	15	324	94	0	475
39	7	331	95	0	475
40	15	346	96	1	476
41	21	367	97	0	476
42	8	375	98	0	476
43	6	381	99	0	476
44	20	401	100	1	477
45	10	411	101	0	477
46	3	414	102	0	477
47	3	417	103	1	478
48	8	425	104	0	478
49	5	430	105	0	478
50	1	431	106	1	479
51	2	433	107	0	479
52	2	435	108	0	479
53	2	437	109	1	480
54	7	444	110	0	480
55	2	446	111	1	481
56	0	446

Table 6. Comparison of goodness-of-fit power of SRGMs for DS-2.

Model No.	Model Name	Model Parameter Estimation Results	MSE	R2	Adjusted R2
1	G-O model	$\widehat{a}=538.1$, $\widehat{b}=0.02575$	804.2202	0.9646	0.9643
2	$m_2(t)$	$\widehat{a}=484.9$, $\widehat{b}=0.06756$, $\widehat{c}=0.06659$	338.3333	0.9852	0.9850
3	$m_3(t)$	$\widehat{a}=488.1$, $\widehat{b}=0.06629$	331.8349	0.9854	0.9853
4	Inflection S-shaped	$\widehat{a}=484.6$, $\widehat{b}=0.06681$, $\widehat{\beta }=3.648$	300.0000	0.9869	0.9867
5	Yamada exponential	$\widehat{a}=6.987\times {10}^4$, $\widehat{\beta }=0.02566$, $\widehat{\gamma }=0.03822$, $\widehat{\alpha }=0.2023$	820.9346	0.9645	0.9635
6	Yamada Rayleigh	$\widehat{a}=568.2$, $\widehat{\beta }=0.001074$, $\widehat{\gamma }=1.325$, $\widehat{\alpha }=1.384$	461.5888	0.9800	0.9795
7	Yamada Weibull	$\widehat{a}=485.4$, $\widehat{r}=1.456$, $\widehat{\alpha }=128.7$, $\widehat{\beta }=3.359\times {10}^{-5}$	308.7850	0.9867	0.9863
8	Delayed S-shaped	$\widehat{a}=488.1$, $\widehat{b}=0.06629$	331.8349	0.9854	0.9853
9	HD/G-O	$\widehat{a}=538.1$, $\widehat{b}=0.02575$, $\widehat{c}=2.849$	811.6667	0.9646	0.9639
10	Yamada imperfect(1)	$\widehat{a}=538.1$, $\widehat{b}=0.02575$, $\widehat{\alpha }=4.124\times {10}^{-10}$	811.6667	0.9646	0.9643
11	Yamada imperfect(2)	$\widehat{a}=538.1$, $\widehat{b}=0.02575$, $\widehat{\alpha }=1.074\times {10}^{-12}$	811.6667	0.9646	0.9643
12	P-Z (1997) model	$\widehat{a}=0.9988$, $\widehat{b}=0.06682$, $\widehat{c}=483.6$, $\widehat{\alpha }=0.5211$, $\widehat{\beta }=3.65$	305.6604	0.9869	0.9864
13	Fault removal model (2003)	$\widehat{a}=468.2$, $\widehat{\alpha }=150.7$, $\widehat{b}=0.8082$, $\widehat{p}=0.9518$, $\widehat{c}=0.03979$, $\widehat{\beta }=0.02274$	419.2381	0.9822	0.9814
14	P-Z coverage model (2003)	$\widehat{a}=488.1$, $\widehat{b}=0.06629$, $\widehat{\alpha }=1.254\times {10}^{-10}$	334.9074	0.9854	0.9853
15	SRGM-3 model (2011)	$\widehat{A}=480.7$, $\widehat{\alpha }=0.02476$, $\widehat{b}=0.3128$, $\widehat{p}=0.1695$	354.8598	0.9847	0.9842
16	proposed model	$\widehat{a}=71.06$, $\widehat{A}=0.9998$, $\widehat{\alpha }=0.942$, $\widehat{c}=0.05328$ $\widehat{b}=0.4515$, $\widehat{\beta }=32.14$, $\widehat{r}=0.1498$	193.8462	0.9919	0.9914

Notes: The bold number means the result of the best SRGM in this column.

From Table 6, we can see that comparing all models using all the three criteria, the new model yields the best criteria values and provides the best descriptive power. All models’ fitting results for DS-2 are graphically illustrated in Figure 5. Figure 6 is three dimensional and the coordinates X, Y and Z illustrate the values of MSE, $R^2$ and Adjusted $R^2$ respectively.

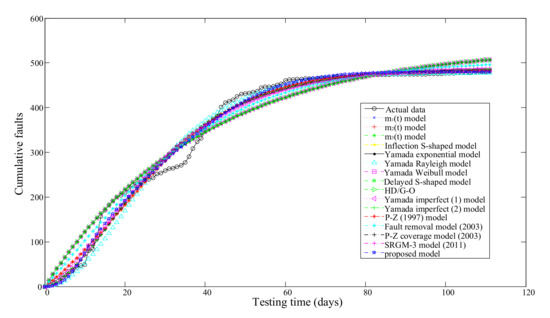
Figure 5. The comparison fitting results of SRGMs for DS-2.

Figure 6. (X, Y, Z) represents (MSE, $R^2$, Adjusted $R^2$ ) values for DS-2.

3.2.3. Tandem Computer Data

Here we examine models using another software’s testing data collected from Tandem Computers Release #1 (Data Set 3, DS-3) [5]. The failure data are recorded by week and are shown in Table 7. We use all data points to fit the models and estimate the parameters in the models. The fault data set also only has the detected fault number. The model parameters, MSE values, $R^2$ values and Adjusted $R^2$ values for goodness-of-fit are listed in Table 8.

Table 7. Failures per week and cumulative failures for DS-3.

Testing Time (Weeks)	CPU (h)	Faults	Cumulative Faults	Testing Time (Weeks)	CPU (h)	Faults	Cumulative Faults
1	519	16	16	11	6539	6	81
2	968	8	24	12	7083	5	86
3	1430	3	27	13	7487	4	90
4	1893	6	33	14	7846	3	93
5	2490	8	41	15	8205	3	96
6	3058	8	49	16	8564	2	98
7	3625	5	54	17	8923	1	99
8	4422	4	58	18	9282	1	100
9	5218	11	69	19	9641	0	100
10	5823	6	75	20	10,000	0	100

Table 8. Comparison of goodness-of-fit power of SRGMs for DS-3.

Model No.	Model Name	Model Parameter Estimation Results	MSE	R2	Adjusted R2
1	G-O model	$\widehat{a}=130.2$, $\widehat{b}=0.08317$	12.9056	0.9857	0.9849
2	$m_2(t)$	$\widehat{a}=130.2$, $\widehat{b}=0.08317$, $\widehat{c}=4.646\times {10}^4$	13.6647	0.9857	0.9840
3	$m_3(t)$	$\widehat{a}=104$, $\widehat{b}=0.2654$	28.0611	0.9689	0.9672
4	Inflection S-shaped	$\widehat{a}=110.8$, $\widehat{b}=0.1721$, $\widehat{\beta }=1.205$	10.5647	0.9890	0.9877
5	Yamada exponential	$\widehat{a}=999.5$, $\widehat{\beta }=0.07685$, $\widehat{\gamma }=0.279$, $\widehat{\alpha }=0.51$	14.8438	0.9854	0.9827
6	Yamada Rayleigh	$\widehat{a}=115.8$, $\widehat{\beta }=0.01721$, $\widehat{\gamma }=3.03$, $\widehat{\alpha }=0.6548$	49.4188	0.9514	0.9422
7	Yamada Weibull	$\widehat{a}=121.1$, $\widehat{r}=1.027$, $\widehat{\alpha }=245.2$, $\widehat{\beta }=3.542\times {10}^{-4}$	15.1750	0.9851	0.9823
8	Delayed S-shaped	$\widehat{a}=104$, $\widehat{b}=0.2654$	28.0611	0.9689	0.9672
9	HD/G-O	$\widehat{a}=130.2$, $\widehat{b}=0.08317$, $\widehat{c}=0.2769$	13.6647	0.9857	0.9840
10	Yamada imperfect(1)	$\widehat{a}=130.2$, $\widehat{b}=0.08317$, $\widehat{\alpha }=9.363\times {10}^{-10}$	13.6647	0.9857	0.9849
11	Yamada imperfect(2)	$\widehat{a}=130.2$, $\widehat{b}=0.08317$, $\widehat{\alpha }=1.04\times {10}^{-9}$	13.6647	0.9857	0.9849
12	P-Z(1997) model	$\widehat{a}=1.589\times {10}^{-8}$, $\widehat{b}=0.1721$, $\widehat{c}=110.8$, $\widehat{\alpha }=0.000368$, $\widehat{\beta }=1.205$	11.9733	0.9890	0.9860
13	Fault removal model (2003)	$\widehat{a}=103.6$, $\widehat{\alpha }=57.49$, $\widehat{b}=0.08193$, $\widehat{p}=0.9993$, $\widehat{c}=4.916$, $\widehat{\beta }=4.827\times {10}^{-5}$	10.8786	0.9906	0.9873
14	P-Z coverage model	$\widehat{a}=73.19$, $\widehat{b}=0.3563$, $\widehat{\alpha }=0.02588$	27.1588	0.9716	0.9683
15	SRGM-3 model (2011)	$\widehat{A}=83.46$, $\widehat{\alpha }=0.3433$, $\widehat{b}=37.1$, $\widehat{p}=0.003678$	14.9250	0.9853	0.9826
16	proposed model	$\widehat{a}=160.4$, $\widehat{A}=0.5101$, $\widehat{\alpha }=0.7292$, $\widehat{c}=87.26$ $\widehat{b}=0.2813$, $\widehat{\beta }=6.468$, $\widehat{r}=7.007$	2.3192	0.9981	0.9973

Notes: The bold number means the result of the best SRGM in this column.

From Table 8, we can see that the new model provides the best descriptive power. The fitting of the models (existing and proposed) to DS-3 is graphically illustrated in Figure 7. Figure 8 is three dimensional and the coordinates X, Y and Z illustrate the values of MSE, $R^2$ and Adjusted $R^2$ respectively.

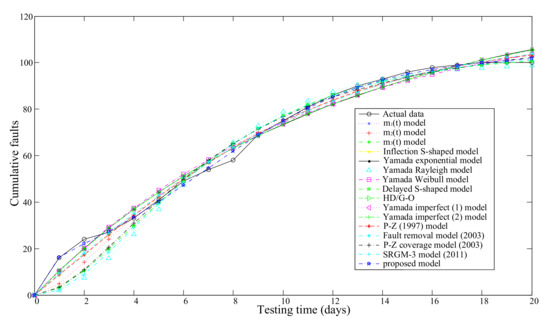
Figure 7. The fitting results of comparison SRGMs compared with actual data for DS-3.

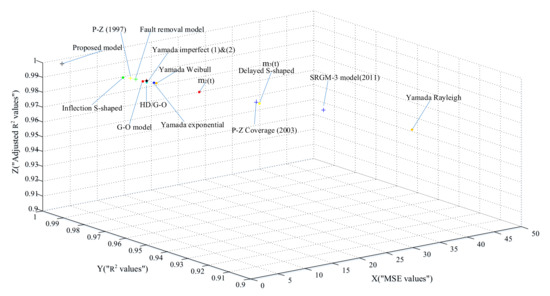
Figure 8. (X, Y, Z) represents (MSE, $R^2$, Adjusted $R^2$ ) values for DS-3.

3.2.4. Comparison of Models’ Predictive Power

For the predictive power comparison, we divide the data set into two parts, 80% and the remaining 20%, respectively. We use the first 80% of data points to estimate the models’ parameters, then use the remaining data points to compare the models’ predictive power. The SSE values for the prediction are 37.0169, 236.0253 and 23.0348, accordingly shown in Table 9. For DS-1, comparing all models, we find that the new model has the smallest SSE value of 37.0169, which are smaller than the values of other models, e.g., others’ SSE values can be 1.87-times (P-Z coverage model’s 69.0496) and even 22.24-times (Yamada imperfect (1) model’s 823.0770) larger than the value of the proposed model. For DS-2, comparing all models, we find that the new model has the smallest SSE value of 236.0253, which are smaller than the values of other models, e.g., others’ SSE values can be 11.75 times (Inflection S-shaped model’s 2.7742 × 10³), even 1468.78 times (Yamada Rayleigh model’s 3.4667 × 10⁵) larger than the value of the proposed model. For DS-3, though SSE = 23.0348 for the proposed model is not the best result, it is only a little larger than the best result, for the smallest SSE value is 6.9655 (given by the delayed S-shaped model), and comparing to other models, we find that the new model’s SSE value is much smaller than the values of other models, e.g., others’ SSE values can be 3.16-times (Yamada Rayleigh model’s 73.4246) and even 555.33-times (SRGM-3 model’s 1.2792 × 10⁴) larger than the value of the proposed model. Additionally, for the delayed S-shaped model, it only provides the best result for DS-3, but does not provide the best results for DS-1 and DS-2. This may indicate that this proposed model gives a better predictive power.

Table 9. Comparison of SRGMs’ predictive power for DS-1, DS-2 and DS-3.

Model No.	Model Name	80% OF DS-1	80% OF DS-2	80% OF DS-3
		SSE	SSE	SSE
1	G-O model(also called $m_1(t)$)	823.0713	6.7713 × 104	147.2964
2	$m_2(t)$	119.7111	7.3709 × 103	356.5743
3	$m_3(t)$	69.0496	3.5343 × 103	6.9655
4	Inflection S-shaped	750.1803	2.7742 × 103	356.5814
5	Yamada exponential	401.7862	6.0381 × 104	377.2231
6	Yamada Rayleigh	197.3302	3.4667 × 105	73.4246
7	Yamada Weibull	553.6076	3.4596 × 103	676.6515
8	Delayed S-shaped	69.0496	3.5343 × 103	6.9655
9	HD/G-O	823.0713	6.7713 × 104	356.5818
10	Yamada imperfect(1)	823.0770	6.7713 × 104	356.5837
11	Yamada imperfect(2)	823.0724	5.7234 × 104	356.5827
12	P-Z (1997) model	595.6770	2.8149 × 103	334.1059
13	Fault removal model (2003)	286.2138	1.9332 × 104	345.1824
14	P-Z coverage model (2003)	69.0496	3.5343 × 103	1.5362 × 103
15	SRGM-3 model (2011)	549.9081	1.1495 × 104	1.2792 × 104
16	proposed model	37.0169	236.0253	23.0348

Notes: The bold number means the result of the best SRGM in this column.

4. Conclusions

In this paper, the problem of modeling software fault-detection processes and fault-correction processes together with imperfect debugging and testing coverage has been investigated. From the viewpoint of fault amount instead of fault correction time delay, a new SRGT model addressing the fault re-introduction and testing coverage is put forward by introducing the relationship function between the MVF of detected faults and corrected faults. The proposed model is applied to two kinds of data sets: one that contains information not only of detected fault numbers but also corrected fault numbers, and another that contains only detected fault numbers. No matter what kind of data sets, the proposed model gives significantly better goodness-of-fit and prediction results comparing with other existing NHPP models for three real data sets according to four criteria. It should be noted that, though adding more parameters makes the software reliability model more complicated and the task of parameter estimation more difficult, by automating the calculations using software tools it is not a critical problem.