Abstract
With the Fourth Industrial Revolution, many factories aim for efficient mass production, and robots are being used to reduce human workloads. In recent years, the field of gripper robots with a soft structure that can grip and move objects without damaging them has attracted considerable attention. This paper proposes a variable-stiffness soft gripper, based on previous designs, with an added silicone coating for increased friction and an EGaIn soft sensor for monitoring grip forces. The variable-stiffness structure used in this study was constructed by connecting soft structures to rigid structures and using tendons fixed to the rigid structures. Furthermore, a more responsive EGaIn soft sensor compared to existing sensors was designed by adding bumps to the path traced by the alloy. After selecting the appropriate fingertip shape, changes in the output of the EGaIn soft sensor corresponding to the object held by the soft gripper were observed, confirming that the strength of the device could be changed according to the intended purpose.
1. Introduction
Robots are employed to complete simple and repetitive tasks on behalf of humans. However, when production processes are modified according to production schedule or situation, some robots can no longer be used. Therefore, robots that can be deployed in different environments are being studied. A successful product of this research field is the DLR hand-arm system, a gripper consisting of a variety of joints and motors that emulate a human hand [1]. This gripper is operated by controlling variable-stiffness structures that change the stiffness of each joint when the system grasps different objects. The DLR hand-arm system is a rigid body robot that exhibits a variety of movements such as a human arm. However, the requisite variable-stiffness structures are complex, and a control system is required to apply a specific gripping force that avoids damaging an object. Hence, different types of multifunctional robots produced in small volumes have been developed, with soft robots created from compliant materials receiving more attention than rigid-type robots, which require precise control when grasping soft objects. In contrast, a soft robot is difficult to control precisely, even though it can hold various soft objects without causing damage. Soft robots are typically controlled using either tendon-driven or pneumatic systems. An example of a research soft robot that works using tendon-driven methods is the Exo-Glove Poly and Soft gripper. Exo-Glove Poly is a wearable robot that helps disabled people who cannot move their fingers to hold objects [2,3]. Soft variable-stiffness grippers actuated with tendon-driven systems have been demonstrated [4,5]. The variable-stiffness structures in such systems are created by securing a tendon to the tip of a rigid structure and passing tendons through soft and rigid structures. Stiffness, controlled by pulling and releasing a tendon, increases nonlinearly when a tendon is pulled while the soft structure is compressed. The dynamic motion of the system can be varied using the placement of tendons. The performance of this type of soft grippers has been verified in experiments in which objects such as spheres, square columns, and bottles containing two liters of water were gripped. Two liters of water was the maximum gripping load of the gripper [5]. Pneumatic soft robots, exemplified by the gripper robot of Soft Robotics Inc. (Bedford, MA, USA) [6] and multigait robot [7], are controlled by adjusting the air pressure in pneumatic chambers. Each chamber is arranged with the soft gripper as a finger on a larger hand structure, enabling the robot to grasp objects when pneumatic pressure is adjusted. With the multigait robot, the air path in each embedded chamber is designed to enable dynamic motion when the system is inflated. This method has the advantage of reducing the size of the system. Other methods for actuating soft robots include the use of chemical reactions [8], material properties [9], and shape memory alloys [10]. A soft robot that utilizes chemical reactions for actuation is the Octobot. With this robot, fuel placed in a configured chamber is decomposed by a catalyst, and the resulting gas expands the chamber, thus driving the robot. The material-actuated jamming gripper [9] consists of a pocket containing granular particles. In an uncompressed state, the pocket wraps around objects with which it is in contact. Grip action is subsequently activated by applying a vacuum to the pocket and compressing the gas between the granular particles, which fixes the pocket to the desired object. Movement with Wang et al.’s gripper [10] depends on the magnitude and location of the temperature applied to the shape memory alloy from which it is created. Methods using chemical reactions, materials properties, and shape memory alloys have the disadvantage of slow operation. In addition, the pneumatic control robot has a complicated process in manufacturing the chamber, and it is difficult to repair the chamber when it is damaged. The tendon-driven control method is more advantageous to construct a system that is more compact than the pneumatic control method. If a soft gripper that implements a strong force through a pneumatic-driven method, a larger pneumatic pump is needed. On the contrary, the tendon-driven method using motors has the advantage of being able to make a compact system with a large gripping force. The forces generated by pneumatically controlled robots are limited by the size of the pump and the pressure the material can sustain. In addition, creating compact pneumatic systems is difficult, as pumps are not easily miniaturized. Thus, tendon-driven soft grippers are more prevalent, as the system’s stiffness can be varied. If the stiffness of the system increases, the gripping force increases, so the weight of the object that the soft gripper can lift increases. However, if these soft grippers gripped objects of more than 2 kg, they would slide due to a weight greater than the maximal static friction force. Therefore, to improve the performance of the soft gripper, it is necessary to monitor the grip of the soft gripper to make sure that it is gripping within the gripper system state.
The rigid condition of typical sensors has limited the ability to monitor grip forces. Because these sensors have a fixed shape, they cannot always produce accurate outputs for every action completed, as their shape can differ from that of the gripper. Soft sensors that conform to the shape of a gripper provide a solution for this discrepancy of shape. A range of soft sensors for monitoring gripping forces has been studied. Reference [11] describes a soft sensor consisting of hydrophilic PTFE as the sensitive dielectric element of the relative humidity–based grasp sensor. In contrast, [12] describes a capacitive strain sensor for force monitoring created by combining silicone and fabric, providing a larger capacity and stiffness than fiber-based sensors and a larger elastic range than silicone-based sensors. Sensors that use EGaIn, a liquid eutectic mixture of gallium and indium as a sensing element, have also been studied. To respond to microstrain, Chen et al., developed an EGaIn sensor with a wavy pattern to reduce hysteresis [13]. Kramer et al., improved the sensing response of their EGaIn sensor by applying pressure to it through a rigid structural block [14]. Park et al., designed their EGaIn sensor path to be thin and fabricated the sensor as a multilayer structure to increase its responsiveness [15]. Finally, Chossat et al., produced a hybrid soft elastomer strain sensor in which signal routing was isolated from detection, such that the sensor reacted less sensitively to unnecessary stresses on wiring [16]. In this paper, a silicone integument was added to the gripper to increase the gripping friction force. Various soft sensors have been considered for application to the integument of this gripper fingertip. Therefore, there is a need for a manufacturing method that can be easily applied to the curved shape and integument of the soft gripper fingertip. The manufacturing method of the EGaIn soft sensor is made easy by injecting EGaIn into a fabricated path. In addition, EGaIn is suitable because of its high conductivity and the small number of processes required for fabricating the soft sensor. The soft gripper is designed based on previous studies [4,5] that performed the optimal design of variable-stiffness soft grippers. The previous study established the basis of the characteristics of each parameter of the variable-stiffness structure and the shape of the gripper.
In this study, a soft gripper with a variable-stiffness structure driven by a tendon was characterized based on the deformation according to the gripping target. This gripper was applied with an EGaIn soft sensor at the end of the grip to increase the gripping freedom and detect the state of the object grip. This EGaIn soft sensor measures the gripping force applied to an object, and the performance of the sensor was verified through an experiment to monitor the sensing response. The soft gripper is capable of autonomous gripping that enables it to firmly fix various objects without damage by checking the sensing value, grasping the grip state, and adjusting the appropriate gripping force. The weight of the gripping target could be inferred from the sensor’s value, and the verification confirmed that an autonomous grip that can firmly grip various objects without damage was possible.
2. Configuration of Variable-Stiffness Gripper
2.1. Design of Variable-Stiffness Structure
Adjustable grippers require variable-stiffness structures to ensure appropriate force when a gripping action is completed. In this study, the variable-stiffness structure was fabricated based on the tendon-drive principle introduced in previous research [17]. Furthermore, soft gripper robots have been studied extensively [18], enabling the design of an appropriate variable-stiffness structure and selection of suitable parameters for this study. The variable-stiffness structure used in this gripper was constructed by fixing a tendon to the rigid structure corresponding to the fingertip and cross-connecting the soft structures with the rigid structure. Rigid structures were built from polylactic acid (PLA) using a Single Plus 3D Printer of Cubicon Inc. (Seongnam, Gyeonggi-do, Korea).
In contrast, soft structures were fabricated by curing Ecoflex0030 silicone in a PLA mold made by the 3D printer. In addition, an integument was coated on the outside of the rigid structure by fixing it to a mold made by the 3D printer. The tendons were constructed using an iron wire with a diameter of 1.59 mm. The dimensions of rigid and flexible structures were set based on [19]. The diameter of each structure was 20 mm, and the lengths of rigid structures 1, 2, and 3 and the flexible structures were 35, 20, 25, and 15 mm. In contrast to the structure in previous research, the variable-stiffness structure designed in this study consists of two inner tendons, as shown in Figure 1, to reduce lateral motion when a finger holds an object. A prototype of this structure is shown in Figure 2.
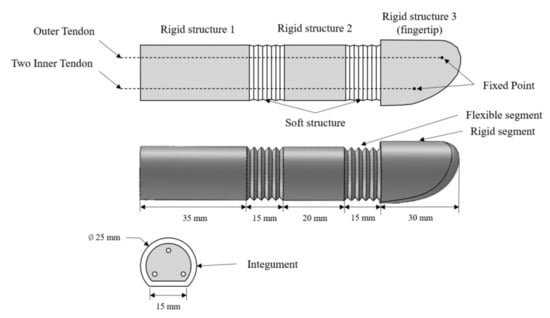
Figure 1.
Illustrative schematic of the variable-stiffness structure.

Figure 2.
A prototype of the variable-stiffness structure.
2.2. Gripper with Variable-Stiffness Structure
Tendon-drive grippers were manufactured and based on the variable-stiffness structure described above. With these devices, gripping is controlled by pulling the steel wire corresponding to the tendon using a motor. The previous gripper design consisted of three fingers. The object can be gripped with two fingers. However, it is not stable, and rotation can occur. To prevent this, the soft gripper was designed with three fingers. However, even if three fingers are used, unintended rotation can occur, but this can be minimized by using a soft structure. The three tendons were embedded into each finger to prevent the rotation. In this research, gripping targets were selected as examples of fruits with similar diameters. The junction between a grasped object and the variable stiffness is a right angle; the proposed soft grippers have a limited ability to hold large objects. Therefore, the size of the gripper in this study was reduced, modifying the joint angle of the variable-stiffness structure to 20°, as shown in Figure 3, to ensure that the gripper could hold large objects firmly and enable a span grip. As for the joint angle, 20 degrees was selected as an angle for which span grip would be capable of enclosing an 80 mm-diameter spherical structure. This also influenced the volume reduction of the gripper. Figure 4 depicts a complete soft gripper module that incorporates these design changes.
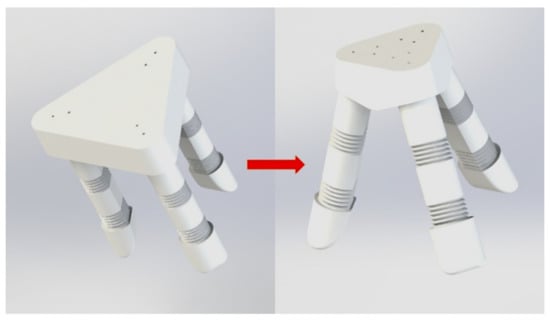
Figure 3.
Illustration of the proposed design change to the gripper geometry.
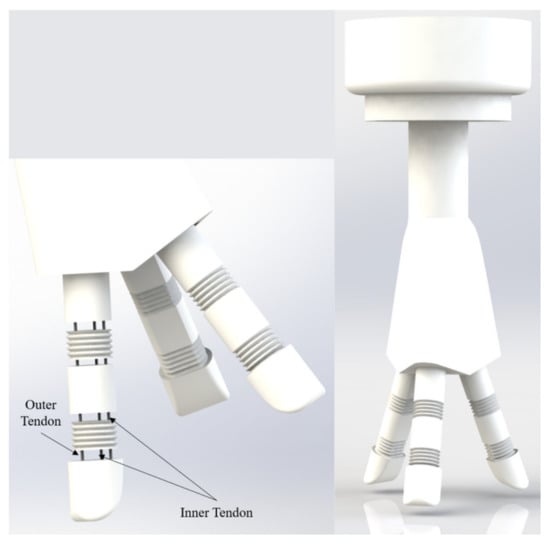
Figure 4.
Illustration of the variable-stiffness structure in the soft gripper.
Figure 5 summarizes the gripper’s control system. Again, Robotis Dynamixel MX-64 motors were used for actuation, while an Arduino Uno with a Bluetooth module was used for control signal output by the motor-drive circuit.
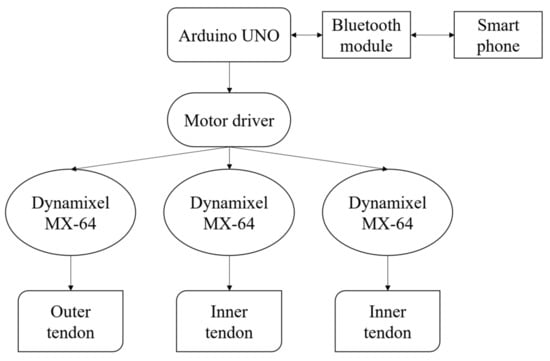
Figure 5.
Diagram of the control system for the gripper.
According to the number of tendons in the variable-stiffness structure, three motors are included in the gripper. Gripping is performed when both inner tendons are pulled at the same time. In addition, if the pulling force on the outer tendon is weaker than those on the inner tendons, the soft structure compresses evenly, and its stiffness increases nonlinearly. Thus, the gripper’s overall stiffness can be adjusted using this characteristic. Furthermore, there are two inner tendons, the gripper can be tilted toward the tendon on which the pulling force is more substantial. This configuration facilitates stronger gripping with less lateral movement. In addition, rotational gripping can be applied by varying the strength of the pulling forces on the inner tendons of each finger, as demonstrated in Figure 6. The movement shown in Figure 6 can be seen in Video S1.

Figure 6.
Image of a soft gripper performing a rotation action.
2.3. EGaIn Soft Sensor
EGaIn is a eutectic mixture of gallium and indium widely used in soft sensors [13,14,15,16]. The mass ratio of EGaIn is 75% gallium and 25% indium. As its melting point is 15.5 °C, it is maintained at a liquid state at room temperature [20]. Compared to other liquid metals, the toxicity and reactivity of EGaIn are low; thus, it is relatively safe [21]. Because of these characteristics, EGaIn has been used in studies of sensors with changing patterns [13], sensors for measuring curvature [14], sensors containing overlapping patterns [15], and sensors consisting of ion solutions [16]. Based on this versatility, an EGaIn soft sensor was developed in this study for application at the tip of a curved finger to enable the sensing of gripping forces performed over a wider area. In previous studies, the EGaIn path was designed and manufactured to be thin, and sensors for measuring tension and pressure were configured such that maximum possible paths pass through the target area. Similar principles were adopted in the soft sensor created in this study, as discussed below.
2.4. Shape of EGaIn Soft Sensor
The sensitivity of EGaIn soft sensors improves with the number of EGaIn placed in a set area. Thus, in previous studies, such as that conducted by Park [15], thin multilayer paths were designed for EGaIn. Although EGaIn soft sensors are used for pressure sensing, they are more suitable for tensile force sensing, as pressure sensors require delicate fabrication processes. In this study, the ability to monitor grip forces requires pressure sensing. To avoid the complex fabrication processes used in previous studies, a new shape suitable for pressure sensing and manufacturing ease was developed. The sensor was designed to attach to a curved fingertip. Therefore, the design and fabrication of the soft sensor should be considered to apply to the curved surface. If the width of the path is too thin, the width of the path can be easily changed. In other words, when sensors are attached to curved surfaces, there may be significant differences in sensor performance due to the thin path. To prevent this effect, the width of the path was increased. The bumps were added to compensate for the shortcomings of increasing path width. Biomimetic design methods were used to maximize the path’s change in area in the limited space. Referring to a previous study [22], bumps were placed in the EGaIn path, emulating the dimples on a person’s skin. When pressure was applied to the sensor, the bumps were pressed together, increasing the change in the area of the EGaIn path. A total of 79 bumps in the shape of truncated cones were arranged on the EGaIn path, and its area was enlarged to ensure that wires could be connected at either end. The path shape of the EGaIn soft sensor was referenced in previous research [15]. Two EGaIn soft sensor molds were designed and fabricated. The first mold was engraved with the path of EGaIn, and the second mold was engraved with the truncated conical bumps on the path of EGaIn. The two molds were printed by 3D printer with the PLA materials, and the sensor body was fabricated by combining two plates made by pouring the Ecoflex0030 into each mold. A schematic of this design is shown in Figure 7a, while the manufactured sensor is shown in Figure 7b. The dimensions of the EGaIn path are summarized in Table 1.

Figure 7.
Illustration of EGaIn soft sensors used for grip force monitoring. (a) Definition of design parameters controlled in manufacture of EGaIn soft sensors. (b) Soft sensors with bumps (left) and without bumps (right) following manufacture.

Table 1.
Design parameters for manufacture of EGaIn soft sensors.
2.5. Verification of Sensor Response
Before finalizing the gripper design, the range of motions possible with the device was studied. Here, the soft sensor developed in the previous section was applied to the fingertips of the gripper, as illustrated in Figure 8.

Figure 8.
Illustration of a gripper with applied EGaIn soft sensors.
The experiment to measure the value of the EGaIn sensor applied to the gripper is shown in Figure 9.
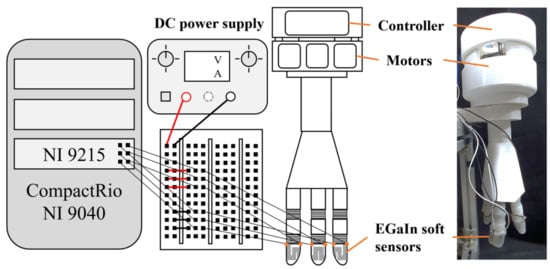
Figure 9.
Illustration of the experimental setup for characterizing the variable-stiffness soft gripper.
3. Results
3.1. Analysis of Variable-Stiffness Structure
The theoretical deflection of the variable-stiffness structure used in this study can be calculated to verify the manufactured structure. This calculation is based on the pseudo-rigid-body model [23], which analyzes soft structures that exhibit nonlinear motion, such as bent thin plates. With this model, soft structures are represented as a series of connected torsion springs to emulate the structure’s nonlinear increase in stiffness when the silicone is compressed. This analytical model can be used to predict stiffness change trends. The terminology used in this analysis is shown in Table 2.

Table 2.
Nomenclature of parameters used in numerical analysis.
Because the cross-section of the variable-stiffness structure is circular and this circular shape is compressed, Chalhoub and Kelly’s Equation (1) can be used to calculate the structure’s change in stiffness as a function of bending [24]. The shape factor used in this expression is defined in (2).
Figure 10 shows the pseudo-rigid-body model of the variable-stiffness structure. Here, the PLA cylinders are assumed to be completely rigid, while soft structures are transformed into torsion springs, connected on either side to rigid structures. For analysis, the stiffness calculated using (1) and (2) is used to determine the stiffnesses of the torsional springs in the model.
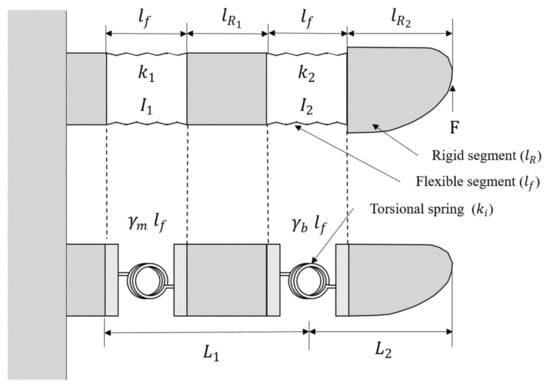
Figure 10.
Pseudo-rigid-body model of the variable-stiffness structure.
Assuming that external forces only act perpendicular to the end of the variable-stiffness structure (i.e., in the vertical direction), the value of in Figure 10 can be obtained as
where is assumed to equal 0.8517, based on the pseudo-rigid-body model from [23]. For the other soft body, it is assumed that the only deformation that occurs is due to moment forces. The value of is thus given by
where is assumed to equal 0.7346, based on the pseudo-rigid-body model in [23].
Using this information, the values of and can be calculated as follows:
The coupling between each length is described by the moment equations below:
where F is the external force acting perpendicular to the end of the variable-stiffness structure. Hence, by combining (7) and (8), and calculating the values of and through numerical analysis, the length of the variable-stiffness structure can be obtained as a function of the external force. For this analysis, the values of and were obtained using a least-squares regression technique. Following the appropriate definition of and , the deflection of the variable-stiffness structure, D, can be calculated using (9).
Experiments were conducted using the setup depicted in Figure 11 and Figure 12 to verify the numerical analysis described above. Here, a force is applied to the end of the variable-stiffness structure while each tendon is pulled 10 mm. The resulting deflection is subsequently compared with the results from theoretical predictions.
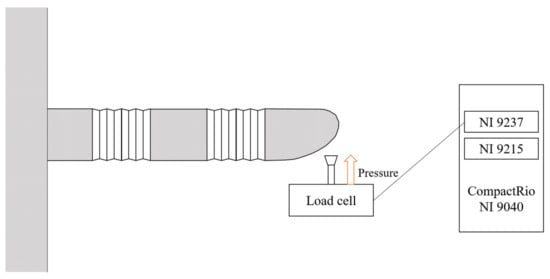
Figure 11.
Diagram of the experimental setup for measuring deflection.

Figure 12.
Illustration of a deflection measurement experiment being conducted.
Comparisons of the measured and predicted deflections are shown in Table 3 and Figure 13. Figure 13 confirms the suitability of this analysis, as the theoretical and experimental results show similar trends with a similar slope.

Table 3.
Comparison of predicted and measured response to applied force.
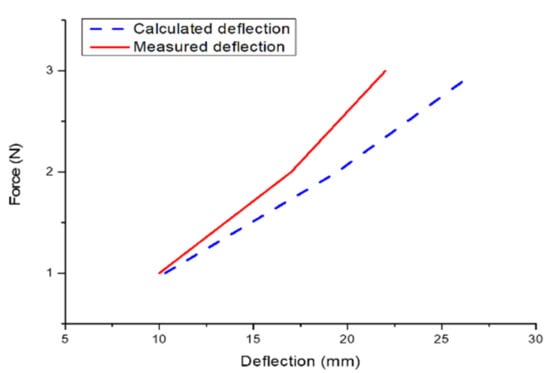
Figure 13.
Comparison of the variation of the predicted and measured deflection with applied force.
3.2. Theoretical Analysis of Sensor Geometry
This section details the analysis conducted to verify the effect of bumps in the EGaIn path, using resistance as the basis of comparison. Here, sensors without bumps are defined as normal-type sensors, while sensors with bumps are defined as bump-type sensors. Figure 14 depicts schematics of the different types of sensors, while the values of the parameters used to calculate the resistance of each sensor type are listed in Table 4.
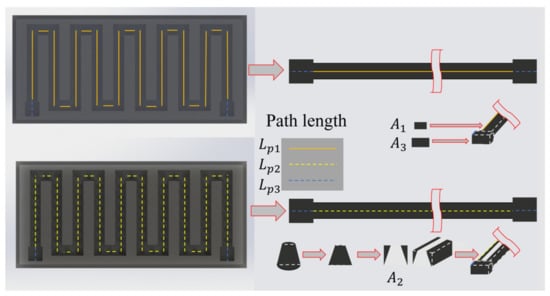
Figure 14.
Definition of the geometrical parameters used to estimate the resistances of the normal- and bump-type EGaIn soft sensors.

Table 4.
Parameters for estimating the resistance of the different EGaIn soft sensors.
The resistance of a given geometry can be calculated as
where ρ is the specific resistance of the constituent material (defined as 29.4 × 10−3 Ω mm for EGaIn [25]), Lp is the length of the geometry, and A is its cross-sectional area. The resistance of a normal-type sensor is calculated using and . Calculating the resistance of bump-type sensors is more complex, as it requires knowledge of the cross-sectional area of a bump. In this study, the cross-sectional areas of the protrusions were modeled as trapezoids. Following this, the resistance of a bump-type sensor is calculated using and . Here, it can be noted that is the difference between a filled EGaIn path area and the total area of the trapezoids constituting bumps (which create spaces on the path), as illustrated in Figure 14. The resistances calculated using this procedure are summarized in Table 5. is the cross-sectional area of the space where the wire will be located; to calculate the resistance of this space, is multiplied by .

Table 5.
Theoretical resistance of the EGaIn soft sensors.
3.3. Verification of Sensor Response
Practical experiments were conducted to validate the theoretical analysis of soft sensors and verify their response to pressure. The equipment used in these experiments is summarized in Table 6.

Table 6.
Summary of equipment used in sensor characterization experiments.
Measurements were obtained using a National Instruments data acquisition unit (DAQ) controlled by a LabVIEW program. This DAQ was installed with a strain/bridge input module (NI 9237) to measure the pressure applied to the sensor through the load cell together with a voltage input module (NI 9215) to measure the sensors’ resistance. Sensors were connected to the data line of the voltage module and the 5 V/1 A power line of a DC power supply to enable resistance measurement using a four-wire method. The EGaIn soft sensors were connected to the breadboard and the voltage input module using ultrafine heat-resistant flame-retardant wire. Here, longer lengths of wire were used to prevent unwanted contact on the breadboard. An illustration of these connections is shown in Figure 15.
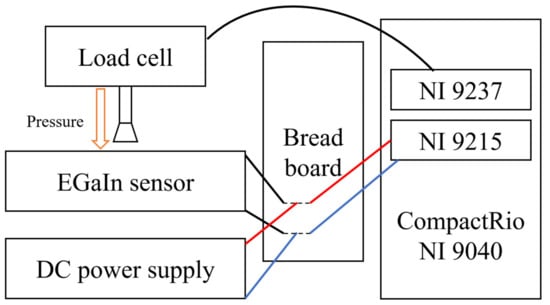
Figure 15.
Illustrative schematic and connection diagram for the resistance measurement experiment.
The calculated resistances in Table 5 only consider the resistances of the EGaIn soft sensors. For accurate comparison with the measurements obtained by the experimental system, a new value, , is defined. This value is the sum of the theoretical sensor resistance, expressed as , with the theoretical resistance of the connecting wires (expressed as ), which can be calculated using Lp3 and A3 in Table 4. Hence, is expressed as
A comparison of the values of for the two types of sensors with the measured resistances is given in Table 7. The difference between the two values is negligible for the bump-type sensor, validating the estimation procedure used in the analysis.

Table 7.
Comparison between calculated and measured sensor resistances.
A force was applied to a flathead bolt for sensing response experiments with a cross-sectional area of 38.5 . The subsequent change in resistance was monitored simultaneously with pressure, confirming that the sensors respond to an applied force. To check the sensor value change more accurately, pressure was applied to a localized area pressing three to four bumps. Figure 16 depicts the variation in sensing resistance with applied pressure. The lines in this image indicate the average value of the measured resistance, while the shaded area represents the standard deviation of these measurements. This image confirms that the inclusion of bumps on an EGaIn soft sensor improves its responsivity, defined as the slope for the range enclosed by the dotted lines in Figure 16. The bump-type sensor is approximately three times more responsive than the normal-type sensor, based on the slopes summarized in Table 8.
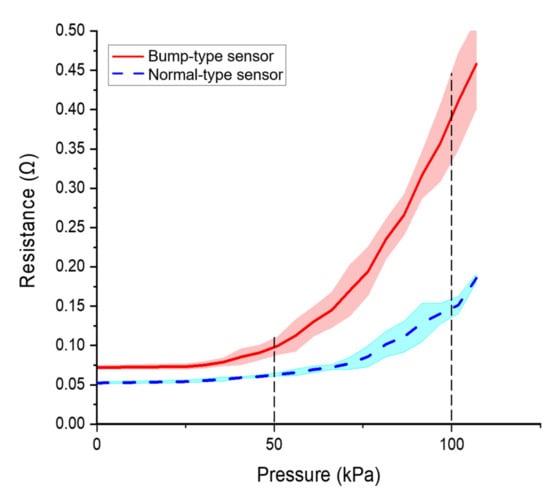
Figure 16.
Variation of resistance with applied pressure in normal- and bump-type sensors.

Table 8.
Comparison of sensor responsivity.
The hysteresis test of the bump-type EGaIn soft sensor used was carried out as shown in Figure 17. This test proves the performance of this sensor. The repeatability test was conducted by placing a weight of 1 kg on a disk with a 2 cm diameter. As a result of performing the sensing test 102 times, it was confirmed that it had an error value of about 6.32%. In addition, it was confirmed that the sensor in a state in which no pressure was applied returned to the existing resistance value.
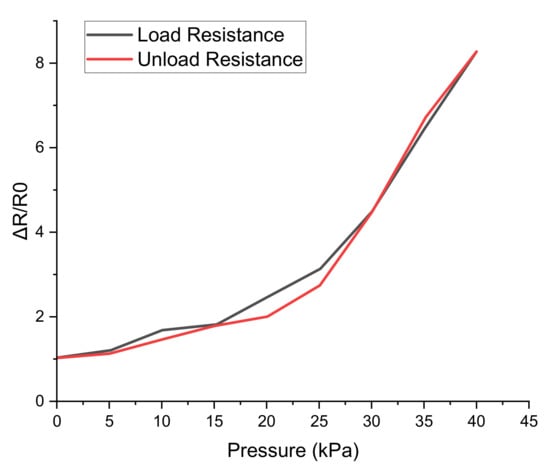
Figure 17.
Hysteresis testing of manufactured bump-type EGaIn soft sensors.
3.4. Analysis of Variable-Stiffness Structure
The EGaIn soft sensor experiment for the variable-stiffness soft gripper with the EGaIn soft sensor was performed as shown in Figure 9. In practical experiments, the gripper was instructed to hold a sphere to ensure that the same pressure was applied to each finger. The lengths of the outer and inner tendons were selected to be 10 and 20 mm, respectively, based on a previous study of variable-stiffness mechanisms [19]. The spherical object used in these experiments consisted of a PLA pocket fabricated with a 3D printer containing an additional 500 g. Hence, the object’s total weight was 613 g. An illustration of the gripper holding this object is shown in Figure 18. If the gripper does not slip an object for 30 s when gripping the object, it is defined as grasp stable; if it does, it is defined as grasp unstable. The movement shown in Figure 18 can be seen in Video S2.
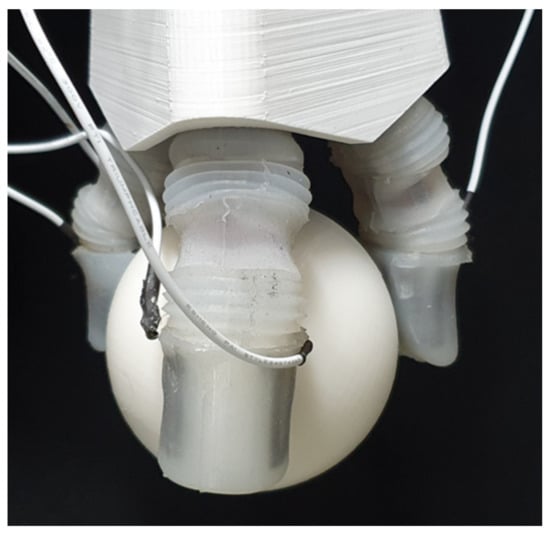
Figure 18.
Gripper holding a spherical object in adhesion experiment.
Figure 19 depicts the change in resistance in each sensor when a fingertip loses grip of the spherical object. The times labeled in this plot correspond to the images labeled in Figure 20.
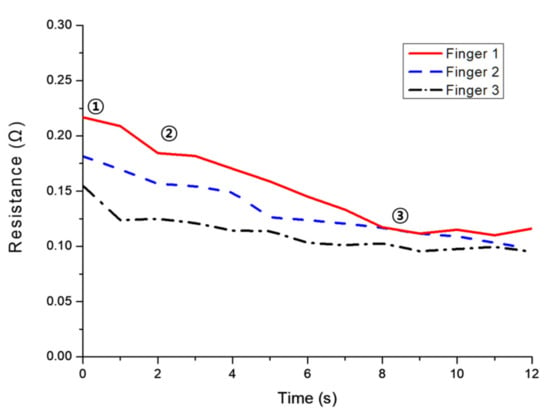
Figure 19.
Variation in sensing resistance according to fingertip shape. Numbered timestamps correspond to the labeled images in Figure 20.
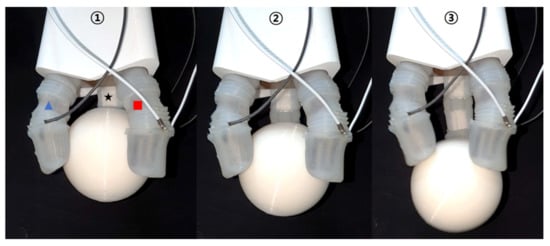
Figure 20.
Images of a spherical object slipping from the gripper during characterization experiments. Labels in this image correspond to the timestamps in Figure 19.
Figure 19 shows the change in resistance of each sensor when the tip of the other finger loses grip on a spherical object. The numbers shown in the graph correspond to the numbers in the image shown in Figure 20. Therefore, the gripper combined with the EGaIn soft sensor could see the change in the sensor’s value in the process of holding and slipping the spherical object, and the steady-state image of this gripper is shown in Figure 21.

Figure 21.
The final prototype of the soft gripper with applied EGaIn soft sensors.
Further experiments were conducted to verify the performance of the EGaIn soft sensors with the selected fingertips. The designed variable-stiffness structure offers the potential to hold objects from their exterior by applying stronger pulling forces to the inner tendons and holding objects by their interior by using stronger pulling forces to the outer tendon. The compression position of the gripper thus varies according to the gripping method. Hence, the experiment depicted in Figure 15 was repeated to determine if the location where pressure was applied on the EGaIn soft sensor could be identified. Here, we anticipated that the deformation of the sensor would vary according to location, as the sensor conforms to the fold in the fingertip shape. Therefore, the different places where pressure was applied in this experiment are as shown in Figure 22. At the same time, Figure 23 depicts experiments in progress, with the front, side, and back of the fingertip applying pressure to a flathead bolt.

Figure 22.
Selection of areas on the finger for application of pressure, for position-based sensor characterization.

Figure 23.
(Left) Front, (Middle) side, and (Right) back of fingers applying pressure to a nail in position-based characterization experiments.
The variation in resistance with applied pressure obtained from the position experiments is shown in Figure 24. From this image, it can be seen that this variation differs depending on whether the force is applied to the side, front, or back of the fingers, indicating that if this combination of soft sensor and finger shape were used in different applications, the location of pressure on each finger of the gripper could be used to identify other gripping states.
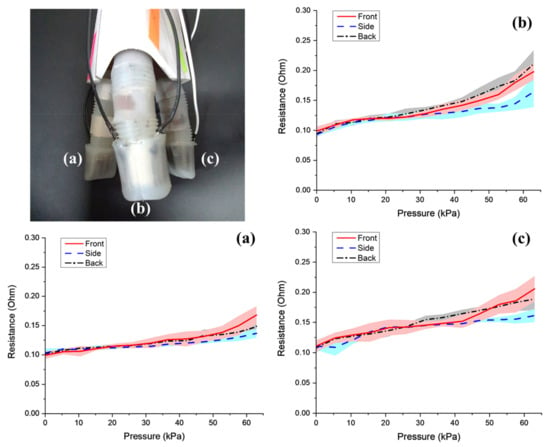
Figure 24.
Position-based sensor response for fingers labeled (a–c) in the top left picture.
The adhesion experiments from the preceding section were repeated to verify its gripping status. Pictures of the spherical object slipping from individual fingers of the gripper and falling are shown in Figure 20. The labels in this image correspond to the timestamps labeled in Figure 19, which plots the change in the resistance of the EGaIn soft sensors with respect to time. The resistance change characteristics of individual soft sensors are not significantly different because the fingertips used in this gripper were all the same shape. However, the actual resistances of the individual sensors confirm that the force an object places on each finger is different. This difference in actual resistance can be used to identify when objects are slipping from the gripper. Overall, these results confirm the feasibility of the EGaIn soft sensor, as it is functional in multiple locations and can be manufactured easily, unlike existing flexible sensors. From Figure 19, it was noted that the weight of the object being gripped could be determined based on how the resistance of an individual sensor varied with applied pressure. To confirm this, a graph of resistance according to the force applied to the front end of each finger was obtained, as shown in Figure 25.
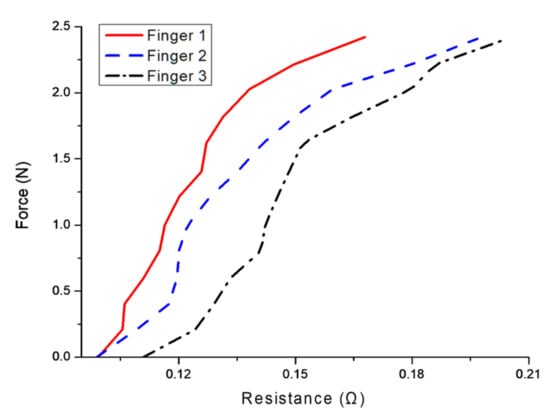
Figure 25.
Graph of force on each finger of the gripper according to the resistance of the corresponding sensor.
To estimate the force from the change in a sensor’s resistance, curve fitting was applied to Figure 25, yielding the following quadratic polynomials:
where the subscript of each function corresponds to the index of the different fingers as labeled in Figure 25. The correlation coefficients for F1(x), F2(x), and F3(x) were 0.9892, 0.9727, and 0.9638, respectively, confirming that they are suitable for estimating the force on each sensor. In theory, these expressions can subsequently be used to estimate the weight of an object. The principle of this estimation procedure is to apply pressure to the object and monitor the change in the resistances of the individual sensors. These changes in resistances are then converted to forces using (12)–(14), and the individual forces on each sensor can then be summed to estimate the weight of the object. Experiments were conducted on a range of objects to test this principle, as shown in Figure 26. In this test, each object gripped for more than 30 s was measured. For 410 g cans, the grip was unstable due to low surface friction and large volume, but griping was possible. It was confirmed that this soft gripper was stable to grip the spherical objects, the can-shaped objects were not held stably due to the low surface friction.

Figure 26.
Images of prototype gripping for a range of targets: (a) 250 mL beverage can, (b) 355 mL beverage can, (c) 410 g can, (d) 500 mL bottle of water, (e) apple, (f) orange.
The results of the experiments in Figure 26 and Table 9 indicate that the sensors can estimate the weight of grasped objects; the percentage difference between their actual and estimated weights is not significant. In Table 9, the coefficient of the friction between a can and the gripper was used to calculate the weight. When soft grippers hold objects vertically, the gripping force multiplied by the coefficient of friction is the weight of the object. The coefficient of friction between the Ecoflex 0030 and steel was found in [26] and its value is 0.918. Although there may be differences in the contact area and detailed types of materials compared to previous experimental data, the estimates of the weight with the soft sensor were calculated. However, the estimates in Figure 26d–f were calculated without considering the coefficient of friction and were not added to Table 9. In addition, the accuracy of these estimates could potentially be improved with a more precise sensor.

Table 9.
Comparison of sensor-estimated measurements and actual weight values for gripping targets.
4. Discussion
A new variable-stiffness gripper was designed in this study, referring to previous research on variable-stiffness structures to improve the performance of existing multifunctional grippers. The movement of the variable-stiffness structure was assessed through theoretical calculations, using a pseudo-rigid-body model, and verified through practical experiments. In addition to including tendons for controlling stiffness, the volume and weight of the newly manufactured gripper were each reduced by 10% and 5%, and a silicone integument was added to its exterior to increase the frictional force and improve adhesion to target objects. In combination, these modifications improve the device’s gripping ability. In addition, an EGaIn soft sensor, applied on the silicone integument, was developed for monitoring the gripping forces exerted on an object, based on changes to sensing resistance with applied pressure. Furthermore, the EGaIn soft sensor’s pressure-based mechanism allows for simultaneous recognition of grip conditions and measurement of the weight of a grasped object. When machine learning is added to a soft gripper with an EGaIn soft sensor, the soft gripper can be configured with automatic grip and it is possible to study autonomous gripping. The limitation of the EGaIn soft sensor described in this paper was that it is necessary to fabricate precisely. In the future, if soft sensors are manufactured by studying more precise manufacturing and filtering functions, it will provide an opportunity to conduct more diverse research.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/app11156957/s1, Video S1: Rotation gripping video, Video S2: Spherical object gripping video.
Author Contributions
Conceptualization, G.-S.C. and Y.-J.P.; methodology, G.-S.C.; software, G.-S.C.; validation, Y.-J.P.; formal analysis, G.-S.C.; investigation, G.-S.C.; resources, Y.-J.P.; data curation, G.-S.C.; writing—original draft preparation, G.-S.C.; writing—review and editing, Y.-J.P.; visualization, G.-S.C.; supervision, Y.-J.P.; project administration, Y.-J.P.; funding acquisition, Y.-J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work is based upon work supported by the National Research Foundation of Korea (NRF) Grant funded by the Korean Government (MSIP) No. NRF-2016R1A5A1938472, Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (2020R1I1A3073575), and 2019 Research Grant from Kangwon National University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Grebenstein, M.; Albu-Schaffer, A.; Bahls, T.; Chalon, M.; Eiberger, O.; Friedl, W.; Gruber, R.; Haddadin, S.; Hagn, U.; Haslinger, R.; et al. The DLR Hand Arm System. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3175–3182. [Google Scholar]
- In, H.; Kang, B.B.; Sin, M.; Cho, K.-J. Exo-Glove: A Wearable Robot for the Hand with a Soft Tendon Routing System. IEEE Robot. Autom. Mag. 2015, 22, 97–105. [Google Scholar] [CrossRef]
- Kang, B.B.; Choi, H.; Lee, H.; Cho, K.-J. Exo-Glove Poly II: A Polymer-Based Soft Wearable Robot for the Hand with a Tendon-Driven Actuation System. Soft Robot. 2019, 6, 214–227. [Google Scholar] [CrossRef]
- Ham, K.; Han, J.; Park, Y.-J. Soft Gripper Using Variable Stiffness Mechanism and Its Application. Int. J. Precis. Eng. Manuf. 2018, 19, 487–494. [Google Scholar] [CrossRef]
- Ham, K.; Han, J.; Jeon, J.K.; Park, Y.-J. Development of Variable Stiffness Soft Robot Hand for Improving Gripping Performance. J. Korea Acad. Ind. Coop. Soc. 2018, 19, 47–53. [Google Scholar] [CrossRef]
- Soft Robotics Inc. Soft Robotics. Available online: https://www.softroboticsinc.com/ (accessed on 1 October 2020).
- Shepherd, R.F.; Ilievski, F.; Choi, W.; Morin, S.A.; Stokes, A.A.; Mazzeo, A.D.; Chen, X.; Wang, M.; Whitesides, G.M. Multigait Soft Robot. Proc. Natl. Acad. Sci. USA 2011, 108, 20400–20403. [Google Scholar] [CrossRef] [Green Version]
- Wehner, M.; Truby, R.L.; Fitzgerald, D.J.; Mosadegh, B.; Whitesides, G.M.; Lewis, J.A.; Wood, R.J. An Integrated Design and Fabrication Strategy for Entirely Soft, Autonomous Robots. Nature 2016, 536, 451–455. [Google Scholar] [CrossRef]
- Brown, E.; Rodenberg, N.; Amend, J.; Mozeika, A.; Steltz, E.; Zakin, M.R.; Lipson, H.; Jaeger, H.M. Universal Robotic Gripper Based on the Jamming of Granular Material. Proc. Natl. Acad. Sci. USA 2010, 107, 18809–18814. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Ahn, S.-H. Shape Memory Alloy-Based Soft Gripper with Variable Stiffness for Compliant and Effective Grasping. Soft Robot. 2017, 4, 379–389. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Lee, S.; Jeong, S.; Jung, U.; Park, K.; Lee, M.; Kim, S.; Lee, J. Enhanced Moisture-Reactive Hydrophilic-PTFE-Based Flexible Humidity Sensor for Real-Time Monitoring. Sensors 2018, 18, 921. [Google Scholar] [CrossRef] [Green Version]
- Atalay, A.; Sanchez, V.; Atalay, O.; Vogt, D.M.; Haufe, F.; Wood, R.J.; Walsh, C.J. Batch Fabrication of Customizable Silicone-Textile Composite Capacitive Strain Sensors for Human Motion Tracking. Adv. Mater. Technol. 2017, 2, 1700136. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zhang, J.; Luo, Z.; Zhang, J.; Li, L.; Su, Y.; Gao, X.; Li, Y.; Tang, W.; Cao, C.; et al. Superelastic, Sensitive, and Low Hysteresis Flexible Strain Sensor Based on Wave-Patterned Liquid Metal for Human Activity Monitoring. ACS Appl. Mater. Interfaces 2020, 12, 22200–22211. [Google Scholar] [CrossRef]
- Kramer, R.K.; Majidi, C.; Sahai, R.; Wood, R.J. Soft Curvature Sensors for Joint Angle Proprioception. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 1919–1926. [Google Scholar]
- Park, Y.-L.; Chen, B.-R.; Wood, R.J. Design and Fabrication of Soft Artificial Skin Using Embedded Microchannels and Liquid Conductors. IEEE Sens. J. 2012, 12, 2711–2718. [Google Scholar] [CrossRef]
- Chossat, J.-B.; Park, Y.-L.; Wood, R.J.; Duchaine, V. A Soft Strain Sensor Based on Ionic and Metal Liquids. IEEE Sens. J. 2013, 13, 3405–3414. [Google Scholar] [CrossRef]
- Huh, T.M.; Park, Y.-J.; Cho, K.-J. Design and Analysis of a Stiffness Adjustable Structure Using an Endoskeleton. Int. J. Precis. Eng. Manuf. 2012, 13, 1255–1258. [Google Scholar] [CrossRef]
- Shintake, J.; Cacucciolo, V.; Floreano, D.; Shea, H. Soft Robotic Grippers. Adv. Mater. 2018, 30, 1707035. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ham, K.; Han, J.; Jeon, J.K.; Park, Y.-J. Parametric Study on the tendency of Stiffness Variation using Variable Stiffness Mechanism. J. Korea Acad. Ind. Coop. Soc. 2016, 17, 750–758. [Google Scholar] [CrossRef] [Green Version]
- French, S.J.; Saunders, D.J.; Ingle, G.W. The system gallium-indium. J. Phys. Chem. 1937, 42, 265–274. [Google Scholar] [CrossRef]
- Chandler, J.E.; Messer, H.H.; Ellender, G. Cytotoxicity of Gallium and Indium Ions Compared with Mercuric Ion. J. Dent. Res. 1994, 73, 1554–1559. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Zhang, K.; Yang, Z.; Jiang, S.; Ju, Z.; Li, Y.; Wang, X.; Wang, D.; Jian, M.; Zhang, Y.; et al. Epidermis Microstructure Inspired Graphene Pressure Sensor with Random Distributed Spinosum for High Sensitivity and Large Linearity. ACS Nano 2018, 12, 2346–2354. [Google Scholar] [CrossRef] [PubMed]
- Howell, L.L. Pseudo-Rigid-Body Model. In Compliant Mechanisms; Wiley-Interscience: New York, NY, USA, 2001; pp. 135–217. [Google Scholar]
- Chalhoub, M.S.; Kelly, J.M. Effect of Bulk Compressibility on the Stiffness of Cylindrical Base Isolation Bearings. Int. J. Solids Struct. 1990, 26, 743–760. [Google Scholar] [CrossRef]
- Zrnic, D.; Swatik, D.S. On the Resistivity and Surface Tension of the Eutectic Alloy of Gallium and Indium. J. Less Common Met. 1969, 18, 67–68. [Google Scholar] [CrossRef]
- Champatiray, C.; Mahanta, G.B.; Pattanayak, S.K.; Mahapatra, R.N. Analysis for Material Selection of Robot Soft Finger Used for Power Grasping. Innov. Prod. Des. Intell. Manuf. Syst. 2020, 961–970. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).