Application of FTA Analysis for Calculation of the Probability of the Failure of the Pressure Leaching Process
Abstract
1. Introduction
2. Characteristics of the Leaching Process in the Context of Risk Assessment
- To calculate the probability of the top event-the failure (early termination) of the leaching process using the FTA.
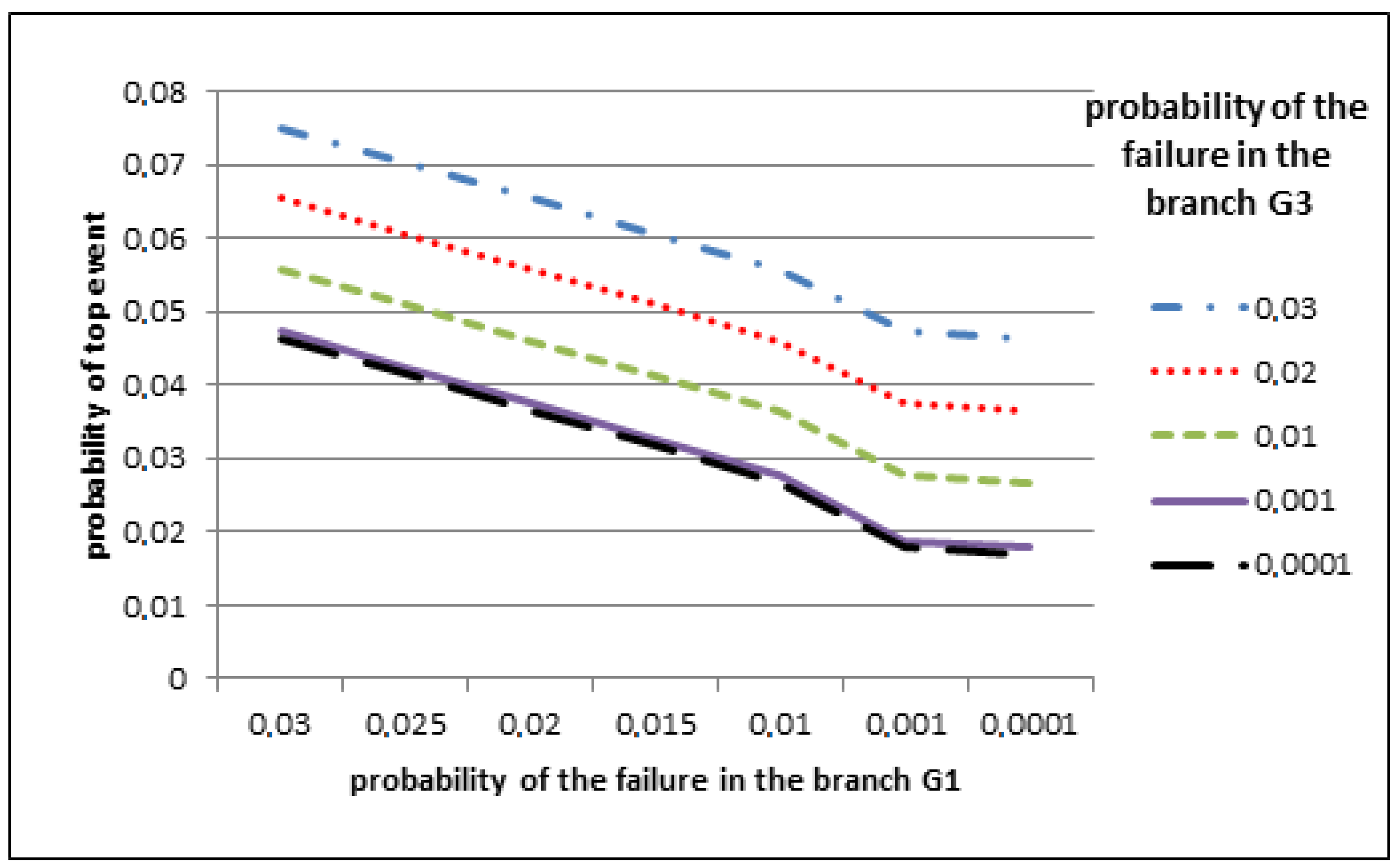
- To model the impact of the dynamic of the probability of base events on the top event using the Monte Carlo method.
- Propose an effective improvement of the leaching process in order to effectively reduce the probability of the top event.
3. Fault Tree Analysis (FTA) Analysis
- The systematic identification of all possible combinations of (basic) causes leading to the top event;
- Easy definition of the top event probability in the system or its arbitrary part;
- Creating a model (causal dependence) for examining the security of the monitored system to know the input/output interactions;
- Modelling for simulation of safety, reliability, etc.;
- Provide a transparent analytical listing of logical operations existing in the tracking system;
- Display of the monitored system in the form of a graphical model in which quantitative and qualitative data are recorded;
- Recognition of individual risk factors in the risk analysis process.
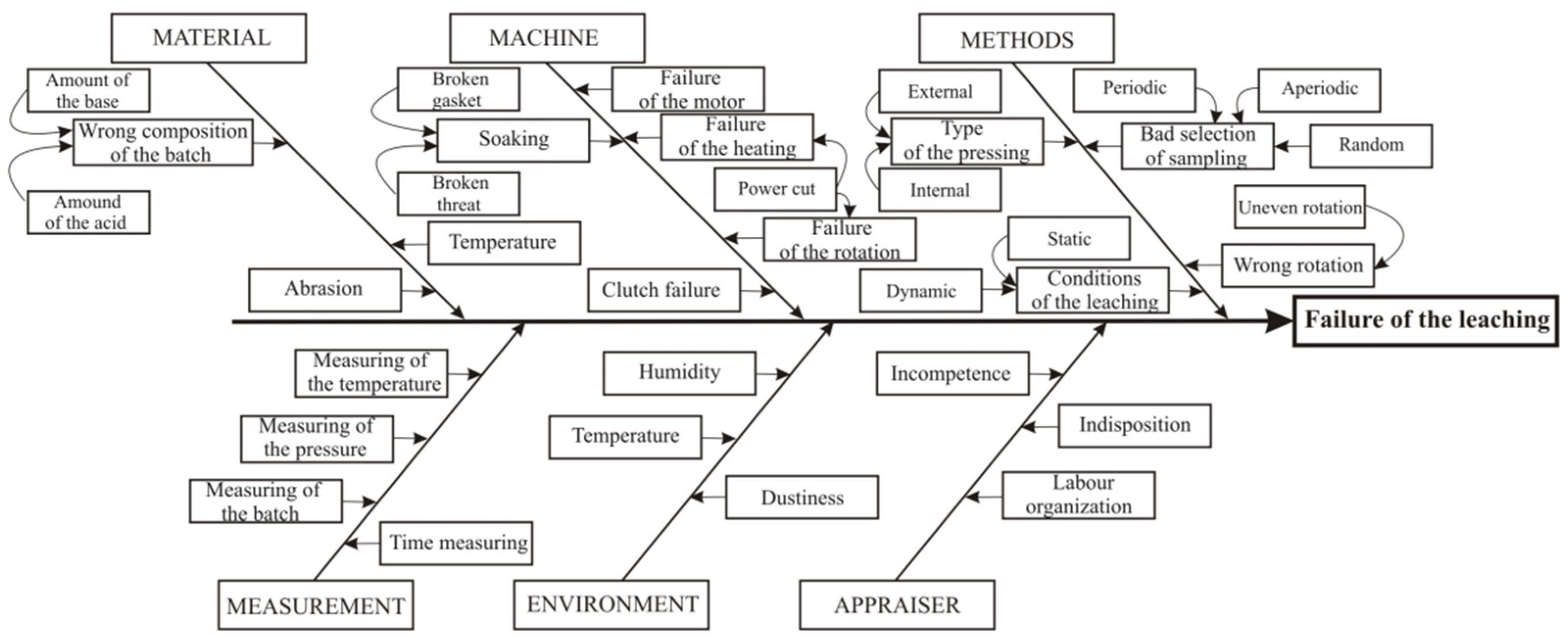
- Definition of the analyzed system, purpose and extent of the analysis, and basic assumptions that have been adopted. Prerequisites should include the conditions under which the monitored system is operated (normal operation, maintenance, special operations...). The amount of information required is subject to the purpose of the analysis. Knowledge of one person is often inadequate, and professional groups need to be set up to obtain sufficient information. In this step, it is useful to use statistical methods and quality tools (e.g., process map, Failure Mode and Effect Analysis FMEA, flowchart, regulatory diagrams, trend analysis, Pareto and Ishikawa diagram).
- Definition of a top event-specifying an undesirable event means defining the onset or existence of dangerous conditions, the inability of the system to perform the required functions. The top event must be defined clearly and unambiguously.
- Construction of the failure tree—the tree is a graphical representation consisting of individual elements that are bound by logical operations describing the observed process. It is necessary to distinguish between conditional and unconditional states in the process of the construction.
4. Monte Carlo Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tavakoli, M.; Nafar, M. Modification of the FFTA method for calculating and analyzing the human reliability of maintenance groups in power transmission grids. Int. J. Syst. Assur. Eng. Manag. 2021, 1–14. [Google Scholar] [CrossRef]
- Luo, W.; Wei, O.; Wan, H. SATMCS: An Efficient SAT-Based Algorithm and Its Improvements for Computing Minimal Cut Sets. IEEE Trans. Reliab. 2021, 70, 575–589. [Google Scholar] [CrossRef]
- Zhu, H.-L.; Liu, S.-S.; Qu, Y.-Y.; Han, X.-X.; He, W.; Cao, Y. A new risk assessment method based on belief rule base and fault tree analysis. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2021, 235, 1748006X2110114. [Google Scholar] [CrossRef]
- Hudák, R.; Šarik, M.; Dadej, R.; Živčák, J.; Harachová, D. Material and Thermal analysis of Laser Sinterted Products. Acta Mech. Autom. 2013, 7, 15–19. [Google Scholar] [CrossRef]
- Rusanen, L.; Aromaa, J.; Forsen, O. Pressure Oxidation of Pyrite-Arsenopyrite Refractory Gold Concentrate. Physicochem. Probl. Miner. Process. 2013, 49. [Google Scholar] [CrossRef]
- Correia, M.N.; Carvalho, J.; Monhemius, A. Study of the autoclave leaching of a tetrahedrite concentrate. Miner. Eng. 1993, 6, 1117–1125. [Google Scholar] [CrossRef]
- Koslides, T.; Ciminelli, V. Pressure oxidation of arsenopyrite and pyrite in alkaline solutions. Hydrometallurgy 1992, 30, 87–106. [Google Scholar] [CrossRef]
- Mikloš, V.; Fröhlich, L. Decomposition of Pyrite and Arsenopyrite by Pressure Oxidation of Tetrahedrite Raw Materials. Metalurgija 2002, 41, 29–32. [Google Scholar]
- Żarczyński, A. Environmental Hazard by Major Accidents in the Polish Chemical Industry. Zagrożenie środowiska Na Terenie Polski Ze Strony Poważnych Awarii w Zakładach Przemysłu Chemicznego. Chem. Rev. 2015, 1, 45–51. [Google Scholar] [CrossRef]
- Dobrzyńska, E. Ocena ryzyka związanego z występowaniem substancji chemicznych na stanowiskach pracy. Metody bezpomiarowe w bazie CHEMPYŁ. Przemysł Chem. 2018, 1, 155–160. [Google Scholar] [CrossRef]
- Shafiee, M.; Enjema, E.; Kolios, A. An Integrated FTA-FMEA Model for Risk Analysis of Engineering Systems: A Case Study of Subsea Blowout Preventers. Appl. Sci. 2019, 9, 1192. [Google Scholar] [CrossRef]
- Dado, M.; Hnilica, R.; Kotus, M.; Kotek, L. Use of virtual reality in machinery safety education. In Proceedings of the ICERI Proceedings, 10th International Conference of Education, Research and Innovation (ICERI2017), Seville, Spain, 16–18 November 2017; Proceedings Paper; WOS: 000429975302127. IATED-INT Association Technology Education & Development: Valencia, Spain, 2017. ISBN 978-84-697-6957-7. [Google Scholar]
- Novakova, R.; Paulikova, A.; Cekanova, K. More Wood, Better Management, Increasing Effectiveness: Starting Points and Perspective. In Proceedings of the Scientific Papers, Prague, Czech Republic, 24–26 May 2017; Dudik, R., Ed.; Česká Zemědělská Univerzita v Praze, Lesnická Fakulta: Prague, Czech Republic; WoodEMA Instituce: Zagreb, Croatia, 2017; ISBN 978-80-213-2761-0. [Google Scholar]
- Gabriska, D. Evaluation of the Level of Reliability in Hazardous Technological Processes. Appl. Sci. 2020, 11, 134. [Google Scholar] [CrossRef]
- Takahashi, M.; Anang, Y.; Watanabe, Y. A Safety Analysis Method for Control Software in Coordination with FMEA and FTA. Information. 2021, 12, 79. [Google Scholar] [CrossRef]
- Girmanová, L.; Mikloš, V.; Palfy, P.; Petrík, J.; Sütőová, A.; Šolc, M. Nástroje a Metódy Manažérstva Kvality; ELFA, s.r.o.: Košice, Slovakia, 2009; ISBN 978-80-553-0144-0. (In Slovak) [Google Scholar]
- Tureková, I.; Tomková, V.; Bagalová, T. Work at Height in Safety Work Plan Management. Adv. Mater. Res. 2014, 919, 523–526. [Google Scholar] [CrossRef]
- Halfarova, P.; Ustyugova, T.; Vykydal, D. The application of Fuzzy FMEA. In Proceedings of the 22nd International Conference on Metallurgy and Materials (METAL), Brno, Czech Republic, 15–17 May 2013; Technical University of Ostrava VSB: Ostrava, Czech Republic, 2013; pp. 1909–1913. [Google Scholar]
- Markulik, S.; Nagyova, A.; Turisova, R.; Villinsky, T. Improving Quality in the Process of Hot Rolling of Steel Sheets. Appl. Sci. 2021, 11, 5451. [Google Scholar] [CrossRef]
- Bujna, M.; Dostál, P. Assessment of Selected Equipment by Method FTA. Acta Univ. Agric. Silvic. Mendel. Brun. 2017, 65, 1655–1661. [Google Scholar] [CrossRef]
- IEC 61025. Fault Tree Analysis (FTA); International Electrotechnical Commission IEC: Geneva, Switzerland, 2006. [Google Scholar]
- Husar, J.; Knapcikova, L.; Balog, M. Implementation of Material Flow Simulation as a Learning Tool. In Advances in Design, Simulation and Manufacturing; Lecture Notes in Mechanical, Engineering; Ivanov, V., Rong, Y., Trojanowska, J., Venus, J., Liaposhchenko, O., Zajac, J., Pavlenko, I., Edl, M., Perakovic, D., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 33–41. ISBN 978-3-319-93586-7. [Google Scholar]
- Toth, T.; Hudak, R.; Zivcak, J. Dimensional verification and quality control of implants by additive manufacturing. Qual. Innov. Prosper. 2015, 19. [Google Scholar] [CrossRef]
- Monkova, K.; Hric, S.; Knapčikova, L.; Vagaska, A.; Matiskova, D. Application of simulation for product quality enhancement. In Proceedings of the International Conference on Informatics, Management Engineering and Industrial Application (IMEIA), Phuket, Thailand, 24–25 April 2016; DEStech Transactions on Engineering and Technology Research: Lancaster, PA, USA, 2016; pp. 216–220. [Google Scholar]
- Patil, R.B.; Waghmode, L.Y.; Chikali, P.B.; Mulla, T.S. An Overview of Fault Tree Analysis (FTA) Method for Reliability Analysis & Life Cycle Cost (LCC) Management. In Proceedings of the Second International Conference on Emerging Trends in Engineering (SICETE), Nagpur, India, 16–18 December 2009; p. 6. [Google Scholar]
- Plura, J. Plánování a Neustálé Zlepšování Jakosti; Computer Press: Praha, Czech Republic, 2001; ISBN 978-80-7226-543-5. (In Czech) [Google Scholar]
- Clemens, P.L. Fault Tree Analysis; Technology Sverdrup: Pittsburg, CA, USA, 1993; 96p, Available online: http://rischioatmosfereesplosive.studiomarigo.it/profiles/marigo2/images/file/1736612536.pdf (accessed on 22 July 2021).
- Vesely, W.; Stamatelatos, M.; Dugan, J.; Fragola, J.; Minarick, J.; Railsback, J. FTA Handbook with Aerospace Applications; NASA Langley Research Center: Washington, DC, USA, 2002. Available online: http://www.hq.nasa.gov/office/codeq/doctree/fthb.pdf (accessed on 22 July 2021).
- Živčák, J.; Šarik, M.; Hudák, R. FEA simulation of thermal processes during the direct metal laser sintering of Ti64 titanium powder. Measurement 2016, 94, 893–901. [Google Scholar] [CrossRef]
- Pačaiová, H.; Andrejiová, M.; Balažiková, M.; Tomašková, M.; Gazda, T.; Chomová, K.; Hijj, J.; Salaj, L. Methodology for Complex Efficiency Evaluation of Machinery Safety Measures in a Production Organization. Appl. Sci. 2021, 11, 453. [Google Scholar] [CrossRef]
- Blaško, P.; Petrík, J. FTA analysis of the failure in the horizontal fluidity test. Met. Mater. Eng. 2015, 21, 229–240. [Google Scholar] [CrossRef]
- Liu, J.; Yang, H.; Wei, D.; Song, X. Time Distribution Simulation of Household Power Load Based on Travel Chains and Monte Carlo–A Study of Beijing in Summer. Sustainability 2021, 13, 6651. [Google Scholar] [CrossRef]
- Knežo, D. O Metóde Monte Carlo a Možnostiach jej Aplikácií. Transf. Inovácií 2012, 24, 178–181. Available online: https://www.sjf.tuke.sk/transferinovacii/pages/archiv/transfer/24-2012/pdf/178-181.pdf (accessed on 22 July 2021). (In Slovak).
- Raychaudhuri, S. Introduction to Monte Carlo simulation. In Proceedings of the 2008 Winter Simulation Conference, Miami, FL, USA, 7–10 December 2008; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2008; pp. 91–100. [Google Scholar]
- Kuselman, I.; Pennecchi, F.; Epstein, M.; Fajgelj, A.; Ellison, S. Monte Carlo simulation of expert judgments on human errors in chemical analysis—A case study of ICP–MS. Talanta 2014, 130, 462–469. [Google Scholar] [CrossRef]
- Sienkowski, S. Estimation of Random Variable Distribution Parameters by the Monte Carlo Method. Metrol. Meas. Syst. 2013, 20, 249–262. [Google Scholar] [CrossRef]
- Sabol, R.; Klein, P.; Ryba, T.; Hvizdos, L.; Varga, R.; Rovnak, M.; Sulla, I.; Mudronova, D.; Galik, J.; Polacek, I.; et al. Novel Applications of Bistable Magnetic Microwires. Acta Physica Polonica A 2017, 131, 1150–1152. [Google Scholar] [CrossRef]
- Özfirat, M.K.; Özkan, E.; Kahraman, B.; Şengün, B.; Yetkin, M.E. Integration of risk matrix and event tree analysis: A natural stone plant case. Sadhana 2017, 42, 1741–1749. [Google Scholar] [CrossRef]

| Concentrate | Fe | As | S | SiO2 | Al2O3 | Au | Sb | Cu |
| 27.00 | 7.78 | 23.76 | 15.6 | 9.88 | 0.0041 | 0.23 | 0.17 |
| Code of Factor | Probability | Code of Factor | Probability | Code of Factor | Probability |
|---|---|---|---|---|---|
| A | 0.001 | B | 0.001 | C | 0.005 |
| D | 0.004 | E | 0.0095 | F | 0.001 |
| G | 0.002 | H | 0.003 | I | 0.0005 |
| J | 0.004 | K | 0.001 | L | 0.002 |
| M | 0.001 | N | 0.001 | O | 0.002 |
| P | 0.0005 | Q | 0.0005 | R | 0.001 |
| S | 0.002 | T | 0.001 | U | 0.001 |
| V | 0.002 | W | 0.0002 | X | 0.0005 |
| Y | 0.002 | Z | 0.001 | AA | 0.0005 |
| AB | 0.001 | AC | 0.00239 | AD | 0.001 |
| AE | 0.0005 | AF | 0.0005 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markulik, S.; Šolc, M.; Petrík, J.; Balážiková, M.; Blaško, P.; Kliment, J.; Bezák, M. Application of FTA Analysis for Calculation of the Probability of the Failure of the Pressure Leaching Process. Appl. Sci. 2021, 11, 6731. https://doi.org/10.3390/app11156731
Markulik S, Šolc M, Petrík J, Balážiková M, Blaško P, Kliment J, Bezák M. Application of FTA Analysis for Calculation of the Probability of the Failure of the Pressure Leaching Process. Applied Sciences. 2021; 11(15):6731. https://doi.org/10.3390/app11156731
Chicago/Turabian StyleMarkulik, Stefan, Marek Šolc, Jozef Petrík, Michaela Balážiková, Peter Blaško, Juraj Kliment, and Martin Bezák. 2021. "Application of FTA Analysis for Calculation of the Probability of the Failure of the Pressure Leaching Process" Applied Sciences 11, no. 15: 6731. https://doi.org/10.3390/app11156731
APA StyleMarkulik, S., Šolc, M., Petrík, J., Balážiková, M., Blaško, P., Kliment, J., & Bezák, M. (2021). Application of FTA Analysis for Calculation of the Probability of the Failure of the Pressure Leaching Process. Applied Sciences, 11(15), 6731. https://doi.org/10.3390/app11156731









