Contribution of Particle–Wall Distance and Rotational Motion of a Single Confined Elliptical Particle to the Effective Viscosity in Pressure-Driven Plane Poiseuille Flows
Abstract
1. Introduction
2. Numerical Methods
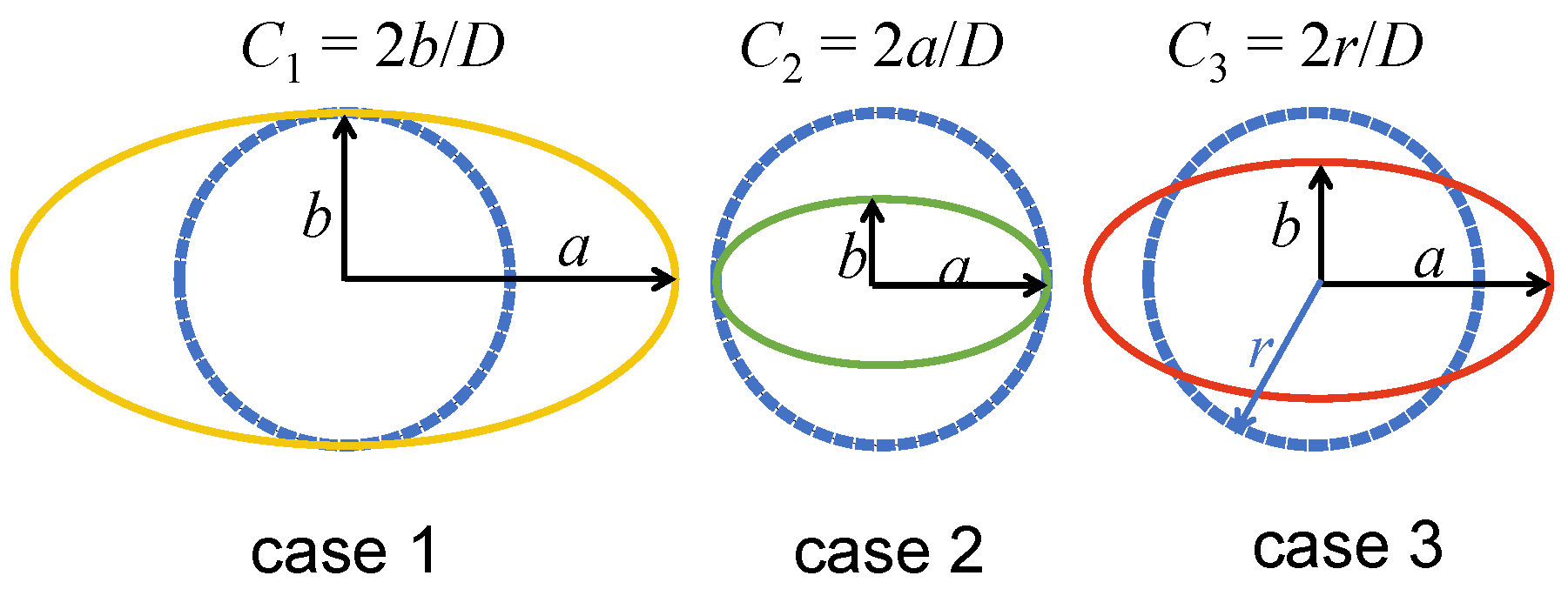
2.1. Computational Models
2.2. Governing Equation for Fluid Part
2.3. Governing Equation for Particles
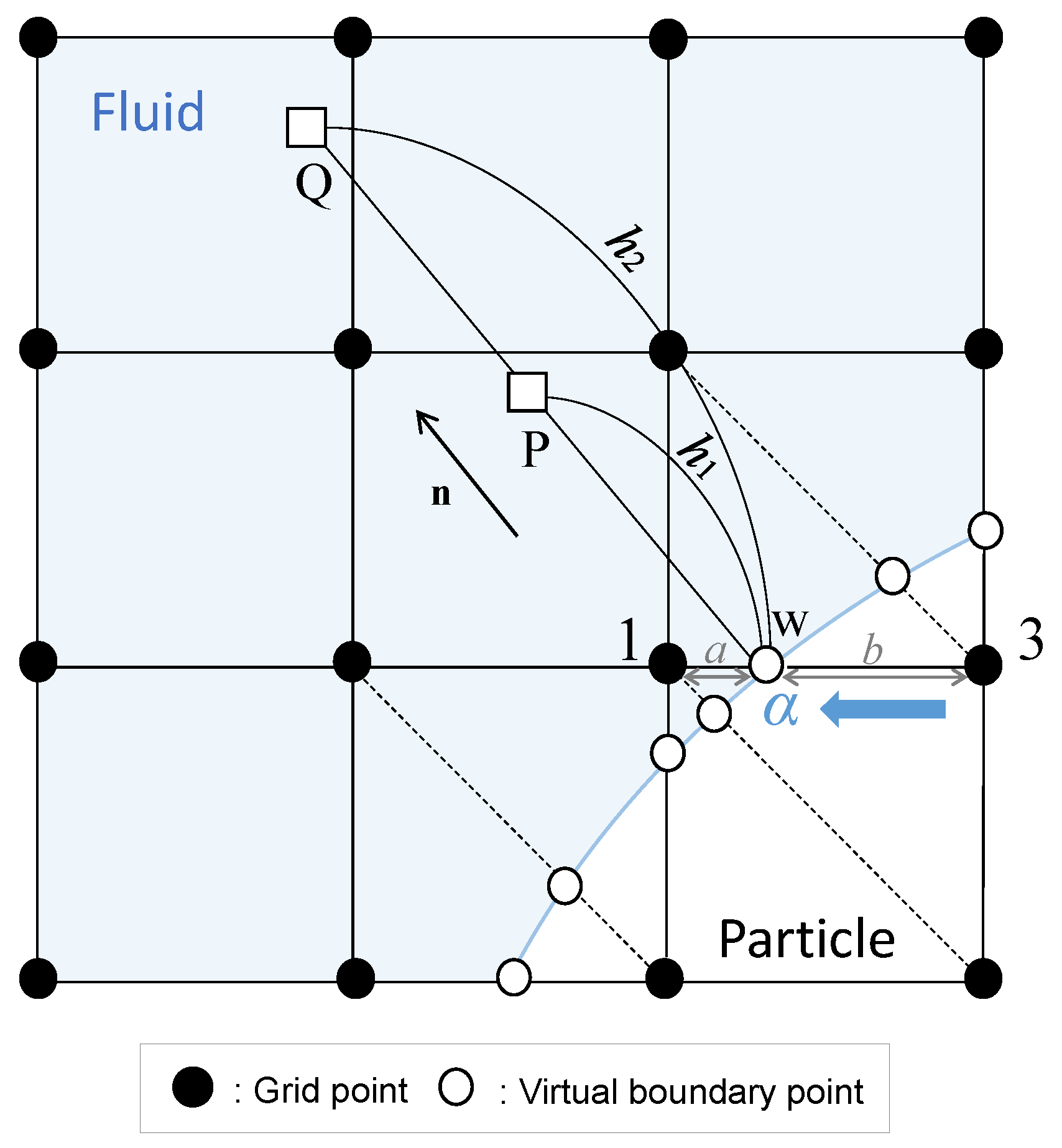
2.4. Virtual Flux Method
2.5. Lift Coefficient
2.6. Relative Viscosity
3. Results and Discussion
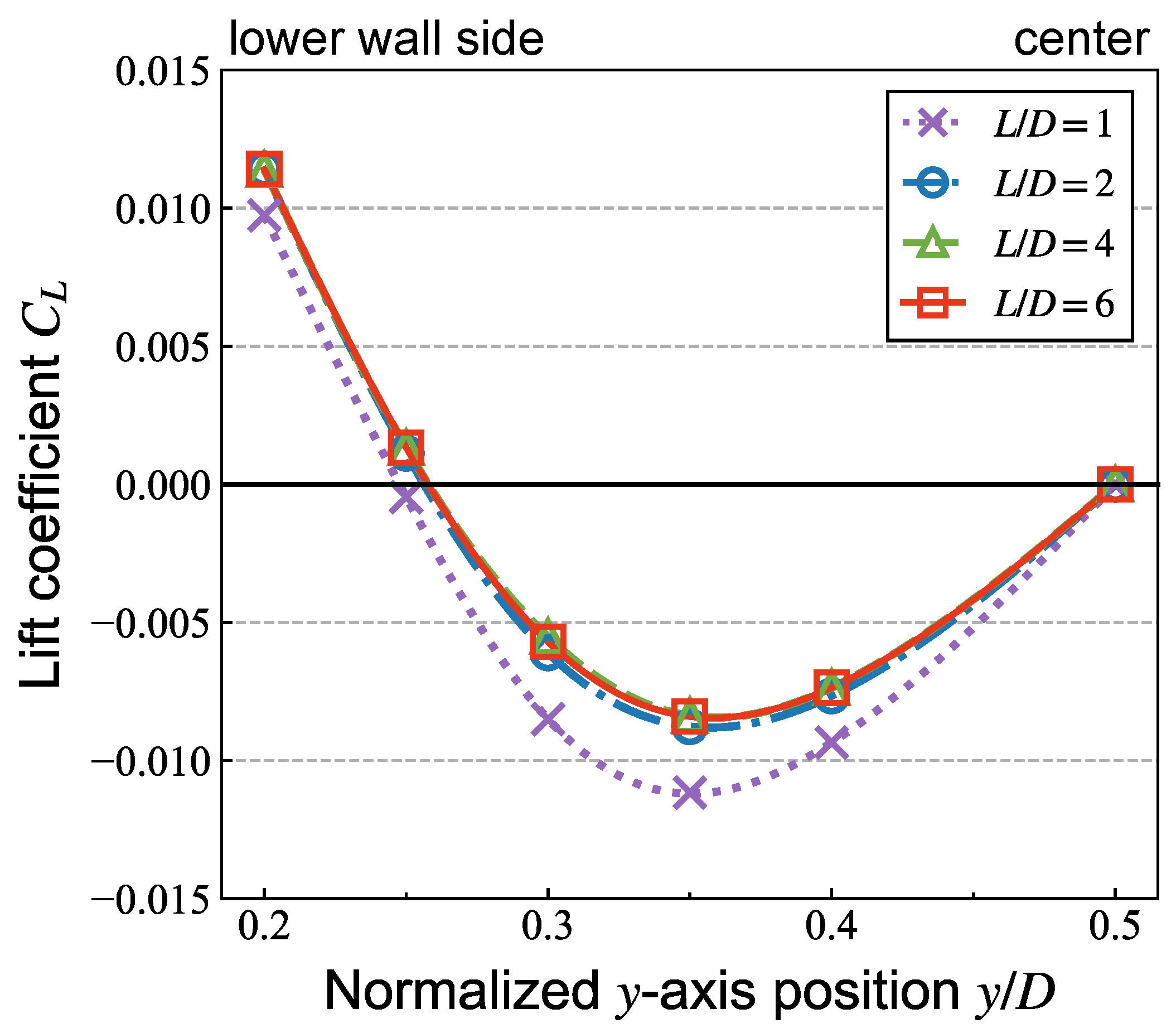
3.1. Periodic Length and Grid Resolution
3.2. Effects of Aspect Ratio of Elliptical Particle on the Equilibrium Position Due to Inertial Migration
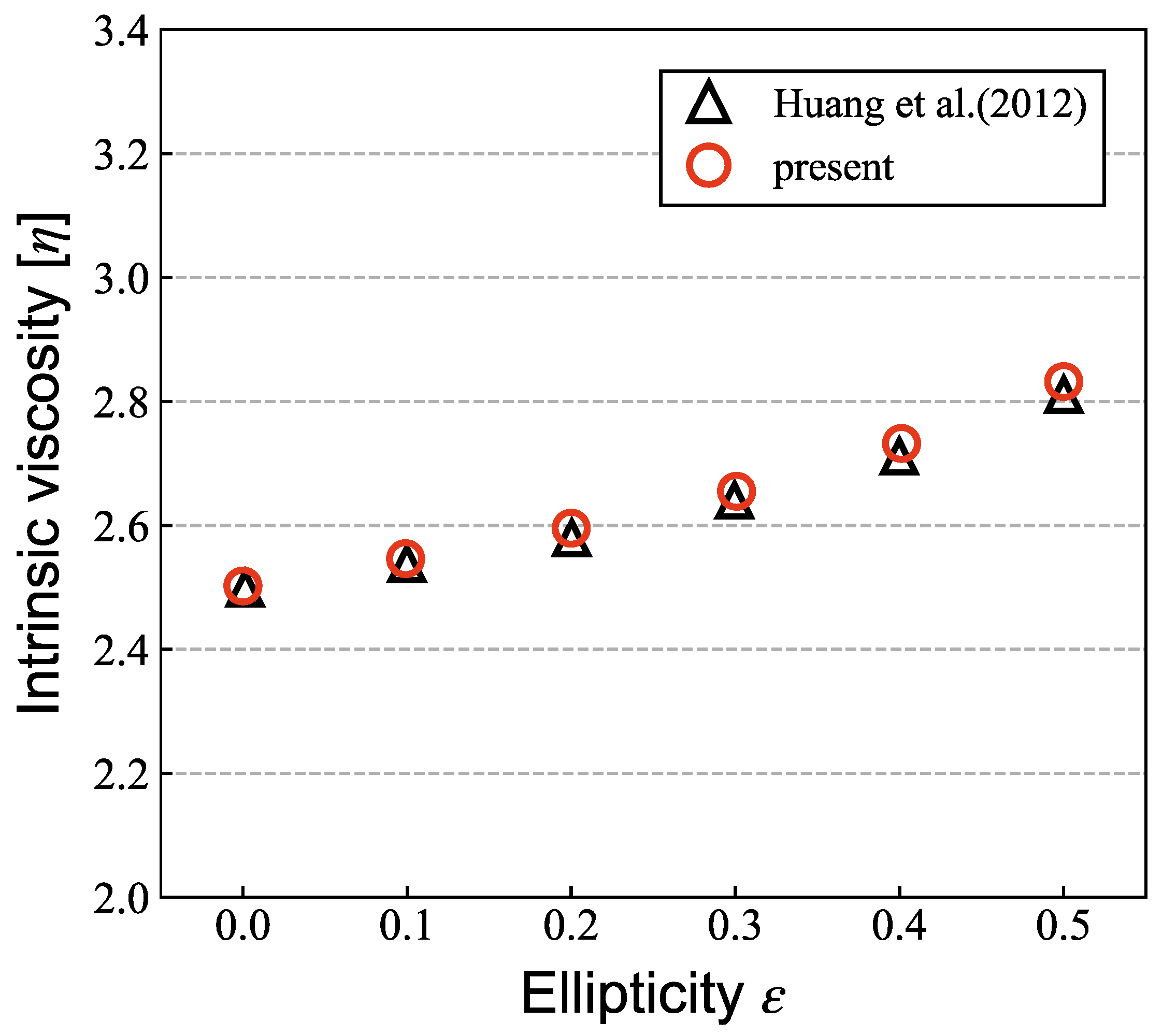
3.3. Effects of Aspect Ratio of Elliptical Particle on the Effective Viscosity
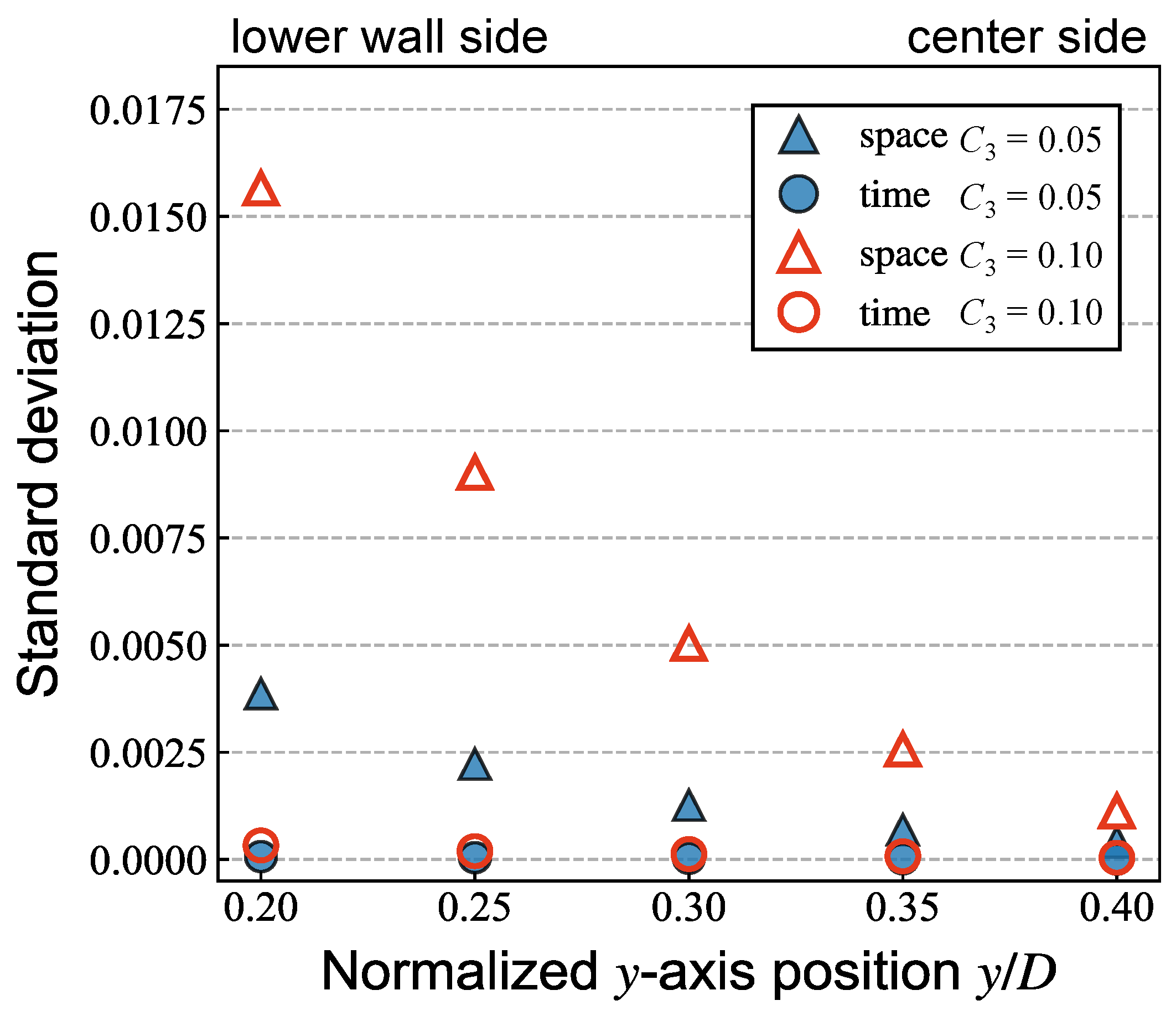
3.4. Spatial and Temporal Changes in the Effective Viscosity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| AR | aspect ratio |
| a | semi-major axis |
| b | semi-minor axis |
| C (C1, C2, C3) | confinement |
| cs | sound speed |
| c | lattice speed |
| D | channel width (characteristic length) |
| Dp | diameter of sphere |
| eα | discrete velocity vector |
| fα | distribution function |
| equilibrium distribution function | |
| non-equilibrium distribution function | |
| virtual distribution function | |
| virtual equilibrium distribution function | |
| Fp | total force vector acting on the particle |
| I | moment of inertia |
| L | channel length |
| m | mass of the suspended particle |
| n | normal unit vector |
| p0 | reference pressure |
| pp | pressure on the solid particle surface |
| Δp0 | pressure drop for particle-free flow |
| Δp | pressure drop |
| pα | pressure distribution function |
| Re | Reynolds number |
| Rep | particle Reynolds number |
| r | radius of circular particle |
| t | time |
| Tp | torque for particle |
| Tw | stress tensor |
| U | characteristic velocity |
| u | fluid velocity vector |
| Δx, Δy | grid resolution |
| xp | position vector for particle |
| yeq | equilibrium position of inertial migration |
| y0 | initial position of a particle in y-coordinate |
| wα | weight coefficients |
| ε | ellipticity |
| effective viscosity | |
| viscosity of solvent | |
| [η] | intrinsic viscosity |
| θp | particle angle |
| non-equilibrium stress tensor | |
| ρ | fluid density |
| τ | single relaxation time |
| τw | shear stress tensor |
| τ0 | wall shear stress for particle-free flow |
| area fraction |
Abbreviations
| eq | equilibrium |
| neq | non-equilibrium |
| eff | effective |
Appendix A
References
- Stickel, J.; Powell, R.L. Fluid Mechanics and Rheology of Dense Suspensions. Annu. Rev. Fluid Mech. 2005, 37, 129–149. [Google Scholar] [CrossRef]
- Segré, G.; Silberberg, A. Behaviour of macroscopic rigid spheres in Poiseuille flow: Part 2. Experimental results and interpretation. J. Fluid Mech. 1962, 14, 136–157. [Google Scholar] [CrossRef]
- Fukui, T.; Kawaguchi, M.; Morinishi, K. Numerical Study of the Microstructure of a Dilute Suspension to Assess Its Thixotropic Behavior by a Two-Way Coupling Scheme. Adv. Fluid Mech. XIII 2020, 128, 47–58. [Google Scholar] [CrossRef]
- Chen, S.-D.; Pan, T.-W.; Chang, C.-C. The motion of a single and multiple neutrally buoyant elliptical cylinders in plane Poiseuille flow. Phys. Fluids 2012, 24, 103302. [Google Scholar] [CrossRef]
- Wen, B.; Chen, H.; Qin, Z.; He, B.; Zhang, C. Lateral migration and nonuniform rotation of suspended ellipse in Poiseuille flow. Comput. Math. Appl. 2019, 78, 1142–1153. [Google Scholar] [CrossRef]
- Einstein, A. Eine neue bestimmung der molekuldimensionenm. Ann. Phys. 1906, 19, 289–306. [Google Scholar] [CrossRef]
- Brady, J.F. The Einstein viscosity correction in n dimensions. Int. J. Multiph. Flow 1984, 10, 113–114. [Google Scholar] [CrossRef]
- Liu, J.; Li, C.; Ye, M.; Liu, Z. On the shear viscosity of dilute suspension containing elliptical porous particles at low Reynolds number. Powder Technol. 2019, 354, 108–114. [Google Scholar] [CrossRef]
- Jeffery, G.B. The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1922, 102, 161–179. [Google Scholar] [CrossRef]
- Huang, H.; Wu, Y.; Lu, X. Shear viscosity of dilute suspensions of ellipsoidal particles with a lattice Boltzmann method. Phys. Rev. E 2012, 86, 046305. [Google Scholar] [CrossRef] [PubMed]
- Doyeux, V.; Priem, S.; Jibuti, L.; Farutin, A.; Ismail, M.; Peyla, P. Effective viscosity of two-dimensional suspensions: Confinement effects. Phys. Rev. Fluids 2016, 1, 043301. [Google Scholar] [CrossRef]
- Fukui, T.; Kawaguchi, M.; Morinishi, K. A two-way coupling scheme to model the effects of particle rotation on the rheological properties of a semidilute suspension. Comput. Fluids 2018, 173, 6–16. [Google Scholar] [CrossRef]
- Fukui, T.; Kawaguchi, M.; Morinishi, K. Numerical study on the inertial effects of particles on the rheology of a suspension. Adv. Mech. Eng. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Xiong, W.; Zhang, J. Shear Stress Variation Induced by Red Blood Cell Motion in Microvessel. Ann. Biomed. Eng. 2010, 38, 2649–2659. [Google Scholar] [CrossRef]
- Jou, L.-D.; Lee, D.; Morsi, H.; Mawad, M. Wall Shear Stress on Ruptured and Unruptured Intracranial Aneurysms at the Internal Carotid Artery. Am. J. Neuroradiol. 2008, 29, 1761–1767. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J.; Guo, Y.; Ku, X. Motion and equilibrium position of elliptical and rectangular particles in a channel flow of a power-law fluid. Powder Technol. 2021, 377, 585–596. [Google Scholar] [CrossRef]
- Başaǧaoǧlu, H.; Succi, S.; Wyrick, D.; Blount, J. Particle Shape Influences Settling and Sorting Behavior in Microfluidic Domains. Sci. Rep. 2018, 8, 8583. [Google Scholar] [CrossRef] [PubMed]
- Izham, M.; Fukui, T.; Morinishi, K. Application of Regularized Lattice Boltzmann Method for Incompressible Flow Simulation at High Reynolds Number and Flow with Curved Boundary. J. Fluid Sci. Technol. 2011, 6, 812–822. [Google Scholar] [CrossRef]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. EPL Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- He, X.; Luo, L.-S. Lattice Boltzmann Model for the Incompressible Navier–Stokes Equation. J. Stat. Phys. 1997, 88, 927–944. [Google Scholar] [CrossRef]
- Mei, R.; Yu, D.; Shyy, W.; Luo, L.-S. Force evaluation in the lattice Boltzmann method involving curved geometry. Phys. Rev. E 2002, 65, 041203. [Google Scholar] [CrossRef]
- Tanno, I.; Morinishi, K.; Matsuno, K.; Nishida, H. Validation of Virtual Flux Method for Forced Convection Flow. JSME Int. J. Ser. B 2006, 49, 1141–1148. [Google Scholar] [CrossRef]
- Morinishi, K.; Fukui, T. An Eulerian approach for fluid–structure interaction problems. Comput. Fluids 2012, 65, 92–98. [Google Scholar] [CrossRef]
- Peskin, C.S. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Su, J.; Chen, X.; Hu, G. Inertial migrations of cylindrical particles in rectangular microchannels: Variations of equilibrium positions and equivalent diameters. Phys. Fluids 2018, 30, 032007. [Google Scholar] [CrossRef]
- Udono, H.; Sakai, M. Numerical evaluation of lift forces acting on a solid particle in a microchannel. J. Soc. Powder Technol. Japan 2017, 54, 454–459. [Google Scholar] [CrossRef][Green Version]
- Pozrikidis, C. Orientation statistics and effective viscosity of suspensions of elongated particles in simple shear flow. Eur. J. Mech. B/Fluids 2005, 24, 125–136. [Google Scholar] [CrossRef]
- Inamuro, T.; Maeba, K.; Ogino, F. Flow between parallel walls containing the lines of neutrally buoyant circular cylinders. Int. J. Multiph. Flow 2000, 26, 1981–2004. [Google Scholar] [CrossRef]
- Freund, J.B.; Vermot, J. The Wall-stress Footprint of Blood Cells Flowing in Microvessels. Biophys. J. 2014, 106, 752–762. [Google Scholar] [CrossRef]

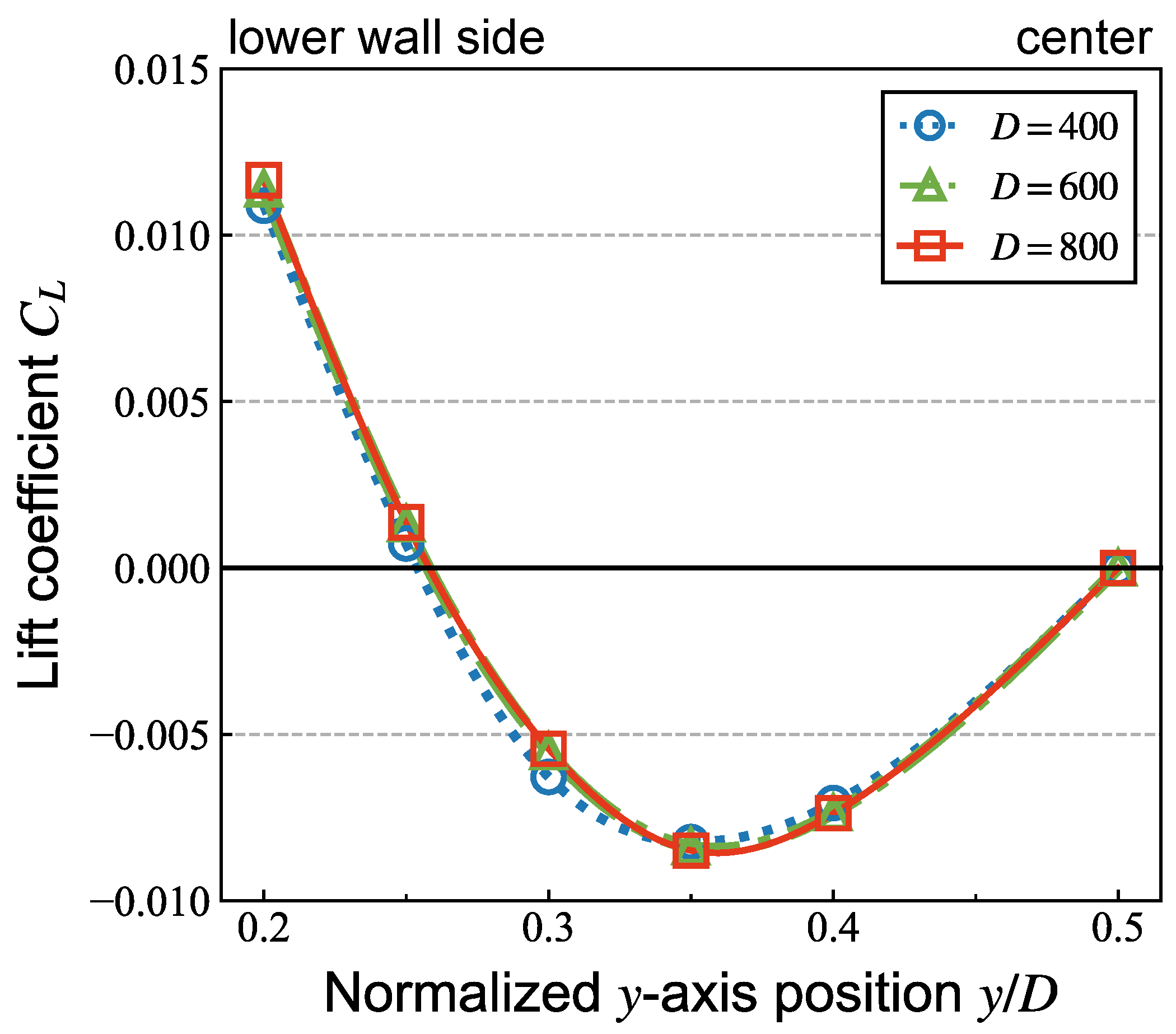
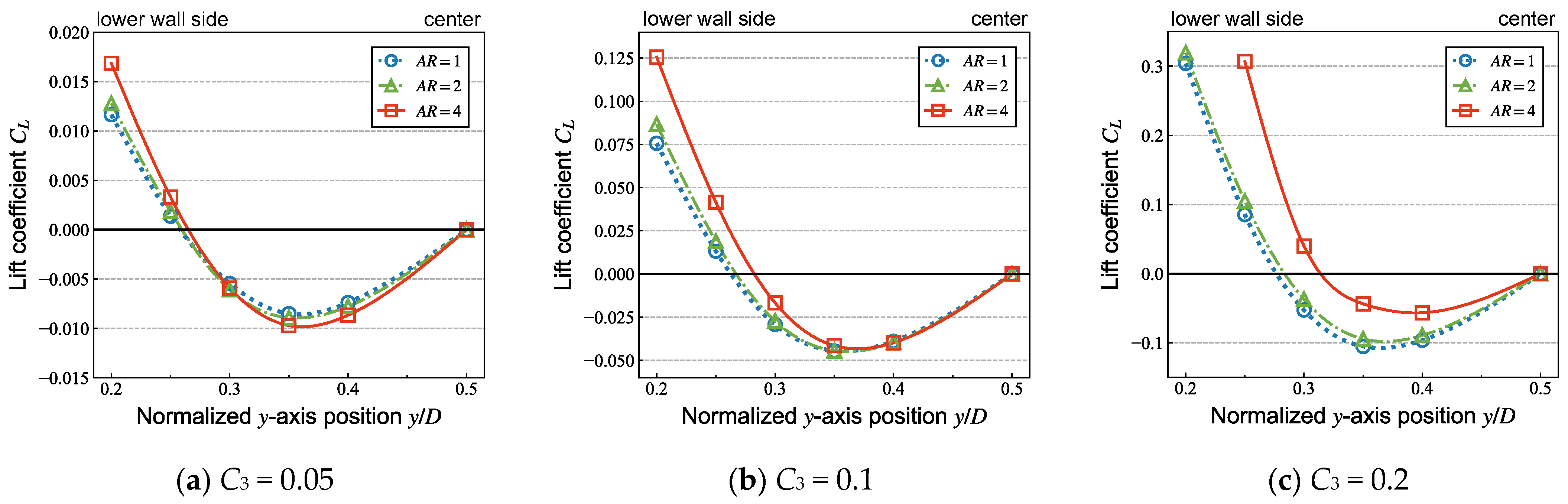


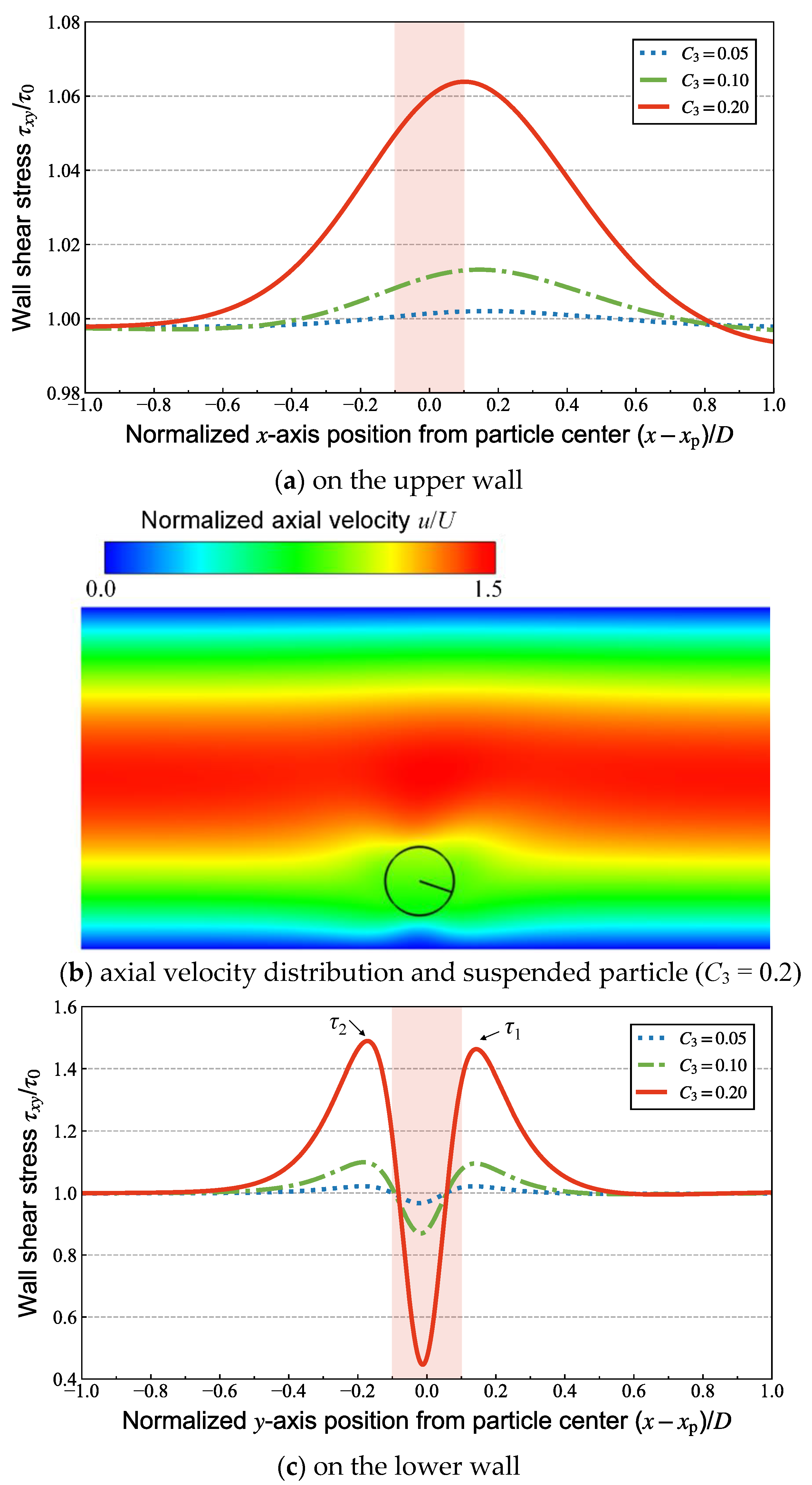
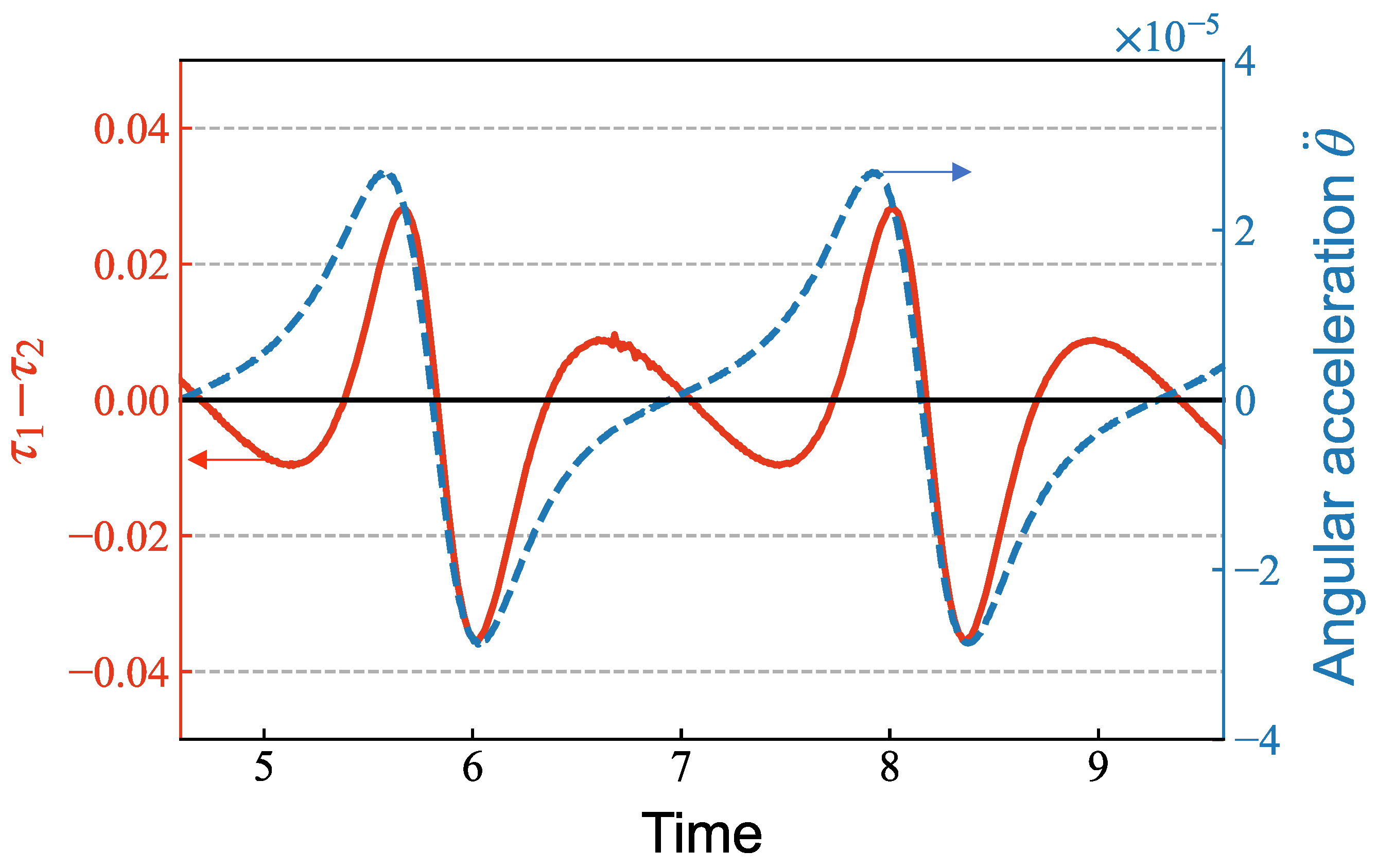
| L/D [-] | yeq/D [-] |
|---|---|
| 1 | 0.248 |
| 2 | 0.256 |
| 4 | 0.258 |
| 6 | 0.258 |
| Number of Cells for D [Cells] | Number of Cells for 2r [Cells] | yeq/D [-] |
|---|---|---|
| 400 | 20 | 0.255 |
| 600 | 30 | 0.258 |
| 800 | 40 | 0.258 |
| AR [-] | yeq/D [-] | ||
|---|---|---|---|
| C3 = 0.05 | C3 = 0.1 | C3 = 0.2 | |
| 1 | 0.258 | 0.263 | 0.277 |
| 2 | 0.260 | 0.267 | 0.284 |
| 4 | 0.260 | 0.282 | 0.314 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawaguchi, M.; Fukui, T.; Morinishi, K. Contribution of Particle–Wall Distance and Rotational Motion of a Single Confined Elliptical Particle to the Effective Viscosity in Pressure-Driven Plane Poiseuille Flows. Appl. Sci. 2021, 11, 6727. https://doi.org/10.3390/app11156727
Kawaguchi M, Fukui T, Morinishi K. Contribution of Particle–Wall Distance and Rotational Motion of a Single Confined Elliptical Particle to the Effective Viscosity in Pressure-Driven Plane Poiseuille Flows. Applied Sciences. 2021; 11(15):6727. https://doi.org/10.3390/app11156727
Chicago/Turabian StyleKawaguchi, Misa, Tomohiro Fukui, and Koji Morinishi. 2021. "Contribution of Particle–Wall Distance and Rotational Motion of a Single Confined Elliptical Particle to the Effective Viscosity in Pressure-Driven Plane Poiseuille Flows" Applied Sciences 11, no. 15: 6727. https://doi.org/10.3390/app11156727
APA StyleKawaguchi, M., Fukui, T., & Morinishi, K. (2021). Contribution of Particle–Wall Distance and Rotational Motion of a Single Confined Elliptical Particle to the Effective Viscosity in Pressure-Driven Plane Poiseuille Flows. Applied Sciences, 11(15), 6727. https://doi.org/10.3390/app11156727





