A Co-Rotational Meshfree Method for the Geometrically Nonlinear Analysis of Structures
Abstract
:1. Introduction
2. Theoretical Formulation
2.1. Basic Assumptions
- The Timoshenko beam hypothesis is valid.
- The theory is limited to elasticity problems.
- The twist rate and unit extension of the centroid axis of the beam are uniform.
- The displacements and rotations of the beam can be large.
- The out-of-plane warping of the cross section is excluded.
2.2. Geometry and Kinematics of Three-Dimensional Beam
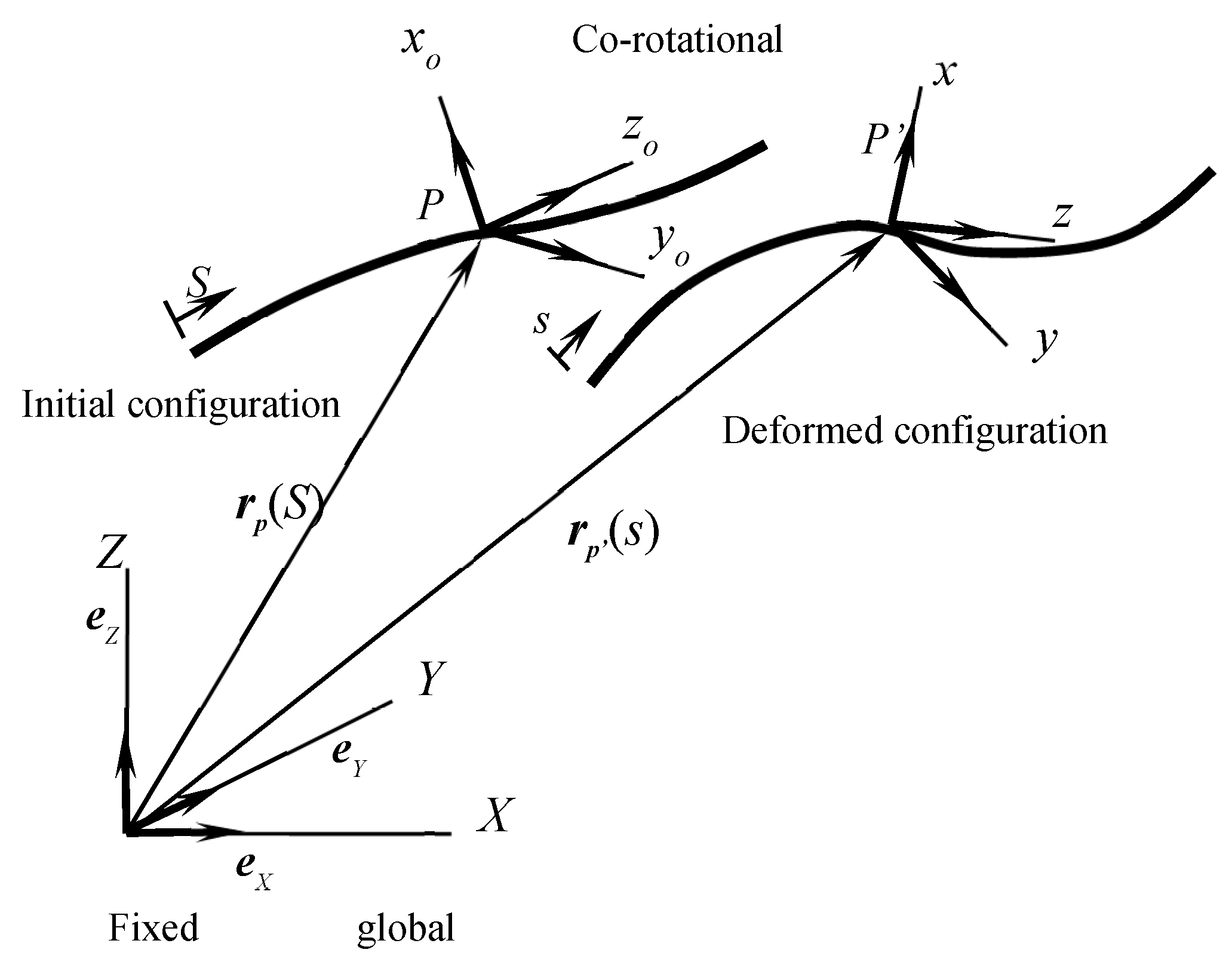
2.2.1. Coordinate System
2.2.2. Kinematics of Deformed Beam
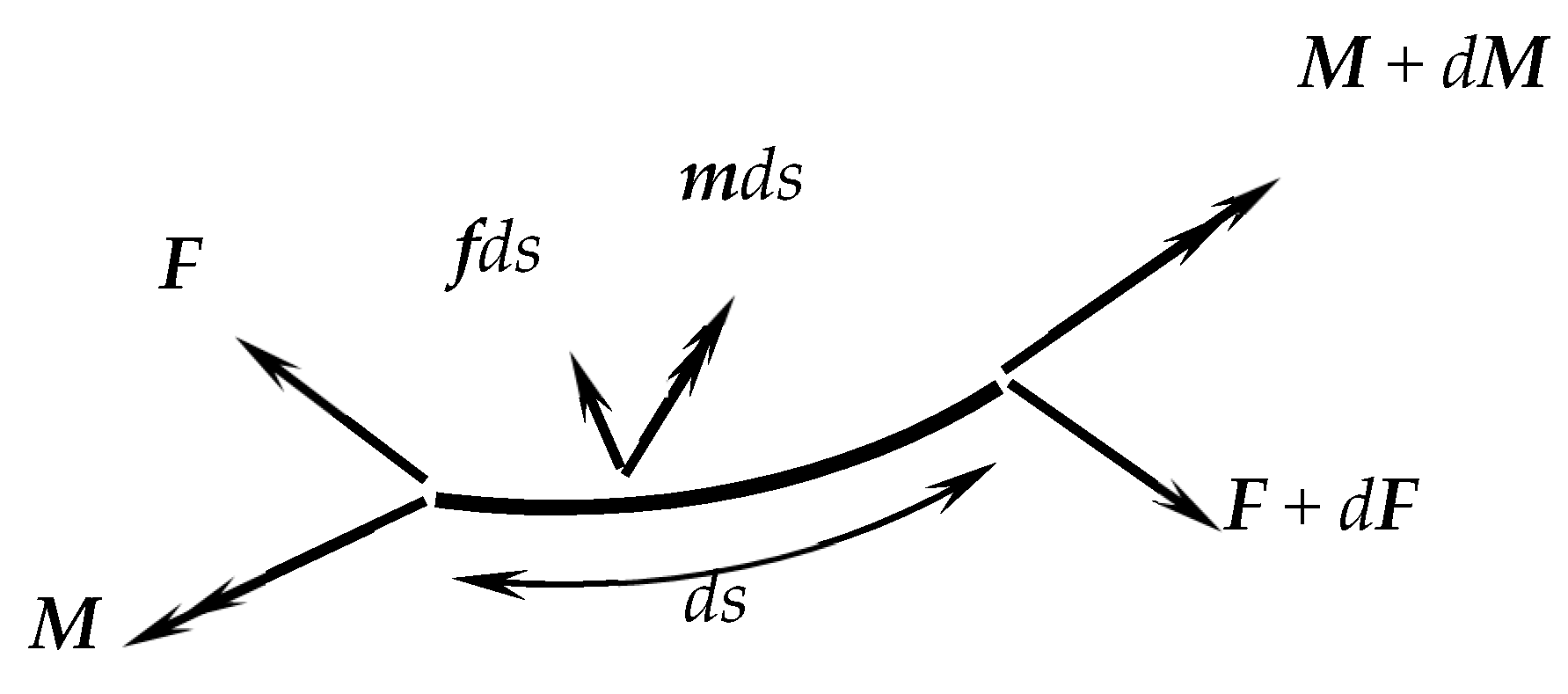
2.3. Equilibrium and Constitutive Equations
2.4. Governing Equations
3. Differential Reproducing Kernel Approximation Collocation Method (DRK)
3.1. Reproducing Kernel Approximation
3.2. Differential Reproducing Kernel Approximation
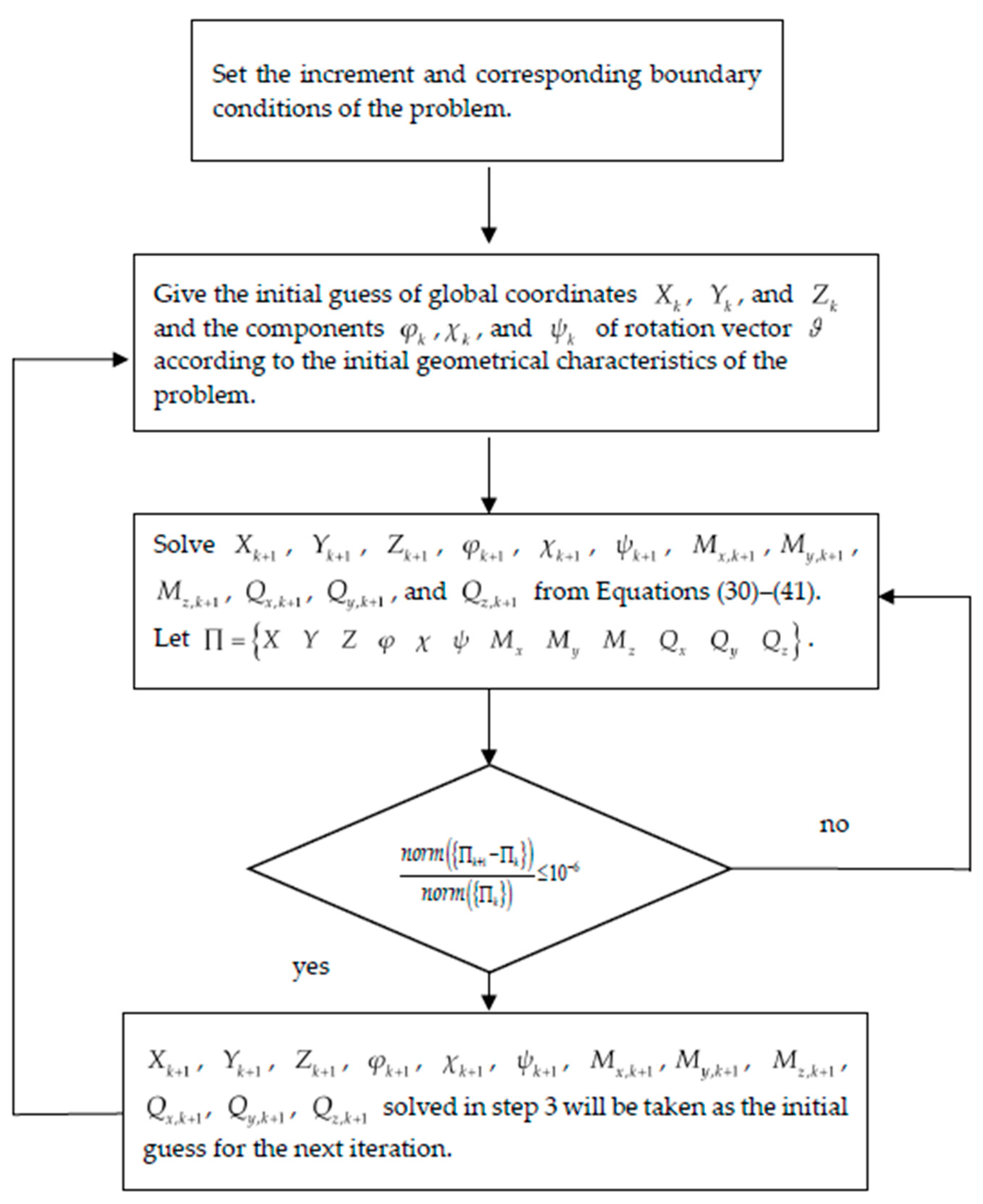
3.3. Strategy for Incremental–Iterative Procedure
4. Numerical Examples
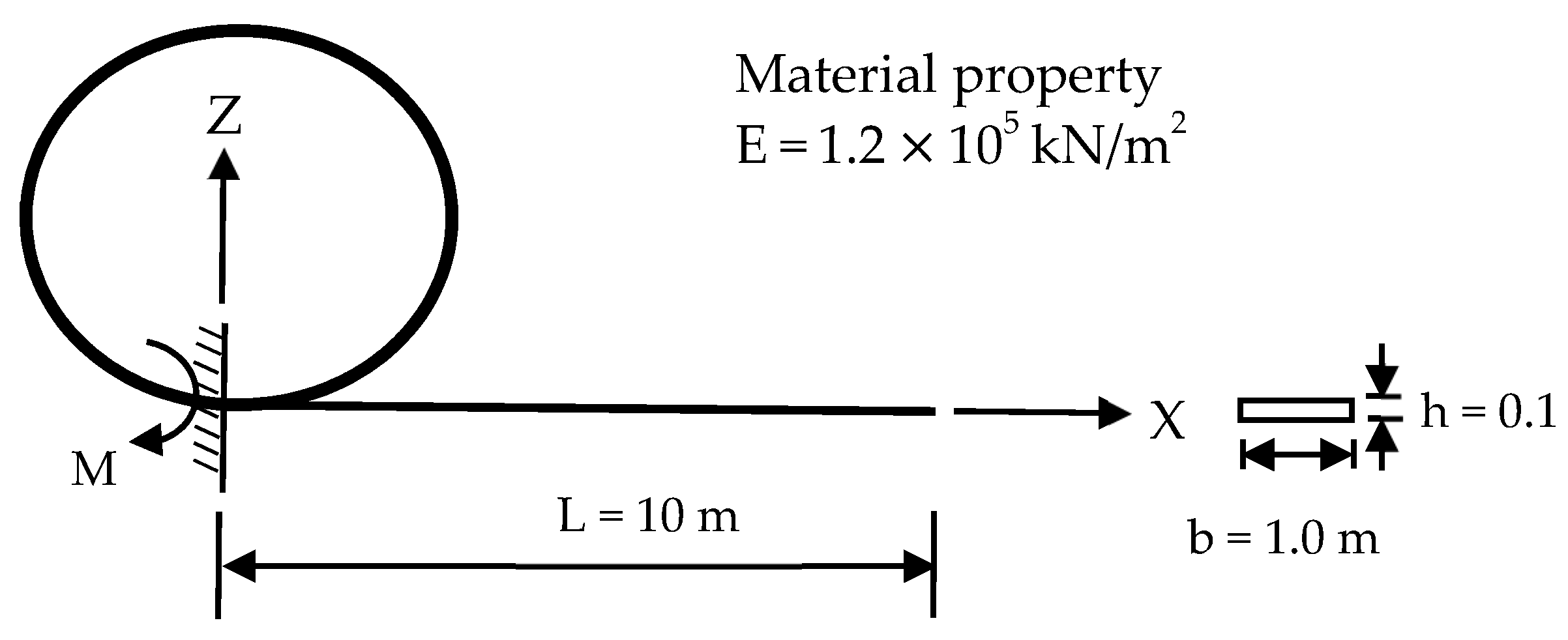
4.1. Cantilever Curved Beam Subjected to End Moment
4.2. A cantilever Beam Initially Curved to π/4 Subjected to a Concentrated Tip Load
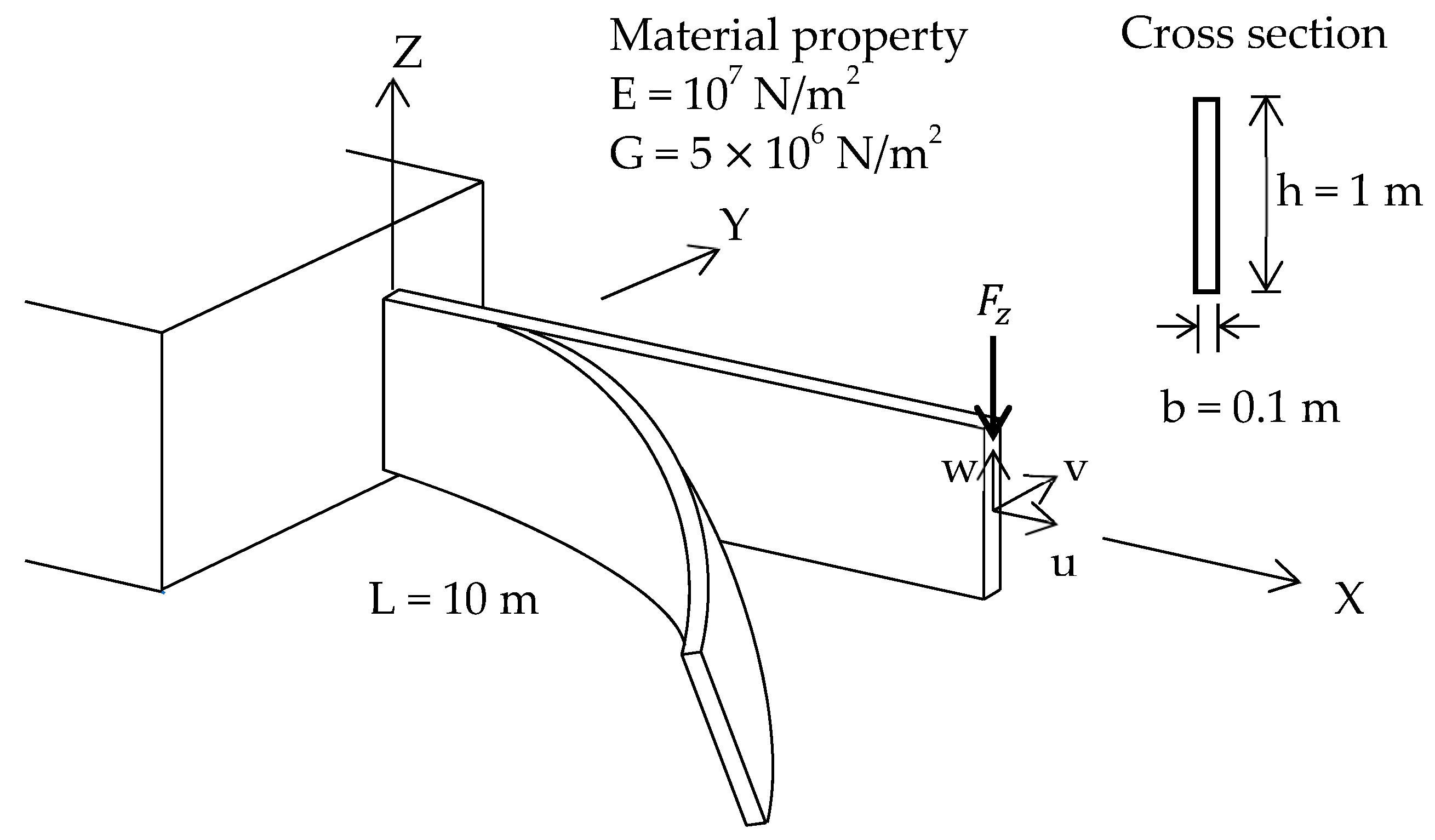
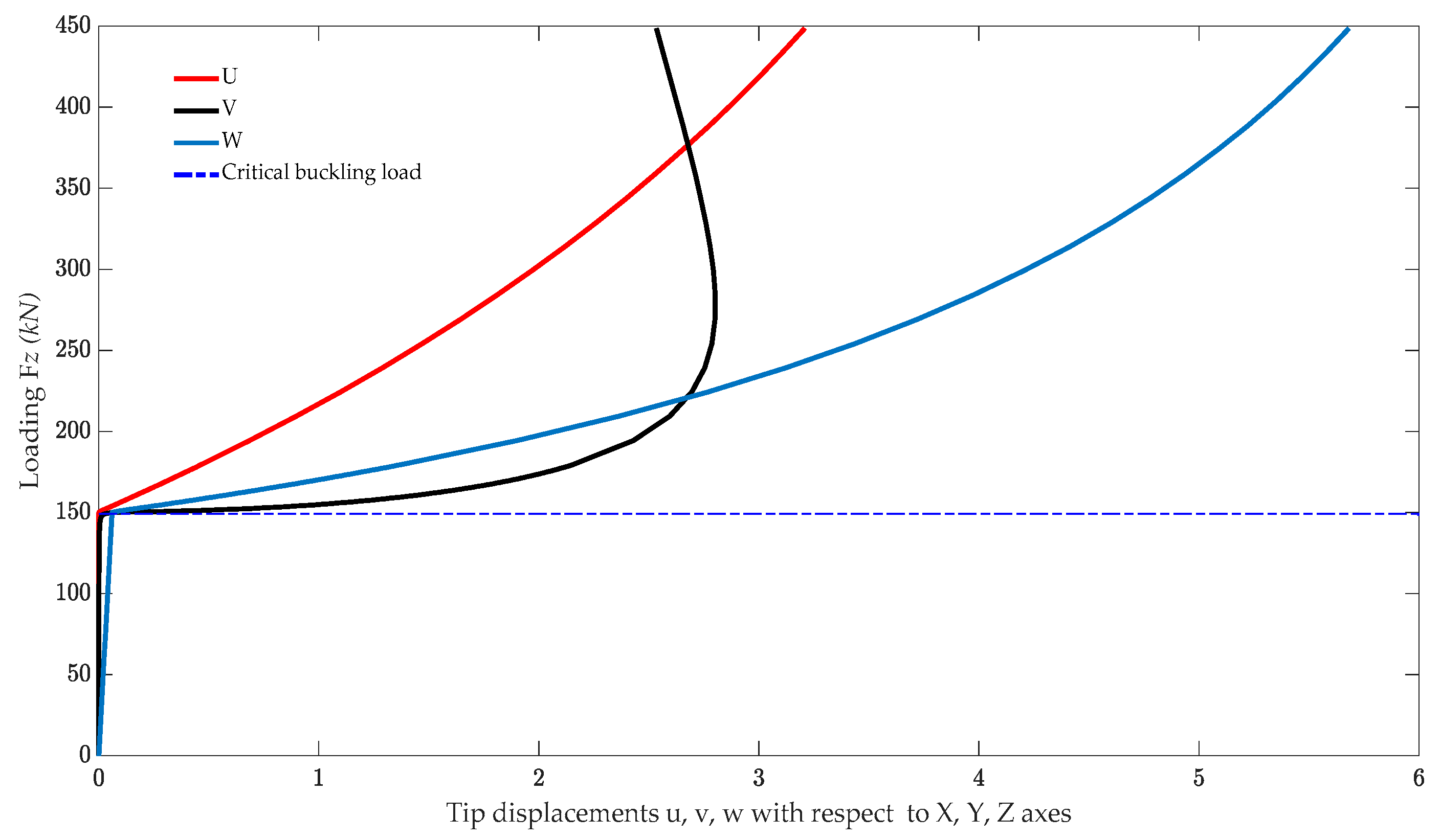
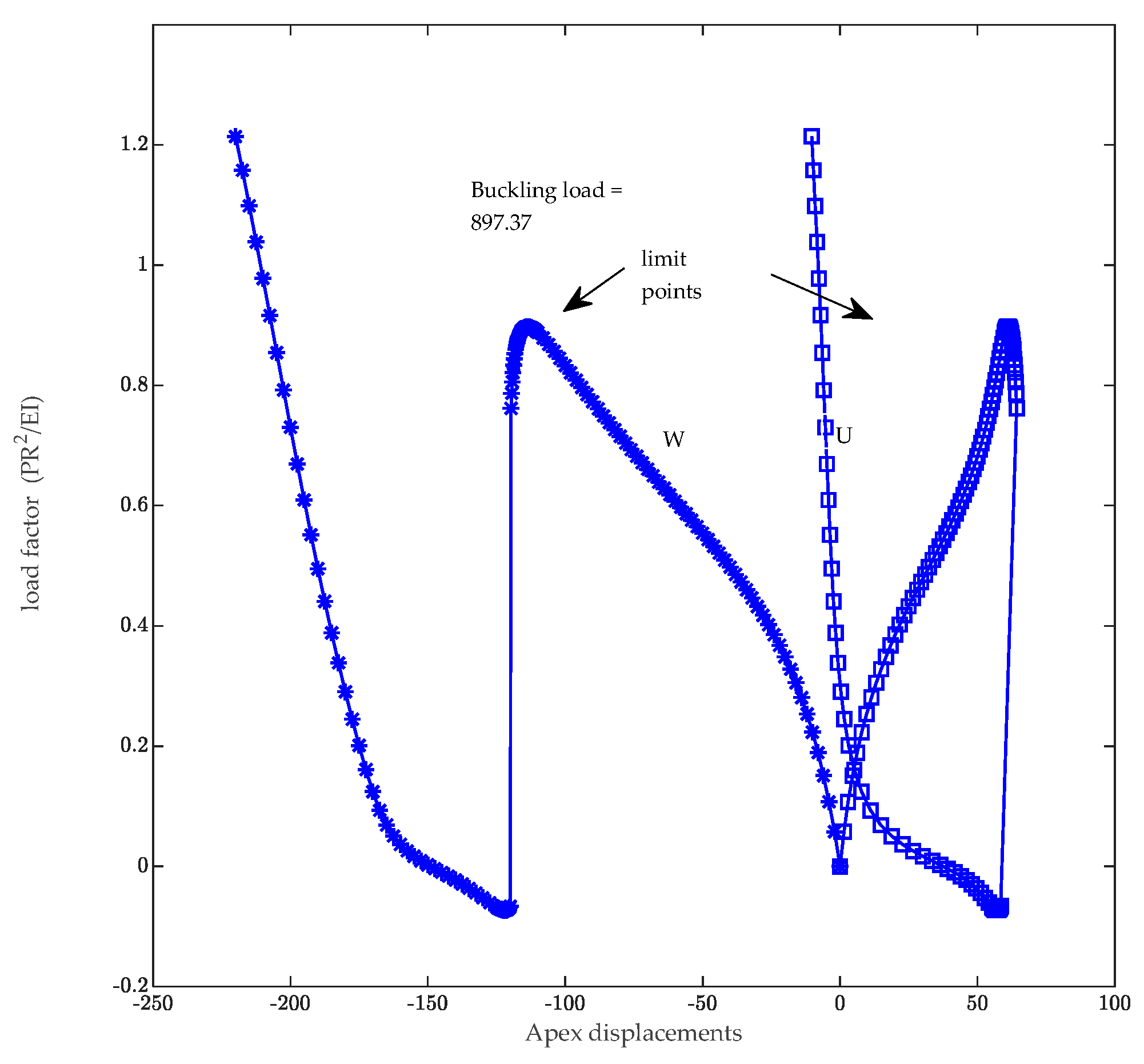
4.3. Lateral Buckling of a Cantilever Beam
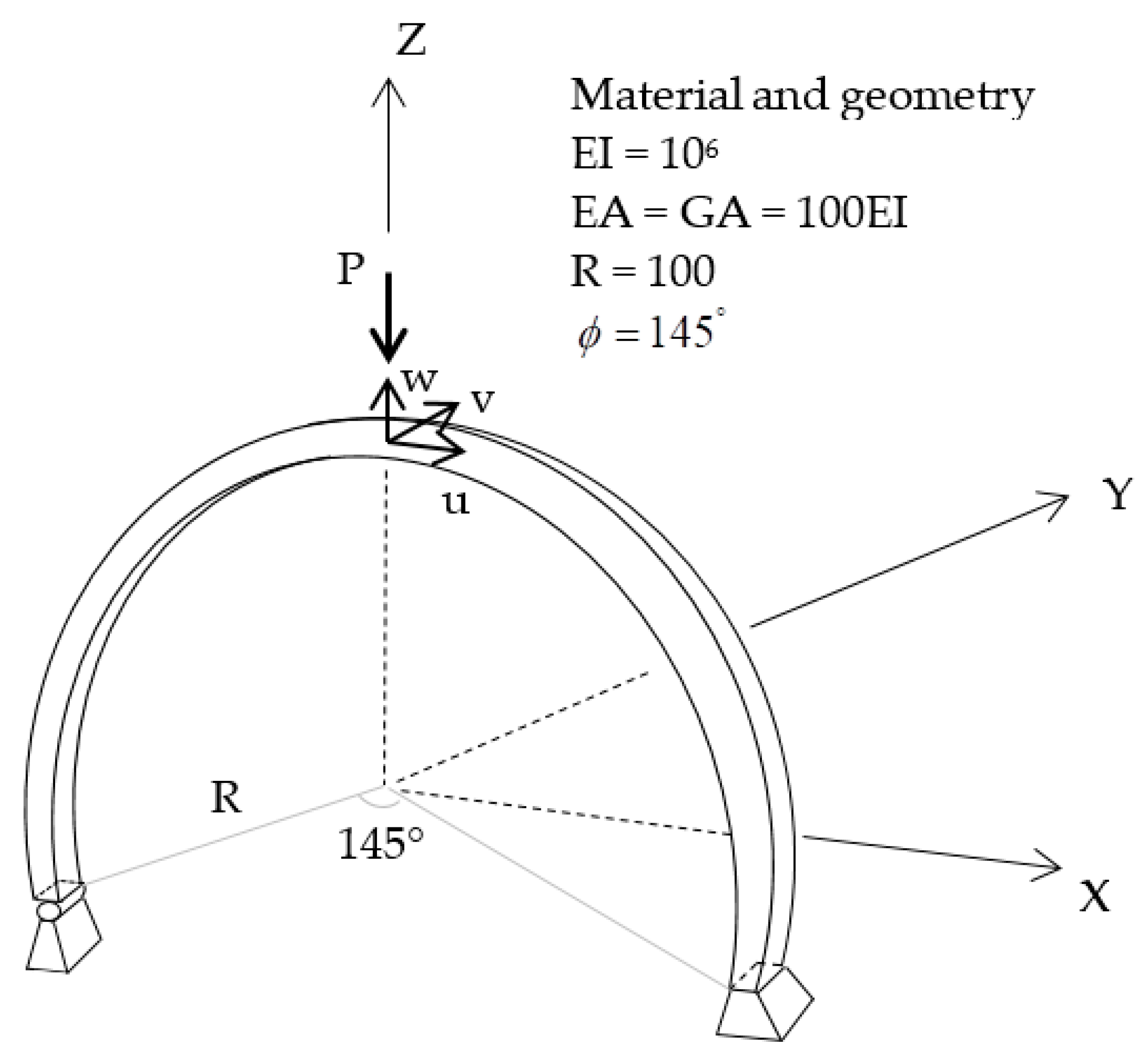
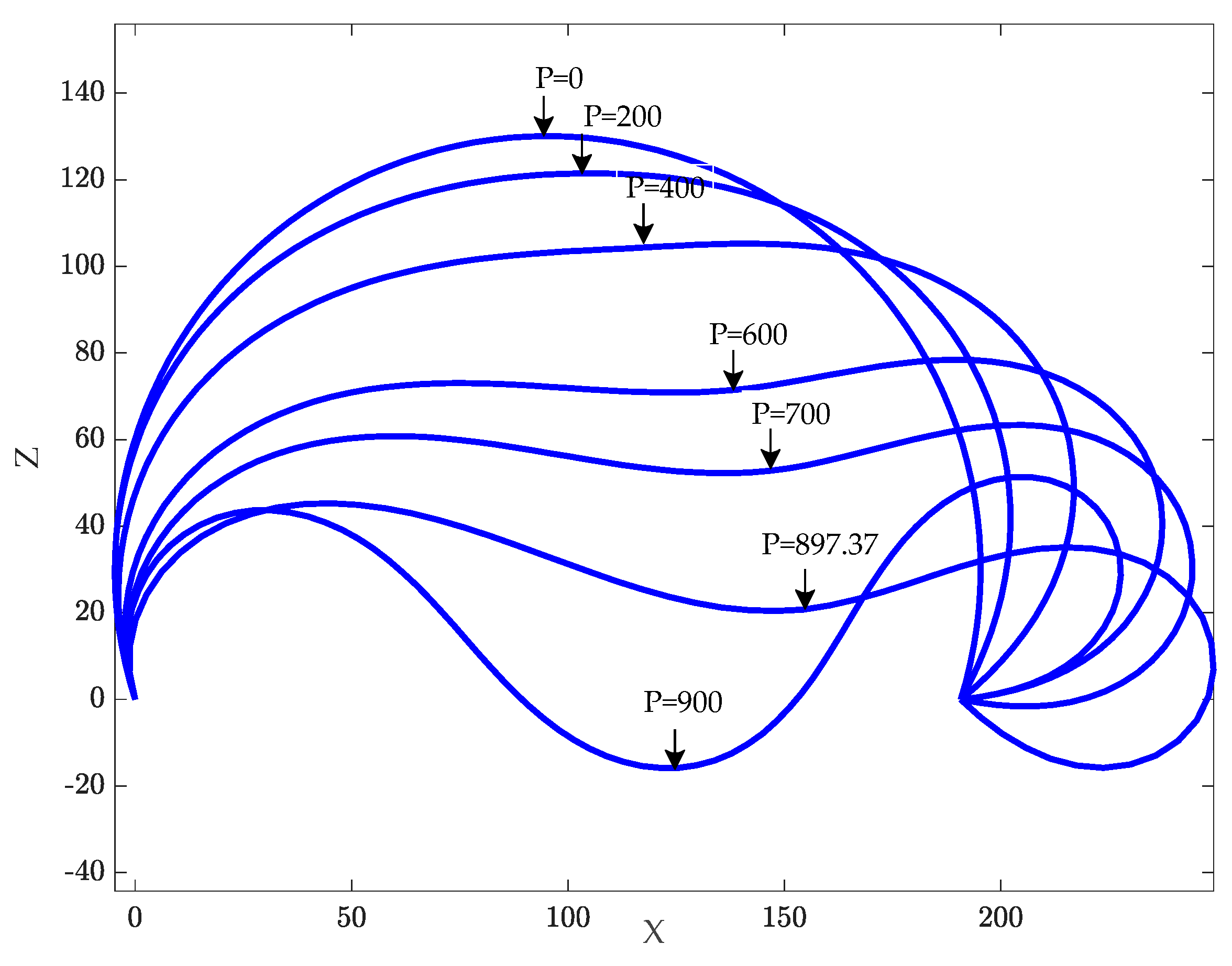
4.4. Postbuckling of a Clamped–Hinged Circular Arch
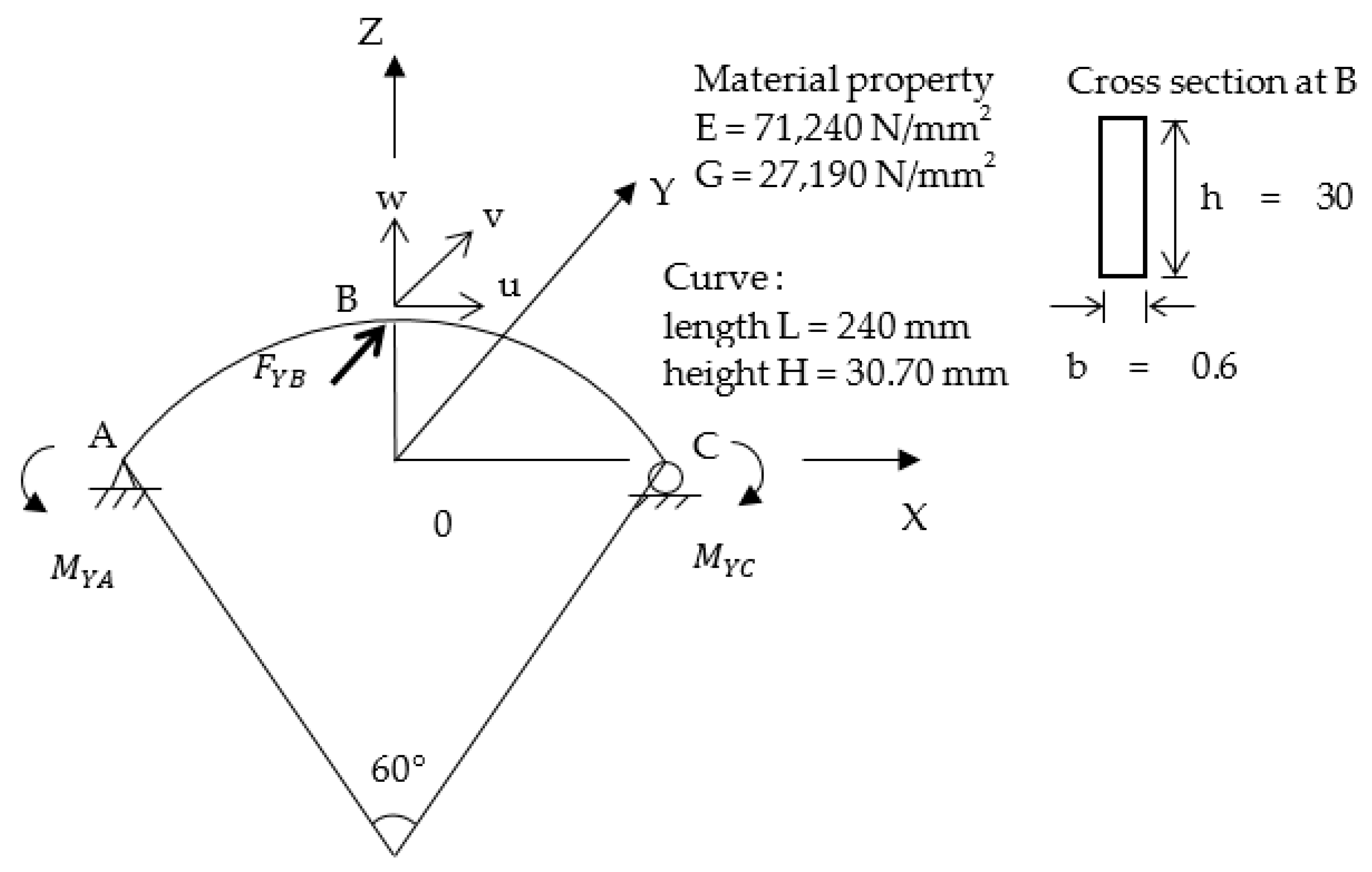
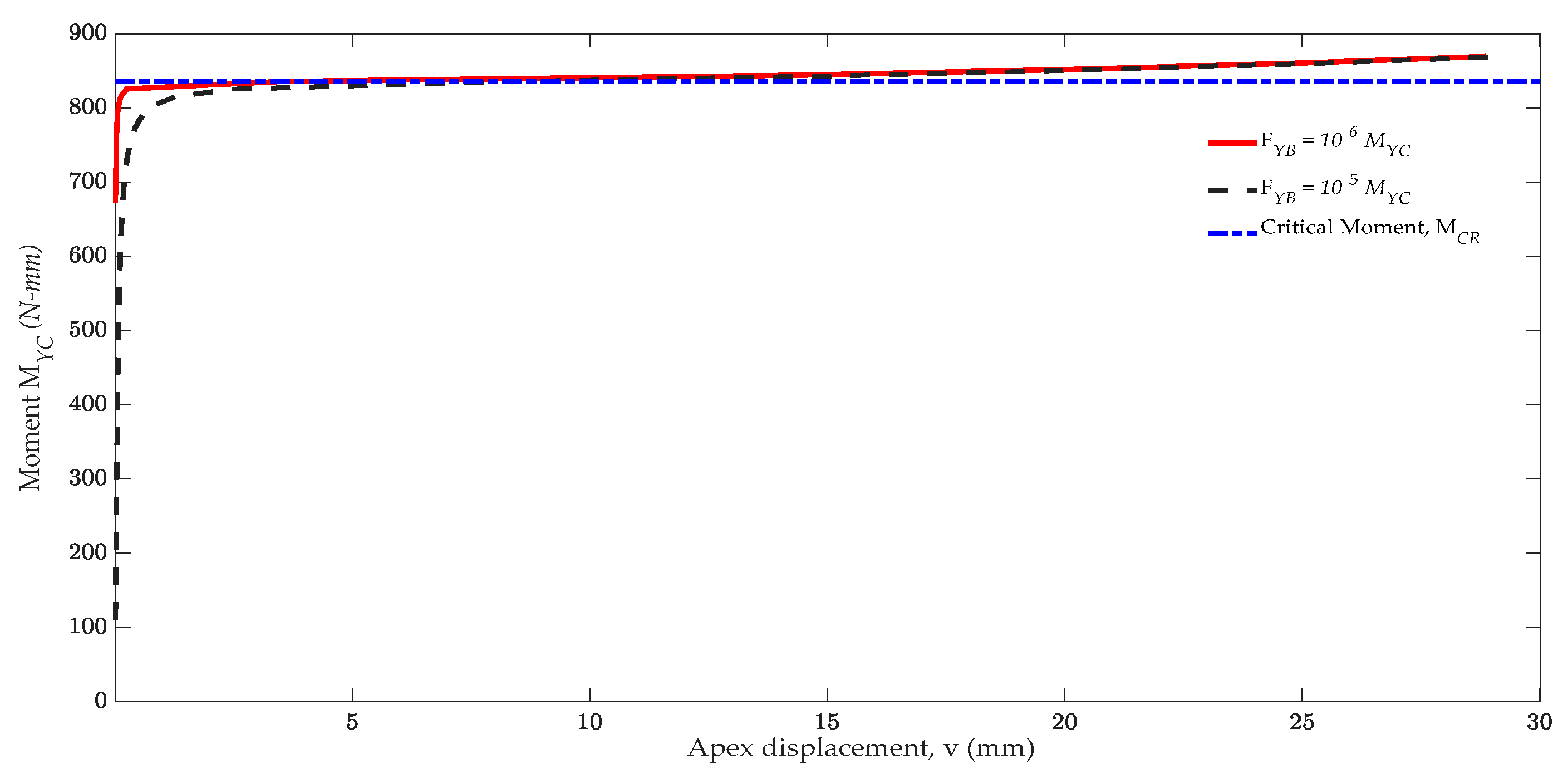
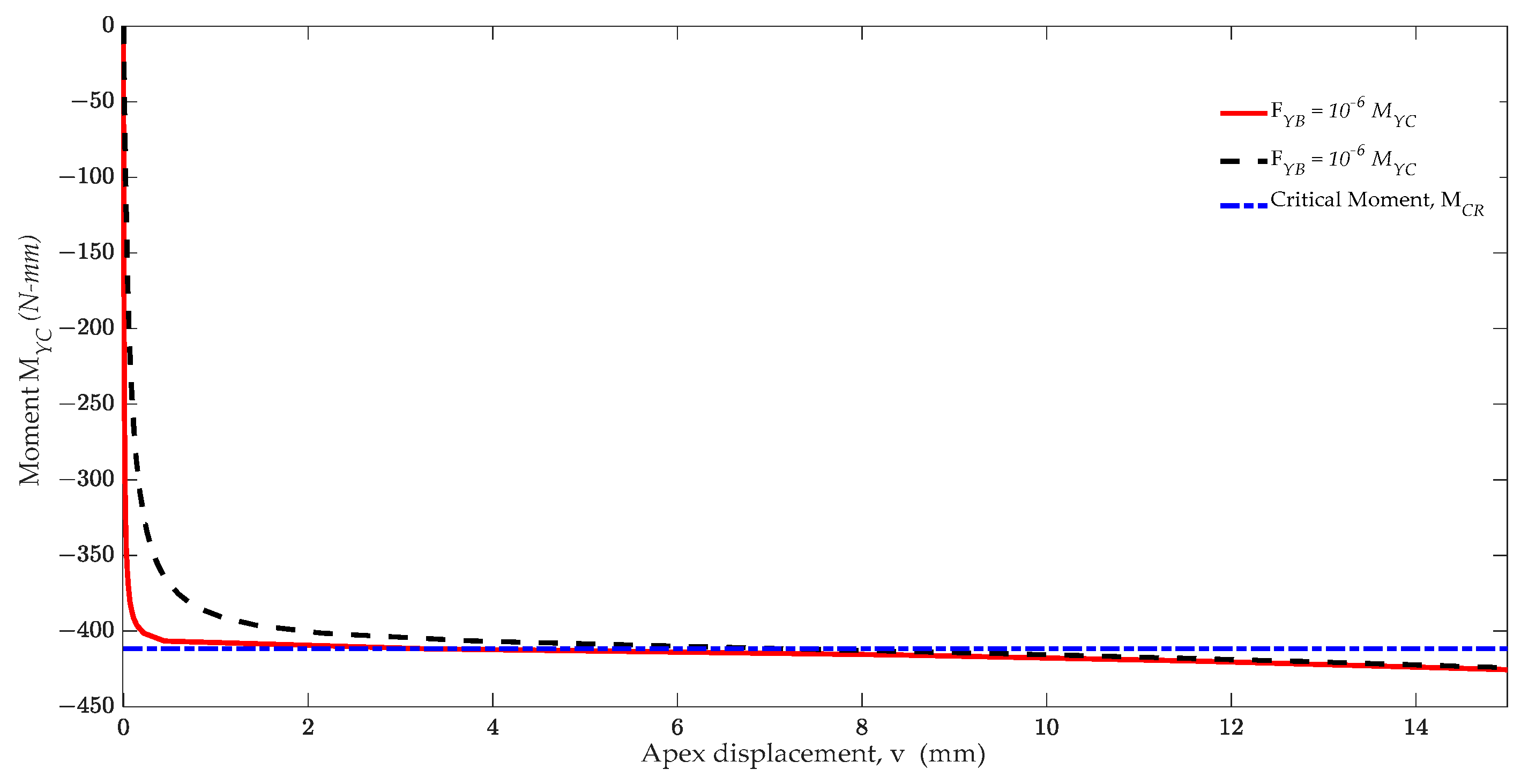
4.5. Lateral Buckling of a Curve Beam
5. Conclusions
Funding
Conflicts of Interest
References
- Bathe, K.; Bolourchi, S. Large displacement analysis of three-dimensional beam structures. Int. J. Numer. Meth. Eng. 1979, 14, 961–986. [Google Scholar] [CrossRef]
- Simo, J.C.; Vu-Quoc, L. A three-dimensional finite-strain rod model. Part II: Computational aspects. Comput. Methods Appl. Mech. Eng. 1986, 58, 79–116. [Google Scholar] [CrossRef]
- Cardona, A.; Geradin, M. A beam finite element non-linear theory with finite rotations. Int. J. Numer. Meth. Eng. 1988, 26, 2403–2438. [Google Scholar] [CrossRef]
- Crisfield, M.A. A consistent co-rotational formulation for non-linear, three-dimensional, beam elements. Comput. Methods Appl. Mech. Eng. 1990, 81, 131–150. [Google Scholar] [CrossRef]
- Jelenic, G.; Saje, M. A kinematically exact space finite strain beam model-finite element formulation by generalized virtual work principle. Comput. Methods Appl. Mech. Eng. 1995, 120, 131–161. [Google Scholar] [CrossRef]
- Ibrahimbegovic, A. On finite element implementation of geometrically nonlinear reissner’s beam theory: Three-dimensional curved beam elements. Comput. Methods Appl. Mech. Eng. 1995, 122, 11–26. [Google Scholar] [CrossRef]
- Ibrahimbegovic, A.; Shakourzadeh, H.; Batoz, J.L.; Mikdad, M.A.; Guo, Y.Q. On the role of geometrically exact and second-order theories in buckling and post-buckling analysis of three-dimensional beam structures. Comput. Struct. 1996, 61, 1101–1114. [Google Scholar] [CrossRef]
- Hsiao, K.M.; Yang, R.T.; Lin, W.Y. A consistent finite element formulation for linear buckling analysis of spatial beams. Comput. Methods Appl. Mech. Eng. 1998, 156, 259–276. [Google Scholar] [CrossRef]
- Jelenic, G.; Crisfield, M.A. Geometrically Exact 3D Beam Theory: Implementation of a strain-invariant finite element for statics and dynamics beams. Comput. Methods Appl. Mech. Eng. 1999, 171, 141–171. [Google Scholar] [CrossRef]
- Hsiao, K.M.; Lin, W.Y. A co-rotational finite element formulation for buckling and postbuckling analyses of spatial beams. Comput. Methods Appl. Mech. Eng. 2000, 188, 567–594. [Google Scholar] [CrossRef]
- Yang, Y.B.; Kuo, S.R.; Wu, Y.S. Incrementally small-deformation theory for nonlinear analysis of structural frames. Eng. Struct. 2002, 24, 783–798. [Google Scholar] [CrossRef]
- Kapania, R.K.; Li, J. A formulation and implementation of geometrically exact curved beam elements incorporating finite strains and finite rotations. Comput. Mech. 2003, 30, 444–459. [Google Scholar] [CrossRef]
- Zupan, D.; Saje, M. Finite-element formulation of geometrically exact three-dimensional beam theories based on interpolation of strain measures. Comput. Methods Appl. Mech. Eng. 2003, 192, 5209–5248. [Google Scholar] [CrossRef] [Green Version]
- Zupan, D.; Saje, M. The three-dimensional beam theory: Finite element formulation based on curvature. Comput. Struct. 2003, 81, 1875–1888. [Google Scholar] [CrossRef]
- Makinen, J. Total lagrangian reissner’s geometrically exact beam element without singularities. Int. J. Numer. Meth. Eng. 2007, 70, 1009–1048. [Google Scholar] [CrossRef]
- Cannarozzi, M.; Molari, L. Stress-based formulation for non-linear analysis of planar elastic curved beams. Int. J. Nonlin. Mech. 2013, 55, 35–47. [Google Scholar] [CrossRef]
- Ye, J.; Xu, L. Member discrete element method for static and dynamic responses analysis of steel frames with semi-rigid joints. Appl. Sci. 2017, 7, 714. [Google Scholar] [CrossRef] [Green Version]
- Silva, R.; Lavall, A.; Costa, R.; Viana, H. Formulation for second-order inelastic analysis of steel frames including shear deformation effect. J. Constr. Steel. Res. 2018, 151, 216–227. [Google Scholar] [CrossRef]
- Piotrowski, R.; Szychowski, A. Lateral torsional buckling of steel beams elastically restrained at the support nodes. Appl. Sci. 2019, 9, 1944. [Google Scholar] [CrossRef] [Green Version]
- Reissner, E. On finite deformation of space-curved beams. J. Appl. Math. Phys. 1981, 32, 734–744. [Google Scholar] [CrossRef]
- Magisano, D.; Leonetti, L.; Madeo, A.; Garcea, G. A large rotation finite element analysis of 3D beams by incremental rotation vector and exact strain measure with all the desirable features. Comput. Methods Appl. Mech. Eng. 2020, 361, 112811. [Google Scholar] [CrossRef]
- Magisano, D.; Leonetti, L.; Garcea, G. How to improve efficiency and robustness of the Newton method in geometrically non-linear structural problem discretized via displacement-based finite elements. Comput. Methods Appl. Mech. Eng. 2017, 313, 986–1005. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin methods. Int. J. Numer. Meth. Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Liu, W.K.; Jun, S.; Zhang, Y.F. Reproducing kernel particle methods. Int. J. Numer. Meth. Fluids 1995, 20, 1081–1106. [Google Scholar] [CrossRef]
- Li, S.; Liu, W.K. Reproducing kernel hierarchical partition of unity. Part I: Formulation and Theory. Int. J. Numer. Meth. Eng. 1999, 45, 251–288. [Google Scholar] [CrossRef]
- Atluri, S.N.; Zhu, T. New concepts in meshless methods. Int. J. Numer. Meth. Eng. 2000, 47, 537–556. [Google Scholar] [CrossRef]
- Atluri, S.N.; Shen, S. The Meshless Local Petrov-Galerkin Method; Tech. Science Press: Los Angeles, CA, USA, 2002. [Google Scholar]
- Aluru, N.R. A point collocation method based on reproducing kernel approximations. Int. J. Numer. Meth. Eng. 2000, 47, 1083–1121. [Google Scholar] [CrossRef]
- Onate, E.; Perazzo, F.; Miquel, J. A finite point method for elasticity problems. Comput. Struct. 2001, 79, 2151–2163. [Google Scholar] [CrossRef]
- Yang, J.P.; Chen, J.Y. Strong-form formulated generalized displacement control method for large deformation analysis. Int. J. Appl. Mech. 2017, 9, 1750101. [Google Scholar] [CrossRef]
- Wang, D.; Wang, J.; Wu, J. Superconvergent gradient smoothing meshfree collocation method. Comput. Methods Appl. Mech. Eng. 2018, 340, 728–766. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chen, S.M.; Wu, C.P. A meshless collocation method based on the differential reproducing kernel interpolation. Comput. Mech. 2010, 45, 585–606. [Google Scholar] [CrossRef]
- Yang, S.W.; Wang, Y.M.; Wu, C.P.; Hu, H.T. A meshless collocation method based on the differential reproducing kernel approximation. Comp. Model. Eng. 2010, 60, 1–39. [Google Scholar]
- Yeh, W.C.; Wang, Y.M. Meshfree method for geometrical nonlinear analysis of curved and twisted beams using a three-dimensional finite deformation theory. Int. J. Struct. Stab. Dyn. 2019, 9, 1950116. [Google Scholar] [CrossRef]
- Argyris, J.H. A excursion into large rotations. Comput. Methods Appl. Mech. Eng. 1982, 32, 85–155. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; Dover Pubns: New York, NY, USA, 2009. [Google Scholar]
- Dadeppo, D.A.; Schmidt, R. Instability of clamped-hinged circular arches subjected to a point load. J. Appl. Mech. 1975, 42, 894–896. [Google Scholar] [CrossRef]
- Yang, Y.B.; Kuo, S.R. Theory and Analysis of Nonlinear Framed Structures; Prentice-Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
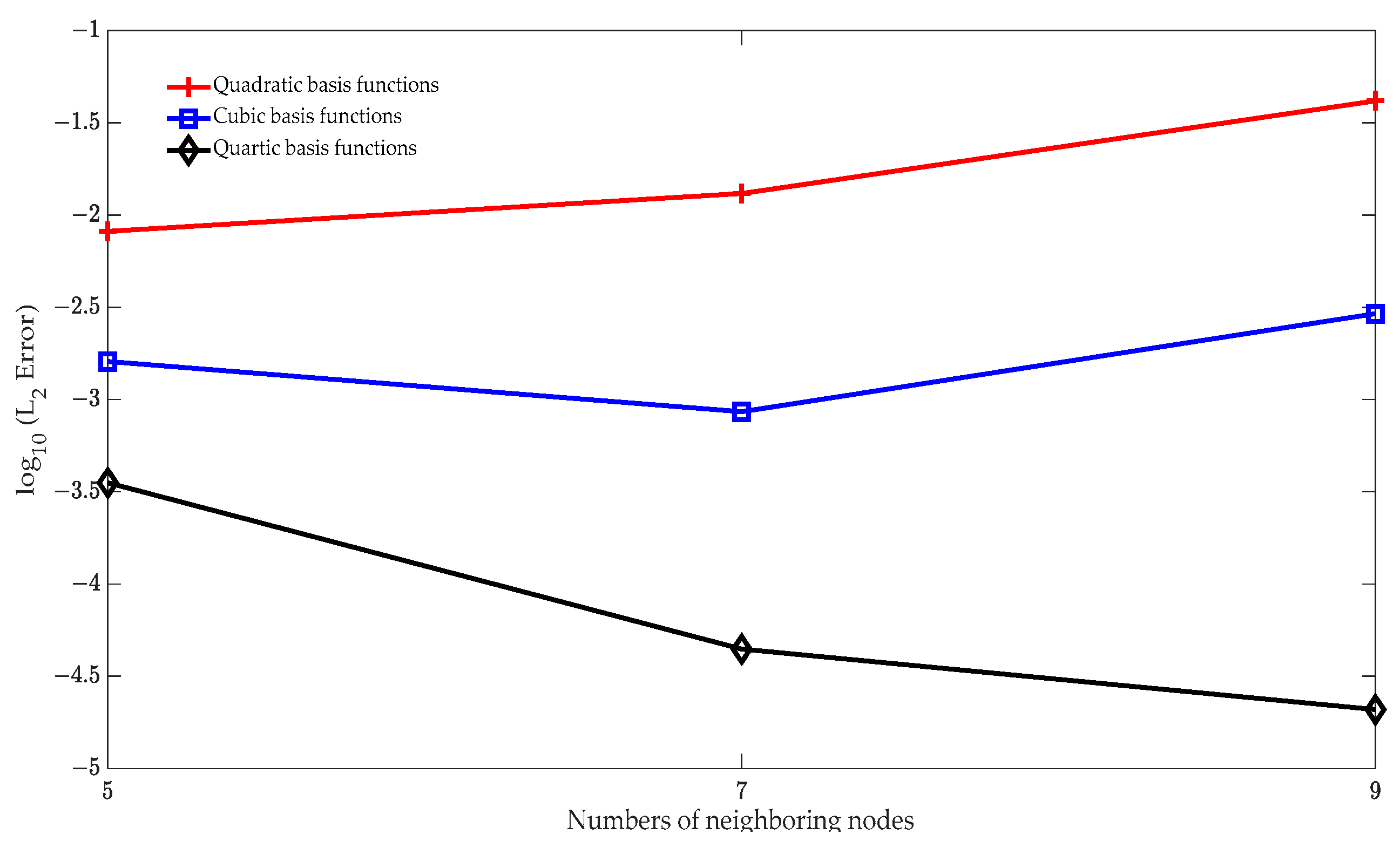
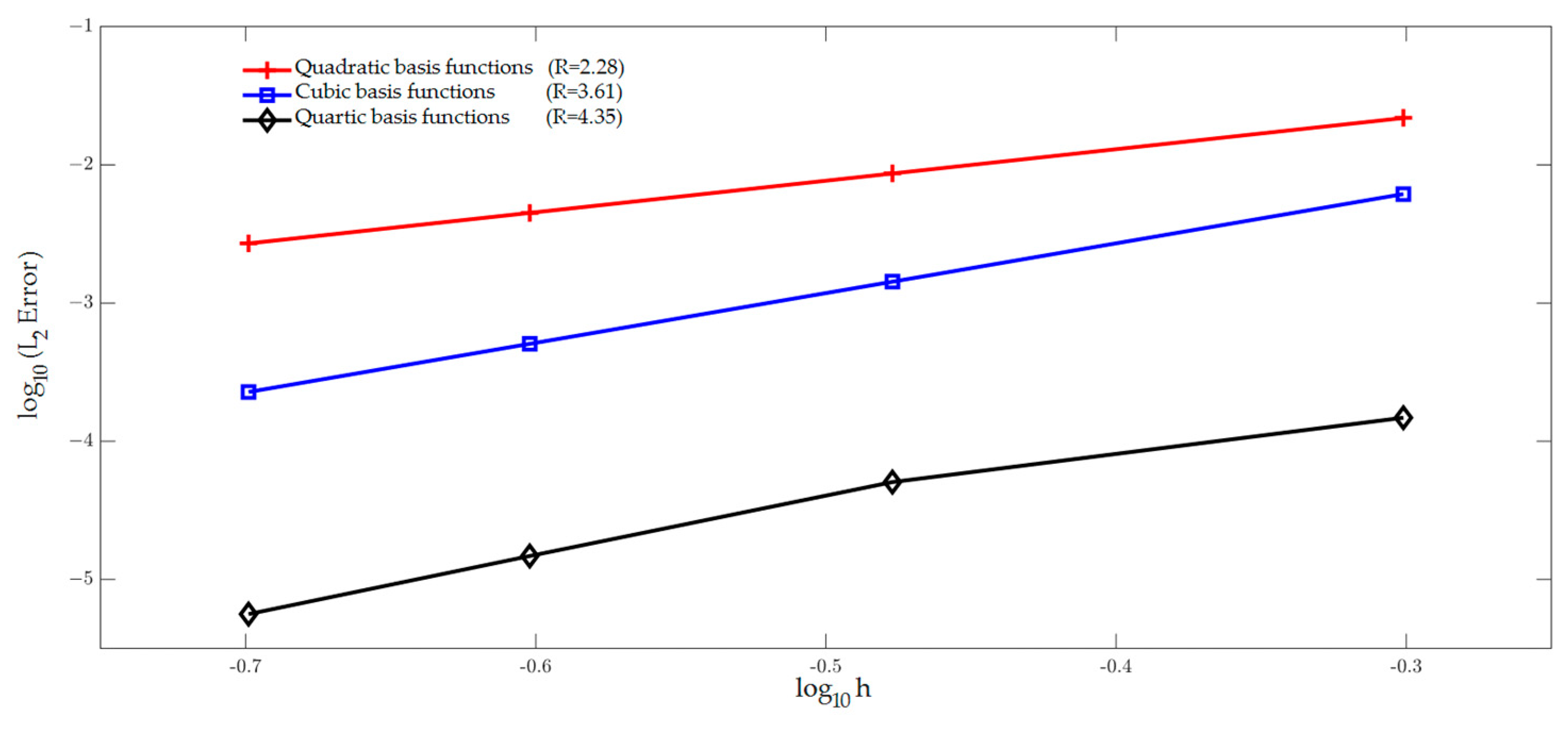

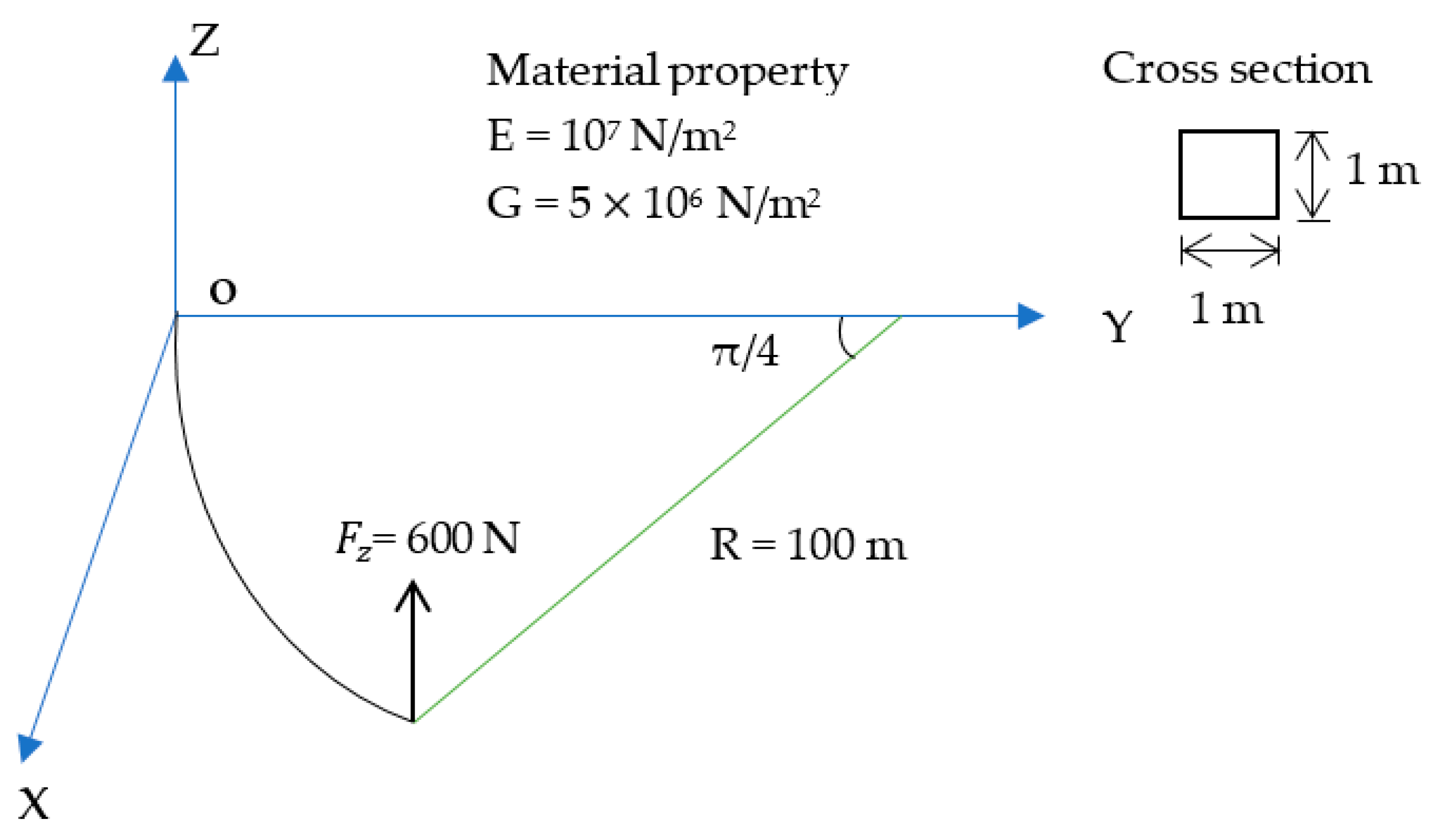
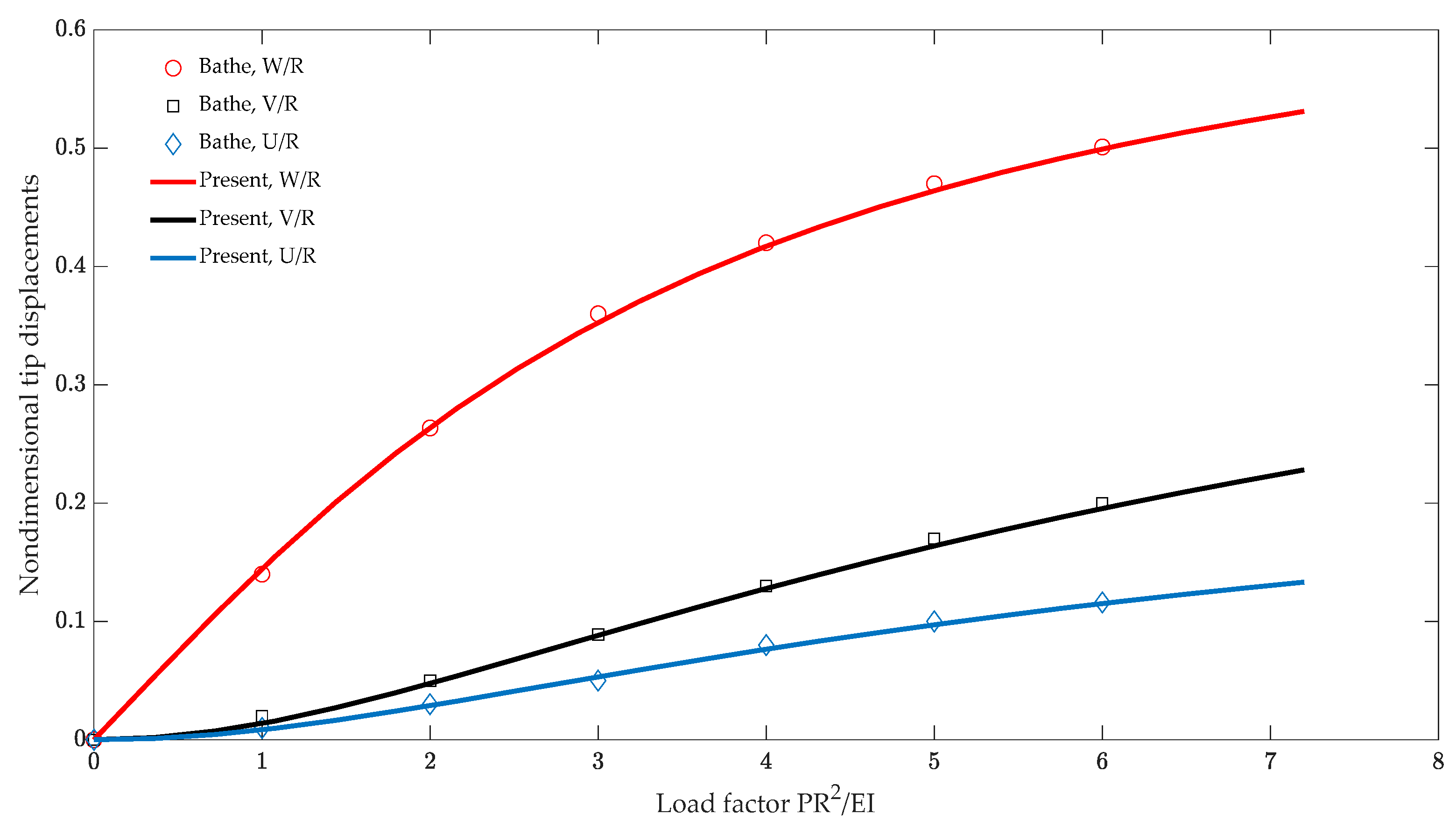

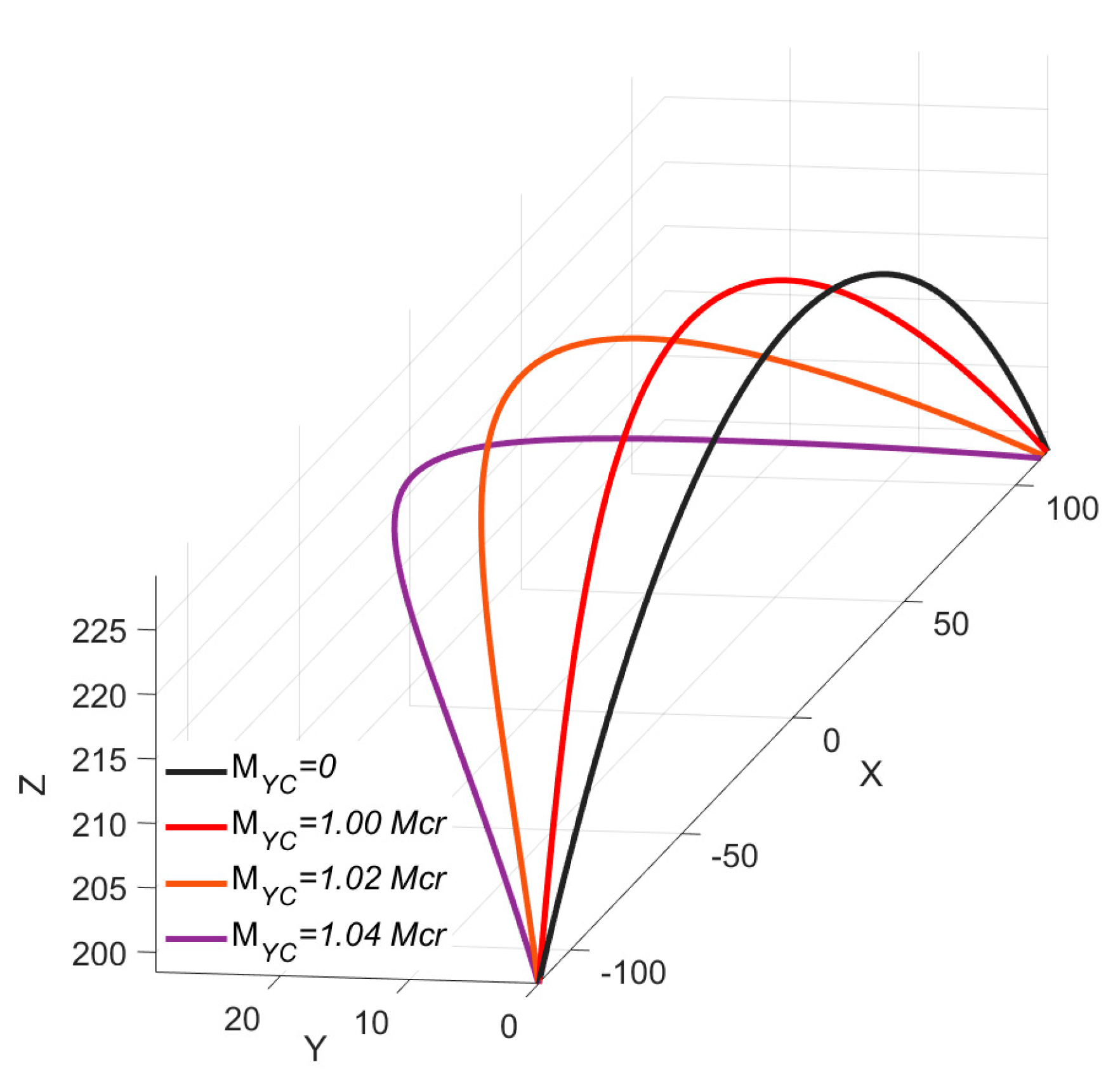
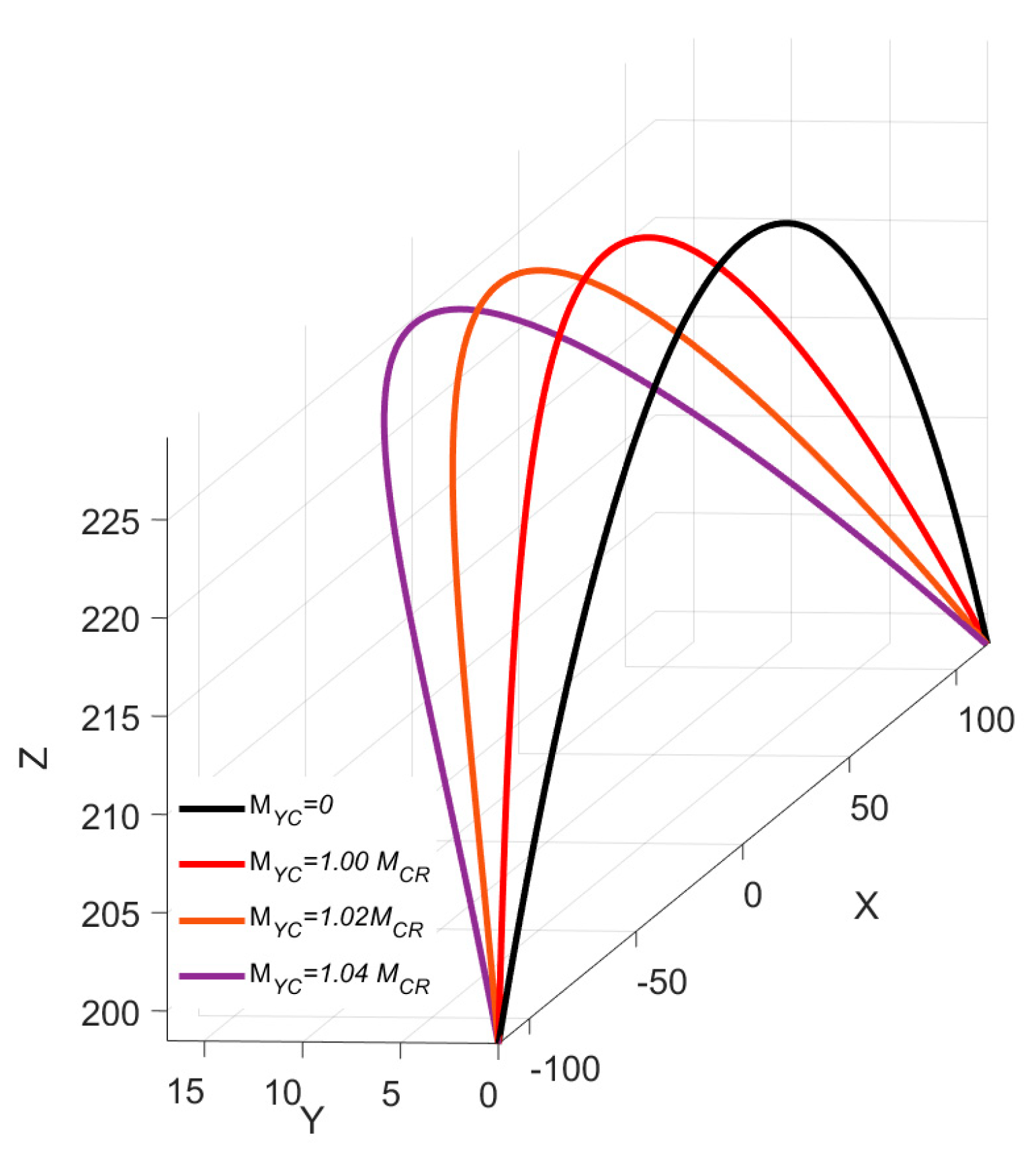
| Model | Nelm | Nnode | X | Y | Z |
|---|---|---|---|---|---|
| Present | 31 | 47.89 | 15.96 | 53.10 | |
| Bathe and Bolourchi [1] | - | 47.20 | 15.90 | 53.4 | |
| Simo and Vu-Quoc [2] | 8 (linear, straight) | 47.23 | 15.79 | 53.37 | |
| Cardona and Geradin [3] | 8 (linear, straight) | 47.04 | 15.96 | 53.50 | |
| Zupan et al. [13] | 8 (linear, curved) | 46.89 | 15.61 | 53.60 | |
| Magisano et al. [21] | 4 (CR-Incremental) | - | - | 53.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, W.-C. A Co-Rotational Meshfree Method for the Geometrically Nonlinear Analysis of Structures. Appl. Sci. 2021, 11, 6647. https://doi.org/10.3390/app11146647
Yeh W-C. A Co-Rotational Meshfree Method for the Geometrically Nonlinear Analysis of Structures. Applied Sciences. 2021; 11(14):6647. https://doi.org/10.3390/app11146647
Chicago/Turabian StyleYeh, Wen-Cheng. 2021. "A Co-Rotational Meshfree Method for the Geometrically Nonlinear Analysis of Structures" Applied Sciences 11, no. 14: 6647. https://doi.org/10.3390/app11146647
APA StyleYeh, W.-C. (2021). A Co-Rotational Meshfree Method for the Geometrically Nonlinear Analysis of Structures. Applied Sciences, 11(14), 6647. https://doi.org/10.3390/app11146647






