Empowering Advanced Parametric Modes Clustering from Topological Data Analysis
Abstract
:Featured Application
Abstract
1. Introduction
- The previously referred mass lumping that transforms the so-called consistent mass matrix into its diagonal counterpart, facilitating an explicit integration;
- In the context of model order reduction—MOR—, in [7], authors proposed a Proper Orthogonal Decomposition—POD—based reduced order modeling operating in the time domain. Ladeveze and coworkers proposed an extension of their radial approximation [8] for addressing mid-frequency dynamics, the so called TVCR (variational theory of complex rays) [9]. In our former works, we considered a PGD formulation for constructing a parametric transfer function [10] that allowed efficient solutions of transient dynamics operating in the time-domain. On the other hand, the separation of variables, at the heart of PGD [11], was extensively employed in the harmonic domain for solving multi-parametric dynamics, and was successfully extended to the nonlinear case, and then combined with modal analysis [4,5,6].
- Modal analysis is one the most widely used techniques for solving dynamical problems. Other than the benefits in the time integration, due to the dynamical system decoupling, the eigenmodes benefit from a physical interpretation, of great interest for the designer or structural analyst. However, when considering parametric models, as is always the case during the design stage, when the material and geometry are not totally defined, the dynamical modes depend on those parameters as previously discussed. Having a surrogate model expressing the parametric evolution of the eigenmodes is of great interest. Constructing those surrogate models is nowadays quite mature, by using usual and advanced nonlinear regressions [12], the last making use of sparsity and appropriate regularizations for operating in high-dimensional settings, while keeping as reduced as possible the number of data (eigenproblem solution), and leading to rich enough (nonlinear) regressions while avoiding overfitting. Here, the trickiest issue is not the regression construction but the fact of ordering the different eigenmodes involved in the modal basis for each parameter choice, in order to create N clusters (or less in the reduced case), and putting in each one a mode of each modal basis, such that modes in each cluster remain close (in certain metrics). The main issue remains the metric to be used to successfully and efficiently accomplishing such clustering. In general, such clustering is performed by operating at the level of the eigenmodes, in the associated vector space, by using, for example, the Modal Assurance Criterion—MAC— [13] that proceed with comparing the modes resulting from each eigenproblem, by using the usual scalar product (modes similar to a given one should remain quite collinear).
2. Methods
2.1. Data Description
2.2. On the Surface Topology
2.2.1. Geometric Features
- A vertex is generated by an individual point ;
- A segment joins two vertex
- A triangle is generated by three different vertexes , such that and are linearly independent, and then:where and are the barycentric coordinates, with ;
- A tetrahedron is generated by four different vertices , such that , , and are linearly independent, and then:where , and are the barycentric coordinates, with .
2.2.2. Features’ Filtration
- For every simplex in , the -dimensional simplices forming it are in (e.g., a triangle is in and its three edges are in );
- If two simplices in have a common element , then there exists such that .
- First, the filtration value of each tetrahedron is computed as the circumradius of the tetrahedron if its circumsphere is empty, and as the minimum of the filtration values of the triangles that are within the circumsphere otherwise.
- Similarly, the filtration value of each triangle is computed as the circumradius of the triangle if the circumcircle is empty, and as the minimum of the filtration values of the segments that are within the circumcircle otherwise.
- Then, the filtration value of each segment is computed as its circumradius.
- Finally, the filtration value of the vertices is set to 0.
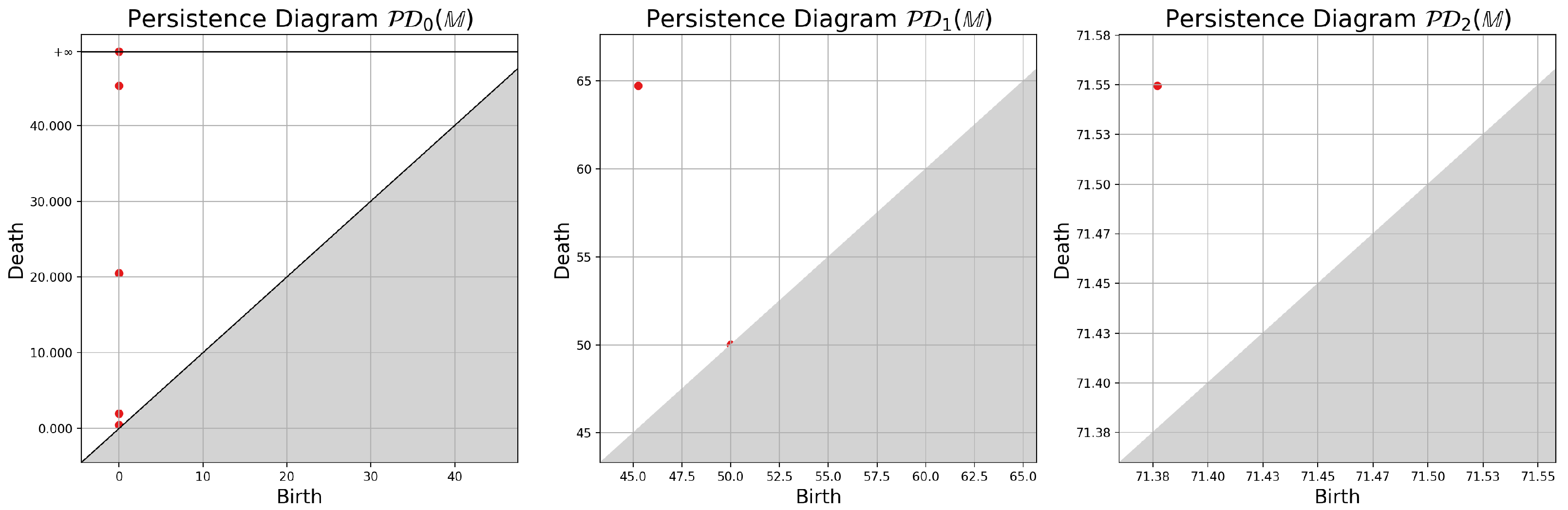
2.2.3. Persistence Diagrams
- The birth scale of the feature at homology k
- The death scale of the feature at homology k
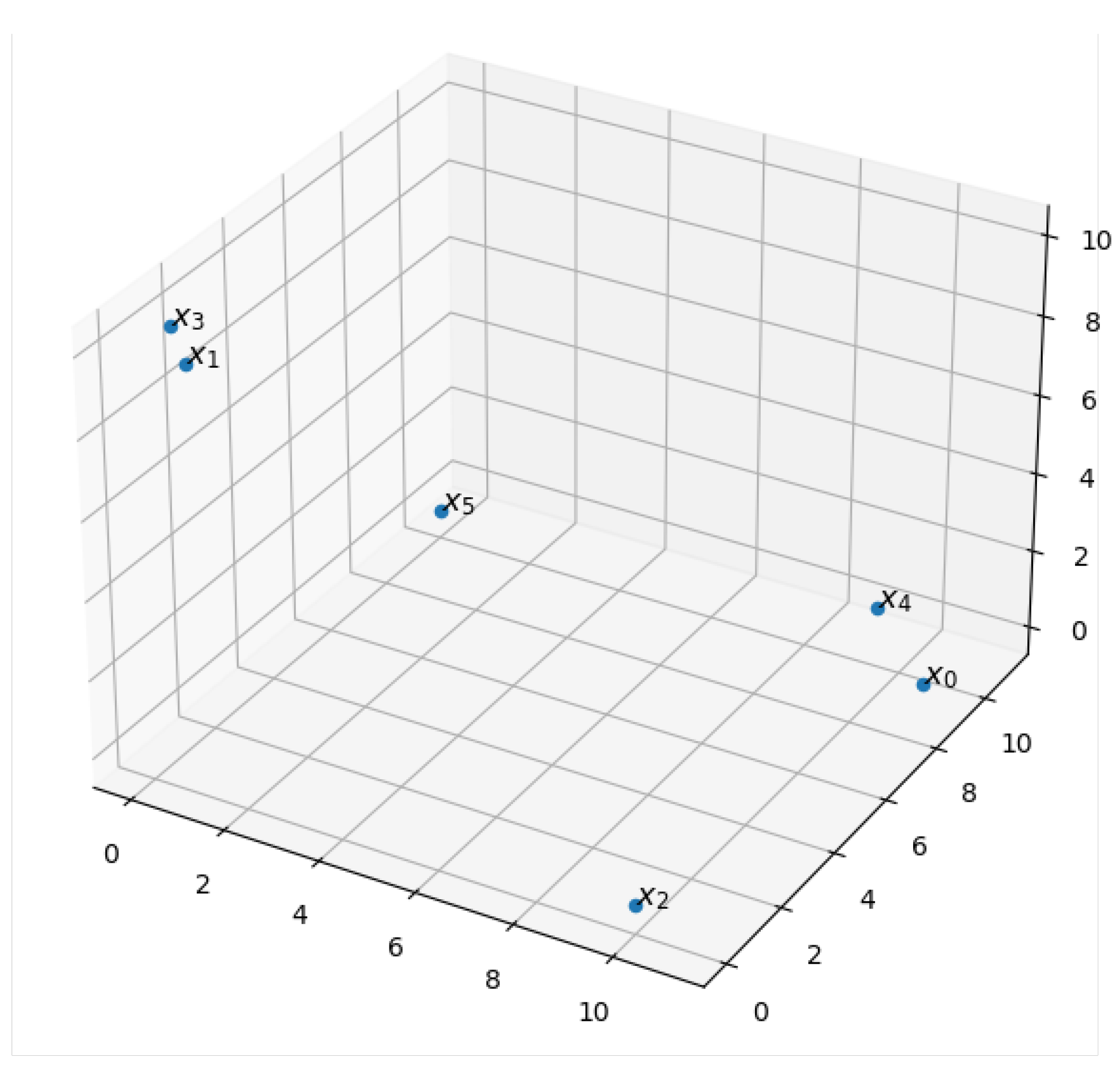
2.2.4. Illustrating the Concepts on an Example
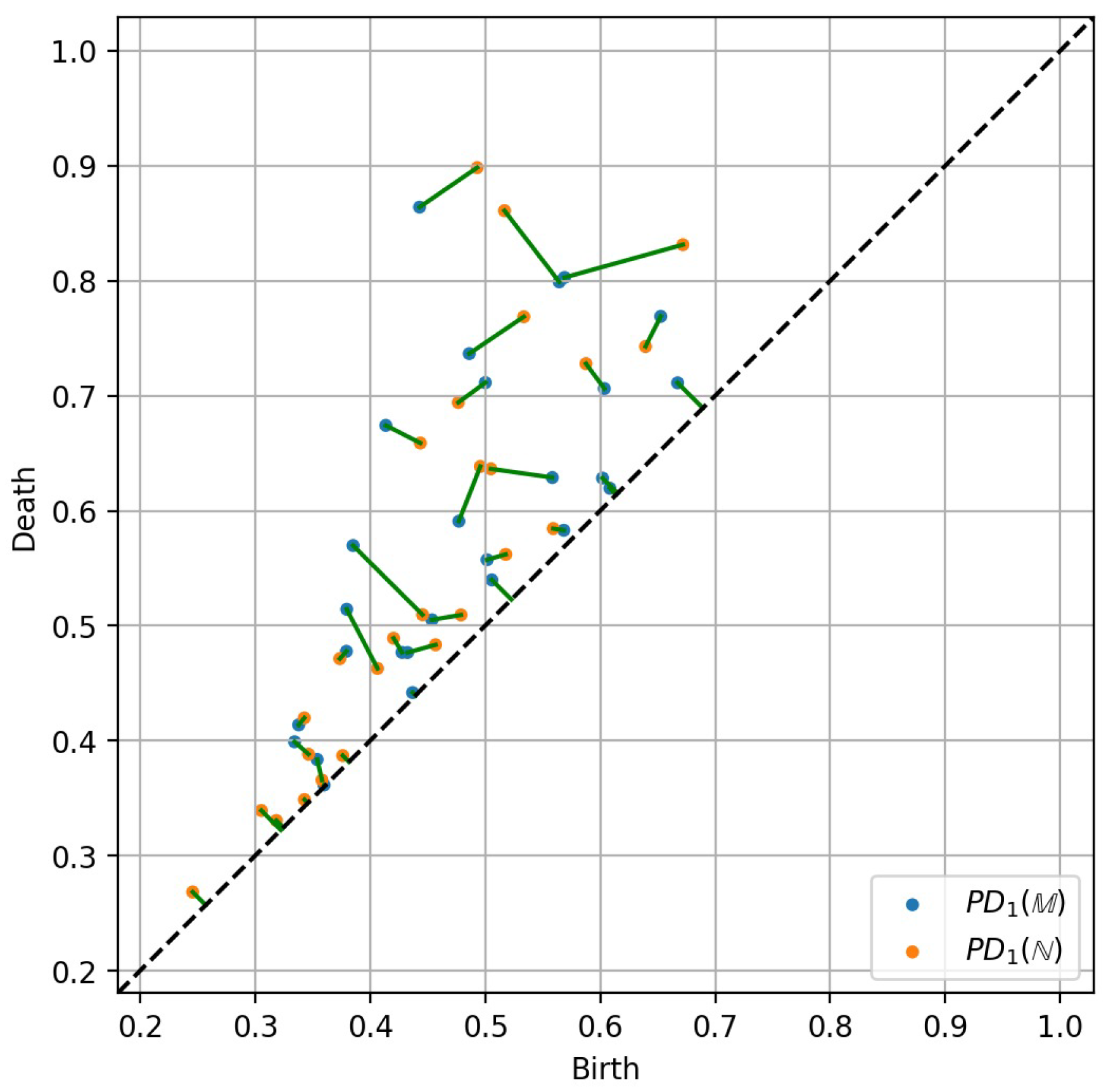
2.2.5. Matching Persistence Diagrams
2.2.6. Multi-Scale Topological Measure of Surface Deformation
2.2.7. Comparing Tropological Descriptions of Deformed Surfaces
2.3. Modal Assurance Criterion
3. Results
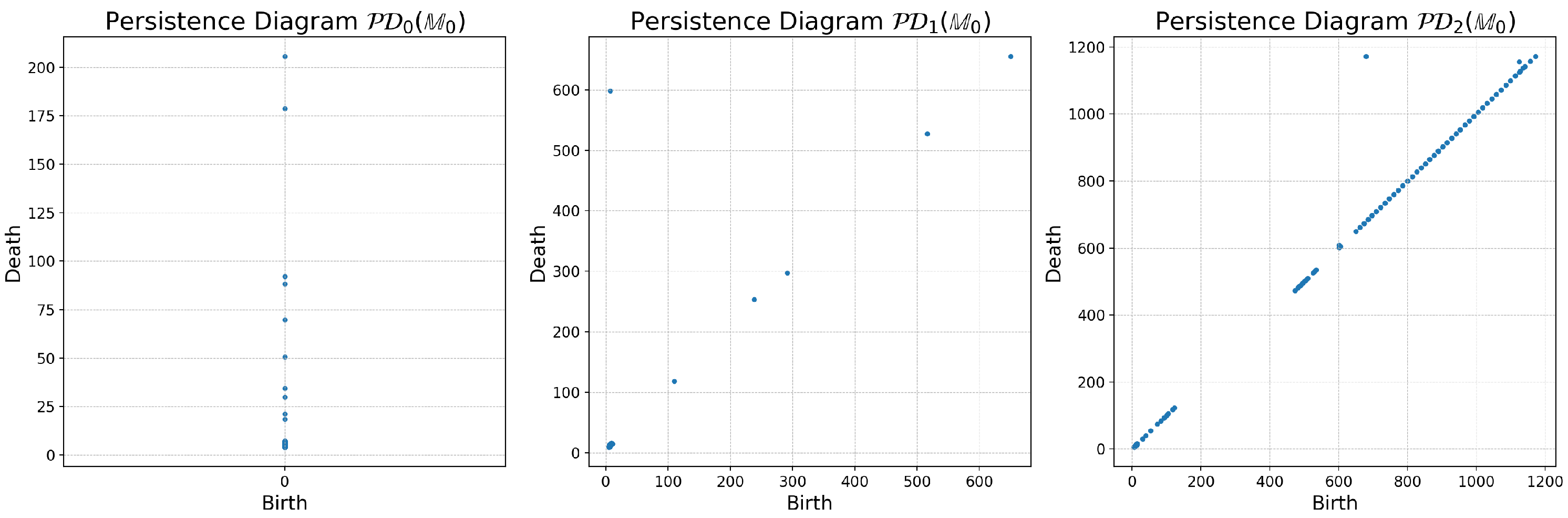
3.1. Topological Modes Identification
3.2. MAC Identification
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Clough, R.W.; Penzien, J. Dynamics of structures; Civil Engineering Series; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar] [CrossRef]
- Bathe, J. Conserving energy and momentum in nonlinear dynamics: A simple implicit time integration scheme. Comput. Struct. 2007, 85, 437–445. [Google Scholar] [CrossRef]
- Germoso, C.; Duval, J.L.; Chinesta, F. Harmonic-Modal Hybrid Reduced Order Model for the Efficient Integration of Non-Linear Soil Dynamics. Appl. Sci. 2020, 10, 6778. [Google Scholar] [CrossRef]
- Malik, M.H.; Borzacchiello, D.; Aguado, J.V.; Chinesta, F. Advanced parametric space-frequency separated representations in structural dynamics: A harmonic–modal hybrid approach. Comptes Rendus MéCanique 2018, 346, 590–602. [Google Scholar] [CrossRef]
- Quaranta, G.; Argerich, C.; Ibañez, R.; Duval, J.L.; Cueto, E.; Chinesta, F. From linear to nonlinear PGD-based parametric structural dynamics. Comptes Rendus MéCanique 2019, 347, 445–454. [Google Scholar] [CrossRef]
- Boucinha, L.; Gravouil, A.; Ammar, A. Space-time proper generalized decompositions for the resolution of transient elastodynamic models. Comput. Methods Appl. Mech. Eng. 2013, 255, 67–88. [Google Scholar] [CrossRef] [Green Version]
- Ladeveze, P. The large time increment method for the analyze of structures with nonlinear constitutive relation described by internal variables. CR Acad. Sci. Paris 1989, 309, 1095–1099. [Google Scholar]
- Ladeveze, P.; Arnaud, L.; Rouch, P.; Blanze, C. The variational theory of complex rays for the calculation of medium-frequency vibrations. Engrg. Comp. 1999, 18, 193–214. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez, D.; Cueto, E.; Chinesta, F. Real-Time Direct Integration of Reduced Solid Dynamics Equations. Int. J. Numer. Methods Eng. 2014, 99/9, 633–653. [Google Scholar] [CrossRef] [Green Version]
- Chinesta, F.; Leygue, A.; Bordeux, F.; Aguado, J.V.; Cueto, E.; Gonzalez, D.; Alfaro, I.; Huerta, A. Parametric PGD based computational vademecum for efficient design, optimization and control. Arch. Comput. Methods Eng. 2013, 20/1, 31–59. [Google Scholar] [CrossRef]
- Sancarlos, A.; Champaney, V.; Duval, J.L.; Cueto, E.; Chinesta, F. PGD-based advanced nonlinear multiparametric regressions for constructing metamodels at the scarce-data limit. arXiv 2021, arXiv:2103.05358. [Google Scholar]
- Pastora, M.; Bindaa, M.; Harcarika, T. Modal Assurance Criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Louis, M.; Bône, A.; Charlier, B.; Durrleman, S. Parallel Transport in Shape Analysis: A Scalable Numerical Scheme. In International Conference on Geometric Science of Information; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; Volume 10589. [Google Scholar]
- Frahi, T.; Argerich, C.; Yun, M.; Falco, A.; Barasinski, A.; Chinesta, F. Tape surfaces characterization with persistence images. AIMS Mater. Sci. 2020, 7, 364–380. [Google Scholar] [CrossRef]
- Frahi, T.; Chinesta, F.; Falco, A.; Badias, A.; Cueto, E.; Choi, H.Y.; Han, M.; Duval, J.L. Empowering Advanced Driver-Assistance Systems from Topological Data Analysis. Mathematics 2021, 9, 634. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Harer, J.L. Computational Topology: An Introduction; American Mathematical Society: Providence, RI, USA, 2009. [Google Scholar]
- GUDHI Project. GUDHI User and Reference Manual. GUDHI Editorial Board. 2021. Available online: https://gudhi.inria.fr/doc/3.4.1/ (accessed on 3 July 2021).
- Carrière, M.; Cuturi, M.; Oudot, S. Sliced Wasserstein Kernel for Persistence Diagrams. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. PMLR 70:664-673. [Google Scholar]




| 0.00 | - | - | - | |
| 0.50 | - | - | ||
| 2.00 | - | - | ||
| 20.50 | - | - | ||
| 45.25 | - | - | ||
| 50.00 | - | - | ||
| 50.02 | - | - | ||
| 64.73 | - | |||
| 70.64 | - | |||
| 71.38 | - | |||
| 71.55 | ||||
| Case | 1st surf. | 2nd surf. | 3rd surf. | 4th surf. | 5th surf. | 6th surf. |
|---|---|---|---|---|---|---|
| 01 | 2828 | 3742 | 6012 | 6281 | 7070 | 7314 |
| 02 | 3839 | 4341 | 5160 | 5269 | 8299 | 9530 |
| 03 | 3540 | 4003 | 4702 | 5536 | 6436 | 8023 |
| 04 | 2971 | 3762 | 5883 | 7481 | 7429 | 9314 |
| 05 | 3062 | 3762 | 5437 | 6156 | 9865 | 10,307 |
| 06 | 4852 | 5239 | 7294 | 8336 | 8237 | 9585 |
| 07 | 3482 | 4411 | 6095 | 6882 | 9319 | 10,627 |
| 08 | 3392 | 3684 | 5903 | 6710 | 9273 | 9438 |
| 09 | 4648 | 5436 | 7986 | 7707 | 10,415 | 9406 |
| 10 | 4425 | 4267 | 5583 | 5811 | 9620 | 9163 |
| 11 | 3256 | 3722 | 4782 | 4888 | 5840 | 8064 |
| 12 | 2993 | 3750 | 5551 | 6885 | 7135 | 8474 |
| 13 | 4281 | 4862 | 7127 | 8230 | 8170 | 9687 |
| 14 | 4367 | 5004 | 7140 | 7036 | 8285 | 8008 |
| 15 | 4937 | 5396 | 6484 | 6446 | 9323 | 10,031 |
| 16 | 3184 | 3941 | 4907 | 4965 | 7205 | 8869 |
| 17 | 2957 | 3652 | 5652 | 6021 | 7659 | 7571 |
| Case | 1st surf. | 2nd surf. | 3rd surf. | 4th surf. | 5th surf. | 6th surf. |
|---|---|---|---|---|---|---|
| 01 | 1 | 2 | 3 | 4 | 5 | 6 |
| 02 | 1 | 2 | 3 | 4 | 5 | 6 |
| 03 | 1 | 2 | 3 | 4 | 5 | 6 |
| 04 | 1 | 2 | 3 | 5 | 4 | 6 |
| 05 | 1 | 2 | 3 | 4 | 5 | 6 |
| 06 | 1 | 2 | 3 | 5 | 4 | 6 |
| 07 | 1 | 2 | 3 | 4 | 5 | 6 |
| 08 | 1 | 2 | 3 | 4 | 5 | 6 |
| 09 | 1 | 2 | 4 | 3 | 6 | 5 |
| 10 | 2 | 1 | 3 | 4 | 6 | 5 |
| 11 | 1 | 2 | 3 | 4 | 5 | 6 |
| 12 | 1 | 2 | 3 | 4 | 5 | 6 |
| 13 | 1 | 2 | 3 | 5 | 4 | 6 |
| 14 | 1 | 2 | 4 | 3 | 6 | 5 |
| 15 | 1 | 2 | 4 | 3 | 5 | 6 |
| 16 | 1 | 2 | 3 | 4 | 5 | 6 |
| 17 | 1 | 2 | 3 | 4 | 6 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frahi, T.; Falco, A.; Mau, B.V.; Duval, J.L.; Chinesta, F. Empowering Advanced Parametric Modes Clustering from Topological Data Analysis. Appl. Sci. 2021, 11, 6554. https://doi.org/10.3390/app11146554
Frahi T, Falco A, Mau BV, Duval JL, Chinesta F. Empowering Advanced Parametric Modes Clustering from Topological Data Analysis. Applied Sciences. 2021; 11(14):6554. https://doi.org/10.3390/app11146554
Chicago/Turabian StyleFrahi, Tarek, Antonio Falco, Baptiste Vinh Mau, Jean Louis Duval, and Francisco Chinesta. 2021. "Empowering Advanced Parametric Modes Clustering from Topological Data Analysis" Applied Sciences 11, no. 14: 6554. https://doi.org/10.3390/app11146554
APA StyleFrahi, T., Falco, A., Mau, B. V., Duval, J. L., & Chinesta, F. (2021). Empowering Advanced Parametric Modes Clustering from Topological Data Analysis. Applied Sciences, 11(14), 6554. https://doi.org/10.3390/app11146554







