Simulation of Self-Consumption Photovoltaic Installations: Profitability Thresholds

Abstract

PV self-consumption can contribute positively to the spread of PV and, therefore, to the progress of renewable energies as a key element in a decarbonized energy model. However, the policies of each country regarding the promotion of this type of renewable technology is fundamental for their growth. Despite the high number of sunshine hours registered in Spain, self-consumption in this country has not been authorized until recently. In this new context, this work presents a systematic study of the profitability limits of a self-consumption PV installation under different conditions of installed peak power, orientation and inclination of the PV panels and level of obstruction of the installation. It was proved that, for the case of study (Córdoba, Spain), the maximum profitability was achieved for PV panels oriented to the south and with an inclination of 15° whereas the most unfavourable conditions are those of PV panels with an orientation and inclination of 180° and 90°, respectively. Furthermore, when the level of obstruction increases the maximum of the Net Present Value of self-consumptions PV installations decreases and this optimal value is achieved for installations with lower power. Finally, empirical adjustment equations have been developed to estimate the profitability parameters of self-consumptions PV installations as a function of their design variables.

1. Introduction

Dependency on energy imports is still a reality in many countries today. Europe suffers from this problem very unevenly. Spain is one of the countries with the greatest demographic and economic weight within Europe that suffers from energy dependency and this shortfall is made up by energy imports of fossil origin. It has only been through applying renewable technologies that in some countries this dependency has improved. At an economic level it has a negative effect on the balance of payments and the country’s debt capacity and also contributes to raising the cost of financing these imports [1]. Also, at an environmental level, the impact on climate change is very high [2].

Specifically, in the case of Spain, dependency stood at around 74% in 2017 (mainly oil and natural gas) and reached 20,700 million euros [3]. Therefore, reducing this dependency is a challenge long discussed at a political level in Spain, although there has not been a clear policy whose objectives were aimed at its reduction. The National Integrated Energy and Climate Plan (PNIEC) 2021–2030 of Spain aims to advance in the improvement of energy dependency abroad to reach 61% in 2030 [4].

Reducing this dependency can be tackled in Spain using its own resources and with a greater share of renewable energies in the country’s energy mix. Specifically, the potential of solar energy in Spain is clear given that it is one of the European countries with the highest rate of solar radiation. Thus, for example, Madrid is the European capital with the highest direct radiation (3.39 kWh·m⁻²·day⁻¹) and the second, after Athens, in global radiation levels (4.88 kWh·m⁻²·day⁻¹) [5]. In this context and due to the sharp decrease in costs that it has experienced in recent years [6], the photovoltaic sector is key to this strategy [7]. It has therefore become the spearhead of the objectives of the Clean energy for all Europeans package [8] to generate a decarbonized energy model. Furthermore, it is a technology with a high capacity to generate employment [9]. However, the different changes that Spanish regulations have undergone regarding energy [10,11,12] have generated certain instability in the solar sector.

In the scope of this work, the authors will focus on photovoltaic (PV) self-consumption. A self-consumption PV installation is a PV plant that allows the owner to generate their own electrical energy from solar energy through PV panels. In addition, the installation is connected to the network, so that when the demand exceeds the self-produced energy, the difference is taken from the electrical network. The concept of pro-sumer is introduced as the user of the electrical system that not only consumes energy but also produces it [13]. It is important to highlight the influence that legislative regulation has on the implementation of such technology. The high impact that the different policies a country may adopt on energy consumption habits [14] and, therefore, on global terms of demand is noteworthy. Osorio-Aravena et al. [15] conclude that without a clear support policy for self-consumption there are many drawbacks, mainly investment, that prosumers encounter for the development of this sector at the residential level in Chile. In this regard, Bertsch et al. [16] have already established the limitations and the technological and administrative possibilities that would generate a profitable system in Germany and Ireland. Masson et al. [17] established the conditions for the development of business models under different regulations, summarising the possible options in five profiles based on the comparison between the retail price and the LCOE. At the time of its publication, it was still in an incipient stage both at the legislative and implementation levels.

To carry out a complete study of the profitability conditions of a photovoltaic installation for self-consumption, it is also necessary to detail the dimensioning of the installations. Thus, Talavera et al. [18] present a methodology that maximises self-consumption based on daily consumption profiles and on the characteristics of the facility itself, regardless of the regulations applied. Posadillo and López-Luque [19] also developed a methodology for isolated installations in which their dimensioning was detailed for changing conditions throughout the year in orientation and demand.

In the literature there are also methodologies that abound in the number of residents of each household. Escobar et al. [20] establish a ranking based on this methodology, as well as on the regulations of several European countries, highlighting the case of France. The complete work developed by Gimeno et al. [21] which, although it focuses empirically on Spanish facilities, establishes a methodology that encompasses the barriers and incentives that prosumers find at various levels (economic, technological and regulatory) in southern European countries and Germany. It is noteworthy that in this work possible changes in the policies of the states leading to an increase in self-consumption are pointed out.

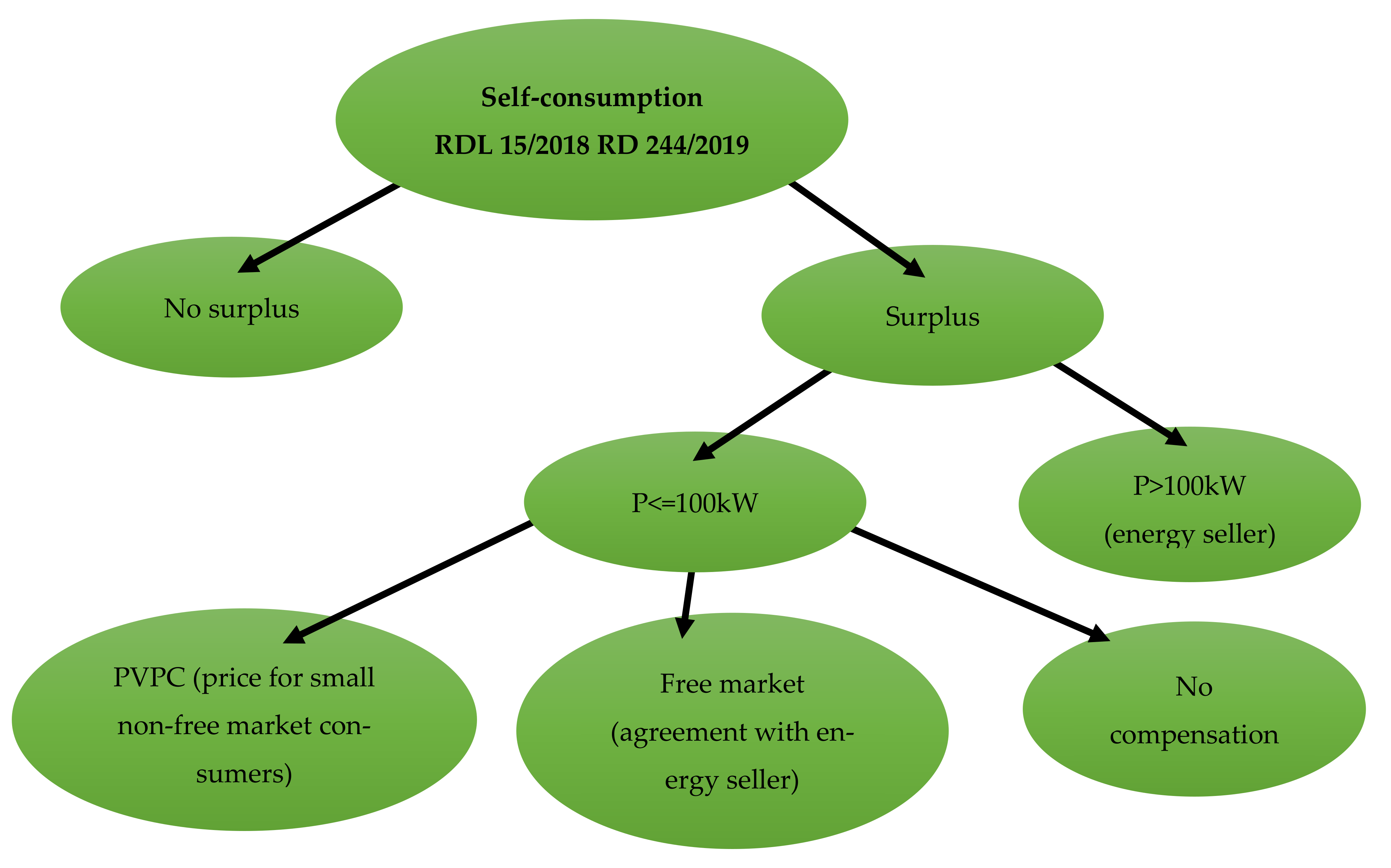
Focusing on the Spanish case, it is worth analysing the evolution of the legislation that has generated an increase in the expectations of the sector in the last three years. The entry into force of Royal Decree 244/2019 [22] together with Royal Decree Law 15/2018 [23] promotes an energy transition towards Renewable Energy Sources (RES) and establishes the following changes regarding self-consumption: the end of any Tax charge on photovoltaic generation (sun tax, Royal Decree 900/2015 [24]), production surpluses can be discharged into the electricity grid in exchange for compensation (Figure 1), there is no limitation to the installed power and there is the possibility of collective self-consumption among several users, allowing the implementation of dynamic coefficients of use.

This new legal framework offers various options for those consumers that feed surpluses into the grid (Figure 1). The surplus compensation mechanism with the demanded energy is available for those stations with power under 100 kW; those whose power exceeds that value or if preferred, will manage the surplus sales directly from the wholesaler market. The rest of the auto consumers, which represent most of the installations in service, have a regulated tariff (PVPC) where the surpluses price is stablished in the 24 h period prior to the service, or have a contract with a trading company, the latter one meaning that the surpluses price is stablished bilaterally.

Since the Spanish regulation came into force, there have been several studies that present a changing and hopeful horizon regarding the increase and profitability of self-consumption in Spain. For an average household, it is more profitable to become a prosumer (1.5–2.0 kWp) than to remain just a consumer [25]. At the same time, another study [10] shows the different options that a prosumer can currently implement to increase the profitability of their installation, detailing the level of increase based on the percentage of self-consumption implemented. It is no less important to note that the authors also point out the possible risks of increased self-consumption with respect to integration costs. The study that shows how, regardless of the region or work zone chosen in Spain and whether or not the prosumer is paid, the performance is guaranteed [26] is interesting. This regional distribution of the study would facilitate the adoption of corrective measures at the legislative level depending on the area in which they worked.

Along with the classic profitability studies in which a standard installation is used, it is interesting to combine the enormous amount of academic work carried out focused on relating urban morphology and possible obstructions with solar capture and energy production. An example is the one developed by Yun et al. [27] in which the impact that the angle of obstruction has on the performance of solar panels in three European cities is studied. Also noteworthy is the relationship between urban morphology, the Sky View Factor or tree shadows and the potential of renewable energies [28,29,30]. Together with the different orientations of the panels, the detailed study of the unobstructed accessibility of the buildings of a city to the solar resource is proposed as a differentiating fact in the design of urban developments [31,32].

However, the works found in the literature study the profitability of PV installations with unrestricted access to solar radiation and optimally oriented. Therefore, there is a lack of studies focused on the large number of urban dwellings in which the possible orientations of collectors are very restricted, or which are subject to a significant level of obstruction. In this context, the aim of the present article is to characterise the profitability of domestic PV installations for self-consumption with orientations different from the optimum and with possible obstructions. The study is completed with adjustment equations that allow an approximate quantification of the profitability indices of PV installations depending on their orientation and degree of obstruction. The current legal framework of self-consumption in Spain will be considered for this.

The remainder of the article is organised as follows. In the next section, Section 2, the characterisations of the power of the collectors, their planes and obstructions, together with energy balance and technical and economic feasibility are presented. Section 3 outlines how the methodology was tested in Córdoba, Spain, and the results are discussed. In Section 4, conclusions are drawn based on the restrictions shown and further research is indicated.

2. Materials and Methods

According to the aforementioned, this work aims to characterise the profitability of PV installations with self-consumption as a function of the orientation and inclination of their panels and the degree of obstruction to which they are exposed. In this sense, it is important to mention that production estimation methods based on the use of databases (Roldan et al., 2021) or prediction equations based on meteorological variables (Amine Allouhi, 2020) are designed for collectors with an orientation close to the optimum and without obstructions. Therefore, they are not applicable to this work. As an alternative, in this work, to simulate the energy production of the installation as a function of the levels of solar obstruction, both variables have been related to the solar irradiance received by the panels. In this way, the methodology uses the rational and empirical models developed to characterise the irradiance on a plane as a function of its orientation and the obstructions to which it is subjected. This methodology was applied by Narvarte and Lorenzo [33] and, with some modifications, it has been implemented in software such as SAM, PVGIS, PVSYST [34,35,36]. Based on this methodology, the study of the profitability of PV self-consumption installations was developed and new mathematical models were proposed to provide simple and immediate information on the profitability of a self-consumption PV installation based on parameters such as the inclination and orientation of its panels and the level of solar obstruction.

2.1. Characterisation of the Power Produced by the Collectors

To evaluate self-consumption systems, in this work the behaviour of a self-consumption photovoltaic plant was simulated in 12 synoptic days of the installation (one for each month of the year). In this way, the simulation method provides a detailed analysis of energy balances every hour, estimating every 10 min the power generated by the PV system and the power demanded/injected into the electrical network.

$$P^{PV}=\eta \left\{\frac{I\left(t\right)}{I_{STC}}PP\left[1-k\left(T_{cell}-T_{STC}\right)\right]\right\},$$

(1)

where:

$I\left(t\right)$ is the irradiance on the plane of the inclined collector (expressed in Wm⁻²) in the instant of time $t$,

$I_{STC}$ is the irradiance under standard conditions (1000 Wm⁻²),

$PP$ is the maximum power generated under standard conditions by the photovoltaic modules (in W),

$k$ is the coefficient of decrease in performance due to the increase in cell temperature, which for silicon cells, is set at 0.004 °C⁻¹,

$\eta$ is a performance factor that groups the investment return and the possible losses in generation and distribution,

$T_{STC}$ is the cell temperature in the standardised assay (25 °C), and

$T_{cell}$ is the actual working temperature of the cell that can be evaluated by means of Equation (2), where $T_a$ is the ambient temperature and $T_{NOC}$ is a parameter of the cell that must be provided by the manufacturer and that represents the temperature of the photovoltaic cells under nominal operating conditions.

$$T_{cell}=T_a+\frac{T_{NOC}-20}{800}I\left(t\right),$$

(2)

In order to estimate the solar irradiance in the collector plane, $I\left(t\right)$, the use of the model of Pérez et al. [37] is proposed, which estimates the global solar irradiance on inclined surfaces as the sum of the direct, reflected and diffuse components, which in turn is decomposed into three terms: diffuse isotropic, diffuse circumsolar and diffuse from the horizon. Thus, the solar irradiance is given by Equation (3) where $\rho$ is the albedo and $F_1$, $F_1$, $a_p$ and $b_p$ are the weighting parameters of the model that allow the diffuse irradiance to be calculated as the sum of the three subcomponents defined above.

$$I=\frac{\cos \theta }{\cos {\theta }_z}{I}_B+\left[\left(1-F_1\right)\frac{1+\cos \beta }{2}+F_1\frac{a_P}{b_P}+F_{2}sin\beta \right]I_D+\rho \frac{1-\cos \beta }{2} \left(I_B+I_D\right),$$

(3)

According to this model, the solar irradiance in the collector plane depends on the direct irradiance, $I_B$, and diffuse, $I_D$, on the horizontal plane, which are estimated from the monthly average radiation on the twelve representative days of each month of the year. using, for this, the model of Collares-Pereira et al. [38]. The dependency at each instant of the irradiance in the collector plane with respect to its geometry is characterised by the variables $\theta$, ${\theta }_z$ and $\beta$ that are defined below.

2.2. Geometric Characterisation of the Collector Plane

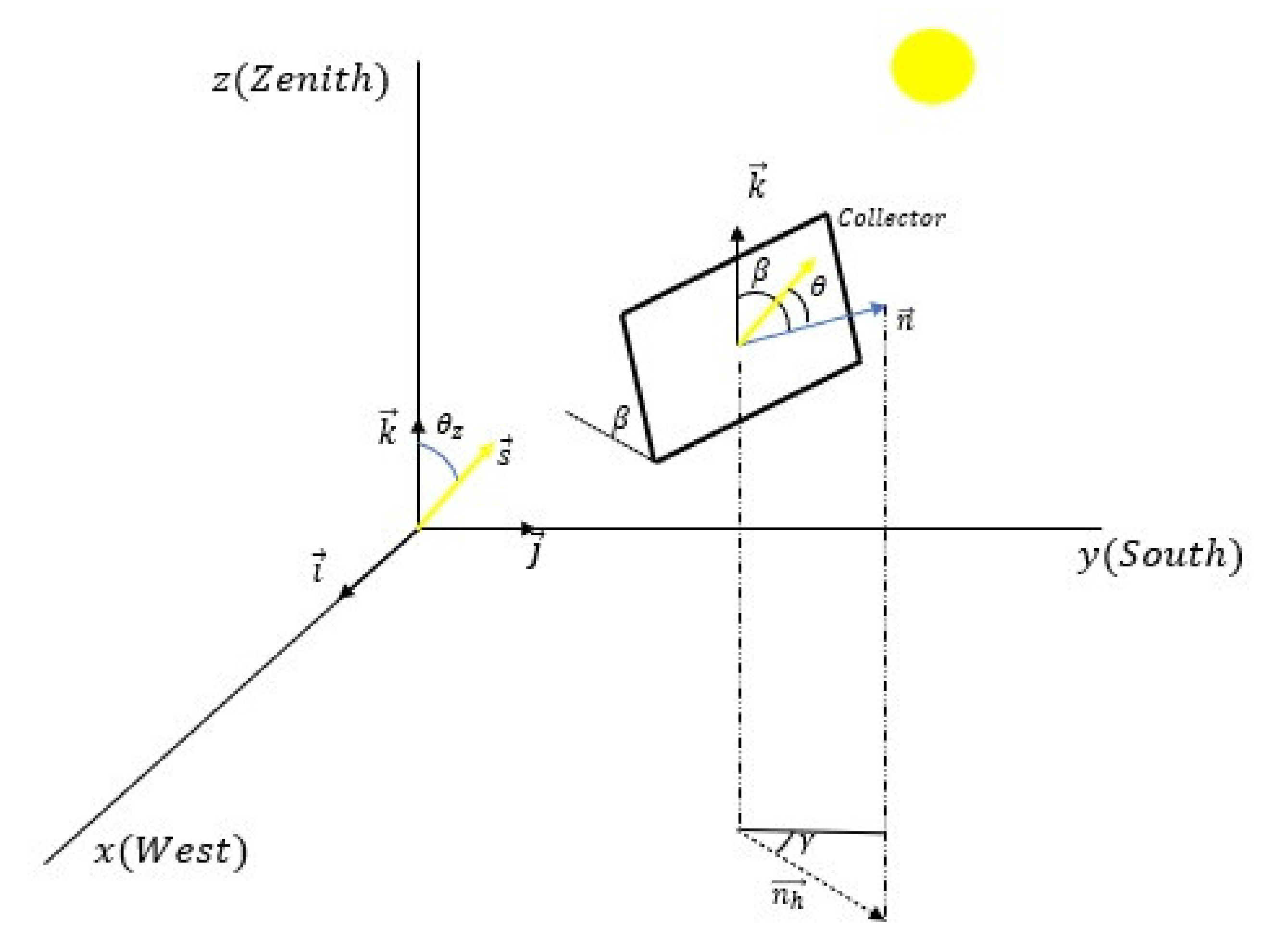
Figure 2 shows, in vector mode, the determining directions of the collector plane’s behaviour regarding solar irradiance collection. To define these characteristic vectors, the terrestrial reference system is used, in which the Ox axis points west, the Oy axis points south, and the Oz axis coincides with the zenith direction, where $\overrightarrow{i}$, $\overrightarrow{j}$ and $\overrightarrow{k}$ are the unit vectors associated with each of these axes, respectively. Thus, in this reference system, the solar vector, $\overrightarrow{s}$, which is defined as a unit vector pointing to the Sun, is given by Equation (4) [39]

$$\begin{array}{c}\overrightarrow{s}=s_x\overrightarrow{i}+s_y\overrightarrow{j}+s_z\overrightarrow{k}=\left(\sin \Omega t\hspace{0.33em}\cos \delta \right)\overrightarrow{i}+\hfill \\ +\left(\cos \Omega t\cos \delta \sin \phi -\sin \delta \cos \phi \right)\overrightarrow{j}+\hfill \\ +\left(\cos \Omega t\cos \delta \cos \phi +\sin \delta \sin \phi \right)\overrightarrow{k},\hfill \end{array}$$

(4)

where:

$\phi$ is the latitude,

$\Omega$ is the speed of rotation of the Earth,

$\delta$ is the declination given by Equation (5) in which $\Gamma$ is the daily angle given by Equation (6).

$$\begin{array}{c}\delta \left(rad\right)=[0.006918 -0.399912\cos \left(\Gamma \right)+\hfill \\ +0.070257\sin \left(\Gamma \right) -0.006758\cos \left(2\Gamma \right)+\hfill \\ +0.000907\sin \left(2\Gamma \right) -0.002697\cos \left(3\Gamma \right)+\hfill \\ +0.00148\sin \left(3\Gamma \right)],\hfill \end{array}$$

(5)

$$\Gamma \left(rad\right)=\frac{2\pi \left(d_j-1\right)}{365}$$

(6)

and $t$ is the true solar time (in hours), whose relationship with GMT time (in hours) is given by Equation (7), in which $L_e$ represents the longitude in degrees of the plant’s geographical location and $E_i$ (in minutes) is the so-called equation of time that is calculated using Equation (8).

$$t=GMT-12+L_e/15+E_i/60$$

(7)

$$\begin{array}{cc}\hfill E_i=229.18& [0.000075+0.001868\cos \left(\Gamma \right)-0.032077\sin \left(\Gamma \right)\hfill \\ & -0.014615\cos \left(2\Gamma \right)-0.04089\sin \left(2\Gamma \right)]\hfill \end{array}$$

(8)

Furthermore, according to Figure 2, from (4), it is found that the solar height, α, that is, the angle that the solar rays form with the horizontal plane, can be determined by the Equation (9)

$$\alpha =\arcsin \left(\cos \Omega t \cos \delta \cos \phi +\sin \delta \sin \phi \right),$$

(9)

Finally, Figure 2 also represents the unit vector $\overrightarrow{n}$ orthogonal to the plane of photovoltaic modules and representative of the spatial position of the collector, which depends on the inclination $\beta$ and the azimuth $\gamma$ of the collectors according to Equation (10). Thus, as seen in Figure 2, the angle between the vector $\overrightarrow{n}$ and the solar vector $\overrightarrow{s}$ is $\theta$, while the angle between $\overrightarrow{n}$ and $\overrightarrow{k}$ coincides with the inclination of the collector,$\beta$. Equations (11)–(13) determine the relationships between the angles and the vectors characteristic of the collector’s position and that determine its radiative uptake.

$$\overrightarrow{n}=\left(\sin \beta \sin \gamma \right)\overrightarrow{i}+\left(\sin \beta \cos \gamma \right)\overrightarrow{j}+\left(\cos \beta \right)\overrightarrow{k}$$

(10)

$$\cos \theta =\overrightarrow{s}·\overrightarrow{n},$$

(11)

$$\cos {\theta }_z=\overrightarrow{s}·\overrightarrow{k}$$

(12)

$$\cos \beta =\overrightarrow{k}·\overrightarrow{n}$$

(13)

2.3. Characterisation of Obstructions

The characterisation of solar incidence in environments with possible solar obstructions requires instruments to determine whether there is an incidence of direct solar rays or not. Cylindrical or hemispherical diagrams, where the apparent horizon line is represented, are often used [31,40,41]. However, characterising the multiple horizon profiles possible in an urban environment (a city) is extremely difficult. Accordingly, in this work, they have been simplified to their average obstruction angle elevation. In this way and as simplification, the obstruction profiles determined by constant obstruction angles $\zeta$ are assumed. Thus, on the cylindrical chart, obstruction profiles such as those represented by the green lines in Figure 3a will be considered, which, geometrically, would be equivalent to the obstruction profile that an observer located in the centre of a circular square with constant height of buildings (Figure 3b).

Accordingly, in the moments of obstruction, that is, when the solar height $\alpha$ is less than the angle of obstruction $\zeta$ and, consequently, the direct irradiance does not reach the PV plates, the global solar irradiance on collectors will be considered with the Equation (14), while, during the moments without obstruction, Equation (3) will be considered.

$$I=\left[\left(1-F_1\right)\frac{1+\cos \beta }{2}+F_1\frac{a_P}{b_P}+F_2\sin \beta \right]I_D+\rho \frac{1-\cos \beta }{2}\left(I_B+I_D\right)\hspace{1em}if \alpha <\zeta ,$$

(14)

2.4. Energy Balance

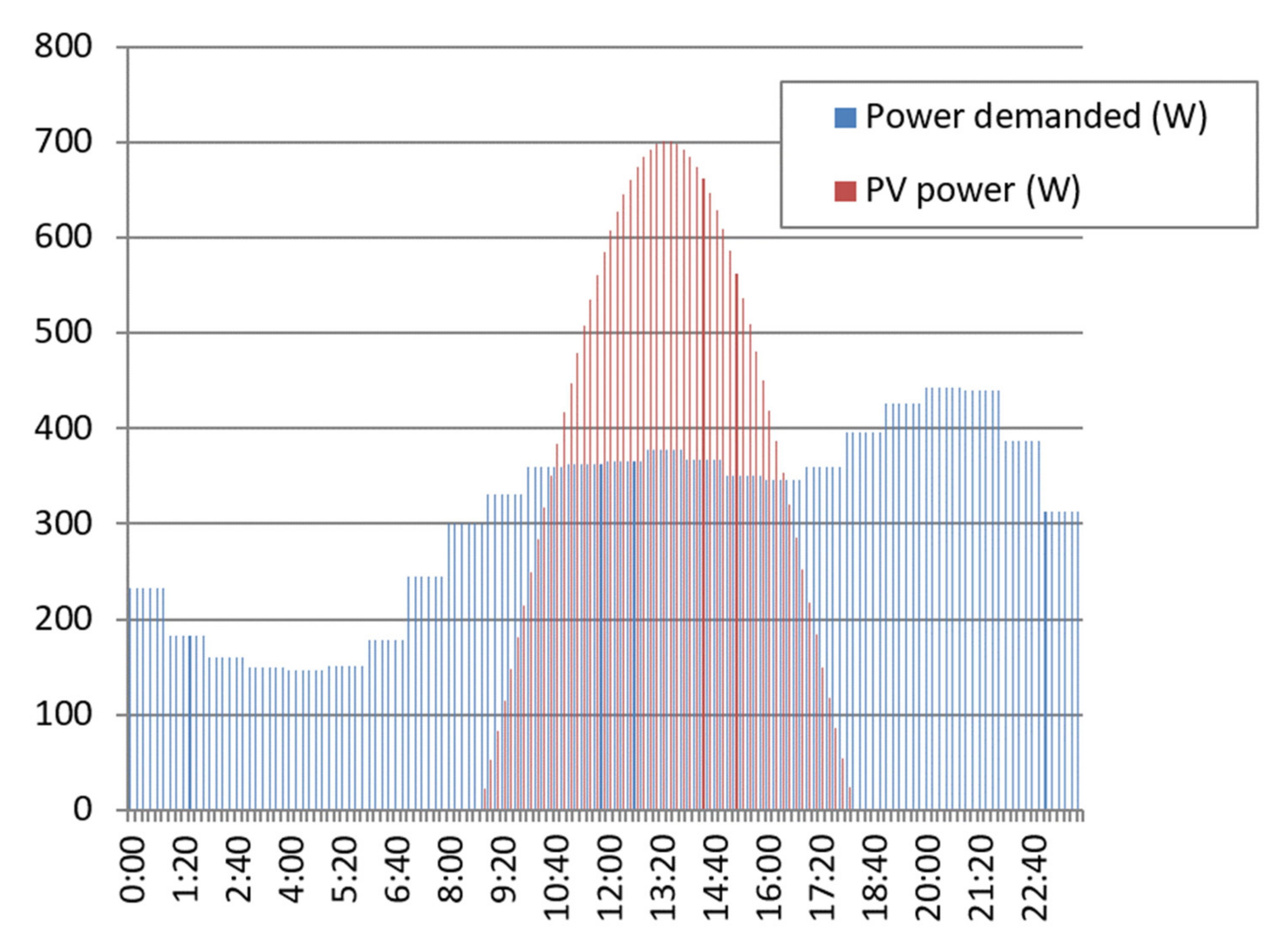
In PV plants with self-consumption, once the curve of photovoltaic power produced in the representative days of the year has been obtained in accordance with the methodology described, it is necessary to compare this curve to that of the demand required by the consumer to obtain an estimate of both the self-contained power submerged as the power taken from or injected into the grid. By way of example, Figure 4 shows in red the values of photovoltaic power generated by an installation, while the curve in blue shows the power demand.

According to Figure 4, in this work, the power balance for a PV installation with self-consumption is estimated according to Equations (15)–(17) in which the central instants of each of the six 10-min intervals in which each GMT hour is decomposed are considered and in which, for each instant $x$ of the representative day of the month $m$, $P_{x,m}^S$ represents the generated and instantaneously self-consumed power, $P_{x,m}^{PV}$ the solar power PV generated (Equation (1)), $P_{x,m}^D$ the power demand required by the consumer, $P_{x,m}^E$ the power imported from the grid and $P_{x,m}^I$ the power injected into the network.

$$P_{x,m}^S=\min \left(P_{x,m}^{PV};P_{x,m}^D\right),$$

(15)

$$\left.\begin{array}{c}{P}_{x,m}^E=P_{x,m}^D-P_{x,m}^{PV}\\ P_{x,m}^I=0\end{array}\right\}\hspace{1em}if\hspace{1em}{P}_{x,m}^S=P_{x,m}^{PV},$$

(16)

$$\left.\begin{array}{c}{P}_{x,m}^E=0\\ P_{x,m}^I=P_{x,m}^{PV}-P_{x,m}^D \end{array}\right\}\hspace{1em}if\hspace{1em}{P}_{x,m}^S=P_{x,m}^D$$

(17)

From Equations (15)–(17) it is possible to perform an hourly balance, integrating the power values obtained for each hour $h$ of the representative days of each month $m$ of the year, through Equations (18)–(20) in which the factor $1/6$ represents the time in hours of which each instant considered is representative.

$$P_{h,m}^S=\frac{1}{6}{\displaystyle \sum }_{x\in h}{P}_{x,m}^S$$

(18)

$$P_{h,m}^E=\frac{1}{6}{\displaystyle \sum }_{x\in h}{P}_{x,m}^E$$

(19)

$$P_{h,m}^I=\frac{1}{6}{\displaystyle \sum }_{x\in h}{P}_{x,m}^I$$

(20)

Finally, the monthly balances of self-consumed energy $\left(S_m\right)$, demanded from the network $\left(E_m\right)$ and injected $\left(I_m\right)$ in each month $m$ can be evaluated with Equations (21)–(23) in which $N_m$ is the number of days in month $m$.

$$S_m=N_m{{\displaystyle \sum }}_{h=1}^{24}{P}_{h,m}^S$$

(21)

$$E_m=N_m{\displaystyle \sum }_{h=1}^{24}{P}_{h,m}^E$$

(22)

$$I_m=N_m{\displaystyle \sum }_{h=1}^{24}{P}_{h,m}^I$$

(23)

Thus, the energy saving in each month, $m$, $F_m$, can be obtained as the sum of two values, a direct saving due to self-consumption and a compensation term, according to Equation (24) in which $p_E$ is the purchase price of the energy and $p_C$ the compensation price

$$F_m=p_E{S}_m+\min \left(p_E{E}_m;p_C{I}_m\right),$$

(24)

From (24), therefore, the annual consumption $F$ will be estimated using Equation (25).

$$F={\displaystyle \sum }_{m=1}^{12}{F}_m$$

(25)

2.5. Technical and Economic Valuation

Finally, this section describes the methodology used to evaluate PV installations with self-consumption, both technically and economically. Thus, as an index of technical valuation of the different facilities, the ratio of annually self-consumed energy versus annual energy needs is proposed.

For the economic assessment of the self-consumption project the evaluation is proposed as that of a conventional project in which, due to the investment of capital, during the useful life of the project, income is obtained that is materialised as a saving with respect to the situation—normally initial—in which there is no PV plant. In this way, saving is quantified as the economic difference between two situations: the first situation in which all electrical energy is taken from the grid and no self-consumption installation is carried out, and the second situation in which a self-consumption PV installation has been implemented and, therefore, only the energy taken from the grid and the possible compensations are valued. Accordingly, for the economic assessment of PV installations with self-consumption, the following parameters will be analysed:

• $Net Present Value, NPV:$ accounts for the present value of all economic flows in the useful life of the project according to Equation (26), in which $F$ is the income of each annual period $j$ updated to the initial year (Equation (25)), $M$ is the maintenance expenses calculated in the initial year, $C_0$ is the initial investment $\left(j=0\right),$ $n$ is the useful life of the installation, $d$ is the discount rate or interest rate required of the investment, $i$ the inflation rate and $\mathsf{\Delta }p$ the rate of year-on-year increase in energy prices.

  $$NPV=-C_0+{\displaystyle \sum }_{j=1}^{n}F\frac{{\left(1+\mathsf{\Delta }p\right)}^j}{{\left(1+d\right)}^j}-{\displaystyle \sum }_{j=1}^{n}M\frac{{\left(1+i\right)}^j}{{\left(1+d\right)}^j}$$

  (26)
• Period of return on investment or$Pay-back$: is an indicator that measures how long the total investment will be recovered at the present value. In this way, it serves to accurately reveal the date on which the initial investment will be covered. When the cash flows are the same every year, the calculation of the Payback will be given by Equation (27).

  $$Pay-back=\frac{C_0}{F}$$

  (27)

3. Results

For the evaluation of PV installations with self-consumption and the study of their profitability limits, in accordance with the exposed methodology, a set of domestic PV installations has been simulated and evaluated technically and economically in which some design variables, such as the inclination of the photovoltaic collector $\left(\beta \right)$, the azimuth of the collector $\left(\gamma \right)$, the nominal power of the installation $\left(PP\right)$ and the degree of obstruction $\left(\zeta \right)$, have been systematically varied. Specifically,

Table 1. Design variables and variation intervals considered for the systematic analysis of PV installations with self-consumption.

Variable	Inclination of Collectors $\left(\mathit{\beta }\right)$	Azimuth of Collectors $\left(\mathit{\gamma }\right)$	Power Peak $\left(\mathit{P}\mathit{P}, \mathit{i}\mathit{n} \mathbf{W}\right)$	Angle of De Obstruction $\left(\mathit{\zeta }\right)$
Number of cases	7	13	7	4
Minimum Value	0°	−180°	500 W	0°
Maximum Value	90°	180°	3500 W	30°
Increase	15°	30°	500 W	10°

shows the values considered for these variables. Thus, their systematic crossing has given rise to 2548 different cases (2548 = 7 · 13 · 7 · 4).

For all these cases, a house located in Córdoba (Spain) has been considered, so the latitude and longitude of the place will be 37.85° N and 4.85 W, respectively, and the values of global horizontal radiation $\left(H\right)$ and the clarity index $\left(k_t\right)$ on the representative days of each month of the year will be those listed in

Table 2. Daily radiation on the horizontal plane (H) and k_t in Córdoba (Spain) [19] and representative day of each month [42].

Month	H (kWh/m2)	kt	Mean Temperature	Representative Julian Day
January	2.06	0.46	9.1	17
February	3.08	0.51	10.7	47
March	3.93	0.50	13.5	75
April	4.81	0.49	16.3	105
May	5.28	0.48	19.4	135
June	6.74	0.59	24.4	162
July	7.14	0.64	27.9	198
August	6.50	0.64	27.6	228
September	5.00	0.58	24.3	258
October	3.30	0.49	18.6	288
November	2.29	0.46	13.6	318
December	1.73	0.42	9.6	344

.

Moreover, regarding energy demand, household consumption data representative of all Spanish households during 2019 was used. Likewise, it was considered that the average Spanish household is covered by the type of regulated contract 2.0 without hourly discrimination, which contracted a power of 3.27 kW and which consumed 2240 kWh/year [25]. For this case, the hourly profiles of demand are characterised and published by Red Eléctrica Española [43]. These data are hourly and were averaged to obtain consumption profiles on the representative days of each month proposed by Klein [42]. 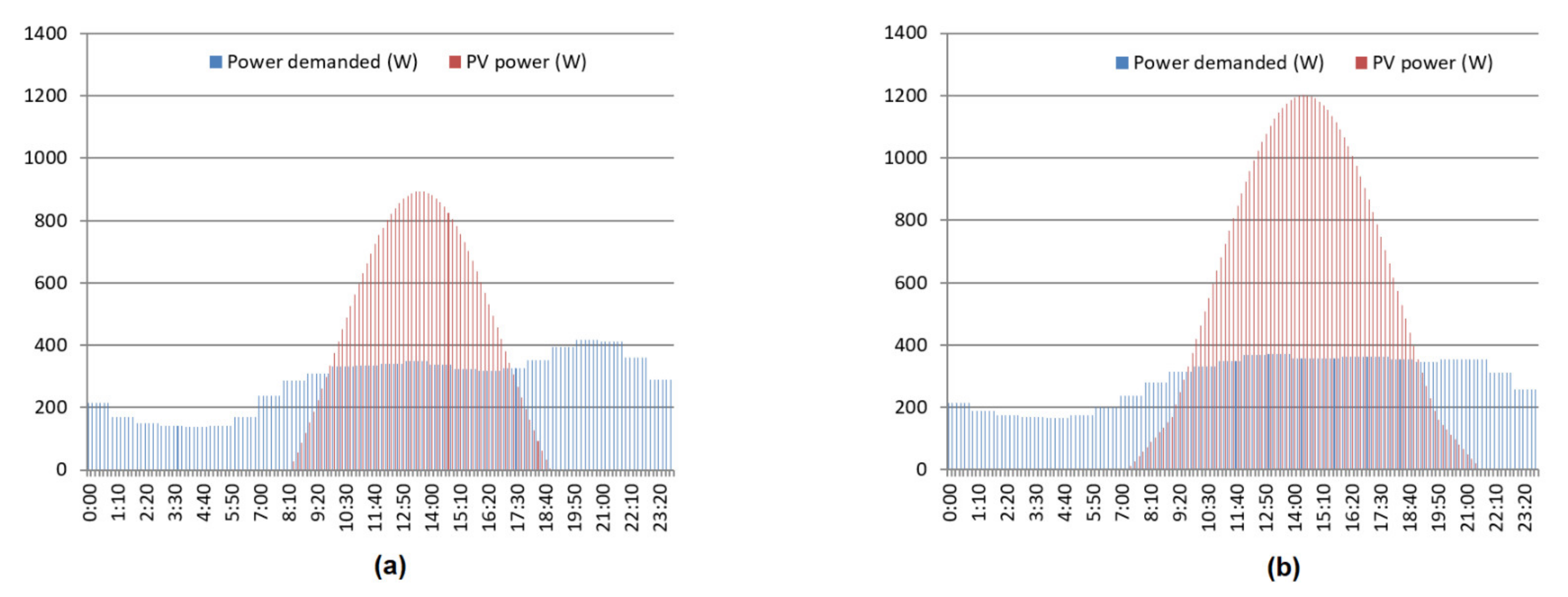Figure 5 shows the profiles obtained in the months of January, April, July, and October. Finally, for the economic evaluation of all the facilities, the values shown in

Table 3. Parameters considered for the economic analysis of PV installations with self-consumption.

Parameters Considered	Value
Installation cost reflected in the power of the CU itself (EUR/Wp)	1.1
Overall return on investment and conversion losses: $\eta$	0.8
Price of energy purchased: $p_E$ (EUR/kWh)	0.16
Compensation price for energy discharged to the grid: $p_C$ (EUR/kWh)	0.04
Maintenance cost reflected in the power of the installation (EUR/Wp)	0.02
Annual discount rate: $d\left(\%\right)$	3
Inflation rate: $i\left(\%\right)$	1
Year-on-year increase in energy Price: $\mathsf{\Delta }p\left(\%\right)$	2.5
Project useful life: $n$ (years)	20

were used.

The simulation of all the cases considered in this study was implemented in VBA-Excel, requiring a total of 1256 s (0.492 s/case) on Intel(R) Core (TM) i5-8250U CPU @ 1.60 GHz.

Thus, the results of the simulation of the different PV installations with self-consumption characterised by the parameters defined above, were tabulated with respect to the azimuth and orientation of collectors as a cylindrical chart, obtaining graphic maps in which the numerical values of the different estimated variables are represented. In these maps, the obstruction level and installed power values have been kept constant. For example,

Table 4. Annual production (in kWh/year) of a 1000 Wp PV installation and an obstruction angle of 30° as a function of the azimuth and inclination of collectors.

Inclination(º)
90	466	496	553	618	671	701	703	700	670	616	552	495	466
75	542	584	659	740	810	856	869	855	808	738	657	584	542
60	664	693	772	859	937	991	1011	990	936	858	770	692	664
45	802	824	889	969	1044	1096	1117	1095	1042	968	887	823	802
30	942	958	1003	1062	1120	1162	1177	1161	1119	1061	1001	958	942
15	1067	1075	1098	1128	1159	1181	1189	1181	1158	1127	1097	1075	1067
0	1151	1151	1151	1151	1151	1151	1151	1151	1151	1151	1151	1151	1151
	−180	−150	−120	−90	−60	−30	0	30	60	90	120	150	180
	Azimuth(º)

,

Table 5. Annual self-consumed energy (in kWh year) of a PV installation of 1000 Wp and an obstruction angle of 30° as a function of the azimuth and inclination of collectors.

Inclination(º)
90	466	496	551	608	661	692	689	680	648	602	550	495	466
75	542	584	640	692	742	780	791	771	727	679	633	581	542
60	655	673	712	755	797	833	847	828	788	742	701	667	655
45	744	748	770	802	838	867	879	865	833	795	763	744	744
30	805	810	821	842	867	887	895	886	864	839	817	807	805
15	853	856	862	873	884	893	896	892	883	871	861	855	853
0	883	883	883	883	883	883	883	883	883	883	883	883	883
	−180	−150	−120	−90	−60	−30	0	30	60	90	120	150	180
	Azimuth(º)

,

Table 6. Annual savings for the first year (in €/year) of a 1000 Wp PV installation and an obstruction angle of 30° as a function of the azimuth and inclination of collectors.

Inclination(º)
90	75	79	88	98	106	111	111	110	105	97	88	79	74.634
75	87	93	103	113	121	128	130	127	120	111	102	93	86.747
60	105	108	116	125	133	140	142	139	132	123	115	108	105.1
45	121	123	128	135	142	148	150	148	142	134	127	122	121.39
30	134	135	139	144	149	153	154	153	148	143	138	135	134.31
15	145	146	147	150	152	154	155	154	152	150	147	146	145.05
0	152	152	152	152	152	152	152	152	152	152	152	152	152.04
	−180	−150	−120	−90	−60	−30	0	30	60	90	120	150	180
	Azimuth(º)

,

Table 7. Net Present Value $NPV$ of a PV installation of 1000 Wp and an obstruction angle of 30° as a function of the azimuth and inclination of collectors.

Inclination(º)
90	-9	81	249	429	590	684	678	655	560	415	246	79	-9
75	222	349	534	714	881	1003	1038	981	846	682	517	343	222
60	570	635	783	947	1104	1227	1273	1215	1081	918	758	621	570
45	880	906	1006	1140	1277	1384	1427	1378	1265	1123	988	895	880
30	1126	1148	1207	1301	1401	1479	1509	1476	1395	1293	1198	1143	1126
15	1330	1342	1374	1421	1470	1508	1521	1506	1467	1418	1371	1340	1330
0	1463	1463	1463	1463	1463	1463	1463	1463	1463	1463	1463	1463	1463
	−180	−150	−120	−90	−60	−30	0	30	60	90	120	150	180
	Azimuth(º)

and

Table 8. $Pay-back$ of a 1000 Wp PV installation and an obstruction angle of 30° as a function of the azimuth and inclination of collectors.

Inclination(º)
90	14.7	13.9	12.5	11.3	10.4	9.9	9.9	10.0	10.5	11.3	12.5	13.9	14.7
75	12.7	11.8	10.7	9.8	9.1	8.6	8.5	8.7	9.2	9.9	10.8	11.8	12.7
60	10.5	10.1	9.5	8.8	8.3	7.9	7.7	7.9	8.3	8.9	9.6	10.2	10.5
45	9.1	9.0	8.6	8.1	7.7	7.4	7.3	7.5	7.8	8.2	8.7	9.0	9.1
30	8.2	8.1	7.9	7.7	7.4	7.2	7.1	7.2	7.4	7.7	8.0	8.1	8.2
15	7.6	7.6	7.5	7.3	7.2	7.1	7.1	7.1	7.2	7.4	7.5	7.6	7.6
0	7.2	7.2	7.2	7.2	7.2	7.2	7.2	7.2	7.2	7.2	7.2	7.2	7.2
	−180	−150	−120	−90	−60	−30	0	30	60	90	120	150	180
						Azimuth(º)

represent, respectively, the maps for the annual photovoltaic production, the annual self-consumed energy, the annual savings achieved, the $NPV$ and the $Pay-back$, for an installation of 1000 Wp of installed peak power and 30° angle of obstruction. In them, the decrease of the variables is observed as the generator is oriented in different directions from the optimal one $\left({\gamma }_{opt}=0°, {\beta }_{opt}=15°\right)$ and they offer the orders of magnitude for all simulations carried out. In general, a high symmetry is observed in the results with respect to azimuth. This is due to the uniformity of the demand curves during the hours of solar incidence.

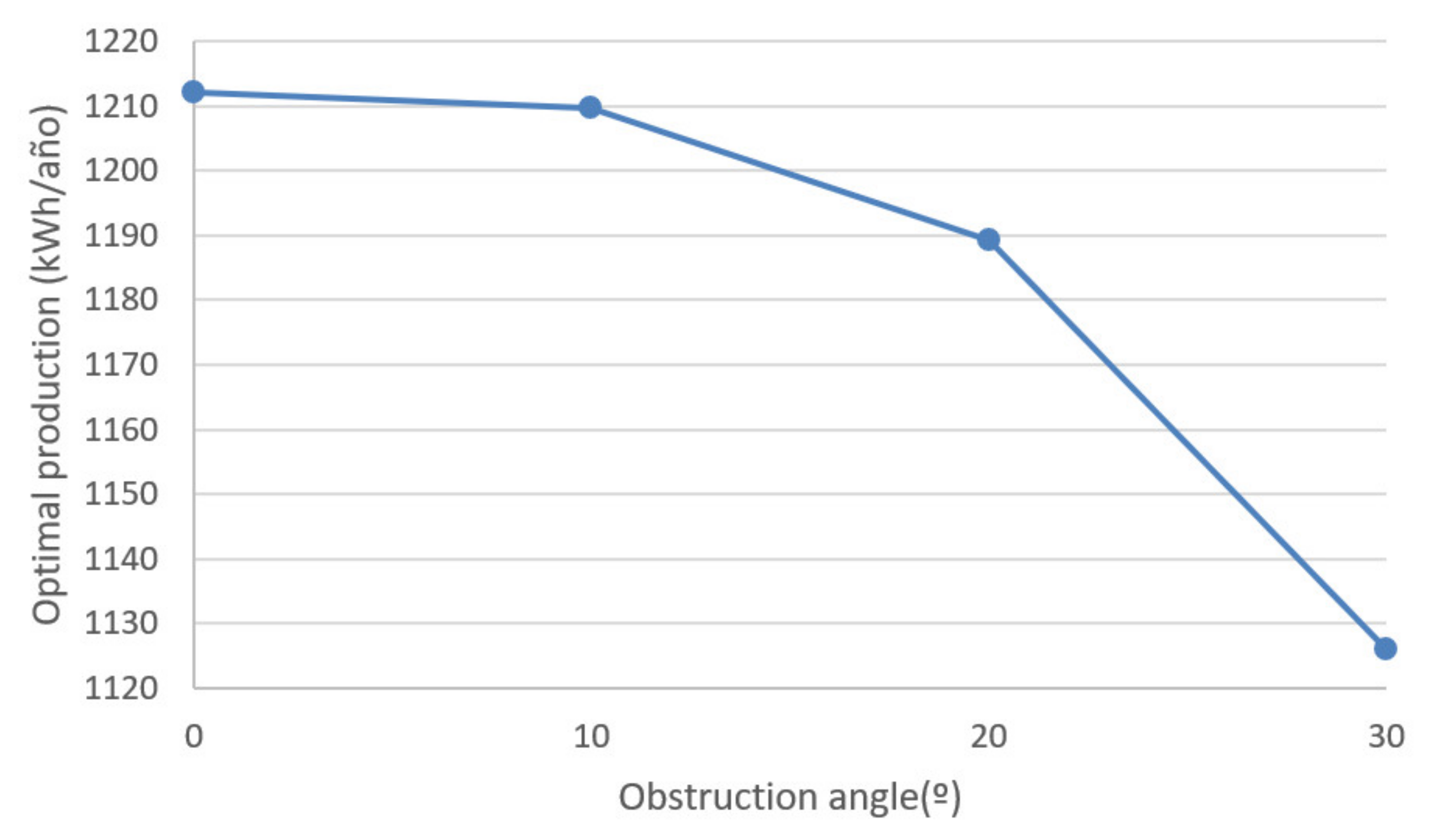
According to Table 4, it is observed that energy production decreases as the obstruction angle increases. Thus, Figure 6 shows the dependency of the optimal production achievable by a 1000 Wp installation as a function of the degree of obstruction. In all cases, as a consequence of Equation (1), energy production, other conditions being equal, will be proportional to its peak power.

Likewise, when comparing Table 5 with Table 4, it is verified that only the solutions with low productivity self-consume all their production. The possibilities of instant self-consumption are saturated when certain productivity limits are exceeded, precisely those that lead to discharges from the network. Thanks to these features, and their economic valuation, the savings achieved (Table 6) are not saturated to the same extent as instant self-consumption.

Finally, based on the annual savings achieved, Table 7 and Table 8 show the $NPV$ and $Pay-back$ obtained for the installation of 1000 Wp of installed peak power and an obstruction angle of 30°, using Equations (26) and (27), respectively, for their calculation. However, it should be noted that in all the $NPV$ tables obtained, for the different values considered for installed power, $PP,$ and degree of obstruction, $\zeta$, the minimum $NPV$ values are reached for the orientation $\gamma =180° \mathrm{and} \beta =90°$. Likewise, in all cases, the optimal $NPV$ corresponds to the orientation $\gamma =0° \mathrm{and}$ $\beta =15°$.

Table 9. Optimal and minimum $NPV$ for different levels of obstruction.

	Optimal $NPV$ for the Best Orientation ($\gamma =0° and \beta =15°$) and Corresponding $PP$		Minimum $NPV$ for the Worst Orientation ($\gamma =180° and \beta =90°$) and Corresponding $PP$
Obstruction	$NPV$ (EUR)	Corresponding PP (Wp)	$NPV$ (EUR)	Corresponding PP (Wp)
$\zeta$ = 0°	1626.0	1500	48.5	1500
$\zeta$ = 10°	1616.1	1500	14.8	1000
$\zeta$ = 20°	1522.2	1500	−4.38	500
$\zeta$ = 30°	1319.1	1000	−11.7	500

shows the $NPV$ values that can be achieved for these two orientations and each degree of obstruction.

From Table 9 it can be deduced that for installations with installed power of 1500 Wp, in the absence of obstructions $\left(\zeta =0°\right)$ all possible orientations give rise to positive $NPV$. Likewise, it is evident that, as the value of the obstruction angle increases, the value of $NPV$ decreases for all the installed powers. Although this occurs, both in the case of worst orientation and in the case of optimal orientation, the reduction is more pronounced in optimally oriented installations compared to those with worst orientation, where the values are negative, but with a low absolute value. Table 9 shows how in the situation of high obstruction the optimal $NPV$ values are achieved with lower peak powers. Therefore, it is found that, as the degree of obstruction increases, installations with lower peak power are recommended, especially in the case of installations that are less well oriented.

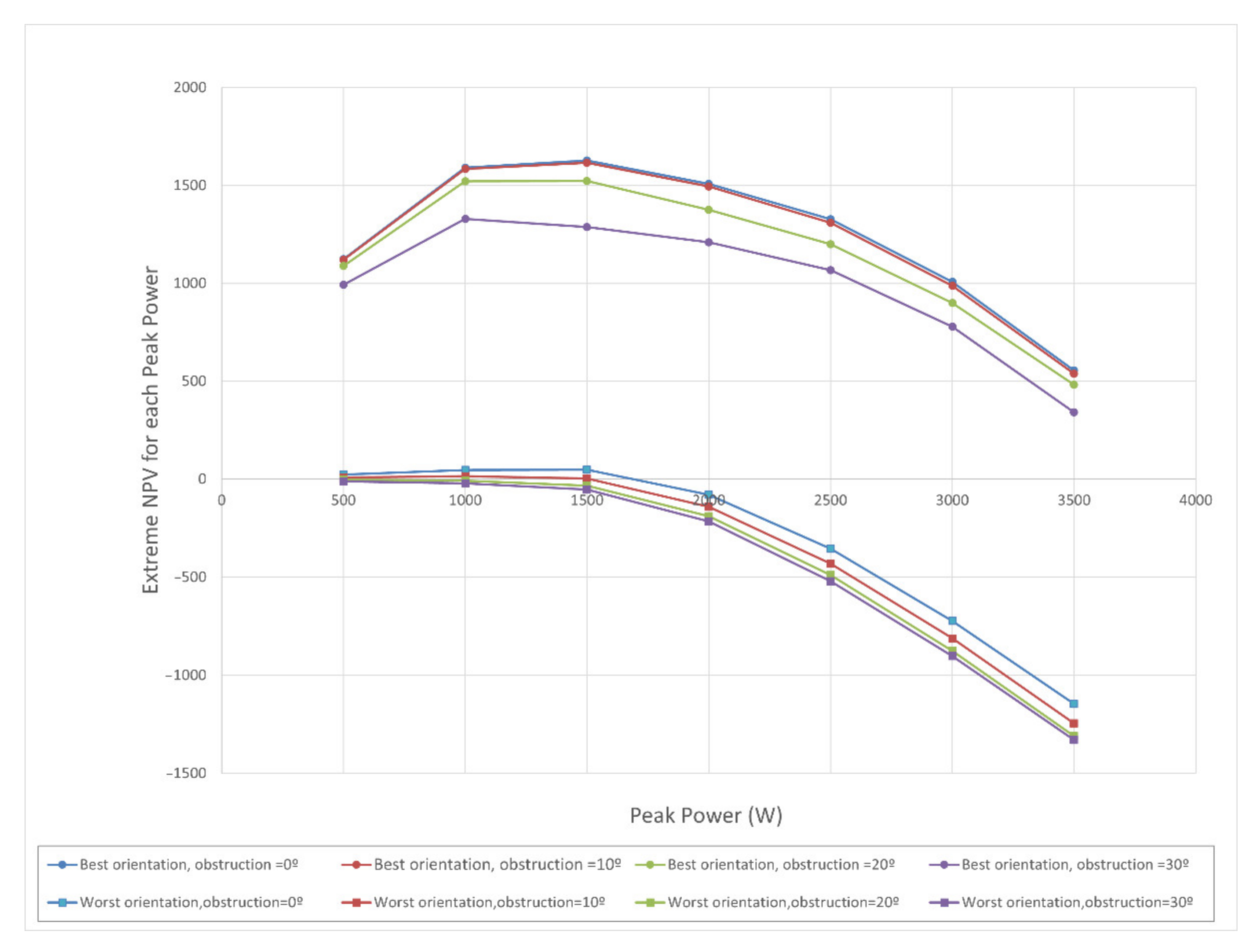
The optimal achievable $NPV$ values for each power and degree of obstruction are represented in Figure 7 (circles) as well as the minimum $NPV$ values in the most unfavourable orientation (squares). In this graph it is observed that the maximum value of $NPV$ (EUR 1626.0), is achieved for the value of $PP=1500 \mathrm{Wp}$ in non-obstruction circumstances. Thus, this figure shows the variation interval of $NPV$ for each power and degree of obstruction. In it, it is observed that, for the most unfavourable orientation ($\gamma =180° \mathrm{and} \beta =90°$), the increase in installed power implies a worsening of the $NPV$, regardless of the angle of obstruction. This graph also shows the inconvenience of increasing the peak power of an installation with a low $NPV$ value. 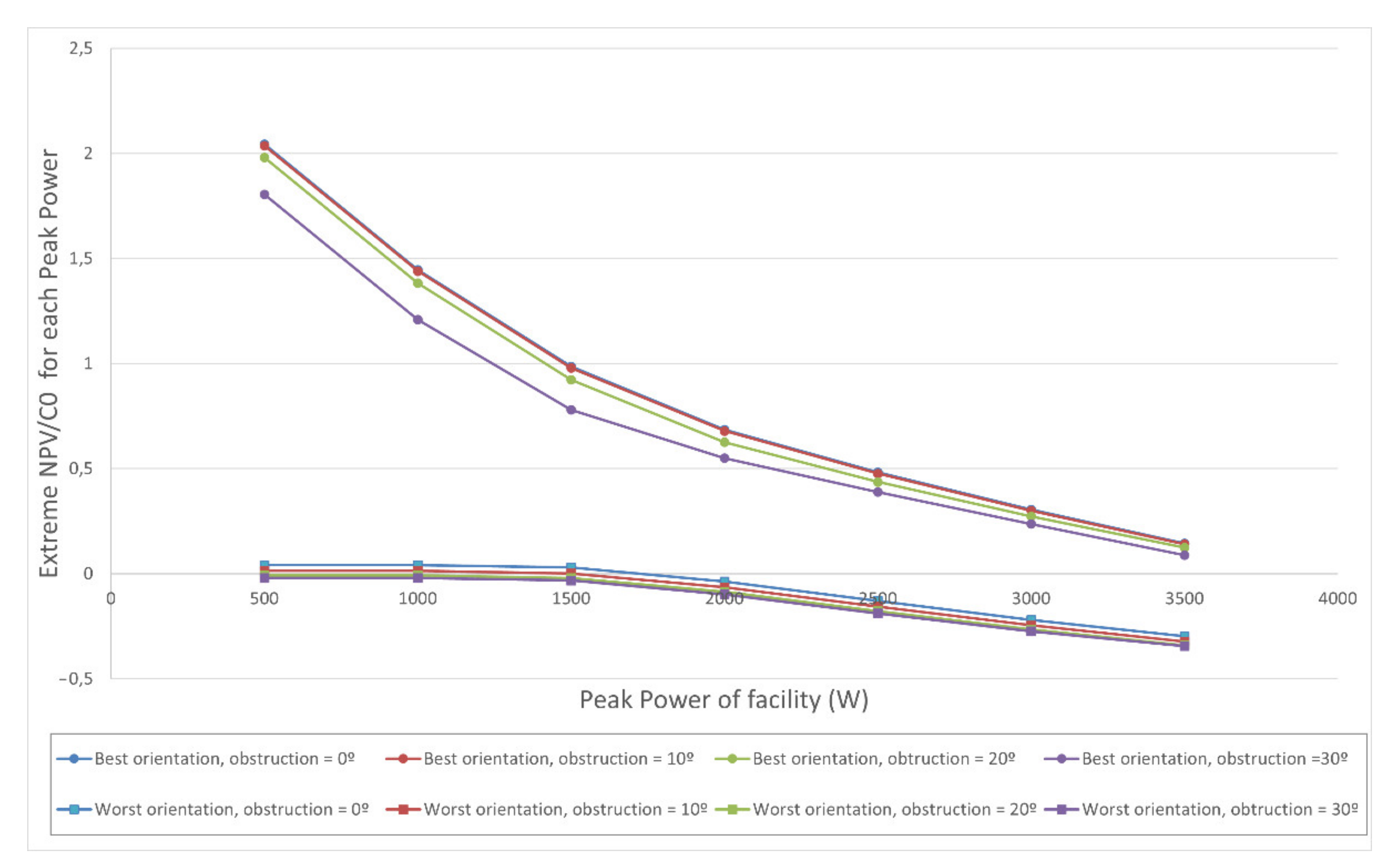However, installations with lower powers may be of great interest in cases where investment capacity is limited and, therefore, the $NPV/investment$ indicator is considered. Figure 8 shows this indicator as a function of peak power and degree of obstruction. It shows the generalised reduction in unit profitability as installed power grows. 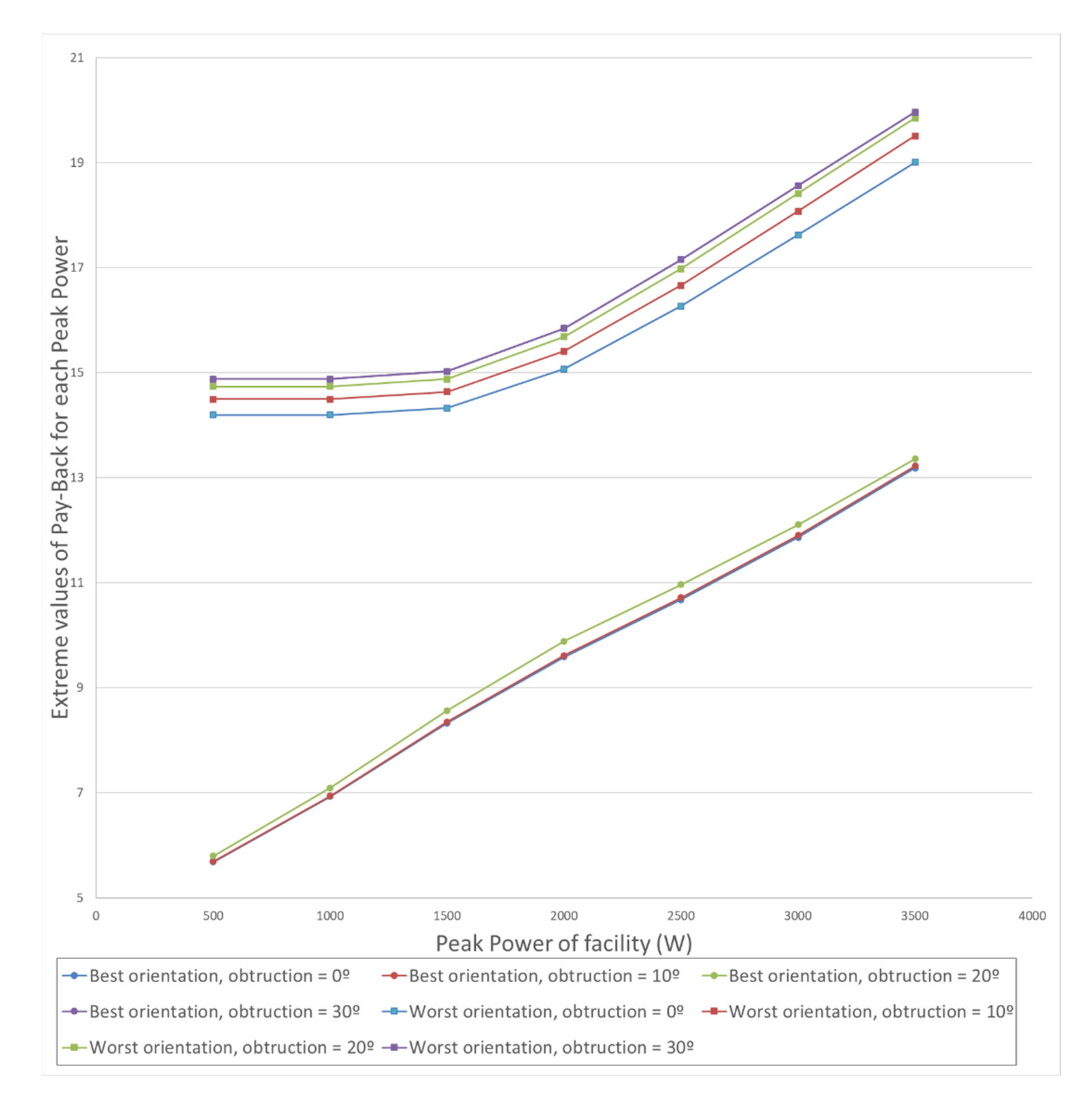Along the same lines, Figure 9 shows the greater ease of recovering the investment in low-power and well-oriented installations, given that the cost is proportional to the installed power and, in addition, they consume all their production. Figure 7, Figure 8 and Figure 9 show, as in Figure 6, the few productive differences for degrees of obstruction $\zeta$ of 0$°$ and 10$°$. The differences in the indicators become more noticeable for $\zeta$ = 30$°$.

Finally, to simplify and generalize the set of results obtained, a way to characterise them mathematically has been sought. In this sense, it should be remembered that the model described and used (for each of the 2548 cases) can be considered as a mathematical function to obtain the study variables from the initial data. However, the complexity of the model and the need to add results on the different representative days makes it difficult, in principle, to know the weight or influence of each variable on the final results. Thus, to overcome this difficulty, in the present work the proposal is to replace this complex function by a mathematical function with a simple expression that reproduces the result of the complex model with the least possible error. In this way, Equations (28)–(30) show the dependency of the technical evaluation variables of the installation (production, compensation and self-consumption) with respect to characteristic parameters of the installation such as inclination $\beta$ and orientation $\gamma$ of the collectors, angle of obstruction $\zeta$ and peak power $PP.$ It should be considered that it is not a statistical problem but rather an adjustment or approximation of a mathematical function with a simple expression to a complex mathematical function, therefore statistical methods are not applicable. To address the adjustment, the set of simple variables was expanded with composite variables obtained as products and quotients of the simple variables. The proposed functions (28)–(30) were selected as the most favourable from the set of fits to linear functions of composite variables. For each of the equations proposed as a quick approximation, the adjustment coefficients are shown as well as the mean of the absolute errors.

• Production, $P$:

  $$\begin{array}{l}P (\mathrm{kWh/year})=73.6+0.5419·PP·\cos \beta +\\ 340.02\sin \beta \sin \gamma + 0.58·PP-0.164·\zeta \\ R^2=0.988& \\ \overline{{\epsilon }_P}=81.2 \mathrm{kWh/año}& \end{array}$$

  (28)
• Compensation, $C$:

  $$\begin{array}{l}C (\mathrm{kWh/year})=-35.65-238.20·\cos \beta +0.529·PP·\\ \cos \beta +289.9\sin \beta \sin \gamma + 8.27·{10}^{-5}·P{P}^2\\ R^2=0.966& \\ \overline{{\epsilon }_C}=110.1 \mathrm{kWh/año}& \end{array}$$

  (29)
• Self-Consumption, $A$:

  $$\begin{array}{l}A (\mathrm{kWh/year})=50.95+ \left(325.02-0.0776·PP\right)·\cos \beta +\\ 0.6540·PP-9.98·{10}^{-5}·P{P}^2-2.1478·\zeta \\ R^2=0.963& \\ \overline{{\epsilon }_A}=35.2 \mathrm{kWh/año}& \end{array}$$

  (30)

Equations (29) and (30) constitute the basis of a simplified model since they allow evaluation of the savings $F$ as a function of design variables by means of Equation (31), where $p_E$ is the energy purchase price and $p_C$ is the compensation price.

$$F\left(PP,\beta ,\gamma ,\zeta ,p_E,p_c\right)=p_{E }A\left(PP,\beta ,\gamma ,\zeta \right)+p_{c}C\left(PP,\beta ,\gamma ,\zeta \right)$$

(31)

Therefore, Equation (31) provides, in a simple way, a first approximation of the possible savings associated to a PV installation for any orientation $\left(\gamma \right)$, tilt $\left(\beta \right)$ and degree of obstruction $\left(\zeta \right)$. In this way, this model allows an easy and immediate evaluation of the profitability and suitability of a domestic PV installation that must be configured according to a set of restrictions imposed by the environment in which it is located.

Moreover, considering that the cost $C_0$ has been considered proportional to the value of the peak power, the Equations (26) and (27) will be approximated by Equations (32) and (33), respectively, with a continuous dependence with respect to the variables of design.

$$\begin{array}{cc}\hfill NP{V}_{ model}=& -C_{0}PP+F\left(PP,\beta ,\gamma ,\zeta ,p_E,p_c\right){\displaystyle \sum }_{j=1}^n\frac{{\left(1+\mathsf{\Delta }p\right)}^j}{{\left(1+d\right)}^j}-\hfill \\ \hfill {\displaystyle \sum }_{j=1}^{n}M\frac{{\left(1+i\right)}^j}{{\left(1+d\right)}^j}& \end{array}$$

(32)

$$Pay-bac{k}_{model}=\frac{C_{0}PP}{F\left(PP,\beta ,\gamma ,\zeta ,p_E,p_c\right)}$$

(33)

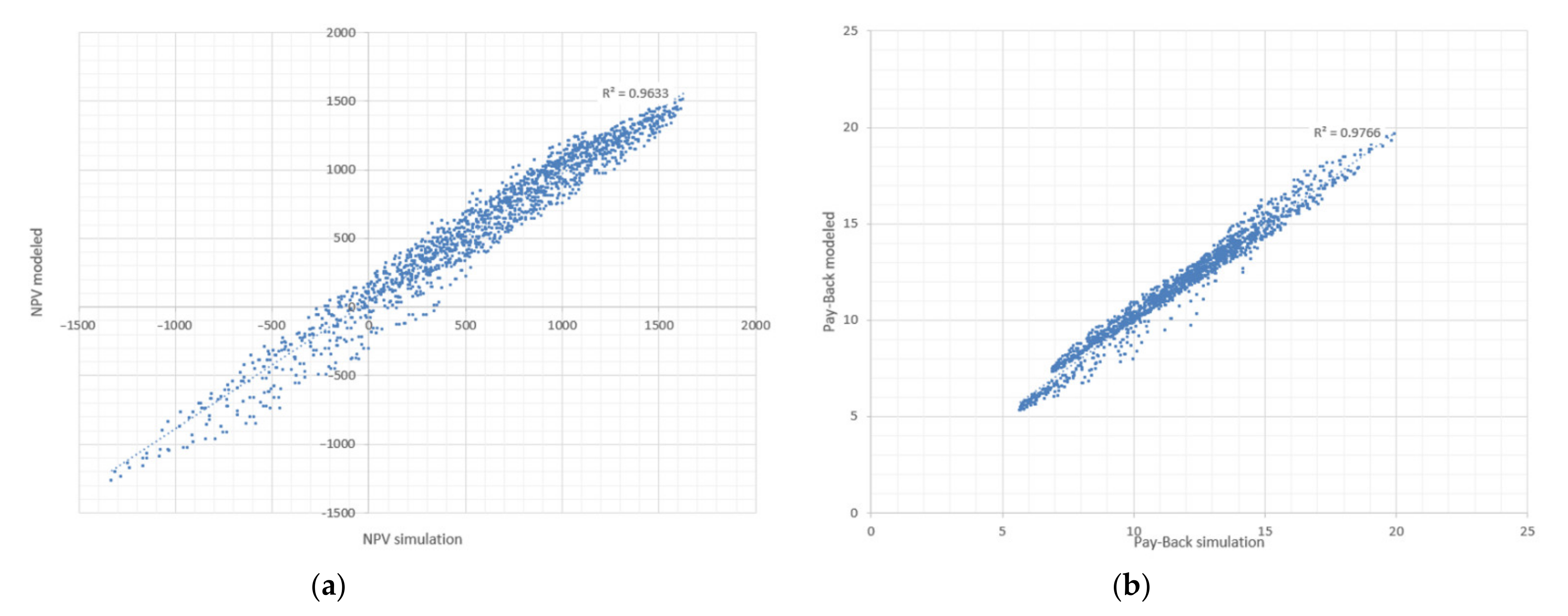
Finally, in Figure 10a the $NPV$ values obtained by means of the model given by Equation (32) are represented against the simulated ones, obtaining a regression coefficient between both of $R^2=0.9633$. Similarly, Figure 10b represents the modelled $Pay-back$ values (Equation (33)) versus the simulated ones, with a regression coefficient between the two of $R^2=0.9766$. Thus, although the model given by Equations (28)–(33) offers approximate values of $NPV$ and $Pay-back$, it notably facilitates the analysis of the qualitative influence of $\gamma$, $\beta$ and $\zeta$ on these indicators.

4. Conclusions

In this work, a complete set of scenarios of domestic self-consumption PV installations located in Córdoba (Spain) has been simulated for a base scenario shown in Table 3. The design variables that were systematically varied were the collector azimuth, inclination of collectors, power of the installation and degree of obstruction. The facilities have been simulated considering the pessimistic hypothesis of energy purchase price values ($p_E=\mathrm{EUR} 0.16 \mathrm{kWh}$) and compensation price $(p_C=\mathrm{EUR} 0.04 /\mathrm{kWh}$) corresponding to the free market.

The “Royal Decree 148/2021” [44], which established the method to calculate the costs of the electric system, is applied from the 1 June 2021 onwards. This new scenario provides two periods for the signed power and three periods for the energy. Initially, there has been an increase in the energy price of both PVPC and free market consumers. Equally, there has been a proportional increase of the energy retribution surplus in PVPC. It is therefore necessary to study this effect with a broader perspective to determine whether it is a temporary disturbance or a trend. This analysis will be addressed in future work.

For all the considered combinations of peak power and angle of obstruction, there are two extreme positions in profitability. The optimal position, $\gamma =0°$ and $\beta =15°$, in which the profitability indices reach maximum profitability, and the most unfavorable position, $\gamma =180° \mathrm{and} \beta =90°$. In the absence of obstructions, the power of 1500 Wp is optimal for all orientations, reaching an optimal $NPV$ of EUR 1626.0 for the most favourable orientation compared to a value of doubtful profitability (EUR 48) in the most unfavourable orientation. If the level of obstruction increases, the $NPV$ interval evolves, decreasing the maximum achievable $NPV$, although the minimum remains at values of doubtful profitability (Table 9). The maximum $NPV$ values obtained for each level of obstruction are compatible with suitable cost-effective installations. Likewise, it is observed that, as the degree of obstruction increases, the optimal $NPV$ values are achieved for installations with powers lower than 1500 W. The preference for powers lower than 1500 W is also justified in cases in which it is intended to improve the profitability unit of invested capital, quantified by the $Pay-back$ or $NPV/investment$ indices. The study of dependency of the profitability indices with respect to the power of the facilities shows a uniform decrease in $Pay-back$ and $NPV/investment$.

Empirical adjustment equations have been developed to estimate profitability parameters in cases of orientation comprised between extreme orientations. From these, a simple model (Equation (32)) is obtained that allows the evaluation of PV installations for self-consumption in Córdoba (Spain) as well as the study of the dependency of the technical and economic evaluation parameters of the installation with respect to other variables of design such as p_E, p_C, C_0, i, d, Δp, and n. Although the values offered by the empirical model are approximate, its advantage lies in being able to carry out an analytical and quantitative study of the influence of the design parameters on the $NPV$ and $Pay-back$ indicators.

This work is a starting point for future work, where climatic considerations or stochastic variations in energy demands can be considered in greater detail.