Abstract
Fiber-optic gyroscopes (FOGs)-based Measurement While Drilling system (MWD) is a newly developed instrument to survey the borehole trajectory continuously and in real time. However, because of the strong vibration while drilling, the measurement accuracy of FOG-based MWD deteriorates. It is urgent to improve the measurement accuracy while drilling. Therefore, this paper proposes an innovative scheme for the vibration error of the FOG-based MWD. Firstly, the nonlinear error models for the FOGs and ACCs are established. Secondly, a 36-order Extended Kalman Filter (EKF) combined with a calibration method based on 24-position is designed to identify the coefficients in the error model. Moreover, in order to obtain a higher accurate error model, an iterative calibration method has been suggested to suppress calibration residuals. Finally, vibration experiments simulating the drilling vibration in the laboratory is implemented. Compared to the original data, compensated the linear error items, the error of 3D borehole trajectory can only be reduced by a ratio from 10% to 34%. While compensating for the nonlinear error items of the FOG-based MWD, the error of 3D borehole trajectory can be reduced by a ratio from 44.13% to 97.22%. In conclusion, compensation of the nonlinear error of FOG-based MWD could improve the trajectory survey accuracy under vibration.
1. Introduction
Accurate borehole trajectory information could help the automatic drilling tool to hit the target [1]. The traditional Measurement While Drilling system (MWD) used to survey the borehole trajectory consists of a triple fluxgate and triple accelerometer (ACC) [2]. The fluxgates determined the azimuth by measuring the components of the geomagnetic field. The accelerometer determined the inclination and toolface angle by measuring the components of the gravity field [3]. This traditional system has two defects. One is that an interfering magnetic field can affect its accuracy. The other is that it must stop drilling work when it needs to measure the borehole trajectory. Another solution that can offer an accurate and continuous borehole trajectory information must be pursued. A fiber-optic gyroscope (FOG) based on an inertial navigation system has been used in aeronautics and astronautics field, such as in airplanes, missiles, and satellites [4]. It can offer real-time position, velocity, and altitude information of the aircraft without relying on other information [5]. These days, with the development of FOG miniaturized technology, the FOG-based MWD has been studied [6,7,8]. The FOG-based MWD consists of triaxial FOGs and triaxial ACCs. The FOGs and ACCs measure the angular rate and acceleration of the automatic drilling tool, respectively. Then, they utilize the inertial navigation algorithm to calculate the three-dimensional (3D) borehole trajectory. However, the bottom hole environment is harsh with a high temperature and strong vibration. Drilling vibrations are a big threat to the MWD [9]. Drilling vibration includes axial vibration, lateral vibrations and torsional vibration [10]. It is characterized by large vibration magnitude, random frequency and a long period of time. Wang et al. [11,12] and Zhang et al. [13] analyzed the influence of downhole vibration on FOG-based MWD measurement accuracy. They gave us the conclusion that the drilling vibrations worsen the measurement accuracy because the error characteristic of the sensors were changed in the vibration. However, it did not propose a solution to solve it.
As we all know, the original data of the FOGs and ACCs have different types of errors, such as bias error, scale factor error and random noise [14]. So, before using them, the error should be compensated by the established error model [15]. In a general way, only the linear error item has been compensated and the nonlinear error items have been ignored [16]. However, while in the drilling environment, downhole vibrations, including non-sinusoidal motions and random high-magnitude shocks, are high dynamic motions. If the nonlinear error is still ignored, it leads to an inaccurate survey result. Aiming to improve the measurement accuracy of the FOG-based MWD under vibration, the nonlinear error must be recognized and compensated correctly.
At present, the centrifuge has been used to calibrate the nonlinear error coefficients of the ACCs [17,18,19]. However, the centrifuge itself has a lot of errors, for example, mechanical structure error, the installation error and the axial rotation dynamic error, which will make the calibration results inaccurate. In addition, using the centrifuge can only recognize the nonlinear error coefficient, while the linear error coefficient needs to calibrate using other equipment. Studies about the nonlinear error model in terms of the FOG seem to be rare. Wang and Ren [20] studied a method to recognize the gyro error coefficient related to the acceleration, but it could not recognize the nonlinear error coefficient related to itself.
In this paper, the nonlinear error item of the FOG-based MWD is recognized and compensated by a turntable instead of a centrifuge. First, taking the nonlinear error item into consideration, the nonlinear error model for the FOG-based MWD is established. Second, a 36-order Extended Kalman Filter (EKF) is designed based on the nonlinear error model [21]. Next, a calibration method based on 24 positions is put forward. With these steps, both the nonlinear and the linear error coefficients could be recognized. Moreover, aiming to decrease calibration residuals, an iterative calibration method is suggested. Finally, in order to verify that compensating the nonlinear error could improve the measurement accuracy of FOG-based MWD under vibration, a calibration experiment and a vibration experiment in the laboratory are implemented.
2. Principle of the FOG-Based MWD
In order to fit the narrow and slim downhole environment, the FOG-based MWD structure should be designed to be slender. A schematic diagram of FOG-based MWD is shown in Figure 1. The FOG-based MWD is mounted in the downhole drilling tools closed to the bit. We just need to install these directional sensors onto a stable platform, which connected with the drilling string by bearings which could separate the motion of directional sensors from the drilling string. It realizes the FOGs-based MWD does not rotate with the drilling string. The FOG-based MWD mainly consists of three FOGs, three ACCs and circuit boards. These FOGs are perpendicular to each other as well as the ACCs. FOG is composed of an optic fiber coil and signal-processing circuit board. The FOG-based MWD has a length of 1 m and its diameter is 35 mm. Its power consumption is 10.4 W. Its supply voltage range is from 18 V to 36 V, and its rated supply voltage is 26 V.
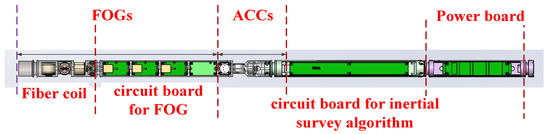
Figure 1.
Schematic diagram of a FOG-based MWD.
The flow chart of the FOG-based MWD measurement algorithm is represented in Figure 2 [6]. The FOG-based MWD are installed into the bottom hole, assembled with their sensitive axes aligned toward the forward direction (Z), the transverse direction (Y) and the vertical direction (X). These three axes form the body frame (b-frame). The local level frame (l-frame), which is the East-North-Up frame with axes along the east, north, and vertical directions, is used as the common reference frame. The earth frame (e-frame) is defined with its Z-axis parallel to and aligned with the direction of the Earth’s rotation. In the equatorial plane, the X-axis locates the Greenwich meridian, and the Y-axis completes the right-hand system. The inertial frame (i-frame) has the common definition that the Z-axis is aligned with the direction of the Earth’s rotation, the X-axis is aligned with the direction of the Earth’s rotation spring equinox in inertial space and the Y-axis completes the right-hand system. Coordinate systems are established to allow information to be exchanged between interfacing systems in a consistent manner and help readers to understand the survey algorithm of the FOG-based MWD.
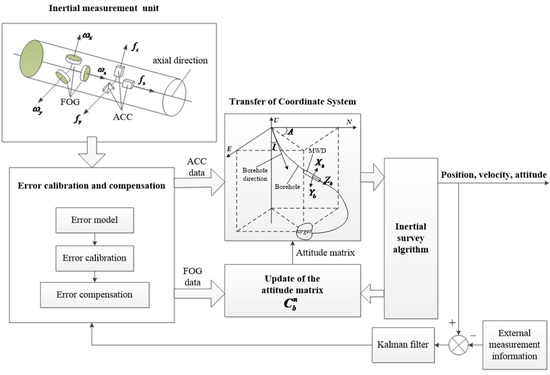
Figure 2.
Flow chart of the FOG-based MWD measurement algorithm.
Firstly, the carrier angular velocity is measured by the FOGs in b-frame. The carrier acceleration is measured by the ACCs in b-frame. Secondly, the errors in the original sensor data should be compensated. and stands for the data whose error has been compensated. Thirdly, the attitude matrix is updated by using angular velocity . Fourthly, and are transferred from b-frame into the l-frame by the updated attitude matrix . The is described in (1) [22].
Whereas, the A is azimuth, T is tool face angle and I is inclination.
In the l-frame, the real-time position, velocity and attitude which describe the 3D borehole trajectory could be calculated by the inertial navigation algorithm. The inertial navigation algorithm has a defect wherein its results could be accumulated over time because of the sensors’ error items. Thus, before using the sensors, we need to calibrate their error items and compensate them. However, there are still residual errors in the sensors’ data. The Kalman filter method could estimate and compensate the sensors’ residual error online by fusing a piece of external information. At this time, the dynamic error navigation error model should be established. The navigation error differential equations include three basic navigation parameters errors, namely the attitude error angles (2), the velocity errors (3) and the position errors (4) [23].
where is the attitude error, is the velocity of the FOG-based MWD and is the velocity error. L, , and h is the latitude, longitude and depth of the FOG-based MWD. , , and is the latitude error, longitude error, and depth error. is the projection of the earth rotation velocity in l-frame. is the angular velocity of the l-frame with respect to e-frame, expressed in the l-frame. is the angular velocity of the l-frame with respect to i-frame, expressed in the l-frame. R is the earth’s diameter. is the error vector of the three FOGs, where . is the error vector of the three ACCs, where .
In Equations (2) and (3), it can be seen that the measurement error of the ACC would influence the velocity and the measurement error of the FOG influence the attitude. When compensated the sensors’ errors online or offline, the sensor error model should be established ahead. The coefficients in the error model should be calibrated by special instrument. Once the error coefficients have been figured out, the error model of the sensor has been obtained. With this error model, the error in the sensor could be compensated. Generally, the linear error model is sufficient for most applications [24]. However, under the drilling conditions, because of the high level of vibration, a linear error model could no longer meet the requirements.
3. Establish of the Nonlinear Error Model
In this paper, only the second-order error is taken into account when establishing the nonlinear error model. Because the third and higher-order error are one-millionth of the linear error coefficient, which could then be ignored [25]. The nonlinear error model of the FOG is given by (5) and the output error of the FOG is given by (6) [23].
In the Equations (5) and (6), subscript g stands for FOG, and superscript b stands for b-frame. is the original output of the FOGs in the b-frame (). The subscript x, y, and z represent the X-axis, Y-axis, and Z-axis. is the ideal output of the FOGs (). is the error between the original output and ideal output. is the bias error of the FOGs (). is the factor error of the three FOGs. is the misalignment matrix, (m = x.y.z, n = x.y.z, ) is the FOGs’ misalignment angle projection of m axis with respect to n axis (rad). stands for the standard deviation of random white noise in FOGs original output (). stands for the second-order error coefficient of the three FOGs ().
In the same way, the nonlinear error model of the ACCs in the FOG-based MWD is given by (7), and the output error of the ACCs is given by (8)
In the Equations (7) and (8), subscript a stands for ACC and superscript b stands for b-frame. The parameters in the Equations (7) and (8) are defined analogously with Equations (5) and (6).
In Equation (6), , the equation can be simplified as follows
is a matrix merged by the factor error matrix and the misalignment matrix .
In the same way, , the equation is simplified as follows:
In this paper, the body frame is defined according to the FOG input axis. First, the axis of the b-frame is defined to coincide with the X-axis FOG input . Then, the axis is defined perpendicular to in the plane and the axis is orthogonal to and [14,26]. The body frame is shown in Figure 3.
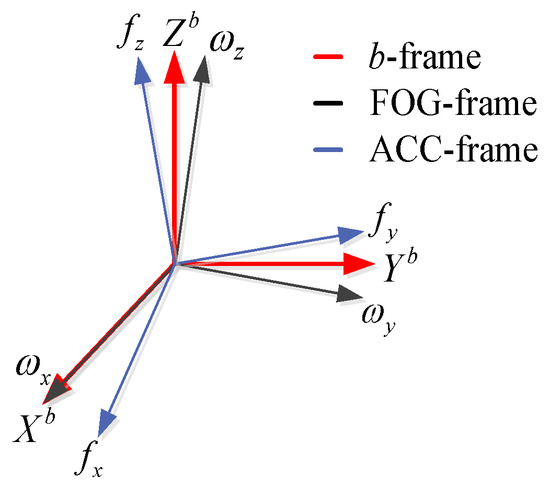
Figure 3.
The relationship between different frames.
Therefore, the matrix could be represented as (11) while the matrix remains still.
4. Recognition of the Coefficient of the Vibration Error
In order to recognize the coefficients in the nonlinear model, the Kalman filter (KF) method should be used. The Kalman filter is an optimized autoregressive data processing algorithm [27]. The basic principle of the algorithm is to use the minimum mean square error as the best estimation criterion, and use the state-space model of signal and noise to introduce the relationship between state variables and observed variables by establishing state equations and observation equations model [28]. KF is a linear filter, which is only suitable for linear systems. EKF (Extended Kalman Filters) and UKF (Unscented Kalman filters) are both developed to work with nonlinear systems. As the EKF linearizes the nonlinear system using Taylor expansion while the UKF propagates the sigma points by function evaluations using the unscented transformation [29]. Several studies have compared these two methods [30].
In this paper, we choose to use the EKF method. UKF is complicated and has a big computation burden. It costs a significant amount of time to select the sigma points. Moreover, the set of the weight for every sigma point is random because it was settled artificially. It often leads to the filter result divergent. Therefore, compared to EKF, UKF does not perform well as it is expected in theory. In order to calibrate more error items, we set 36 parameters in the state vector. If UKF is used, the computation will be greatly increased. In addition, the EKF accuracy is enough for the FOG-based MWD. Therefore, we choose to use EKF.
4.1. The 36-Order EKF
The 36-order EKF is designed. The EKF method has two equations (Statement equation and Observation equation), which are given by:
where X is the state vector, Z is the measurement vector, and are nonlinear function. is zero-mean uncorrelated “state noise” process, is zero-mean uncorrelated “measurement noise” process.
In order to estimate and recognize the coefficients of the error items, the state vector is designed to include the linear error and nonlinear error coefficients. The state vector is given in (13). There are 36 elements in the state vector in total.
In this paper, the EKF is designed based on the nonlinear error model of the FOGs-based MWD. The ACC’s error model and FOG’s error model used in Equations (2) and (3) are the already established nonlinear error model in Equations (9) and (10). With this nonlinear error model, both the linear error item and the nonlinear error item could be recognized and compensated.
The state noise matrix in the statement equation includes the ACC noise and the FOG noise. Therefore, it is given by
In this paper, the local position is already known and remains unchanged when the calibration experiment is done. Hence, we can use this fixed position as one of the external measurements. Besides, the velocity of the FOG-based MWD keeps zero while doing the calibration experiment. Thus, the zero velocity could be another external measurement. Because the external measurement in the measurement equation does not changed with time. Thus, the measurement equation is a linear system. The nonlinear function h( ) could be replaced by the linear function . The observation vector Z and the measurement matrix H can be written as follows:
where , and is the local latitude, longitude, height which is known ahead. is the identity matrix with six rows and six columns. is the zero matrix with six rows and thirty columns.
However, as mentioned above, the state equation is nonlinear. So, before using the Kalman filter method, we needed to linearize the state equation using the Taylor expansion [31].
is the estimate of the state vector. To obtain the first-order approximation of Taylor’s expansion, the linear linearization equation of the system can obtained by:
F is the Jacobian matrix of , which is expressed as [32].
Then, the samples of continuous signals are subject to discrete changes, the sampling period is constant, that its discrete linear error equation is:
On the basis of the discrete linear equation, the Kalman filter equation of linear Kalman filter can be used [32]:
P is the covariance matrix and K is the Kalman gain [33]. I is the identify matrix.
With the EKF method above, the error coefficients could be estimated optimally. Once the error coefficients are obtained, the nonlinear error model could be established. With the nonlinear error model, the errors in the FOG-based MWD could be compensated by (25) and (26)
4.2. Calibration Design
Different error items need different motions to motivate. The error of the ACC needs the positive and negative acceleration to motivate and the error of the FOG needs the positive and negative angular velocity to motivate. In addition, every particular motion should be maintained for a period of time to fully motivate the error. Additionally, in order to save time, the calibration procedure should be kept as simple as possible [26]. In this paper, relying on the turntable, a calibration method based on 24 positions has been designed. The process of calibration is reported in Table 1. The process of the calibration experiment has been carried out in the following steps.

Table 1.
The calibration path based on 24 positions.
To start, the FOG-based MWD is static with the X, Y, Z axes pointed to the East, North and Up directions for 600 s. Secondly, the Y-axis should be rotated at a speed of 30°/s by 90° and then keep static for 180 s. Next, the Y-axis is rotated at a speed of 30°/s by 180° and then kept static for 180 s. After that, the Y-axis is rotated at a speed of 30°/s by 180° again and then keep static for 180 s. The rest can be conducted in the same manner.
After the 18th step, the FOG-based MWD returns to its original position. Then, X-axis, Y-axis, and Z-axis are rotated at a speed of 30°/s clockwise and then counter-clockwise for 180 s, respectively. In this way, the calibration path has 24 positions in total, as reported in Figure 4.
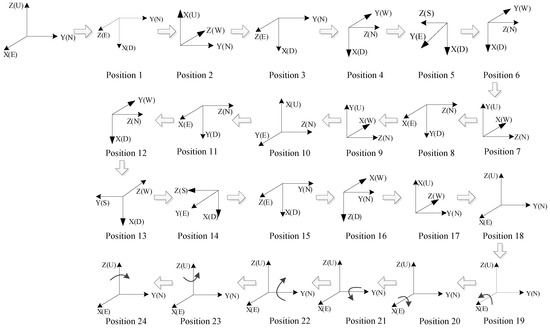
Figure 4.
The 24 positions of the calibration.
When the calibration experiment is performed, the sensors’ output data should be collected simultaneously. Then, using the 36-order EKF to deal with the sensors’ output, the coefficients of the error model can be recognized.
5. An Iterative Calibration Method
The error coefficients recognized by the 36-order EKF are not the true value of the error items. Between the true coefficients and the recognized coefficients, there are still some residual errors. If the residual error of these coefficients could be estimated and compensated, the accuracy of the calibration could be improved. Therefore, this paper proposed a calibration residual suppression method based on an iterative algorithm.
Assuming that the true value of the error coefficients is , for the first calibration, its estimated results is . The relation between and is described as follows:
where is a unit matrix and is the error matrix with the same size with . Thus, the residual error of the coefficients of the error items is :
Next, we use Equations (25) and (26) to compensate for the error in the original data. Here we rewrite the Equations (25) and (26) as follows:
The superscript 1 in , , , , , means the error coefficients which is estimated for the first time. The and are the FOG and ACC data, which are compensated the error by using the first estimate of the coefficients.
Then, we use the 36-order EKF again to estimate the residual in and again. If the estimated result is , the relation between and is given by:
Whereas is an error matrix of the second time estimation. Then after the second time estimation, the residual error is .
According to the second estimation, the error coefficients should be adjusted as follows:
The superscript 2 in , , , , , represents the error coefficients that are estimated for the second time. Then, Equations (25) and (26) are used to compensate for the error. Next, the 36-order EKF is used again to estimate the residual error after the second estimation. The rest may be deduced in the same way. According to the induction method, the results of the n times estimation is :
Then after n times estimation, the calibration residual is:
Except for the first-time calibration, the rest of the calibrations are all aiming to estimate the residual error. Therefore, after n times iterative calibrations, the state vector as well as the error coefficient could be obtained by Equation (36):
The more times the error is estimated, the more accurate the error coefficients could be obtained. But it is impossible to iterate forever. The iteration is stopped when the spectral radius of the error matrix is less than 1. When , it indicates that the error matrix M converges to a stable value [6]. Although we can continue to estimate the error coefficients, the effect is not obvious.
6. Simulation Experiment
In this part, the simulation data with known error coefficients are generated using the trajectory generator. We applied two versions of the error model and the EKF method to these data. One version, called nonlinear EKF, applies all 36 error terms described in Section 4.1. In the other version, called linear EKF, we excluded the six nonlinear terms from the model. A comparison of the outputs from the two methods will indicate the importance of including the nonlinear terms in the model.
6.1. Simulation Data
The pure FOG and ACC measurementsare generated by a trajectory generator according to the 24-position calibration process. The data is demonstrated in Figure 5. It can be seen that the measurements of the FOG and ACC consistent with the calibration process. Then, the error items were added to the pure data. The value of each error item is shown in Table 2. Utilizing Equations (5) and (7), the simulation data with the known quantitative error items could be obtained.
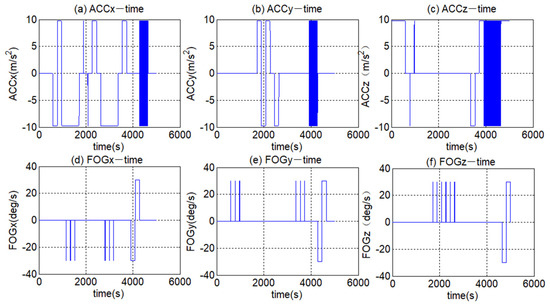
Figure 5.
The sensor measurements generated according to the 24-position calibration.

Table 2.
The values of each error coefficient.
6.2. Simulation Results
Then we used the nonlinear EKF and liner EKF to recognize the error items. Their results are demonstrated in Figure 6, Figure 7 and Figure 8. The blue line represents the error coefficient estimated by the linear EKF, while the red line represents the error coefficient estimated by the nonlinear EKF.
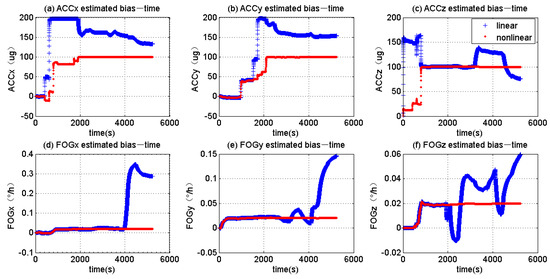
Figure 6.
The estimated results of the bias error.
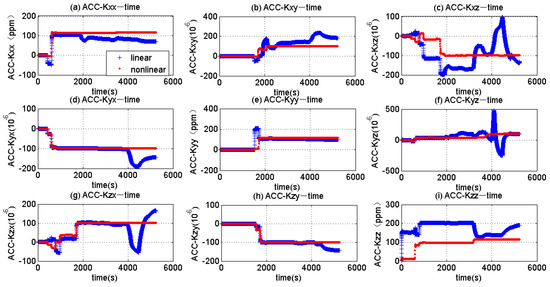
Figure 7.
Estimated results of the scale factor error and misalignment error (ACCs).
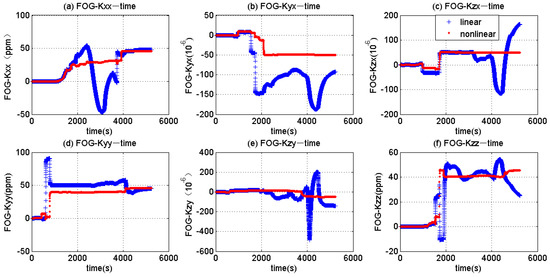
Figure 8.
Estimated results of the scale factor error and misalignment error (FOGs).
Figure 6 shows the bias error coefficients recognized by the two methods. In Figure 6a–c, the red lines converge to 100 μg (the true value) after 2000 s, indicating that nonlinear EKF could recognize the bias error correctly. However, the blue line in Figure 6a,b converges to 150 μg, indicating that the bias error coefficients of X-axial ACC and Y-axial ACC estimated by linear EKF is incorrect. The blue line in Figure 6c does not converge to a stable value, indicating that the bias error coefficient of Z-axial ACC could not be recognized by linear EKF. The nonlinear EKF could recognize the bias error successfully because the red lines in Figure 6d–f all converge to the true value 0.01°/h. The linear EKF is a failure to recognize the bias error because the blue lines in Figure 6d–f diverge to a high value after 4000 s. The reason is that at the time of 3912 s, we began to rotate the turntable around X-axis, Y-axis and Z-axis at the speed of 30°/s for 180 s (Table 1). At this dynamic state, though the nonlinear error coefficients are small (10 × 10−6 s/rad), the nonlinear error items are large to 0.098°/h. For the linear EKF, its state vector only has the linear error coefficients, and it could not separate the nonlinear error from all the errors. However, the state vector of the nonlinear EKF, which includes the linear and nonlinear error coefficients, which can recognize the error items effectively.
Figure 7 shows the estimated results of the scale factor error and misalignment error of the ACCs. The three figures located in the diagonal place in Figure 7 are the estimation results of the scale factors. The others are the estimation results of the misalignment angle. It can be seen that the linear EKF could not recognize any of the misalignment angles, while the nonlinear EKF could recognize each error item correctly (100 ppm). The linear EKF misidentifies the scale factors and could not recognize the scale factors . On the contrary, the nonlinear error EKF recognizes all of the scale factors of the ACCs.
Figure 8 exhibits the estimated results of the scale factor and misalignment angle of the FOGs. Figure 8a,d,f are the estimation results of the scale factor. The others are the results of the misalignment error. It can be seen that the nonlinear error EKF recognizes each error item correctly. The linear EKF only recognizes Kgxx and Kgyy. Compared to the nonlinear EKF, the linear EKF oscillates a great deal before it can converge to stable.
Figure 9 shows the estimated results of the nonlinear error of the FOG-based MWD. The nonlinear error coefficients are all estimated correctly by the nonlinear EKF. It also could be seen that the nonlinear error of ACCs is recognized at the time of 2000 s and the nonlinear errors of the FOGs were not recognized until 4000 s. The reason for this is that before 2000 s, the calibration path changes the orientation of the ACCs many times. When the ACCs pointed to the straight direction, the gravity acceleration could motivate the ACCs’ error. Until 4000 s, the turntable had an angular velocity (30°/s) that could motivate the errors of the FOGs. This high speed of the rotation could motivate the nonlinear error of the FOGs. It could also prove that the calibration path is reasonably designed.
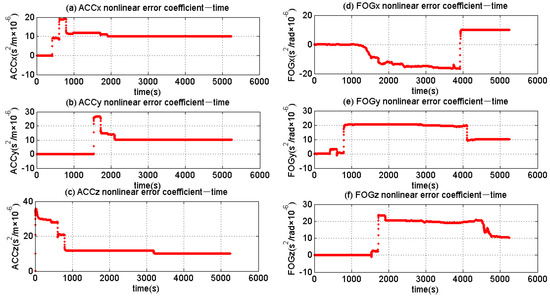
Figure 9.
The estimated results of the nonlinear error.
Table 3 lists the estimated results of the error items by the linear EKF and nonlinear EKF. It can be seen that the linear EKF only recognizes eight error items and have significant errors. The relative error of the estimated Bgx is 1333.50%. The relative error of the estimated Bay is 53.98%. The relative error of the estimated Kaxx is 30.25%. It illustrates that when the original data includes nonlinear errors, the linear EKF could not recognize the error items coefficients. However, the nonlinear EKF method could recognize all the error items. Compared to the true value, the relative error of estimated results is less than 10%. However, it can be noticed that the relative error of the ACCs scale factor error is about 15% and the scale factor error of the ACCs is about 15 ppm (parts per million). Therefore, a method to suppress the residual calibration error should be adopted to improve the calibration accuracy.

Table 3.
The estimated results of all the error items.
In order to improve the calibration accuracy, we make use of the iterative calibration method to suppress the residual. It takes four times the iteration to achieve this goal. The estimated results of each iteration are shown in Figure 10. By doing the fourth iteration, the residual error in theACC scale factor is only reduced by 0.4 ppm, which is 2.60% of the total residual error, indicating that all error parameters have converged to the ultimate accuracy after the third iteration. Thus, the fourth or subsequent iteration has little effect. By conducting these iterations three times, the residual of the ACC scale factor error was reduced by 53.3%.
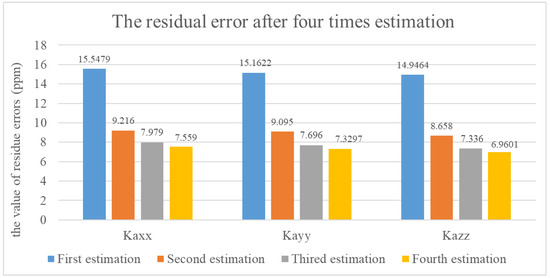
Figure 10.
The residual error after each iteration of the scale factor error ACCs.
7. Experiment
7.1. Calibration Experiment
Before this calibration experiment was carried out, the temperature calibration for the FOG-based MWD was implemented from 0 °C to 150 °C with the thermostat. It makes it so the remaining errors in the FOG-based MWD have nothing with the temperature. The FOG-based MWD was mounted on the three-axis turntable, as shown in Figure 11. Its performance parameters are listed in Table 4. Then, the calibration experiment was carried out according to the calibration path designed in Table 1. The sensors’ data was collected and saved during the calibration experiment.

Figure 11.
The calibration experiments.

Table 4.
The performance parameter of the three-axis turntable.
Then, the nonlinear EKF was utilized to recognize the error item of ACCs and FOGs. Figure 12 illustrates the estimated results of the nonlinear error coefficients by the nonlinear EKF.The estimated results of the bias error for FOG-based MWD are illustrated in Appendix A. The estimated results of the scale factor error and misalignment error (ACCs) are illustrated in Appendix B. The estimated results of the scale factor error and misalignment error (FOGs) are illustrated in Appendix C.
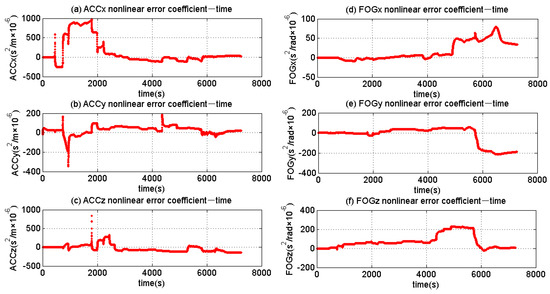
Figure 12.
The estimated results of nonlinear error items.
Based on Figure 12, it can be seen that the nonlinear error coefficients all converged to a stable value at the end of the calibration experiment. The nonlinear error coefficients of the X axial ACC, Y axial ACC, and Z axial ACC are 29.26 × 10−6 s/m2, 20.81 × 10−6 s/m2 and s/m2, respectively. The nonlinear error coefficients of the X axial FOG, Y axial FOG and Z axial FOG are s/rad, s/rad and s/rad, respectively. The recognition results of all the error items are listed below. With the error coefficients, the nonlinear error model could be established. Thus, the error items could be compensated.
7.2. Vibration Experiment
In order to verify that compensating the nonlinear error of the FOG-based MWD could improve its measurement accuracy under vibration, vibration experiments simulating the drilling vibration have been accomplished. One is the sinusoidal periodic vibration; the other is the random vibration. Figure 13 illustrates the vibration setup. The vibration table is made by the Ling company in USA with product number 1216VH-219.

Figure 13.
Vibration experimental set-up.
7.2.1. The Periodic Vibration
The FOG-based MWD was mounted on the vibration table with its Y-axis along the vibration direction. The experiment was carried out according to the following steps: first, the vibration table was kept stationary for 15 min, then the vibration table started to vibrate and kept vibrating for 1 h. The frequency of the vibration was 20 Hz, and the amplitude of the vibration is 5 g. Lastly, the vibration table went back to stationary and was kept for 5 min. The experiment time was 80 min in total, which is close to a Schuler Period [34]. The sampling rate of the FOG-based MWD is 100 Hz.
Figure 14 shows the original data of the FOG-based MWD. It is can be seen that the fluctuation amplitude of the data in the vibrations is much larger than that is in the stationary. One reason is that the sensors could sense the vibration motion; the other one is that the error performance of the sensors is different from that in the stationary. Though the vibration direction is aligned Y-axis, the X axial ACC and Z axial ACC were also influenced greatly. The reason is that the misalignment error is existing in the FOG-based MWD. In addition, the fluctuation amplitude of X-axial ACC and Z-axial ACC did not line up with the horizontal axis in terms of vibration. The reason is that the bias error changed during the vibration. Therefore, it is important to recognize the vibration error and compensate for them.
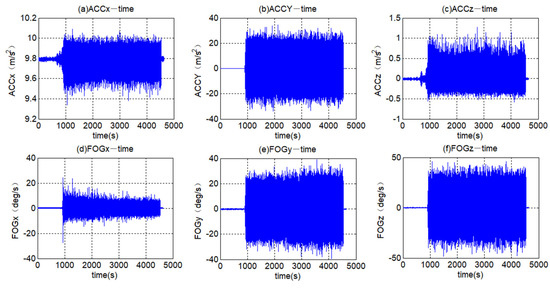
Figure 14.
The original data of the FOG-based MWD in the vibration experiment.
The error items recognized in Section 7.1 were compensated. Thus, we can obtain three sets of data. One set is the original data. The second set is the data that only compensated the linear error items. The third one is the data that compensated both the linear and nonlinear error items. Then using the inertial navigation algorithm to calculate the position, velocity and attitude of the FOG-based MWD with the three sets of data. The results are illustrated in Figure 15.
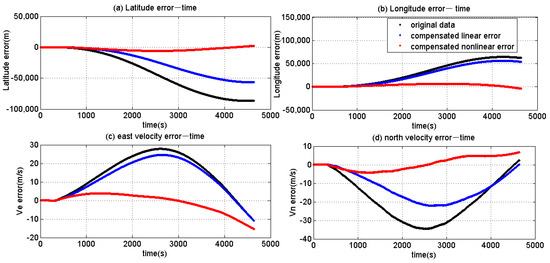
Figure 15.
Position error and velocity error.
It can be seen that the latitude error and longitude error calculated by the original data is m and m. With the second set of data, the latitude error and longitude error is reduced to m and m. It shows that the linear error items were compensated, and the error of latitude and longitude was only reduced by 34.45% and 13.50%, respectively. However, with the third set of data, the error of latitude and longitude was reduced to 2402 m and 4089 m. Compared to the original data, the ratio of the decreased errors was 97.22% and 93.42%. The conclusion could be made that compensating the nonlinear error items of the FOG-based MWD can improve the measurement accuracy.
The FOG-based MWD was mounted on the vibration table with the attitude of inclination 0.09°, the toolface angle −90.05° and the azimuth 186.77°. Taking this attitude as a standard, the attitude error of the three sets of data could be obtained. The attitude error is illustrated in Figure 16. It can be seen that without compensating for any sensors error, the attitude error increases over time quickly. At the end of the experiment, the error of inclination, toolface angle and azimuth is 1.77°, 1.42° and 4.53°, respectively. It obviously cannot satisfy the requirement of the drilling operation.
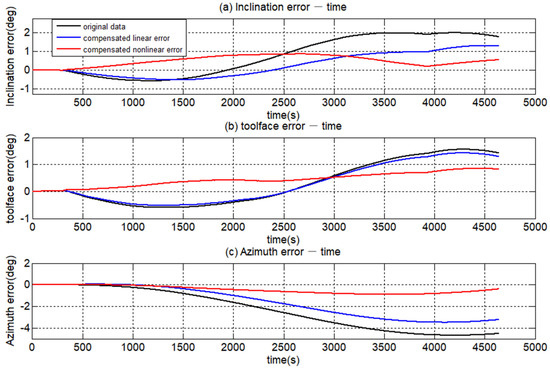
Figure 16.
The attitude error.
When the data was compensated for the linear error items, the error of inclination, toolface angle and azimuth were reduced to 1.29°, 1.28° and 3.23°, respectively. When the data was compensated, both the linear error items and nonlinear error items, the error of inclination, the toolface angle and azimuth were reduced to 0.55°, 0.81° and 0.42°. Basically, it can meet the requirement of the drilling operation. Table 5 lists the measurement error of the borehole trajectory. While the nonlinear error items of the FOG-based MWD were compensated, the error of 3D borehole trajectory can be reduced by a ratio from 44.13% to 97.22%.

Table 5.
The measurement error of the borehole trajectory.
7.2.2. The Random Vibration
The second experiment is the random vibration. When the random vibration was conducted, the FOG-based MWD was mounted on the vibration table with its X-axis along the vibration direction. The experiment was carried out according to the following steps: first, the vibration table was kept stationary for 20 min, then the vibration table started to vibrate and kept vibrating for 1 h.
The power density spectrum of random vibration is shown in the Figure 17 below. Lastly, the vibration table went back to stationary and was kept for 10 min. The experiment time was 90 min. The sampling rate of the FOG-based MWD was 100 Hz.
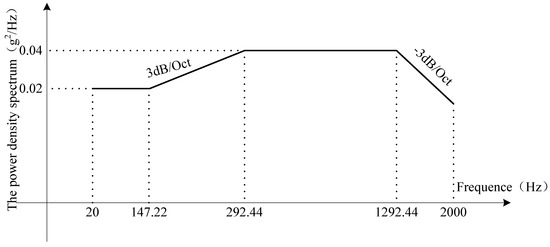
Figure 17.
The power density spectrum of random vibration.
As mentioned in the above experiment, three sets of data were used to compare the trajectory survey result, which is shown in Figure 18 and Figure 19.
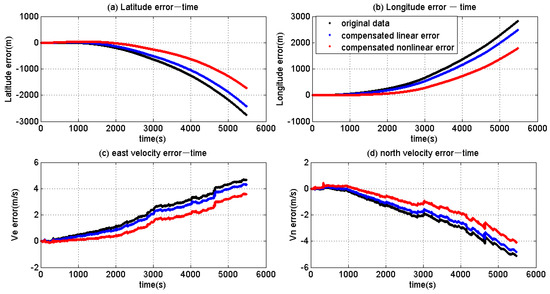
Figure 18.
Position error and velocity error.
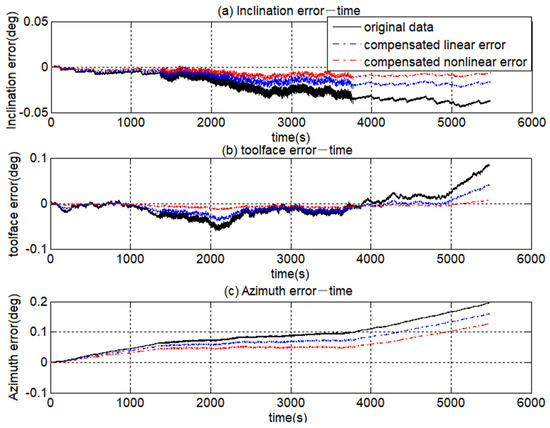
Figure 19.
The attitude errors.
In Figure 18, it can be seen that the latitude error and longitude error calculated with the original data is 2754 m and 2828 m. With the second set of data, the latitude error and longitude error were reduced to 2420 m and 2487 m. However, with the third set of data, the error of latitude and longitude was reduced to 1716 m and 1786 m. In Figure 19, the error of inclination, toolface angle and azimuth calculated with the original data is −0.04°, 0.08° and 0.20°, respectively. After the data compensated the linear error items, its error of inclination, toolface angle and azimuth were reduced to −0.016°, 0.04° and 0.16°, respectively. When the data was compensated, both the linear error items and nonlinear error items, the error of inclination, toolface angle and azimuth were reduced to −0.006°, 0.007° and 0.13°. Compared to the original data, the attitude error decreased by 83.78%, 91.25%, and 34.80%.
The results of the random vibration experiment are not as promising as the periodic experiment. In addition, the position error shown in Figure 18 and the azimuth error shown in Figure 19 increased with time. As we all know, the defect of the inertial navigation algorithm is that its error results accumulate over time, which is mainly caused by the sensor’s error. Although we have compensated the linear error items and nonlinear error items of the FOGs and ACCs, there are still some residual errors in the FOGs and ACCs. The residual errors could also lead to the position and attitude error divergent. However, compared to the first two sets of data, the results of the third set of data diverge much slow over time. It can prove that the proposed method of this paper could suppress the error. Moreover, according to Equations (5) and (7), the nonlinear error is directly related to the quadratic term of angular velocity and acceleration. Therefore, the more intense the carrier motion, the greater the angular velocity and acceleration, and the larger resulting residual nonlinear error. This is why the results of the periodic vibration experiment accumulated slowly over time and look to be stable, while the results of the random vibration experiment accumulated quickly over time. However, for each vibration experiment, compared to the results of the original data and the data only compensated the linear error items, the results of the data compensated the linear error items and nonlinear error items accumulate much slower with time. It could help prove the effectiveness of our proposed method.
8. Discussion
8.1. Repeatability of Nonlinear Error
With the limit of sensor manufacturing technology, the nonlinear error of FOGs and ACCs sometimes does not have good repeatability. When the working environment has been changed, the nonlinear error changes with it. So, some researchers held the opinion that not compensating the nonlinear error is better than wrongly compensating it. The sensors used in this paper have been selected carefully and the nonlinear error coefficients of the sensors all have good repeatability. In the authors’ opinion, an adaptive calibration method for the nonlinear error should be studied in the future.
8.2. Error Terms Related to Acceleration in FOG
The FOGs in the FOG-based MWD could be influenced by the acceleration. As is known, the vibration acceleration downhole is very large. Therefore, if higher precision is required, the error terms of the FOG related to acceleration should also be recognized and compensated.
9. Conclusions
In order to improve the measurement accuracy of the FOG-based MWD under conditions of drilling vibrations, this paper proposed an innovative scheme for the vibration error of FOGs-based MWD. First, a nonlinear error model was established. Second, a 36-order nonlinear EKF combined with a 24-position calibration method was designed. Additionally, in order to obtain more accurate error models, an iterative calibration method was put forward to suppress calibration residuals. Then a simulation experiment was carried out to verify the effectiveness and correctness of this proposed method. Next, a calibration experiment and vibration experiments under the lab conditions were accomplished. With the nonlinear EKF method, the coefficients of the linear and nonlinear error items could be calibrated correctly. The periodic and random vibration experiments verified the effectiveness of compensating nonlinear error items. Compared to the original data, the linear error items are compensated; the error of 3D borehole trajectory can only be reduced by a ratio from 10% to 34%. While the nonlinear error items of the FOG-based MWD were compensated, the error of 3D borehole trajectory can be reduced by a ratio from 44.44% to 97.22%. In conclusion, the compensated vibration nonlinear error items of the FOG-based MWD can improve the measurement accuracy under the process of drilling vibration. The new method can also be applied to other high dynamic fields.
Author Contributions
Conceptualization, L.W. and Y.H.; methodology, L.W. and B.L.; software, L.W. and T.W.; validation, L.W. and T.W.; writing—original draft preparation, L.W. and Y.H.; writing—review and editing, T.W. and B.L.; supervision, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China, grant number 41902320, the Fundamental Research Funds for the Central Universities, grant number 2652018089, National Key Research and Development Program, grant number 2018YFC0603405, and Key laboratory of deep GeoDrilling Technology, Ministry of Natural Resources 2018 Open Project Fund, grant number PY201801.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
The authors would like to express their appreciation to Chunxi Zhang and Shuang Gao at Beihang University who provided the experimental instrument for this research work. The authors would like to thank greatly Yu Wang and Qilong Xue at the China University of Geoscience (Beijing) for their helpful discussions and comments.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Estimated Results of the Bias Error for FOG-Based MWD
The estimate of the Bias error derived by the linear EKF and nonlinear EKF were compared in Figure A1. The ACC bias error of X-axis, Y-axis and Z-axis is illustrated in Figure A1a–c, respectively. The FOG bias error of X-axis, Y-axis and Z-axis is illustrated in Figure A1d–f, respectively. It can be seen that the sensor bias errors estimated by the two filters all converge to a stable value. However, the bias errors of the ACCz estimated by the two EKF are different as well as that of the three FOGs. Among them, the bias errors of the three FOGs estimated by the nonlinear EKF are 0.99°/h, 0.58°/h and −1.66°/h, while by the linear EKF is 1.21°/h, 0.80°/h and −2.08°/h. The bias errors of the three ACCs estimated by the nonlinear EKF are −116.39 μg, −1.74 μg and 164.89 μg while they are 100.69 μg, 136.16 μg and 90.65 μg by the linear EKF. In Figure A1a,e, the estimation of the linear EKF has a large fluctuation. Most of the bias errors estimated by the linear EKF is a little bigger than that of the nonlinear EKF. The reason is that there is nonlinear error item in the sensors, but the linear EKF cannot recognize the nonlinear error and regards the nonlinear error as the bias error. Moreover, in the nonlinear error model (5) and (7), it can be seen that the nonlinear error item varies with the motion state of the sensor. It is obvious that it cannot be regarded as the constant bias error.
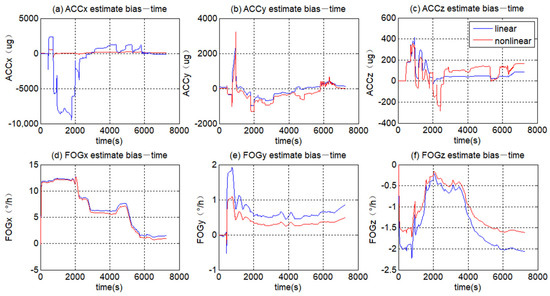
Figure A1.
The estimated results of the Bias error.
Appendix B. Estimated Results of the Scale Factor Error and Misalignment Error (ACCs)
Figure A2 showed that the estimation of the ACC scale factor error and the misalignment error derived from the two EKFs all converge to the stable value. The scale factor errors Kxx, Kyy, and Kzz of the three-axis ACC estimated by the nonlinear EKF are 14.77 ppm, 99.64 ppm and 358.00 ppm, respectively. The misalignment errors Kxy, Kxz, Kyx, Kyz, Kzx and Kzy of the ACC as estimated by the nonlinear EKF are 8280.74 μrad, 690.50 μrad, −8397.52 μrad, −604.28 μrad, −996.20 μrad, and 472.14 μrad. The scale factor errors Kxx, Kyy, and Kzz estimated by the linear EKF are −25.71 ppm, 121.58 ppm and 532.47 ppm, respectively. The misalignment errors Kxy, Kxz, Kyx, Kyz, Kzx and Kzy of the ACC as estimated by the linear EKF are 8041.73 μrad, 849.80 μrad, −8284.30 μrad, −188.45 μrad, −1089.58 μrad and 420.35 μrad.
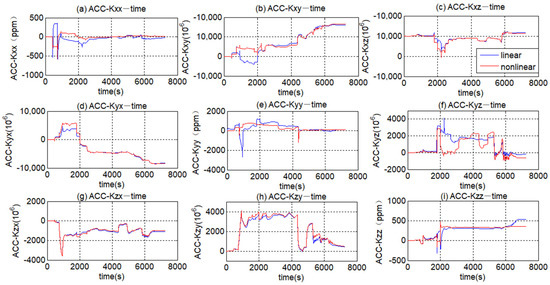
Figure A2.
Estimated results of the scale factor error and misalignment error (ACCs).
Appendix C. Estimated Results of the Scale Factor Error and Misalignment Error (FOGs)
In Figure A3, it can be seen that the estimation of the FOG scale factor error and the misalignment error derived from the two EKFs all converge to the stable value. The scale factor errors Kxx, Kyy, and Kzz of the three-axis FOG estimated by the nonlinear EKF are 186.11 ppm, −663.73 ppm and −632.08 ppm, respectively. The scale factor errors Kxx, Kyy, and Kzz estimated by the linear EKF are 177.93 ppm, −724.73 ppm and −633.40 ppm, respectively. The three misalignment errors Kyx, Kzx and Kzy of the FOG as estimated by the nonlinear EKF are −9818.57 μrad, 1878.28 μrad and 100.68 μrad. The three misalignment errors Kyx, Kzx and Kzy of the FOG as estimated by the 30-order filter are −9735.09 μrad, 1940.04 μrad and −732.83 μrad.
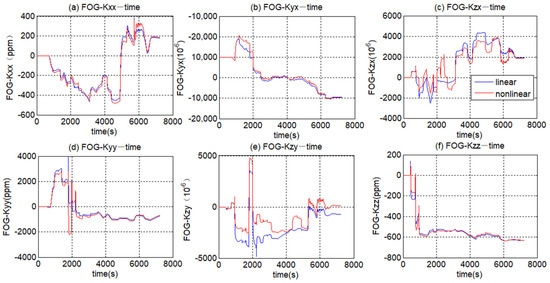
Figure A3.
Estimated results of the scale factor error and misalignment error (FOGs).
References
- Qilong, X.; Ruihe, W.; Feng, S.; Leilei, H.; Laiju, H. Continuous Measurement-While-Drilling Utilizing Strap-Down Multi-Model Surveying System. IEEE Trans. Instrum. Meas. 2014, 63, 650–657. [Google Scholar] [CrossRef]
- Yang, Y.; Li, F.; Gao, Y.; Mao, Y. Multi-Sensor Combined Measurement While Drilling Based on the Improved Adaptive Fading Square Root Unscented Kalman Filter. Sensors 2020, 20, 1897. [Google Scholar] [CrossRef] [Green Version]
- ElGizawy, M.L. Continuous Measurement-While-Drilling Surveying System Utilizing MEMS Inertial Sensors; Department of Geomatics Engineering, University of Calgary: Calgary, AB, Canada, 2009. [Google Scholar]
- Silva, T.; Batista, P. Long baseline navigation filter with clock offset estimation. Nonlinear Dyn. 2020, 100, 2557–2573. [Google Scholar] [CrossRef]
- De Celis, R.; Cadarso, L. GNSS/IMU laser quadrant detector hybridization techniques for artillery rocket guidance. Nonlinear Dyn. 2018, 91, 2683–2698. [Google Scholar] [CrossRef]
- Dorveaux, E.; Vissiere, D.; Martin, A.-P.; Petit, N. Iterative calibration method for inertial and magnetic sensors. In Proceedings of the Joint 48h IEEE Conference on Decision and Control (CDC) and 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 8296–8303. [Google Scholar] [CrossRef] [Green Version]
- Lefevre, H.C. The fiber-optic gyroscope: Actually better than the ring-laser gyroscope? In Proceedings of the OFS2012 22nd International Conference on Optical Fiber Sensor, Beijing, China, 15–17 October 2012. [Google Scholar] [CrossRef]
- Noureldin, A.; Irvine-Halliday, D.; Mintchev, M.P. Accuracy limitations of fog-based continuous measurement-while-drilling surveying instruments for horizontal wells. IEEE Trans. Instrum. Meas. 2002, 51, 1177–1191. [Google Scholar] [CrossRef]
- Xu, X.; Gu, H.; Kan, Z.; Zhang, Y.; Cheng, J.; Li, Z. Properties of Drillstring Vibration Absorber for Rotary Drilling Rig. Arab. J. Sci. Eng. 2020, 45, 5849–5858. [Google Scholar] [CrossRef]
- Xue, Q.; Leung, H.; Huang, L.; Zhang, R.; Liu, B.; Wang, J.; Li, L. Modeling of torsional oscillation of drillstring dynamics. Nonlinear Dyn. 2019, 96, 267–283. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Lin, T.; Li, X.; Wang, T. Characterization of a fiber optic gyroscope in a measurement while drilling system with the dynamic Allan variance. Measurement 2015, 75, 263–272. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Gao, S.; Lin, T.; Li, X. Influence of linear vibration on the errors of three-axis FOGs in the measurement while drilling systems. Optik 2018, 156, 204–223. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Gao, S.; Lin, T.; Li, X. Vibration Noise Modeling for Measurement While Drilling System Based on FOGs. Sensors 2017, 17, 2367. [Google Scholar] [CrossRef] [Green Version]
- Volynskii, D.V.; Odintsov, A.A.; Dranitsyna, E.V.; Untilov, A.A. Calibration of fiber-optic gyros within strapdown inertial measurement units. Gyroscopy Navig. 2012, 3, 194–200. [Google Scholar] [CrossRef]
- Dzhashitov, V.E.; Pankratov, V.M.; Barulina, M.A. Mathematical models of thermal stress-strain state and scale factor error of fiber optic gyro sensors. J. Mach. Manuf. Reliab. 2013, 42, 124–131. [Google Scholar] [CrossRef]
- Nikolaev, S.; Golota, A.; Ivshina, I. Identification modeling of inertial sensors’ parameters of strapdown inertial navigation systems. In Proceedings of the 2nd International Ural Conference on Measurements (UralCon), Chelyabinsk, Russia, 16–19 October 2017; pp. 149–155. [Google Scholar] [CrossRef]
- IEEE Recommended Practice for Precision Centrifuge Testing of Linear Accelerometers. In IEEE Std 836-2001; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2001; pp. 1–96. [CrossRef]
- Ren, S.-Q.; Liu, Q.-B.; Zeng, M.; Wang, C.-H. Calibration Method of Accelerometer’s High-Order Error Model Coefficients on Precision Centrifuge. IEEE Trans. Instrum. Meas. 2019, 69, 2277–2286. [Google Scholar] [CrossRef]
- Kau, D.S.; Boutelle, J.; Lawdermilt, L. Accelerometer input axis angular acceleration sensitivity. IEEE Aerosp. Electron. Syst. Mag. 2005, 14, 449–456. [Google Scholar] [CrossRef]
- Wang, S.; Ren, S. Calibration of cross quadratic term of gyro accelerometer on centrifuge and error analysis. Aerosp. Sci. Technol. 2015, 43, 30–36. [Google Scholar] [CrossRef]
- Einicke, G.A.; White, L.B. Robust extended Kalman filtering. IEEE Trans. Signal Process. 1999, 47, 2596–2599. [Google Scholar] [CrossRef]
- Schwarz, K.P.; Wei, M. INS/GPS Integration for Geodetic Applications; Lecture Notes of ENGO 623; Department of Geomatics Engineering at the University of Calgary: Calgary, AB, Canada, 1999. [Google Scholar]
- Peng, H.; Zhi, X.; Wang, R.; Liu, J.; Zhang, C. A new dynamic calibration method for IMU deterministic errors of the INS on the Hypersonic Cruise Vehicles. Aerosp. Sci. Technol. 2014, 32, 121–130. [Google Scholar] [CrossRef]
- Yu, Z. Design and implementation of linear error modelling in a wireless inertial localization system. In Proceedings of the 2014 Asia-Pacific Conference on Computer Aided System Engineering (APCASE), South Kuta, Indonesia, 10–12 February 2014; pp. 71–75. [Google Scholar] [CrossRef]
- Yu, H.; Lv, X.; Tang, J.; Wei, G.; Wang, Y.; Rao, G. Establishment and analysis of high-order error model of laser gyro SINS. Infrared Laser Eng. 2013, 42, 2375–2379. [Google Scholar]
- Li, B.G.; Lu, J.Z.; Xiao, W.H.; Lin, T. In-field fast calibration of FOG-based MWD IMU for horizontal drilling. Meas. Sci. Technol. 2015, 26, 7. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Wang, S.; Wu, B.; Fernandez, C.; Xiong, X.; Coffie-Ken, J. A state-of-charge estimation method of the power lithium-ion battery in complex conditions based on adaptive square root extended Kalman filter. Energy 2021, 219, 119603. [Google Scholar] [CrossRef]
- Gustafsson, F.; Hendeby, G. Some Relations Between Extended and Unscented Kalman Filters. IEEE Trans. Signal Process. 2012, 60, 545–555. [Google Scholar] [CrossRef] [Green Version]
- Chao, D.; Zhuang, Y.; El-Sheimy, N. An Innovative MEMS-Based MWD Method for Directional Drilling. In Proceedings of the SPE/CSUR Unconventional Resources Conference, Calgary, AB, Canada, 20–22 October 2015. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Z.-Y.; Xie, R.-R. Quadratic extended Kalman filter approach for GPS/INS integration. Aerosp. Sci. Technol. 2006, 10, 709–713. [Google Scholar] [CrossRef]
- Zhang, X.; Mu, X.; Liu, H.; He, B.; Yan, T. Application of Modified EKF Based on Intelligent Data Fusion in AUV Navigation. In Proceedings of the 2019 IEEE Underwater Technology Conference, Kaohsiung, Taiwan, 16–19 April 2019. [Google Scholar] [CrossRef]
- Ribas, D.; Ridao, P.; Carreras, M.; Cufi, X. An EKF vision-based navigation of an UUV in a structured environment. IFAC Proc. Vol. 2003, 36, 287–292. [Google Scholar] [CrossRef]
- IEEE Standard for Inertial Systems Terminology. In IEEE Std 1559-2009; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2009; pp. 1–30. [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).