Abstract
In the last few years, we witnessed a growing body of literature about automated negotiation. Mainly, negotiating agents are either purely self-driven by maximizing their utility function or by assuming a cooperative stance by all parties involved in the negotiation. We argue that, while optimizing one’s utility function is essential, agents in a society should not ignore the opponent’s utility in the final agreement to improve the agent’s long-term perspectives in the system. This article aims to show whether it is possible to design a social agent (i.e., one that aims to optimize both sides’ utility functions) while performing efficiently in an agent society. Accordingly, we propose a social agent supported by a portfolio of strategies, a novel tit-for-tat concession mechanism, and a frequency-based opponent modeling mechanism capable of adapting its behavior according to the opponent’s behavior and the state of the negotiation. The results show that the proposed social agent not only maximizes social metrics such as the distance to the Nash bargaining point or the Kalai point but also is shown to be a pure and mixed equilibrium strategy in some realistic agent societies.
1. Introduction
Automated negotiation is an iterative and distributed search process between multiple intelligent agents exchanging offers, with the goal of finding a mutual agreement that allows for cooperation between the different parties [1,2,3,4,5]. The applications of automated negotiation range from electronic commerce [6,7], coordination in robotics [8], energy markets [9], computer networks [10], video games [11], and even traffic control [12]. Despite the large and growing body of literature about automated negotiation, there are still challenges and issues to be solved.
Open multi-agent systems are systems where heterogeneous agents may enter and leave the system [13,14]. Consequently, one may face a variety of agent behaviors when interacting with other agents in the system. This heterogeneity precludes agents from assuming a fully cooperative behavior by other agents, and it forces agents to do their best effort to try to achieve a good performance and to guarantee high utility. Therefore, in negotiation scenarios, agent designers have focused on developing the best performing agent among all competitors, that is, the agent that obtained the best utility for itself [15], with less focus on the utility achieved by its opponent. While achieving a high utility for itself is an interesting property for an automated agent, it may not be the best strategy in an agent society [16], where agents may need to collaborate on multiple occasions. For instance, an agent may act selfishly, may obtain the maximum utility for itself, and may exploit the opponent, ending up in an agreement that may portray a low utility for its opponent. In that case, what would be the incentive for the opponent to collaborate with us? One should take into consideration that, in an agent society, agents may share opinions about their counterparts. This may make it difficult for selfish agents to collaborate with other agents in the future. As a result, this may harm the agent’s long-term interests.
Although an agent may need to achieve the best utility for itself, it cannot ignore the utility achieved by its opponent. Therefore, one may be tempted to think that the solution to this problem is for all agents to take a fully cooperative approach to negotiation. In the past, there have been proposals of negotiation models and strategies that assume cooperative behaviors during the negotiation. In many of these proposals, the authors assume either that both parties play the same cooperative strategy or that the other party also employs a cooperative strategy [17,18,19,20]. While this is a feasible assumption in some domains, it is not appropriate for open environments where agents may display a plethora of behaviors and strategies. Previous works have shown how social or cooperative agents may be exploited by competitive agents [15,21,22]. Ideally, a good balance should be struck between both taking a social attitude and preserving one’s own utility. In open environments, one may negotiate with a wide range of strategies, and a social agent should be prepared to attain mutually attractive utilities independently of the other agents’ attitudes. The hypothesis that we aim to answer in this article is whether we can design a social agent that performs well against a wide range of opponents in an open and dynamic society. Several difficulties hinder the design of such an agent, as we discuss in the following paragraphs.
First, agents should reach a consensus before their deadline, and that typically entails some type of reciprocal concessions. Constant and timely concessions regardless of the opponent’s moves mostly end up in situations where the agent can be exploited, such as the case of ANAC2011 [23,24], where the Hardheaded agent [25] won the competition by just waiting for its opponents’ concessions. When the opponent concedes, a social agent should reciprocate to some extent to build a good long-term relationship and to encourage further cooperation. In contrast, if the opponent’s strategy is designed in a way that it does not respond to a nice move, it may not be beneficial to sustain the negotiation or to make any further concessions. In those cases, it may be good to signal when we are not pleased with an opponent’s attitude during the negotiation. For example, given a selfish opponent, a counter selfish move may help the opponent notice that we are not inclined to concede against its selfish attitude [26]. Therefore, concessions should be carried out attending to one’s own and the opponent’s moves.
Second, achieving a social agreement, one that is appealing for both parties, requires understanding the other side’s preferences/needs; thus, the agent needs to follow up its opponent’s moves and accordingly make mutually beneficial offers. It has been shown that learning an opponent’s preferences in negotiation is not trivial by any means [3,27,28]. For instance, non-exploratory behaviors, such as an opponent constantly making the same bids, prevents the agent from learning its opponent’s preferences (especially in large-sized domains). The repetition results in overestimated preferences for repeated bids while underestimating preferences for less repeated or non-explored bids. Even when the opponent concedes, it should be taken into consideration that a concession at the start of the negotiation may not imply the same about the opponent’s preferences as a concession towards the end. That is, while one may not concede on important issues at the start of the negotiation, this may prove false as the negotiation advances. As the opponent explores the bid space, one may be able to utilize the learned information to make better estimations, but a social agent should also be prepared for situations where the exploration of the bid space carried out by the opponent is scarce.
In this article, we aim to find whether it is possible to design a social agent capable of negotiating efficiently in a competitive agent society. That is, while the agent should attempt to ensure an appropriate utility for itself, it should also strive to find a good agreement for the opponent. This should improve the long-term perspectives of the agent in a dynamic agent society. More specifically, we aim to answer the following research questions:
- Q1. Can a social agent obtain high utility in heterogeneous environments?
- Q2. Can a social agent achieve socially efficient agreements in heterogeneous environments?
- Q3. Can social negotiation strategies be an efficient choice for self-interested agents in agent societies?
With these questions in mind, we designed an adaptive social strategy that considers both the opponent’s moves and the context of the negotiation to adapt its social behavior accordingly. More specifically, our agent employs a portfolio of strategies supported by a new variant of the Tit-For-Tat strategy [29] that is based on the robust analysis of windows of opponent’s bids and smooth transitions between target utility updates; a new frequency-based opponent modeling mechanism that aims to be robust against some of the aforementioned problems; and an adaptive behavior strategy that depends on the time pressure, the opponent’s moves, and the information available about the opponent during the negotiation. The assumptions made by the proposed negotiation strategy are the following: (i) it assumes that agents’ preferences are portrayed by linear additive utility functions; (ii) it assumes no previous knowledge or model about the opponents’ preferences during the negotiation, with all the learning taking place from the information collected during the negotiation; (iii) it assumes bounded rationality by the agents and, therefore, agents employ heuristics rather than game-theoretic mechanisms to make decisions during the negotiation; and (iv) it assumes no particular behavior for the opponents. Thus, this negotiation strategy is designed to work on heterogeneous and imperfect knowledge negotiations where no prior information is available about the opponent and where preferences are represented through linear additive utility functions.
The remainder of this article is organized as follows. First, we describe the general negotiation setting that we considered for the design of our social agent. Then, we describe the specific design of our social agent by providing details about its portfolio of negotiation strategies, the concession mechanism, the bidding mechanisms, the acceptance mechanisms, and the opponent modeling component. Afterwards, we describe the experiments that we carried out to assess the performance of our social agent in a stationary and non-stationary agent society, composed by some of the top performing agents from the state-of-the-art. Finally, we conclude by comparing our approach to related approaches in the literature and by providing some concluding remarks about this work and future lines of work.
2. Negotiation Setting
In this section, we introduce what the general negotiation setting for the design of our agent is. First, we describe the negotiation protocol followed by our agent. Finally, we describe the type of utility functions employed by our social agent to describe agent’s preferences and we discuss the impact of reservation utilities on our social agent proposal.
2.1. Negotiation Protocol
Our social agent were designed to participate in bilateral negotiations similar to many of the negotiation scenarios described in the literature [19,23,28,30]. More specifically, our agent follows the alternating offers protocol [21,31].
In this protocol, both parties take turns in proposing offers and counter-offers. First, one of the agents proposes an offer. The opponent agent either makes a counter-offer or accepts the offer. In the following round, they switch roles and interaction continues in a turn, taking fashion until reaching a termination condition. When they reach an agreement/deadline or one of the agents decides to withdraw from the negotiation (i.e., negotiation failure), the negotiation ends.
2.2. Utility Functions and Reservation Utility
In principle, this social agent is designed to negotiate in domains with linear additive utility functions. In this setting, the negotiation scenario consists of negotiation issues (or attributes) in which the domain values are represented by . An offer is represented by o, while represents the set of all possible offers in the negotiation domain. The agents’ preferences are represented by means of linear additive utility functions in the following form:
where represents the importance of the negotiation issue i for the agent, represents the value for issue i in offer o, and is the valuation function for issue i, which returns the desirability of the issue value. Without losing generality, it is assumed that and the domain of is in the range of [0,1] for any i.
This assumption is taken by the opponent modeling mechanism employed by the agent, as the agent attempts to learn each and for the opponent’s utility function. However, as the reader also observes, the rest of the agent’s components (e.g., concession tactic, bidding strategies, etc.) are independent of the learning mechanism employed by the agent. That is, one can think of the opponent modeling mechanism as an interchangeable module or service that provides information to the agent about the utility provided by an offer to the opponent. This is similar to the philosophy followed by the BOA framework [32], which allows agent designers to implement their bidding strategy, opponent modeling, and accepting strategy separately so that the performance of any components can be compared with the others by keeping other components the same. Therefore, the agent could easily be adapted to other domains with other types of utility functions [33].
We also assume that the utility functions are non-discounted. That means that offers do not lose value as the negotiation process unfolds. We believe that discounted domains do not represent a notable majority of the negotiation scenarios. In any case, without any loss of generality, the social component of our agent would only require small adjustments to be employed in such domains.
In the experiments that we carried out, we assume that the reservation value is zero. That is, if a negotiation fails, agents do not obtain any value from the negotiation. This decision is employed to ensure compatibility with some of the state-of-the-art opponents selected in the experiments section. Our agent can work in both domains with and without reservation utility by filtering out those offers that are not above the reservation utility and capping concession.
3. Proposed Social Agent
Our social agent employs a range of negotiation behaviors. The agent shifts behaviors depending on the negotiation conditions and the information that is gradually available about the opponent’s preferences. In this section, we first describe the general ideas behind the negotiation strategy of our social agent and then explain our concession strategy elaborately. After that, we describe how our agent switches bidding and acceptance behaviors during the negotiation. Finally, we describe the opponent modeling mechanism that we propose to estimate the opponent’s preference profile.
3.1. Negotiation Strategy
The behavior of our social agent is determined by a finite state machine that specifies the negotiation behavior to be followed during the negotiation. Each state corresponds to a behavior adopted by the agent in particular circumstances, depending on some factors such as attitude of the opponent, remaining time, or agent’s current state. To sum up, our agent’s negotiation strategy is composed of five negotiation behaviors.
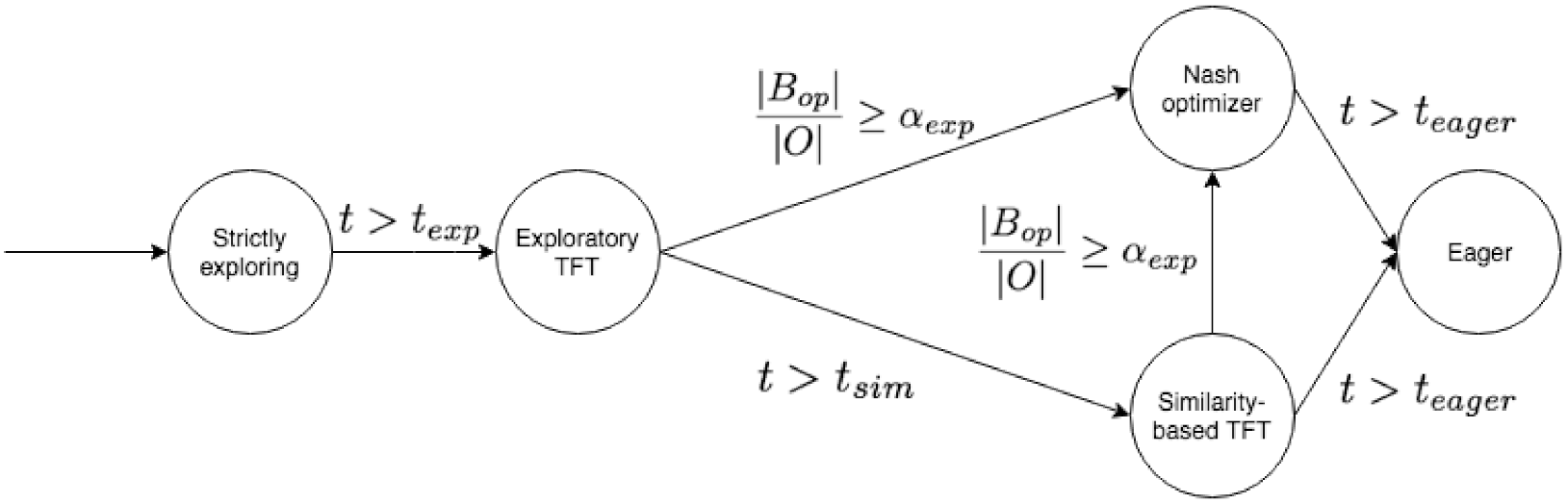
The representation of the finite state machine is shown in Figure 1, and the state transition rules can be explained as follows. In the beginning, our agent aims to get to know its opponent from the bid exchanges. The goal is obtaining knowledge to use in the rest of the negotiation. Therefore, the initial negotiation behavior is Strictly Exploring, which is employed until a strict exploration time threshold ( is surpassed. After the strict exploration phase, the agent may have learned to some extent about its opponent’s preferences, but it may be the case that the learned model is not reliable yet to accurately estimate the bids maximizing the social welfare. In that case, until receiving a certain proportion of unique bids (), the agent employs a Exploratory Tit-For-Tat behavior. Whenever the agent receives the specified proportion of unique bids, the agent’s negotiation behavior turns to be Nash Optimizer. In that behavior, the estimated Nash product bid is offered. If the negotiation time surpasses the time threshold () and the proportion of unique bids is not received, the Similarity-Based Tit-For-Tat behavior is followed. During this phase, the agent may transit to Nash Optimizer as it receives enough bids. The final behavior Eager, occurs only when the negotiation time approaches the deadline ().
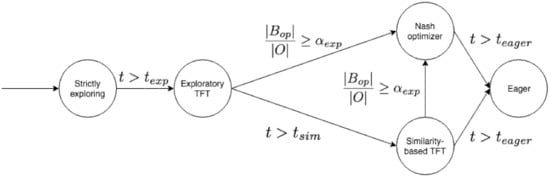
Figure 1.
Finite state machine representing the behavior of the proposed social agent.
The next list briefly describes each of the behaviors:
- Strictly Exploring: at the start of the negotiation, the agent aims to explore the negotiation space. Therefore, it is not inclined to accept the opponent’s bids. The aspiration of the agent is controlled by a special window-based tit-for-tat mechanism that is described in Section 3.2.
- Exploratory TFT: After a certain time threshold in the negotiation, the agent transits to this state. Even though the agent still explores the negotiation space, the agent may accept incoming offers if they are above the current aspiration of the agent (see Section 3.2).
- Nash optimizer: As mentioned, our agent’s orientation is social. Thus, the agent aims to find a fair deal for both parties, regardless of the opponent’s behavior. The strategy of the proposed agent is finding a deal that is as close as possible to the Nash bargaining point. To achieve this, the agent needs to learn an accurate model of the opponent’s preferences. Learning an accurate model about the opponent’s preferences involves receiving several unique bids from the opponent. When the agent has received a proportion of the negotiation space, the agent considers the opponent model to be approximately accurate. Then, the agent is ready to change to the Nash optimizer behavior. In this state, the bidding and acceptance strategy try to be as close as possible to the estimated Nash point.
- Similarity-based TFT: Although our agent aims to be social and it tries to get as close as possible to the Nash bargaining point, in some situations, the opponent may not reveal many unique bids. Then, in such a case, learning an accurate opponent model becomes hard. Consequently, the agent starts using a similarity-based heuristic when the negotiation is approaching a threshold (i.e., ). The aspiration of the agent is again controlled by a special tit-for-tat concession mechanism (see Section 3.2).
- Eager: In the last moments of the negotiation (i.e., ), the agent tries to close an agreement by proposing back the best offer sent by the opponent or by accepting any offer that improves or equalizes the best offer received so far.
The reader can find the specific details of our agent strategy in Section 3.2, Section 3.3 and Section 3.4.
3.2. Concession Mechanism
Concession mechanisms generally determine a target utility for an agent in a given negotiation round. The concession mechanism is tightly linked to what offers are considered acceptable in a negotiation round, as well as the minimum utility demanded when bidding, both typically relying on such target utility. In this article, we propose a new and robust variant of the Tit-for-Tat tactic [21].
Tit-for-Tat tactics respond to the concession moves carried out by the opponent in a reciprocal way. In other words, when the opponent concedes, so does in a certain magnitude the agent. If the opponent does not concede neither does the agent. While basic and classic Tit-for-Tat considers the opponent’s current move (i.e., by comparing the last two offers made by the opponent), our new Tit-for-Tat strategy analyzes a non-sliding window of the opponent’s consecutive offers (e.g., windows formed by k offers). The primary motivation of considering “windows of negotiation history” rather than the current move is to avoid mimicking the irregular fluctuations in utility changes that prevent us from understanding the opponent’s general concession trend. Next, we describe the non-sliding window mechanism.
3.2.1. Bid Windows
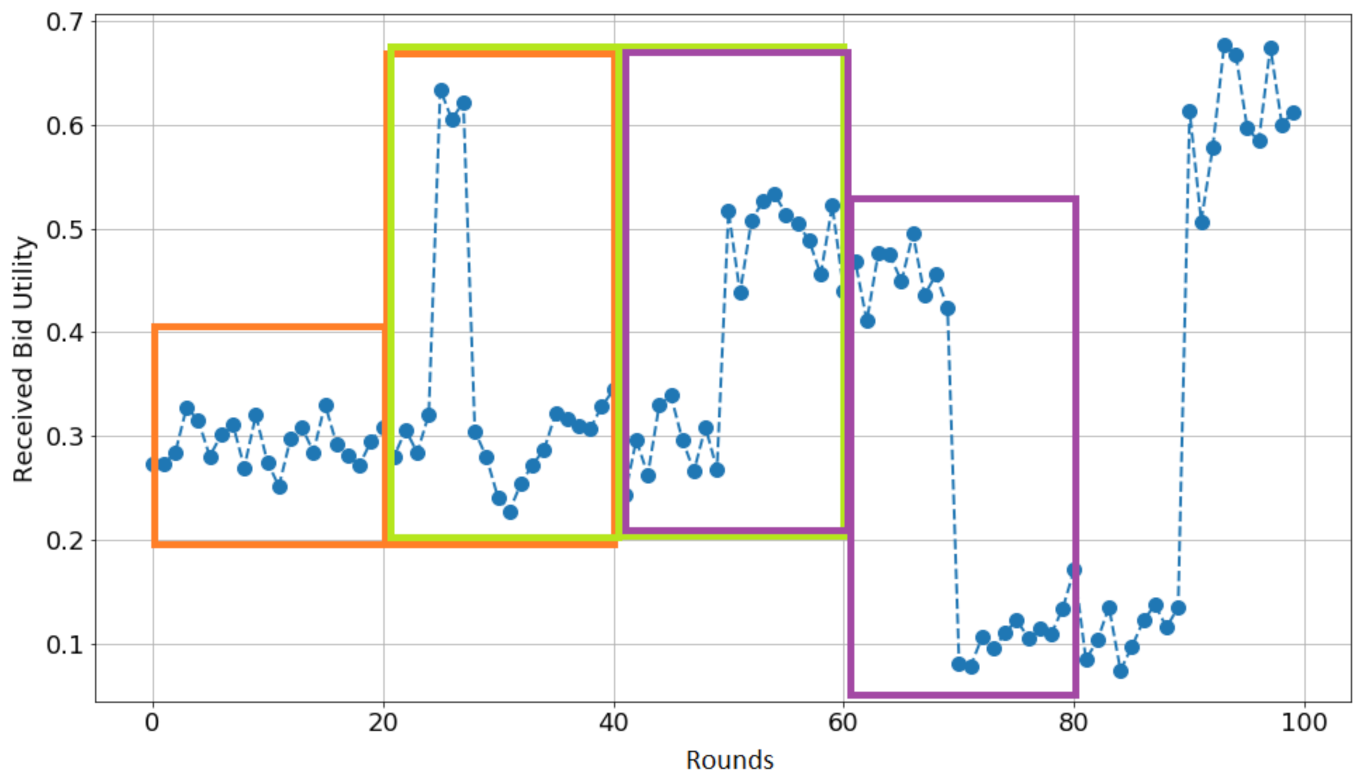
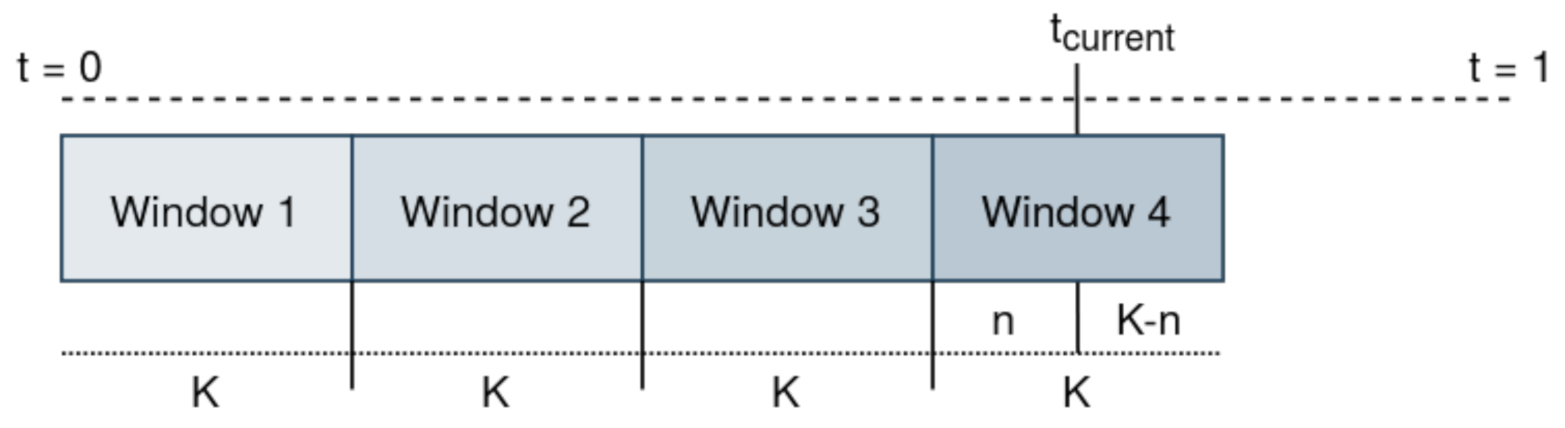
The proposed agent employs non-sliding windows of bids in many of its components. In general, the negotiation history is split into disjoint and successive windows of bids received from the opponent. These windows can contain at most k bids. The most recent window may contain less than k bids as it is filled with new offers received from the opponent. Both Figure 2 and Figure 3 contain examples of this concept. On the one hand, Figure 2 is an example of a sequence of received bids by an opponent. The horizontal axis shows the negotiation rounds while the vertical axis denotes the received utility of the opponent’s bids at each round. Each bid window is shown by colored rectangles. One may think of windows as consecutive slices of received bids. In this figure, there are four completed windows of offers and one that is currently being filled with opponent offers (the last one to the right). On the other hand, Figure 3 shows a conceptual example with offers and three complete bid windows, and one that is currently being filled at .
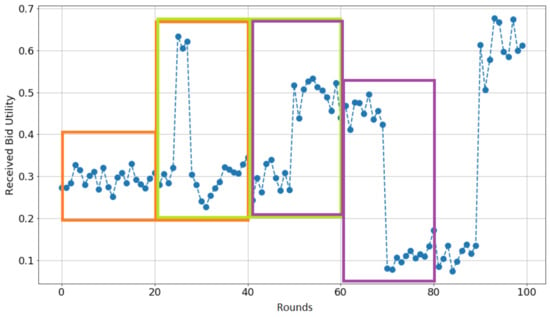
Figure 2.
The concept of bid window. In the figure, the reader can observe four consecutive windows of k offers.
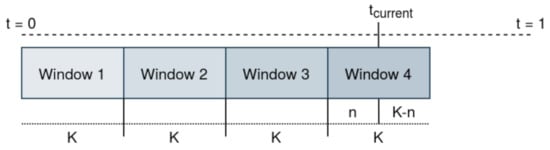
Figure 3.
The bid windows that split the negotiation history into partitions of K bids.
In the new Tit-for-Tat concession mechanism, the agent considers the most recent complete window pairs, and (just filled), in the history of bid windows . If we consider an example with , the concession mechanism would work with two consecutive windows of bids of size . In this example, one can formulate the current window of bids as = [, ..., ], where t is current time step and denotes the offer sent by the opponent at round i. For instance, the agent would take into account Window 2 and Window 3 at for the given example in Figure 3. Only when the current window is filled with k bids is the concession mechanism executed again. Therefore, the concession and update of the target utility occur in window-sized mini-batches. After the update, the current window is added to the history of previous bid windows, and it is emptied to start a new bid window.
3.2.2. Target Utility Update
After explaining the concept of a bid window, let us formalize some parameters and data employed by the target utility update mechanism, which is carried out only when the concession mechanism is executed (i.e., after comparing two non-sliding windows as described in the previous subsection). Coupled with the non-sliding window mechanism, the target utility update mechanism is what makes our proposed Tit-for-Tat strategy different from classic variants. First, represents the best offer received from the opponent, considering our utility function. Second, represents the maximum utility update at each concession step. This new parameter, which is not included in classic Tit-for-Tat variants, avoids abrupt concessions and forces a more thorough exploration of the utility space. The details of our proposed target utility update mechanism can be found in Algorithm 1. Next, let us explain how this mechanism works in detail.
| Algorithm 1: The target utility update mechanism. |
 |
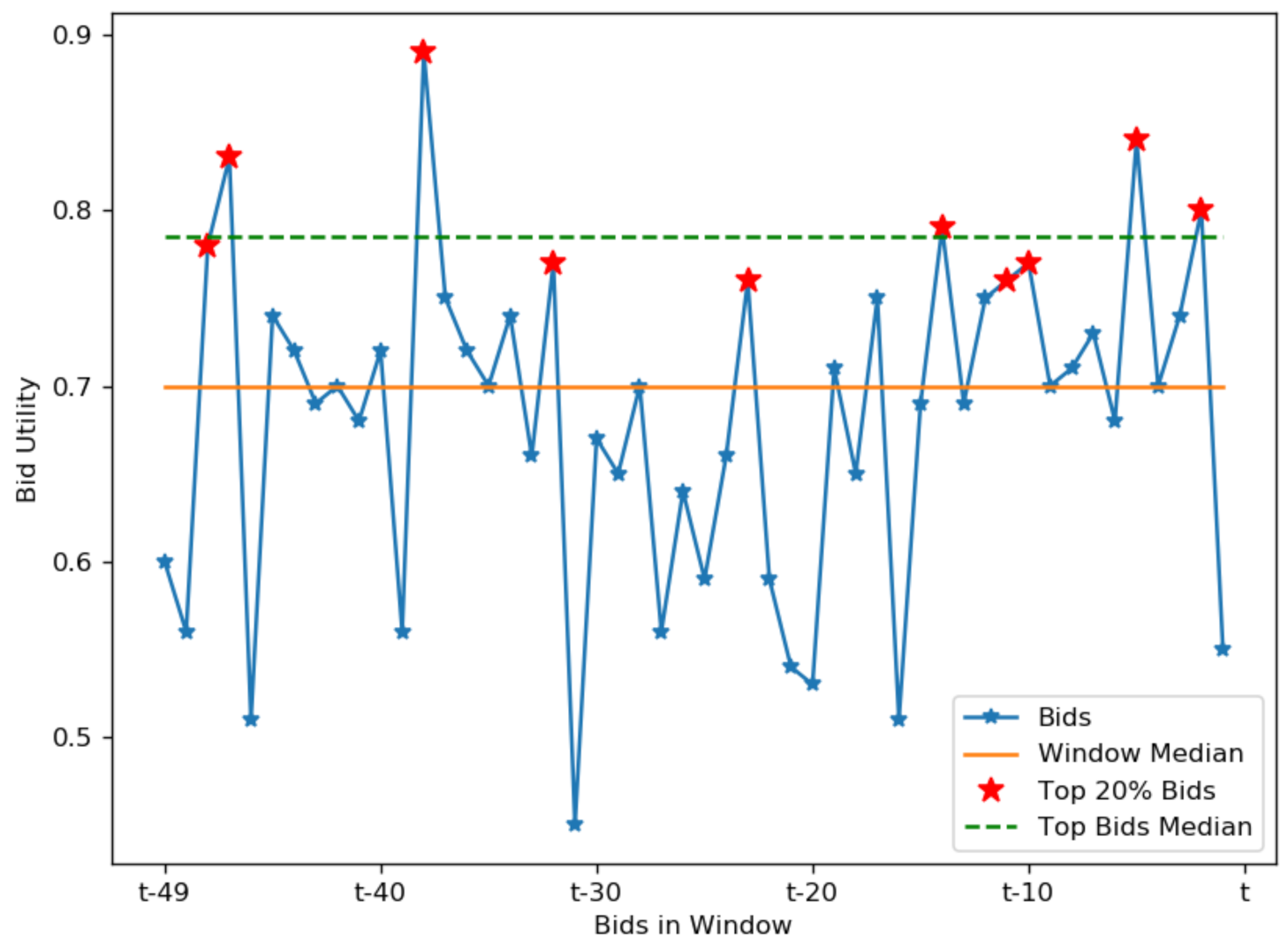
The first steps (lines 1–4) consist of estimating a central measure of utility received from the opponent in the current window of bids. For that, bids in a window first need to be transformed to a utility space. The agent uses a median utility calculation mechanism as a measure of centrality due to the abrupt and unintended changes in utilities of bids sent by the opponent. In fact, instead of considering the whole window of bids, we propose for the agent to just consider those offers whose utility are above a given percentile (i.e., , with z being the specific percentile). We experimentally found that many windows of bids only contain a few reasonable offers for the agent even though the opponent may have conceded. In some scenarios, this is caused by inaccurate opponent models in the early and middle stages and, in others, just due to the exploratory nature of the opponent. Therefore, we believe that concessions should only be detected with the top offers from the window of bids rather than just two consecutive offers or from the whole set of offers, as proposed by classic Tit-for-Tat variants. After filtering out those offers above the percentile in the windows of bids, its median is calculated. From this point on, we refer to this median calculation on the top bids in a window as the top median. Figure 4 shows a bid window collected from a real negotiation and illustrates how calculating the median on the offers above a given percentile (, 20% top offers) may better represent concessions carried out by the opponent.
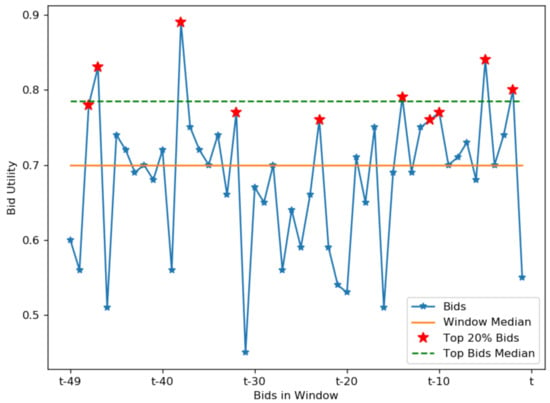
Figure 4.
An example of the top median mechanism for .
After that, the agent checks the previous window of bids to calculate the best top median received so far from previous windows (lines 5–12). Please, notice that this median calculation follows the same procedure as described in the paragraph above (i.e., median on the top offers from the window of bids). We consider that a concession has been carried out by the opponent if the top median in the current window is above the best top median from previous bid windows. The concession step is the difference between both top medians (line 13) and, if necessary, truncated to the maximum concession step . Finally (line 14), the target utility is recalculated as the previous target utility minus the concession step calculated before. Then, the calculated target utility is compared with the utility of the best offer received so far, and the higher value is set to be the current target utility.
3.3. Bidding Mechanism
While the concession and target utility update mechanism are the same regardless of the underlying behavior followed by our agent, the bidding behavior changes accordingly. This section describes the bidding strategy followed by our agent depending on the underlying negotiation behavior. The general description of each behavior is not repeated to avoid redundancy; the reader can find it in Section 3.1.
3.3.1. Strictly Exploring and Exploratory Tit-For-Tat
Both the Strictly Exploring and the Exploratory Tit-For-Tat behaviors employ the same bidding strategy. This bidding strategy allows the agent to explore the negotiation space with the opponent. It should be highlighted that, in this case, the target utility is employed to filter which offers can be sent to the opponent. That is, in these strategies, offers sent to the opponent are at least as good as the target utility. The agent sorts the outcome/offer space in descending order according to its utility function. This bidding mechanism iteratively sends offers in descending order from the best possible offer in the domain to the current target utility. Then, once all the offers in the interval have been sent at least once, the agent starts sending random offers from the utility range. It should be highlighted that, once the target utility is updated, the agent starts sending new and unexplored offers again in descending order until no more new offers are available, turning back again to the random bidding in the utility range.
3.3.2. Nash Optimizer
In Nash Optimizer behavior, the agent believes that the opponent model gained significant information and it can be used to estimate what the opponent gets from any bid. In addition, this is the behavior that makes the agent social since it offers the bid that maximizes the product of the utility it gets and what the opponent is estimated to get. The selection of prospective bids is, again, regulated by the current target utility. More specifically, the agent always sends this offer given a current target utility:
where is the estimated utility function of the opponent, estimated as described in Section 3.5, , and is the current target utility.
3.3.3. Similarity-Based TFT
The Similarity-Based TFT is employed when the agent abandons the exploratory behaviors and it considers that it does not have enough data to model the opponent correctly. In that case, a simple similarity mechanism is employed to propose offers to the opponent. Again, the set of available offers to be sent to the opponent is regulated by the current target utility . From that set of offers, the agent selects the offer that maximizes the similarity to the best offer sent by the opponent so far . Notably, the mechanism can be described as follows:
where is a similarity function between 0 and 1 that indicates how similar two offers are. In the case of our experiments, as we worked with discrete issues, this similarity was calculated as the percentage of common values in both offers. It should be highlighted that this strategy includes a small exploration mechanism that allows it to propose random offers in the current utility range. This exploration mechanism is activated with a probability that depends on the remaining negotiation time:
where t is the current time and T is the total negotiation time.
3.3.4. Eager
Since the negotiation is about to end, the agent offers the best offer received from the opponent in an attempt to successfully close the negotiation.
3.4. Acceptance Mechanism
As with the bidding mechanism, the behavior of the agent changes with regard to bidding acceptance. Next, we briefly describe each of these acceptance mechanisms.
3.4.1. Strictly Exploring
As the agent solely aims to explore the negotiation space and to know the opponent, it rejects all incoming offers from the opponent.
3.4.2. Exploratory TFT and Similarity-Based TFT
Unlike the Strictly Exploring behavior, in these behaviors, the agent accepts the offer when . That is, when the utility received in the offer is at least as good as the current target utility.
3.4.3. Nash Optimizer
Considering that this behavior is active when the agent has explored the negotiation space and it can rely on its opponent model, the agent accepts an offer if it is at least as good as the next offer to be sent, that is, if the received offer is at least as good as the bid sent by the Nash bidding mechanism: .
3.4.4. Eager
As it is mentioned in the bidding strategy, in this behavior, the negotiation time is about to end. Therefore, the agent aims to reach an agreement on a bid that provides at least the highest utility it has received (i.e., ).
3.5. Opponent Modeling
For modeling the preferences of the opponent, we proposed a frequency-based opponent modeling mechanism, in which the earlier version was presented in [28]. The model is developed for a time-bounded negotiation setting where each of the agents has a linear additive utility function, as described in Section 2. The opponent modeling mechanism proposed for our social agent covers the modeling and update mechanisms for both relative issue preferences and the issue value evaluations.
3.5.1. Value Function Estimation
The value function estimation aims to estimate the function for each of the negotiation issues. It assumes that the most preferred issue values appear more frequently in offers than others. Hence, the frequent issue values are assumed to present more utility than those that are less frequent. The estimation of the issue value evaluation is made by a max-normalization function. The function estimates the relative importance of each of the issues’ values compared to the most frequent value of that issue. Formally, the estimation is calculated by the following formula:
where is 1 if the value j is used for issue i in offer o and 0 otherwise. We propose the use of Laplace smoothing to the value occurrences. The reason behind this approach is to initialize the issue values that have never been received. In addition, the ratio is filtered by an exponential filter with coefficient , having the range of . The proposed filter is one of the main differences of this value function estimation component with respect to the classic frequentist opponent modeling approaches. It controls the relative importance of repeatedly received issue values by suppressing their growth. When the constant is assigned to be 1, the estimation function turns into a classic frequency model with a Laplace smoothing.
3.5.2. Issue Weight Estimation
The proposed model seeks statistically significant changes in issue value distributions of the two consecutive, disjoint and time-sorted window of offers as shown in Figure 3. The underlying assumption is that, when a concession is carried out, the distribution of issue values changes from window to window. Thus, if one detects changes between in the distribution of issue values sent by the opponent, one may detect concession moves.
Before going further, we explain the concept of issue value distribution in more detail. Equation (6) formulates the issue value distributions in a list of offers . Given a window of bids, the formula calculates the occurrence frequencies of each of the issue i’s negotiation values j, . The returns 1 if the value j of issue i exists in the offer o. The || denotes the length of the bid window. The formula applies Laplace smoothing to handle the erroneous outcomes of the statistical significance test in the Algorithm 2. Table 1 demonstrates how this calculation is performed for a given example.
| Algorithm 2: The issue weight update mechanism |
 |

Table 1.
Issue values’ smooth frequency calculation given an example window of bids.
The proposed algorithm departs from classic frequentist opponent modeling approaches in two ways: it employs non-sliding windows rather than two consecutive offers to decide how to update weights, and it is based on statistical tests of significance to compare the issue value distribution in windows of bids. The proposed algorithm iterates over every single negotiation issue i and calculates the frequency distribution of the issue values in the previous window and the frequency distribution of the issue values in the current window (lines 3–5). Then, a Chi-squared test is carried out with the null hypothesis being that both frequency distributions, and , are statistically equivalent (line 6). The main goal behind this test is to check whether the distribution of issue values for i changed from the previous window of offers to the current one. This information helps us determine if, overall, the opponent changed the type of offers sent. In the case that the null hypothesis cannot be rejected, we add the issue i to the set of issues e for which the distribution did not change from the previous to the current window (lines 7–8).
When the null hypothesis is rejected (line 9), it means that the frequency distribution for issue i is different from the past to the current window. The question is in what direction the change points for that issue (e.g., concession and increase of utility). More specifically, inspired by classic frequency approaches, we are interested in checking if the opponent conceded in the issue because then we can update the weights for those issues that remained the same. Again, the assumption is that opponents tend not to change the most important issues more often than less preferred issues. In order to estimate if the opponent conceded in the issue, we employ the frequency distribution for issue i during the whole negotiation as an approximation of the actual valuations, as specified in Equation (5). Then, the expected utility obtained in issue i for the previous window of opponent offers is calculated (line 10). The same procedure is applied to obtain the expected utility obtained in issue i for the current window (line 11). Then, both expected utilities are compared to assess if a concession has been carried out in the issue i (lines 12). If the value distribution of an issue does not change significantly over the consecutive windows and the expected utility of the previous window is higher than that of the current window, it is considered as a concession (lines 13).
We propose to take an aggressive strategy to detect overall concessions over two consecutive windows of opponent offers. We consider that there is a concession as long as the opponent conceded in any of the issues (line 14). In that case, we update the importance for those issues that stayed in the same frequency distribution by adding a parameter that is calculated by a time-dependent decay function denoted in Equation (7) where tunes the speed of the decay (lines 15–16). We understand that there are other strategies to detect an overall concession, and we are currently exploring the performance of more conservative approaches and probabilistic approaches. If there is no concession in any of the issues, then issue weights stay the same (line 17).
Figure 5 shows how the issue weight update parameter, , is calculated for varying values over negotiation time.
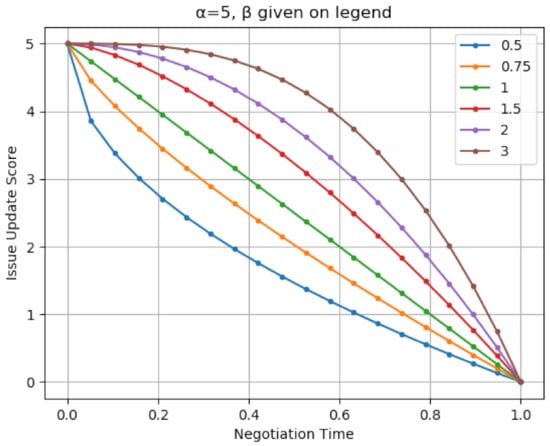
Figure 5.
The issue weight update for various levels of .
4. Experiments
In this section, we assess the empirical performance of the proposed agent and aim to answer the initial question raised at the start and title of this article: Can social agents efficiently perform in automated negotiation? To answer that general question, we proposed three different research questions in Section 1. The three research questions were as follows:
- Q1. Can a social agent obtain a high utility in heterogeneous environments?
- Q2. Can a social agent achieve socially efficient agreements in heterogeneous environments?
- Q3. Can social negotiation strategies be an efficient choice for self-interested agents in agent societies?
To answer these questions, we designed three types of experiments. The first experiment serves to analyze the impact of the length of the window of bids on the performance of our social agent. The second experiment aims to analyze the behavior and performance of our social agent in a static society of agents. By a static society of agents, we mean a society where multiple types of agents exist, but they do not change their strategies. With this experiment, we aim to find if our social agent can achieve socially efficient agreements in heterogeneous environments. Lastly, we carry out a theoretical analysis using game theory to find out about the prospective use of our social strategy in a society where agents can decide their negotiation strategies. This experiment aims to find if a social strategy such as the one proposed in this article may be efficient even for self-interested agents. The structure of this section is organized as follows. First, we describe the experimental settings common to all our experiments. Then, we describe and analyze the experiments carried out to identify an appropriate window size for the proposed agents. After that, we provide the empirical results for the experiment carried out to determine the behavior and performance of our agent in a static agent society. Finally, we describe the insights arising from the theoretical analysis carried out in a dynamic setting.
4.1. General Experimental Setting
In this subsection, we describe the settings and design decisions common to all the experiments carried out to assess the performance of our social agent. To be more specific, we describe the metrics employed to evaluate the performance of the agents as well as the agents that form the agent society in which our agent interacts.
4.1.1. Quality Metrics
As mentioned throughout the article, the goal of the proposed agent is to be social and reaching an agreement that is as fair as feasible for both agents. For that reason, most of the metrics employed to assess the performance of the agent aim to measure the fairness/quality of the agreement from both agents’ perspectives. Next, we describe each of the metrics that we use in our experimental setting:
- Individual utility: This is the utility received by the agent at the end of the negotiation. When the negotiation ends with no agreement, then the agent gets an individual utility of 0.0. Otherwise, the utility obtained by the agent is that of the individual utility reported by the agreement.
- Nash bargaining point distance: The Nash bargaining point is the Pareto optimal point that maximizes the product of both agents’ utilities. Traditionally, as the product of the two utilities penalizes scenarios where one of the agents gets a very high utility while the other agent gets a low utility, the Nash bargaining point is considered as an indicator of the fairness of the resulting agreement. Thus, in practice, the closer an agreement is to the Nash bargaining point, the fairer it should be for both involved parties.
- Kalai point distance: The Kalai point also seeks to find an outcome that is fair for both parties. However, differently from the Nash bargaining point, the Kalai point considers the initial reservation utilities of the agents (i.e., the status quo solution) when computing the fairness of the agreement. In essence, both parties should gain in the same proportion from their status-quo point. Thus, the Kalai point is the Pareto optimal solution that maximizes the ratio of the gains of both agents. In practice, the closer an agreement is to the Kalai point, the fairer it should be for both involved parties.
- Negotiation time: Although it is not related to the fairness of the agreement found by negotiating agents, the negotiation time helps to see the performance of the different strategies from a different perspective. The sooner agreements are closed, the more time that the spare time and computational power can be allocated to other relevant tasks. Therefore, other aspects being equal, one should prefer negotiation agents that close deals more rapidly.
The aforementioned metrics are employed to analyze the empirical performance of our social agent and other agents employed in the experiments.
4.1.2. Negotiation Domains
In these experiments, we considered four different negotiation domains with a medium or large number of possible negotiation outcomes to reduce the odds of the Nash point or agreements close by mere chance. Next, we briefly describe the negotiation domains chosen for the experiments:
- Itex vs. Cypress (ANAC 2010, [34]): This is a classic buyer–seller setting where a bike manufacturing company negotiates on the sale of a commodity with a bike retail shop. There are a total of 180 possible outcomes.
- England vs. Zimbabwe (ANAC 2010, [34]): This is a negotiation domain consisting of the national negotiations between England and Zimbabwe on the application of the World’s Health Organization Framework on Tobacco Control. The negotiation domain consists of 576 possible negotiation outcomes and 5 negotiation issues.
- Grocery domain (ANAC 2011, [35]): This domain involves agents negotiating on the type of groceries to purchase from a supermarket. There are a total of 1600 possible outcomes distributed across 5 negotiation issues.
- Amsterdam Trip (ANAC 2011, [35]): This is a negotiation domain where two parties of friends negotiate on the details of a trip to Amsterdam. The negotiation domain contains 3024 possible outcomes distributed across 6 negotiation issues.
- Party domain: This is a negotiation party where two hosts negotiate on how to organize a party for their friends. The negotiation scenario contains 3072 possible negotiation outcomes and 6 negotiation issues.
- Camera domain (ANAC 2012, [36]): The camera domain contains preference profiles that describe the purchase of a camera and its accessories for a specific budget. More specifically, the negotiation domain contains 3600 prospective outcomes distributed across 6 negotiation issues.
4.1.3. Agents
Another critical decision to make for the experimental setting is deciding on the opponent agents to negotiate with. Some factors influenced our decision in this matter. First, our proposed agent is an agent that models the opponent from the data leaked in the current negotiation process, and we assume that no other data from the opponent is available. This is the situation faced in case of a cold start in an agent society, in case that the preferences of agents change from negotiation to negotiation, or in the case that negotiation partners rarely interact more than once. Therefore, negotiating agents that learn from multiple negotiations are excluded from this experimental setting, as introducing these agents would result in an unfair comparison. Second, we want to evaluate the performance of our agent in an agent society that shows a range of behaviors and bidding strategies, as it would probably happen in a real agent society. For that reason, we employ the following state-of-the-art agents to represent a realistic agent society:
- AgentK (K) [37]: This is the winning agent of the 2010 ANAC negotiation competition. It is an agent for which the concession speed is regulated by the average utility of all received bids and its standard deviation. In terms of offer proposal, it selects any offer from above the current aspiration. Therefore, it does not model the opponent’s preferences on offers.
- IAmHaggler2011 (IH2011) [38]: A negotiating agent that uses Gaussian processes to predict the future concession of its opponent and then adjust its concession rate accordingly to get the most from the negotiation. The goal of this agent is that of optimizing one’s utility while also trying to get more utility than the opponent. Bids are only selected from a small range around the target utility. This aggressive stance usually results in the agent repeating the same offers. This agent placed third in the ANAC 2011 competition.
- Gahboninho (GAH) [39]: This agent finished second in the ANAC 2011 competition. Gahboninho employs an adaptive concession strategy that attempts to detect if agents are susceptible to being pressured or if they are stubborn. For that, Gahboninho limits most of the outcomes sent to outcomes that report a low utility value for the opponent.
- Hardheaded (HH) agent [25]: The winning agent of the 2011 ANAC competition. This agent follows a time-based bidding strategy that consists of not conceding until almost the end of the negotiation. While not conceding, the agent performs opponent modeling on the opponent’s preferences by using a frequency modeling mechanism. Then, in the last states of the negotiation, the agent attempts to find an agreement by using the trained model on the opponent’s preferences and finding outcomes that have the same target utility for one’s own but maximize the preferences of the opponent.
- IAmHaggler2012 (IH2012) [36]: The 2012 version of IAmHaggler ranked as the most social agent in the ANAC 2012 competition (i.e., maximization of the sum of the opponent’s and one’s utility). This agent was employed to compare the performance of our social agent against some state-of-the-art social agents.
- TheNegotiatorReloaded (TNR) [40]: This agent is the best performing agent in non-discounted domains for the ANAC 2012 agent competition. The agent divides the negotiation into non-sliding windows, similarly to our approach. For each window, the agent estimates the type of agent behavior that it is facing and adjusts its concession rate accordingly. The agent employs Bayesian learning for modeling the opponents’ preferences and having an updated estimation of the Kalai point.
- CUHK Agent (CUHK) [41]: This agent won the ANAC 2012 agent competition for discounted domains. The agent adopts an adaptive concession strategy that sets a minimum target utility depending on both the behavior of the opponent and the characteristics of the domain (i.e., discount factor). In general, the agent will attempt to exploit the opponent as much as possible by not conceding. Compromises are only taken at the end of the negotiation after a time threshold that is set dynamically according to the opponent’s behavior. In this case, the agent attempts to model the opponent preferences by attempting to estimate a rank for proposed outcomes.
From the agents selected, one can observe that we have both agents that carry out opponent modeling (i.e., IAmHaggler2011, Hardheaded, TheNegotiatorReloaded, CUHK Agent, and IAmHaggler2012), agents that show an adaptive concession behavior (e.g., AgentK, IAmHaggler2011, TheNegotiatorReloaded, CUHK Agent, Gahboninho, and IAmHaggler2012), and agents that consider the opponent’s preferences when constructing bids (e.g., Hardheaded, TheNegotiatorReloaded, and IAmHaggler2012). They are agents that performed among the best in the International Automated Negotiating Agents Competition (ANAC) editions of 2010, 2011, and 2012. It should be noted that agents from the 2013 competition onward were discarded as they specialize in different problems to the ones covered in this article (e.g., learning over multiple negotiations, non-linear utility functions, multi-lateral negotiations, etc.). Thus, we argue that a realistic agent society would be formed by top-performing agents as most of the ones employed in this setting.
4.1.4. Social Agent Configuration
As the reader may have realized, our agent’s behavior is controlled by many hyperparameters. After an initial exploration of our agent, we found a set of parameter values that generally performed well in practice. To avoid overfitting of our agent to the agents selected for the experiments, we carried out manual tests using GENIUS with our agent and Agent K in one of the domains: the party domain. During the tests, we observed both the outcome obtained by our agent and the evolution during the negotiation. After a few manual tests, we found a combination of hyperparameters (see Table 2) that obtained good joint utility and distances to both Nash point and the Pareto frontier. Of course, we do not claim that the configuration results in an optimal configuration of the agent, but as the reader will appreciate, these values are enough to prove the main contribution of this article: how a social agent can efficiently perform in an agent society. As only one agent and domain were employed for finding this combination of hyperparameters, we argue that there is no risk of overfitting, as there are five negotiation domains and six opponents that were not employed during this exploration. Therefore, we used the parameter values found in Table 2 for the subsequent experiments carried out to assess the performance of our social agent.

Table 2.
General configuration for our social agent during the experiments.
4.2. Analyzing the Impact of the Window Size
In this first batch of experiments, we study to what extent the length of the window, employed by our agent to carry out the different behavioral analyses, impacts the social performance of our agent. The main goal of this experiment is to identify an adequate window size for properly and socially reacting to the moves of the agents in the agent society. For this first experiment, we set the value of the window size to . The rest of the parameters of the agent were set according to the values represented in Table 2.
Each configuration of our agent faced a subset of four agents (i.e., AgentK, IAmHaggler2011, Hardheaded agent, and TheNegotiator Reloaded) in a subset of three negotiation domains (i.e., party, Amsterdam trip, and England vs. Zimbabwe domains) and negotiation profiles. The reason we carried out these experiments with just a subset of the opponents and domains is to avoid overfitting. In these experiments, each instance of our agent faced each of the four opponent agents for all three negotiation domains, using both preference profiles, and repeating each negotiation setting 10 times (a total of negotiations per our social agent configuration). In addition, we measured the distance to the Nash bargaining point, the distance to the Kalai point, and the negotiation time at the end of each negotiation. The experiments were conducted using a Genius simulator [42] using bilateral negotiations with a common deadline of 90 s.
Table 3 contains the results of this first experiment. As the reader may observe, a window size of 25 is capable of obtaining a lower distance to the Nash bargaining point and the Kalai point, resulting in a more social outcome than the other two configurations. More interestingly, there were no observable differences in the individual utility obtained by the proposed agent. This means that smaller window sizes also impacted the learning carried out by the agent. In fact, the larger the window sizes, the fewer updates that are carried out on the opponent model. We could not observe a notable difference between the three studied configurations in terms of speed, with negotiations taking approximately 82% of the total time.

Table 3.
Average distance to the Nash bargaining point, to the Kalai point, average individual utility, and ratio of negotiation time consumed for three window sizes.
4.3. Performance in a Stationary Agent Society
As mentioned at the start of this section, the second experiment studies the behavior and performance of the proposed agent in a static society. The society is formed by the top-performing agents described in Section 4.1.3 and our social agent. For this analysis, we assumed that agents may face any other agent in society, including versions of themselves. Another assumption for this first experiment is that the agents face the same number of times each other in the experiment. The game-theoretic analysis carried out in Section 4.4 helps us to answer what would happen if the agent society started from other different agent distributions in the society.
To carry out an experiment with this type of setting, we run a GENIUS tournament between all of the agents described in Section 4.1.3 and our agent. Each agent faces each other agent (including itself) 10 times in every single domain and for every possible profile in that domain. This means that each pair of agents faces in negotiations. In order to analyze the behavior and performance of each agent, we record the utility achieved at the end of the negotiation, the distance to the Nash bargaining and Kalai point, and the time taken to finish the negotiation. The parameters of our social agent are set at the ones described in Table 2 and the appropriate negotiation window size highlighted in the previous experiment (i.e., 25 bids).
First, we focus on analyzing the overall performance of our social agent in this tournament. The overall results of this experiment can be found in Table 4. The table shows the average individual utility, distance to the Nash bargaining point, distance to the Kalai point, and negotiation time in the negotiations carried out by each of the agents in the society. As it can be observed, our social agent obtains the best average utility, distance to the Nash bargaining point, and distance to the Kalai point. These overall results point to various insights.

Table 4.
Average utility, distance to the Nash point, distance to the Kalai point, and negotiation time for the agents when facing themselves and all other opponents in the specified domains. The best performing values are in boldface.
First, the distance to the Nash and Kalai points corroborates that our agent is indeed a social agent. It is, in fact, the most social agent among the agents in this society, including IAmHaggler2012, which was awarded as the most social agent in the ANAC 2012 competition. The reader should be reminded that both the Nash bargaining and the Kalai point are considered fair outcomes in negotiation settings. Therefore, the closer that the agreements are to these points, the fairer outcome that is achieved. A social agent should aim to be fair, as it tends to maximize the utility of both parties at the same time. Hence, our agent outperforms the current state of the art in terms of social agents. These results corroborate our second research question Q2 (i.e., Can a social agent achieve socially efficient agreements in heterogeneous environments?).
Second, one can also observe that our agent is capable of obtaining competitive results concerning the individual utility of the agent. Our social agent obtains the best average utility for the agents included in the experiment. This includes winning agents from the ANAC competition such as Agent K, CUHK Agent, and HardHeaded. This positive result for the individual utility of the agent is related to the fact that the agent achieves deals that are close to the Kalai and Nash bargaining point. Usually, these points contain agreements that have a high utility for both parties, and no party suffers from exploitation. Therefore, by securing the socially optimal outcome, one can also guarantee a high utility for oneself. In this case, it was the highest overall average utility. This helps us answer our initial research question regarding the prospective performance of social agents in automated negotiation. Particularly, these results support one of our initial research questions, Q1 (i.e., Can a social agent obtain a high utility in heterogeneous environments?).
These results regarding the individual utility of agents are surprising at first, as most of the rest of the agents have been designed to be competitive and maximize one’s utility as much as possible. Therefore, we carried out a more in-depth analysis of the negotiations of the tournament. This analysis showed why competitive agents were not able to guarantee the highest average utility. Many negotiations where these competitive agents participated finished without any agreement due to the competitive nature of agents participating in the tournament. For instance, 12.5% of the negotiations for The Negotiator Reloaded, 8.33% of the negotiations for HardHeaded, 5.52% of the negotiations for Gahboninho, and 4.68% of the negotiations for CUHK Agent finished without an agreement. The numbers were particularly worrying when some of these competitive agents faced themselves (e.g., 26.67% of negotiations failed when TheNegotiator Reloaded faced itself). No negotiation in which our agent participated finished in failure.
We argue that, in an agent society, achieving agreements is of utmost importance as, otherwise, business opportunities and partnerships may be missed, and the reputation of the agent in the society may also decrease among other negotiators. In the end, if other agents in the society had bad experiences negotiating against another agent, they may avoid selecting the agent as a negotiating partner in the future, further decreasing the performance of that agent in the society.
From these initial experiments, one can conclude that (i) the proposed agent indeed shows a social behavior by minimizing the distance of agreements achieved to both the Nash and the Kalai point, both measures of fairness in negotiation; (ii) although the design of the agent focuses on social performance and behavior, the agent is capable of achieving efficient results in terms of the individual utility of the agent. This latter result supports our initial hypothesis that social agents can also perform efficiently in automated negotiation. These results were obtained based on the assumption that there is a static agent society composed of the agents included in the experiment. In the next experiment, we show how our agent would perform in case that the agent society is dynamic and agents can decide on what strategy to play in negotiations.
4.4. Performance in a Non-Stationary and Utilitarian Agent Society
In this case, we plan to study the appropriateness of the proposed agent in a dynamic agent society, where agents can change their negotiation strategy prior to engaging in a negotiation with another agent. More specifically, assuming that agents can choose based on a range of available negotiation strategies, is our proposed strategy attractive even for self-interested agents? For that, we analyze the agent society from a game-theoretic perspective. First, we formulate a game where two agents have to negotiate, and each of them can decide to play according to one of the strategies mentioned in Section 4.1.3 or the proposed social agent. Then, the agents negotiate, and by the end of the negotiation, they achieve a utility. In this game, we assume that agents are rational, and their choice is purely driven by the individual utility expected at the end of the game. Therefore, we formulate a game with two players and eight possible strategies for each agent. The payoff of each strategy combination is obtained from the average utility achieved by that pair of agents across all domains and profiles in the previous tournament. The payoff matrix arising from the definition of this game can be observed in Table 5.

Table 5.
Payoff matrix for a bilateral negotiation in an agent society formed by the studied agents. Bold represents the pure equilibrium of the game
First, we carried out a pure and a mixed equilibrium analysis on the resulting game using the algorithm described in [43]. In the game, there is a single pure equilibrium consisting of one of the players using our social strategy and the other agent employing The Negotiator Reloaded strategy. A total of four mixed equilibria were found for the game, and they can be observed in Table 6. As it is observable both in Table 5 and Table 6, our social agent has a significant contribution (i.e., most used strategy) to the strategy profile of at least one of the two players in the negotiation. In fact, it is the most used negotiation strategy for the two players in three out of the four mixed strategies of the game. Overall, even in a society where agents can rationally adapt their strategies for the negotiation, our social agent has a prevalence over the rest of most competitive strategies. Both game-theoretic results support the fact that our proposed agent can be an efficient choice even for self-interested agents, answering our initial research question Q3 (i.e., Can social negotiation strategies be an efficient choice for self-interested agents in agent societies?).

Table 6.
Mixed Nash equilibrium for the dynamic agent society. Each row represents a different mixed equilibrium. In each cell, the first number represents the ratio of use of the strategy for the first player, while the second represents the ratio of use of the same strategy for the second player.
5. Related Work
The literature on cooperative agents is extensive, and it includes work as relevant as collaborative knowledge networks [44,45,46], multi-agent teams [7,47,48], cooperative agent planning [49,50], coalition formation [51], etc. Despite social and cooperative negotiating agents having links with many other areas of cooperative agents, in this section, we aim to review work that is the most related to our social agent proposal. Mainly, we aim to discuss cooperative and adaptive negotiation agent proposals and highlight the differences between these agents and our proposal.
Lai et al. [18] proposed a multi-issue bilateral negotiation agent that is based on a bidding mechanism that proposes offers in the iso-utility curve. The agent sends up to k offers per round to its counterpart, who may accept or propose new counteroffers. The offers sent to the opponent are the most similar to the previous offers sent by the opponent. The results show that, when both agents employ this model, they are capable of reaching agreements that are very close to Pareto optimality. Our agent also employs similarity metrics when there is insufficient information to estimate the other agent’s preferences correctly. However, there are several differences between our proposal and [18]. Our agent focuses on reaching social agreements, and it does not require the counterpart to be cooperative. In addition to it, our agent changes its behavior depending on available information and the opponent’s moves.
The Nice Tit-For-Tat [29] strategy was proposed in one of the Automated Negotiating Agents Competitions to reciprocate the opponents’ behavior. Similar to our proposal, the agent is equipped with an opponent model, one based on Bayesian learning, that helps to estimate the opponent’s preferences on bids. This opponent model guides the concession strategy carried out by the tit-for-tat agent. When the opponent carries out a concession, the agent reciprocates some proportion of the opponent’s concession and selects the bid that is the most likely to be accepted by the opponent according to the opponent model. Our agent also employs an opponent model to drive bidding, but it is aware when the model may not be trusted due to the lack of information about the opponent. In addition to this, concessions are not detected solely based on a single pair of bids, but a window of bids is employed to ensure that the concession is a byproduct of a general and genuine change by the opponent, and it is not a byproduct of mere chance.
Ilany et al. [52] proposed an interesting approach that combines machine learning and statistics for appropriately selecting a negotiation strategy. Two mechanisms are proposed: one based on supervised learning that selects a negotiation depending on the negotiation domain characteristics and another based on multi-armed bandits that selects the negotiation strategy during the negotiation. The results showed that the agent was capable of over-performing agents for the previous negotiation competitions. Our agent also adapts its behavior during the negotiation. Even though the adaptive mechanism is not as sophisticated, it is engineered based on the prospective problems that may arise during the negotiation. On top of that, the main contribution of the article is not the adaptation mechanism itself, but the proposal of a social strategy that is capable of efficiently performing in an agent society. Moreover, the focus of the agent proposed in [52] is not necessarily social utility maximization but individual utility maximization.
Proposing another agent that is supported by a variety of negotiation strategies [53], the authors presented a multi-party negotiation agent for which the decisions (e.g., bidding, acceptance, etc.) are built by aggregating the decisions of multiple winning agents from previous ANAC competitions. While our agent is also supported by several strategies, the behavior of the agent proposed in [53] does not adapt according to the negotiation context, as the aggregation rules remain the same. In addition, the objective of our agent is that of being social, while the work presented in Güneş et al. [53] solely strives for utility maximization.
Katsuhide [54] proposed an adaptive agent that changes the concession speed according to previous negotiation sessions with the opponent and the current negotiation state. The strategy uses an opponent modeling mechanism that maps the opponent bids to its utility function by considering time, mean received utility, and the deviation of the received utility. Then, the agent classifies opponents according to the Thomas–Killman Conflict Mode Instrument and adapts its concession speed accordingly. If the opponent is classified as cooperative or passive, the proposed agent demonstrates a more cooperative behavior. In addition to this, the agent also employs a genetic algorithm to search for Pareto optimal bids by generating variations of the opponent’s first bid. It assumes, with a high likelihood, that bids generated from the first opponent’s bids are the best for the opponent. The work presented in [54] also adapts its behavior and may respond cooperatively to other agents’ cooperation. However, the agent requires multiple negotiation sessions to learn about the opponent’s style, while our agent is designed to work for single negotiations where we may not have information about the opponent.
Pan et al. [55] proposed a distributed multi-objective genetic algorithm for solving bilateral negotiations. In their proposal, each agent carries out an NSGA-II genetic algorithm that employs one’s utility function and the evaluation of the opponent for a subset of offers (i.e., partial disclosure on one’s preferences). Once near Pareto optimal bids are generated, the agents negotiate on which bid from the estimated Pareto frontier they should agree on. The agents proposed by Pan et al. are cooperative, as they disclose information about their preferences. However, the negotiation carried out on the estimated Pareto frontier does not necessarily need to be cooperative and ends up in a social agreement. In addition to our agent aiming for social agreements, the other main difference between the proposal presented in Pat et al. and our proposal is that we do not assume any information disclosure in the negotiation apart from exchanged bids. Therefore, our negotiation strategy is also adequate for less cooperative scenarios.
Liu et al. [56] presented a negotiating agent that searches high joint utility agreements around the Nash bargaining solution. This agent also employs a frequentist opponent model, assuming that the most frequently received issue values are the most important for the opponent. In their work, these values are named as prior values. On the other hand, issues with high deviation are priors for the opponent. In their study, the agent calculates standard deviations for each of the issue values, and then it estimates the standard deviation of the aforementioned deviations, coined as the Issue Standard Deviation (ISD). ISD is used as a bridge to estimate the opponent’s preferences on issues. In contrast to our work, they do not have a bid/time window approach in the opponent model, which may face the problems mentioned throughout our article. Moreover, our social agent strategy adapts its bidding and acceptance strategy based on the information available during the negotiation, while the proposal in Liu et al. does not.
Jonker and Aydoğan presented a negotiating agent aiming not only to optimize its utility but also to optimize an outcome in combination with acceptability for human negotiators [26]. The agent determines its moves by following a set of predefined rules considering the opponent’s last three moves. Similar to our work, that agent deploys an adaptive behavior-based mechanism. However, in contrast to our strategy, it has been mainly designed for human-agent negotiation settings where the negotiators have fewer rounds with limited bid exchanges.
Another related negotiating agent was proposed by M. Amini et al. [57]. Their agent follows an extension of the Boulware time-based concession tactic where the agent does not concede at the beginning of the negotiation while adjusting its target utility based on the highest estimated utility to be received. Unlike our time-independent target utility update mechanism with bid windows analysis, they strictly follow a time-based concession strategy led by the best-estimated bid for opponents given the list of acceptable bids for the agent itself. The opponent model is also implemented in a frequentist fashion, prioritizing received bid issues with the highest repetition having the least variation of values, but as mentioned, opponents’ bid histories are not evaluated in windows. On the other hand, the opponent model is designed as an ensemble of individual models that learn each opponent separately, unlike our work. They also introduce the “attention coefficient”, which is used to aggregate opponent models with higher values for the more conceding opponents. Given the adaptive expected utility-based target utility setting and weighted opponent modeling components, they claim that the agent seeks to maximize social welfare.
Azaria et al. [58] proposed a social agent aiming to provide strategic advice in repeated interactions between humans and self-interested software agents. In the proposed model, the agent has complete information about the state of the world, but the human participant may not. The challenge of advice provision is choosing proposals that have some utility for the software agent and have high probabilities of being accepted by the human counterpart. The authors propose an adaptive model capable of gradually changing the weights assigned to each participant when providing advice. The experiments carried out by the authors show how the proposed social agent outperforms behavioral economics and psychological models. Both our agent and the agent proposed in [58] are social, and they show some form of adaptability. The main difference between [58] and our proposed agent is that we focus on bilateral negotiations between software agents where multiple bids may be exchanged between involved parties and where both parties have imperfect knowledge about the world. In addition to this, software agents may exhibit different behavior to that of human beings.
6. Conclusions
Many negotiator agents are selfish and purely driven by one’s utility function maximization. Unfortunately, this means that they usually ignore the other counterparts’ utility in the final agreed outcome. While this strategy may be apt for non-repeated interactions, we argue that, while optimizing one’s utility function is important, agents in a society should not ignore the opponent’s utility in the final agreement since this should improve the long-term perspectives of the agent in the system.
In this article, we presented a social agent proposal supported by a portfolio of negotiation behaviors for which the selection depends on both the information about the negotiation and the behavior of the opponent. The agent employs a new variant of Tit-for-Tat based on a robust analysis of non-adjacent windows of bids and a new and robust frequency opponent modeling mechanism. The opponent modeling mechanism proposed in this article is a frequentist model that is based on the novel idea of windows of bids to detect general changes in the opponent’s bidding and to avoid unwanted effects on the opponent model by abrupt and punctual changes in the opponent’s concession and hardheaded behaviors. The overall negotiation strategy represents different general states that may be faced by a negotiating strategy: a strict exploration where no offers are accepted, an exploration phase where offers may be accepted, two optimizer phases where the agent aims to employ the available information about the opponent to ensure a social deal by using similarity metrics or a frequentist opponent model, and an eager state where the agent aims to close a deal as soon as possible. The agent moves through these states as more information is available about the opponent. First, the agent explores the negotiation space to understand the opponent’s preferences. If enough information is available about the opponent’s preferences, the social agent then exploits the available information by proposing estimated Nash bids and attempt to end up with a social agreement. If no information is available, the agent resorts to a similarity metric that aims to offer bids that are the most similar to the best offer received from the opponent, trying to be social with the scarce information available. Finally, when the deadline approaches, the agent aims to close an agreement.
We have carried out experiments in an agent society formed by some top-performing agents from previous negotiation competitions and some social agents. The experiments have shown that our agent is not only the top-performing with respect to one’s utility maximization but also the agent that participates in those negotiations that are the closest to the Nash Bargaining and the Kalai point, both measures of social fairness. A more in-depth analysis also revealed that our social agent is one of the pure equilibrium strategies to play in the proposed agent society. Furthermore, our social agent also has notorious importance in all of the mixed equilibrium strategies carried out by agents in an agent society. This shows how an agent can be social yet can efficiently perform in an agent society, confirming our main claim in this article. These results suggest that our social agent (i) obtains a high utility in heterogeneous environments, (ii) achieves socially efficient agreements in heterogeneous environments, and (iii) represents a rational and efficient choice even for self-interested agents in an agent society.
Author Contributions
Conceptualization, V.S.-A., O.T., R.A., and V.J.; methodology, V.S.-A., R.A. and V.J.; software, V.S.-A. and O.T.; validation, V.S.-A., V.S.-A., O.T., R.A., and V.J.; formal analysis, V.S.-A.; writing—original draft preparation, V.S.-A., O.T., R.A.; supervision, V.J.; funding acquisition, R.A. and V.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the MINECO/FEDER RTI2018-095390-B-C31 project of the Spanish government and partially supported by a grant of The Scientific and Research Council of Turkey (TÜBİTAK) with grant number 118E197. The contents of this article reflect the ideas and positions of the authors and do not necessarily reflect the ideas or positions of TÜBİTAK.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sanchez-Anguix, V.; Julian, V.; Botti, V.; García-Fornes, A. Tasks for agent-based negotiation teams: Analysis, review, and challenges. Eng. Appl. Artif. Intell. 2013, 26, 2480–2494. [Google Scholar] [CrossRef]
- Fatima, S.; Kraus, S.; Wooldridge, M. Principles of Automated Negotiation; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Baarslag, T.; Hendrikx, M.J.; Hindriks, K.V.; Jonker, C.M. Learning about the opponent in automated bilateral negotiation: A comprehensive survey of opponent modeling techniques. Auton. Agents Multi-Agent Syst. 2016, 30, 849–898. [Google Scholar] [CrossRef] [Green Version]
- Sanchez-Anguix, V.; Chalumuri, R.; Aydoğan, R.; Julian, V. A near Pareto optimal approach to student–supervisor allocation with two sided preferences and workload balance. Appl. Soft Comput. 2019, 76, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Aydoğan, R.; Øzturk, P.; Razeghi, Y. Negotiation for Incentive Driven Privacy-Preserving Information Sharing. In PRIMA 2017: Principles and Practice of Multi-Agent Systems; An, B., Bazzan, A., Leite, J., Villata, S., van der Torre, L., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 486–494. [Google Scholar]
- Cao, M.; Luo, X.; Luo, X.R.; Dai, X. Automated negotiation for e-commerce decision making: A goal deliberated agent architecture for multi-strategy selection. Decis. Support Syst. 2015, 73, 1–14. [Google Scholar] [CrossRef]
- Sanchez-Anguix, V.; Aydoğan, R.; Julian, V.; Jonker, C. Unanimously acceptable agreements for negotiation teams in unpredictable domains. Electron. Commer. Res. Appl. 2014, 13, 243–265. [Google Scholar] [CrossRef]
- Botelho, S.C.; Alami, R. M+: A scheme for multi-robot cooperation through negotiated task allocation and achievement. In Proceedings of the 1999 IEEE International Conference on Robotics and Automation (Cat. No. 99CH36288C); IEEE: New York, NY, USA, 1999; Volume 2, pp. 1234–1239. [Google Scholar]
- Lopes, F.; Rodrigues, T.; Sousa, J. Negotiating bilateral contracts in a multi-agent electricity market: A case study. In Proceedings of the 2012 23rd International Workshop on Database and Expert Systems Applications; IEEE: New York, NY, USA, 2012; pp. 326–330. [Google Scholar]
- De la Hoz, E.; Gimenez-Guzman, J.M.; Marsa-Maestre, I.; Orden, D. Automated negotiation for resource assignment in wireless surveillance sensor networks. Sensors 2015, 15, 29547–29568. [Google Scholar] [CrossRef] [Green Version]
- Iuhasz, G.; Munteanu, V.I.; Negru, V. Evolutionary approach to negotiation in game AI. In Proceedings of the 2013 15th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing; IEEE: New York, NY, USA, 2013; pp. 296–302. [Google Scholar]
- Takahashi, J.; Kanamori, R.; Ito, T. Evaluation of automated negotiation system for changing route assignment to acquire efficient traffic flow. In Proceedings of the 2013 IEEE 6th International Conference on Service-Oriented Computing and Applications; IEEE: New York, NY, USA, 2013; pp. 351–355. [Google Scholar]
- Payne, T.R.; Paolucci, M.; Singh, R.; Sycara, K. Communicating Agents in Open Multi Agent Systems. In Proceedings of the First GSFC/JPL Workshop on Radical Agent Concepts (WRAC), McLean, VA, USA, 16–18 January 2002; pp. 365–371. [Google Scholar]
- Sanchez-Anguix, V.; Espinosa, A.; Hernandez, L.; Garcia-Fornes, A. Mamsy: A management tool for multi-agent systems. In Proceedings of the 7th International Conference on Practical Applications of Agents and Multi-Agent Systems (PAAMS 2009); Springer: Berlin/Heidelberg, Germany, 2009; pp. 130–139. [Google Scholar]
- Baarslag, T.; Aydoğan, R.; Hindriks, K.V.; Fujita, K.; Ito, T.; Jonker, C.M. The automated negotiating agents competition, 2010–2015. AI Mag. 2015, 36, 115–118. [Google Scholar] [CrossRef] [Green Version]
- Billhardt, H.; Julian Inglada, V.J.; Corchado, J.; Fernández, A. Human-agent societies: Challenges and issues. Int. J. Artif. Intell. 2015, 13, 28–44. [Google Scholar]
- Chen, J.H.; Chao, K.M.; Godwin, N.; Soo, V.W. A multiple-stage cooperative negotiation. In Proceedings of the IEEE International Conference on e-Technology, e-Commerce and e-Service; IEEE: New York, NY, USA, 2004; pp. 131–138. [Google Scholar]
- Lai, G.; Sycara, K.; Li, C. A decentralized model for automated multi-attribute negotiations with incomplete information and general utility functions. Multiagent Grid Syst. 2008, 4, 45–65. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Anguix, V.; Valero, S.; Julián, V.; Botti, V.; GarcíA-Fornes, A. Evolutionary-aided negotiation model for bilateral bargaining in ambient intelligence domains with complex utility functions. Inf. Sci. 2013, 222, 25–46. [Google Scholar] [CrossRef]
- Zheng, S.; Xiang, Y.; Shi, L.; Liao, K.; Yang, J.; He, Z. A Cooperative Game-based Negotiation Strategy of Electric Vehicle Discharging Price. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC); IEEE: New York, NY, USA, 2019; pp. 2437–2442. [Google Scholar]
- Faratin, P.; Sierra, C.; Jennings, N.R. Negotiation decision functions for autonomous agents. Robot. Auton. Syst. 1998, 24, 159–182. [Google Scholar] [CrossRef] [Green Version]
- Baarslag, T.; Gerding, E.H.; Aydogan, R.; Schraefel, M.C. Optimal negotiation decision functions in time-sensitive domains. In Proceedings of the 2015 IEEE/WIC/ACM International Joint Conference on Web Intelligence and Intelligent Agent Technology WI-IAT 2015; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2016; Volume 2, pp. 190–197. [Google Scholar]
- Jonker, C.M.; Aydoğan, R.; Baarslag, T.; Fujita, K.; Ito, T.; Hindriks, K. Automated negotiating agents competition (ANAC). In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017. [Google Scholar]
- Aydoğan, R.; Keskin, O.; Çakan, U. Let’s negotiate with Jennifer! Towards a Speech-based Human-Robot Negotiation. In Advances in Automated Negotiations; Ito, T., Aydoğan, R., Zhang, M., Eds.; Springer: Singapore, 2020; pp. 3–16. [Google Scholar]
- Van Krimpen, T.; Looije, D.; Hajizadeh, S. Hardheaded. In Complex Automated Negotiations: Theories, Models, and Software Competitions; Springer: Berlin/Heidelberg, Germany, 2013; pp. 223–227. [Google Scholar]
- Jonker, C.M.; Aydoğan, R. Deniz: A Robust Bidding Strategy for Negotiation Support Systems. In Advances in Automated Negotiations; Ito, T., Zhang, M., Aydoğan, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 29–44. [Google Scholar]
- Baarslag, T.; Hendrikx, M.; Hindriks, K.; Jonker, C. Predicting the performance of opponent models in automated negotiation. In Proceedings of the 2013 IEEE/WIC/ACM International Joint Conferences on Web Intelligence (WI) and Intelligent Agent Technologies (IAT); IEEE: New York, NY, USA, 2013; Volume 2, pp. 59–66. [Google Scholar]
- Tunalı, O.; Aydoğan, R.; Sanchez-Anguix, V. Rethinking frequency opponent modeling in automated negotiation. In Proceedings of the International Conference on Principles and Practice of Multi-Agent Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 263–279. [Google Scholar]
- Baarslag, T.; Hindriks, K.; Jonker, C. A Tit for Tat Negotiation Strategy for Real-Time Bilateral Negotiations; Springer: Berlin/Heidelberg, Germany, 2013; Volume 435, pp. 229–233. [Google Scholar]
- Fujita, K. Automated strategy adaptation for multi-times bilateral closed negotiations. In Proceedings of the 2014 International Conference on Autonomous Agents and Multi-Agent Systems, Paris, France, 5–9 May 2014; pp. 1509–1510. [Google Scholar]
- Aydoğan, R.; Festen, D.; Hindriks, K.V.; Jonker, C.M. Alternating offers protocols for multilateral negotiation. In Modern Approaches to Agent-Based Complex Automated Negotiation; Springer: Berlin/Heidelberg, Germany, 2017; pp. 153–167. [Google Scholar]
- Baarslag, T.; Hindriks, K.; Hendrikx, M.; Dirkzwager, A.; Jonker, C. Decoupling negotiating agents to explore the space of negotiation strategies. In Novel Insights in Agent-Based Complex Automated Negotiation; Springer: Berlin/Heidelberg, Germany, 2014; pp. 61–83. [Google Scholar]
- Ito, T.; Hattori, H.; Klein, M. Multi-issue Negotiation Protocol for Agents: Exploring Nonlinear Utility Spaces. In Proceedings of the IJCAI’07: The 20th International Joint Conference on Artifical Intelligence, Hyderabad, India, 6–12 January 2007; Volume 7, pp. 1347–1352. [Google Scholar]
- Baarslag, T.; Hindriks, K.; Jonker, C.; Kraus, S.; Lin, R. The first automated negotiating agents competition (ANAC 2010). In New Trends in Agent-Based Complex Automated Negotiations; Springer: Berlin/Heidelberg, Germany, 2012; pp. 113–135. [Google Scholar]
- Fujita, K.; Ito, T.; Baarslag, T.; Hindriks, K.; Jonker, C.; Kraus, S.; Lin, R. The second automated negotiating agents competition (ANAC2011). In Complex Automated Negotiations: Theories, Models, and Software Competitions; Springer: Berlin/Heidelberg, Germany, 2013; pp. 183–197. [Google Scholar]
- Williams, C.R.; Robu, V.; Gerding, E.H.; Jennings, N.R. An overview of the results and insights from the third automated negotiating agents competition (ANAC2012). In Novel Insights in Agent-Based Complex Automated Negotiation; Springer: Berlin/Heidelberg, Germany, 2014; pp. 151–162. [Google Scholar]
- Kawaguchi, S.; Fujita, K.; Ito, T. AgentK: Compromising strategy based on estimated maximum utility for automated negotiating agents. In New Trends in Agent-Based Complex Automated Negotiations; Springer: Berlin/Heidelberg, Germany, 2012; pp. 137–144. [Google Scholar]
- Williams, C.R.; Robu, V.; Gerding, E.H.; Jennings, N.R. Iamhaggler2011: A gaussian process regression based negotiation agent. In Complex Automated Negotiations: Theories, Models, and Software Competitions; Springer: Berlin/Heidelberg, Germany, 2013; pp. 209–212. [Google Scholar]
- Adar, M.B.; Sofy, N.; Elimelech, A. Gahboninho: Strategy for balancing pressure and compromise in automated negotiation. In Complex Automated Negotiations: Theories, Models, and Software Competitions; Springer: Berlin/Heidelberg, Germany, 2013; pp. 205–208. [Google Scholar]
- Dirkzwager, A.; Hendrikx, M. An adaptive negotiation strategy for real-time bilateral negotiations. In Novel Insights in Agent-based Complex Automated Negotiation; Springer: Berlin/Heidelberg, Germany, 2014; pp. 163–170. [Google Scholar]
- Hao, J.; Leung, H.f. CUHKAgent: An adaptive negotiation strategy for bilateral negotiations over multiple items. In Novel Insights in Agent-Based Complex Automated Negotiation; Springer: Berlin/Heidelberg, Germany, 2014; pp. 171–179. [Google Scholar]
- Hindriks, K.; Jonker, C.M.; Kraus, S.; Lin, R.; Tykhonov, D. Genius: Negotiation environment for heterogeneous agents. In Proceedings of the 8th International Conference on Autonomous Agents and Multiagent Systems, Budapest, Hungary, 10–15 May 2009; pp. 1397–1398. [Google Scholar]
- Nisan, N.; Roughgarden, T.; Tardos, E.; Vazirani, V.V. Algorithmic Game Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Ioannidis, E.; Varsakelis, N.; Antoniou, I. Communication Policies in Knowledge Networks. Phys. A Stat. Mech. Its Appl. 2018, 492, 360–374. [Google Scholar] [CrossRef]
- Ioannidis, E.; Varsakelis, N.; Antoniou, I. Experts in Knowledge Networks: Central Positioning and Intelligent Selections. Phys. A Stat. Mech. Its Appl. 2018, 509, 890–905. [Google Scholar] [CrossRef]
- Ioannidis, E.; Varsakelis, N.; Antoniou, I. Intelligent Agents in Co-Evolving Knowledge Networks. Mathematics 2021, 9, 103. [Google Scholar] [CrossRef]
- Hafızoğlu, F.M.; Sen, S. The Effects of Past Experience on Trust in Repeated Human-Agent Teamwork. In Proceedings of the 17th International Conference on Autonomous Agents and MultiAgent Systems, Stockholm, Sweden, 10–15 July 2018; pp. 514–522. [Google Scholar]
- Dunin-Keplicz, B.; Verbrugge, R. Teamwork in Multi-Agent Systems: A Formal Approach; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 21. [Google Scholar]
- Torreno, A.; Onaindia, E.; Sapena, O. FMAP: Distributed cooperative multi-agent planning. Appl. Intell. 2014, 41, 606–626. [Google Scholar] [CrossRef] [Green Version]
- Nissim, R.; Brafman, R. Distributed heuristic forward search for multi-agent planning. J. Artif. Intell. Res. 2014, 51, 293–332. [Google Scholar] [CrossRef] [Green Version]
- Ruan, L.; Chen, J.; Guo, Q.; Jiang, H.; Zhang, Y.; Liu, D. A coalition formation game approach for efficient cooperative multi-UAV deployment. Appl. Sci. 2018, 8, 2427. [Google Scholar] [CrossRef] [Green Version]
- Ilany, L.; Gal, Y. Algorithm selection in bilateral negotiation. Auton. Agents Multi-Agent Syst. 2016, 30, 697–723. [Google Scholar] [CrossRef] [Green Version]
- Güneş, T.D.; Arditi, E.; Aydoğan, R. Collective voice of experts in multilateral negotiation. In Proceedings of the International Conference on Principles and Practice of Multi-Agent Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 450–458. [Google Scholar]
- Fujita, K. Efficient Strategy Adaptation for Complex Multi-times Bilateral Negotiations. In Proceedings of the Proceedings IEEE 7th International Conference on Service-Oriented Computing and Applications, SOCA 2014, Matsue, Japan, 17–19 November 2014; pp. 207–214. [Google Scholar]
- Li, P.; Luo, X.; Meng, X.; Miao, C.; He, M.; Guo, X. A two-stage win-win multiattribute negotiation model: Optimization and then concession. Comput. Intell. 2013, 29, 577–626. [Google Scholar]
- Liu, S.; Okuhara, S.; Moustafa, A.; Ito, T. An Automated Negotiating Agent that Searches the Bids Around Nash Bargaining Solution to Obtain High Joint Utilities. In Proceedings of the Annual Conference of the Japanese Society for Artificial Intelligence, Kumamoto, Japan, 9–12 June 2020; pp. 66–76. [Google Scholar]
- Amini, M.; Fathian, M.; Ghazanfari, M. A BOA-based adaptive strategy with multi-party perspective for automated multilateral negotiations. Appl. Intell. 2020, 50, 1–31. [Google Scholar] [CrossRef]
- Azaria, A.; Gal, Y.; Kraus, S.; Goldman, C.V. Strategic advice provision in repeated human-agent interactions. Auton. Agents Multi-Agent Syst. 2016, 30, 4–29. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).