Investigations for a Trajectory Variation to Improve the Energy Conversion for a Four-Stroke Free-Piston Engine
Abstract
:Featured Application
Abstract
1. Introduction
2. Consideration of the Energy Losses for Converting Chemically Stored Energy into Electrical Energy
3. Experimental Prototype
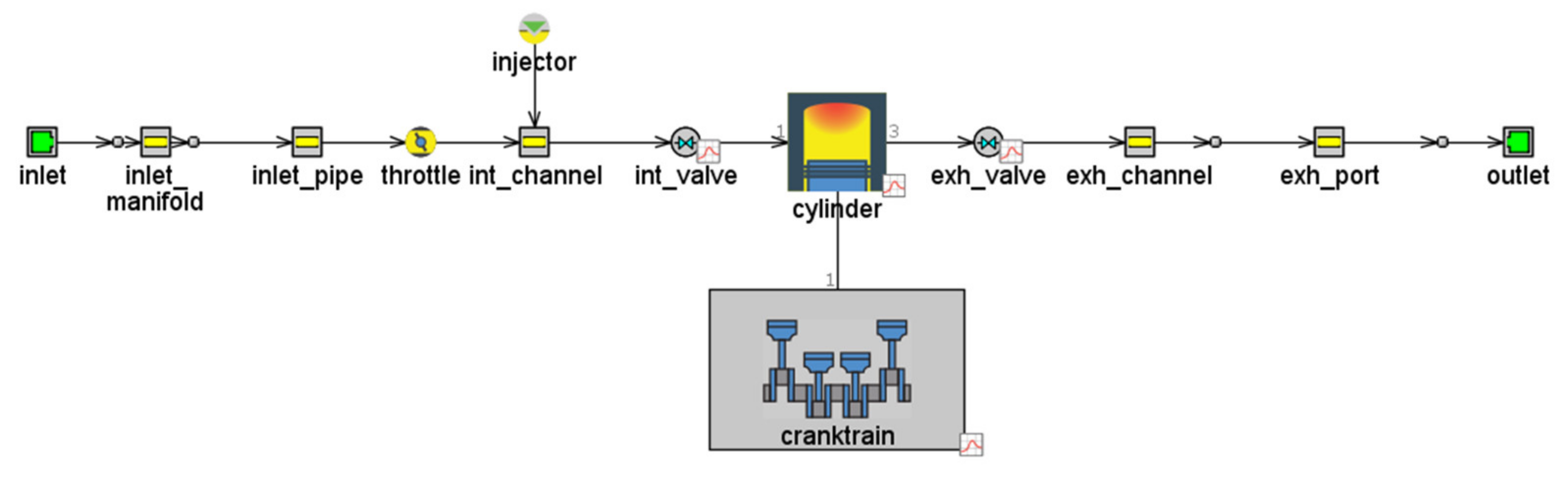
4. Thermodynamic Model of the Free-Piston Engine
5. Simulation Model of the Linear Permanent Magnet Synchronous Machine
6. Trajectory Variation
6.1. Specificity of the Free-Piston Engine
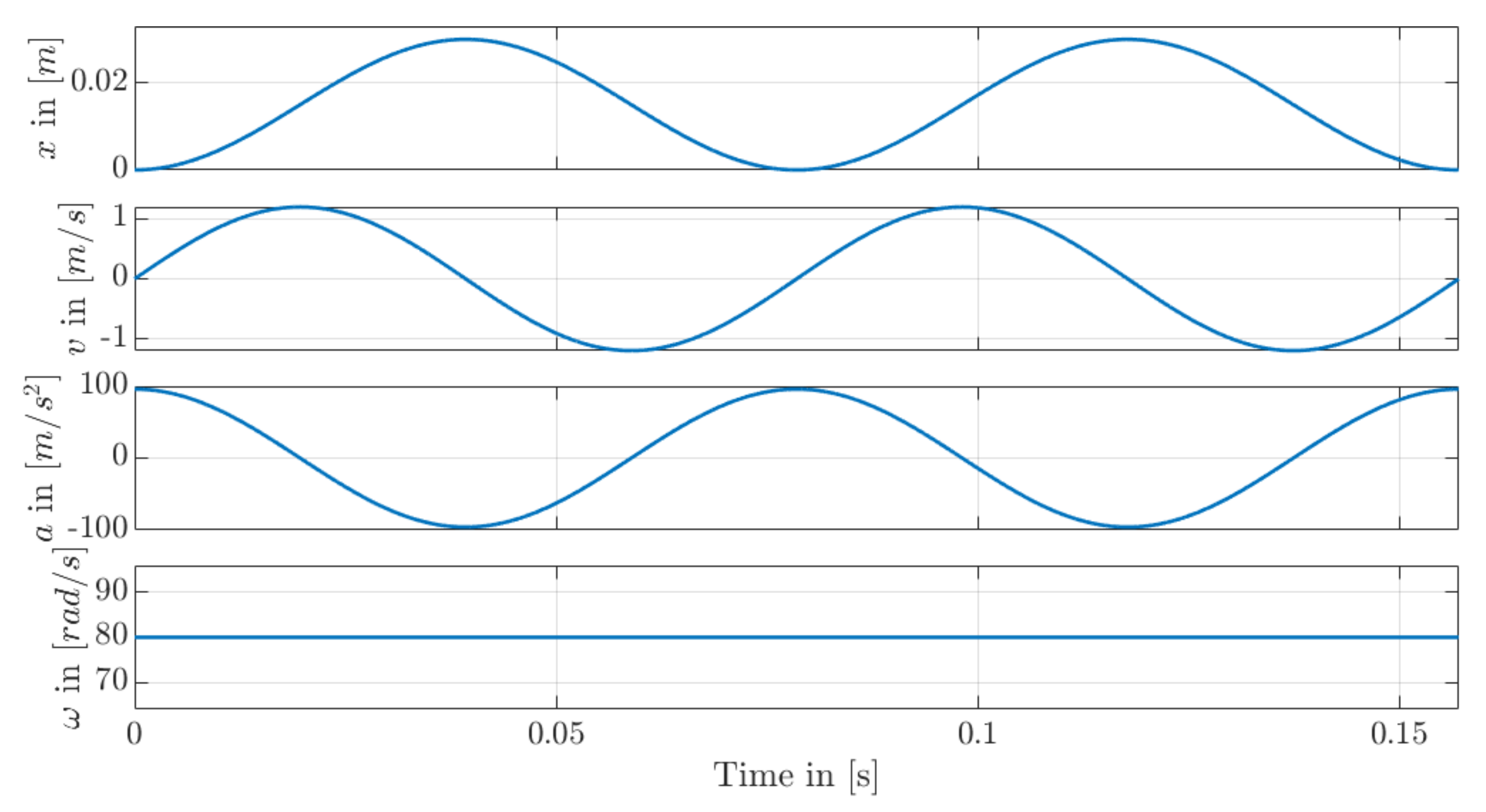
6.2. Reference Stroke
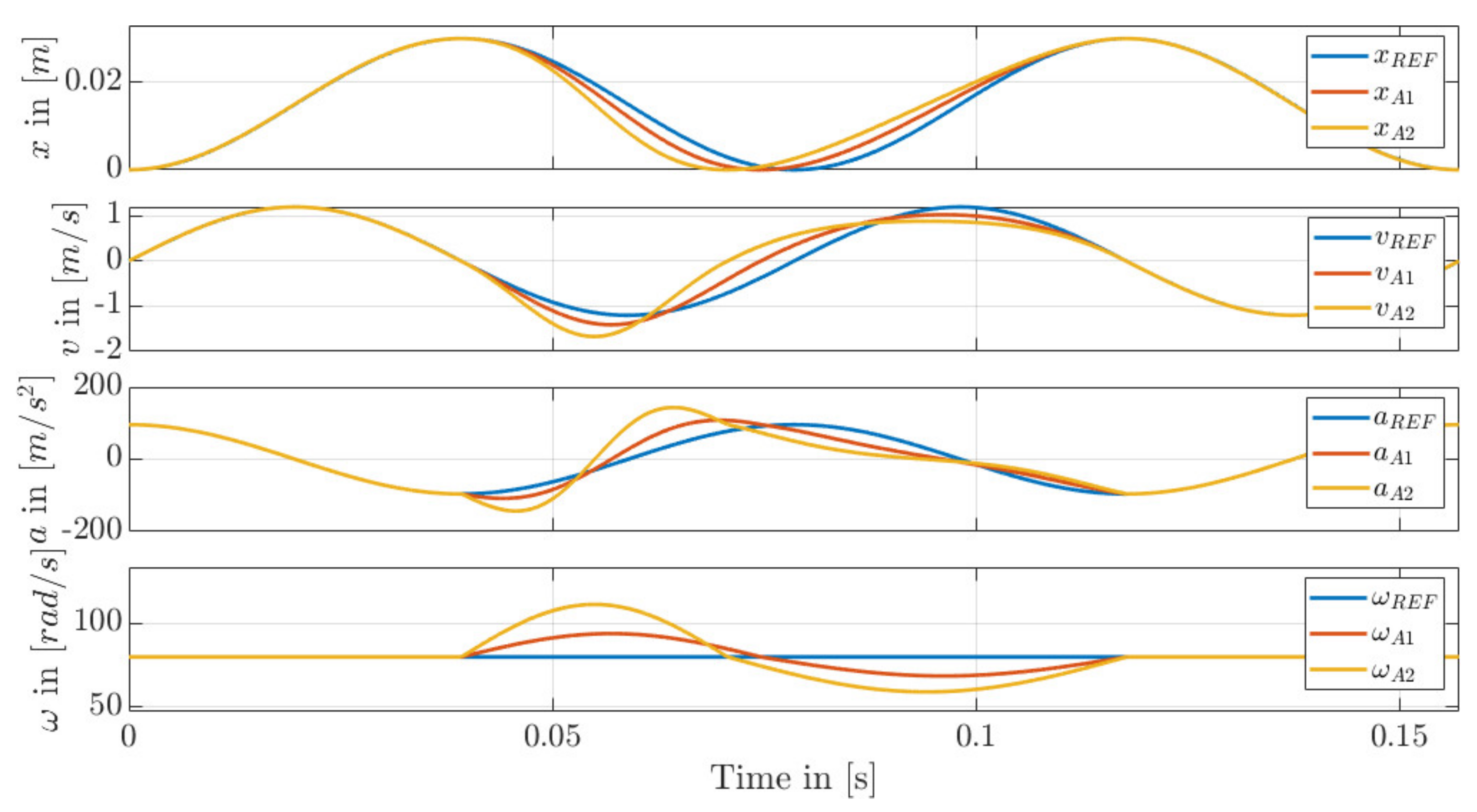
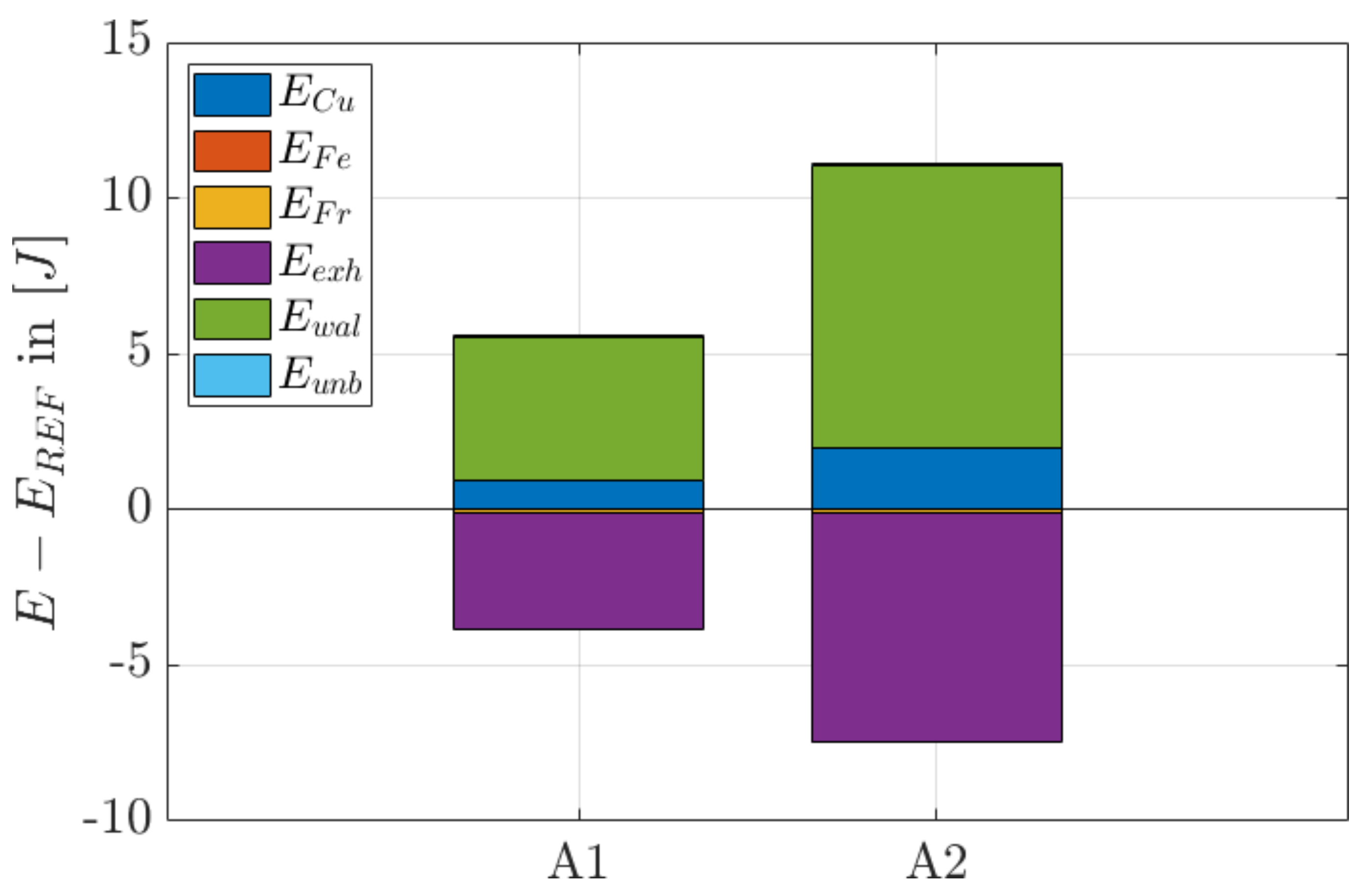
6.3. Time Displacement of the Dead Center (Trajectory A)
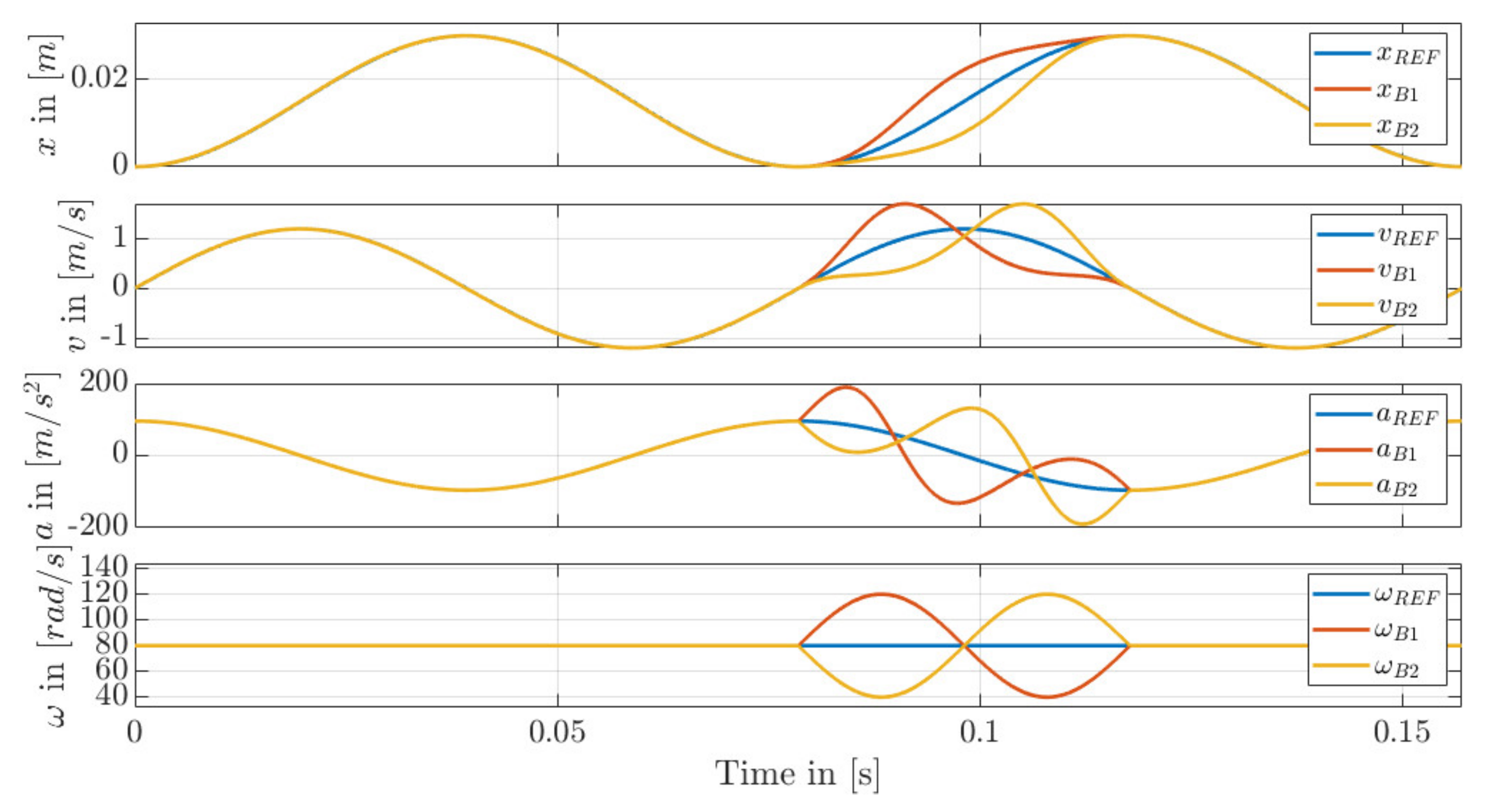
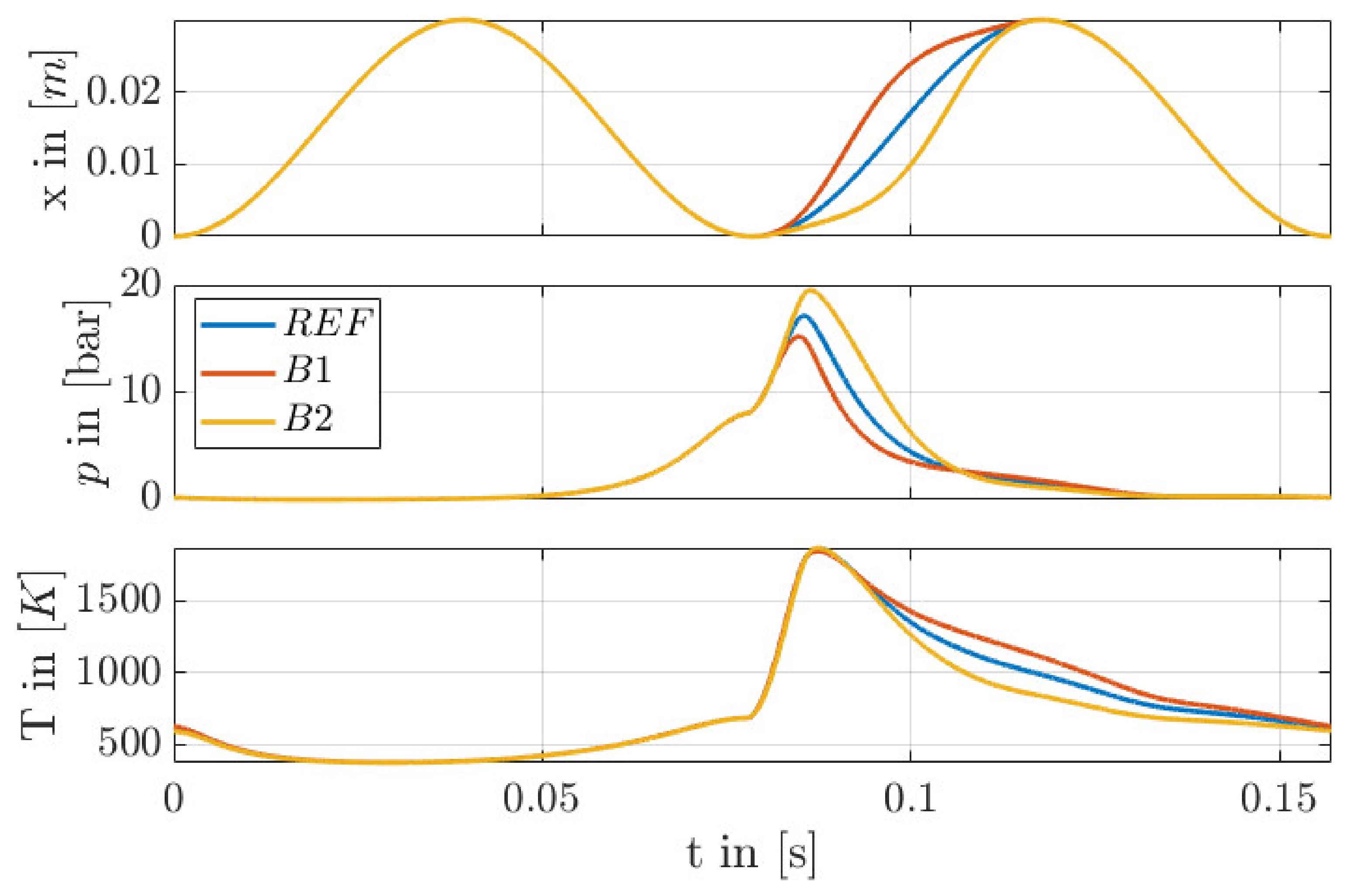
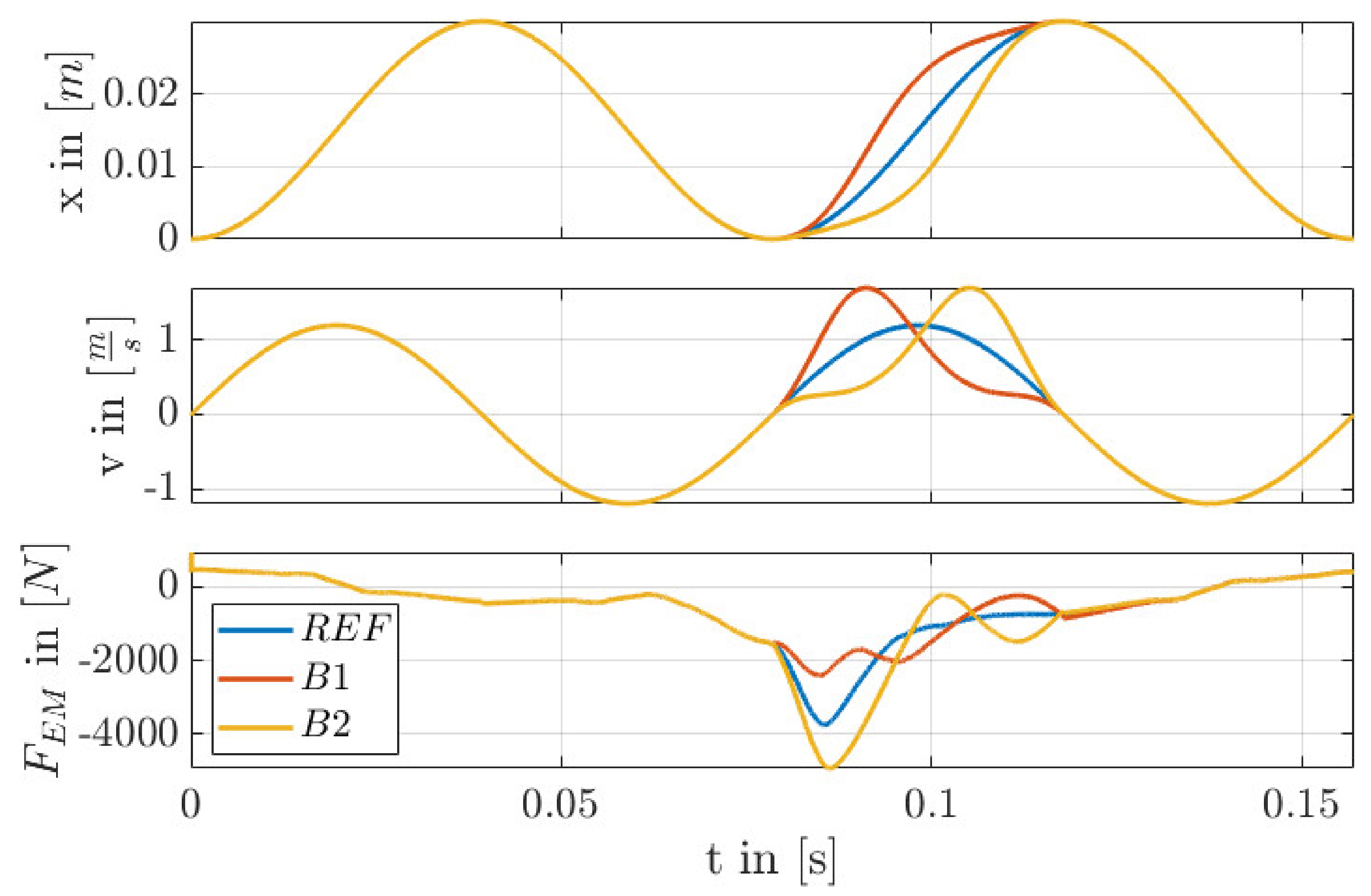
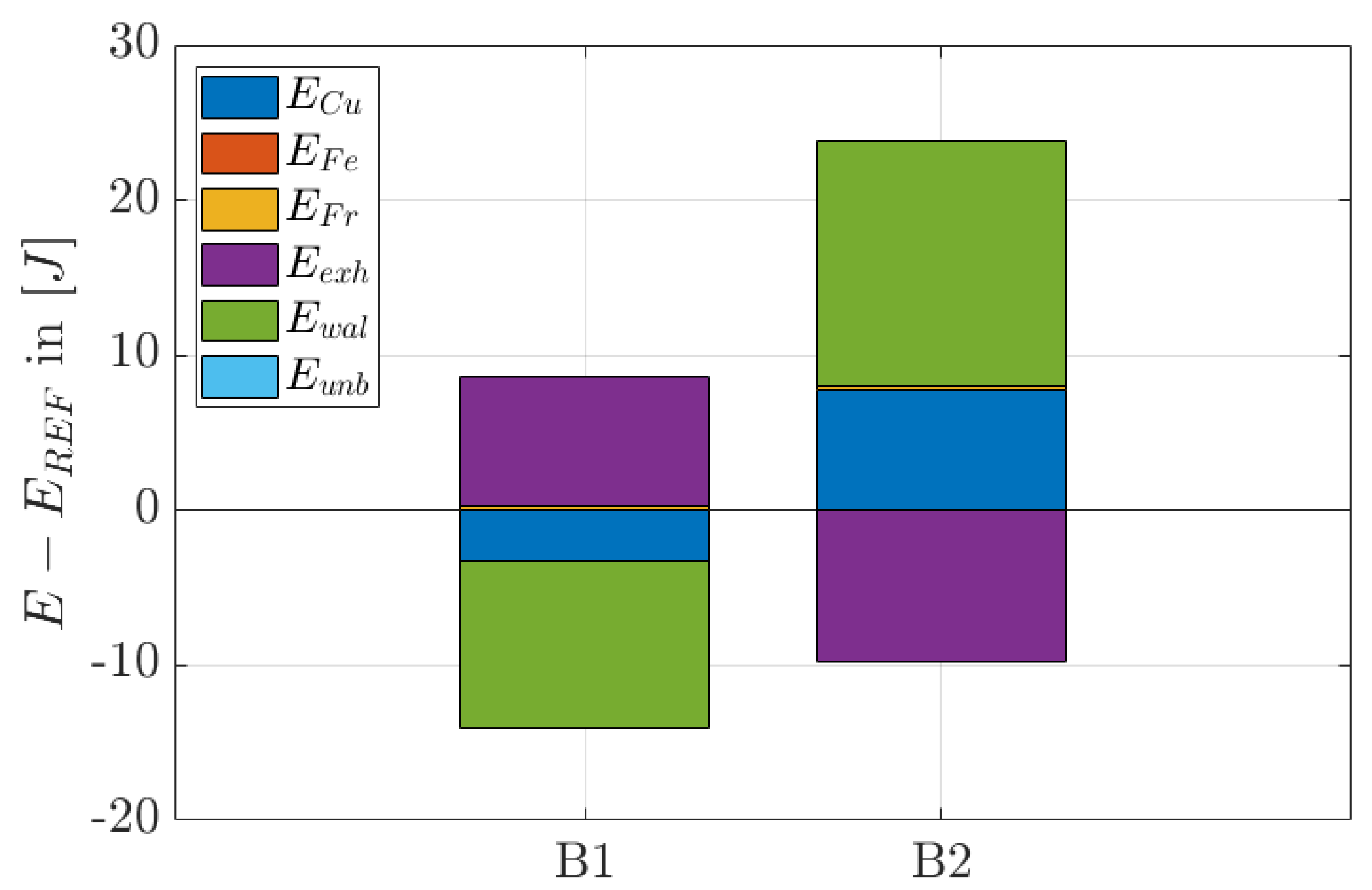
6.4. Compression and Extension of the Stroke (Trajectory B)
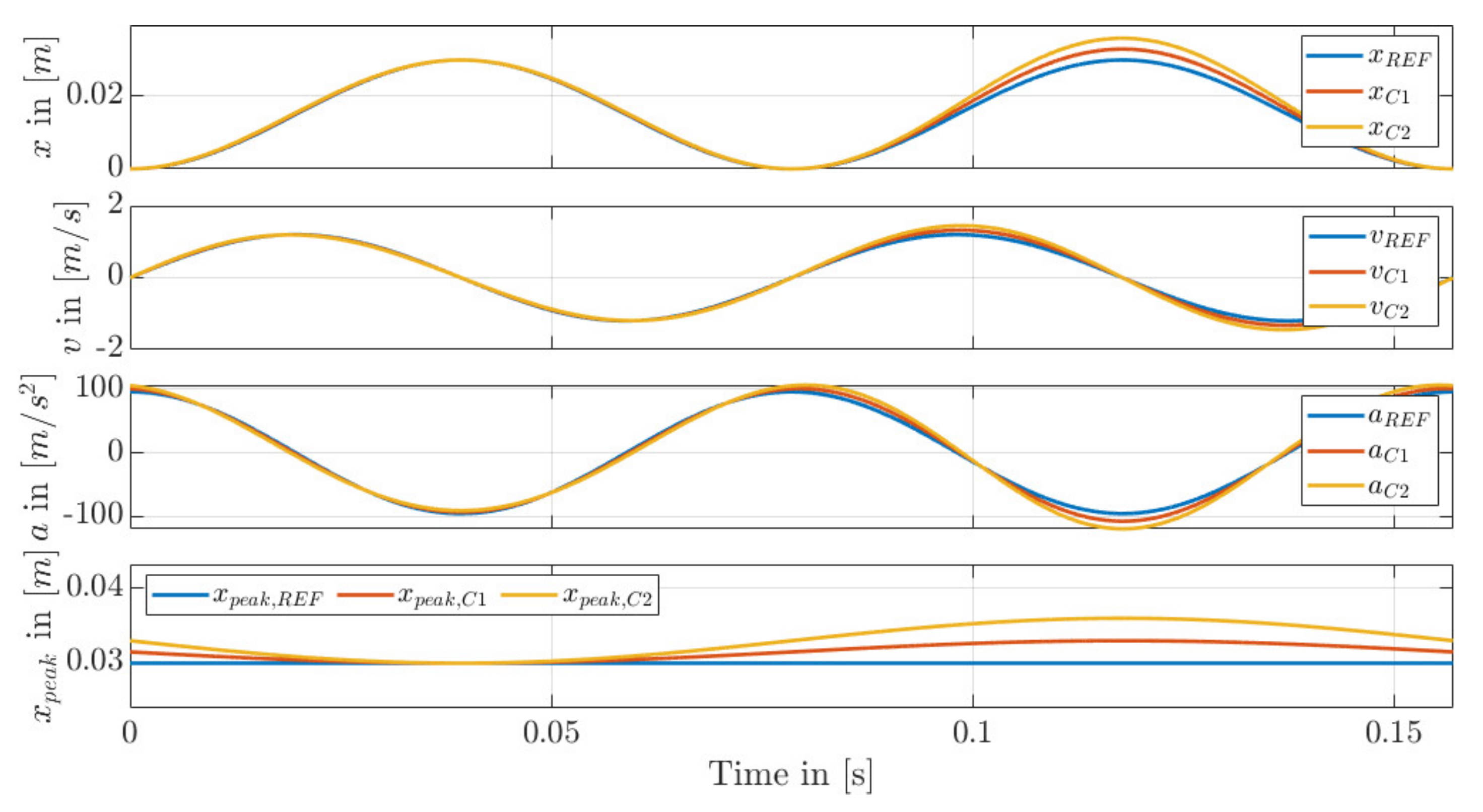
6.5. Variation of the Stroke Amplitude (Trajectory C)
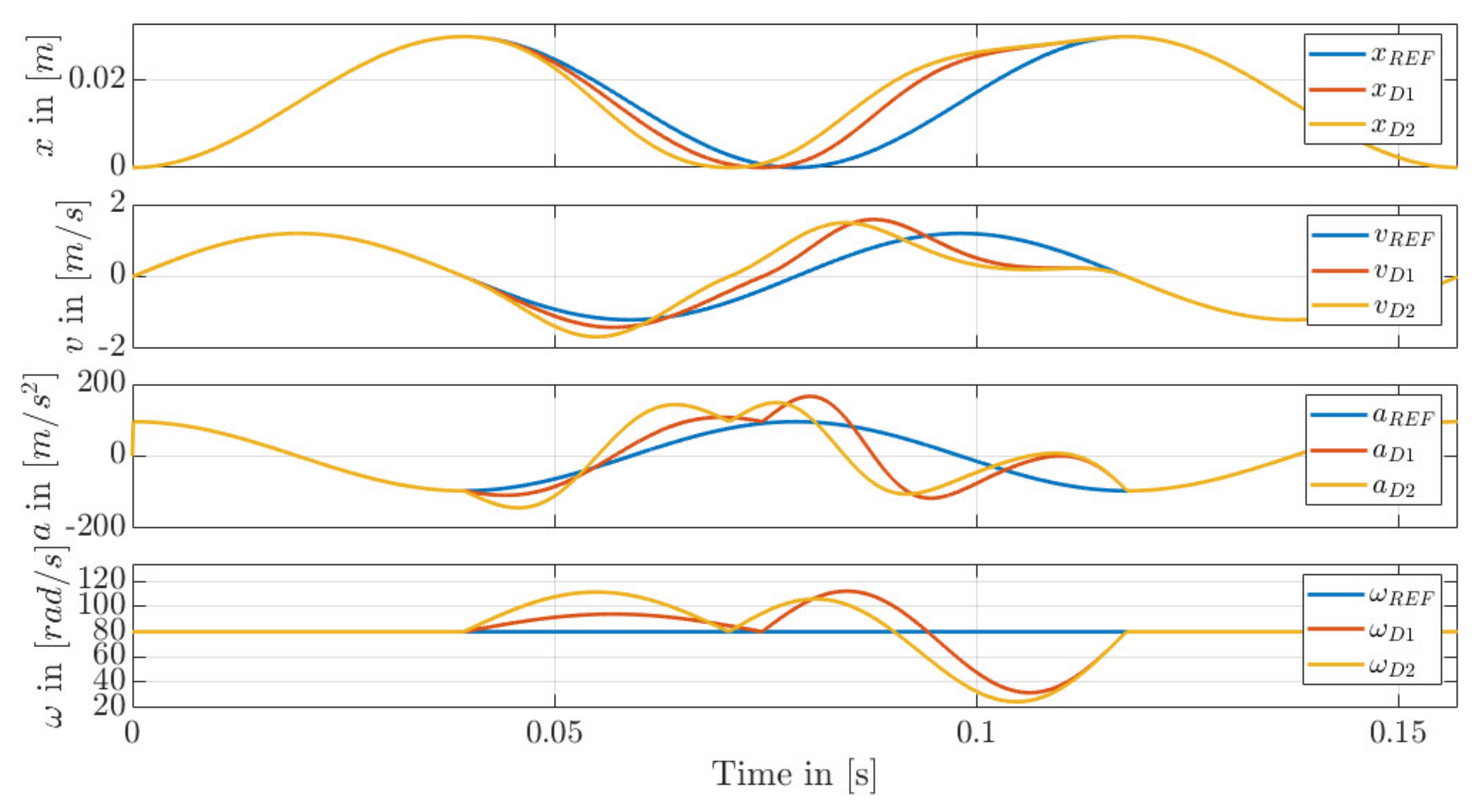
6.6. Combination of Proposed Trajectories (Trajectory D)
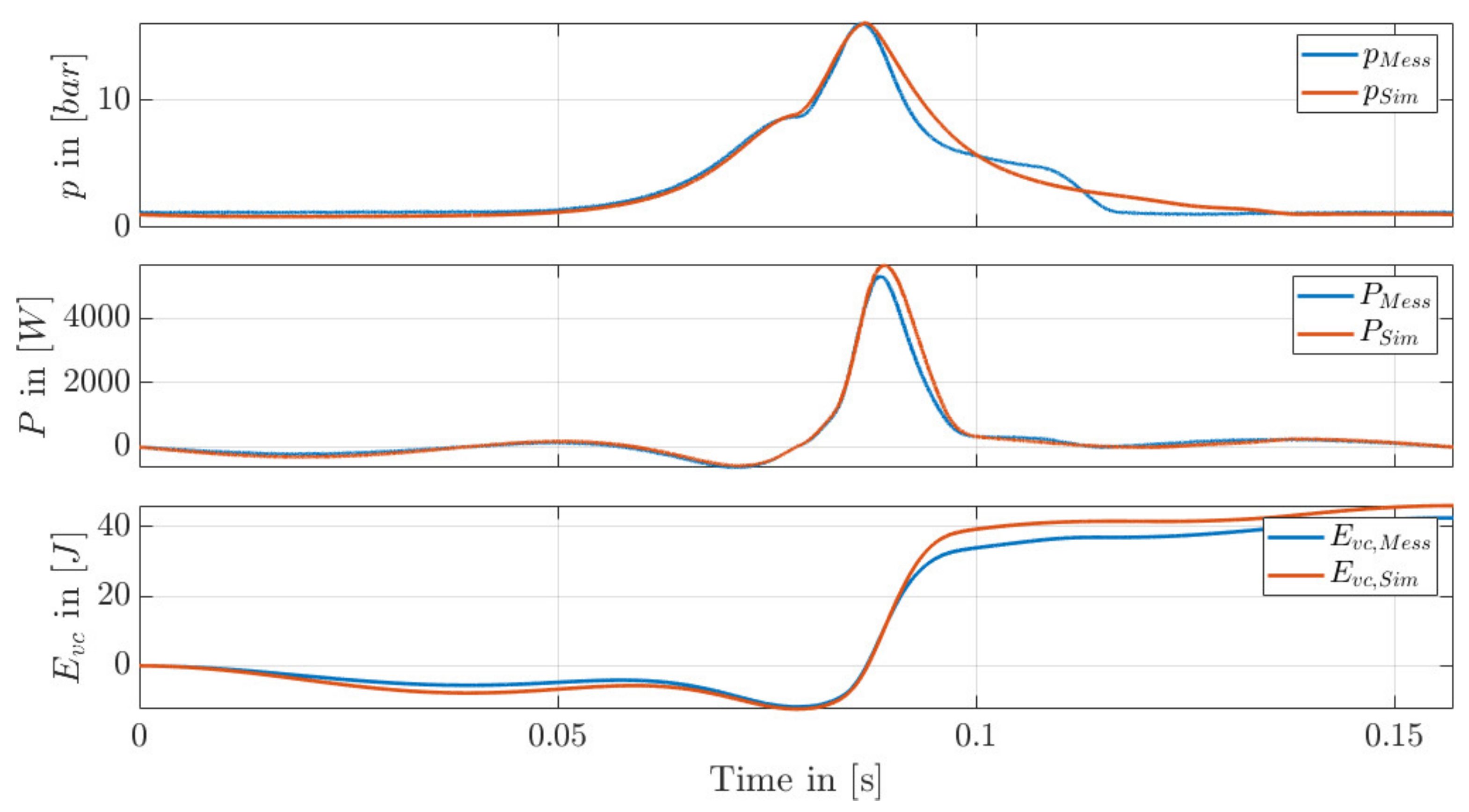
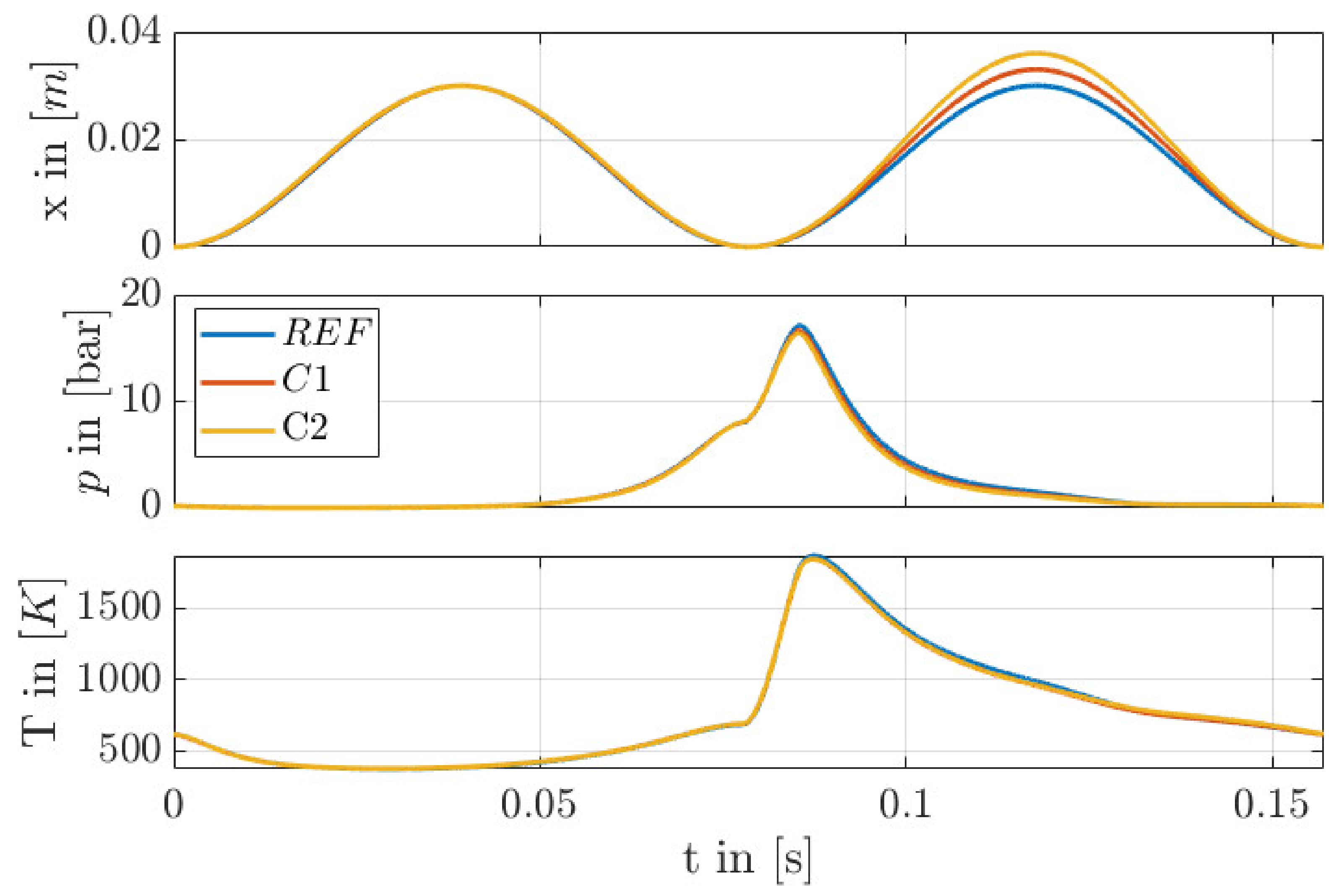
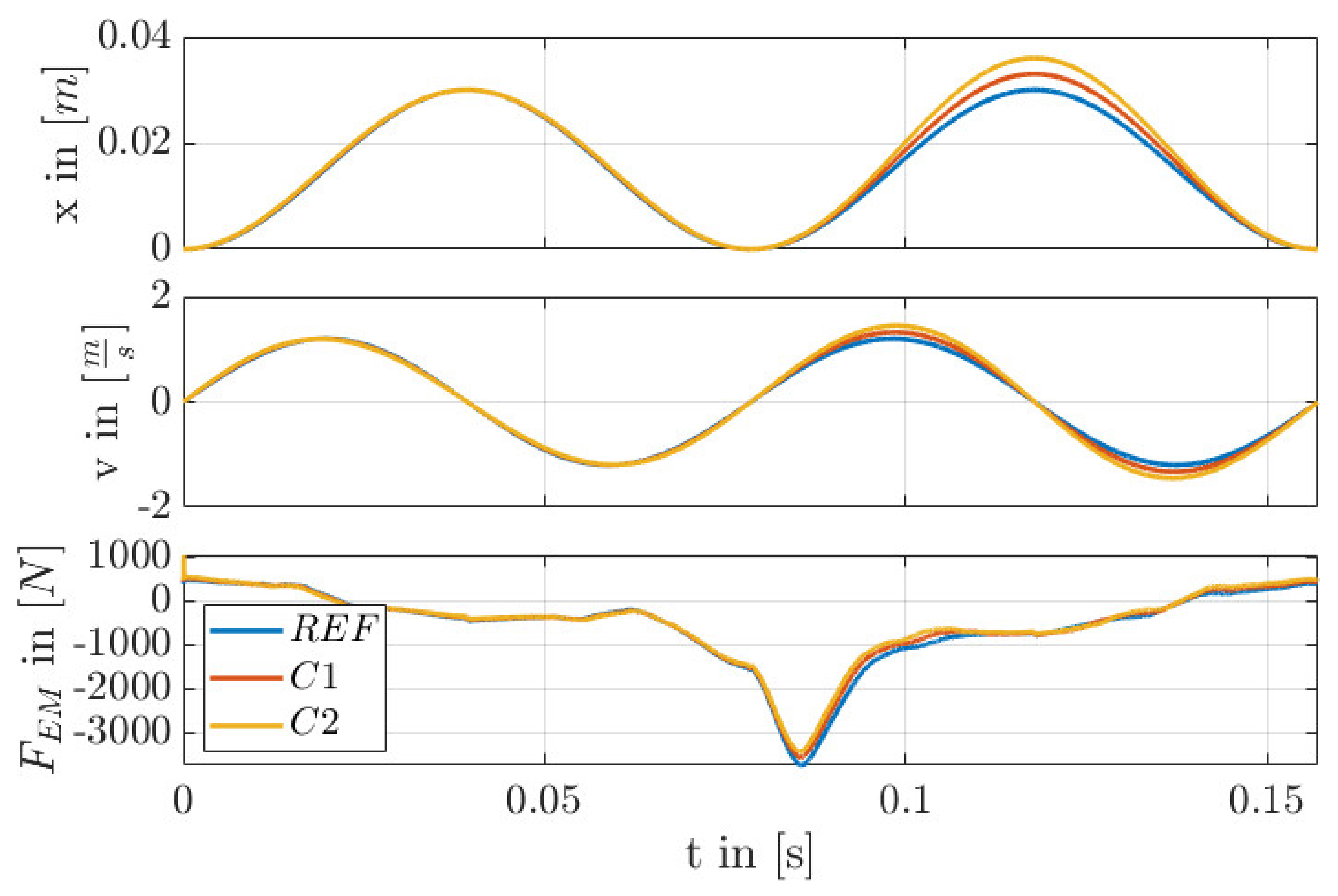
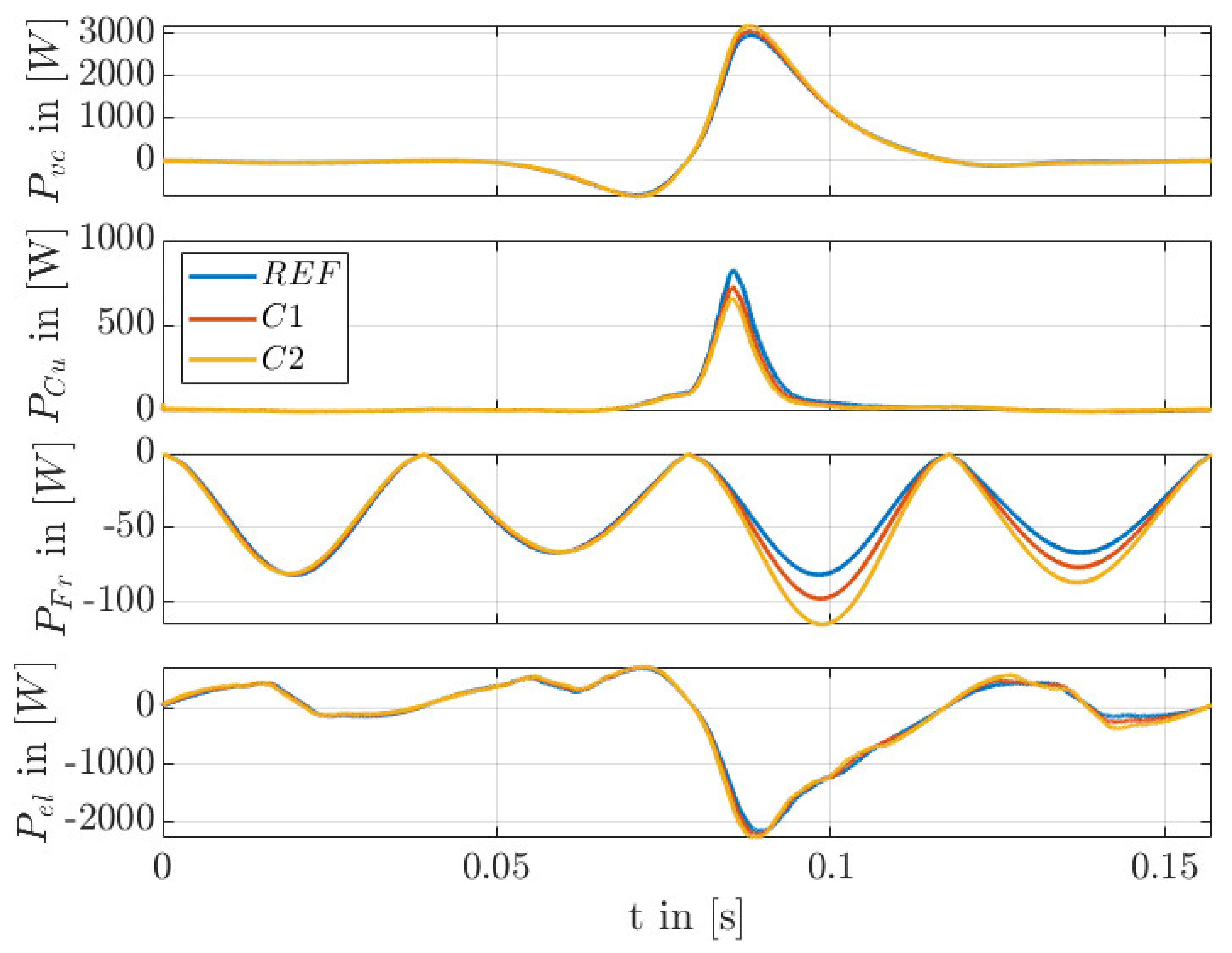
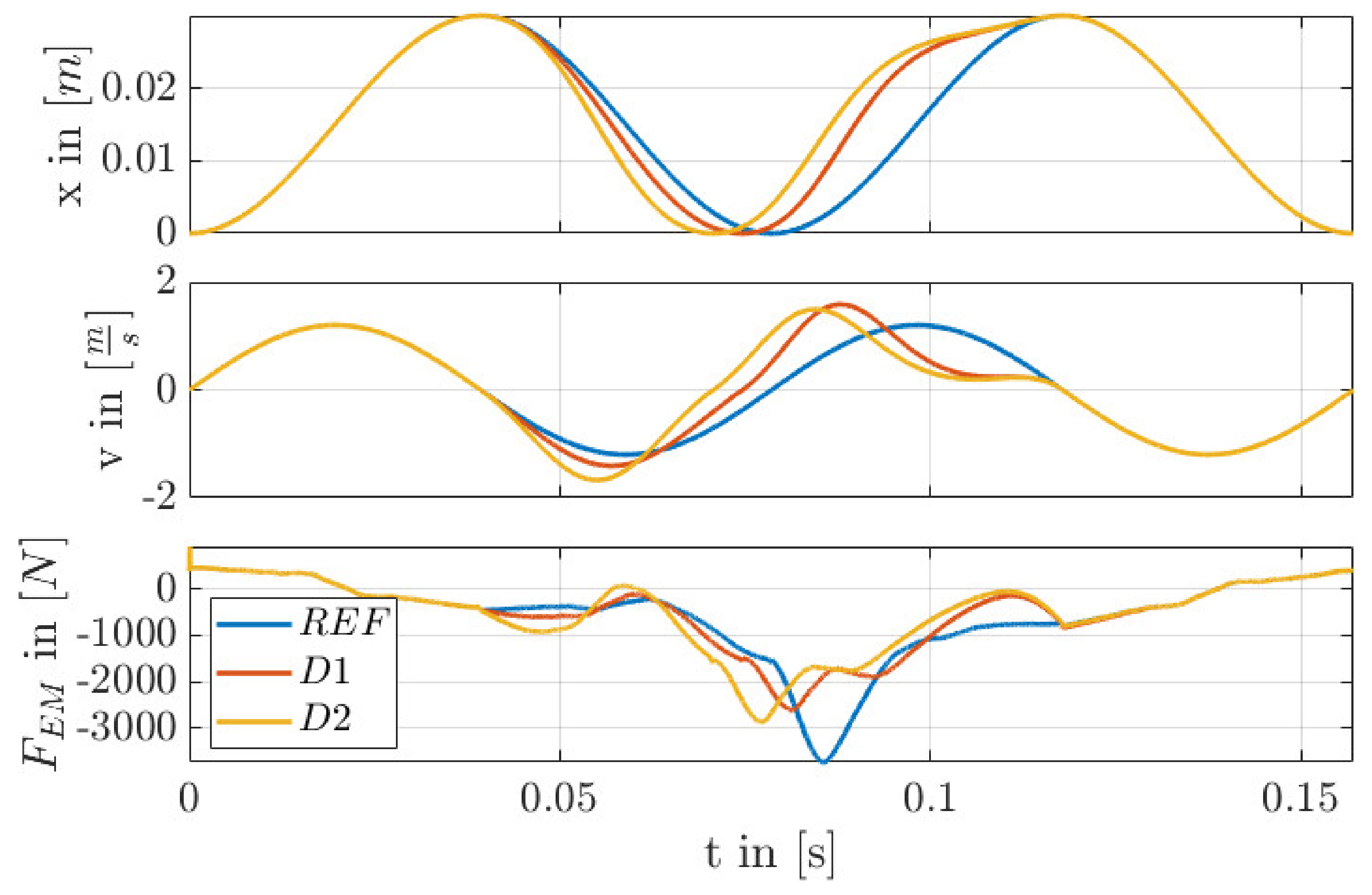
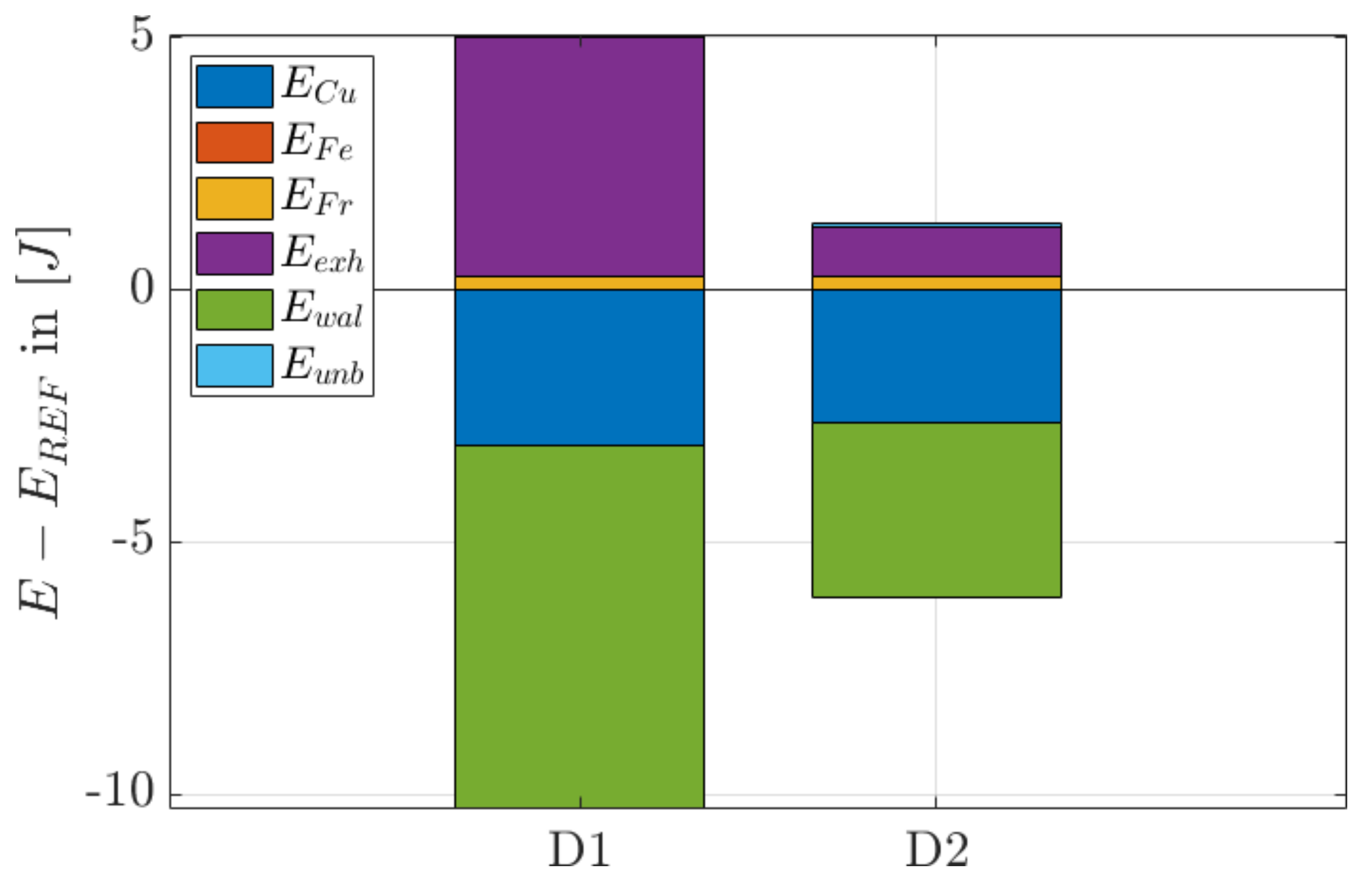
7. Results
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature and Abbreviations
| LHV | Lower heat value | Energy [J] | |
| HTC | Heat transfer coefficient | Mass [kg] | |
| PC | Personal computer | Efficiency [-] | |
| PMSM | Permanent magnet excited synchronous machine | Area [] | |
| IMEP | Indicated mean effective pressure | Temperature [K] | |
| SI-Turb | Spark-Ignition Turbulent Flame Model | Inlet temperature [K] | |
| TDCF | Top dead center firing | ||
| REF | Reference case | Outlet temperature [K] | |
| A1 | Low TDC shift | Time [s] | |
| A2 | High TDC shift | Heat transfer coefficient [W/(m2 K)] | |
| B1 | Early piston acceleration | Mean specific heat capacity [J/(kg K)] | |
| B2 | Late piston acceleration | Power [W] | |
| C1 | Low stroke amplitude change | Velocity [m/s] | |
| C2 | High stroke amplitude change | Force [N] | |
| D1 | Combination of early piston acceleration and low TDC shift | Friction coefficient [-] | |
| D2 | Combination of early piston acceleration and high TDC shift | Cylinder pressure [Pa] | |
| Stroke [m] | Current [A] | ||
| Duration of the cycle [s] | Virtual angular velocity | ||
| Relative duration change [-] | Virtual angle | ||
| Force constant [N/A] | Frequency [Hz] | ||
| Ohmic resistance [] | Magnetic flux density [T] | ||
| Voltage [V] | Equivalence ratio [-] | ||
| Unburned density [kg/m3] | Acceleration [m/s2] | ||
| Turbulent flame speed [m/s] | Laminar flame speed [m/s] | ||
| Turbulent flame speed multiplier [-] | Flame kernel growth multiplier [-] | ||
| Flame radius [m] | Integral length scale [-] | ||
| Maximum laminar speed [m/s] | Laminar speed roll-off value [m/s] | ||
| Equivalence ratio at maximum speed [m/s] | Unburned gas temperature [K] | ||
| Temperature exponent [-] | Pressure exponent [-] | ||
| Average cylinder gas velocity [m/s] | Model constant [-] |
References
- Rahman, S.M.A.; Rizwanul Fattah, I.M.; Ong, H.C.; Zamri, M.F.M.A. State-of-the-Art of Strategies to Reduce Exhaust Emissions from Diesel Engine Vehicles. Energies 2021, 14, 1766. [Google Scholar] [CrossRef]
- Burnete, N.V.; Mariasiu, F.; Moldovanu, D.; Depcik, C. Simulink Model of a Thermoelectric Generator for Vehicle Waste Heat Recovery. Appl. Sci. 2021, 11, 1340. [Google Scholar] [CrossRef]
- Woo, S.; Lee, J.; Han, Y.; Yoon, Y. Experimental Study of the Combustion Efficiency in Multi-Element Gas-Centered Swirl Coaxial Injectors. Energies 2020, 13, 6055. [Google Scholar] [CrossRef]
- Chen, P.-T.; Yang, C.-J.; Huang, K.D. Dynamic Simulation and Control of a New Parallel Hybrid Power System. Appl. Sci. 2020, 10, 5467. [Google Scholar] [CrossRef]
- Gerlach, A.; Fritsch, M.; Benecke, S.; Rottengruber, H.; Leidhold, R. Variable Valve Timing With Only One Camshaft Actuator for a Single-Cylinder Engine. IEEE/ASME Trans. Mechatron. 2019, 24, 1839–1850. [Google Scholar] [CrossRef]
- Wrobel, R.; Sierzputowski, G.; Sroka, Z.; Dimitrov, R. Comparison of Diesel Engine Vibroacoustic Properties Powered by Bio and Standard Fuel. Energies 2021, 14, 1478. [Google Scholar] [CrossRef]
- Sato, M.; Goto, T.; Zheng, J.; Irie, S. Resonant Combustion Start Considering Potential Energy of Free-Piston Engine Generator. Energies 2020, 13, 5754. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, H.; Zuo, Z. Numerical Investigation of a Free-Piston Hydrogen-Gasoline Engine Linear Generator. Energies 2020, 13, 4685. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, Z.; Liu, S.; Liu, L. Effects of Injector Spray Angle on Performance of an Opposed-Piston Free-Piston Engine. Energies 2020, 13, 3735. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, Z.; Sun, Y.; Liu, L. Electromagnetic Characteristics Analysis of a Tubular Moving Magnet Linear Generator System. Appl. Sci. 2020, 10, 3713. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, Z.; Yang, L.; Liu, L. Electromagnetic Loss Analysis of a Linear Motor System Designed for a Free-Piston Engine Generator. Electronics 2020, 9, 621. [Google Scholar] [CrossRef] [Green Version]
- Graef, M.; Treffinger, P.; Pohl, S.-E.; Rinderknecht, F. Investigation of a high efficient Free Piston Linear Generator with variable Stroke and variable Compression Ratio A new Approach for Free Piston Engines. World Electr. Veh. J. 2007, 1, 116–120. [Google Scholar] [CrossRef] [Green Version]
- Kock, F.; Haag, J.; Friedrich, H.E. The Free Piston Linear Generator-Development of an Innovative, Compact, Highly Efficient Range-Extender Module. In SAE 2013 World Congress & Exhibition, APR. 16; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2013. [Google Scholar]
- Kosaka, H.; Akita, T.; Moriya, K.; Goto, S.; Hotta, Y.; Umeno, T.; Nakakita, K. Development of Free Piston Engine Linear Generator System Part 1-Investigation of Fundamental Characteristics. In SAE 2014 World Congress & Exhibition, APR. 08; SAE International400 Commonwealth Drive: Warrendale, PA, USA, 2014. [Google Scholar]
- Virsik, R.; Heron, A. Free piston linear generator in comparison to other range-extender technologies. World Electr. Veh. J. 2013, 6, 426–432. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Chen, F.; Li, L.; Xu, Z.; Liu, L.; Yang, G.; Lian, H.; Tian, Y. A Free-Piston Linear Generator Control Strategy for Improving Output Power. Energies 2018, 11, 135. [Google Scholar] [CrossRef] [Green Version]
- Gerlach, A.; Rottengruber, H.; Leidhold, R. Control of a Directly Driven Four-Stroke Free Piston Engine. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 4525–4530, ISBN 978-1-5090-6684-1. [Google Scholar]
- Li, K.; Zhang, C.; Sun, Z. Precise piston trajectory control for a free piston engine. Control Eng. Pract. 2015, 34, 30–38. [Google Scholar] [CrossRef]
- Vu, D.N.; Lim, O. Piston motion control for a dual free piston linear generator: Predictive-fuzzy logic control approach. J. Mech. Sci. Technol. 2020, 34, 4785–4795. [Google Scholar] [CrossRef]
- Bashir, A.; Zulkifli, S.A.; Abidin, E.Z.Z.; Aziz, A.R.A. Control of Piston Trajectory in a Free-Piston Linear Electric Generator by Load Current Modulation. In Proceedings of the 2020 IEEE Student Conference on Research and Development (SCOReD), Batu Pahat, Malaysia, 27–29 September 2020; pp. 465–470, ISBN 978-1-7281-9317-5. [Google Scholar]
- Zhang, C.; Li, K.; Sun, Z. Modeling of piston trajectory-based HCCI combustion enabled by a free piston engine. Appl. Energy 2015, 139, 313–326. [Google Scholar] [CrossRef]
- Kim, J.; Bae, C.; Kim, G. Simulation on the effect of the combustion parameters on the piston dynamics and engine performance using the Wiebe function in a free piston engine. Appl. Energy 2013, 107, 446–455. [Google Scholar] [CrossRef]
- Feng, H.; Guo, C.; Yuan, C.; Guo, Y.; Zuo, Z.; Roskilly, A.P.; Jia, B. Research on combustion process of a free piston diesel linear generator. Appl. Energy 2016, 161, 395–403. [Google Scholar] [CrossRef]
- Yuan, C.; Feng, H.; He, Y.; Xu, J. Combustion characteristics analysis of a free-piston engine generator coupling with dynamic and scavenging. Energy 2016, 102, 637–649. [Google Scholar] [CrossRef]
- Chiang, C.-J.; Yang, J.-L.; Lan, S.-Y.; Shei, T.-W.; Chiang, W.-S.; Chen, B.-L. Dynamic modeling of a SI/HCCI free-piston engine generator with electric mechanical valves. Appl. Energy 2013, 102, 336–346. [Google Scholar] [CrossRef]
- Jia, B.; Smallbone, A.; Feng, H.; Tian, G.; Zuo, Z.; Roskilly, A.P. A fast response free-piston engine generator numerical model for control applications. Appl. Energy 2016, 162, 321–329. [Google Scholar] [CrossRef]
- Arshad, W.M.; Thelin, P.; Backstrom, T.; Sadarangani, C. Use of Transverse-Flux Machines in a Free-Piston Generator. IEEE Trans. Ind. Applicat. 2004, 40, 1092–1100. [Google Scholar] [CrossRef]
- Xu, Z.; Chang, S. Improved Moving Coil Electric Machine for Internal Combustion Linear Generator. IEEE Trans. Energy Convers. 2010, 25, 281–286. [Google Scholar] [CrossRef]
- Benecke, S.; Gerlach, A.; Leidhold, R. Design Principle for Linear Electrical Machines to Minimize Power Loss in Periodic Motions. IEEE Trans. Ind. Applicat. 2020, 56, 4820–4828. [Google Scholar] [CrossRef]
- Zhang, C.; Sun, Z. Trajectory-based combustion control for renewable fuels in free piston engines. Appl. Energy 2017, 187, 72–83. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Yuan, C.; He, Y.; Wang, R. An optimization of free-piston engine generator combustion using variable piston motion. Adv. Mech. Eng. 2017, 9, 168781401772087. [Google Scholar] [CrossRef]
- Tipler, P.A.; Mosca, G. Physics for Scientists and Engineers: With Modern Physics, 6th ed.; Extended Version; Chapter 1–41; Freeman: New York, NY, USA, 2008; ISBN 1429202653. [Google Scholar]
- Rinderknecht, F. A highly efficient energy converter for a hybrid vehicle concept-focused on the linear generator of the next generation. In Proceedings of the 8th International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER), Grimaldi Forum, Monte Carlo, Monaco, 27–30 March 2013; IEEE: Piscataway, NJ, USA, 2013; ISBN 9781467352710. [Google Scholar]
- Li, Q.-F.; Xiao, J.; Huang, Z. Flat-type permanent magnet linear alternator: A suitable device for a free piston linear alternator. J. Zhejiang Univ. Sci. A 2009, 10, 345–352. [Google Scholar] [CrossRef]
- Zhang, B. Modellierung und Hocheffiziente Berechnung der Lastabhängigen Eisenverluste in Permanentmagneterregten Synchronmaschinen; KIT Scientific Publishing: Karlsruhe, Germany, 2019. [Google Scholar]
- Rhodes, D.B.; Keck, J.C. Laminar Burning Speed Measurements of Indolene-Air-Diluent Mixtures at High Pressures and Temperatures. In SAE International Congress and Exposition, FEB. 25; SAE International: Warrendale, PA, USA, 1985. [Google Scholar]
- Gamma Technologies LLC. GT-SUITE-Engine Performance-Application Manual; Gamma Technologies LLC: Westmont, IL, USA, 2019. [Google Scholar]

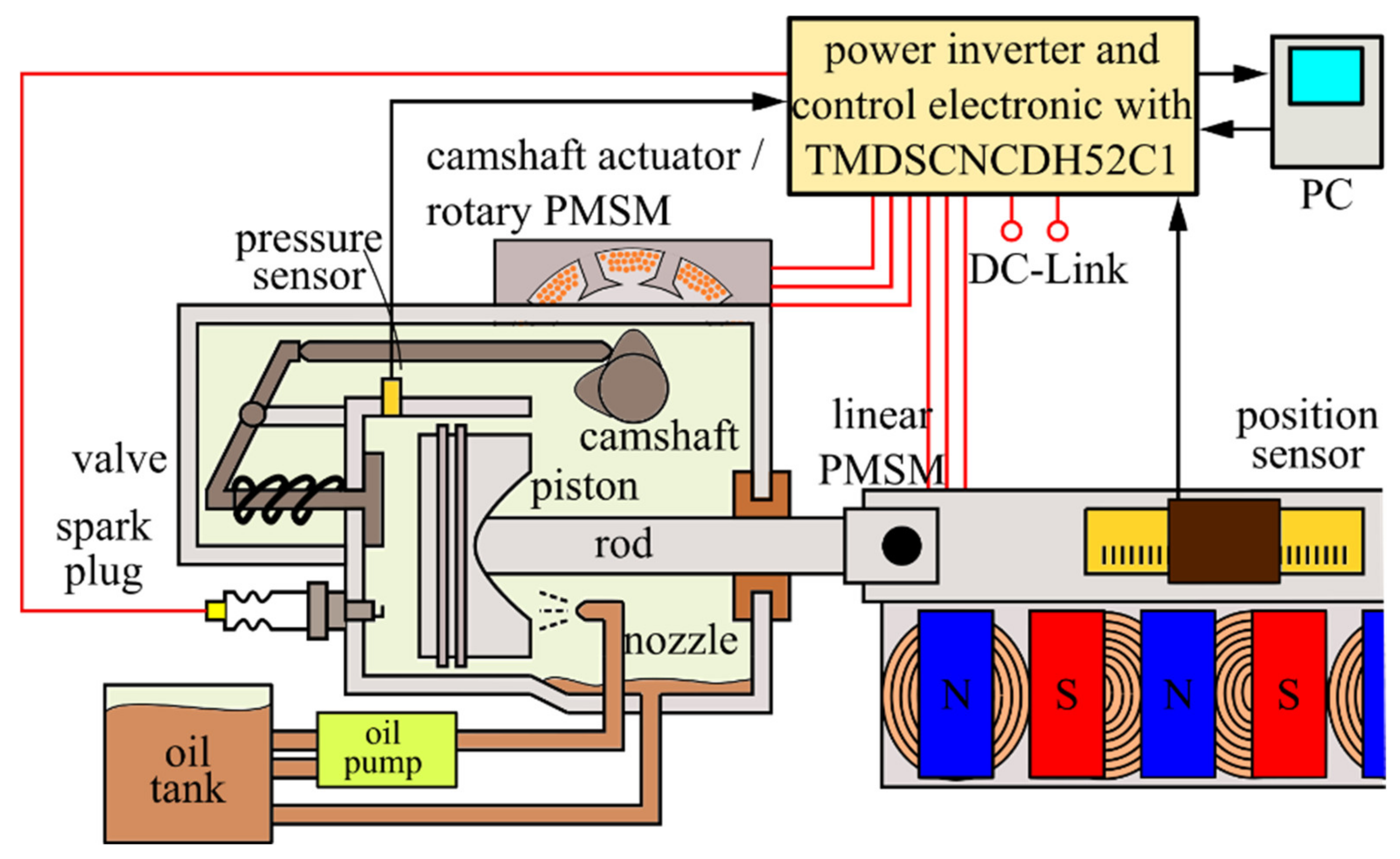
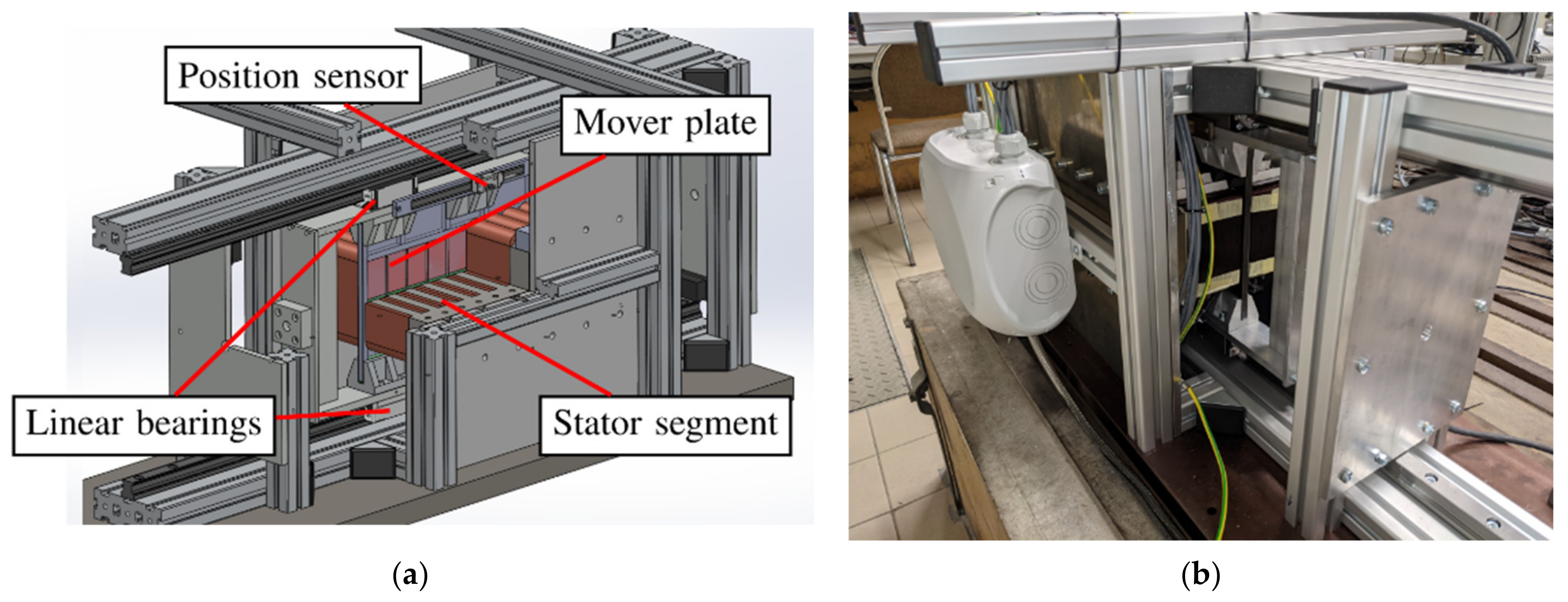
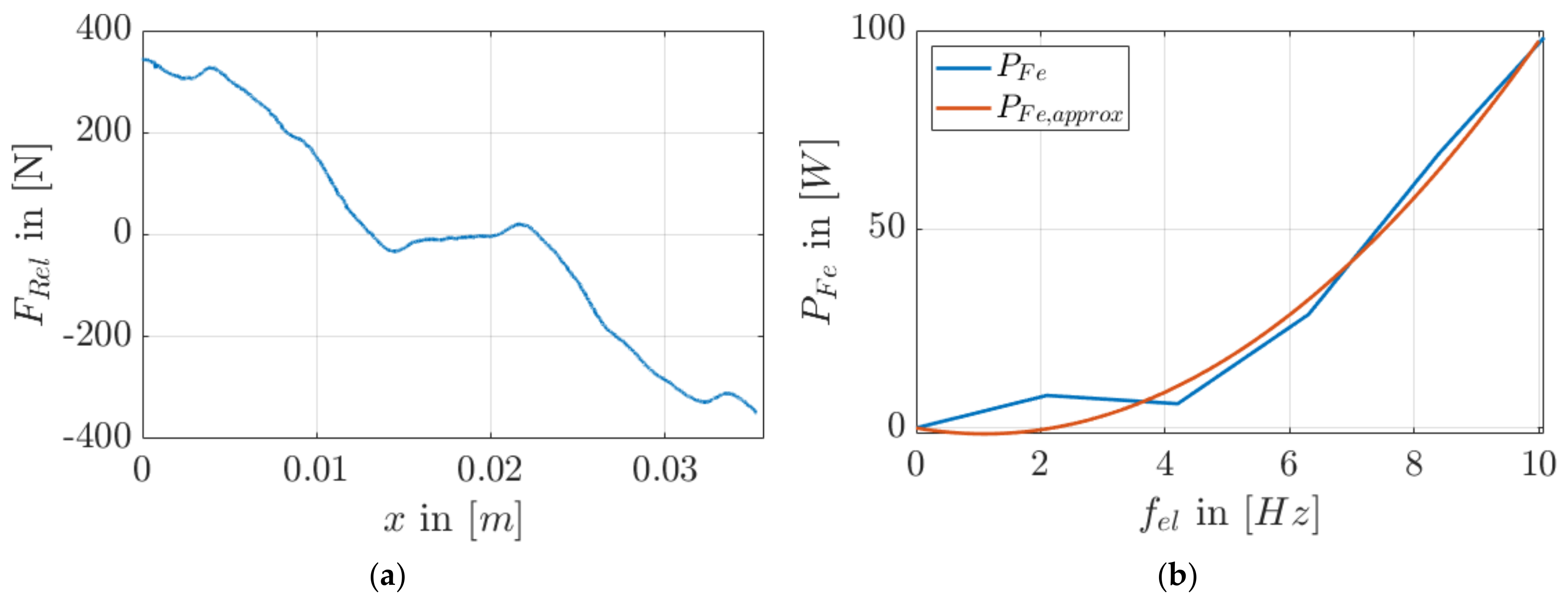
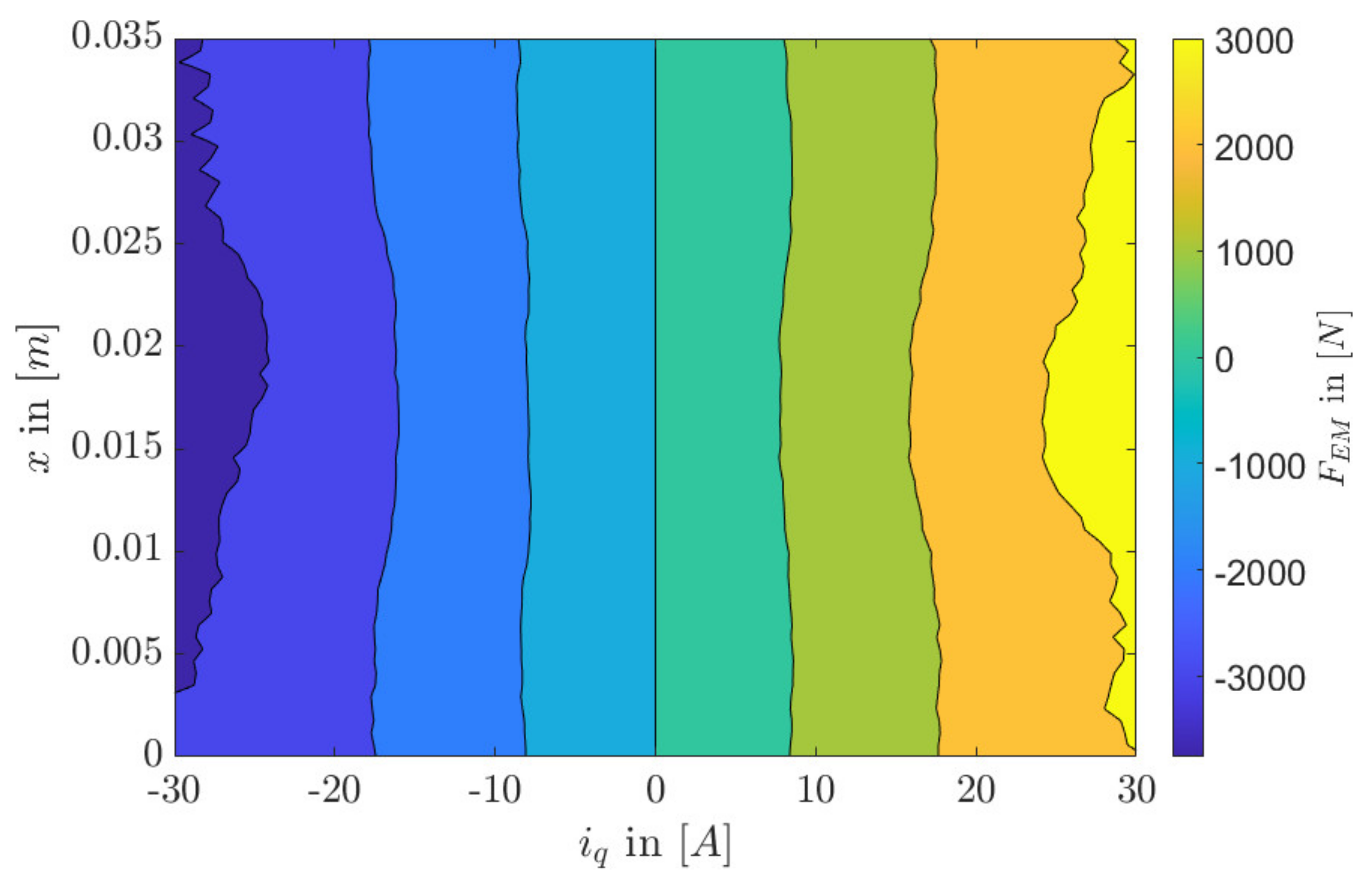

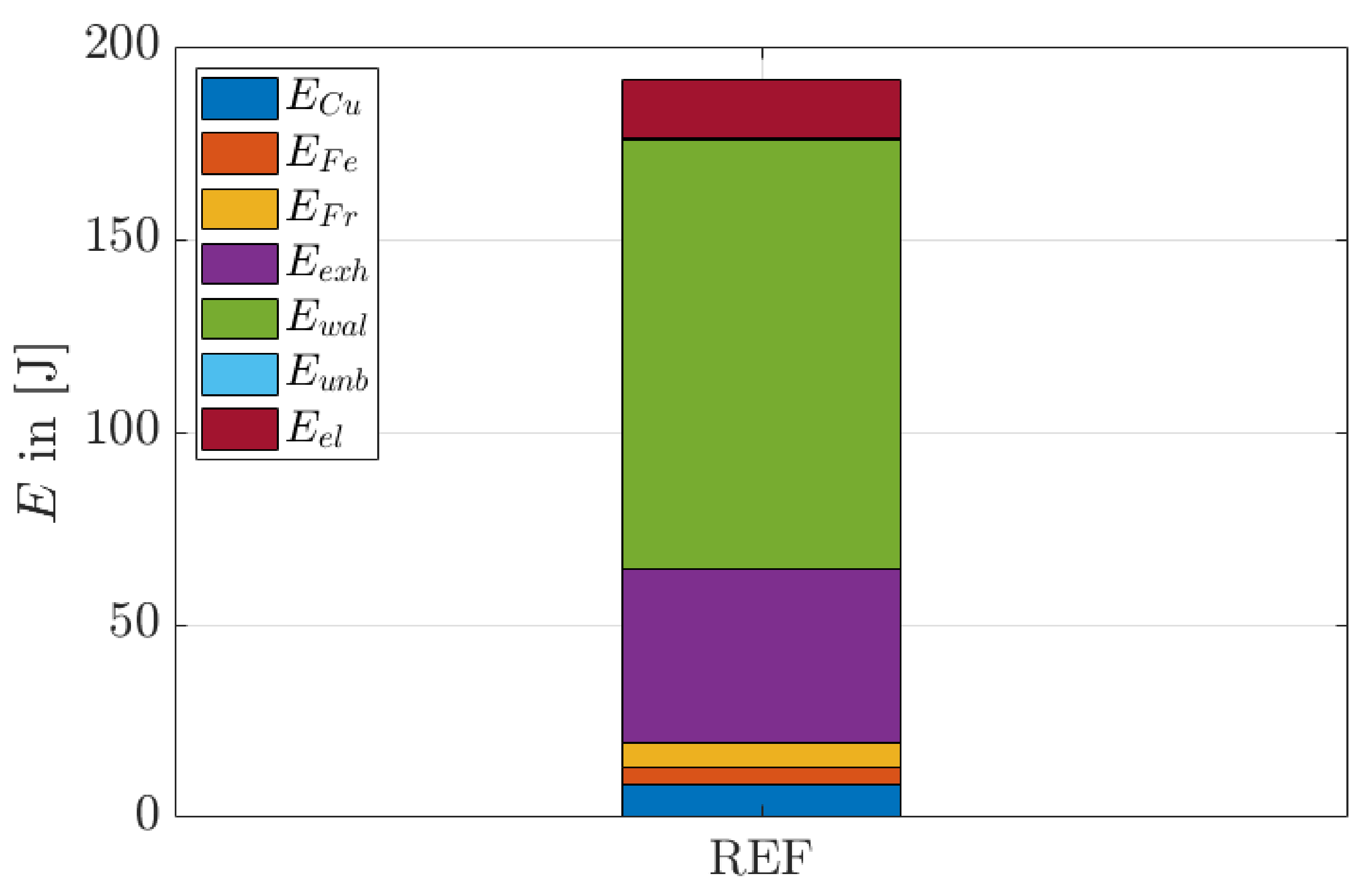
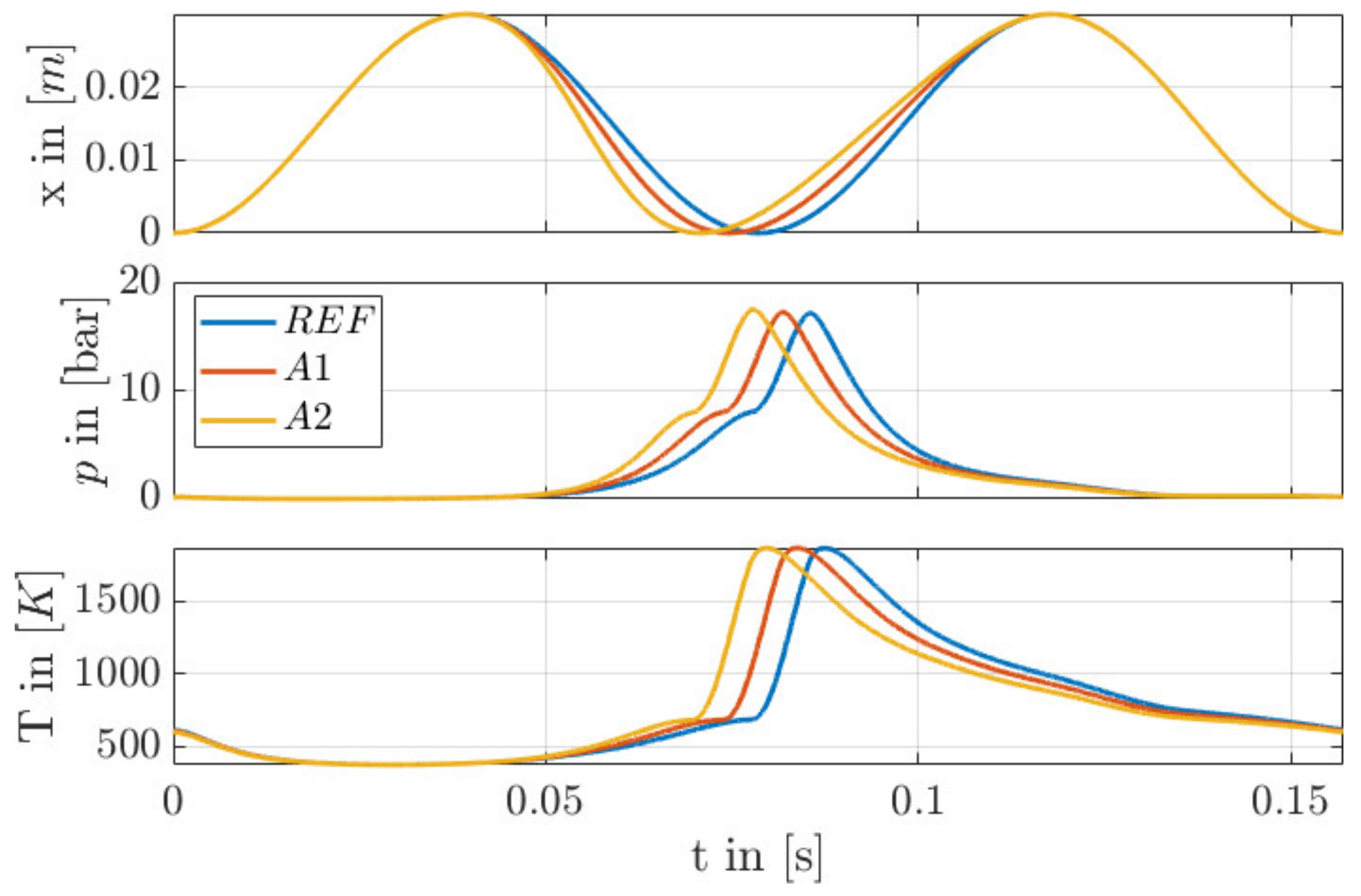
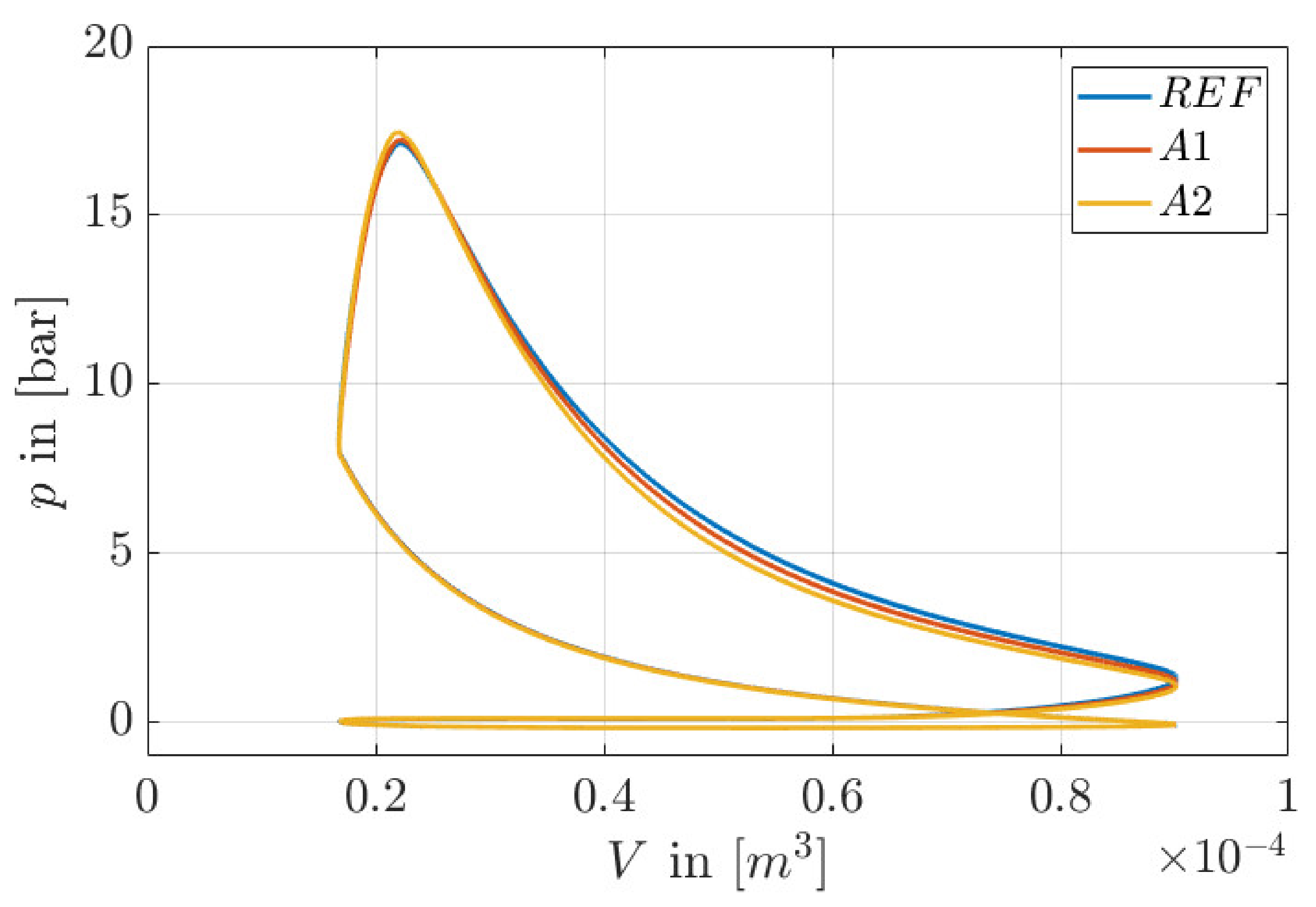
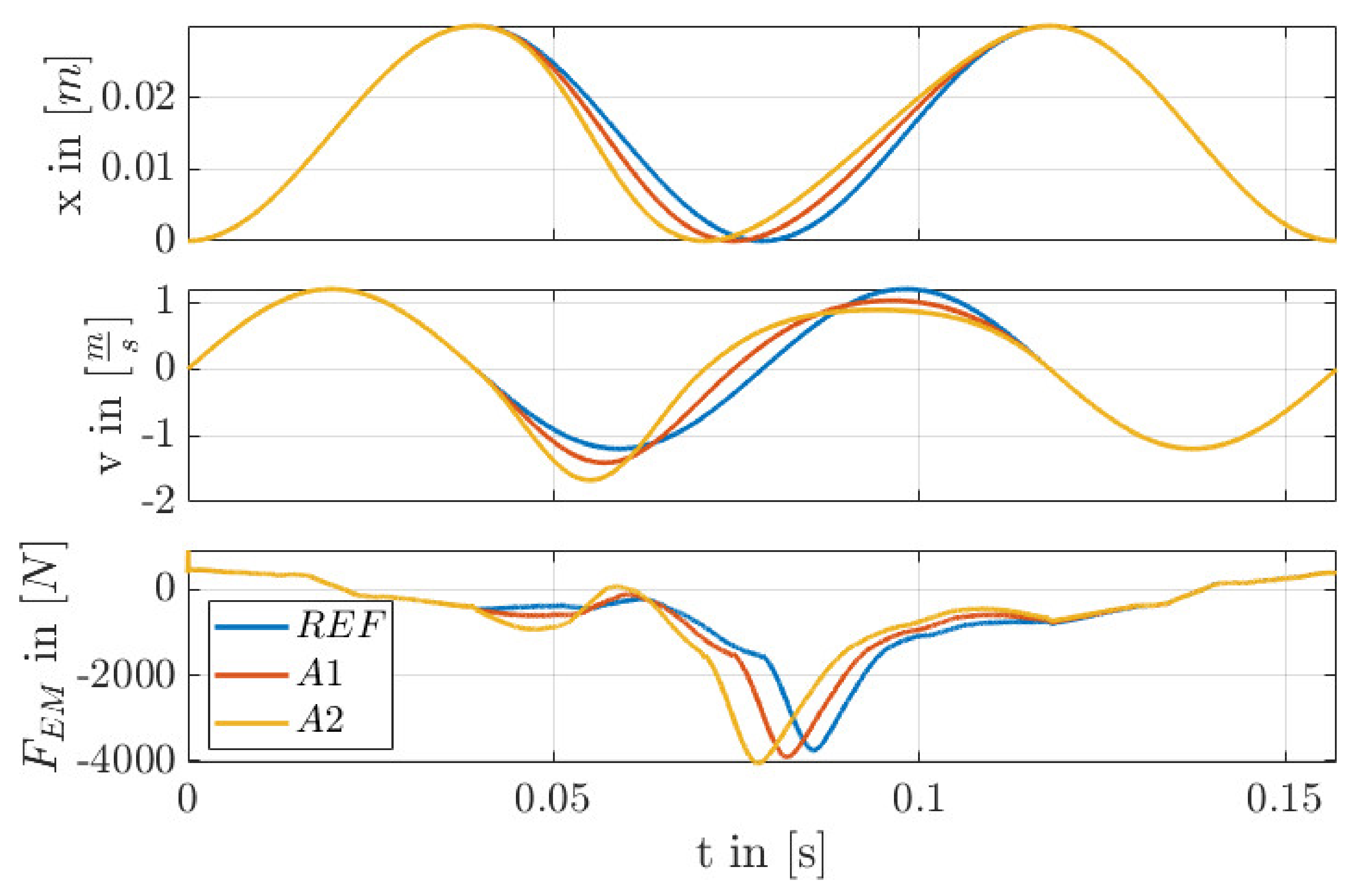
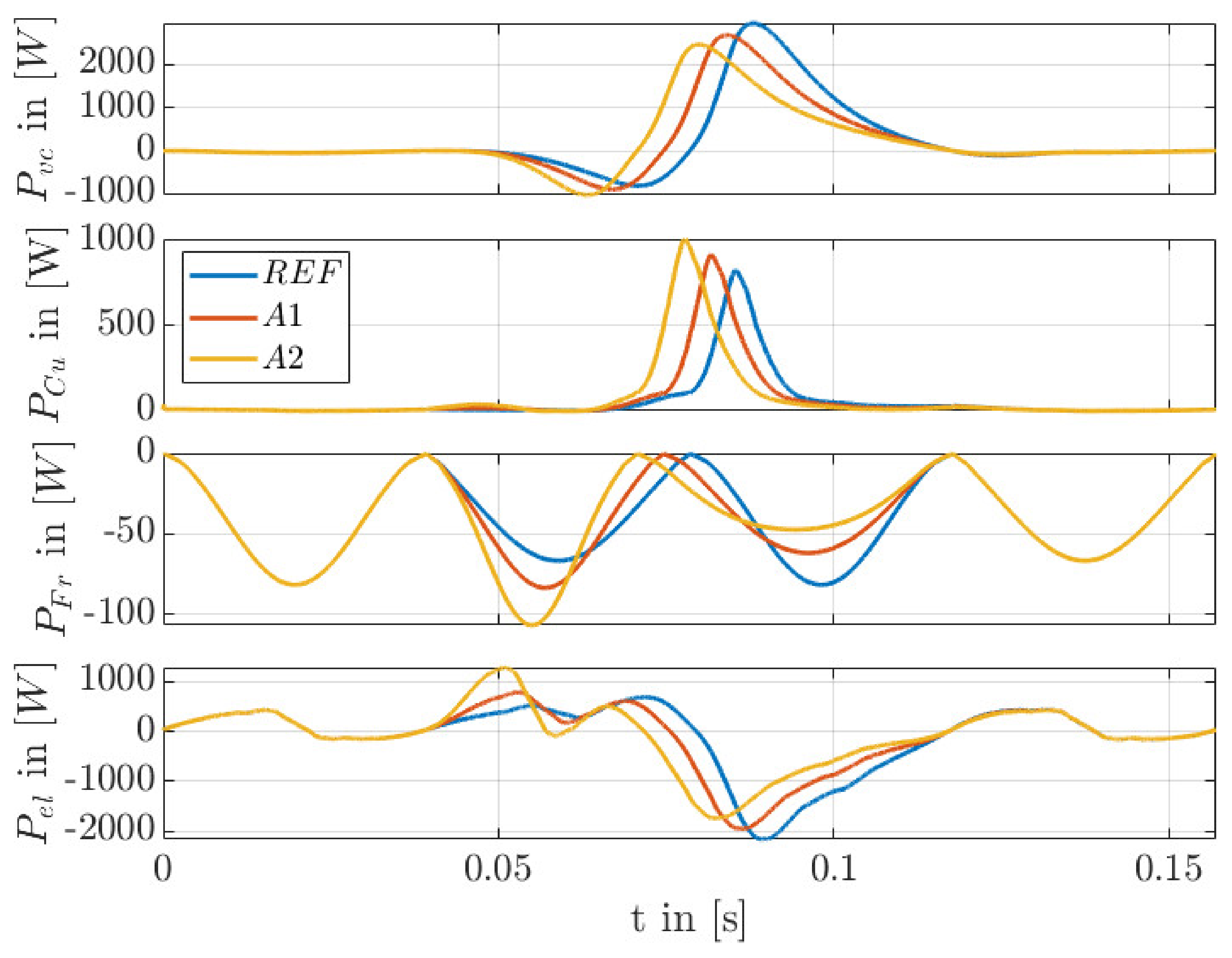



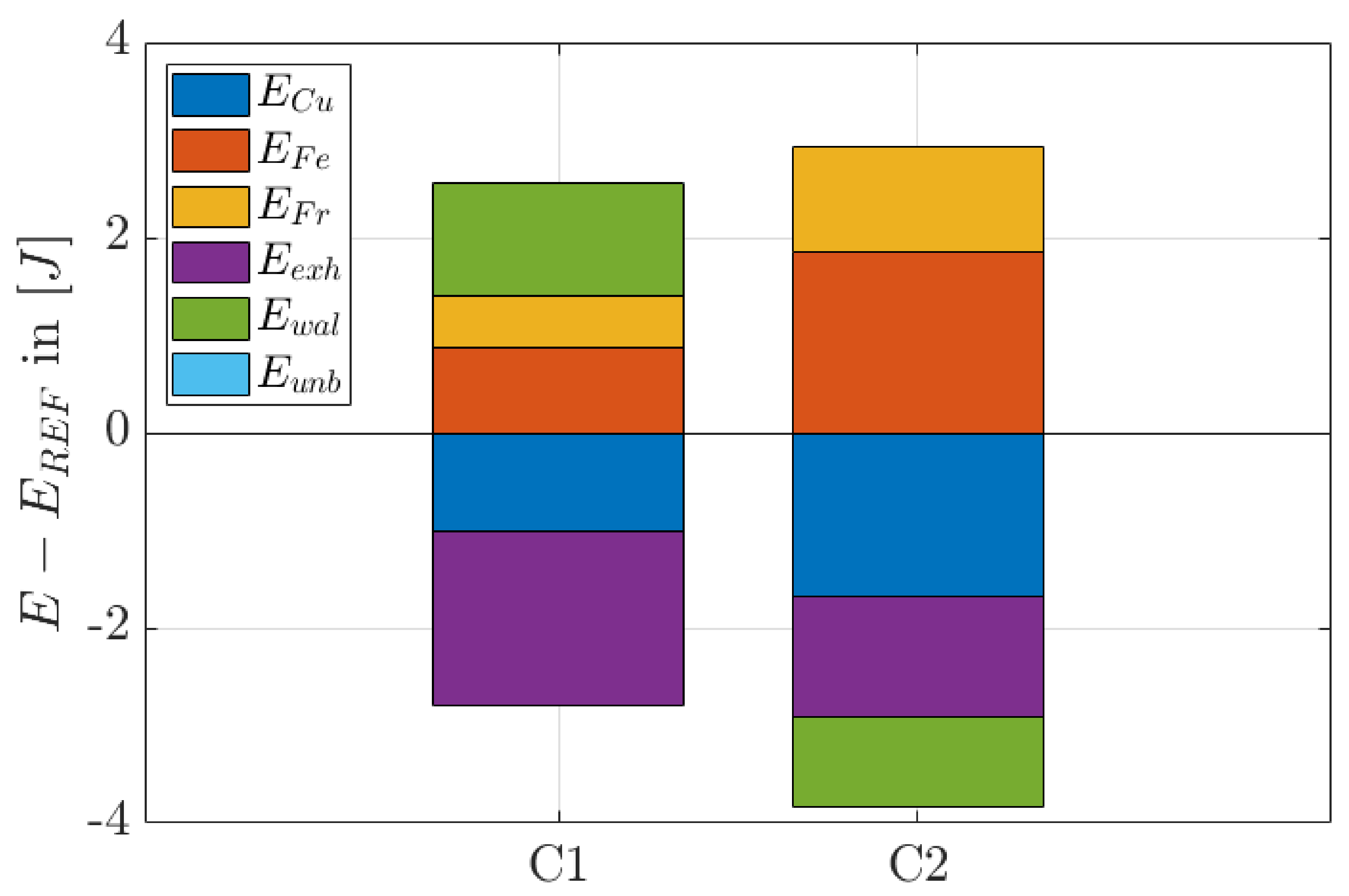




| Linear PMSM | Combustion Engine | ||
|---|---|---|---|
| Rated Power | Engine Type | Four-Stroke | |
| Rated Speed | Engine Displacement | ||
| Rated Current | Rated Power | ||
| Peak Current | Bore Diameter | ||
| Rated Force | Number of Cylinders | ||
| Peak Force | Conventional Stroke | ||
| Mover Mass | Maximal Stroke | ||
| Mover Length | Rated Speed | ||
| Magnet Yoke length | Rated Force | ||
| Maximum stroke | Moving Mass | ||
| Resistance per phase | 1.29 Ω | ||
| Linear PMSM | |
|---|---|
| Rated Power | |
| Rated Speed | |
| Rated Current | |
| Peak Current | |
| Rated Force | |
| Peak Force | |
| Mover Mass | |
| Mover Length | |
| Magnet Yoke length | |
| Maximum stroke | |
| Resistance per phase | 0.441 Ω |
| Combustion Engine | Combustion Model: SI-Turb | ||
|---|---|---|---|
| Engine Speed | Turbulent Flame Speed Multiplier | 0.025 | |
| IMEP | 4.7 bar | Flame Kernel Growth Multiplier | 0.01 |
| Injected fuel mass | Taylor Length Scale Multiplier | 0.001 | |
| Injected fuel | indolene | ||
| LHV of the fuel | |||
| Initial Stroke | |||
| Effective compression ratio | 5.368 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tempelhagen, R.; Gerlach, A.; Benecke, S.; Klepatz, K.; Leidhold, R.; Rottengruber, H. Investigations for a Trajectory Variation to Improve the Energy Conversion for a Four-Stroke Free-Piston Engine. Appl. Sci. 2021, 11, 5981. https://doi.org/10.3390/app11135981
Tempelhagen R, Gerlach A, Benecke S, Klepatz K, Leidhold R, Rottengruber H. Investigations for a Trajectory Variation to Improve the Energy Conversion for a Four-Stroke Free-Piston Engine. Applied Sciences. 2021; 11(13):5981. https://doi.org/10.3390/app11135981
Chicago/Turabian StyleTempelhagen, Robin, Andreas Gerlach, Sebastian Benecke, Kevin Klepatz, Roberto Leidhold, and Hermann Rottengruber. 2021. "Investigations for a Trajectory Variation to Improve the Energy Conversion for a Four-Stroke Free-Piston Engine" Applied Sciences 11, no. 13: 5981. https://doi.org/10.3390/app11135981
APA StyleTempelhagen, R., Gerlach, A., Benecke, S., Klepatz, K., Leidhold, R., & Rottengruber, H. (2021). Investigations for a Trajectory Variation to Improve the Energy Conversion for a Four-Stroke Free-Piston Engine. Applied Sciences, 11(13), 5981. https://doi.org/10.3390/app11135981






