Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading
Abstract
:1. Introduction
2. Mixed Mode Fatigue Life Evaluation Procedure Using ANSYS
3. Numerical Results and Discussion
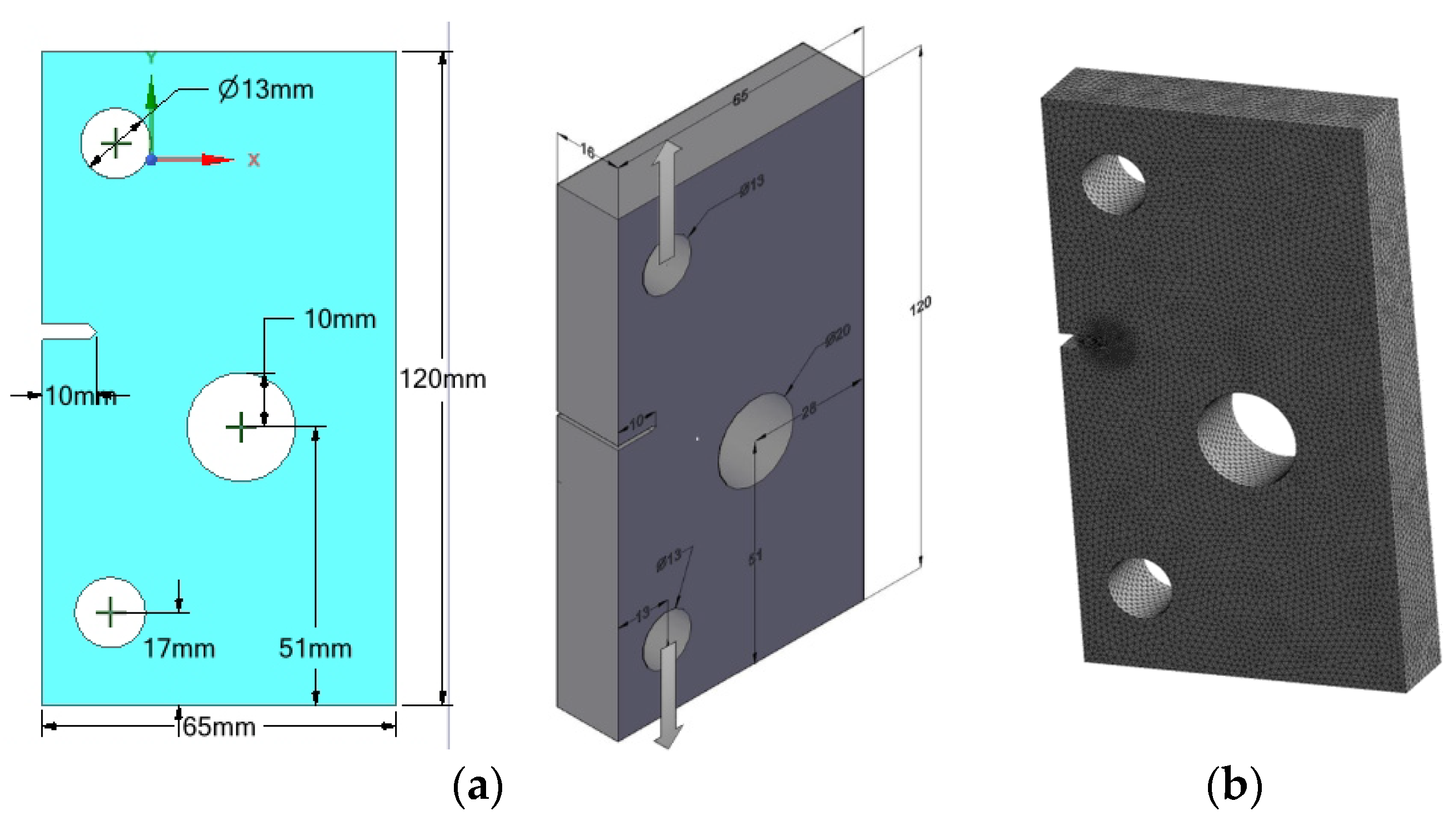
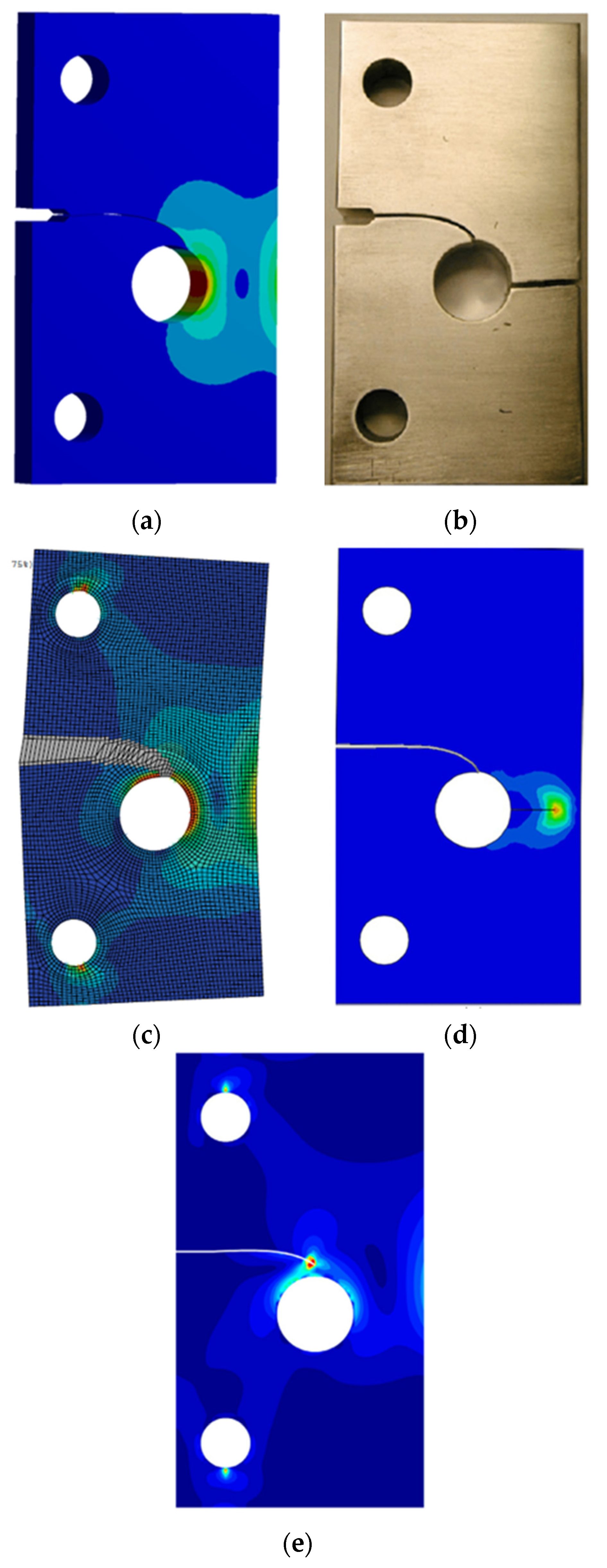
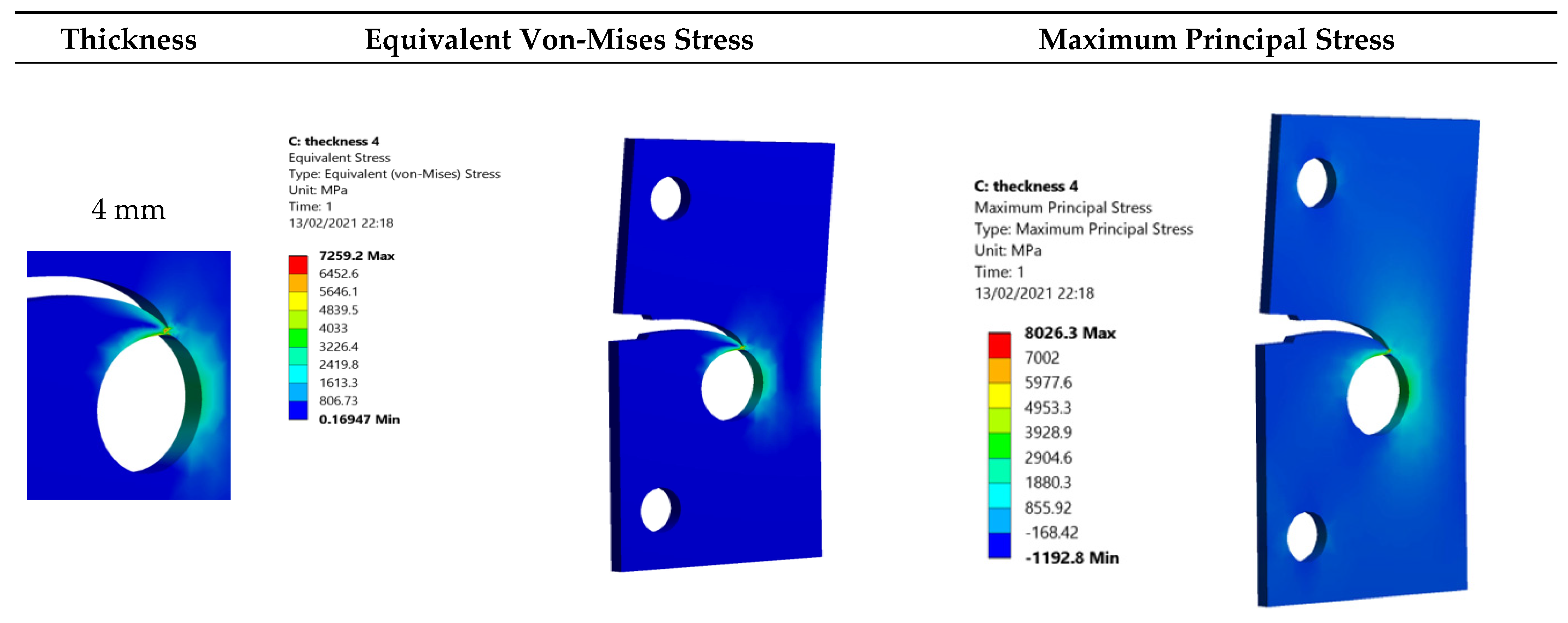
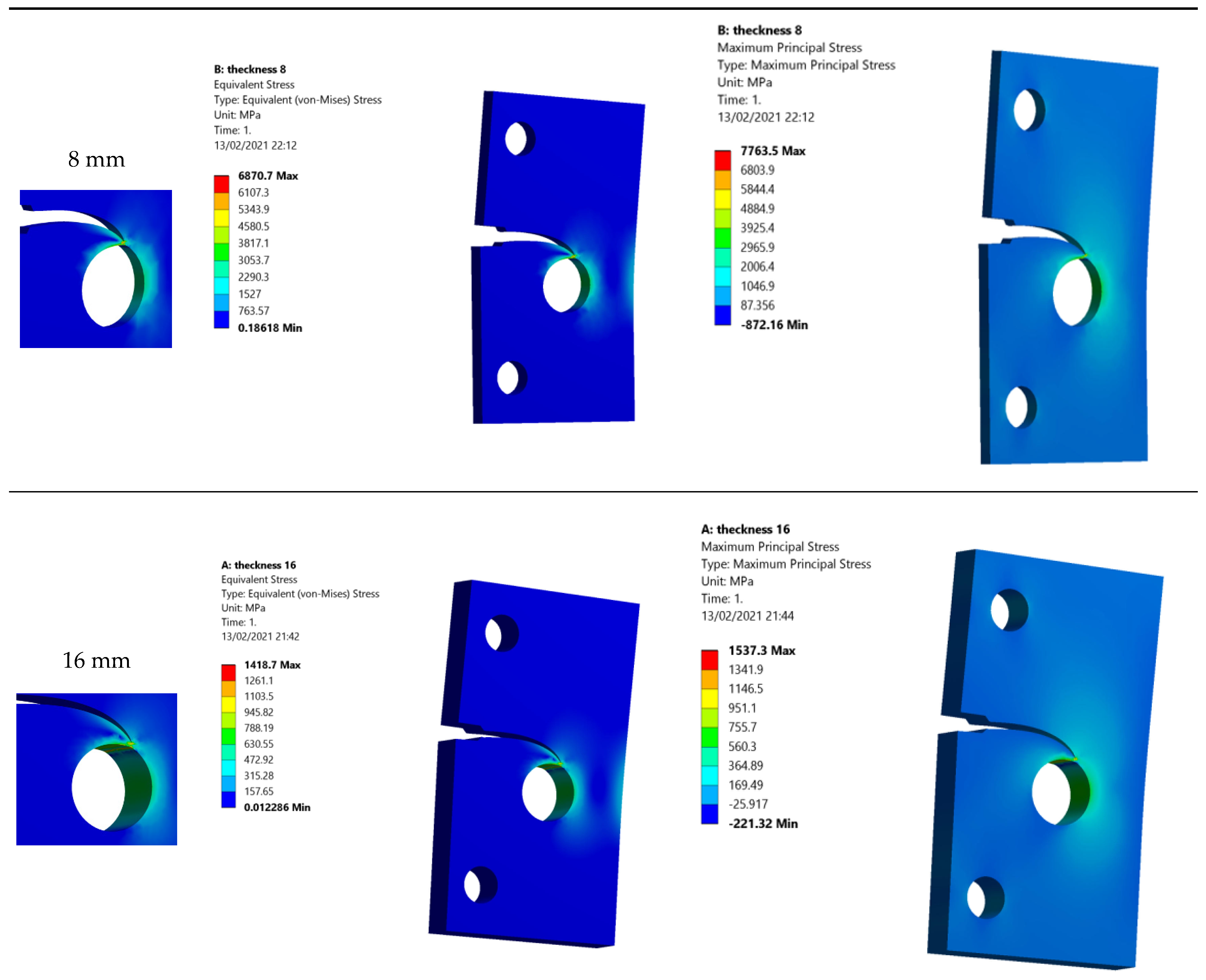
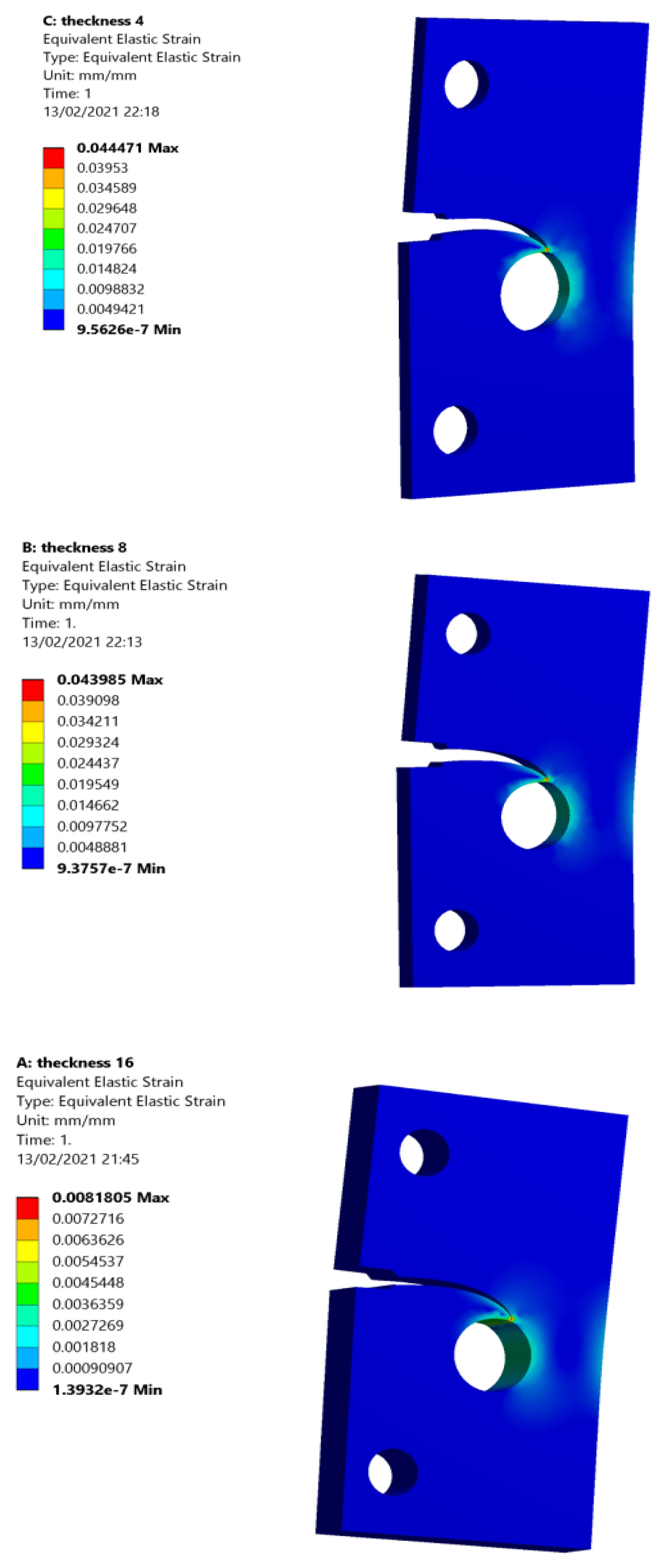
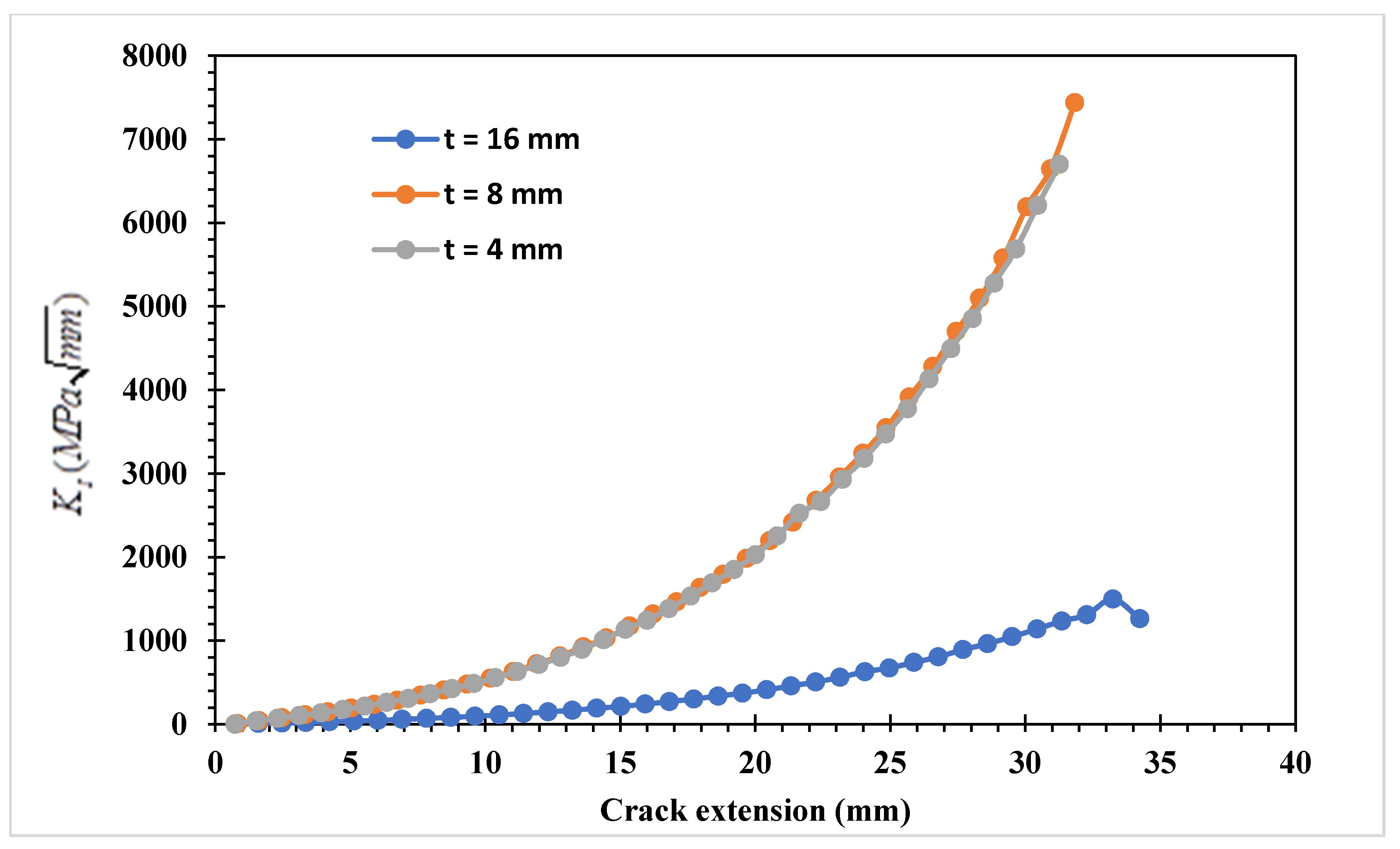
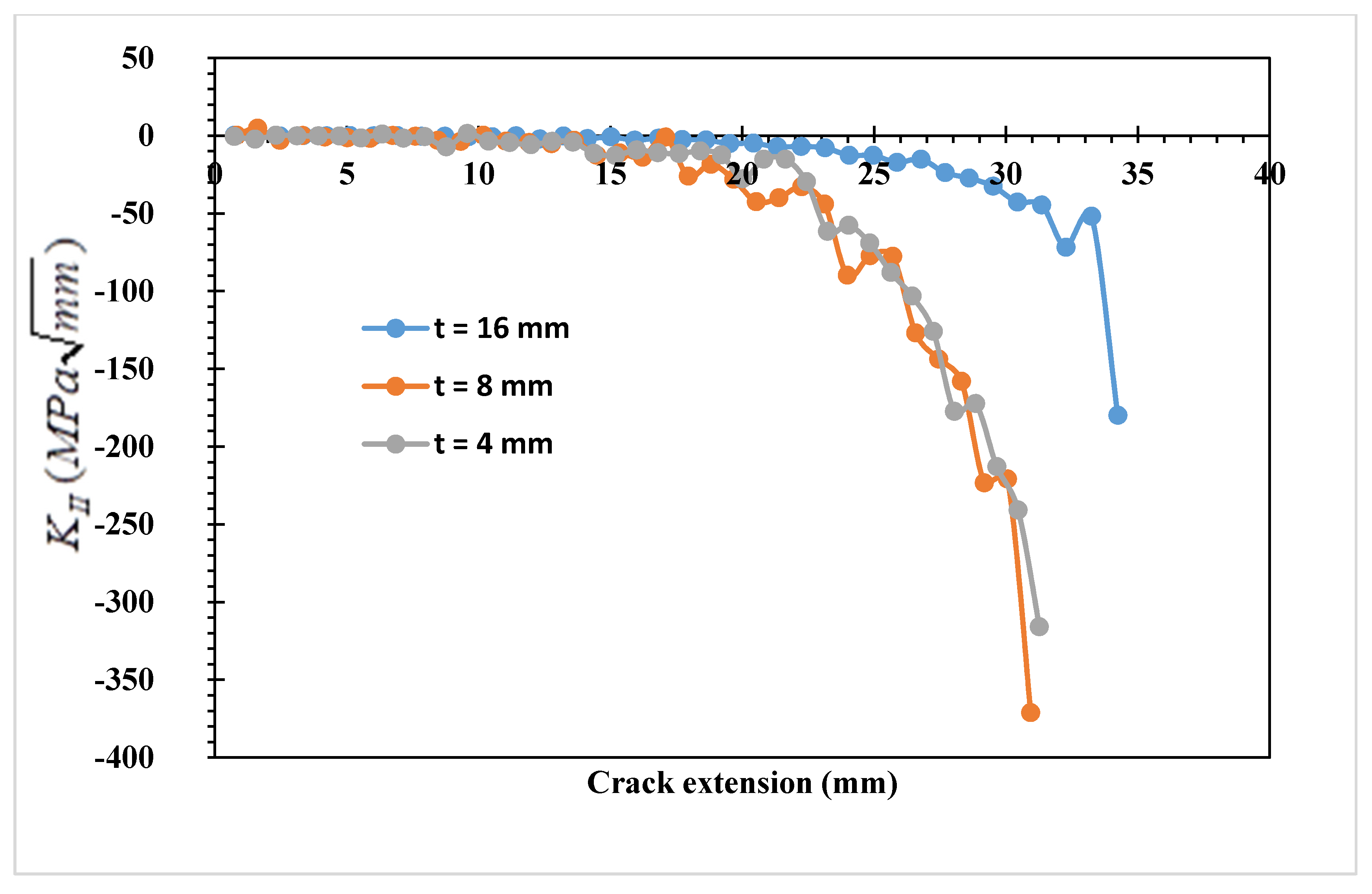
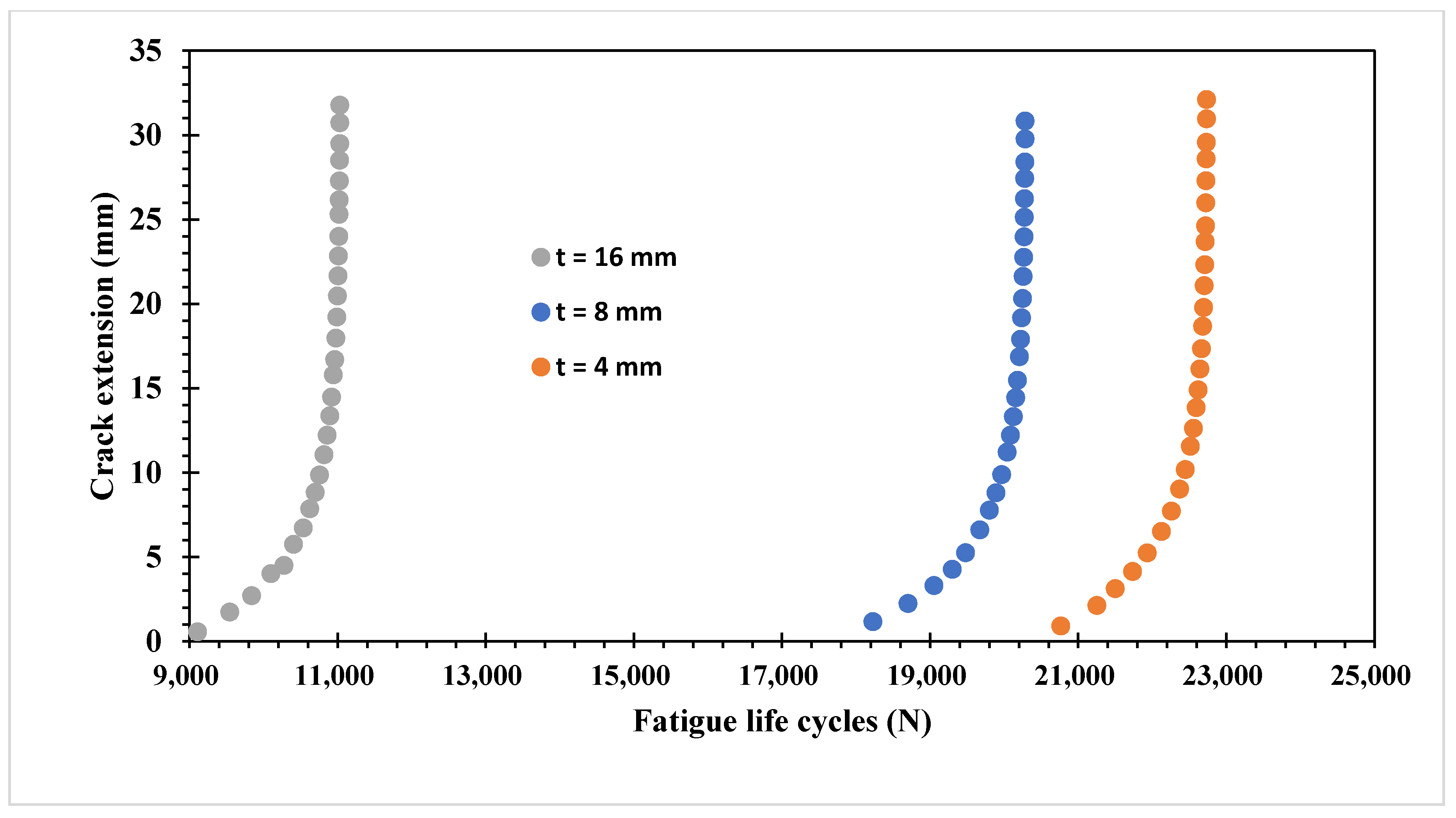
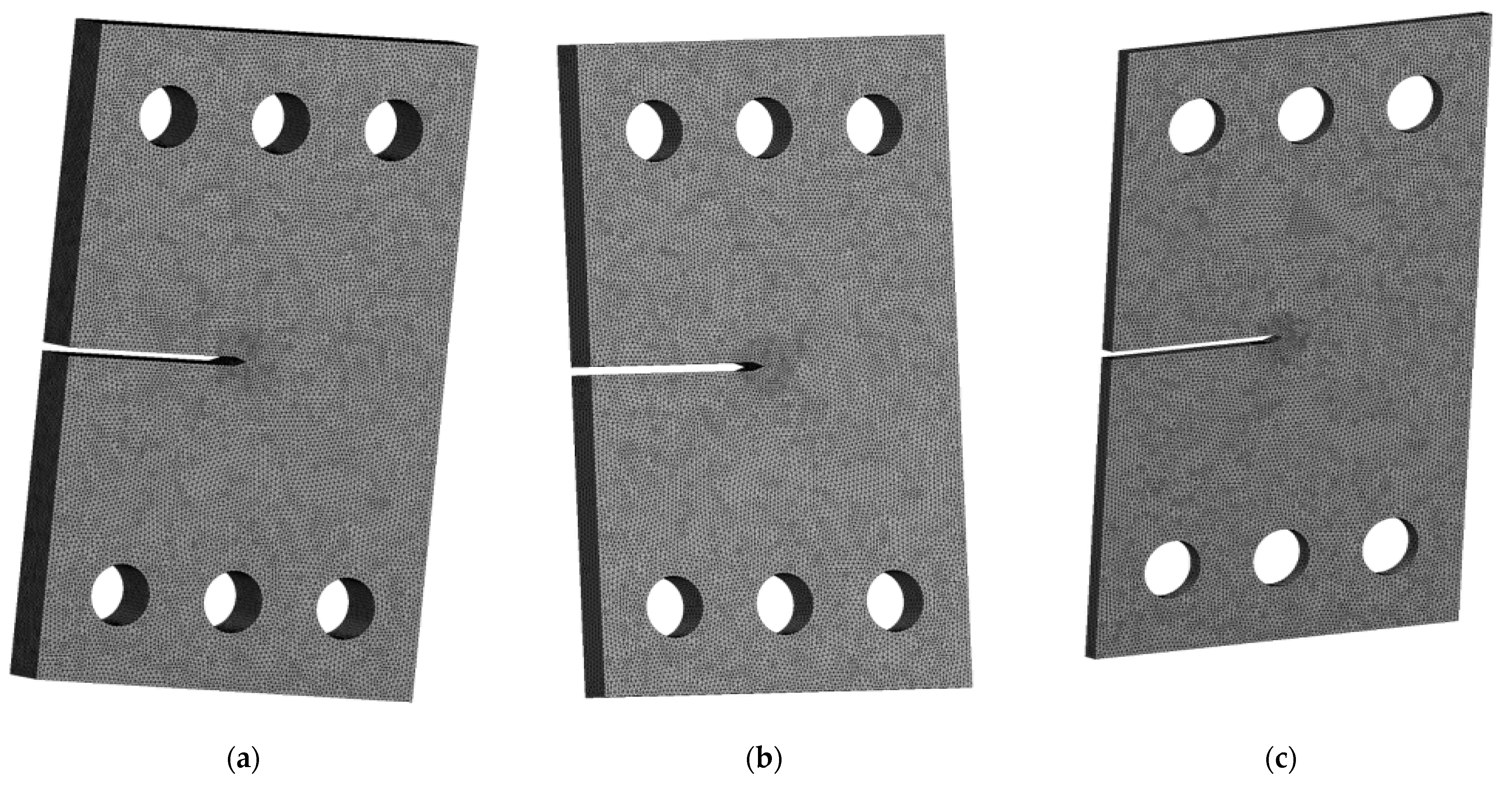
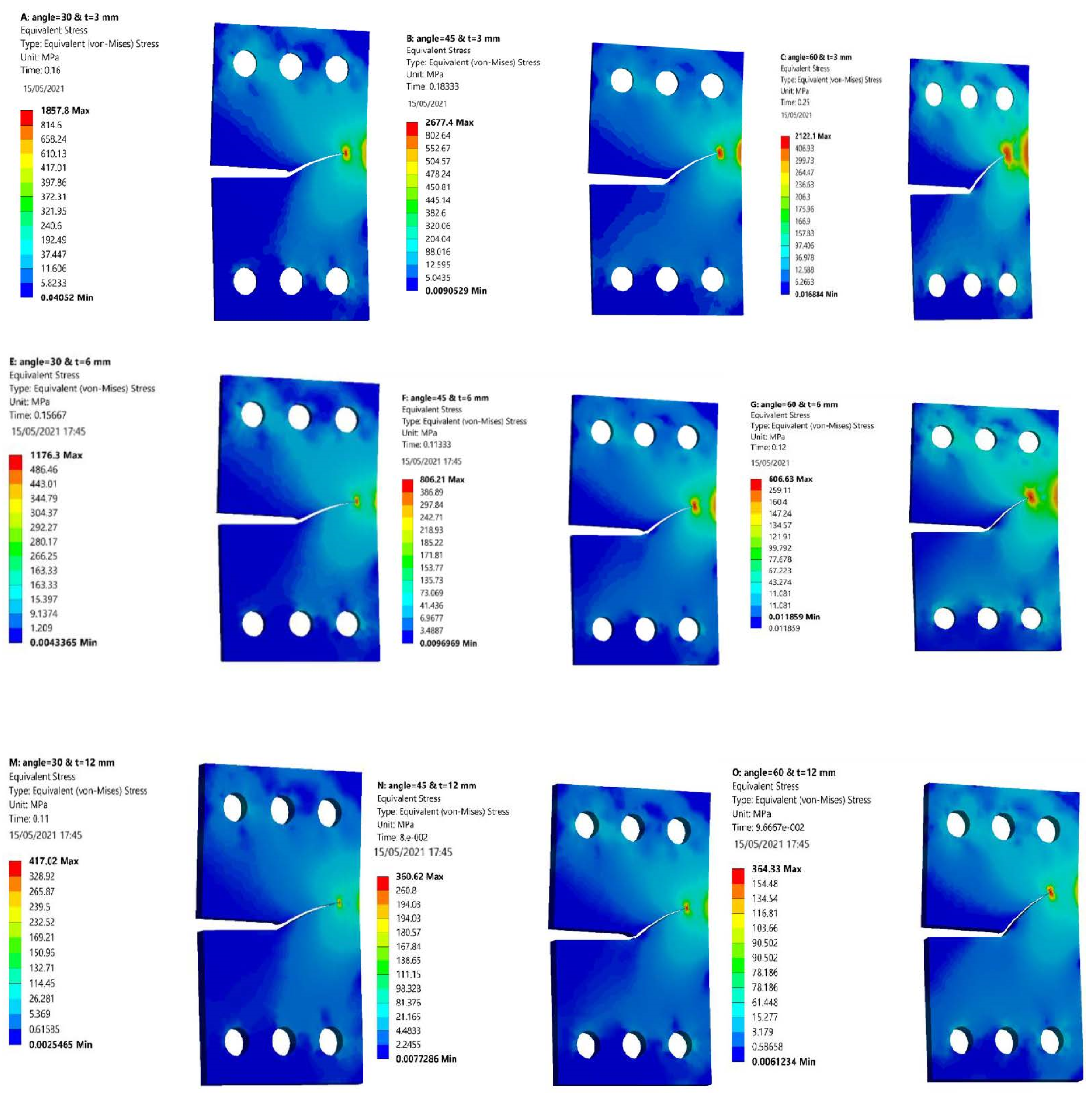
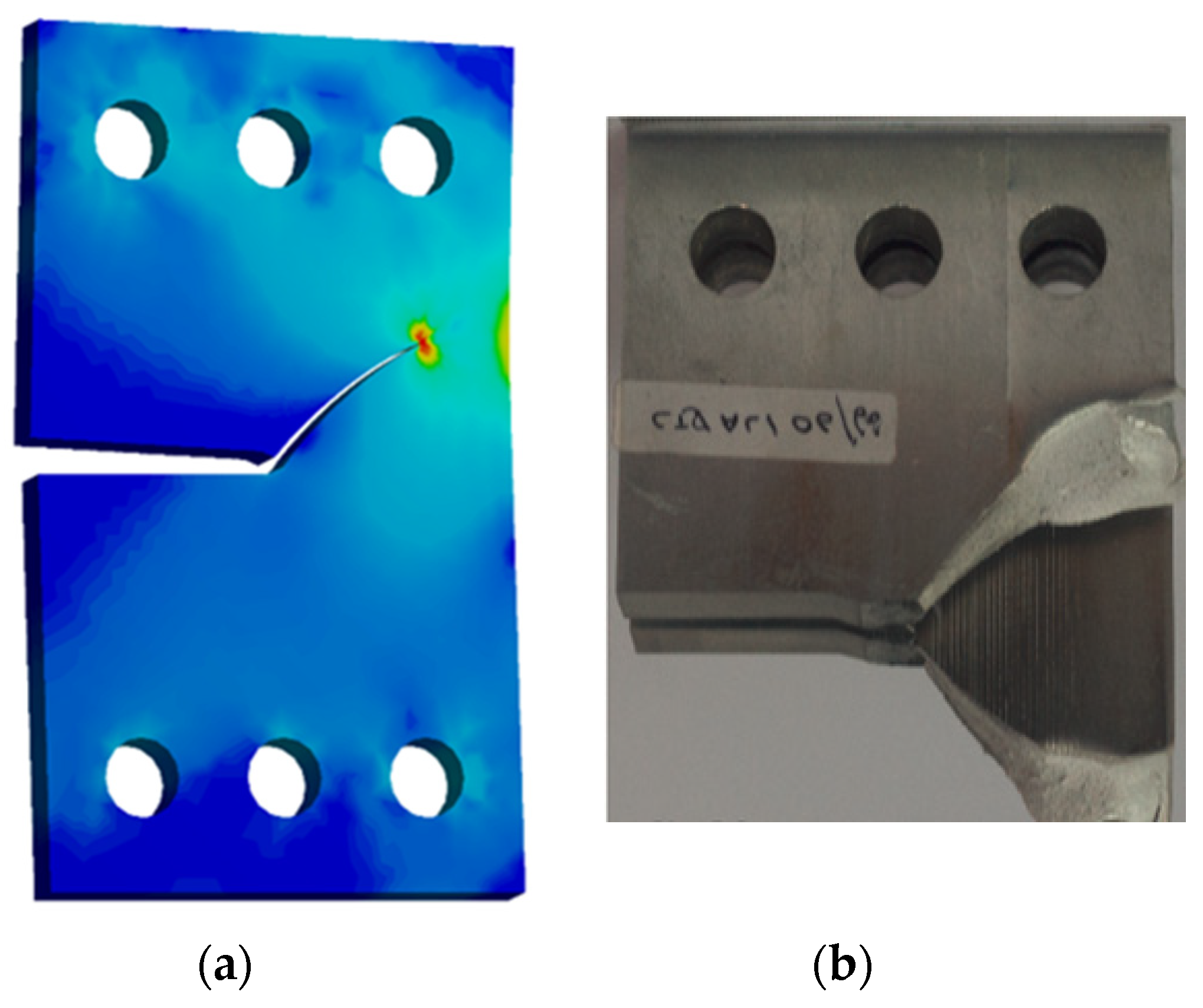
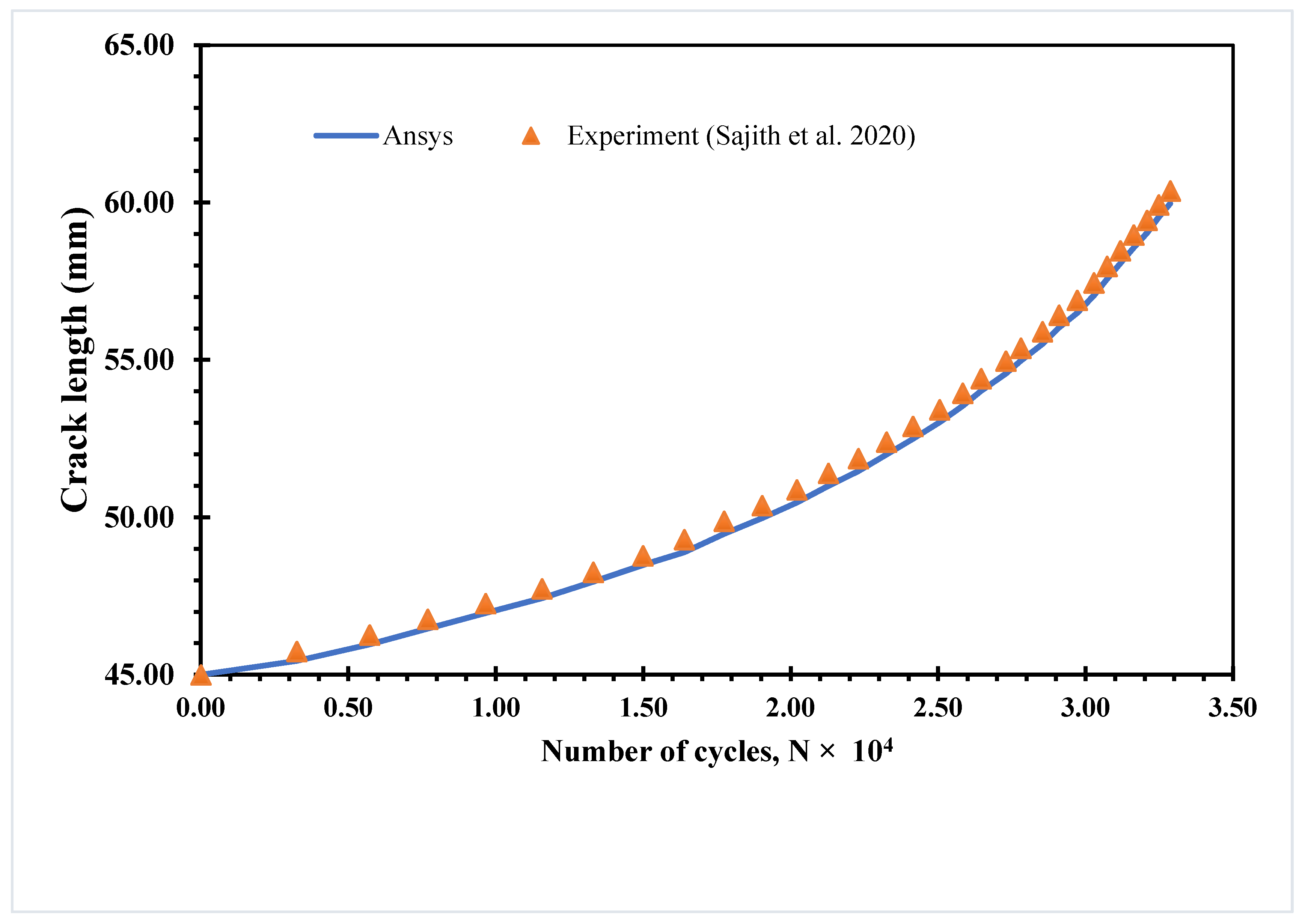
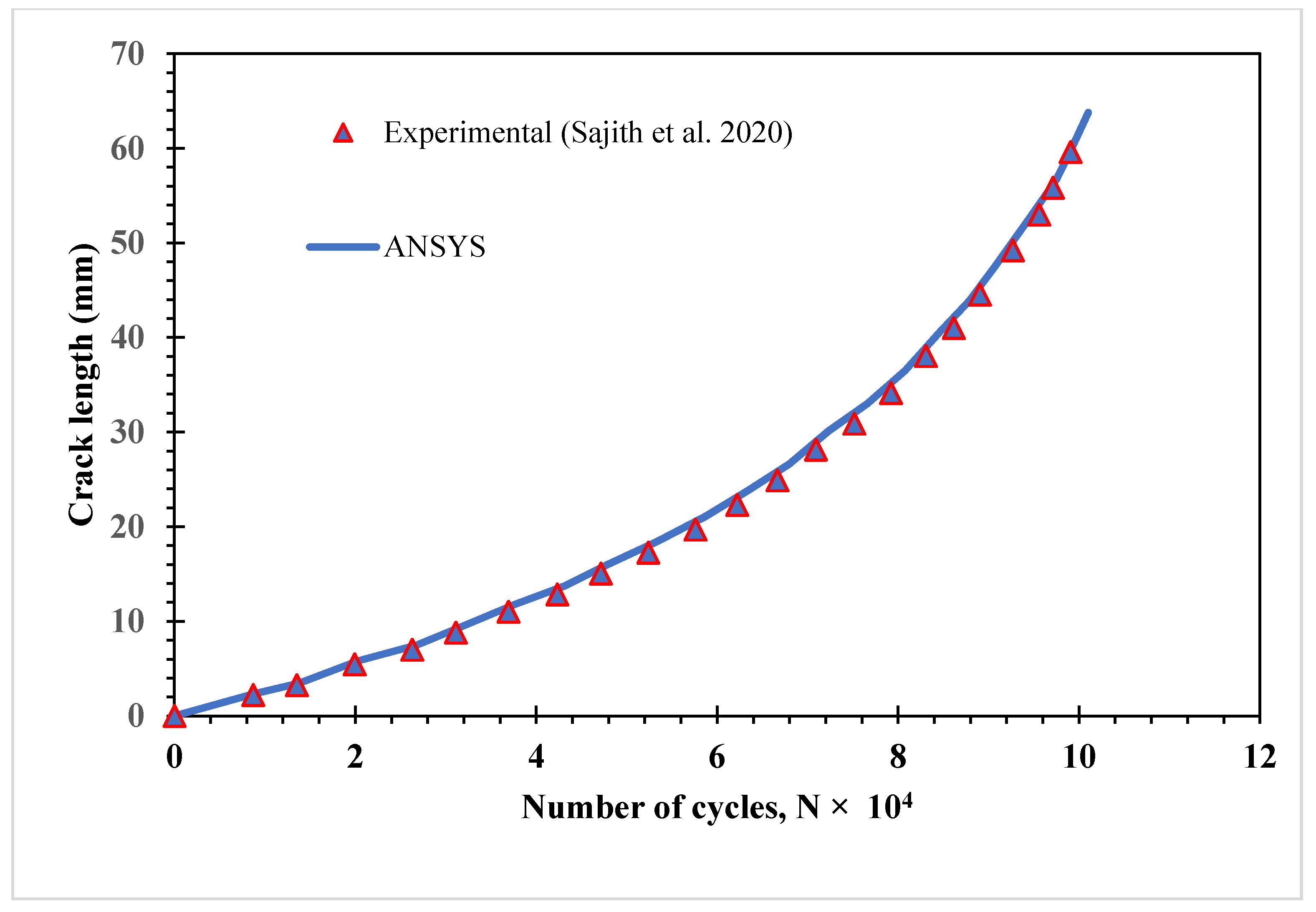
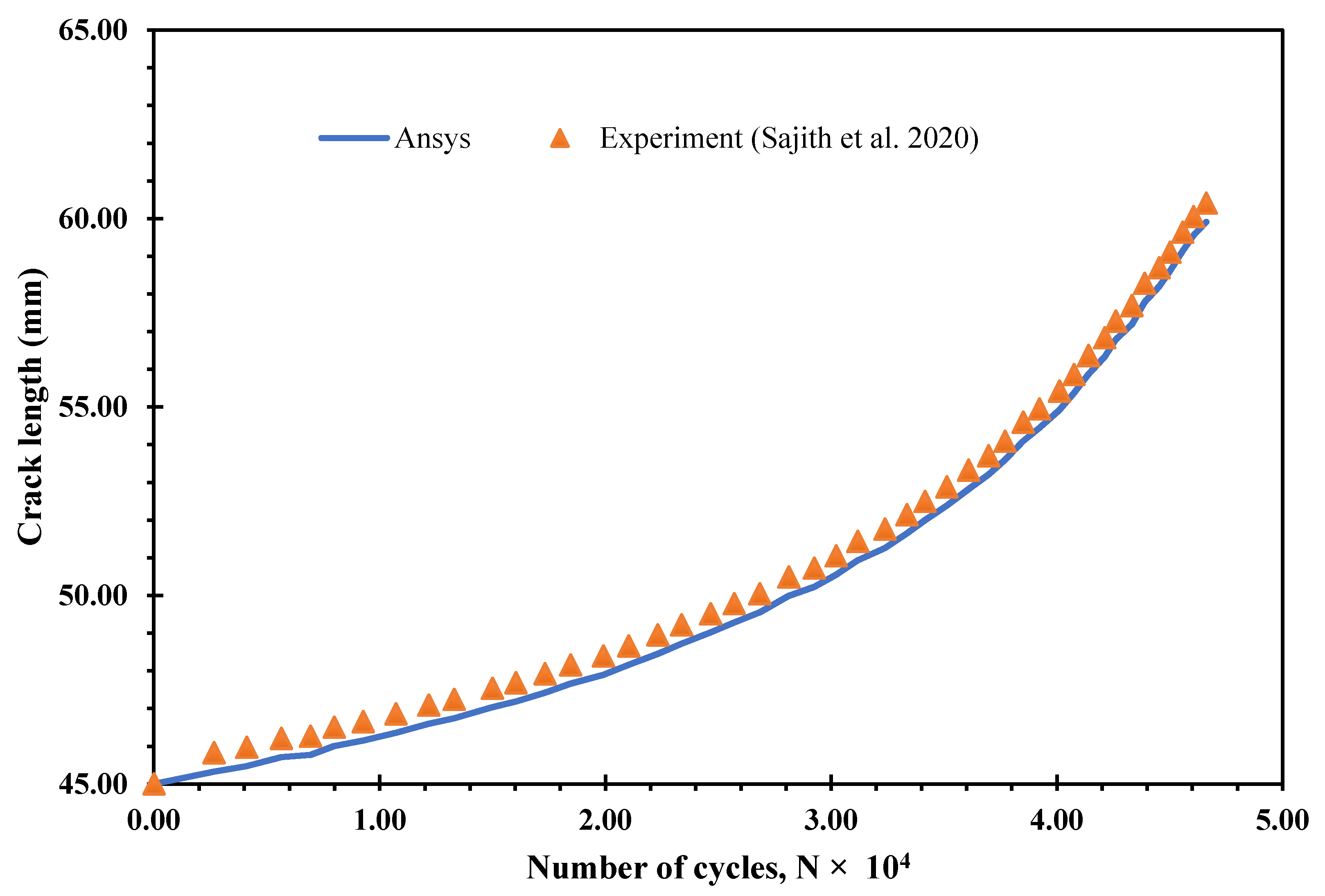
3.1. Single Edge Cracked Plate with a Three-Hole
3.2. Compact Tension Shear Specimen (CTS)
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tada, H.; Paris, P.C.; Irwin, G.R.; Tada, H. The Stress Analysis of Cracks Handbook; ASME Press: New York, NY, USA, 2000; Volume 130. [Google Scholar]
- Dirik, H.; Yalçinkaya, T. Crack path and life prediction under mixed mode cyclic variable amplitude loading through XFEM. Int. J. Fatigue 2018, 114, 34–50. [Google Scholar] [CrossRef]
- Sih, G.; Liebowitz, H. Mathematical Fundamentals. In Fracture; Academic Press: New York, NY, USA, 1968; Volume 2, pp. 67–190. [Google Scholar]
- Hellan, K. Introduction to Fracture Mechanics; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Barsom, J.; Rolfe, S. Fracture and Fatigue in Structure: Application of Fracture Mechanics; American Society for Testing and Materials: Philadelphia, PA, USA, 1999. [Google Scholar]
- Broek, D. Elementary Engineering Fracture Mechanics; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Huynh, H.D.; Nguyen, M.N.; Cusatis, G.; Tanaka, S.; Bui, T.Q. A polygonal XFEM with new numerical integration for linear elastic fracture mechanics. Eng. Fract. Mech. 2019, 213, 241–263. [Google Scholar] [CrossRef]
- Surendran, M.; Natarajan, S.; Palani, G.; Bordas, S.P. Linear smoothed extended finite element method for fatigue crack growth simulations. Eng. Fract. Mech. 2019, 206, 551–564. [Google Scholar] [CrossRef]
- Rozumek, D.; Marciniak, Z.; Lesiuk, G.; Correia, J. Mixed mode I/II/III fatigue crack growth in S355 steel. Procedia Struct. Integr. 2017, 5, 896–903. [Google Scholar] [CrossRef]
- Giannella, V.; Dhondt, G.; Kontermann, C.; Citarella, R. Combined static-cyclic multi-axial crack propagation in cruciform specimens. Int. J. Fatigue 2019, 123, 296–307. [Google Scholar] [CrossRef]
- Giannella, V.; Fellinger, J.; Perrella, M.; Citarella, R. Fatigue life assessment in lateral support element of a magnet for nuclear fusion experiment “Wendelstein 7-X”. Eng. Fract. Mech. 2017, 178, 243–257. [Google Scholar] [CrossRef] [Green Version]
- Alshoaibi, A.M. Numerical Modeling of Crack Growth under Mixed-Mode Loading. Applied Sciences 2021, 11, 2975. [Google Scholar] [CrossRef]
- Shlyannikov, V.; Yarullin, R.; Yakovlev, M.; Giannella, V.; Citarella, R. Mixed-mode crack growth simulation in aviation engine compressor disk. Eng. Fract. Mech. 2021, 246, 107617. [Google Scholar] [CrossRef]
- Sih, G.; Barthelemy, B. Mixed mode fatigue crack growth predictions. Eng. Fract. Mech. 1980, 13, 439–451. [Google Scholar] [CrossRef]
- Sih, G.; Moyer, E., Jr. Path dependent nature of fatigue crack growth. Eng. Fract. Mech. 1983, 17, 269–280. [Google Scholar] [CrossRef]
- Giannella, V. Stochastic approach to fatigue crack-growth simulation for a railway axle under input data variability. Int. J. Fatigue 2021, 144, 106044. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Finite element procedures for the numerical simulation of fatigue crack propagation under mixed mode loading. Struct. Eng. Mech. 2010, 35, 283–299. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Comprehensive Comparisons of Two and Three Dimensional Numerical Estimation of Stress Intensity Factors and Crack propagation in Linear Elastic Analysis. Int. J. Integr. Eng. 2019, 11, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Alshoaibi, A.M.; Fageehi, Y.A. 2D finite element simulation of mixed mode fatigue crack propagation for CTS specimen. J. Mater. Res. Technol. 2020, 9, 7850–7861. [Google Scholar] [CrossRef]
- Fageehi, Y.A.; Alshoaibi, A.M. Numerical Simulation of Mixed-Mode Fatigue Crack Growth for Compact Tension Shear Specimen. Adv. Mater. Sci. Eng. 2020, 2020. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Wang, Q.; Zeng, W.; Liu, G.; Sun, J.; He, L.; Bui, T.Q. Dynamic brittle crack propagation modeling using singular edge-based smoothed finite element method with local mesh rezoning. Eur. J. Mech. A Solids 2019, 76, 208–223. [Google Scholar] [CrossRef]
- Gomes, G.; Miranda, A.C. Analysis of crack growth problems using the object-oriented program bemcracker2D. Frat. Integr. Strutt. 2018, 12, 67–85. [Google Scholar] [CrossRef] [Green Version]
- Fageehi, Y.A.; Alshoaibi, A.M. Nonplanar Crack Growth Simulation of Multiple Cracks Using Finite Element Method. Adv. Mater. Sci. Eng. 2020, 2020. [Google Scholar] [CrossRef] [Green Version]
- Mirsayar, M. A generalized criterion for fatigue crack growth in additively manufactured materials–Build orientation and geometry effects. Int. J. Fatigue 2021, 145, 106099. [Google Scholar] [CrossRef]
- Paris, P.; Erdogan, F. A critical analysis of crack propagation laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Coffin, L. Cyclic Deformation and Fatigue of Metals; Fatigue and Endurance of Metals [Russian translation]; USSR: Moscow, Russia, 1963; pp. 257–272. [Google Scholar]
- Wöhler, A. Versuche zur Ermittlung der auf die Eisenbahnwagenachsen einwirkenden Kräfte und die Widerstandsfähigkeit der Wagen-Achsen. Z. Bauwes. 1860, 10, 583–614. [Google Scholar]
- Wawrzynek, P.; Carter, B.; Banks-Sills, L. The M-Integral for Computing Stress Intensity Factors in Generally Anisotropic Materials; National Aeronautics and Space Administration, Marshall Space Flight Center: Huntsville, AL, USA, 2005. [Google Scholar]
- Citarella, R.; Giannella, V.; Lepore, M.; Dhondt, G. Dual boundary element method and finite element method for mixed-mode crack propagation simulations in a cracked hollow shaft. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 84–98. [Google Scholar] [CrossRef]
- Dhondt, G.; Hackenberg, H.-P. Use of a rotation-invariant linear strain measure for linear elastic crack propagation calculations. Eng. Fract. Mech. 2021, 247, 107634. [Google Scholar] [CrossRef]
- Bjørheim, F. Practical Comparison of Crack Meshing in ANSYS Mechanical APDL 19.2; University of Stavanger: Stavanger, Norway, 2019. [Google Scholar]
- ANSYS. Academic Research Mechanical, Release 19.2, Help System. In Coupled Field Analysis Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Walters, M.C.; Paulino, G.H.; Dodds, R.H., Jr. Interaction integral procedures for 3-D curved cracks including surface tractions. Eng. Fract. Mech. 2005, 72, 1635–1663. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Giner, E.; Sukumar, N.; Tarancón, J.; Fuenmayor, F. An Abaqus implementation of the extended finite element method. Eng. Fract. Mech. 2009, 76, 347–368. [Google Scholar] [CrossRef] [Green Version]
- Malekan, M.; Carvalho, H. Analysis of a main fatigue crack interaction with multiple micro-cracks/voids in a compact tension specimen repaired by stop-hole technique. J. Strain Anal. Eng. Des. 2018, 53, 648–662. [Google Scholar] [CrossRef]
- Cheng, Z.; Wang, H. How to control the crack to propagate along the specified path feasibly? Comput. Methods Appl. Mech. Eng. 2018, 336, 554–577. [Google Scholar] [CrossRef] [Green Version]
- Richard, H. Fracture Predictions for Cracks Exposed to Superimposed Normal and Shear Stresses; International Nuclear Information System: Vienna, Austria, 1985. [Google Scholar]
- Antunes, F.V.; Branco, R.; Ferreira, J.A.M.; Borrego, L. Stress Intensity Factor Solutions for CTS Mixed Mode Specimen. Frat. Integr. Strutt. 2019, 13, 676–692. [Google Scholar] [CrossRef]
- DEMIR, O.; Ayhan, A.O.; Sedat, I.; LEKESIZ, H. Evaluation of mixed mode-I/II criteria for fatigue crack propagation using experiments and modeling. Chin. J. Aeronaut. 2018, 31, 1525–1534. [Google Scholar] [CrossRef]
- Sajith, S.; Murthy, K.; Robi, P. Experimental and numerical investigation of mixed mode fatigue crack growth models in aluminum 6061-T6. Int. J. Fatigue 2020, 130, 105285. [Google Scholar] [CrossRef]
- Demir, O.; Ayhan, A.O.; İriç, S. A new specimen for mixed mode-I/II fracture tests: Modeling, experiments and criteria development. Eng. Fract. Mech. 2017, 178, 457–476. [Google Scholar] [CrossRef]
- Sajith, S.; Shukla, S.; Murthy, K.; Robi, P. Mixed mode fatigue crack growth studies in AISI 316 stainless steel. Eur. J. Mech. A Solids 2020, 80, 103898. [Google Scholar] [CrossRef]
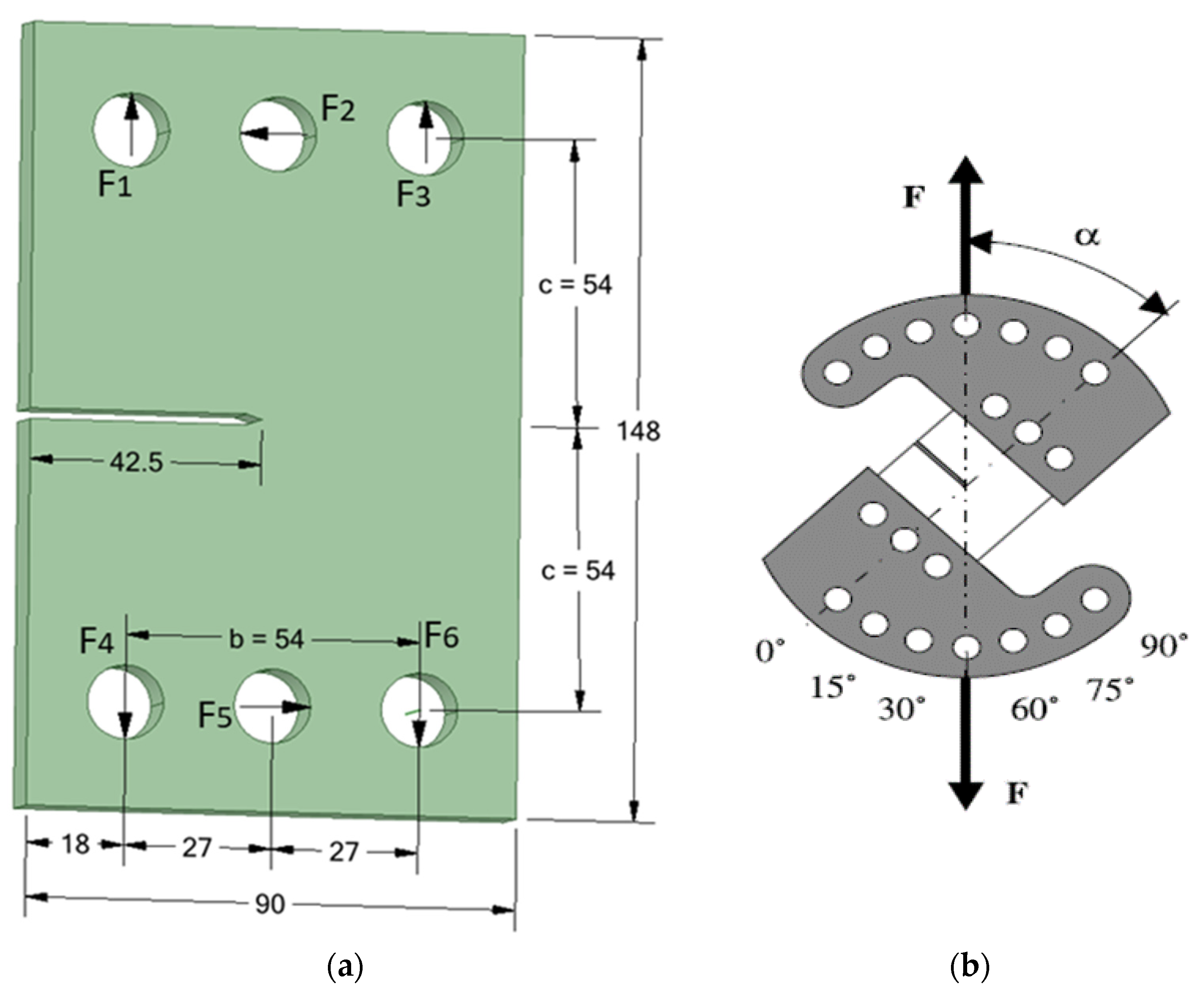


| α | F2 = F5 | F1 = F6 | F3 = F4 |
|---|---|---|---|
| 30 | 0.5 F | 0.933 F | –0.067 F |
| 45 | 0.707 F | 1.061 F | –0.354 F |
| 60 | 0.866 F | 1.116 F | −0.616 F |
| Properties | Metric Units Value |
|---|---|
| Elasticity Modulus, E | 74 GPa |
| Poisson’s ratio, υ | 0.33 |
| Yield strength, σy | 517 MPa |
| Ultimate strength, σu | 579 MPa |
| Threshold SIF, Kth | 3.15 MPa |
| Fracture toughness, KIC | 32.95 MPa |
| Paris’ law coefficient, C | 4.3378 × 10−7 |
| Paris law exponent, m | 2.6183 |
| t = 12 mm | t = 6 mm | t = 3 mm | |
|---|---|---|---|
| No. of nodes | 897,045 | 623,867 | 443,766 |
| No. of elements | 615,479 | 419,579 | 288,809 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshoaibi, A.M. Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading. Appl. Sci. 2021, 11, 5953. https://doi.org/10.3390/app11135953
Alshoaibi AM. Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading. Applied Sciences. 2021; 11(13):5953. https://doi.org/10.3390/app11135953
Chicago/Turabian StyleAlshoaibi, Abdulnaser M. 2021. "Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading" Applied Sciences 11, no. 13: 5953. https://doi.org/10.3390/app11135953
APA StyleAlshoaibi, A. M. (2021). Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading. Applied Sciences, 11(13), 5953. https://doi.org/10.3390/app11135953






