Recirculated Wave Undulators for Compact FELs
Abstract
1. Introduction
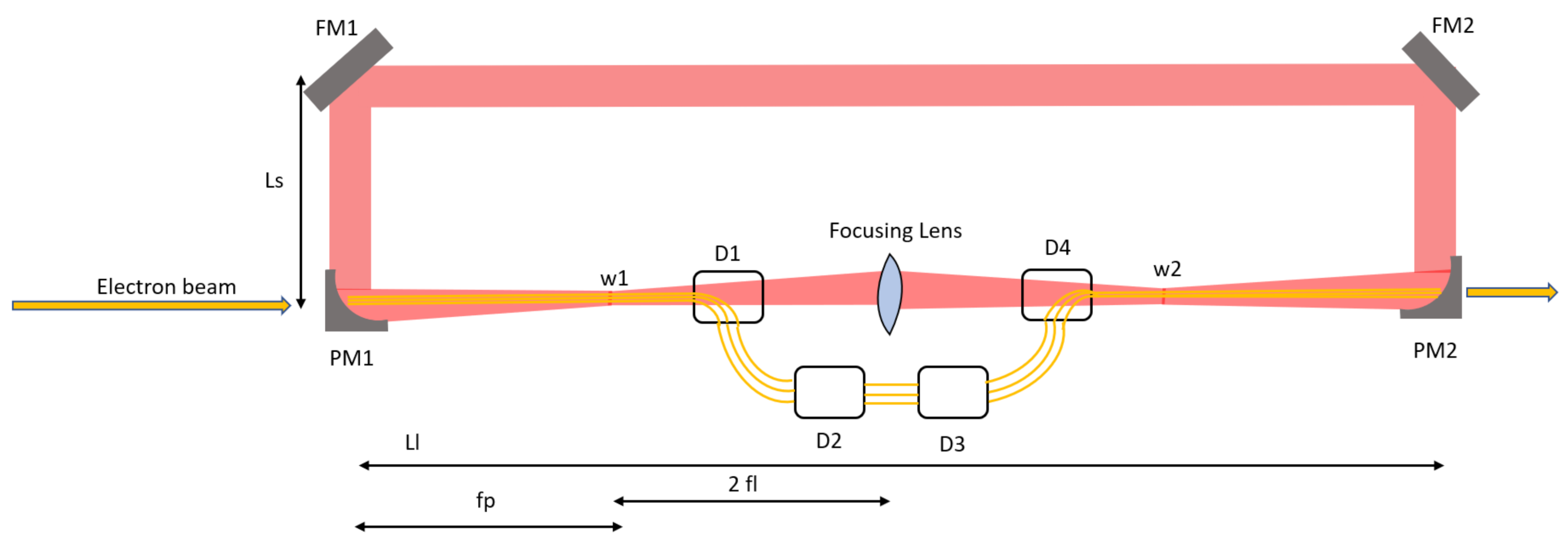
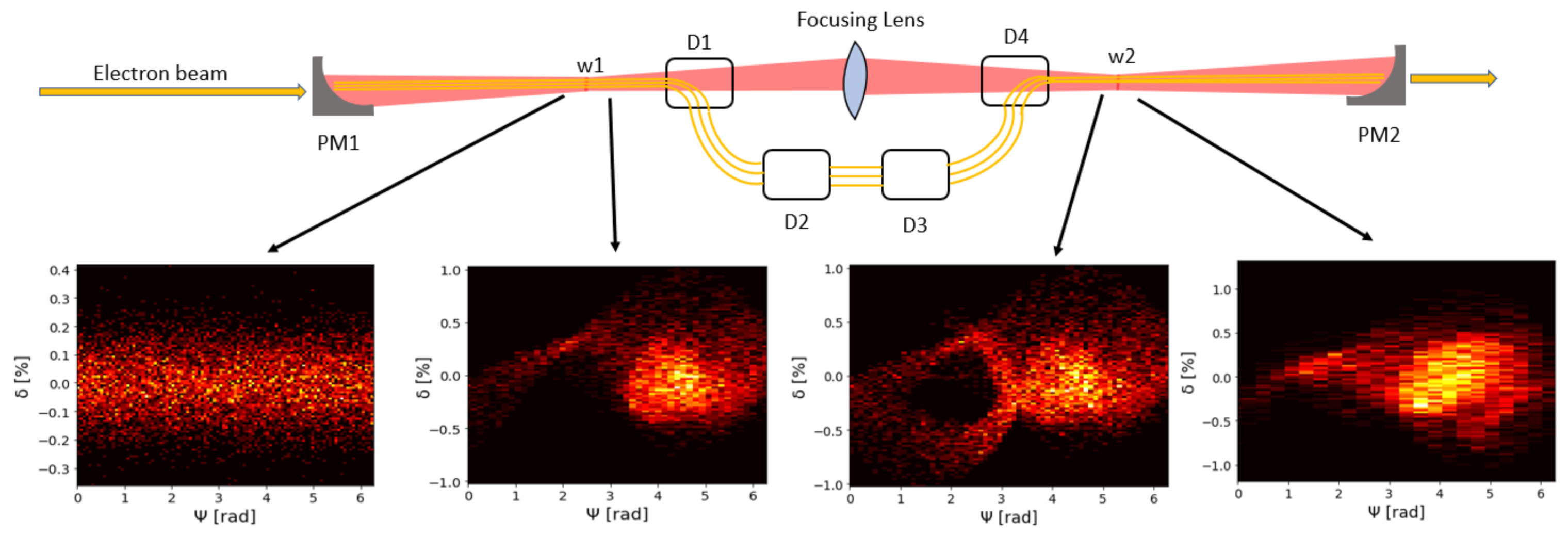
2. The Optical Cavity
3. Solution of the Liouville Equation for Longitudinal Beam Dynamics in Magnetic Chicanes
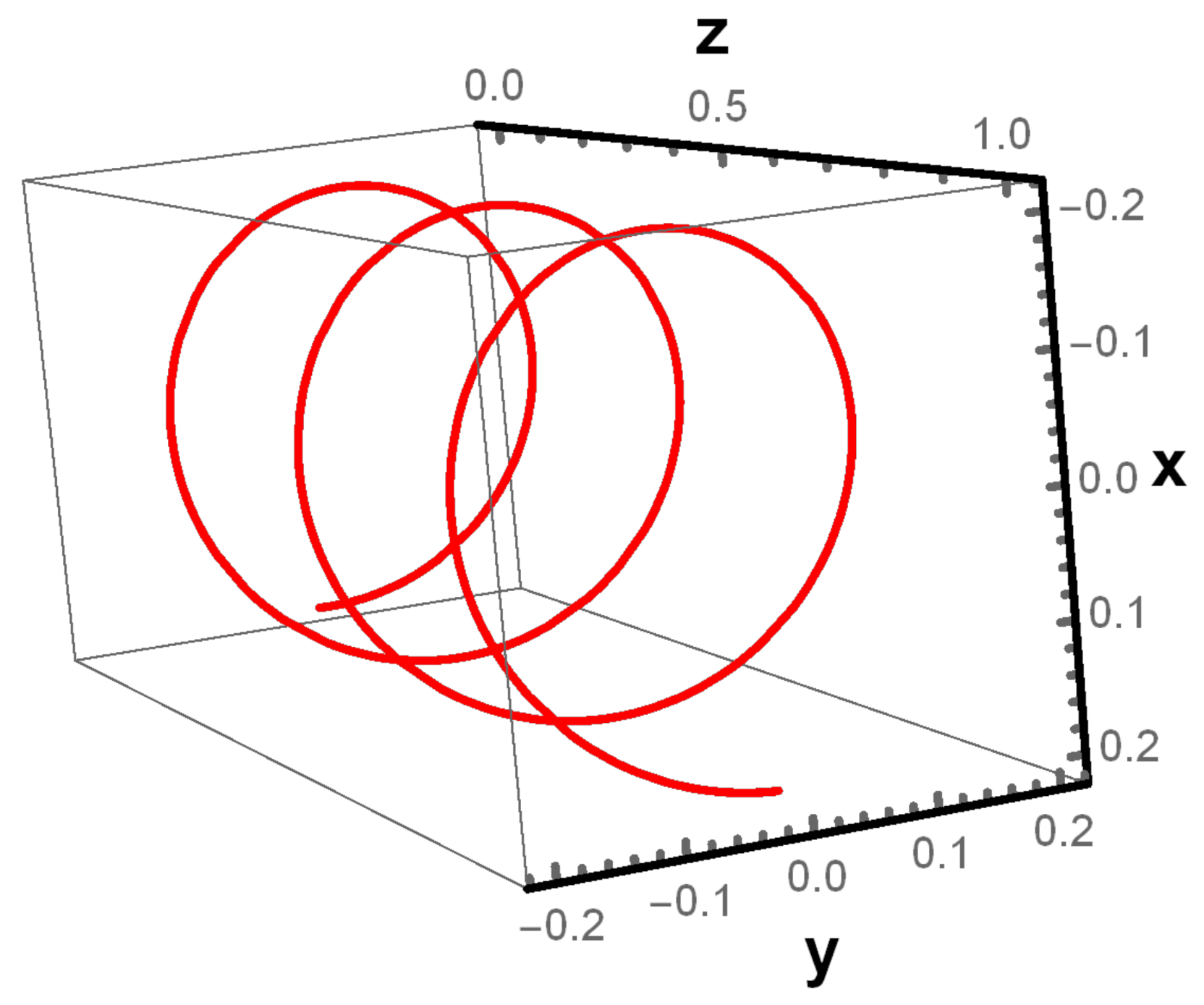
4. Dynamics of Relativistic Electrons Inside an Electromagnetic Undulator
5. 1D FEL Equations
6. Discussions on the Recirculated Wave Undulator FEL Scheme
7. Coherent Synchrotron Radiation
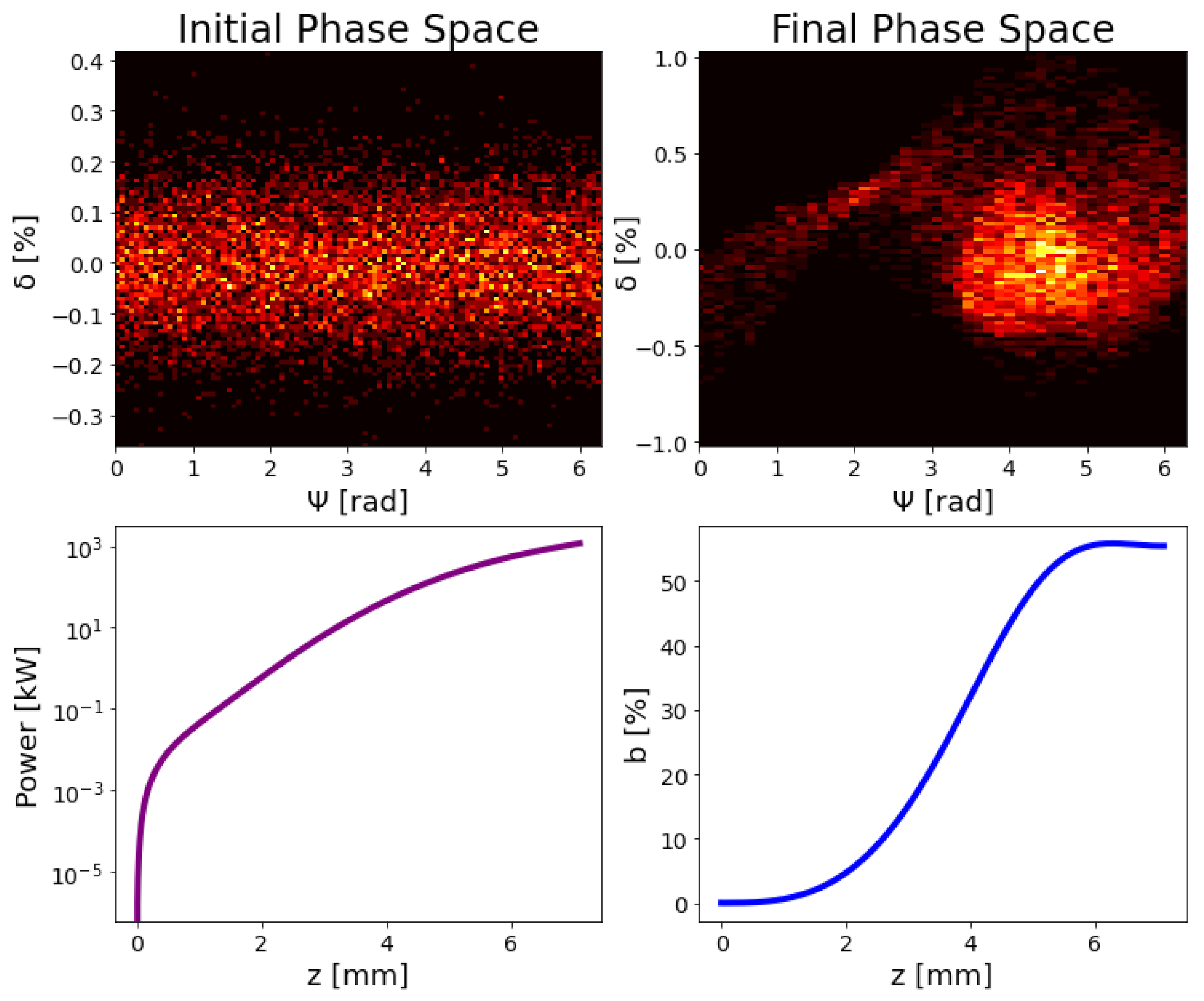
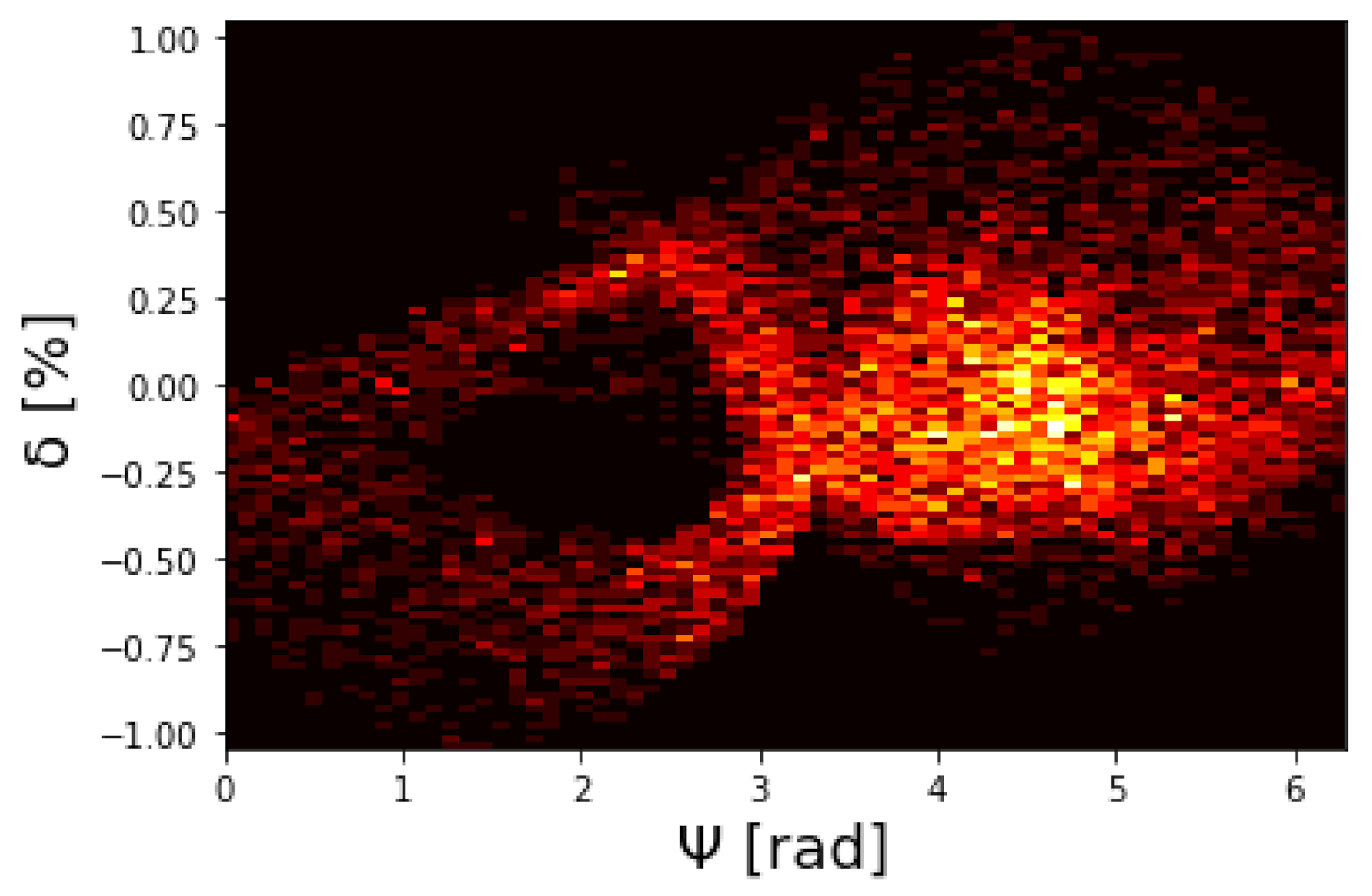
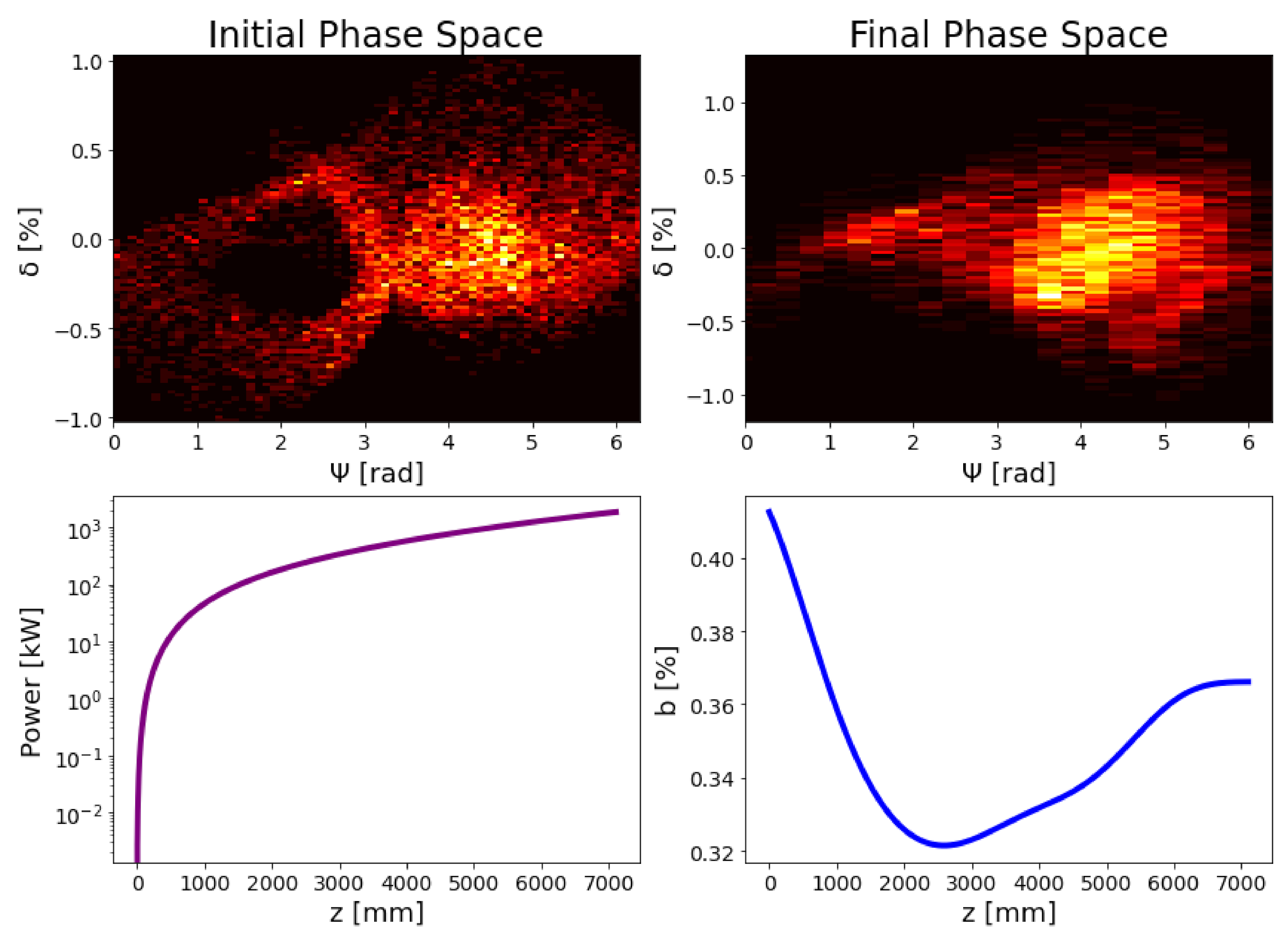
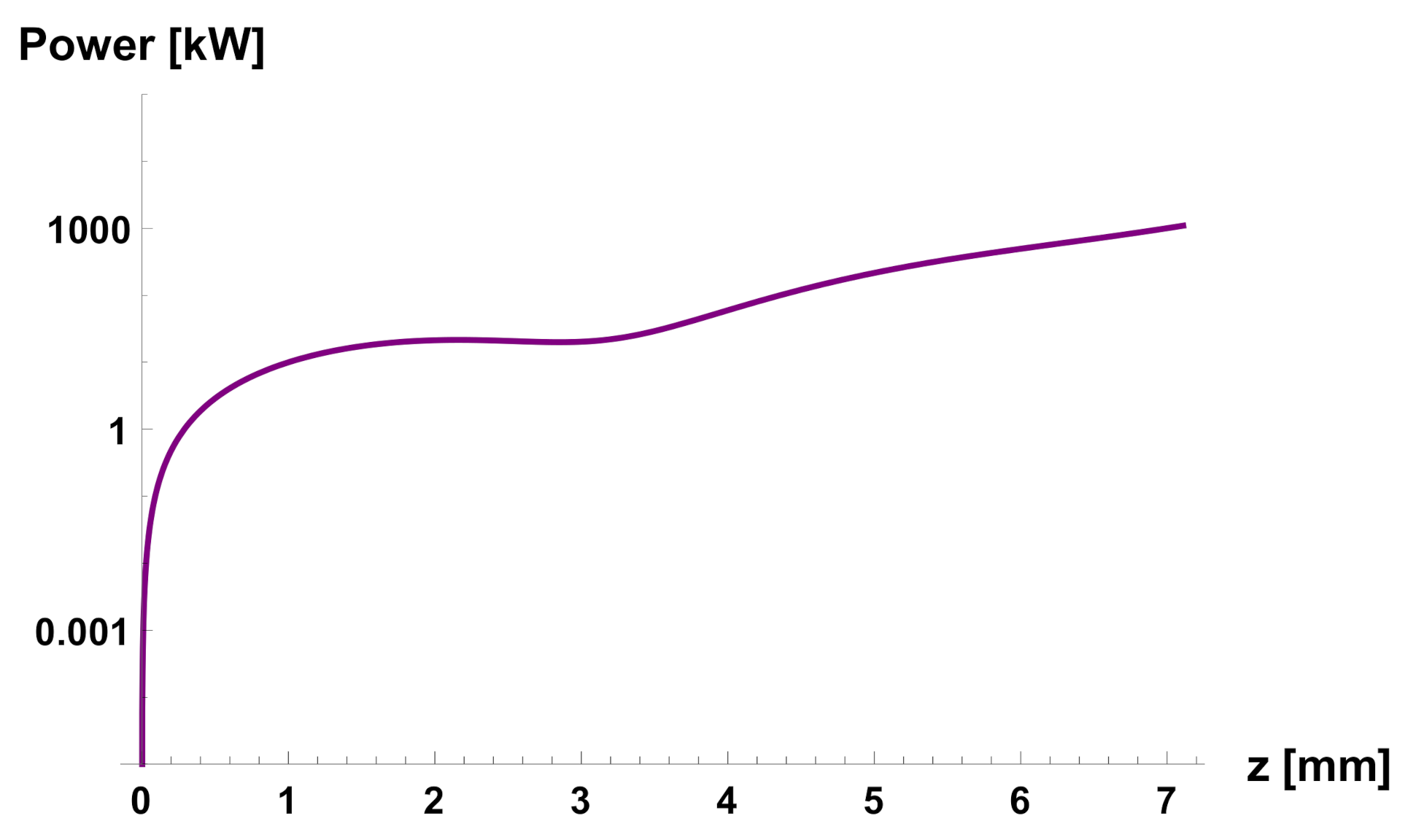
8. FEL Radiation: Numerical Simulations
9. FEL Radiation: Comparison with the Analytic Model
10. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Derivation of the 1D FEL Equations for the Wave Undulator
References
- O’Shea, P.G.; Freund, H.P. Free-electron lasers: Status and applications. Science 2001, 292, 1853–1858. [Google Scholar] [CrossRef] [PubMed]
- McNeil, B.W.; Thompson, N.R. X-ray free-electron lasers. Nat. Photonics 2010, 4, 814–821. [Google Scholar] [CrossRef]
- Brau, C.A. Free-electron lasers. Science 1988, 239, 1115–1121. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Barletta, W.A.; Bisognano, J.; Corlett, J.N.; Emma, P.; Huang, Z.; Kim, K.J.; Lindberg, R.; Murphy, J.B.; Neil, G.R.; Nguyen, D.C.; et al. Free electron lasers: Present status and future challenges. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2010, 618, 69–96. [Google Scholar] [CrossRef]
- Colson, W.B.; Sessler, A.M. Free electron lasers. Annu. Rev. Nucl. Part. Sci. 1985, 35, 25–54. [Google Scholar] [CrossRef][Green Version]
- Allaria, E.; Badano, L.; Bassanese, S.; Capotondi, F.; Castronovo, D.; Cinquegrana, P.; Danailov, M.B.; D’Auria, G.; Demidovich, A.; Monte, R.D.; et al. The FERMI free-electron lasers. J. Synchrotron Radiat. 2015, 22, 485–491. [Google Scholar] [CrossRef]
- Schmüser, P.; Dohlus, M.; Rossbach, J.; Behrens, C. Free-Electron Lasers in the Ultraviolet and X-ray Regime; Springer Tracts in Modern Physics; Springer: Berlin/Heidelberg, Germany, 2014; Volume 258. [Google Scholar]
- Pellegrini, C.; Marinelli, A.; Reiche, S. The physics of X-ray free-electron lasers. Rev. Mod. Phys. 2016, 88, 015006. [Google Scholar] [CrossRef]
- Feng, C.; Deng, H.X. Review of fully coherent free-electron lasers. Nucl. Sci. Tech. 2018, 29, 1–15. [Google Scholar] [CrossRef]
- Pellegrini, C. The history of X-ray free-electron lasers. Eur. Phys. J. H 2012, 37, 659–708. [Google Scholar] [CrossRef]
- Margaritondo, G.; Rebernik Ribic, P. A simplified description of X-ray free-electron lasers. J. Synchrotron Radiat. 2011, 18, 101–108. [Google Scholar] [CrossRef]
- Curcio, A.; Dattoli, G.; Di Palma, E.; Petralia, A. Free electron laser oscillator efficiency. Opt. Commun. 2018, 425, 29–37. [Google Scholar] [CrossRef]
- Honkavaara, K. Status of the FLASH FEL User Facility at DESY. In Proceedings of the 38th International Free Electron Laser Conference, Santa Fe, NM, USA, 20–25 August 2017. [Google Scholar]
- Rönsch-Schulenburg, J.; Honkavaara, K.; Schreiber, S.; Treusch, R.; Vogt, M. FLASH-Status and Upgrades. In Proceedings of the 39th International Free Electron Laser Conference (FEL’19), Hamburg, Germany, 26–30 August 2019. [Google Scholar]
- Corde, S.; Phuoc, K.T.; Lambert, G.; Fitour, R.; Malka, V.; Rousse, A.; Beck, A.; Lefebvre, E. Femtosecond X rays from laser-plasma accelerators. Rev. Mod. Phys. 2013, 85, 1–58. [Google Scholar] [CrossRef]
- Esarey, E.; Shadwick, B.A.; Catravas, P.; Leemans, W.P. Synchrotron radiation from electron beams in plasma-focusing channels. Phys. Rev. E 2002, 65, 056505. [Google Scholar] [CrossRef]
- Aschikhin, A.; Behrens, C.; Bohlen, S.; Dale, J.; Delbos, N.; Di Lucchio, L.; Elsen, E.; Erbe, J.-H.; Felber, M.; Foster, B.; et al. The FLASHForward facility at DESY. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 806, 175–183. [Google Scholar] [CrossRef]
- Dobsiach, P.; Meystre, P.; Scully, M.O. Optical wiggler free-electron X-ray laser in the 5 Å region. IEEE J. Quantum Electron. 1983, 19, 1812–1820. [Google Scholar] [CrossRef]
- Ciocci, F.; Dattoli, G.; Walsh, J. A short note on the wave-undulator FEL operation. Nucl. Instrum. Methods A 1985, 237, 401–403. [Google Scholar] [CrossRef]
- Banacloche, J.G.; Moore, G.T.; Schlicher, R.R.; Scully, M.O.; Walther, H. Soft X-Ray freeelectron laser with a laser undulator. IEEE J. Quantum Electron. 1987, 23, 1558–1570. [Google Scholar] [CrossRef]
- Tang, C.M.; Hafizi, B.; Ride, S.K. Thomson backscattered X-rays from an intense laser beam. Nucl. Instrum. Methods A 1993, 331, 371–378. [Google Scholar] [CrossRef]
- Dattoli, G.; Letardi, T.; Vazquez, L.R. FEL SASE WAVE undulators. Opt. Commun. 2012, 285, 5341–5346. [Google Scholar] [CrossRef]
- Bacci, A.; Ferrario, M.; Maroli, C.; Petrillo, V.; Serafini, L. Transverse effects in the production of x rays with a free-electron laser based on an optical undulator. Phys. Rev. Spec. Top.-Accel. Beams 2006, 9, 060704. [Google Scholar] [CrossRef]
- Polyanskiy, M.N.; Pogorelsky, I.V.; Yakimenko, V. Picosecond pulse amplification in isotopic CO2 active medium. Opt. Express 2011, 19, 7717–7725. [Google Scholar] [CrossRef] [PubMed]
- Bazarov, I.V.; Dunham, B.M.; Sinclair, C.K. Maximum achievable beam brightness from photoinjectors. Phys. Rev. Lett. 2009, 102, 104801. [Google Scholar] [CrossRef] [PubMed]
- Dattoli, G.; Petrillo, V.; Rau, J.V. FEL SASE and wave-undulators. Opt. Commun. 2012, 285, 5341–5346. [Google Scholar] [CrossRef]
- Curcio, A.; Dattoli, G.; Ferrario, M.; Giulietti, D.; Nguyen, F. An optical cavity design for a compact wave-undulator based-FEL. Opt. Commun. 2017, 405, 197–200. [Google Scholar] [CrossRef]
- Curcio, A.; Panas, R.; Knafel, M.; Wawrzyniak, A.I. Liouville theory for fully analytic studies of longitudinal beam dynamics and bunch profile reconstruction in dispersive lines. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2021, 986, 164755. [Google Scholar] [CrossRef]
- Svelto, O. Principles of Lasers; Plenum Press: New York, NY, USA, 1976; p. 386. [Google Scholar]
- Babusci, D.; Dattoli, G.; Quattromini, M. Relativistic equations with fractional and pseudodifferential operators. Phys. Rev. A 2011, 83, 062109. [Google Scholar] [CrossRef]
- Di Mitri, S. Bunch length compressors. CERN Yellow Rep. Sch. Proc. 2018, 1, 363. [Google Scholar] [CrossRef]
- Landau, L.D. (Ed.) The Classical Theory of Fields; Elsevier: Amsterdam, The Netherlands, 2013; Volume 2. [Google Scholar]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Nonlinear harmonic generation in high-gain free-electron lasers. J. Appl. Phys. 2005, 97, 113102. [Google Scholar] [CrossRef]
- Dattoli, G.; Ottaviani, P.L.; Pagnutti, S. Booklet for FEL Design; ENEA-Edizioni Scientifiche: Frascati, Italy, 2007. [Google Scholar]
- Lau, Y.Y.; He, F.; Umstadter, D.P.; Kowalczyk, R. Nonlinear Thomson scattering: A tutorial. Phys. Plasmas 2003, 10, 2155–2162. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Curcio, A. Recirculated Wave Undulators for Compact FELs. Appl. Sci. 2021, 11, 5936. https://doi.org/10.3390/app11135936
Curcio A. Recirculated Wave Undulators for Compact FELs. Applied Sciences. 2021; 11(13):5936. https://doi.org/10.3390/app11135936
Chicago/Turabian StyleCurcio, Alessandro. 2021. "Recirculated Wave Undulators for Compact FELs" Applied Sciences 11, no. 13: 5936. https://doi.org/10.3390/app11135936
APA StyleCurcio, A. (2021). Recirculated Wave Undulators for Compact FELs. Applied Sciences, 11(13), 5936. https://doi.org/10.3390/app11135936





