Experimental Analysis and Prediction Model of Milling-Induced Residual Stress of Aeronautical Aluminum Alloys
Abstract
:Featured Application
Abstract
1. Introduction
2. Milling-Induced Residual Stress Experiment of 7075 Aluminum Alloy
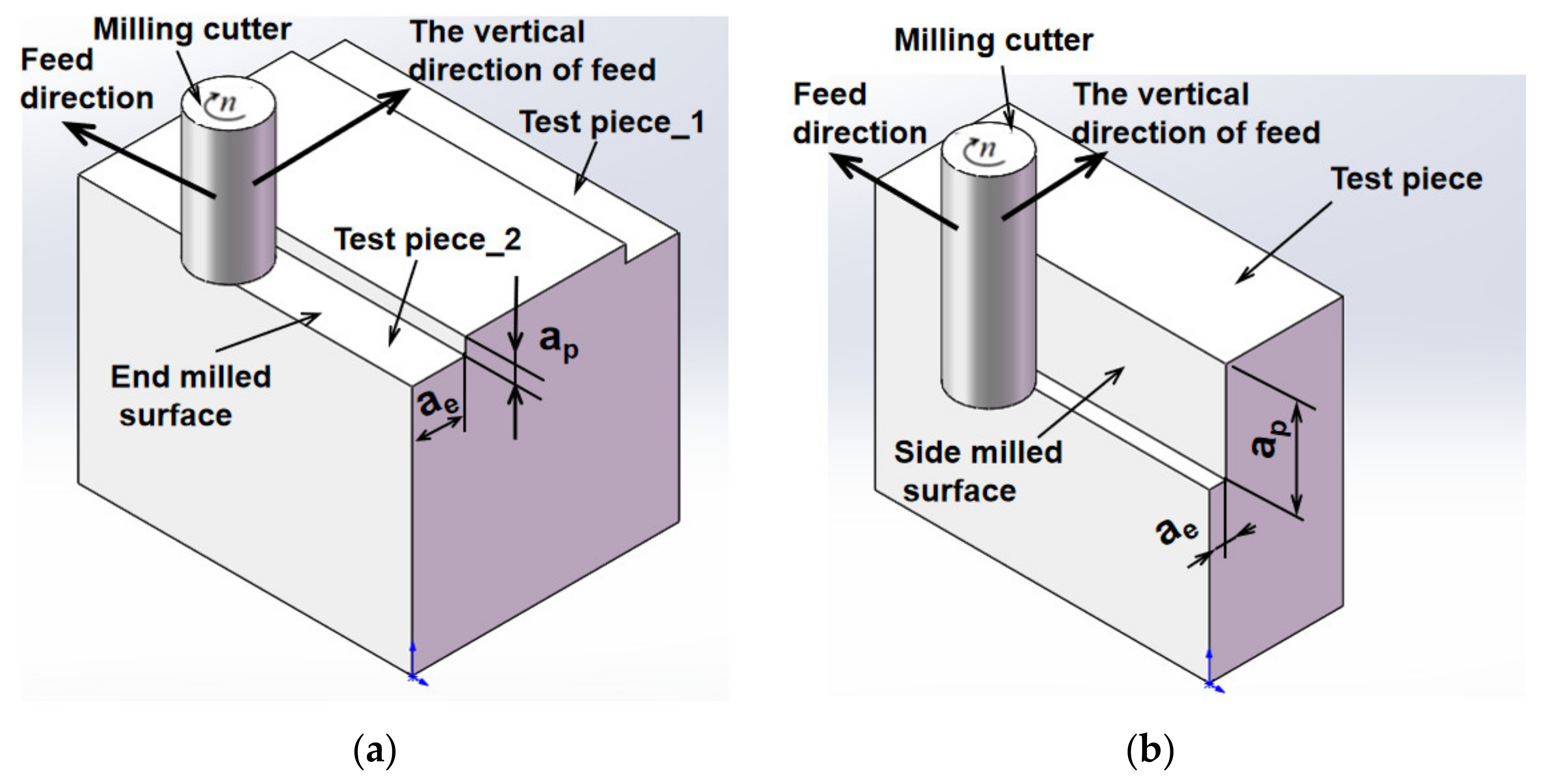
2.1. Design of the Experimental Study
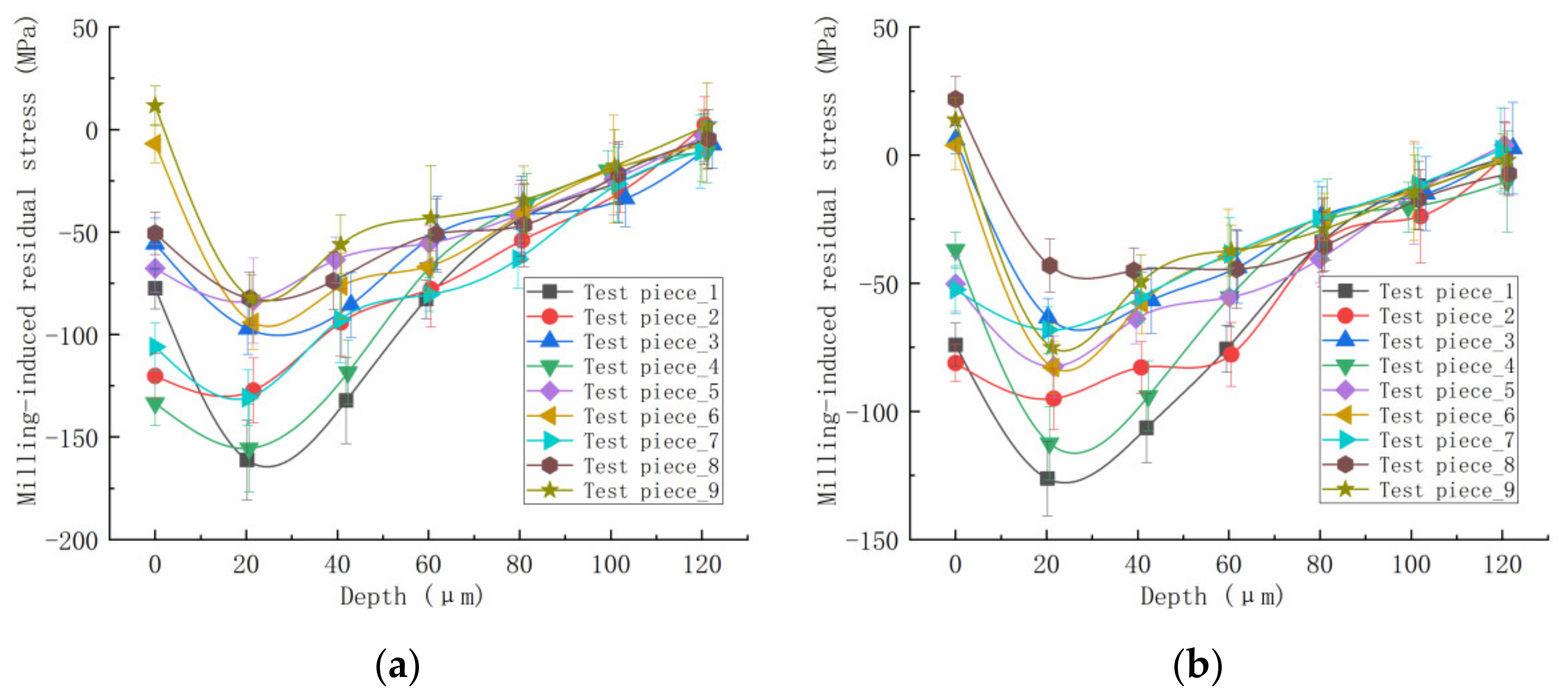
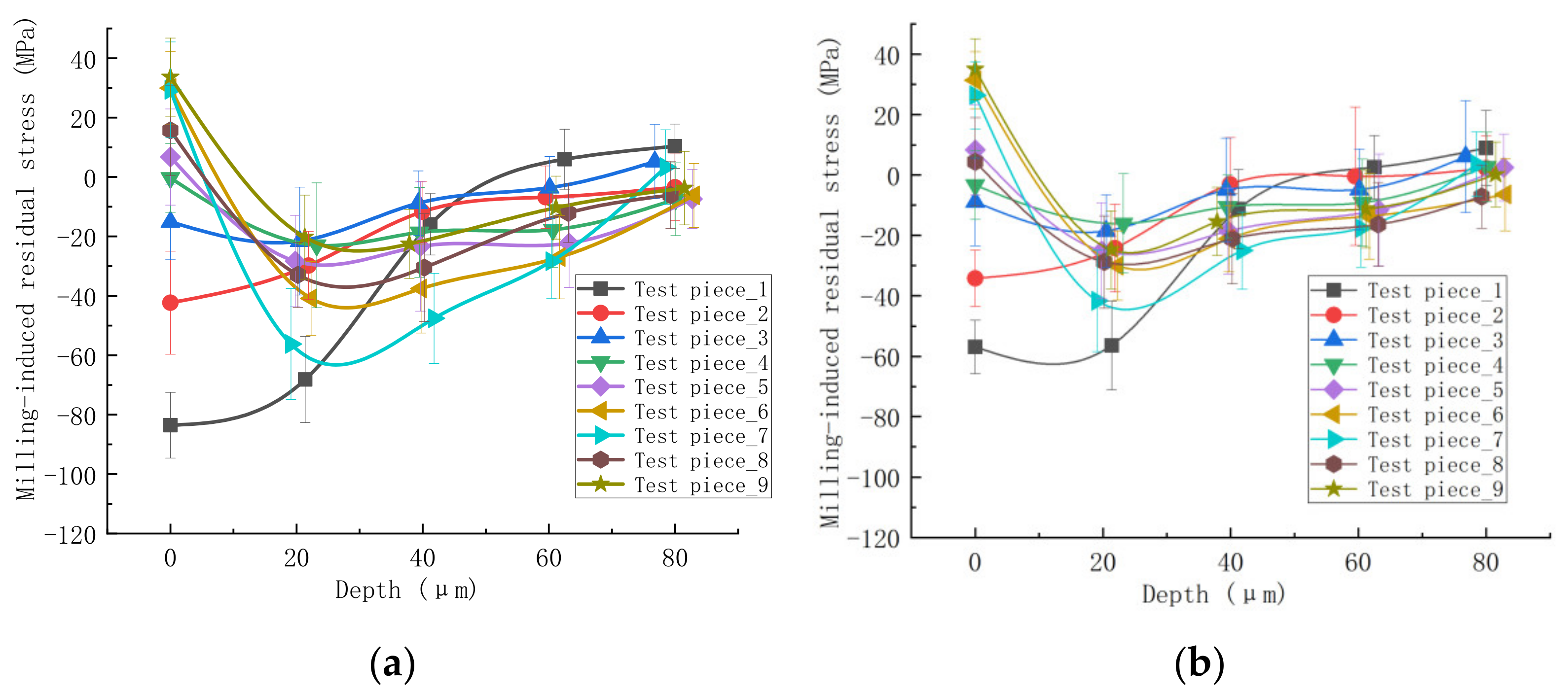
2.2. Test Results of Milling-Induced Residual Stress
- (1)
- The condition of end milling.
- (2)
- The condition of side milling.
3. Prediction Model of Milling-Induced Residual Stress
3.1. Formulation of BP Neural Network
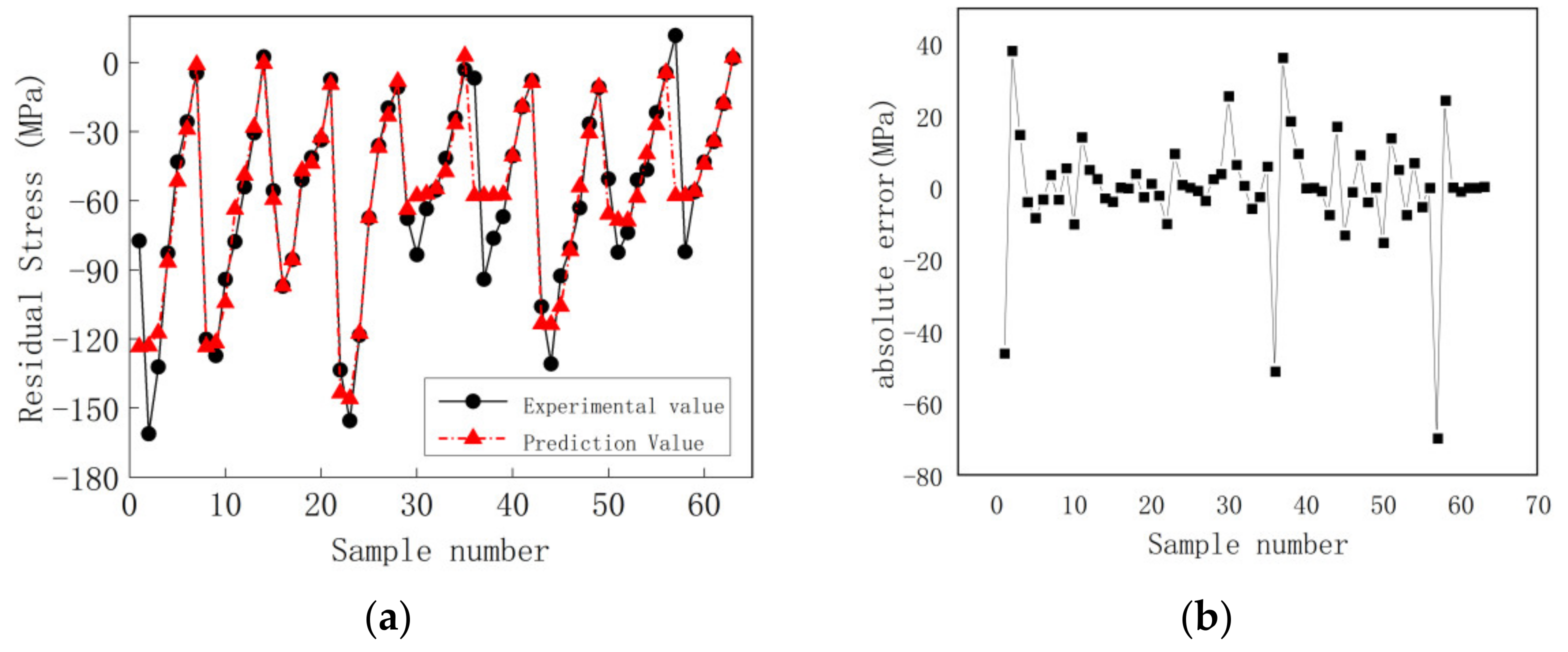
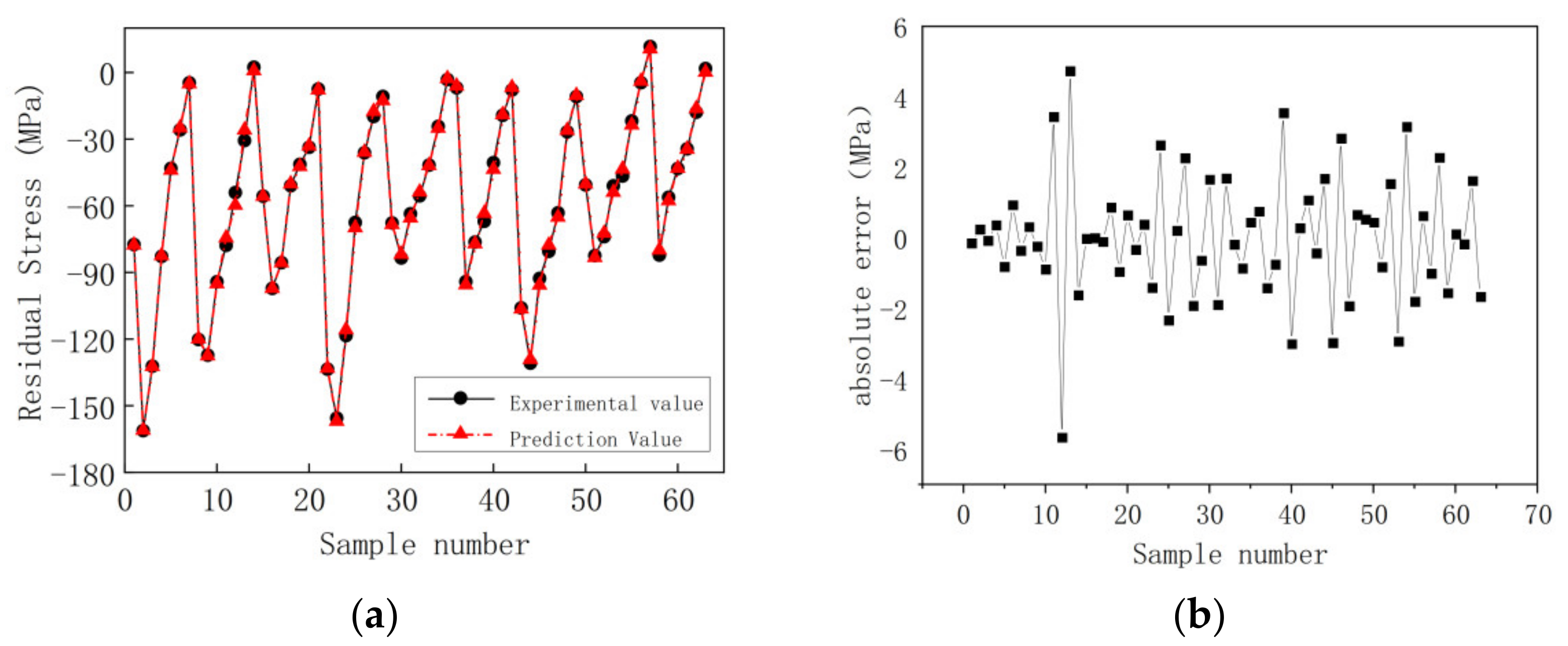
3.2. BP Neural Network Optimized by Genetic Algorithm
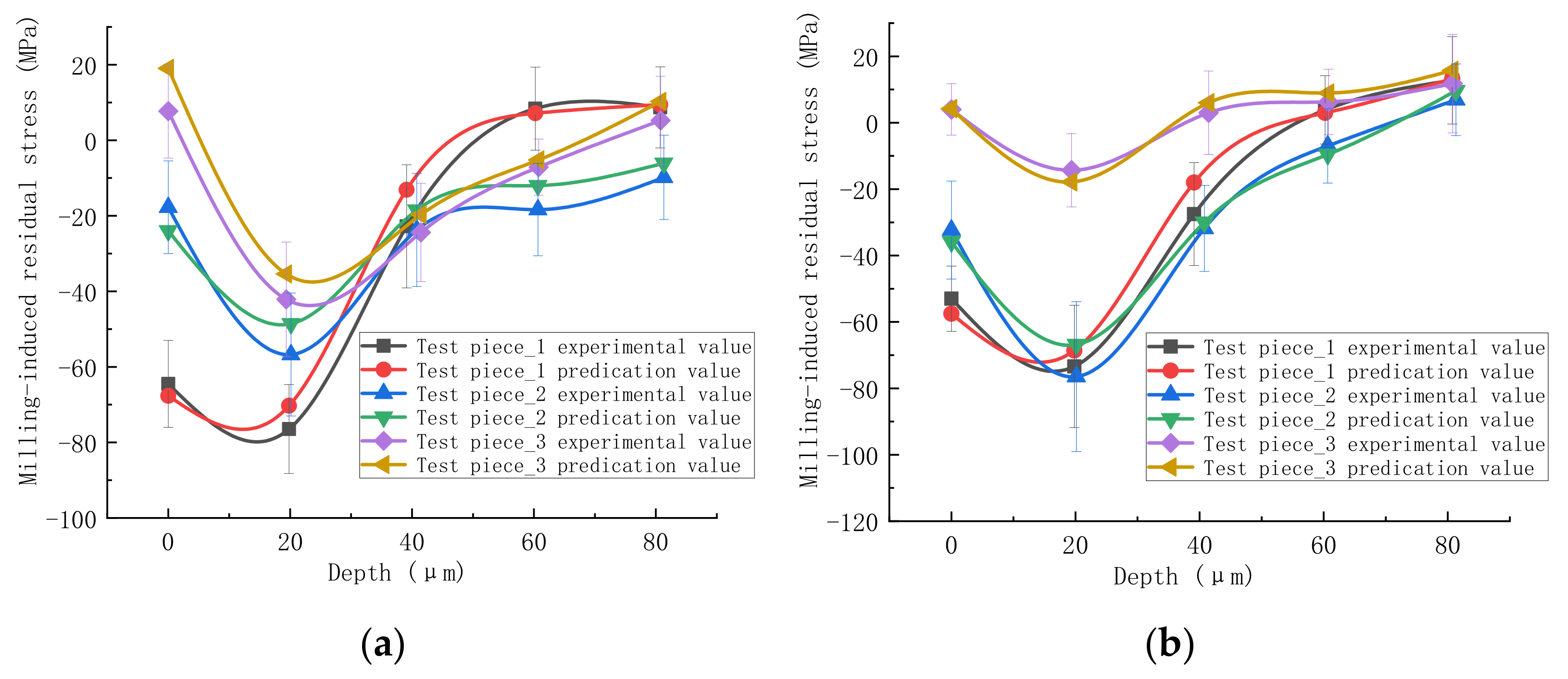
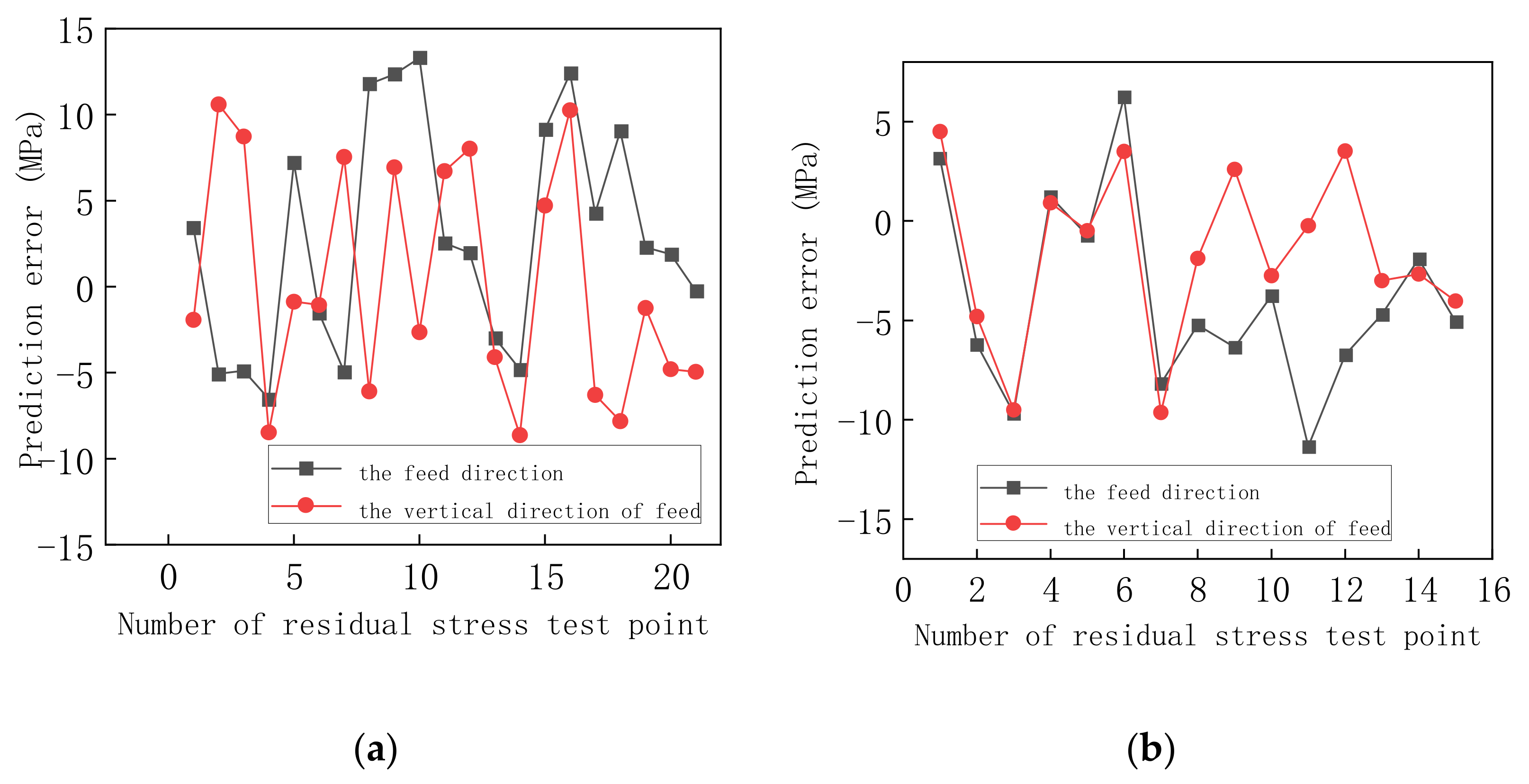
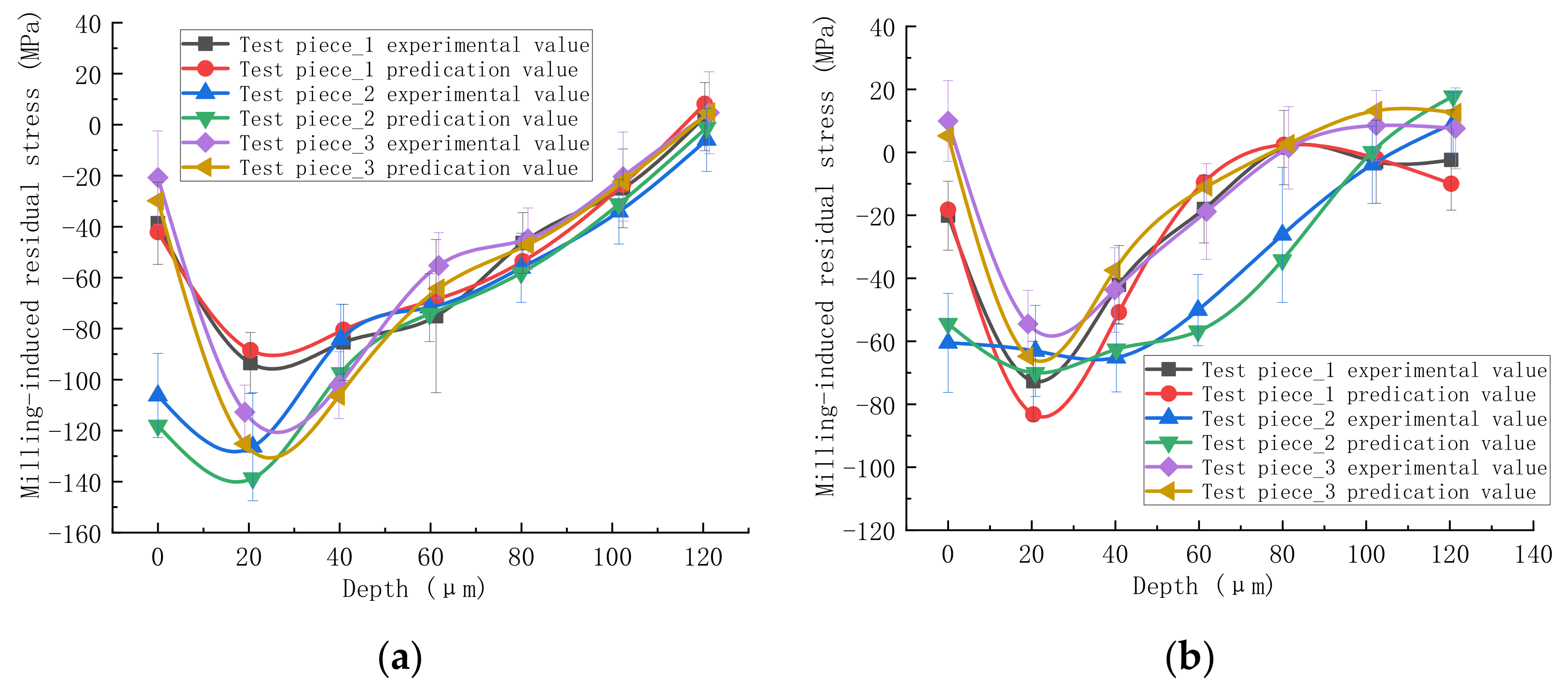
3.3. Validation of BP Neural Network Model
4. Conclusions
5. Replication of Results
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duan, Z.; Li, C.; Ding, W.; Zhang, Y.; Yang, M.; Gao, T.; Cao, H.; Xu, X.; Wang, D.; Mao, C.; et al. Milling Force Model for Aviation Aluminum Alloy: Academic Insight and Perspective Analysis. Chin. J. Mech. Eng. 2021, 34, 18. [Google Scholar] [CrossRef]
- Li, H.; Jia, L.; Huang, J.; Ma, Y. Precipitation behavior and properties of extruded 7136 aluminum alloy under different aging treatments. Chin. J. Aeronaut. 2021, 34, 612–619. [Google Scholar] [CrossRef]
- Chatterjee, B.; Bhowmik, S. Evolution of material selection in commercial aviation industry—A review. Sustain. Eng. Prod. Manuf. Technol. 2019, 199–219. [Google Scholar] [CrossRef]
- Ji, M.; Li, W.; Liu, H.; Zhu, L.; Chen, H.; Li, W. Effect of titanium sol on sulfuric-citric acids anodizing of 7150 aluminum alloy. Surf. Interfaces 2020, 19, 100479. [Google Scholar] [CrossRef]
- He, S.; Chen, S.; Zhao, Y.; Qi, N.; Zhan, X. Study on the intelligent model database modeling the laser welding for aerospace aluminum alloy. J. Manuf. Process. 2021, 63, 121–129. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, X.; Xia, Q.; Yan, C. Strengthening effect of laser shock peening on 7075-T6 aviation aluminum alloy. Adv. Mech. Eng. 2020, 12, 1687814020952177. [Google Scholar] [CrossRef]
- Zhong, H.; Liu, Z.; Qin, H.; Liu, Y. Static analysis of thin-walled space frame structures with arbitrary closed cross-sections using transfer matrix method. Thin Walled Struct. 2018, 123, 255–269. [Google Scholar] [CrossRef]
- Sedeh, M.R.N.; Ghaei, A. The effects of machining residual stresses on springback in deformation machining bending mode. Int. J. Adv. Manuf. Technol. 2021, 114, 1087–1098. [Google Scholar] [CrossRef]
- Sahraei, A.; Pezeshky, P.; Sasibut, S.; Rong, F.; Mohareb, M. Closed form solutions for shear deformable thin-walled beams including global and through-thickness warping effects. Thin Walled Struct. 2021, 158, 107190. [Google Scholar] [CrossRef]
- Singh, A.; Agrawal, A. Comparison of deforming forces, residual stresses and geometrical accuracy of deformation machining with conventional bending and forming. J. Mater. Process. Technol. 2016, 234, 259–271. [Google Scholar] [CrossRef]
- Santos, M.C.; Machado, A.R.; Sales, W.F.; Barrozo, M.A.S.; Ezugwu, E.O. Machining of aluminum alloys: A review. Int. J. Adv. Manuf. Technol. 2016, 86, 3067–3080. [Google Scholar] [CrossRef]
- Ruitao, P.; Linfeng, Z.; Jiawei, T.; Xiuli, F.; Meiliang, C. Application of pre-stressed cutting to aviation alloy: The effect on residual stress and surface roughness. J. Manuf. Process. 2021, 62, 501–512. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, M.; Tang, K.; Zhang, D. A new in-processes active control method for reducing the residual stresses induced deformation of thin-walled parts. J. Manuf. Process. 2020, 59, 316–325. [Google Scholar] [CrossRef]
- Li, J.G.; Wang, S.Q. Distortion caused by residual stresses in machining aeronautical aluminum alloy parts: Recent advances. Int. J. Adv. Manuf. Technol. 2017, 89, 997–1012. [Google Scholar] [CrossRef]
- Guo, J.; Fu, H.; Pan, B.; Kang, R. Recent progress of residual stress measurement methods: A review. Chin. J. Aeronaut. 2021, 34, 54–78. [Google Scholar] [CrossRef]
- Mirkoohi, E.; Bocchini, P.; Liang, S.Y. Inverse analysis of residual stress in orthogonal cutting. J. Manuf. Process. 2019, 38, 462–471. [Google Scholar] [CrossRef]
- Shan, C.; Zhang, M.; Zhang, S.; Dang, J. Prediction of machining-induced residual stress in orthogonal cutting of Ti6Al4V. Int. J. Adv. Manuf. Technol. 2020, 107, 2375–2385. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, Z.; Hua, Y.; Zhao, J.; Lv, W.; Hassan Mohsan, A.U. Effects of cutting edge micro-geometry on residual stress in orthogonal cutting of Inconel 718 by FEM. Materials 2018, 11, 1015. [Google Scholar] [CrossRef] [Green Version]
- Ji, C.; Sun, S.; Lin, B.; Fei, J. Effect of cutting parameters on the residual stress distribution generated by pocket milling of 2219 aluminum alloy. Adv. Mech. Eng. 2018, 10, 1687814018813055. [Google Scholar] [CrossRef]
- Liu, X.; Xiong, R.; Xiong, Z.; Zhang, S.; Zhao, L. Simulation and experimental study on surface residual stress of ultra-precision turned 2024 aluminum alloy. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–7. [Google Scholar] [CrossRef]
- Salvati, E.; Korsunsky, A.M. A simplified FEM eigenstrain residual stress reconstruction for surface treatments in rbitrary 3D geometries. Int. J. Mech. Sci. 2018, 4, 138–139. [Google Scholar]
- Meng, L.; Khan, A.M.; Zhang, H.; Fang, C.; He, N. Research on surface residual stresses generated by milling Ti6Al4V alloy under different pre-stresses. Int. J. Adv. Manuf. Technol. 2020, 107, 2597–2608. [Google Scholar] [CrossRef]
- Zhang, S.; Gong, M.; Zeng, X.; Gao, M. Residual stress and tensile anisotropy of hybrid wire arc additive-milling subtractive manufacturing. J. Mater. Process. Technol. 2021, 293, 117077. [Google Scholar] [CrossRef]
- Xiong, Y.; Wang, W.; Shi, Y.; Jiang, R.; Shan, C.; Liu, X.; Link, K. Investigation on surface roughness, residual stress and fatigue property of milling in-situ TiB2/7050Al metal matrix composites. Chin. J. Aviat. 2021, 34, 451–464. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, X.; Leopold, J.; Ding, H. Analytical Model for Prediction of Residual Stress in Dynamic Orthogonal Cutting Process. ASME J. Manuf. Sci. Eng. 2018, 140, 011002. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, L.; Yan, P.; Feng, L.; Qiu, T.; Wang, X.; Zhang, N. Prediction of surface residual stress in end milling with Gaussian process regression. Measurement 2021, 178, 109333. [Google Scholar] [CrossRef]
- Vovk, A.; Sölter, J.; Karpuschewski, B. Finite element simulations of the material loads and residual stresses in milling utilizing the CEL method. Procedia CIRP 2020, 87, 539–544. [Google Scholar] [CrossRef]
- Zhou, R.; Yang, W. Analytical modeling of machining-induced residual stresses in milling of complex surface. Int. J. Adv. Manuf. Technol. 2019, 105, 565–577. [Google Scholar] [CrossRef]
- Reimer, A.; Luo, X. Prediction of residual stress in precision milling of AISI H13 steel. Procedia CIRP 2018, 71, 329–334. [Google Scholar] [CrossRef]
- Morin, L.; Braham, C.; Tajdary, P.; Seddik, R.; Gonzalez, G. Reconstruction of heterogeneous surface residual-stresses in metallic materials from X-ray diffraction measurements. Mech. Mater. 2021, 158, 103882. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| Stroke (mm) | X = 630, Y = 560, Z = 560 |
| B-axis swing angle (°) | −120~+30 |
| Maximum spindle speed (r/min) | 12,000 |
| Maximum feed rate of linear axis (mm/min) | 30,000 |
| Positioning accuracy (mm) | 0.006 |
| Control system | Heidenhain iTNC530 |
| Test Piece Number | vc (m/min) | fz (mm) | ap (mm) | ae (mm) |
|---|---|---|---|---|
| 1 | 125.6 | 0.01 | 0.5 | 10 |
| 2 | 125.6 | 0.025 | 1 | 15 |
| 3 | 125.6 | 0.05 | 1.5 | 20 |
| 4 | 376.8 | 0.01 | 1 | 20 |
| 5 | 376.8 | 0.025 | 1.5 | 10 |
| 6 | 376.8 | 0.05 | 0.5 | 15 |
| 7 | 628 | 0.01 | 1.5 | 15 |
| 8 | 628 | 0.025 | 0.5 | 20 |
| 9 | 628 | 0.05 | 1 | 10 |
| Test Piece Number | vc (m/min) | fz (mm) | ap (mm) | ae (mm) |
|---|---|---|---|---|
| 1 | 125.6 | 0.01 | 15 | 0.2 |
| 2 | 125.6 | 0.025 | 25 | 0.6 |
| 3 | 125.6 | 0.05 | 35 | 1 |
| 4 | 376.8 | 0.01 | 25 | 1 |
| 5 | 376.8 | 0.025 | 35 | 0.2 |
| 6 | 376.8 | 0.05 | 15 | 0.6 |
| 7 | 628 | 0.01 | 35 | 0.6 |
| 8 | 628 | 0.025 | 15 | 1 |
| 9 | 628 | 0.05 | 25 | 2 |
| X-ray Diffraction Parameters | Specification/Values |
|---|---|
| Tube type | Cr |
| Supplied current during the experiment | 6.7 mA |
| Supplied voltage during the experiment | 30 kV |
| Exposure time for the calibration | 8 s |
| Exposure time for measurement | 10 s |
| Collimator diameter | 3 mm |
| Collimator distance | 10.390 mm |
| 2-theta angle | 138.75° |
| Tilt angle | −45° to 45° |
| Number of tilts | 5/5 |
| Rotation angle | 0° to 90° |
| Number of rotations | 2 |
| Stress resolution | ±10 MPa |
| Poisson ratio | 0.33 |
| Young’s modulus | 70.3 GPa |
| Electrolytic Polishing Parameters | Specification/Values |
|---|---|
| Electrolyte | NaCl |
| Voltage | 40 V |
| Flowrate | 10 |
| Working current | 2 A |
| Area | 63.59 mm2 |
| Test Piece Number | vc (m/min) | fz (mm/z) | ap (mm) | ae (mm) | (MPa) | (MPa) |
|---|---|---|---|---|---|---|
| 1 | 125.6 | 0.01 | 0.50 | 10.00 | −84.77 | −67.56 |
| 2 | 125.6 | 0.025 | 1.00 | 15.00 | −76.56 | −61.18 |
| 3 | 125.6 | 0.05 | 1.50 | 20.00 | −60.34 | −36.40 |
| 4 | 376.8 | 0.01 | 1.00 | 20.00 | −80.45 | −58.48 |
| 5 | 376.8 | 0.025 | 1.50 | 10.00 | −52.16 | −48.36 |
| 6 | 376.8 | 0.05 | 0.50 | 15.00 | −53.78 | −39.35 |
| 7 | 628 | 0.01 | 1.50 | 15.00 | −77.18 | −38.26 |
| 8 | 628 | 0.025 | 0.50 | 20.00 | −51.93 | −31.72 |
| 9 | 628 | 0.05 | 1.00 | 10.00 | −41.43 | −36.46 |
| Test Piece Number | vc (m/min) | fz (mm/z) | ap (mm) | ae (mm) | (MPa) | (MPa) |
|---|---|---|---|---|---|---|
| 1 | 125.6 | 0.01 | 15.00 | 0.20 | −31.32 | −25.17 |
| 2 | 125.6 | 0.025 | 25.00 | 0.60 | −18.65 | −12.17 |
| 3 | 125.6 | 0.05 | 35.00 | 1.00 | −10.69 | −8.74 |
| 4 | 376.8 | 0.01 | 25.00 | 1.00 | −17.34 | −10.40 |
| 5 | 376.8 | 0.025 | 35.00 | 0.20 | −21.57 | −14.96 |
| 6 | 376.8 | 0.05 | 15.00 | 0.60 | −27.22 | −16.17 |
| 7 | 628 | 0.01 | 35.00 | 0.60 | −34.04 | −21.65 |
| 8 | 628 | 0.025 | 15.00 | 1.00 | −19.96 | −18.86 |
| 9 | 628 | 0.05 | 25.00 | 0.20 | −11.18 | −11.49 |
| Source | The Feed Direction | The Vertical Direction of Feed | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SS | df | MS | F-Value | p-Value | SS | df | MS | F-Value | p-Value | |
| Regression analysis | 1616.59 | 4 | 404.15 | 4.91 | 0.0762 | 1177.22 | 4 | 294.31 | 6.97 | 0.0433 |
| Vc | 435.71 | 1 | 435.71 | 5.29 | 0.0829 | 574.28 | 1 | 574.28 | 13.59 | 0.0211 |
| fz | 1146.41 | 1 | 1146.41 | 13.93 | 0.0203 | 451.56 | 1 | 451.56 | 10.69 | 0.0308 |
| ap | 0.1067 | 1 | 0.1067 | 0.0013 | 0.973 | 40.61 | 1 | 40.61 | 0.9612 | 0.3824 |
| ae | 34.37 | 1 | 34.37 | 0.4176 | 0.5534 | 110.77 | 1 | 110.77 | 2.62 | 0.1807 |
| Residual | 329.24 | 4 | 82.31 | 169.01 | 4 | 42.25 | ||||
| Cor Total | 1945.83 | 8 | 1346.23 | 8 | ||||||
| Source | The Feed Direction | The Vertical Direction of Feed | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| SS | df | MS | F-Value | p-Value | SS | df | MS | F-Value | p-Value | |
| Regression analysis | 245.43 | 4 | 61.36 | 0.8409 | 0.5647 | 143.36 | 4 | 35.84 | 1.45 | 0.3638 |
| Vc | 3.41 | 1 | 3.41 | 0.0467 | 0.8395 | 5.84 | 1 | 5.84 | 0.2363 | 0.6523 |
| fz | 174.12 | 1 | 174.12 | 2.39 | 0.1973 | 69.84 | 1 | 69.84 | 2.83 | 0.1681 |
| ap | 24.81 | 1 | 24.81 | 0.34 | 0.5911 | 36.75 | 1 | 36.75 | 1.49 | 0.2897 |
| ae | 43.09 | 1 | 43.09 | 0.5906 | 0.4851 | 30.92 | 1 | 30.92 | 1.25 | 0.326 |
| Residual | 291.87 | 4 | 72.97 | 98.88 | 4 | 24.72 | ||||
| Cor Total | 537.31 | 8 | 242.24 | 8 | ||||||
| Test Piece Number | vc (m/min) | fz (mm/z) | ap (mm) | ae (mm) |
|---|---|---|---|---|
| 1 | 188.4 | 0.04 | 0.5 | 15 |
| 2 | 251.2 | 0.02 | 1.2 | 12 |
| 3 | 376.8 | 0.04 | 0.6 | 13 |
| Test Piece Number | vc (m/min) | fz (mm/z) | ap (mm) | ae (mm) |
|---|---|---|---|---|
| 1 | 188.4 | 0.01 | 15 | 0.2 |
| 2 | 251.2 | 0.02 | 18 | 0.5 |
| 3 | 376.8 | 0.03 | 24 | 0.9 |
| Filename | Description |
|---|---|
| ED-RS.xlsx | Experimental data on residual stress |
| VD-RS.xlsx | Verification data of residual stress experiment |
| P_ESRS.m | Calculation program of equivalent side milling residual stress |
| P_EERS.m | Calculation program of equivalent end milling residual stress |
| Basic data for(eq.2-eq.5).xlsx | Basic data for Equations (2)–(5) |
| CC_EQ2_3.m | Procedure for calculating the coefficients and exponents of Equations (2) and (3) |
| CC_EQ4_5.m | Procedure for calculating the coefficients and exponents of Equations (4) and (5) |
| Main_BP_TP_E_FD.m | Training program of BP neural network for residual stress in feed direction in end milling mode |
| Main_BP_TP_E_VFD.m | Training program of BP neural network for residual stress in vertical feed direction in end milling mode |
| Main_BP_TP_S_FD.m | Training program of BP neural network for residual stress in feed direction in side milling mode |
| Main_BP_TP_S_VFD.m | Training program of BP neural network for residual stress in vertical feed direction in side milling mode |
| Main_BP_PP_E_FD.m | BP neural network prediction program for residual stress in feed direction in end milling mode |
| Main_BP_PP_E_VFD.m | BP neural network prediction program for residual stress in vertical feeding direction in end milling mode |
| Main_BP_PP_S_FD.m | BP neural network prediction program for residual stress in feed direction in side milling mode |
| Main_BP_PP_S_VFD.m | BP neural network prediction program for residual stress in vertical feeding direction in side milling mode |
| BP-END-feed direction.rar | Summary of BP neural network program for residual stress in the feed direction of end milling |
| BP-END-vertical feed direction.rar | Summary of BP neural network program for residual stress in the vertical feed direction of end milling |
| BP-SIDE-feed direction.rar | Summary of BP neural network program for residual stress in the feed direction of side milling |
| BP-SIDE-vertical feed direction.rar | Summary of BP neural network program for residual stress in the vertical feed direction of side milling |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yi, S.; Wu, Y.; Gong, H.; Peng, C.; He, Y. Experimental Analysis and Prediction Model of Milling-Induced Residual Stress of Aeronautical Aluminum Alloys. Appl. Sci. 2021, 11, 5881. https://doi.org/10.3390/app11135881
Yi S, Wu Y, Gong H, Peng C, He Y. Experimental Analysis and Prediction Model of Milling-Induced Residual Stress of Aeronautical Aluminum Alloys. Applied Sciences. 2021; 11(13):5881. https://doi.org/10.3390/app11135881
Chicago/Turabian StyleYi, Shouhua, Yunxin Wu, Hai Gong, Chenxi Peng, and Yongbiao He. 2021. "Experimental Analysis and Prediction Model of Milling-Induced Residual Stress of Aeronautical Aluminum Alloys" Applied Sciences 11, no. 13: 5881. https://doi.org/10.3390/app11135881
APA StyleYi, S., Wu, Y., Gong, H., Peng, C., & He, Y. (2021). Experimental Analysis and Prediction Model of Milling-Induced Residual Stress of Aeronautical Aluminum Alloys. Applied Sciences, 11(13), 5881. https://doi.org/10.3390/app11135881






