Modeling a New AQM Model for Internet Chaotic Behavior Using Petri Nets
Abstract
:1. Introduction
2. Related Work and Motivation
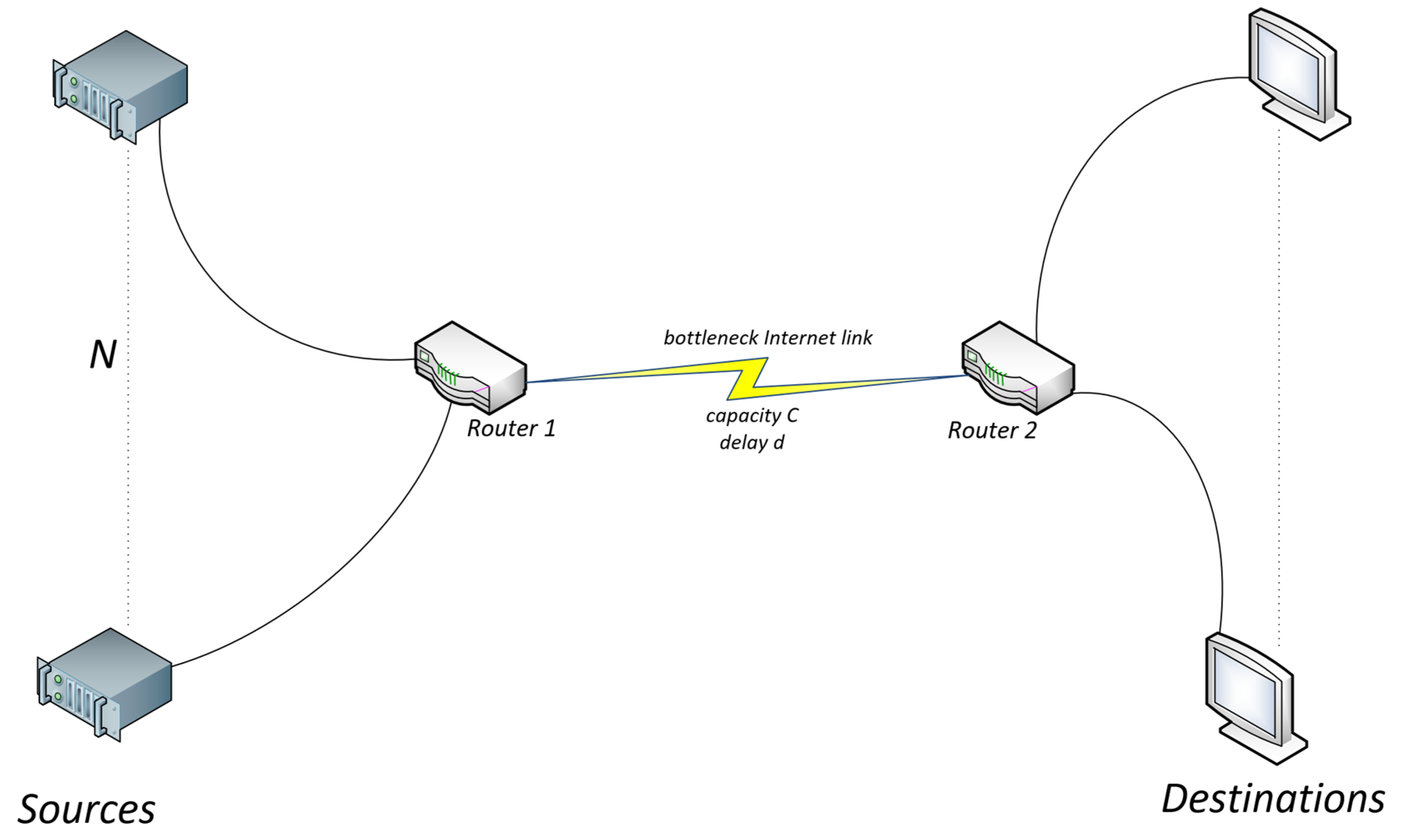
3. Dynamical Model for Congestion Control
Definition of Our Dynamical Model
| Algorithm 1. Drop mechanism for each packet arrival. |
 |
4. Formal Description of Our Dynamical Model Using Petri Nets
5. Validation
5.1. Matrix Equation
5.2. Reachability Tree
5.3. Invariance Analysis
5.4. Analysis of Properties
5.4.1. Reachability
5.4.2. Boundedness
5.4.3. Reversibility
5.4.4. Deadlock
5.4.5. Liveness
6. Numerical Simulations
6.1. Simulation Scenario
6.2. Performance Study
7. Conclusions
Ongoing Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kleinrock, L. An early history of the internet [History of Communications]. IEEE Commun. Mag. 2010, 48, 26–36. [Google Scholar] [CrossRef]
- Leiner, B.; Cerf, V.; Clark, D.; Kahn, R.; Kleinrock, L.; Lynch, D.; Postel, J.; Roberts, L.; Wolff, S. The past and future history of the Internet. Commun. ACM 1997, 40, 102–108. [Google Scholar] [CrossRef]
- Candela, M.; Luconi, V.; Vecchio, A. Impact of the COVID-19 pandemic on the Internet latency: A large-scale study. Comput. Netw. 2020, 182, 107495. [Google Scholar] [CrossRef]
- Duran, G.; Valero, J.; Amigó, J.M.; Giménez, A.; Bonastre, O.M. Bifurcation analysis for the Internet congestion. In Proceedings of the IEEE INFOCOM, Paris, France, 29 April–2 May 2019; pp. 1073–1074. [Google Scholar]
- Lorenz, E. Deterministic Non periodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef] [Green Version]
- Moon, F.C. Chaotic and Fractal Dynamics: An Introduction for Applied Scientists and Engineers; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Banerjee, S.; Mitra, M.; Rondoni, L. Applications of Chaos and Nonlinear Dynamics in Engineering; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1. [Google Scholar]
- Karimov, A.; Tutueva, A.; Karimov, T.; Druzhina, O.; Butusov, D. Adaptive Generalized Synchronization between Circuit and Computer Implementations of the Rössler System. Appl. Sci. 2021, 11, 81. [Google Scholar] [CrossRef]
- Karimov, T.; Nepomuceno, E.G.; Druzhina, O.; Karimov, A.; Butusov, D. Chaotic Oscillators as Inductive Sensors: Theory and Practice. Sensors 2019, 19, 4314. [Google Scholar] [CrossRef] [Green Version]
- Tutueva, A.V.; Artur, I.K.; Moysis, L.; Volos, C.; Butusov, D.N. Construction of one-way hash functions with increased key space using adaptive chaotic maps. Chaos Solitons Fractals 2020, 141, 110344. [Google Scholar] [CrossRef]
- Veres, A.; Boda, M. The chaotic nature of TCP congestion Control. In Proceedings of the IEEE INFOCOM, Tel Aviv, Israel, 26–30 March 2000; pp. 1715–1723. [Google Scholar]
- Leland, W.E.; Taqqu, M.S.; Willinger, W.; Wilson, D.V. On the self-similar nature of Ethernet traffic. IEEE/ACM Trans. Netw. 1994, 2, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Cai, L.; Li, H.; Chen, B.; Wang, J. On the Chaotic Dynamics Analysis of Internet Traffic. In Proceedings of the International Workshop on Chaos-Fractals Theories and Applications, Shenyang, China, 6–8 November 2009; pp. 361–364. [Google Scholar]
- Kaklauskas, L.; Sakalauskas, L. Application of Chaos Theory to Analysis of Computer Network Traffic. In Proceedings of the International Conference Applied Stochastic Models and Data Analysis, Vilnius, Lithuania, 30 June–3 July 2009; pp. 407–411. [Google Scholar]
- Yan, G. Internet Congestion Control based on the Controlling Bifurcation and Chaos algorithm. In Proceedings of the IEEE International Conference on Mechatronics and Control, Jinzhou, China, 3–5 July 2014; pp. 1500–1503. [Google Scholar]
- Rezaie, B.; Motlagh, M.; Khorsandi, S.; Analoui, M. Analysis and control of bifurcation and chaos in TCP-like Internet congestion control model. In Proceedings of the 15th International Conference on Advanced Computing and Communications, Guwahati, India, 18–21 December 2007; pp. 111–116. [Google Scholar]
- Huang, Z.; Yang, Q.; Cao, J. The stochastic stability and bifurcation behavior of an Internet congestion control model. Math. Comput. Model. 2011, 54, 1954–1965. [Google Scholar] [CrossRef]
- Jacobson, V. Congestion avoidance and control. ACM SIGCOMM Comput. Commun. Rev. 1998, 18, 314–329. [Google Scholar] [CrossRef]
- Adams, R. Active queue management: A survey. IEEE Commun. Surv. Tutor. 2013, 5, 1425–1476. [Google Scholar] [CrossRef]
- Nichols, K.; Jacobson, V. Controlling Queue Delay. ACM Queue 2012, 55, 42–50. [Google Scholar]
- Alwahab, D.; Laki, S. A Simulation-Based Survey of Active Queue Management Algorithms. In Proceedings of the 6th International Conference on Communications and Broadband Networking, Singapore, 24–26 February 2018; pp. 71–77. [Google Scholar]
- Chitra, K.; Padamavathi, G. Classification and Performance of AQM-Based Schemes for Congestion Avoidance. Int. J. Comput. Sci. Inf. Secur. 2010, 8, 331–340. [Google Scholar]
- Zheng, Y.G.; Wang, Z.H. Stability and Hopf bifurcation of a class of TCP/AQM networks. Nonlinear Anal. Real World Appl. 2010, 11, 1552–1559. [Google Scholar] [CrossRef]
- Ranjan, P.; Abed, E.H.; La, R.J. Nonlinear instabilities in TCP-RED. IEEE/ACM Trans. Netw. 2004, 12, 1079–1092. [Google Scholar] [CrossRef] [Green Version]
- Ding, D.; Zhu, J.; Luo, X. Hopf bifurcation analysis in a fluid flow model of Internet congestion control algorithm. Nonlinear Anal. Real World Appl. 2009, 10, 824–839. [Google Scholar] [CrossRef]
- Beneš, N.; Brim, L.; Pastva, S.; Šafránek, D. Digital Bifurcation Analysis of Internet Congestion Control Protocols. Int. J. Bifurc. Chaos 2020, 30, 2030038. [Google Scholar] [CrossRef]
- Babich, F.; Deotto, L. Formal methods for specification and analysis of communication protocols. IEEE Commun. Surv. Tutor. 2002, 4, 2–20. [Google Scholar] [CrossRef] [Green Version]
- Murata, T. Petri nets: Properties, analysis and applications. Proc. IEEE 1989, 77, 541–580. [Google Scholar] [CrossRef]
- Tang, S.; Hu, X.; Zhao, L. Modeling and Security Analysis of IEEE 802.1AS Using Hierarchical Colored Petri Nets. In Proceedings of the IEEE GLOBECOM, Taipei, Taiwan, 8–10 December 2020; pp. 1–6. [Google Scholar]
- Mahendran, V.; Gunasekaran, R.; Siva, C. Performance Modeling of Delay-Tolerant Network Routing via Queueing Petri Nets. IEEE Trans. Mob. Comput. 2014, 13, 1816–1828. [Google Scholar] [CrossRef]
- Wang, C.; Tao, Y.; Zhou, Y. Protocol Verification by Simultaneous Reachability Graph. IEEE Commun. Lett. 2017, 21, 1727–1730. [Google Scholar] [CrossRef]
- Floyd, S.; Jacobson, V. Random early detection gateways for congestion avoidance. IEEE Trans. Netw. 1993, 1, 397–413. [Google Scholar] [CrossRef]
- Koo, J.; Song, B.; Chung, K.; Lee, H.; Kahng, H. MRED: A new approach to random early detection. In Proceedings of the 15th International Conference on Information Networking, Beppu City, Oita, Japan, 31 January–2 February 2001; pp. 347–352. [Google Scholar]
- Misra, S.; Oommen, B.; Yanamandra, S.; Obaidat, M. Random Early Detection for Congestion Avoidance in Wired Networks: A Discretized Pursuit Learning-Automata-Like Solution. IEEE Trans. Syst. Man Cybern. 2010, 40, 66–76. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Athuraliya, S.; Low, S.H.; Li, V.H.; Yin, Q. REM: Active queue management. IEEE Netw. 2001, 15, 48–53. [Google Scholar] [CrossRef] [Green Version]
- Lin, D.; Morris, R. Dynamics of random early detection. In Proceedings of the ACM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communication, 14–18 September 1997; pp. 127–137. Available online: https://dl.acm.org/doi/abs/10.1145/263105.263154 (accessed on 22 June 2021).
- Lim, C.; Choi, C.; Lim, H. A weighted RED for alleviating starvation problem in wireless mesh networks. In Proceedings of the 33rd IEEE Conference on Local Computer Networks, Montreal, QC, Canada, 14–17 October 2008; pp. 841–842. [Google Scholar]
- Zala, D.D.; Vyas, A.K. Comparative Analysis of RED Queue Variants for Data Traffic Reduction over Wireless Network. In Recent Advances in Communication Infrastructure; Lecture Notes in Electrical Engineering; Springer: Singapore, 2020; Volume 618, pp. 131–139. [Google Scholar]
- Danladi, S.B.; Ambursa, F.U. DyRED: An Enhanced Random Early Detection Based on a new Adaptive Congestion Control. In Proceedings of the 15th International Conference on Electronics, Computer and Computation, Abuja, Nigeria, 10–12 December 2019; pp. 1–5. [Google Scholar]
- Amigó, J.M.; Duran, G.; Giménez, A.; Bonastre, O.M.; Valero, J. Generalized TCP-RED dynamical model for Internet congestion control. Elsevier Commun. Nonlinear Sci. Numer. Simul. 2020, 82, 105075. [Google Scholar] [CrossRef]
- Duran, G.; Valero, J.; Amigó, J.M.; Giménez, A.; Bonastre, O.M. Stabilizing Chaotic Behavior of RED. In Proceedings of the IEEE International Conference on Network Protocols, Cambridge, UK, 24–27 September 2018; pp. 241–242. [Google Scholar]
- NS-3, A Discrete-Event Network Simulator for Internet Systems. Available online: https://www.nsnam.org/ (accessed on 27 May 2021).
- Rampfl, S. Network simulation and its limitations. In Proceedings of the zum Seminar Future Internet (FI), Innovative Internet Technologien und Mobile Communication (IITM) und Autonomous Communication Networks (ACN), Munich, Germany, 30 April–31 July 2013; Volume 57, pp. 57–63. [Google Scholar]
- Crovella, M.E.; Bestavros, A. Self-similarity in World Wide Web traffic: Evidence and possible causes. IEEE/ACM Trans. Netw. 1997, 5, 835–846. [Google Scholar] [CrossRef] [Green Version]
- Williamson, C. Internet traffic measurement. IEEE Internet Comput. 2001, 5, 70–74. [Google Scholar] [CrossRef]
- Jiayue, H.; Rexford, J.; Chiang, M. Design for optimizability: Traffic management of a future Internet. In Algorithms for Next Generation Architectures; Springer: London, UK, 2010; pp. 3–18. [Google Scholar]
- Wu, X.-L.; Li, W.-M.; Liu, F.; Yu, H. Packet size distribution of typical Internet applications. In Proceedings of the International Conference on Wavelet Active Media Technology and Information Processing, Chengdu, China, 17–19 December 2012; pp. 276–281. [Google Scholar]
- Awduche, D.; Chiu, A.; Elwalid, A.; Widjaja, I.; Xiao, X. Overview and Principles of Internet Traffic Engineering. Internet Engineering Task Force (IETF) RFC 3272. 2002. Available online: https://datatracker.ietf.org/doc/rfc3272/ (accessed on 15 June 2021).
- Pandora FMS (for Pandora Flexible Monitoring System), a Software for Monitoring Computer Networks. Available online: https://pandorafms.com/ (accessed on 15 June 2021).







| Place | Description |
|---|---|
| P1 | A new packet comes from the Internet (network) to the router, which is ready. |
| P2 | The packet is received. |
| P3 | The AQM gets the average queue length (AQL) at the router. |
| P4 | The packet is accepted because the AQL is below the min. threshold. |
| P5 | The AQM gets the probability pmax Iz (α, β). |
| P6 | The packet is rejected because the AQL is over the max. threshold. |
| P7 | The packet is accepted (not discard the result of pmax Iz (α, β)). |
| P8 | The packet is rejected (discard the result of pmax Iz (α, β)). |
| P9 | The packet is put into the buffer queue to be transmitted to the destination. |
| P10 | The AQM ready for receiving the next packet. |
| Transition | Description |
| T1 | Input a new packet; the router is ready. |
| T2 | Start the transmission of the packet once received. |
| T3 | The AQL is below the min. threshold. Check guard G1. |
| T4 | The AQL is between thresholds. Check guard G2. |
| T5 | The AQL is over the max. threshold. Check guard G3. |
| T6 | Fill the buffer with the received packet. |
| T7 | Drop the packet; the AQL is over the max. threshold. |
| T8 | Do not discard the packet. Check guard G4. |
| T9 | Discard the packet. Check guard G5. |
| T10 | Input the packet into the buffer. |
| T11 | Reject the packet. |
| T12 | Leave the buffer. The packet is transmitted. |
| Guard | Description |
| G1 | . Guard associated to transition T3 |
| G2 | . Guard associated to transition T4 |
| G3 | . Guard associated to transition T5 |
| G4 | Not Discard = True. Guard associated to transition T8 |
| G5 | Discard = True. Guard associated to transition T9 |
| T-Invariant | Content | Description |
|---|---|---|
| 1T-inv | (1,1,1,0,0,1,0,0,0,0,0,1) | Accept packet, AQL below min. threshold |
| 2T-inv | (1,1,0,0,1,0,1,0,0,0,0,0) | Drop packet, AQL over max. threshold |
| 3T-inv | (1,1,0,1,0,0,0,1,0,1,0,1) | Accept packet, AQM probability function |
| 4T-inv | (1,1,0,1,0,0,0,0,1,0,1,0) | Reject packet, AQM probability function |
| P-Invariant | Content | Description |
|---|---|---|
| 1P-inv | (1,1,0,0,0,0,0,0,0,0) | Router ready, received packet |
| 2P-inv | (0,1,1,1,1,1,1,1,1,1) | AQM in process, received packet |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amigó, J.M.; Duran, G.; Giménez, Á.; Valero, J.; Bonastre, O.M. Modeling a New AQM Model for Internet Chaotic Behavior Using Petri Nets. Appl. Sci. 2021, 11, 5877. https://doi.org/10.3390/app11135877
Amigó JM, Duran G, Giménez Á, Valero J, Bonastre OM. Modeling a New AQM Model for Internet Chaotic Behavior Using Petri Nets. Applied Sciences. 2021; 11(13):5877. https://doi.org/10.3390/app11135877
Chicago/Turabian StyleAmigó, José M., Guillem Duran, Ángel Giménez, José Valero, and Oscar Martinez Bonastre. 2021. "Modeling a New AQM Model for Internet Chaotic Behavior Using Petri Nets" Applied Sciences 11, no. 13: 5877. https://doi.org/10.3390/app11135877
APA StyleAmigó, J. M., Duran, G., Giménez, Á., Valero, J., & Bonastre, O. M. (2021). Modeling a New AQM Model for Internet Chaotic Behavior Using Petri Nets. Applied Sciences, 11(13), 5877. https://doi.org/10.3390/app11135877







