Optimum Shape Design of Geometrically Nonlinear Submerged Arches Using the Coral Reefs Optimization with Substrate Layers Algorithm
Abstract
:1. Introduction
2. Problem Statement: Nonlinear Submerged Arches Design
2.1. Funicular Equilibrium of Submerged Arches
2.2. Structural Stability: Buckling Analysis of Submerged Arches
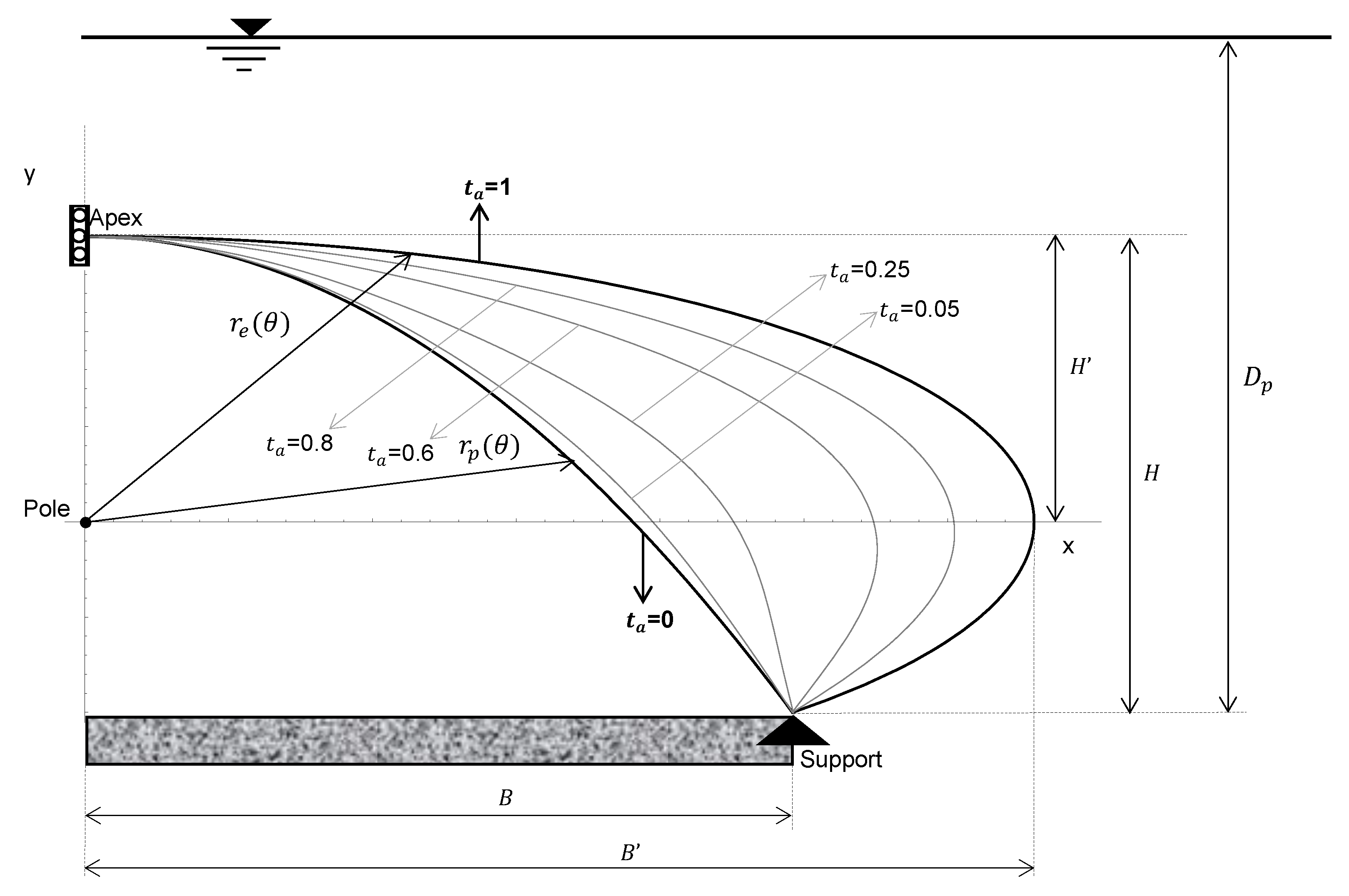
2.3. Alternative Approach: Shape Parameterization
2.4. Geometrical Nonlinear Analysis and Optimal Design
3. The CRO-SL: A Low-Level Ensemble Evolutionary Algorithm
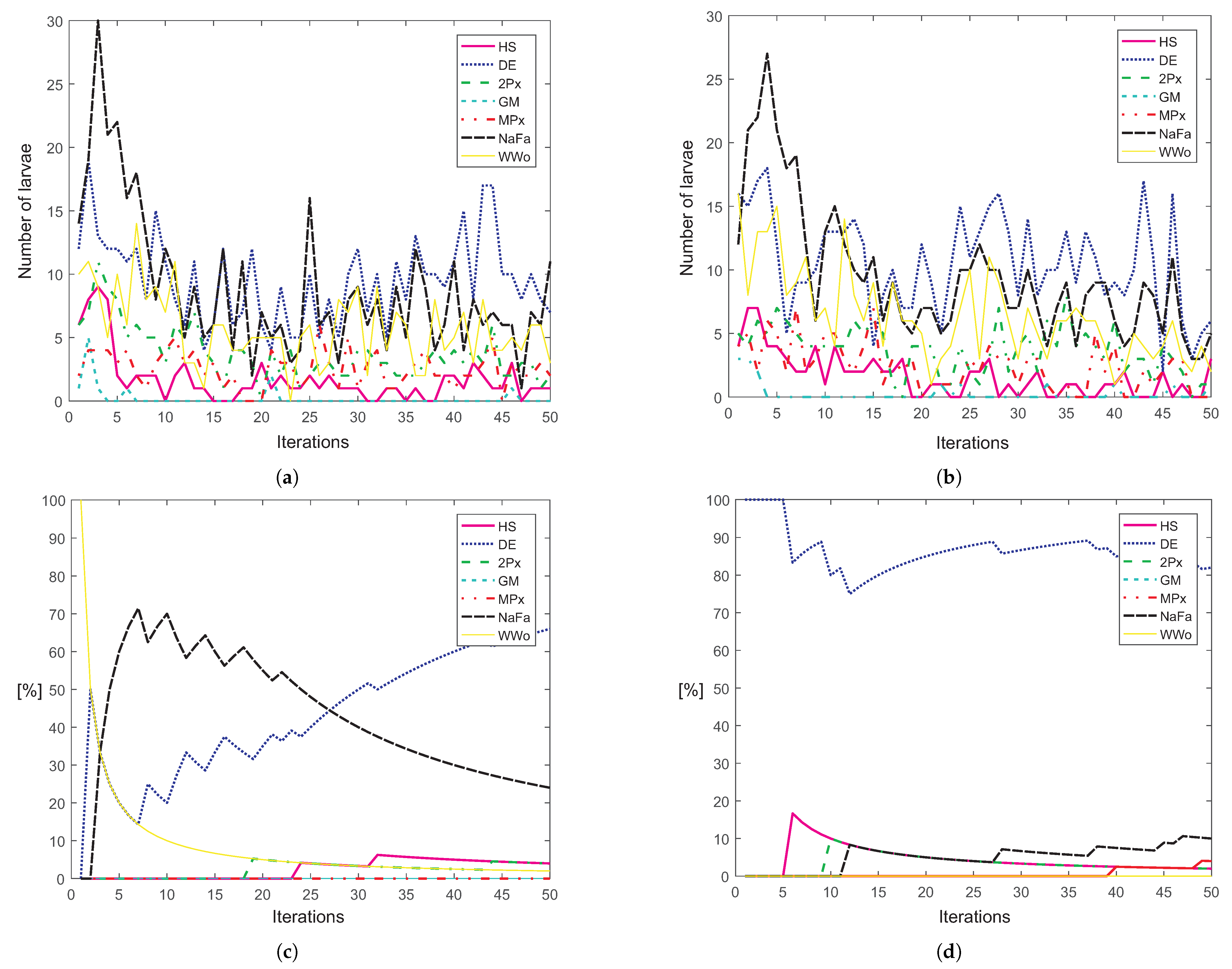
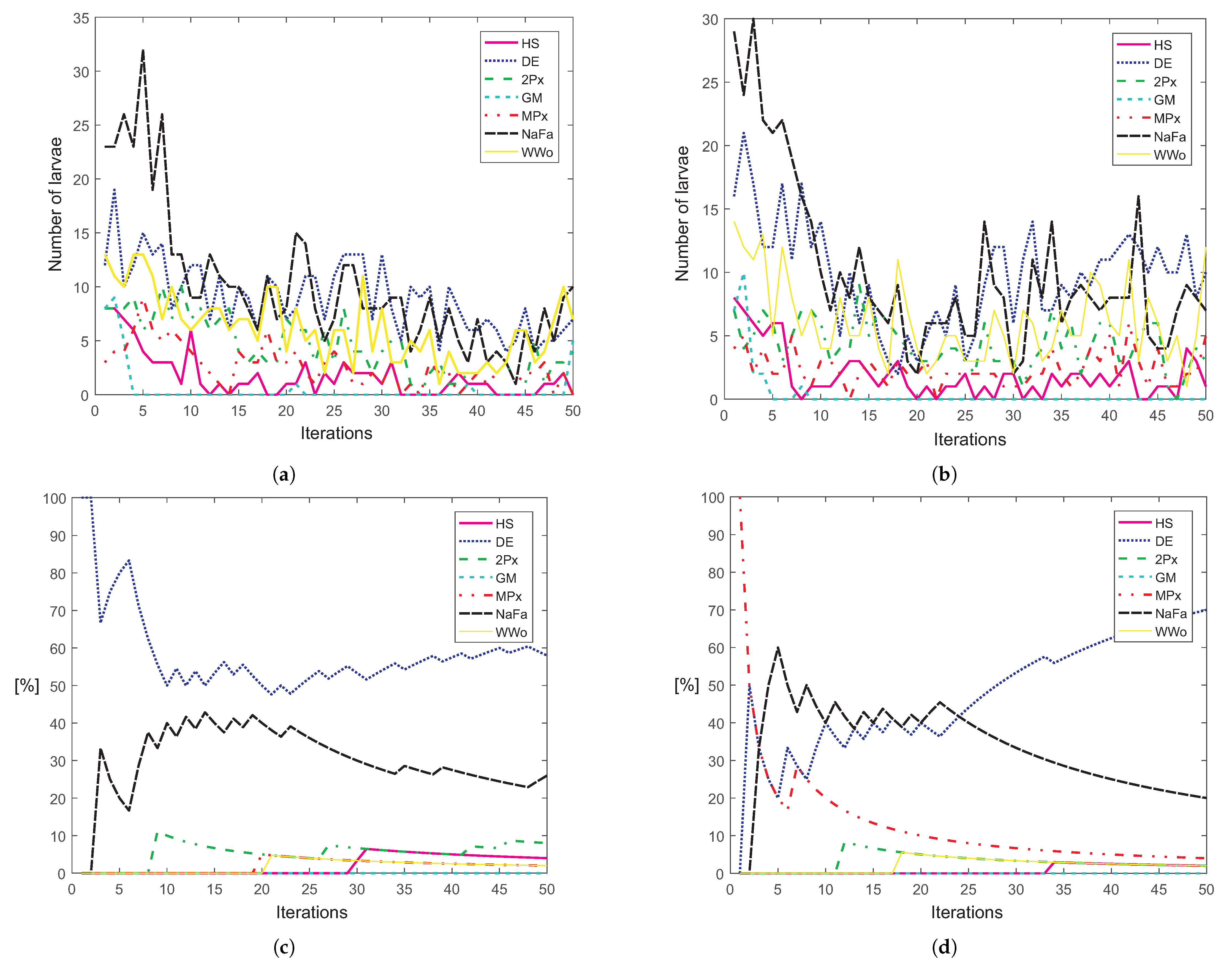
Substrate Layers Defined in the CRO-SL
- HS: Mutation from the Harmony Search algorithm. Harmony Search [52] is a population-based meta-heuristic that mimics the improvisation of a music orchestra while it is composing a melody. HS controls how new larvae are generated in one of the following ways: (i) with a probability HMCR (Harmony Memory Considering Rate), the value of a component of the new larva is drawn uniformly from the same values of the component in the other corals, and (ii) with a probability PAR (Pitch Adjusting Rate), subtle adjustments are applied to the values of the current larva, replaced by any of its neighboring values (upper or lower, with equal probability).
- DE: Mutation from Differential Evolution algorithm (with ). This operator is based on the evolutionary algorithm with the same name [53], a method with powerful global search capabilities. DE introduces a differential mechanism for exploring the search space. Therefore, new larvae are generated by perturbing the population members using vector differences of individuals. Perturbations are introduced by applying (where F determines the evolution factor weighting the perturbation amplitude) for each encoded parameter on a random basis. After this perturbation, final perturbed vector is combined with an alternative coral in the reef following a classical 2-points crossover, as defined next.
- 2Px: Classical 2-points crossover. The crossover operator is the most classical exploration mechanism in genetic and evolutionary algorithms [54]. It consists of coupling to individuals at random, choosing two points for the crossover, and interchanging the genetic material in-between both points. In the CRO-SL, one individual to be crossed is from the 2Px substrate, whereas the couple can be chosen from any part of the reef.
- MPx: Multi-points crossover. Similar to the 2-points crossover, but in this case a number k of crossover points are selected, and a binary template decides whether parts of the individuals are interchanged.
- GM: Gaussian Mutation, with a value linearly decreasing during the run, from to , where is the domain search. Specifically, the Gaussian probability density function isThe reason of adapting the value of along the generations is to provide a stronger mutation in the beginning of the optimization, while fine-tuning with smaller displacements nearing the end. The mutated larva is thus calculated as , where is a random number following the Gaussian distribution.
- Firefly Optimization (Fa): The Fa is a kind of swarm intelligence algorithm, first introduced by Yang in [55]. The Fa is based on the flashing patterns and behaviour of fireflies in nature. The pattern movement of a firefly i attracted to another (brighter) firefly j is calculated as follows:where stands for the attractiveness at distance . The specific Fa mutation implemented in the CRO-SL is a modified version of the algorithm known as Neighborhood Attraction Firefly Algorithm (NaFa) [56]. It has been implemented as follows. When a coral (solution) in the reef belongs to the NaFa substrate, it is updated by following Equation (12). All the parameters of the equation are tuned during the CRO-SL evolution. The corals in the NaFa substrate consider as swarm a neighborhood among all the other corals in the reef (not only the NaFa substrate). Thus, the corals in the NaFa substrate are updated taking into account some solutions from other substrates, as all the corals in the reef share the same objective function (brightness for the NaFa substrate). Note that the Fa algorithms has been applied to different structural problems in previous works [57,58], showing a good behaviour.
- Water Wave Optimization (WWo): The WWo [59] is a recently proposed meta-heuristic based on the phenomena of water waves, such as propagation, refraction, and breaking. Three different procedures are then defined in this algorithm: Wave propagation: at each generation of the algorithm, each wave in the population is propagated, to generate another wave in the following way:where is a uniformly distributed random number within the range [−1,1], and is the length of the dth dimension of the search space (see in [59] for reference). Then, Wave refraction is simulated aswhere is the best solution found so far, and is a Gaussian random number with mean and standard deviation . Finally, a wave breaking process is also simulated aswhere is the breaking coefficient.The implementation of the algorithm as CRO-SL is straightforward, as any solution within the substrate is just applied the set of operators described above, with the algorithm’s parameters described in [59].
4. Numerical Examples
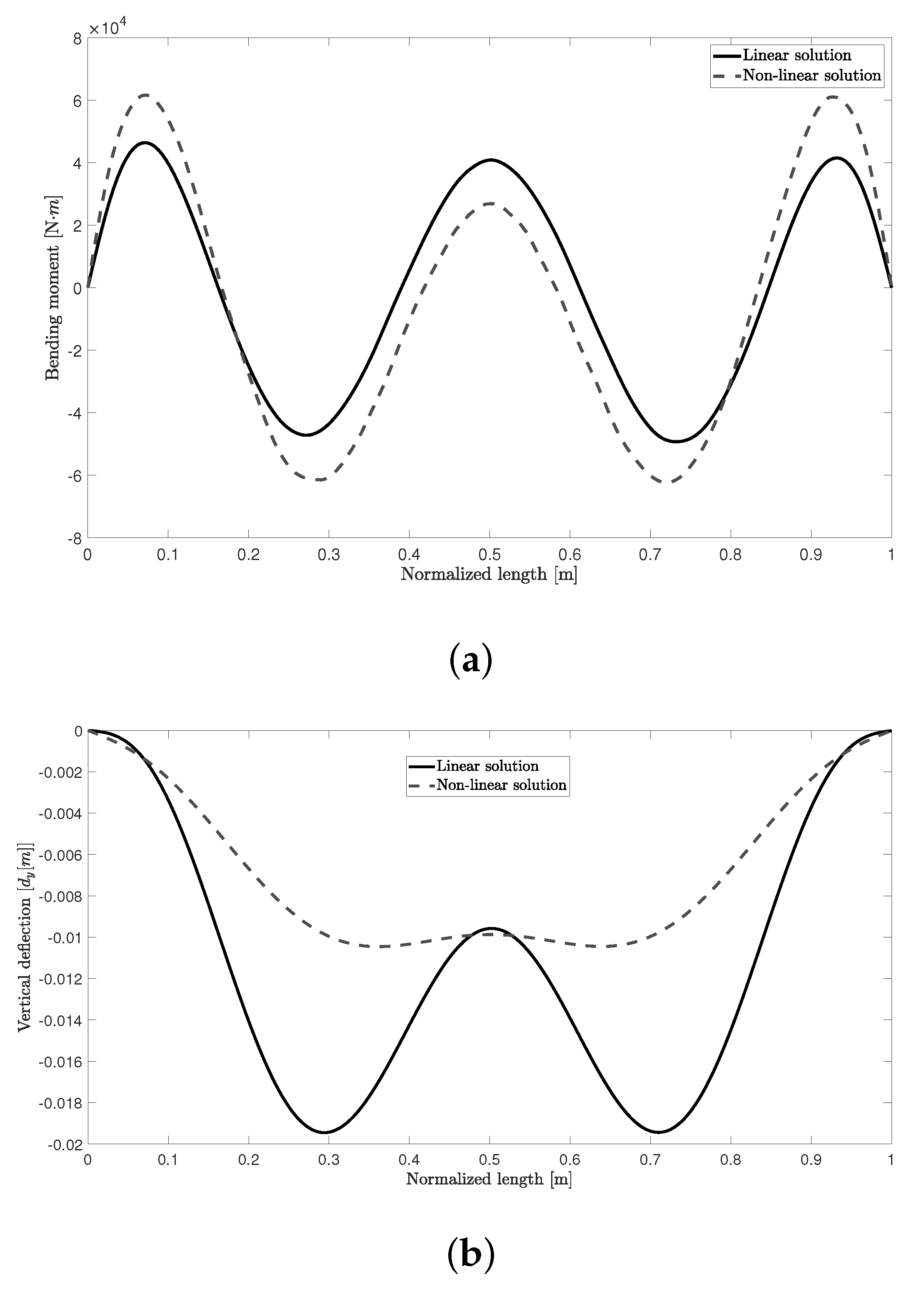
4.1. Case in Which the Height H Is Fixed
4.2. Case in Which the Span B Is Fixed
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tadjbakhsh, I.G. Stability and optimum design of arch-type structures. Int. J. Solids Struct. Struct. Eng. 1981, 17, 565–574. [Google Scholar] [CrossRef]
- Pepinato, A. (Ed.) Innovative Bridge Design Handbook; Butterworth-Heinemann: Woburn, MA, USA; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Wang, C.M.; Wang, C.Y. Funicular shapes for submerged arches. J. Struct. Eng. 2002, 128, 266–270. [Google Scholar] [CrossRef]
- Pi, Y.L.; Trahair, N.S. Non-linear buckling and postbuckling of elastic arches. Eng. Struct. 1998, 20, 571–579. [Google Scholar] [CrossRef]
- Pi, Y.L.; Bradford, M.A. Elasto-plastic buckling and postbuckling of arches subjected to a central load. Comput. Struct. 2003, 81, 1811–1825. [Google Scholar] [CrossRef]
- Bradford, M.A.; Pi, Y.L.; Yang, G.; Fan, X.C. Effects of approximations on non-linear in-plane elastic buckling and post buckling analyses of shallow parabolic arches. Eng. Struct. 2015, 101, 58–67. [Google Scholar] [CrossRef]
- Bateni, M.; Eslami, M.R. Non-linear in-plane stability analysis of FG circular shallow arches under uniform radial pressure. Thin-Walled Struct. 2015, 94, 302–313. [Google Scholar] [CrossRef]
- Chengyi, C.; Genshu, T.; Lei, Z. In-plane nonlinear buckling analysis of circular arches considering shear deformation. J. Constr. Steel Res. 2020, 164, 105762. [Google Scholar] [CrossRef]
- Casapulla, C.; Mousavian, E.; Zarghani, M. A Digital Tool to Design Structurally Feasible Semi-Circular Masonry Arches Composed of Interlocking Blocks. Comput. Struct. 2019, 221, 111–126. [Google Scholar] [CrossRef]
- Jorquera-Lucerga, J.; Manterola-Armisén, J. An iterative form-finding method for antifunicular shapes in spatial arch bridges. Comput. Struct. 2012, 108–109, 42–60. [Google Scholar] [CrossRef]
- Espa na, R.M.; Hernández-Díaz, A.M.; Cecilia, J.M.; García-Román, M.D. Evolutionary strategies as applied to shear strain effects in reinforced concrete beams. Appl. Soft Comput. 2017, 57, 164–176. [Google Scholar] [CrossRef]
- Cecilia, J.M.; Hernández-Díaz, A.M.; Castrillo, P.; Jiménez-Alonso, J.F. Enhanced calculation of eig-en-stress field and elastic energy in atomistic interdiffusion of alloys. Comput. Phys. Commun. 2017, 211, 23–30. [Google Scholar] [CrossRef]
- Pérez-Aracil, J.; Hernández-Díaz, A.M.; Jiménez-Alonso, J.F.; Puerta-Lopez, F.J. Fatigue Assessment of a Slender Footbridge Based on an Updated Finite Element Model. Key Eng. Mater. 2018, 774, 589–594. [Google Scholar] [CrossRef]
- Jamshidi, M.; Arghavani, J.; Maboudi, G. Post-Buckling Optimization of Two-Dimensional Functionally Graded Porous Beams. Int. J. Mech. Mater. Des. 2019, 15, 801–815. [Google Scholar] [CrossRef]
- Daxini, D.S.; Prajapati, J.M. Structural Shape Optimization with Meshless Method and Swarm-Intelligence Based Optimization. Int. J. Mech. Mater. Des. 2020, 16, 167–190. [Google Scholar] [CrossRef]
- Hernández-Díaz, A.M.; García-Román, M.D. Computing the refined compression field theory. Int. J. Concr. Struct. Mater. 2016, 10, 143–147. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.M.; Ler, C.W. Optimization of Submerged Funicular Arches. Mech. Based Des. Struct. Mach. 2003, 31, 181–200. [Google Scholar] [CrossRef]
- Hernández-Díaz, A.M.; Mu noz, A.; Jiménez-Alonso, J.F.; Sáez, A. Buckling design of submerged arches via shape parameterization. Comput. Math. Methods 2019, 1, e1057. [Google Scholar] [CrossRef] [Green Version]
- He, L.; Li, W.; Zhang, Y.; Cao, Y. A Discrete Multi-Objective Fireworks Algorithm for Flowshop Sched-uling with Sequence-Dependent Setup Times. Swarm Evol. Comput. 2019, 51, 100575. [Google Scholar] [CrossRef]
- Hernández-Díaz, A.M.; Bueno-Crespo, A.; Pérez-Aracil, J.; Cecilia, J.M. Multi-objective optimal design of submerged arches using extreme learning machine and evolutionary algorithms. Appl. Soft Comput. 2018, 71, 826–834. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Camacho-Gómez, C.; Molina, D.; Herrera, F. A Coral Reefs Optimization algorithm with substrate layers and local search for large scale global optimization. In Proceedings of the IEEE Conference on Evolutionary Algorithms, Vancouver, BC, Canada, 24–29 July 2016; pp. 3574–3581. [Google Scholar]
- Lynn, N.; Ponnuthurai, N.S. Ensemble Particle Swarm Optimizer. Appl. Soft Comput. 2017, 55, 533–548. [Google Scholar] [CrossRef]
- Wu, G.; Mallipeddi, R.; Suganthan, P.N. Ensemble strategies for population based optimization algorithms—A survey. Swarm Evol. Comput. 2019, 44, 695–711. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Camacho-Gómez, C.; Magdaleno, A.; Pereira, E.; Lorenzana, A. Structures vibration control via Tuned Mass Dampers using a co-evolution Coral Reefs Optimization algorithm. J. Sound Vib. 2017, 393, 62–75. [Google Scholar] [CrossRef]
- Camacho-Gómez, C.; Wang, X.; Pereira, E.; Díaz, I.M.; Salcedo-Sanz, S. Active vibration control design using the Coral Reefs Optimization with Substrate Layer algorithm. Eng. Struct. 2018, 157, 14–26. [Google Scholar] [CrossRef] [Green Version]
- Bermejo, E.; Chica, M.; Damas, S.; Salcedo-Sanz, S.; Cordón, O. Coral Reef Optimization with Substrate Layers for Medical Image Registration. Swarm Evol. Comput. 2018, 42, 138–159. [Google Scholar] [CrossRef]
- Marcelino, C.G.; Camacho-Gómez, C.; Jiménez-Fernández, S.; Salcedo-Sanz, S. Optimal Generation Scheduling in Hydro-Power Plants with the Coral Reefs Optimization Algorithm. Energies 2021, 14, 2443. [Google Scholar] [CrossRef]
- Pérez-Aracil, J.; Camacho-Gomez, C.; Hernandez-Diaz, A.M.; Pereira, E.; Salcedo-Sanz, S. Submerged Arches Optimal Design With a Multi-Method Ensemble Meta-Heuristic Approach. IEEE Access 2020, 8, 215057–215072. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S. Modern meta-heuristics based on nonlinear physics processes: A review of models and de-sign procedures. Phys. Rep. 2016, 655, 1–70. [Google Scholar] [CrossRef]
- Chai, Y.; Kunnath, S. Geometry of submerged funicular arches in Cartesian coordinates. J. Struct. Eng. 2003, 129, 1087–1092. [Google Scholar] [CrossRef]
- Chai, Y.; Wang, C. Approximate solution for the shape of submerged funicular arches with self-weight. J. Struct. Eng. 2005, 131, 399–404. [Google Scholar] [CrossRef]
- Karnovsky, I.A. Theory of Arched Structures: Strength, Stability, Vibration; Springer Science & Business Media: New York, NY, USA, 2011. [Google Scholar]
- Timoshenko, S. Strength of Materials, Part II: Advanced Theory and Problems, 3rd ed.; CBS Publishers and Distributors, Pvt. Ltd.: New Delhi, India, 2019. [Google Scholar]
- Zienckiewicz, O.C.; Taylor, R.L. The Finite Element Method: Solid Mechanics, 5th ed.; Butter-Worth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Dinnik, A. Stability of Arches; OGIS, Gostechizdat: Moscow, Russia, 1946. [Google Scholar]
- Inglis, C. Applied Mechanics for Engineers; Cambridge University Press: Cambridge, UK, 1951. [Google Scholar]
- Gil-Martín, L.M.; Hernández-Montes, E.; Palomares, A.; Pasadas-Fernández, M. The optimum shape of an arch under non-symmetric loading conditions. Arch. Appl. Mech. 2016, 86, 1509–1520. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Attard, M.M.; Zhu, J.; Kellerman, D.C. In-plane buckling of prismatic funicular arches with shear defor-mation. Arch. Appl. Mech. 2014, 84, 693–713. [Google Scholar] [CrossRef]
- Houst, V.; Elias, J.; Micas, L. Shape optimization of concrete buried arches. Eng. Struct. 2012, 48, 716–726. [Google Scholar] [CrossRef]
- Gavin, H.P.; Reilly, K.J. Submerged Funicular Arches. J. Struct. Eng. 2000, 126, 627–629. [Google Scholar] [CrossRef]
- Wood, R.D.; Zienkiewicz, O.C. Geometrically nonlinear finite element analysis of beams, frames, arches and axisymmetric shells. Comput. Struct. 1977, 7, 725–735. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures, 1st ed.; Prentice-Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Miller, K.; Joldes, G.; Lance, D.; Wittek, A. Total Lagrangian explicit dynamics finite element algorithm for computing soft tissue deformation. Commun. Numer. Methods Eng. 2007, 23, 121–134. [Google Scholar] [CrossRef]
- Available online: https://www.ansys.com/ (accessed on 15 June 2021).
- Bathe, K.J.; Ozdemir, H. Elastic-plastic large deformation static and dynamic analysis. Comput. Struct. 1976, 6, 81–92. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; MIT Press: Boston, MA, USA, 2006. [Google Scholar]
- Hernández-Díaz, A.M.; Pérez, J.; Ruiz, R.; Jiménez, J.F. Assessment of the seismic behaviour of the original and modified structure of the Veronicas market at Murcia (Spain). Inf. Constr. 2019, 71, e291. [Google Scholar] [CrossRef] [Green Version]
- Salcedo-Sanz, S.; del Ser, J.; Landa-Torres, I.; Gil-López, S.; Portilla-Figueras, J.A. The Coral Reefs Opti-mization algorithm: A novel metaheuristic for efficiently solving optimization problems. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Salcedo-Sanz, S. A review on the coral reefs optimization algorithm: New development lines and current ap-plications. Prog. Artif. Intell. 2017, 6, 1–15. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Mu noz-Bulnes, J.; Vermeij, M. New Coral Reefs-based Approaches for the Model Type Selection Problem: A Novel Method to Predict a Nation’s Future Energy Demand. Int. J. Bioinspired Comput. 2017, 10, 145–158. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony Search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A simple and efficient heuristic for global optimization over con-tinuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin, Germany, 2003. [Google Scholar]
- Yang, X.S. Firefly algorithm. Nat. Inspired Metaheuristic Alg. 2008, 20, 79–90. [Google Scholar]
- Wang, H.; Wang, W.; Zhou, X.; Sun, H.; Zhao, J.; Yua, X.; Cui, Z. Firefly algorithm with neighborhood attraction. Inf. Sci. 2017, 382–383, 374–387. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Mixed variable structural optimization using firefly algorithm. Comput. Struct. 2011, 89, 2325–2336. [Google Scholar] [CrossRef]
- Kaveh, A.; Javadi, S.M. Chaos-based firefly algorithms for optimization of cyclically large-size braced steel domes with multiple frequency constraints. Comput. Struct. 2019, 214, 28–39. [Google Scholar] [CrossRef]
- Zheng, Y.J. Water wave optimization: A new nature-inspired metaheuristic. Comput. Oper. Res. 2015, 55, 1–11. [Google Scholar] [CrossRef] [Green Version]
- European Committee for Standardization (CEN). Eurocode 2: Design of Concrete Structures, Part 1-1: General Rules and Rules for Buildings; EN 1992-1-1; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]







| Parameter | Description | Value |
|---|---|---|
| Reef | Reef size | 100 |
| Fraction of reef capacity initially occupied | 80% | |
| Frequency of broadcast spawning | 97% | |
| Percentage of asexual reproduction | 5% | |
| Fraction of corals for depredation | 5% | |
| Probability of depredation | 10% | |
| Maximum number of iterations | 50 |
| Type of Parameter | Parameter | Value [m] |
|---|---|---|
| Fixed parameters | 10 | |
| H | 6 | |
| Variable parameters | ||
| B | ||
| h | ||
| (dimensionless) |
| Optimal Solution | |||||||
|---|---|---|---|---|---|---|---|
| Analysis | f | ||||||
| Linear | 8.99 m | 15.00 m | 0.25 m | 0.52 | 126.14 m | 5.05 × N·m | 4.04 × |
| Non-linear | 8.97 m | 15.02 m | 0.44 m | 0.51 | 126.95 m | 6.32 N·m | 5.06 × |
| Type of Parameter | Parameter | Value [m] |
|---|---|---|
| Fixed parameters | 10 | |
| B | 30 | |
| Variable parameters | H | |
| h | ||
| (dimensionless) |
| Optimal Solution | |||||||
|---|---|---|---|---|---|---|---|
| Analysis | f | ||||||
| Linear | 5.26 m | 8.00 m | 0.35 m | 0.22 | 215.41 m | 1.74 × N·m | 1.22 × |
| Non-linear | 6.43 m | 7.50 m | 0.55 m | 0.18 | 267.97 m | 3.88 × N·m | 2.72 × |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Aracil, J.; Camacho-Gómez, C.; Hernández-Díaz, A.M.; Pereira, E.; Salcedo-Sanz, S. Optimum Shape Design of Geometrically Nonlinear Submerged Arches Using the Coral Reefs Optimization with Substrate Layers Algorithm. Appl. Sci. 2021, 11, 5862. https://doi.org/10.3390/app11135862
Pérez-Aracil J, Camacho-Gómez C, Hernández-Díaz AM, Pereira E, Salcedo-Sanz S. Optimum Shape Design of Geometrically Nonlinear Submerged Arches Using the Coral Reefs Optimization with Substrate Layers Algorithm. Applied Sciences. 2021; 11(13):5862. https://doi.org/10.3390/app11135862
Chicago/Turabian StylePérez-Aracil, Jorge, Carlos Camacho-Gómez, Alejandro Mateo Hernández-Díaz, Emiliano Pereira, and Sancho Salcedo-Sanz. 2021. "Optimum Shape Design of Geometrically Nonlinear Submerged Arches Using the Coral Reefs Optimization with Substrate Layers Algorithm" Applied Sciences 11, no. 13: 5862. https://doi.org/10.3390/app11135862
APA StylePérez-Aracil, J., Camacho-Gómez, C., Hernández-Díaz, A. M., Pereira, E., & Salcedo-Sanz, S. (2021). Optimum Shape Design of Geometrically Nonlinear Submerged Arches Using the Coral Reefs Optimization with Substrate Layers Algorithm. Applied Sciences, 11(13), 5862. https://doi.org/10.3390/app11135862









