Prediction of Transient Temperature Distributions for Laser Welding of Dissimilar Metals
Abstract
:1. Introduction
2. Definition of the Model
- (a)
- Radiation and convection heat loss from the surface are considered for modeling.
- (b)
- The ambient temperature is 298 K and the system is within good thermal isolation from the environment.
- (c)
- The change in phase during the process is also taken into account.
- (d)
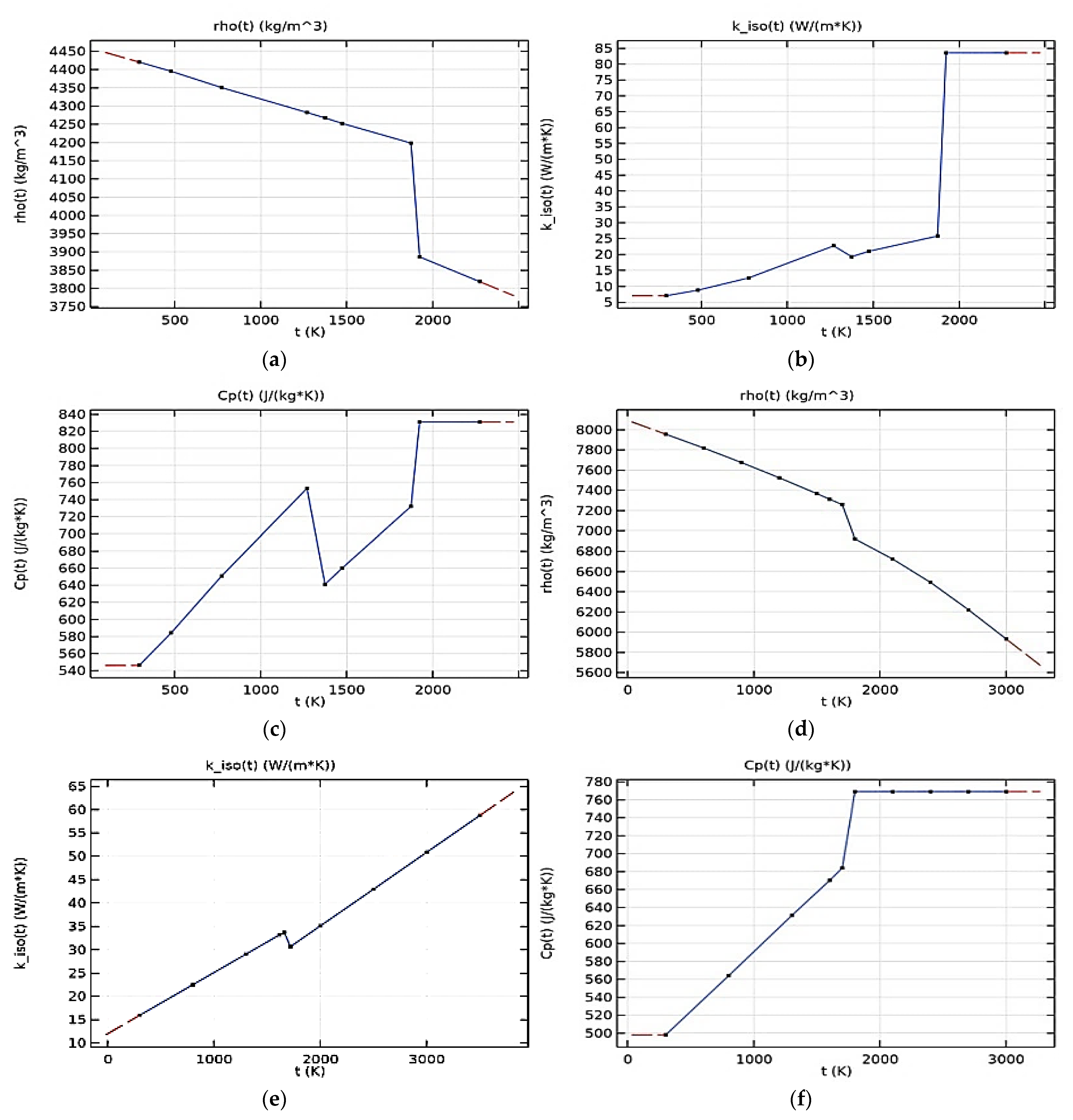
- The thermo physical properties of the materials change with the change of temperature.
- (e)
- The position of the laser beam is vertical to the surface.
- (f)
- Latent heat during a phase change is considered for simulation. Latent heat for melting of Ti6Al4V and AISI 316L is 286 kJ/kg and 260 kJ/kg respectively.
3. Numerical Model
Mesh Convergence Analysis
4. Results
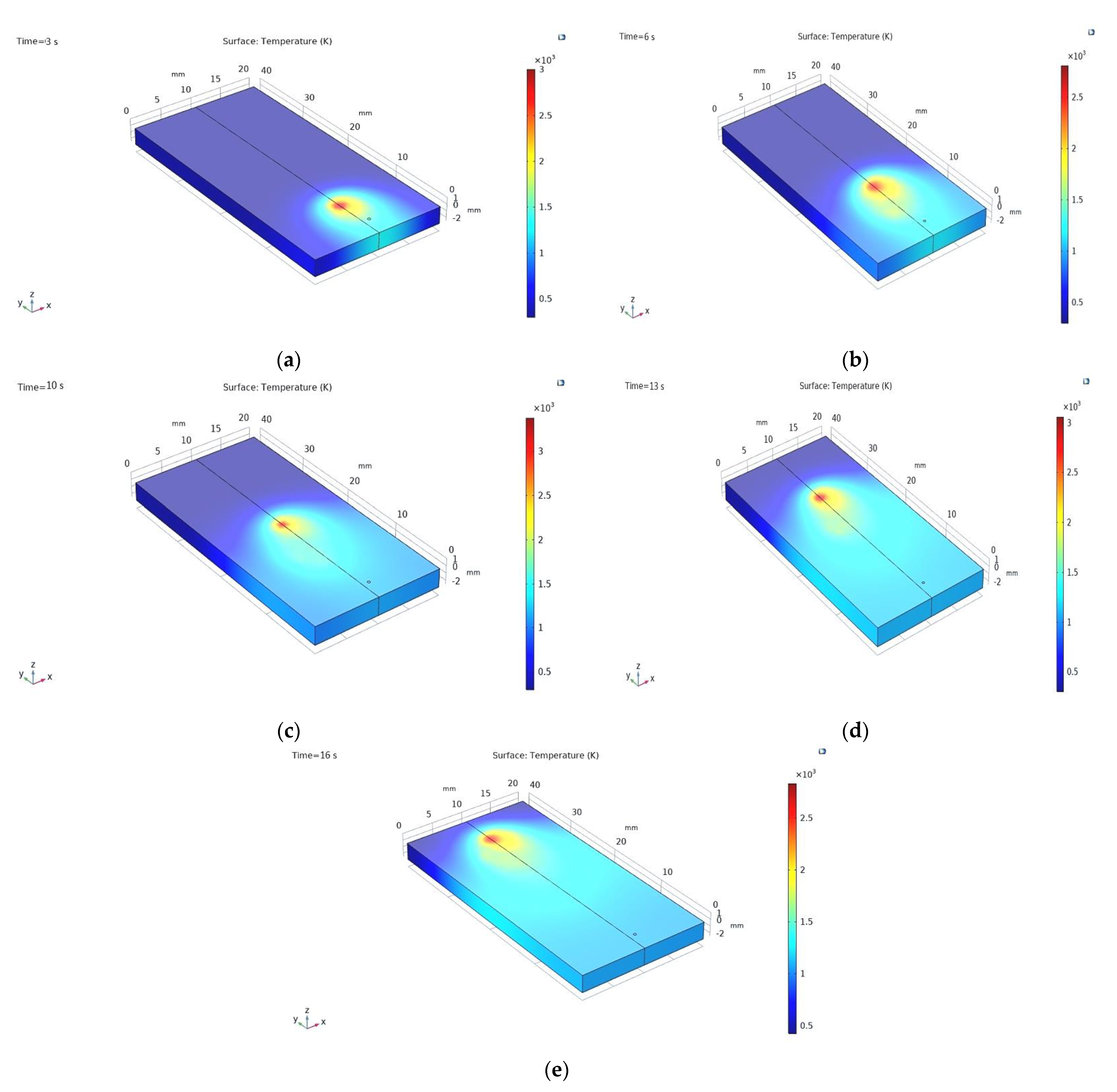
4.1. Temperature Propagation during the Welding
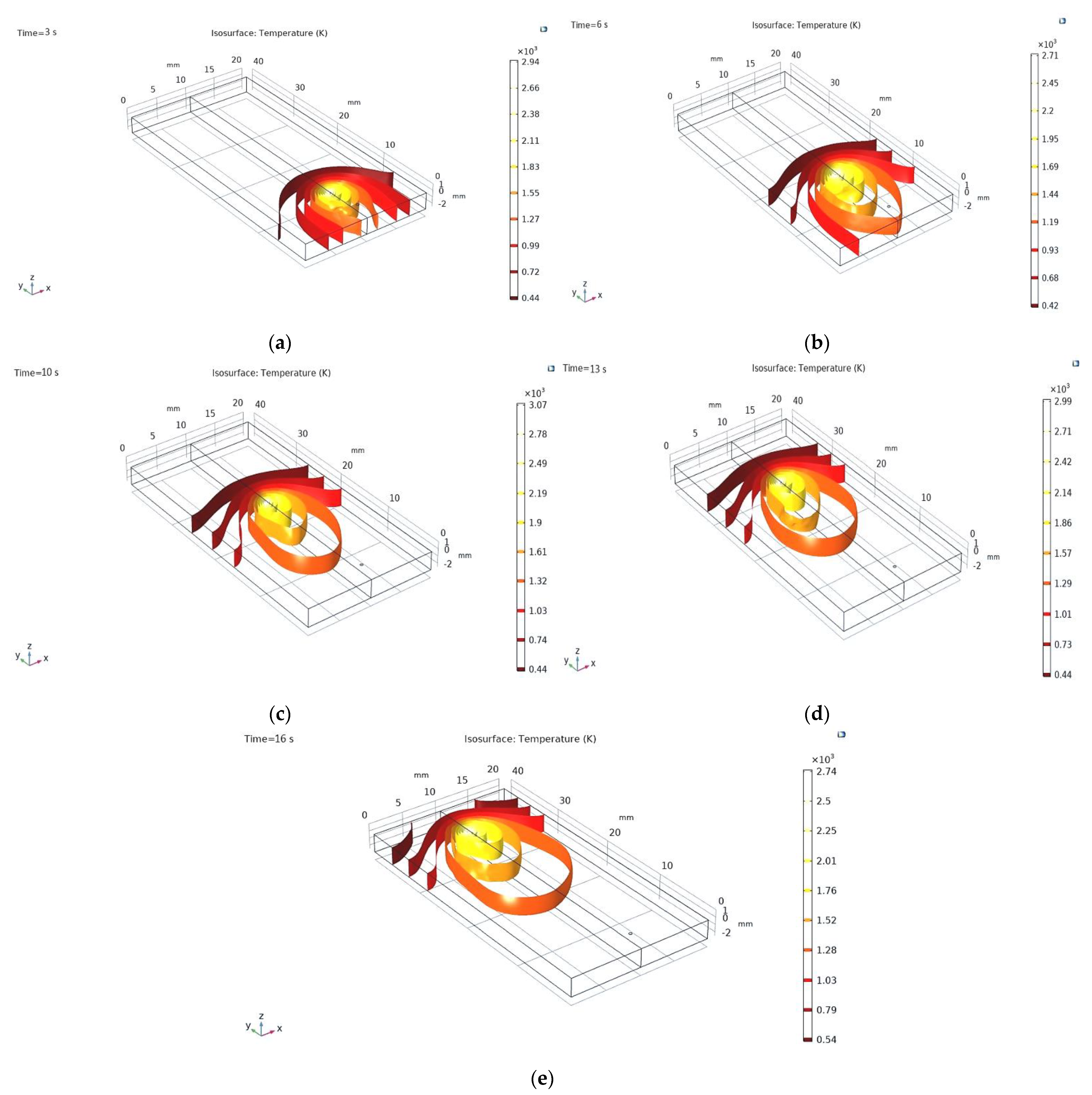
4.2. Isothermal Contours
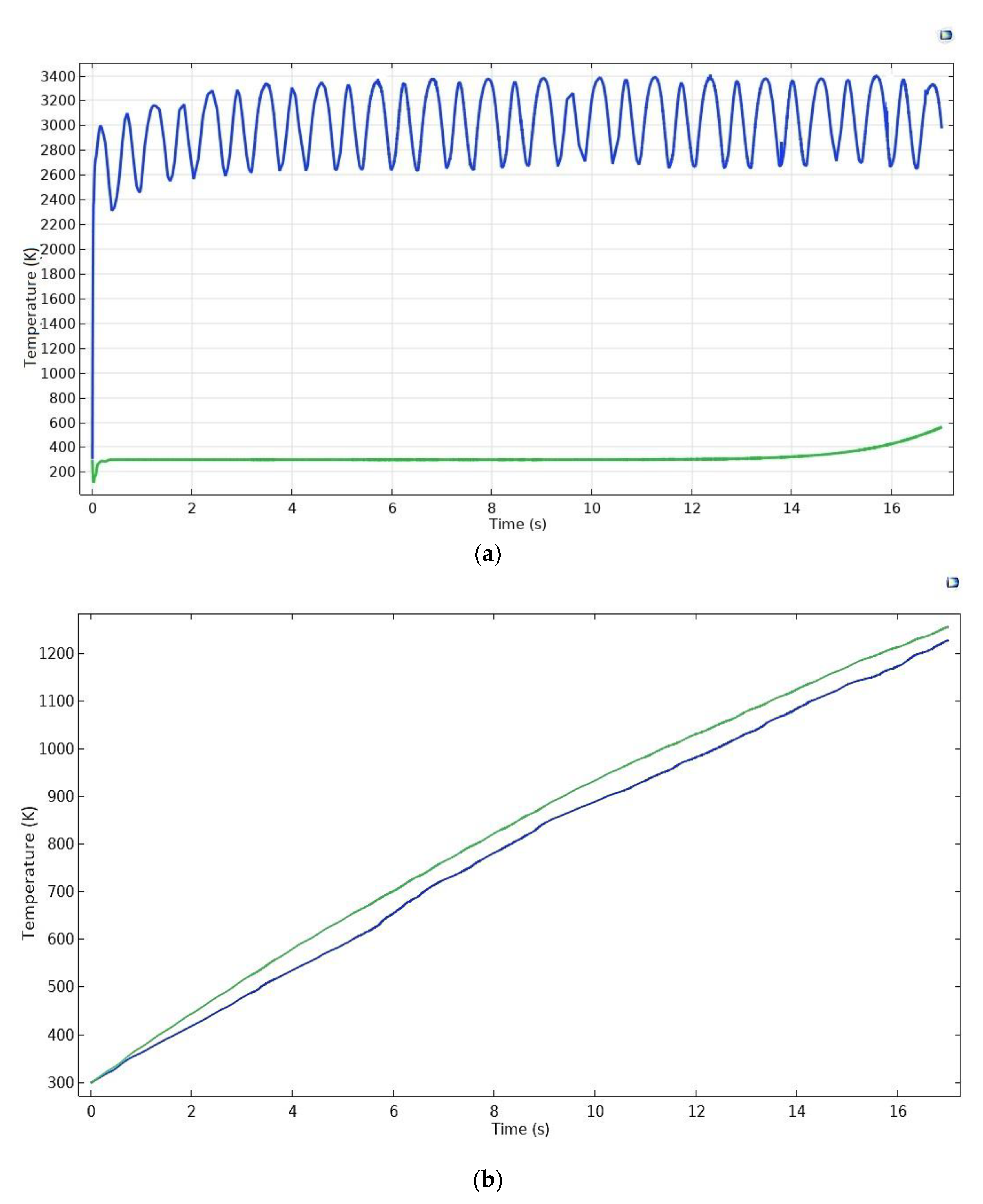
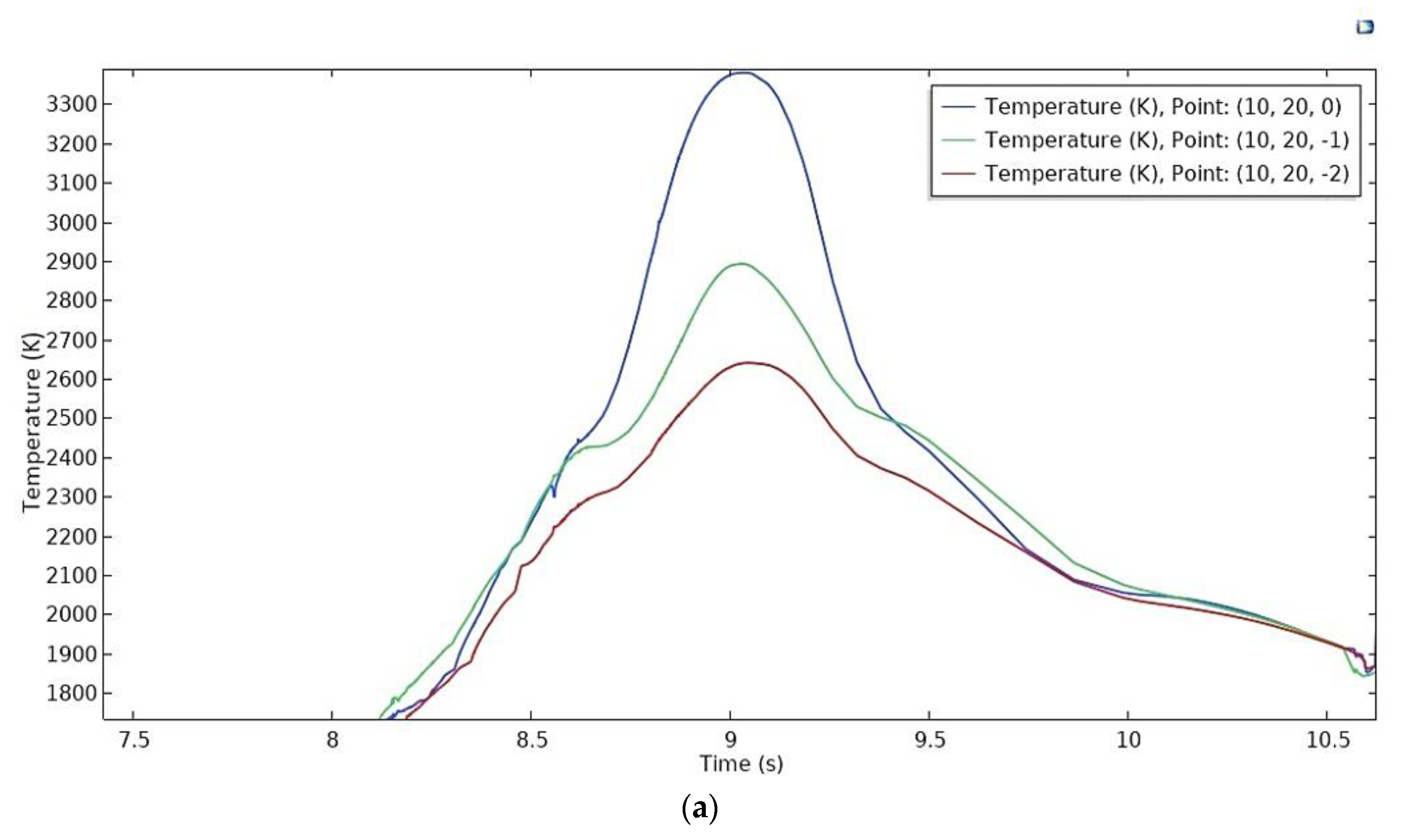
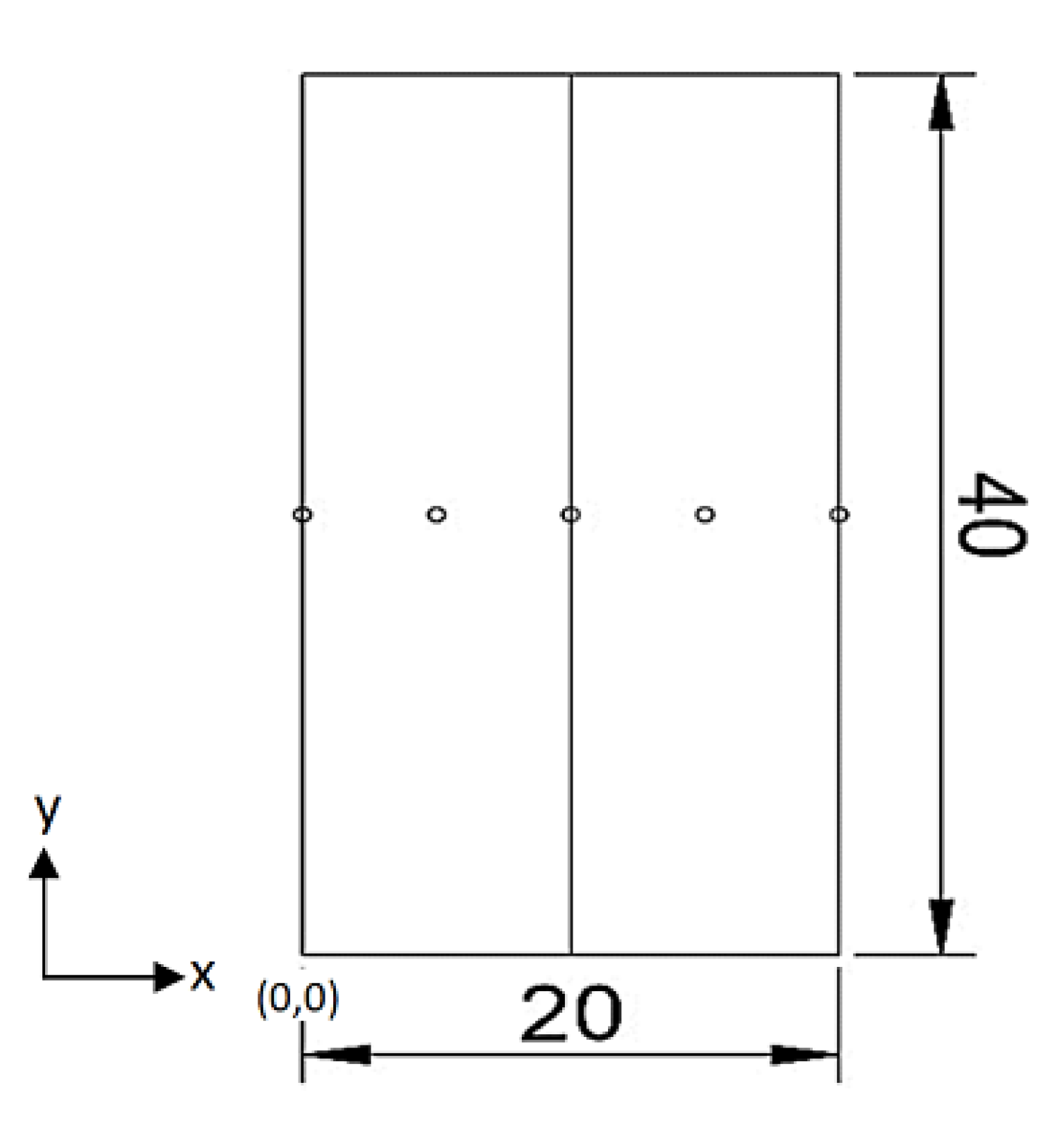
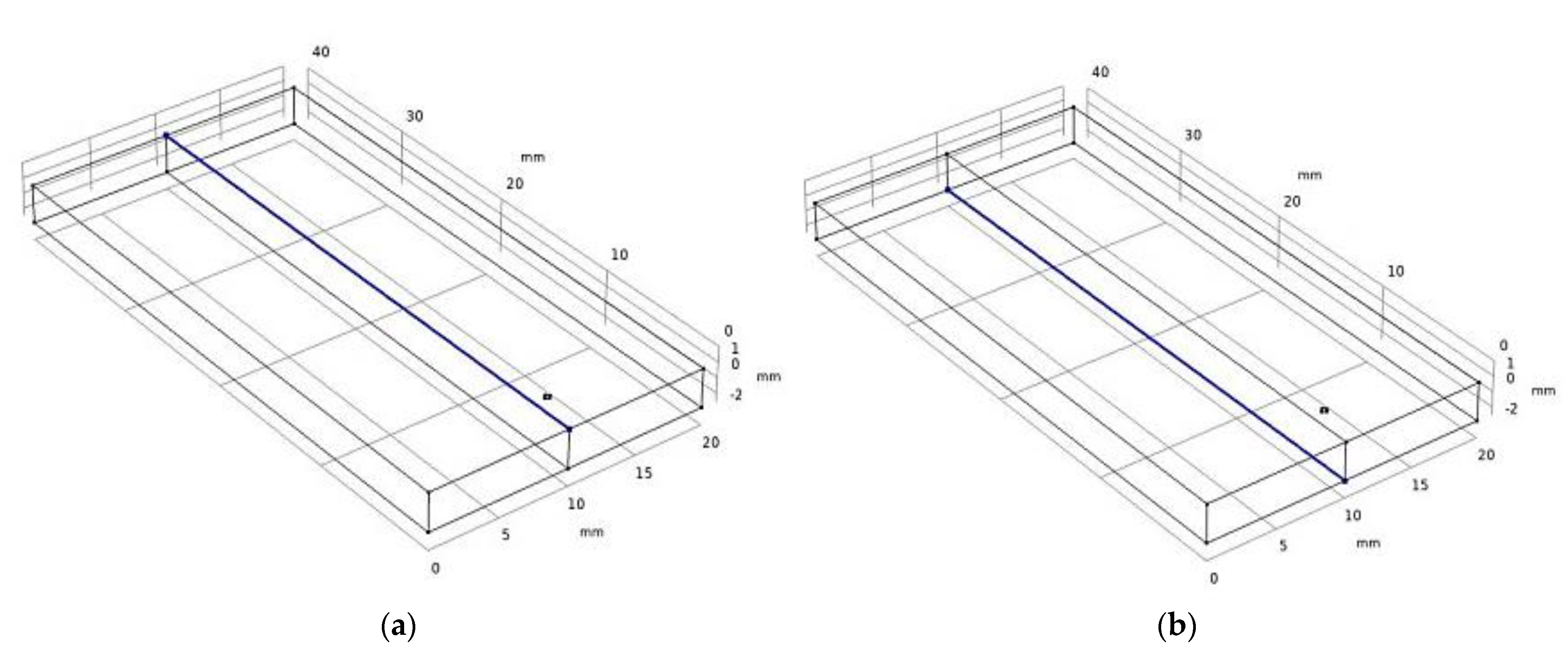
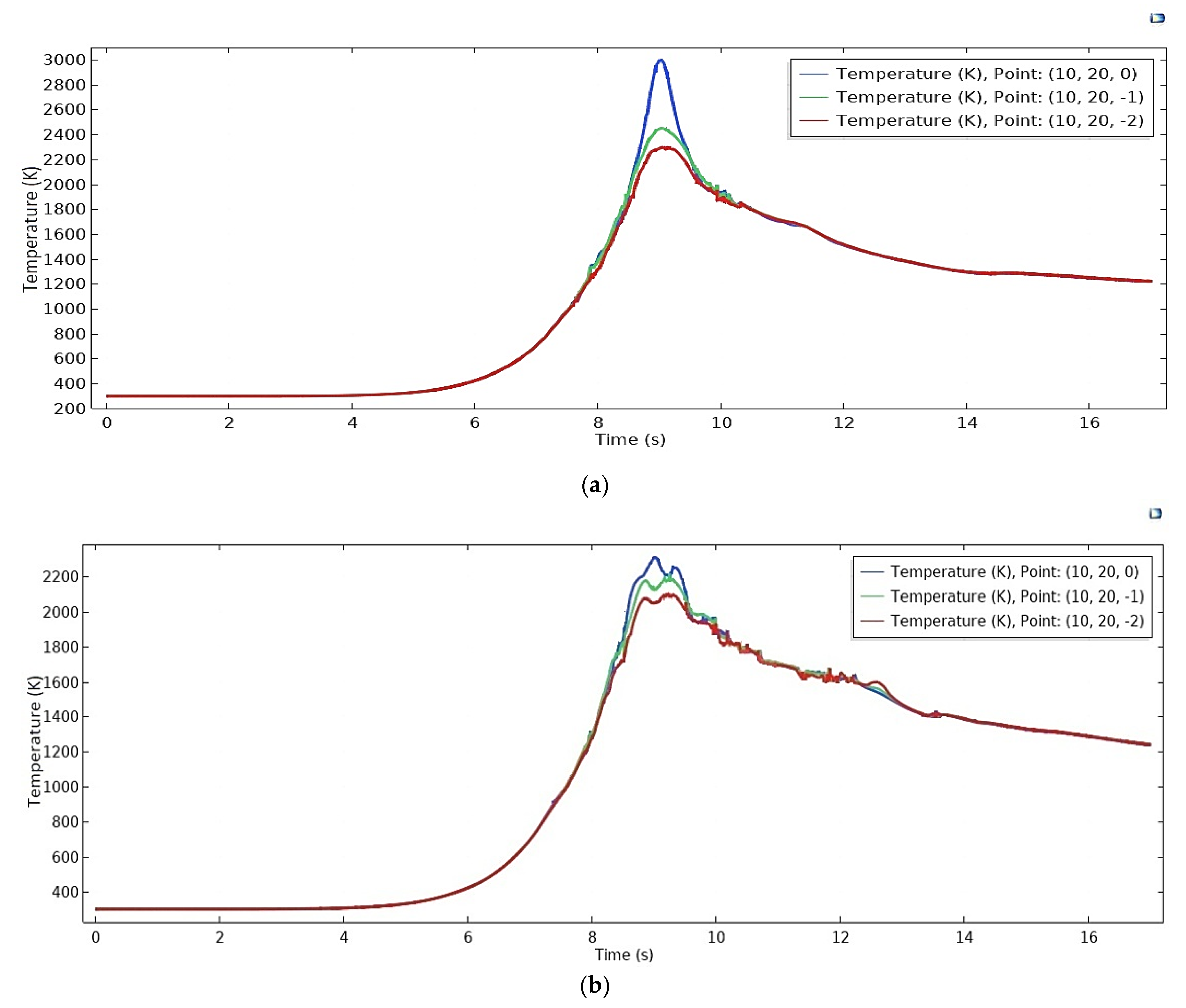
4.3. Temperature Probes
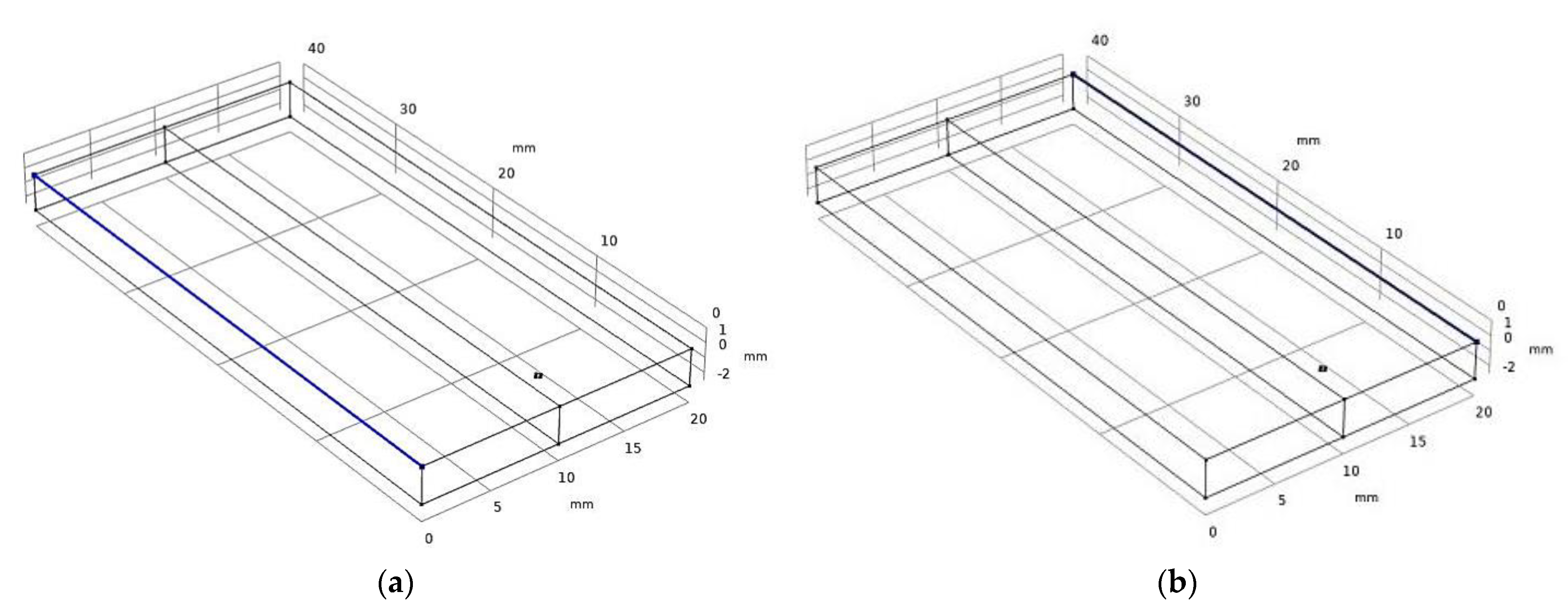
4.4. Offsetting the Laser Beam toward Ti-6Al-4V
5. Conclusions
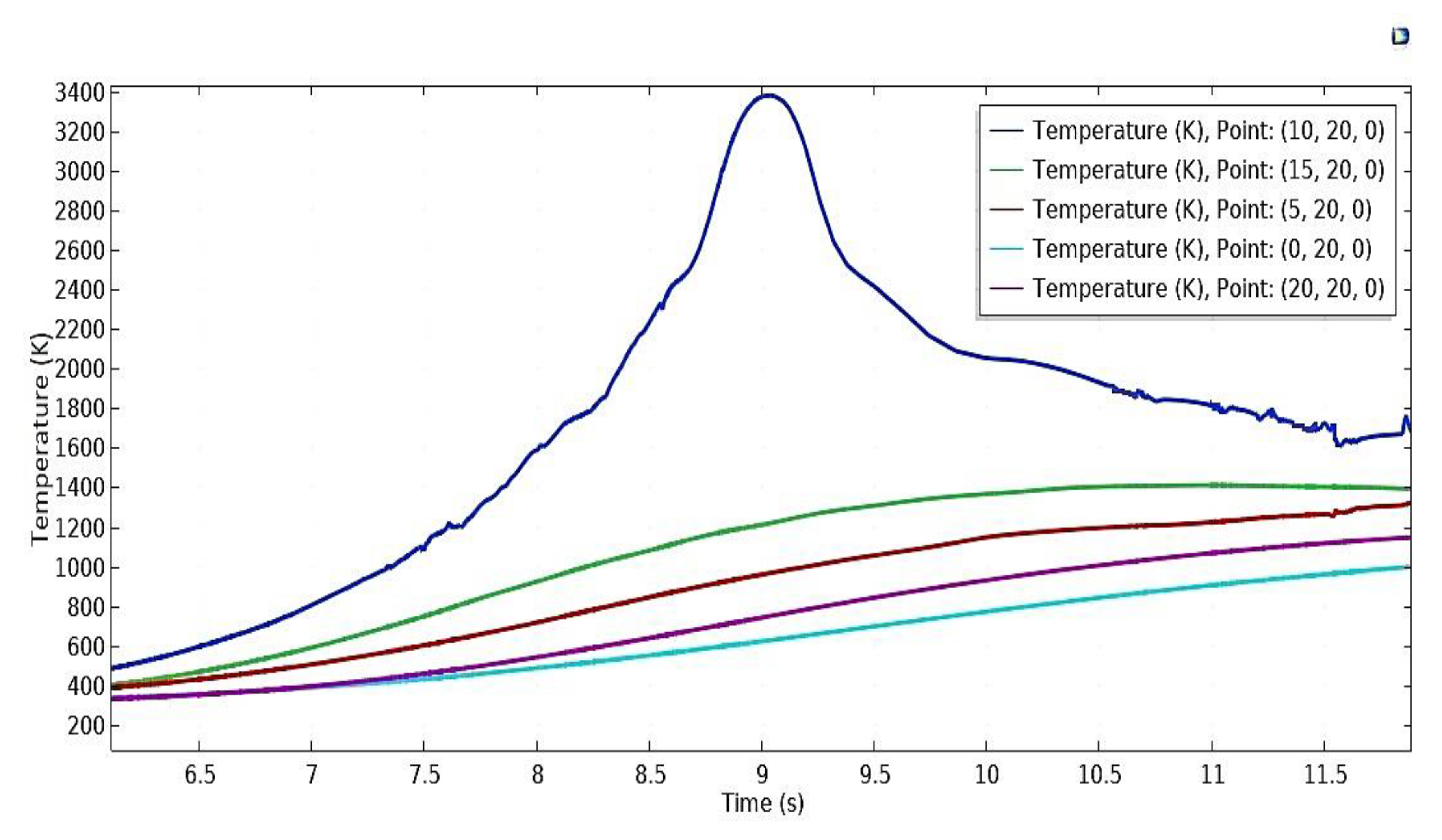
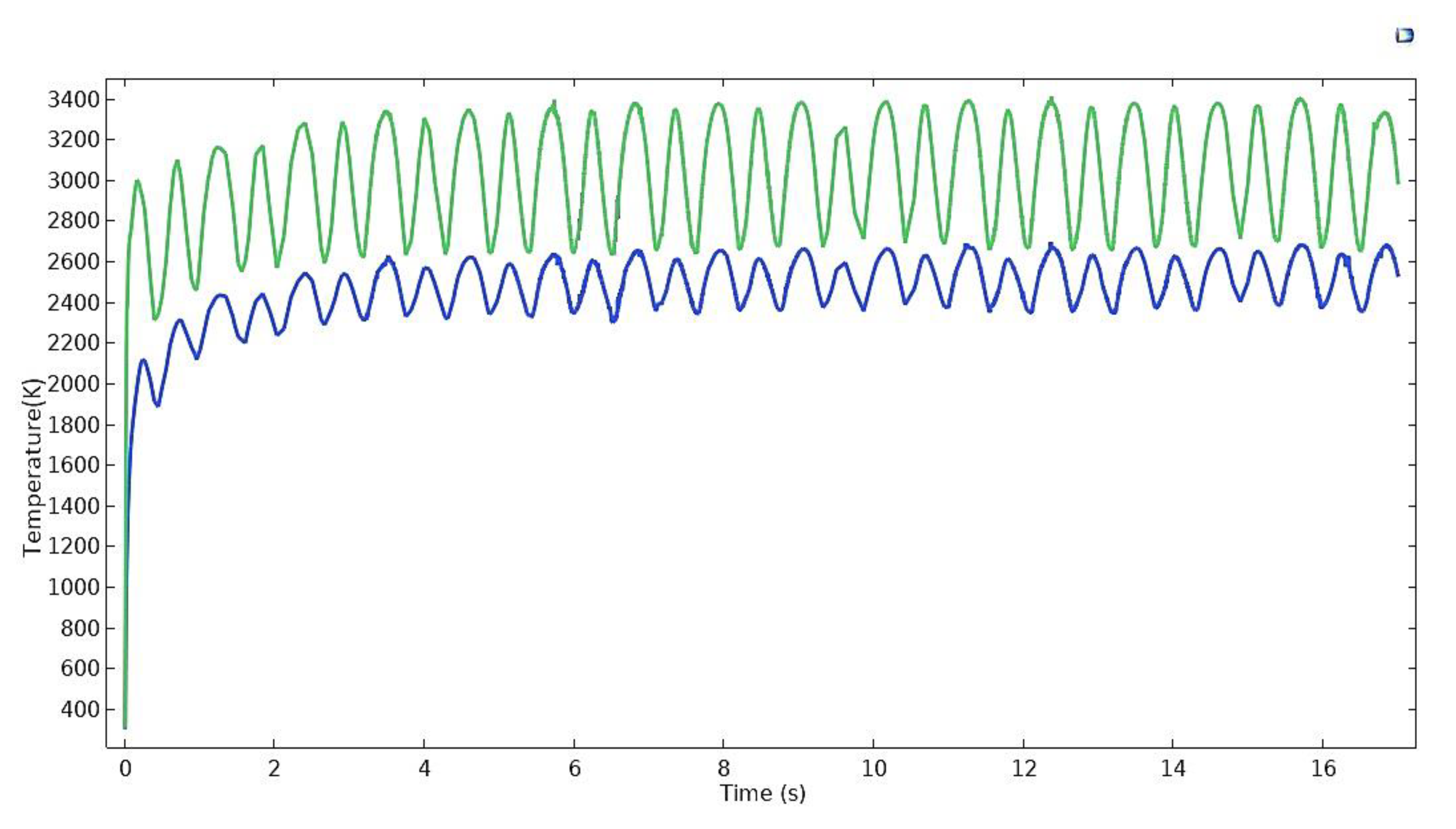
- Temperature distribution along the weld line throughout the process at laser spot irradiation shows that the average maximum temperature generated is near 3300 K. Maximum temperatures along the traverse direction (for fixed y value) on z = 0 plane in the middle (x = 5 and x = 15) and edges (x = 0 and x = 20) of the work pieces are approximately 1200 and 1000 K, respectively.
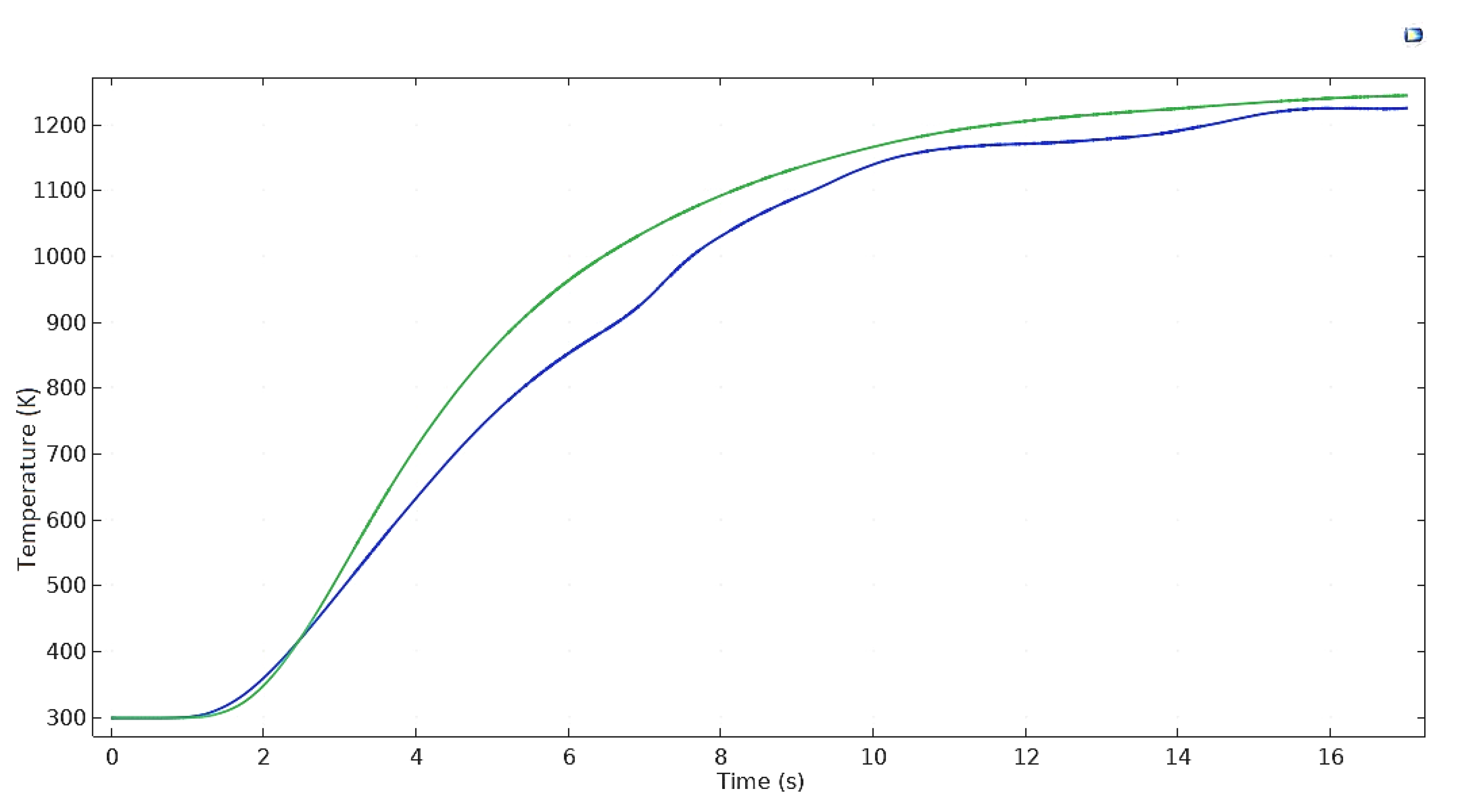
- Temperature distribution along the thickness shows that even the bottom-most surface along the z-axis achieves an average temperature near 2400 K. A significant penetration depth can be achieved. The average temperature of the two domains ranges from 1150 K to 1200 K during the process.
- There are differences in the thermal properties of these two materials. Ti6Al4V has a higher melting temperature. It would take more time than 316L to reach it, as the model was done in zero offsets. The offset of the laser heat source in the same arrangement can create a better-quality welding by adjusting the variations in thermal properties as predicted from the model. Welding interface temperature can be minimized up to 500–1000 K by offsetting the laser beam toward the Ti-6Al-4V side.
- Transient distribution of peak temperature from the weld line along the x-axis is plotted and it decreases as it moves far from the source, for obvious reason. Near the weld line, it decreases sharply and the sharpness decreases as the distance increases from the weld line. The difference of maximum temperature between the edge lines (along x = 0 and x = 20) on the z = 0 plane lies between 20 and 100 K. The maximum temperatures can reach up to 1200 K for both samples along the edges mentioned, which indicates recrystallization for AISI 316 and presence of both α phase and β phase for Ti6Al4V that occur within the sample width range.
- Transient isothermal contours help to understand the heating and cooling phenomena during the process. At higher temperature, AISI316L has a lower thermal conductivity compared to Ti6Al4V; thus, the steel part attains a higher temperature near the weld zone. Temperature history of two nearby points in traverse direction makes it understandable that even within two nearer points; one can be in heating mode and one in cooling mode. This fact demonstrates the complex type of deformation, which is the main source of residual stresses.
6. Future Scope
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, J.H.; Liaw, P.K.; Corum, J.M.; McCoy, H.E. High-temperature mechanical behavior of Ti-6Al-4V alloy and TiC p /Ti-6Al-4V composite. Met. Mater. Trans. A 1999, 30, 1569–1578. [Google Scholar] [CrossRef]
- Baqer, Y.M.; Ramesh, S.; Yusof, F.; Manladan, S.M. Challenges and advances in laser welding of dissimilar light alloys: Al/Mg, Al/Ti, and Mg/Ti alloys. Int. J. Adv. Manuf. Technol. 2018, 95, 4353–4369. [Google Scholar] [CrossRef]
- Kotadia, H.R.; Franciosa, P.; Ceglarek, D. Challenges and Opportunities in Remote Laser Welding of Steel to Aluminium. In Proceedings of the MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2019; Volume 269, p. 02012. [Google Scholar]
- Pouranvari, M. Critical assessment 27: Dissimilar resistance spot welding of aluminium/steel: Challenges and opportunities. Mater. Sci. Technol. 2017, 33, 1705–1712. [Google Scholar] [CrossRef] [Green Version]
- Szymlek, K. Review of Titanium and Steel Welding Methods. Adv. Mater. Sci. 2008, 8, 186–194. [Google Scholar] [CrossRef] [Green Version]
- Emmelmann, C.; Lunding, S. Introduction to Industrial Laser Materials Processing; Rofin-Sinar Laser: Hamburg, Germany, 2000. [Google Scholar]
- Jakubczak, K. Lasers: Applications in Science and Industry; Jakubczak, K., Ed.; BoD–Bookson Demand: Norderstedt, Germany, 2011. [Google Scholar]
- Castillejo, M. Lasers in Materials Science; Ossi, P.M., Zhigilei, L., Eds.; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Benyounis, K.; Olabi, A.; Hashmi, M. Effect of laser welding parameters on the heat input and weld-bead profile. J. Mater. Process. Technol. 2005, 164–165, 978–985. [Google Scholar] [CrossRef] [Green Version]
- Falvo, A.; Furgiuele, F.; Maletta, C. Laser welding of a NiTi alloy: Mechanical and shape memory behaviour. Mater. Sci. Eng. A 2005, 412, 235–240. [Google Scholar] [CrossRef]
- Wang, P.; Chen, X.; Pan, Q.; Madigan, B.; Long, J. Laser welding dissimilar materials of aluminum to steel: An overview. Int. J. Adv. Manuf. Technol. 2016, 87, 3081–3090. [Google Scholar] [CrossRef]
- Chen, H.-C.; Pinkerton, A.J.; Li, L. Fibre laser welding of dissimilar alloys of Ti-6Al-4V and Inconel 718 for aerospace applications. Int. J. Adv. Manuf. Technol. 2011, 52, 977–987. [Google Scholar] [CrossRef]
- Azizpour, M.; Ghoreishi, M.; Khorram, A. Numerical simulation of laser beam welding of Ti6Al4V sheet. J. Comput. Appl. Res. Mech. Eng. 2015, 4, 145–154. [Google Scholar] [CrossRef]
- Turňa, M.; Taraba, B.; Ambroz, P.; Sahul, M. Contribution to Numerical Simulation of Laser Welding. Phys. Procedia 2011, 12, 638–645. [Google Scholar] [CrossRef] [Green Version]
- Kazemi, K.; Goldak, J.A. Numerical simulation of laser full penetration welding. Comput. Mater. Sci. 2009, 44, 841–849. [Google Scholar] [CrossRef]
- Tsirkas, S.; Papanikos, P.; Kermanidis, T. Numerical simulation of the laser welding process in butt-joint specimens. J. Mater. Process. Technol. 2003, 134, 59–69. [Google Scholar] [CrossRef]
- Guoming, H.; Jian, Z.; JianQang, L. Dynamic simulation of the temperature field of stainless steel laser welding. Mater. Des. 2007, 28, 240–245. [Google Scholar] [CrossRef]
- Mohanty, S.; Laldas, C.K.; Roy, G.G. A New Model for Keyhole Mode Laser Welding Using FLUENT. Trans. Indian Inst. Met. 2012, 65, 459–466. [Google Scholar] [CrossRef]
- Attarha, M.; Sattari-Far, I. Study on welding temperature distribution in thin welded plates through experimental measurements and finite element simulation. J. Mater. Process. Technol. 2011, 211, 688–694. [Google Scholar] [CrossRef]
- Shanmugam, N.S.; Buvanashekaran, G.; Sankaranarayanasamy, K.; Kumar, S.R. A transient finite element simulation of the temperature and bead profiles of T-joint laser welds. Mater. Des. 2010, 31, 4528–4542. [Google Scholar] [CrossRef]
- Multiphysics COMSOL. Introduction to COMSOL Multiphysics®; COMSOL Multiphysics: Burlington, MA, USA, 2018. [Google Scholar]
- Dickinson, E.; Ekström, H.; Fontes, E. COMSOL Multiphysics®: Finite element software for electrochemical analysis. A mini-review. Electrochem. Commun. 2014, 40, 71–74. [Google Scholar] [CrossRef]
- Ranjbarnodeh, E.; Serajzadeh, S.; Kokabi, A.H.; Fischer, A. Prediction of temperature distribution in dissimilar arc welding of stainless steel to carbon steel. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 117–125. [Google Scholar] [CrossRef]
- Akbari, M.; Saedodin, S.; Toghraie, D.; Shoja-Razavi, R.; Kowsari, F. Experimental and numerical investigation of temperature distribution and melt pool geometry during pulsed laser welding of Ti6Al4V alloy. Opt. Laser Technol. 2014, 59, 52–59. [Google Scholar] [CrossRef]
- Kumar, P.; Sinha, A.N. Studies of temperature distribution for laser welding of dissimilar thin sheets through finite element method. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 455. [Google Scholar] [CrossRef]
- Attar, M.A.; Ghoreishi, M.; Beiranvand, Z.M. Prediction of weld geometry, temperature contour and strain distribution in disk laser welding of dissimilar joining between copper & 304 stainless steel. Optik 2020, 219, 165288. [Google Scholar] [CrossRef]
- Li, Z.; Rostam, K.; Panjehpour, A.; Akbari, M.; Karimipour, A.; Rostami, S. Experimental and numerical study of temperature field and molten pool dimensions in dissimilar thickness laser welding of Ti6Al4V alloy. J. Manuf. Process. 2020, 49, 438–446. [Google Scholar] [CrossRef]
- Ai, Y.; Jiang, P.; Wang, C.; Mi, G.; Geng, S. Experimental and numerical analysis of molten pool and keyhole profile during high-power deep-penetration laser welding. Int. J. Heat Mass Transf. 2018, 126, 779–789. [Google Scholar] [CrossRef]
- Akbari, M.; Saedodin, S.; Panjehpour, A.; Hassani, M.; Afrand, M.; Torkamany, M.J. Numerical simulation and designing artificial neural network for estimating melt pool geometry and temperature distribution in laser welding of Ti6Al4V alloy. Optik 2016, 127, 11161–11172. [Google Scholar] [CrossRef]
- Fey, A.; Ulrich, S.; Jahn, S.; Schaaf, P. Numerical analysis of temperature distribution during laser deep welding of duplex stainless steel using a two-beam method. Weld. World 2020, 64, 623–632. [Google Scholar] [CrossRef]
- Kumar, K.S. Analytical Modeling of Temperature Distribution, Peak Temperature, Cooling Rate and Thermal Cycles in a Solid Work Piece Welded by Laser Welding Process. Procedia Mater. Sci. 2014, 6, 821–834. [Google Scholar] [CrossRef] [Green Version]
- Tsirkas, S. Numerical simulation of the laser welding process for the prediction of temperature distribution on welded aluminium aircraft components. Opt. Laser Technol. 2018, 100, 45–56. [Google Scholar] [CrossRef]
- Shah, A.; Kumar, A.; Ramkumar, J. Analysis of transient thermo-fluidic behavior of melt pool during spot laser welding of 304 stainless-steel. J. Mater. Process. Technol. 2018, 256, 109–120. [Google Scholar] [CrossRef]
- Wang, R.; Lei, Y.; Shi, Y. Numerical simulation of transient temperature field during laser keyhole welding of 304 stainless steel sheet. Opt. Laser Technol. 2011, 43, 870–873. [Google Scholar] [CrossRef]
- Lee, K.-H.; Yun, G.J. A novel heat source model for analysis of melt Pool evolution in selective laser melting process. Addit. Manuf. 2020, 36, 101497. [Google Scholar] [CrossRef]
- Steen, W.M.; Dowden, J.; Davis, M.; Kapadia, P. A point and line source model of laser keyhole welding. J. Phys. D Appl. Phys. 1988, 21, 1255–1260. [Google Scholar] [CrossRef]
- Tseng, W.; Aoh, J. Simulation study on laser cladding on preplaced powder layer with a tailored laser heat source. Opt. Laser Technol. 2013, 48, 141–152. [Google Scholar] [CrossRef]
- Xu, G.X.; Wu, C.S.; Qin, G.L.; Wang, X.Y.; Lin, S.Y. Adaptive volumetric heat source models for laser beam and laser + pulsed GMAW hybrid welding processes. Int. J. Adv. Manuf. Technol. 2011, 57, 245–255. [Google Scholar] [CrossRef]
- Jayanthi, A.; Venkatramanan, K.; Kumar, K. Modeling and simulation for welding of AISI316l stainless steels using Pulsed Nd:YAG Laser. Int. J. Mater. Sci. 2017, 12, 39–50. [Google Scholar]
- Indhu, R.; Tak, M.; Vijayaraghavan, L.; Soundarapandian, S. Microstructural evolution and its effect on joint strength during laser welding of dual phase steel to aluminium alloy. J. Manuf. Process. 2020, 58, 236–248. [Google Scholar] [CrossRef]
- Indhu, R.; Divya, S.; Tak, M.; Soundarapandian, S. Microstructure development in Pulsed Laser Welding of Dual Phase Steel to Aluminium Alloy. Procedia Manuf. 2018, 26, 495–502. [Google Scholar] [CrossRef]
- Indhu, R.; Soundarapandian, S.; Vijayaraghavan, L. Yb: YAG laser welding of dual phase steel to aluminium alloy. J. Mater. Process. Technol. 2018, 262, 411–421. [Google Scholar] [CrossRef]
- Indhu, R.; Tak, M.; Vijayaraghavan, L.; Soundarapandian, S. Microstructural and mechanical properties of complex phase steel to aluminium alloy welded dissimilar joint. Procedia Manuf. 2020, 48, 267–272. [Google Scholar] [CrossRef]
- Paschotta, R. Encyclopedia of Laser Physics and Technology; Wiley-Vch: Berlin, Germany, 2008; Volume 1. [Google Scholar]
- Noy, A. (Ed.) Handbook of Molecular Force Spectroscopy; Springer Science & Business Media: Heidelberg, Germany, 2007. [Google Scholar]
- Lakoba, T.I.; Kaup, D.J. Hermite-Gaussian expansion for pulse propagation in strongly dispersion managed fibers. Phys. Rev. 1998, 58, 6728–6741. [Google Scholar] [CrossRef]
- Balasubramanian, K.R.; Shanmugam, N.S.; Buvanashekaran, G.; Sankaranarayanasamy, K. Numerical and experimental investigation of laser beam welding of AISI304 stainless steel sheet. Adv. Prod. Eng. Manag. 2008, 3, 93–105. [Google Scholar]
- Shanmugam, N.S.; Buvanashekaran, G.; Sankaranarayanasamy, K. Experimental investigation and finite element simulation oflaser beam welding of AISI304 stainless steel sheet. Exp. Tech. 2010, 34, 25–36. [Google Scholar] [CrossRef]
- Boivineau, M.; Cagran, C.; Doytier, D.; Eyraud, V.; Nadal, M.-H.; Wilthan, B.; Pottlacher, G. Thermophysical Properties of Solid and Liquid Ti-6Al-4V (TA6V) Alloy. Int. J. Thermophys. 2006, 27, 507–529. [Google Scholar] [CrossRef]
- Kim, C.S. Thermophysical Properties of Stainless Steels; (No.ANL-75-55); Argonne National Lab.: Lemont, IL, USA, 1975.
- Xiong, L.; Mi, G.; Wang, C.; Zhu, G.; Xu, X.; Jiang, P. Numerical Simulation of Residual Stress for LaserWelding of Ti-6Al-4VAlloy Considering Solid-State Phase Transformation. J. Mater. Eng. Perform. 2019, 28, 3349–3360. [Google Scholar] [CrossRef]
- Mertens, A.; Reginster, S.; Paydas, H.; Contrepois, Q.; Dormal, T.; Lemaire, O.; Lecomte-Beckers, J. Mechanical properties of alloy Ti–6Al–4V and of stainless steel 316L processed by selective laser melting: Influence of out-of-equilibrium microstructures. Powder Met. 2014, 57, 184–189. [Google Scholar] [CrossRef]
- Nguyen, Q.; Azadkhou, A.; Akbari, M.; Panjehpour, A.; Karimipour, A. Experimental investigation of temperature field and fusion zone microstructure in dissimilar pulsed laser welding of austenitic stainless steel and copper. J. Manuf. Process. 2020, 56, 206–215. [Google Scholar] [CrossRef]
- Casalino, G.; Mortello, M. Modeling and experimental analysis of fiber laser offset welding of Al-Ti butt joints. Int. J. Adv. Manuf. Technol. 2015, 83, 89–98. [Google Scholar] [CrossRef]
- Ganeriwala, R.; Strantza, M.; King, W.; Clausen, B.; Phan, T.; Levine, L.; Brown, D.; Hodge, N. Evaluation of a thermomechanical model for prediction of residual stress during laser powder bed fusion of Ti-6Al-4V. Addit. Manuf. 2019, 27, 489–502. [Google Scholar] [CrossRef]
- Casalino, G.; Mortello, M.; Peyre, P. FEM Analysis of Fiber Laser Welding of Titanium and Aluminum. Procedia CIRP 2016, 41, 992–997. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Zhou, J.; Sun, D.; Gu, X. Nd:YAG laser welding of dissimilar metals of titanium alloy to stainless steel without filler metal based on a hybrid connection mechanism. J. Mater. Res. Technol. 2020, 9, 1662–1672. [Google Scholar] [CrossRef]
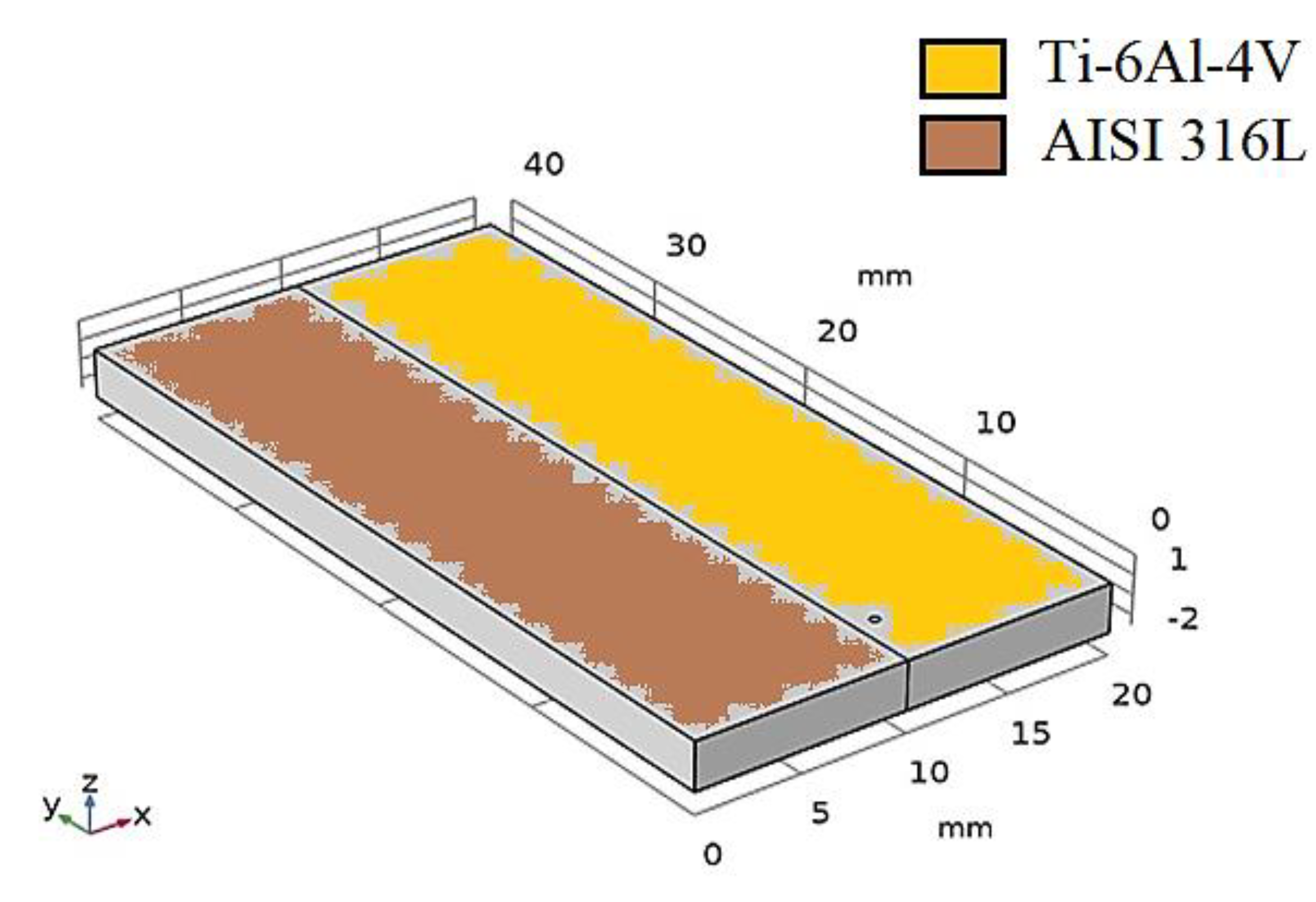
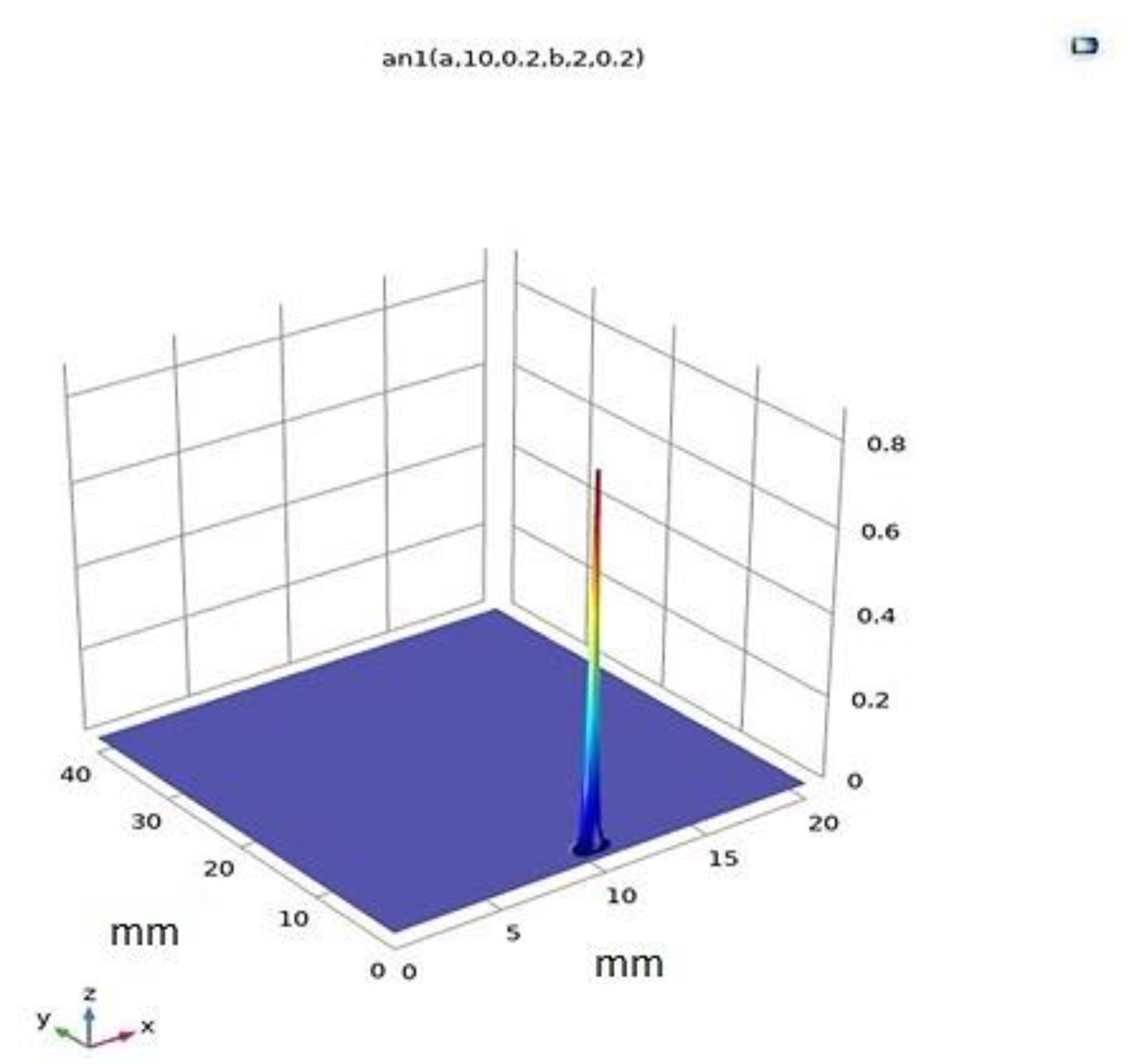
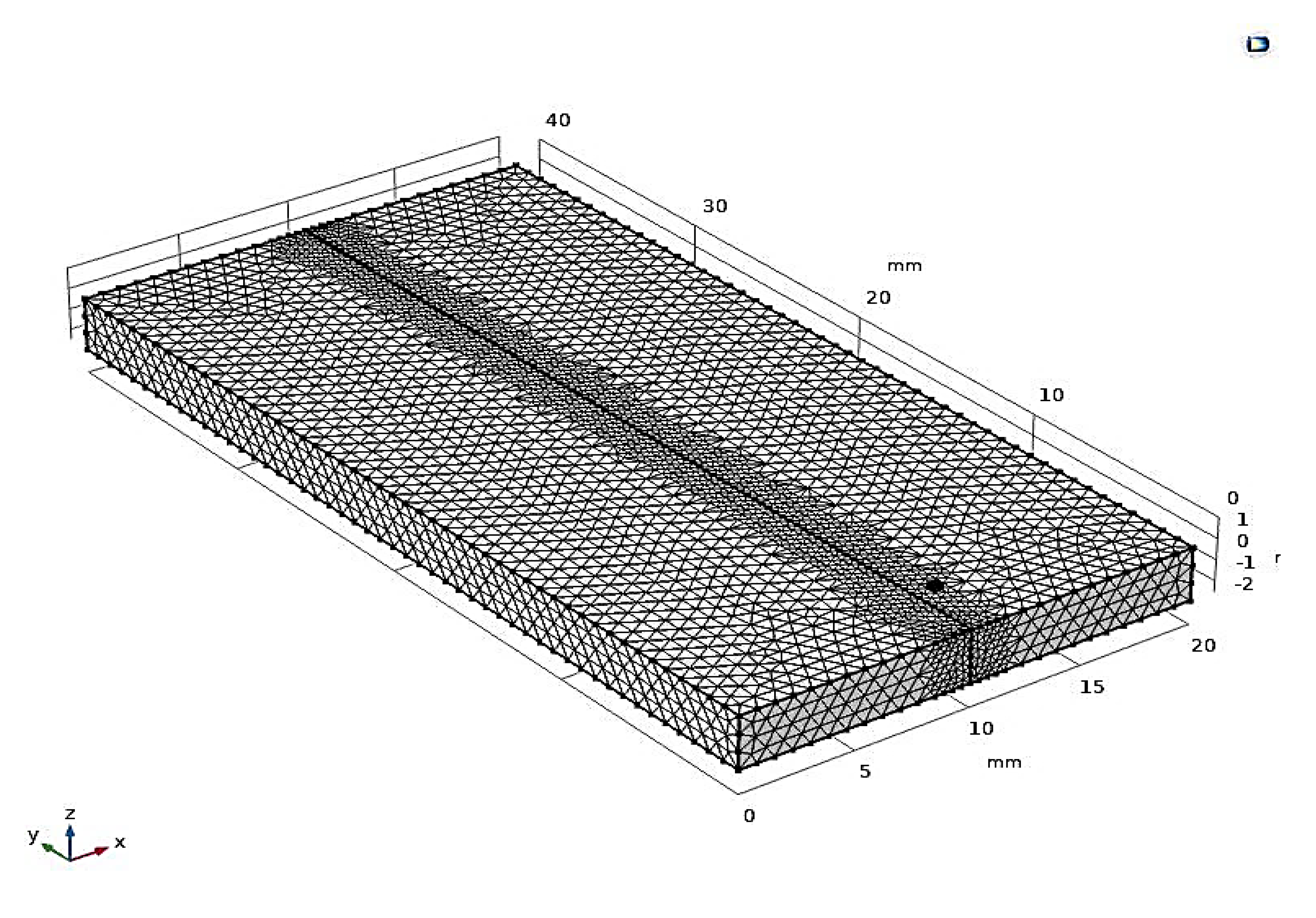
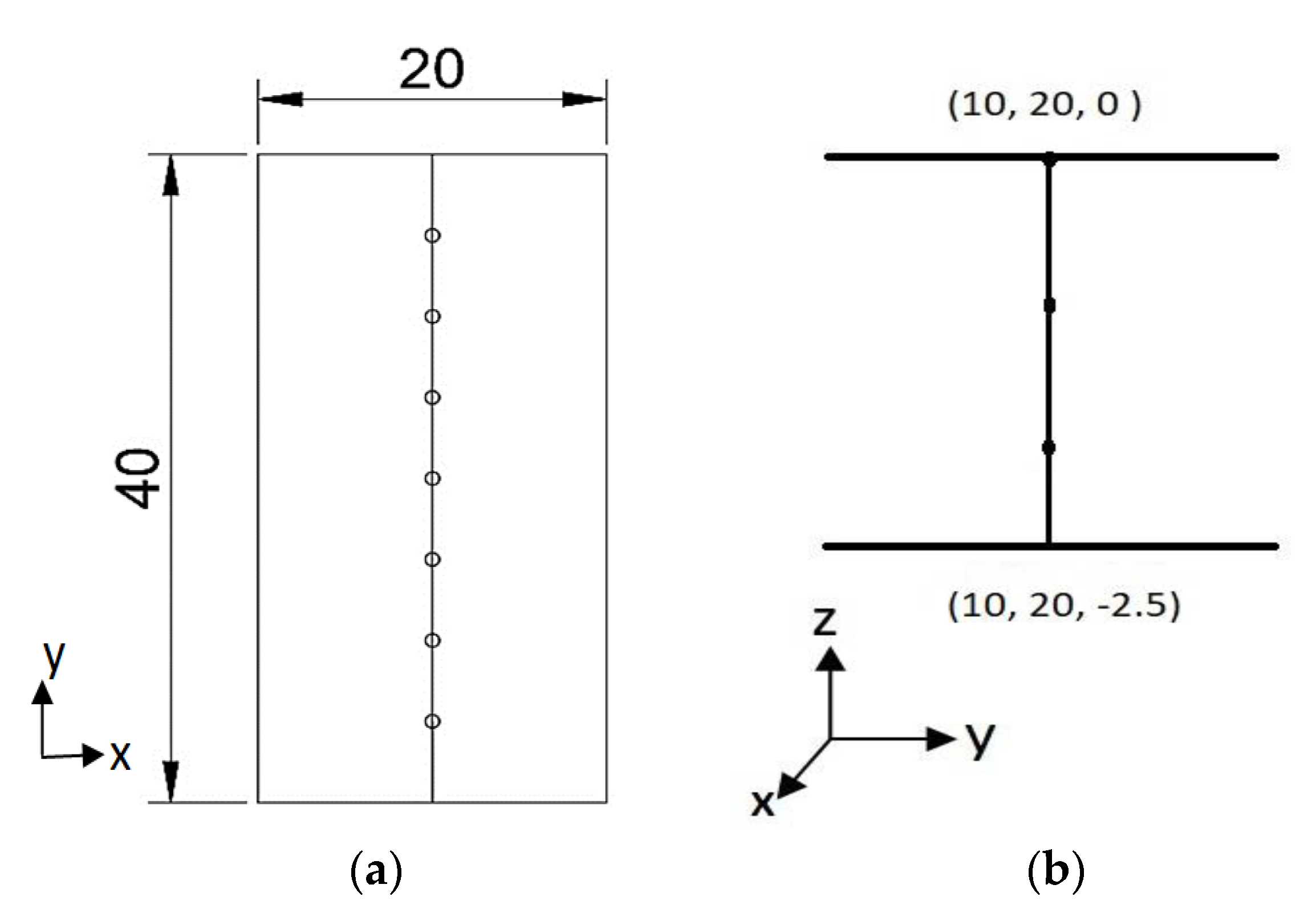

| Parameters | Value | Details |
|---|---|---|
| x0 | 10 [mm] | x coordinate |
| y0 | 2 [mm] | y coordinate |
| Sigx | 0.200 [mm] | Deviation along x |
| Sigy | 0.200 [mm] | Deviation along y |
| Rc | 0.001 | Reflection coefficient |
| Ac | 5 [1/cm] | Absorption coefficient |
| Q0 | 300 [W] | Laser power |
| L1 | 10 [mm] | Material size 1 |
| L2 | 10 [mm] | Material size 2 |
| LZ | 2.5 [mm] | Thickness of the sheet |
| Time step | 0.2 | Time step for storing solution |
| End time | 17 [s] | End time step |
| V | 2.0 [mm/s] | Laser velocity |
| L | 40 [mm] | Length of sheet |
| Arguments | Upper Limit | Lower Limit |
|---|---|---|
| a | (L1 + L2) | 0 |
| a0 | x0 | x0 |
| Siga | Sigx | Sigx |
| b | 2(L1 + L2) | 0 |
| b0 | y0 | y0 |
| sigb | sigy | Sigy |
| Name | Value | Unit |
|---|---|---|
| Density | rho(T) | kg/m³ |
| Thermal conductivity | k_iso(T) | W/(m·K) |
| Heat capacity at constant pressure | Cp(T) | J/(kg·K) |
| Name | Value |
|---|---|
| Convective heat transfer of air(h) | 10 W/m2K |
| Emissivity(ε) | 0.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, P.S.; Sen, A.; Chattopadhyaya, S.; Sharma, S.; Singh, J.; Dwivedi, S.P.; Saxena, A.; Khan, A.M.; Pimenov, D.Y.; Giasin, K. Prediction of Transient Temperature Distributions for Laser Welding of Dissimilar Metals. Appl. Sci. 2021, 11, 5829. https://doi.org/10.3390/app11135829
Ghosh PS, Sen A, Chattopadhyaya S, Sharma S, Singh J, Dwivedi SP, Saxena A, Khan AM, Pimenov DY, Giasin K. Prediction of Transient Temperature Distributions for Laser Welding of Dissimilar Metals. Applied Sciences. 2021; 11(13):5829. https://doi.org/10.3390/app11135829
Chicago/Turabian StyleGhosh, Partha Sarathi, Abhishek Sen, Somnath Chattopadhyaya, Shubham Sharma, Jujhar Singh, Shashi Parkash Dwivedi, Ambuj Saxena, Aqib Mashood Khan, Danil Yurievich Pimenov, and Khaled Giasin. 2021. "Prediction of Transient Temperature Distributions for Laser Welding of Dissimilar Metals" Applied Sciences 11, no. 13: 5829. https://doi.org/10.3390/app11135829
APA StyleGhosh, P. S., Sen, A., Chattopadhyaya, S., Sharma, S., Singh, J., Dwivedi, S. P., Saxena, A., Khan, A. M., Pimenov, D. Y., & Giasin, K. (2021). Prediction of Transient Temperature Distributions for Laser Welding of Dissimilar Metals. Applied Sciences, 11(13), 5829. https://doi.org/10.3390/app11135829










