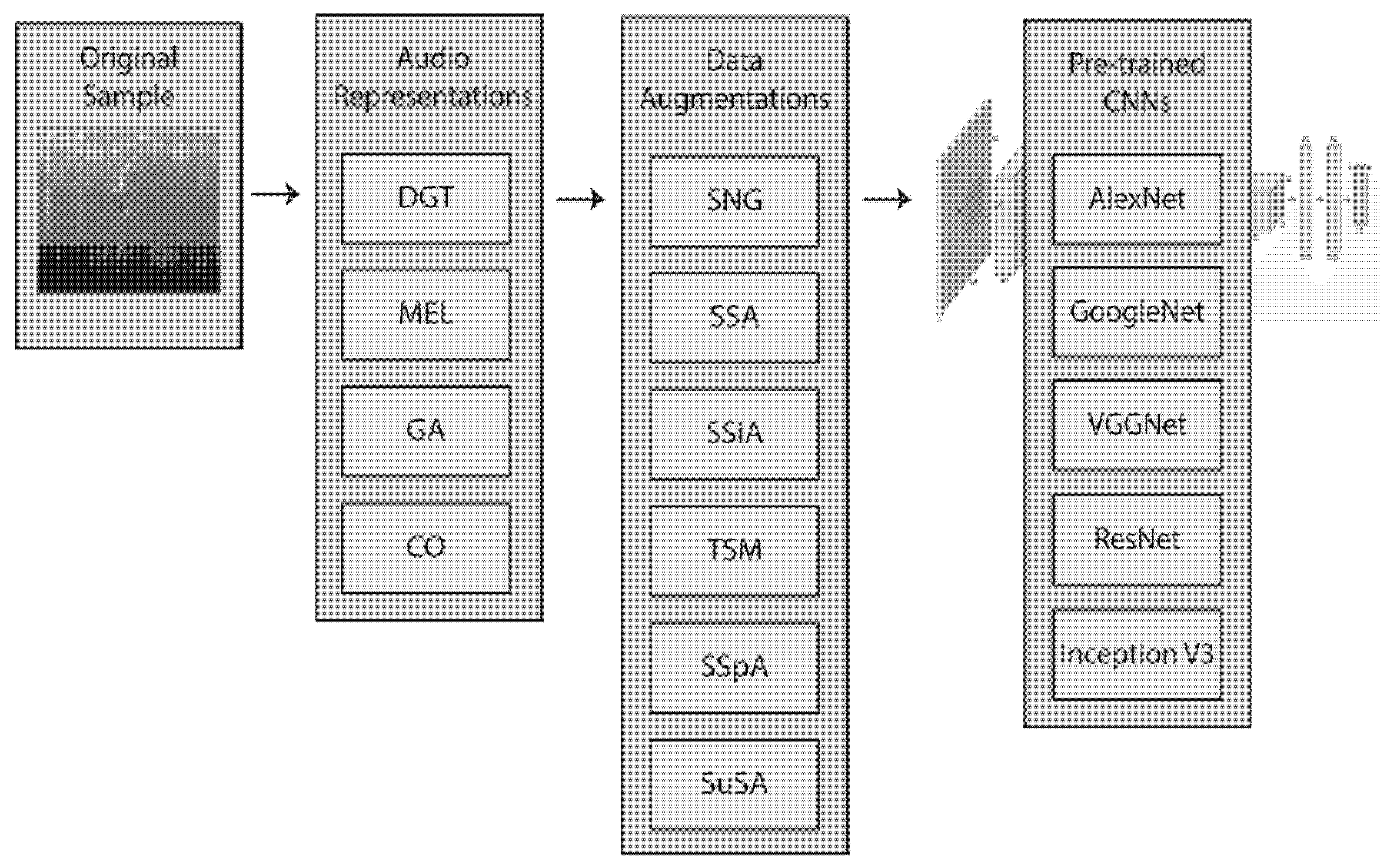
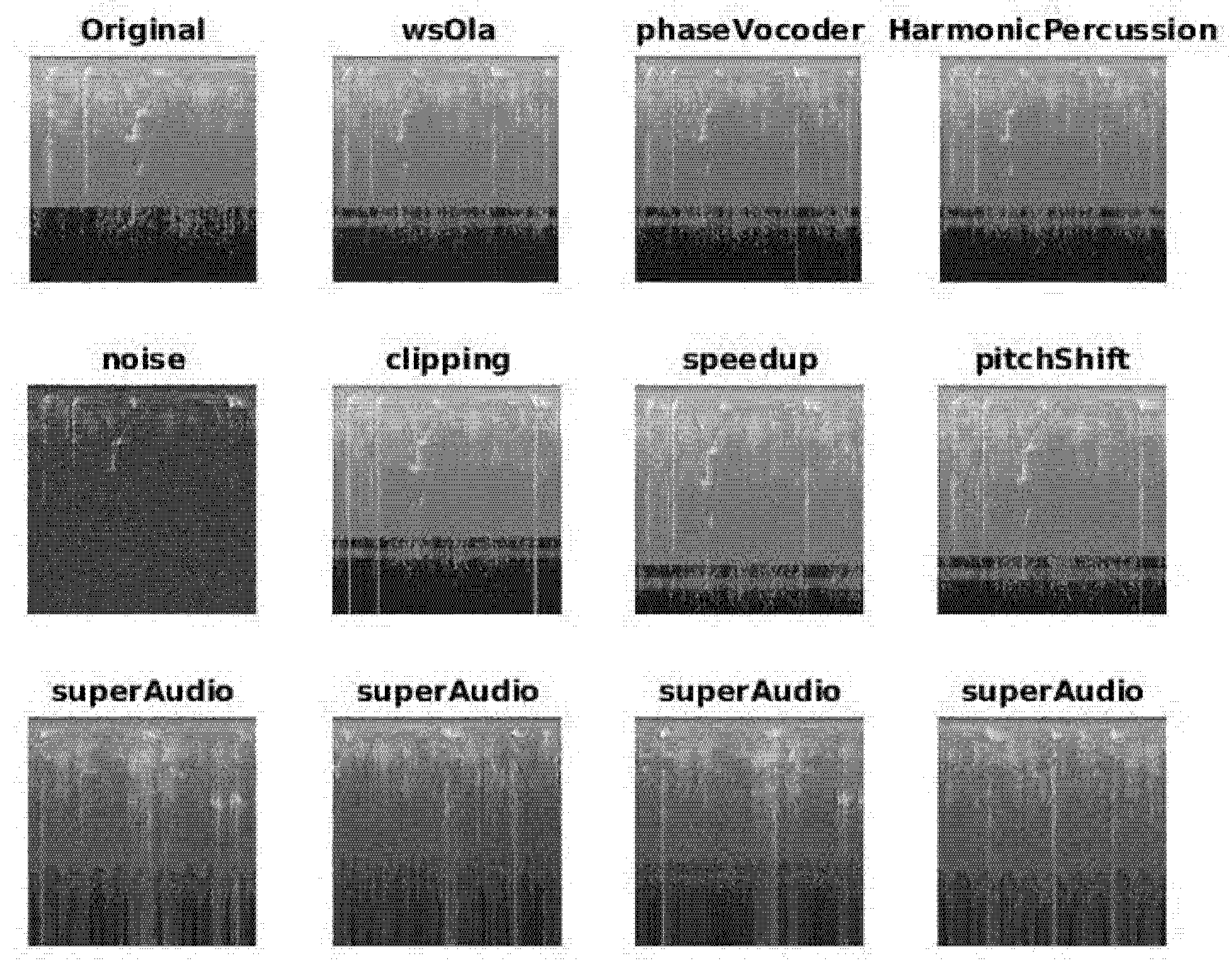
1. Introduction
Sound classification and recognition have long been included in the field of pattern recognition. Some of the more popular application domains include speech recognition [
1], music classification [
2], biometric identification [
3], and environmental sound recognition [
4], the topic of interest in this work. Following the three classical pattern recognition steps of (i) preprocessing, (ii) feature/descriptor extraction, and (iii) classification, most early work in sound classification began by extracting features from audio recordings such as the Statistical Spectrum Descriptor or Rhythm Histogram [
5]. Once it was recognized, however, that visual representations of audio, such as spectrograms [
6] and Mel-frequency Cepstral Coefficients spectrograms (Mel) [
7], contain valuable information, powerful texture extraction techniques like local binary patterns (LBP) [
8] and its many variants [
9] began to be explored for audio classification [
2,
10]. In [
2], for example, ensembles of classifiers designed to fuse sets of the most robust texture descriptors with acoustic features extracted from the audio traces on multiple datasets were exhaustively investigated; this study showed that the accuracy of systems based solely on acoustic or visual features could be enhanced by combining texture features.
Recently, deep learners have proven even more robust in image recognition and classification than have texture analysis techniques. In audio biodiversity assessment, for example, a task that intends to monitor animal species at risk, convolution neural networks (CNNs) have greatly enhanced the performance of animal [
11] and bird identification [
12,
13,
14]. Deep learners have also been adapted to identify the sounds of marine animals [
11] and fish [
15]. In both these works, the authors combined CNN with visual features; the fusion of CNNs with traditional techniques was shown to outperform both the stand-alone conventional and single deep learning approaches.
Another environmental audio recognition problem that is growing in relevancy has to do with identifying sources of noise in environments. This audio classification problem is of particular concern for cell phone developers since noise interferes with conversation. Consequently, datasets of extraneous sounds have been released to develop systems for handling different kinds of noise. The Environmental Sound Classification (ESC-50) dataset, for instance, contains 2000 labeled samples divided into fifty classes of environmental sounds that range from dogs barking to the sound of sea waves and chainsaws. In [
16], a deep CNN achieved results superior to human classification on this dataset. Other work of interest in this area includes [
17,
18,
19,
20,
21].
For all its power, deep learning also has significant drawbacks when it comes to environmental sound classification. For one, deep learning approaches require massive training data [
22]. For audio classification, this means collecting large numbers of labeled audio signals and transforming them into visual representations, a task that is prohibitively expensive and labor-intensive. Fortunately, there are methods for increasing the number of images in small datasets. One such method is to apply data augmentation techniques. Audio signals can be augmented in both the time and frequency domains, and these augmentation techniques can be directly applied either on the raw signals themselves or on the images obtained after they have been converted into spectrograms. In [
23], for example, several augmentation techniques were applied to the training set in the BirdCLEF 2018 dataset. The augmentation pipeline involved taking the original bird audio signals, chunking them, and then augmenting them in the time domain (e.g., by adding background/atmospheric noise) and in the frequency domain (e.g., by applying pitch shifts and frequency stretches). This augmentation process not only enlarged the dataset but also produced nearly a 10% improvement in identification performance. Similarly, some standard audio augmentation techniques such a time and pitch shifts for bird audio classification were applied in [
24]. Samples were also generated in [
24] by summing separate samples belonging to the same class. This summing technique was used for domestic sound classification in [
25,
26]. In [
27], new data was generated by computing the weighted sum of two samples belonging to different classes and teaching the network to predict the weights of the sum. Audio signal augmentation on a domestic cat sound dataset was produced in [
28] by random time stretching, pitch shifting, compressing the dynamic range, and inserting noise. Data augmentation techniques that are standard in speech recognition have also proven beneficial for animal sound identification, as in [
29,
30].
The goal of this work is to perform an extensive study of CNN classification using different architectures combined with an investigation of multiple sets of different data augmentation approaches and methods for representing audio signals as images. Building such ensembles is motivated by two observations: (1) it is well known that ensembles of neural networks generally perform better than stand-alone models due to the instability of the training process [
31], and (2) it has been shown in other classification tasks that an ensemble of multiple networks trained with different augmentation protocols performs much better than do stand-alone networks [
32]. The classification scores of the CNNs are combined by sum rule and compared and tested across three different audio classification datasets: domestic cat sound classification [
28,
33], bird call classification [
34], and environmental noise classification [
4].
The main contribution of this study is the exhaustive tests performed on ensembles made by fusing (see
Figure 1) five CNNs trained with four audio representations of raw sound signals combined with six different data augmentation methods (totaling thirty-five subtypes). The performances of the best performing ensembles are compared across the three datasets and with the state of the art. In the fair comparisons, our method outperforms all others. Another contribution of this work is the free availability of the MATLAB source code used in this study, available at
https://github.com/LorisNanni.
2. Audio Image Representations
Since the input to a CNN is in the form of a matrix, the following four methods were used to map the audio signals into spectrograms:
The Discrete Gabor Transform (DGT): this is a short-time Fourier transform (STFT) with a Gaussian kernel as the window function. The continuous version of DGT can be defined as the convolution between the product of the signal with a complex exponential and a Gaussian, as:
where s
is the signal,
is a frequency, and
is the imaginary unit. The width of the Gaussian window is defined by
. The discrete version of DGT applies the discrete convolution rather than the continuous convolution. The output
is a matrix, where the columns represent the frequencies of the signal at a fixed time. The DGT implementation used in this study (see, [
35]) is available at
http://ltfat.github.io/doc/gabor/sgram.html (accessed on 6 January 2021).
Mel spectrograms (MEL) [
36]: these spectrograms are computed by extracting the coefficients relative to the compositional frequencies with STFT. Extraction is accomplished by passing each frame of the frequency-domain representation through a Mel filter bank (the idea is to mimic the non-linear human ear perception of sound, which discriminates lower frequencies better than higher frequencies). Conversion between Hertz (
) and Mel (
) is defined as:
The filters in the filter bank are all triangular, which means that each has a response of 1 at the center frequency, which decreases linearly towards 0 until it reaches the center frequencies of the two adjacent filters, where the response is 0.
- 3.
Gammatone (GA) band-pass filters: this is a bank of GA filters whose bandwidth increases with the increasing central frequency. The functional form of Gammatone is inspired by the response of the cochlea membrane in the inner ear of the human auditory system [
37]. The impulse response of a Gammatone filter is the product of a statistical distribution (Gamma) and a sinusoidal carrier tone. This response can be defined as:
where
is the central frequency of the filter and
its phase. Gain is controlled by the constant
, and
is the order of the filter.
is a decay parameter that determines the bandwidth of the band-pass filter.
- 4.
Cochleagram (CO): this mapping models the frequency selectivity property of the human cochlea [
38]. To extract a cochleagram, it is first necessary to filter the original signal with a gammatone filter bank (see, Equation (3) above). The filtered signal must then be divided into overlapping windows. For each window and every frequency, the energy of the signal is calculated.
Each of the four spectrograms is then mapped to a gray-scale image using a linear transformation that maps the minimum value to 0 and the maximum value to 255, with the value of each pixel rounded to the closest smaller integer.
3. Convolutional Neural Networks (CNNs)
Aside from the input and output layers, CNNs are composed of one or more of the following specialized hidden layers: convolutional (CONV), activation (ACT), pooling (POOL), and fully-connected (FC), or classification layer. The CONV layers pull out features from the input volume and work by convolving a local region of the input volume (the receptive field) to filters of the same size. Once the convolution is computed, these filters slide into the next receptive field, where once again, the convolution between the new receptive field and the same filter is computed. This process is iterated over the entire input image, whereupon it produces the input for the next layer, a non-linear ACT layer, which improves the learning capabilities and classification performance of the network. Typical activation functions include (i) the non-saturating Rectified Linear Activation Function (ReLU) function , (ii) the saturating hyperbolic tangent , , and (iii) the sigmoid function . Pool layers are often interspersed between CONV layers and perform non-linear downsampling operations (max or average pool) that serve to reduce the spatial size of the representation, which in turn has the benefit of reducing the number of parameters, the possibility of overfitting, and the computational complexity of the CNN. FC layers typically make up the last hidden layers and have FC neurons to all the activations in the previous layer. SoftMax is generally used as the activation function for the output CLASS layer, which performs the final classification (also typically using the SoftMax function).
In this study, five CNNs pre-trained on ImageNet [
39] or Places365 [
40] are adapted to the problem of environmental sound classification as defined in the datasets used in this work. The architecture of the following pre-trained CNNs remains unaltered except for the last three layers, which are replaced by an FC layer, an ACT layer using SoftMax, and a CLASS layer also using SoftMax:
AlexNet [
41] was the first neural network to win (and by a large margin) the ILSVRC 2012 competition. AlexNet has a structure composed of five CONV blocks followed by three FC layers. The dimension of the hidden layers in the network is gradually reduced with max-pooling layers. The architecture of AlexNet is simple since every hidden layer has only one input layer and one output layer.
GoogleNet [
42] is the winner of ILSVRC 2014 challenge. The architecture of GoogleNet involves twenty-two layers and five POOL layers. GoogleNet was unique in its introduction of a novel Inception module, which is a subnetwork made up of parallel convolutional filters. Because the output of these filters is concatenated, the number of learnable parameters is significantly reduced. This study uses two pre-trained GoogleNets: the first is trained on the ImageNet database [
39], and the second is trained on the Places365 [
40] datasets.
VGGNet [
43] is a CNN that took second place in ILSVRC 2014. Because VGGNet includes 16 (VGG-16) or 19 (VGG-19) CONV/FC layers, it is considered extremely deep. All the CONV layers are homogeneous. Unlike AlexNet [
41], which applies a POOL layer after every CONV layer, VGGNet is composed of relatively tiny 3 × 3 convolutional filters with a POOL layer applied every two to three CONV layers. Both VGG-16 and VGG-19 are used in this study, and both are pre-trained on the ImageNet database [
39].
ResNet [
44] was the winner of ILSVRC 2015 and is much deeper than VGGNet. ResNet is distinguished by introducing a novel network-in-network architecture composed of residual (RES) layers. ResNet is also unique in applying global average pooling layers at the end of the network rather than the more typical set of FC layers. These architectural advances produce a model that is eight times deeper than VGGNet yet significantly smaller in size. Both ResNet50 (a 50-layer residual network) and ResNet101 (the deeper variant of ResNet50) are investigated in this study. Both CNNs have an input size of 224 × 224 pixels.
InceptionV3 [
45] advances GoogleNet by making the auxiliary classifiers perform as regulators rather than as classifiers. This is accomplished by factorizing 7 × 7 convolutions into two or three consecutive layers of 3 × 3 convolutions and applying the RMSProp Optimizer. InceptionV3 accepts images of size 299 × 299 pixels.
In
Table 1, we report the specifications of the different network architectures that we used in our paper.
6. Conclusions
In this paper, we presented the largest study conducted so far that investigates ensembles of CNNs using different data augmentation techniques for audio classification. Several data augmentation approaches designed for audio signals were tested and compared with each other and with a baseline approach that did not include data augmentation. Data augmentation methods were applied to the raw audio signals and their visual representations using different spectrograms. CNNs were trained on different sets of data augmentation approaches and fused via the sum rule.
Experimental results clearly demonstrate that ensembles composed of fine-tuned CNNs with different architectures maximized performance on the tested three audio classification problems, with some of the ensembles obtaining results comparable with the systems, including on the ESC-50 dataset. To the best of our knowledge, this is the largest, most exhaustive study of CNN ensembles applied to the task of audio classification. Our best ensemble, FusionGlobal is composed of 63 networks with nine different architectures and seven different trainings for every network. Four of the networks were obtained using different data augmentation strategies and three different methods to create a spectrogram. It is worth noting that the same ensemble is competitive with the state of the art on the three datasets. To be more precise, we reach 96.82% on the BIRDZ dataset, 90.51% on the CAT dataset, and 88.65% on ESC-50.
This work can be expanded further by investigating which augmentation methods (spectrogram augmentation vs. signal augmentation) work best for classifying different kinds of sounds. We also plan to apply transfer learning using spectrograms instead of natural images. A systematic selection of augmentation approaches, e.g., by iteratively evaluating an increasing subset of augmentation techniques (as is typical when evaluating different features), would require an enormous amount of time and computation power. An expert-based approach that utilizes the knowledge of environmental scientists would be the best way of handling this challenge.
This study could also be expanded by including more datasets, which would provide a more comprehensive validation of the proposed fusions. Furthermore, there is a need to investigate the impact on performance when different CNN topologies and parameter settings in the retuning step are combined with different types of data augmentation.
The technique proposed here is not exclusively applicable to environmental sound classification but can be applied to many related audio tasks. For example, this technique should work well for real-time audio event detection and speech recognition. An important application area related to the ESC-50 dataset for noise identification would be to apply our approach to the more refined problem of fault diagnosis of drilling machines and other machinery [
57,
58]. Most studies in this area have focused on extracting handcrafted texture features from visual representations of sound [
58]. But recently, there has been some interesting work that has successfully used deep learning to solve this problem [
57]. Investigating the performance of our proposed method to tasks such as these would involve combining a different set of network architectures, but the main idea of ensembling different models obtained from many audio augmentation protocols should increase classification performance on these novel tasks and would be worth investigating in the future. Finally, we plan on exploring some possibilities presented in [
59].