Comparative and Cost Analysis of a Novel Predictive Power Ramp Rate Control Method: A Case Study in a PV Power Plant in Puerto Rico
Abstract
:1. Introduction
2. Overview of the Power Ramp-Rate Control Methods
2.1. Ramp Saturation (RS) Method
2.2. Simple Moving Average (SMA) Method
2.3. Exponential Moving Average (EMA) Method
2.4. First Order Low-Pass Filter (FOLPF) Method
2.5. Second Order Low-Pass Filter (SOLPF) Method
2.6. Enhanced Linear Exponential Smoothing (ELES)
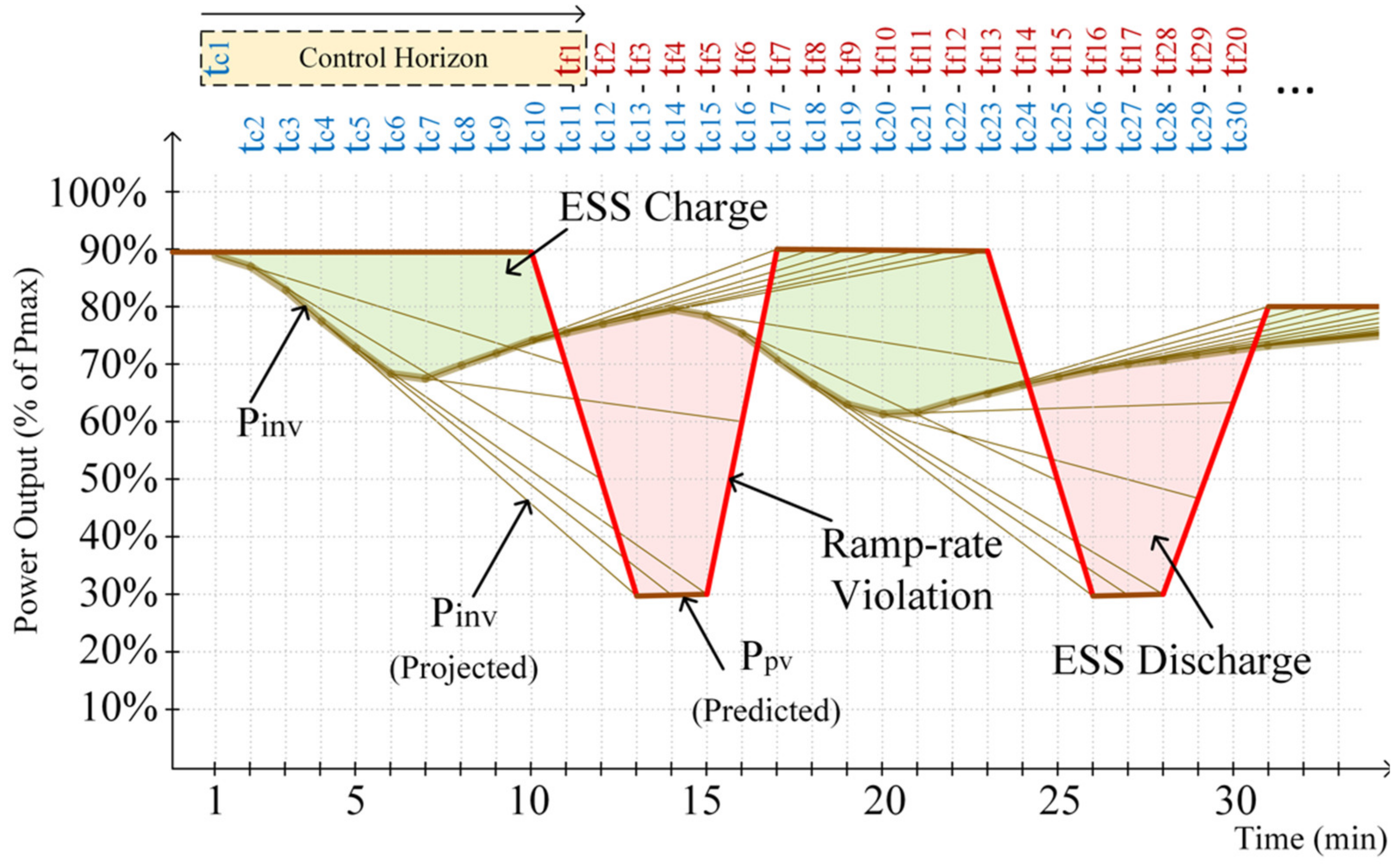
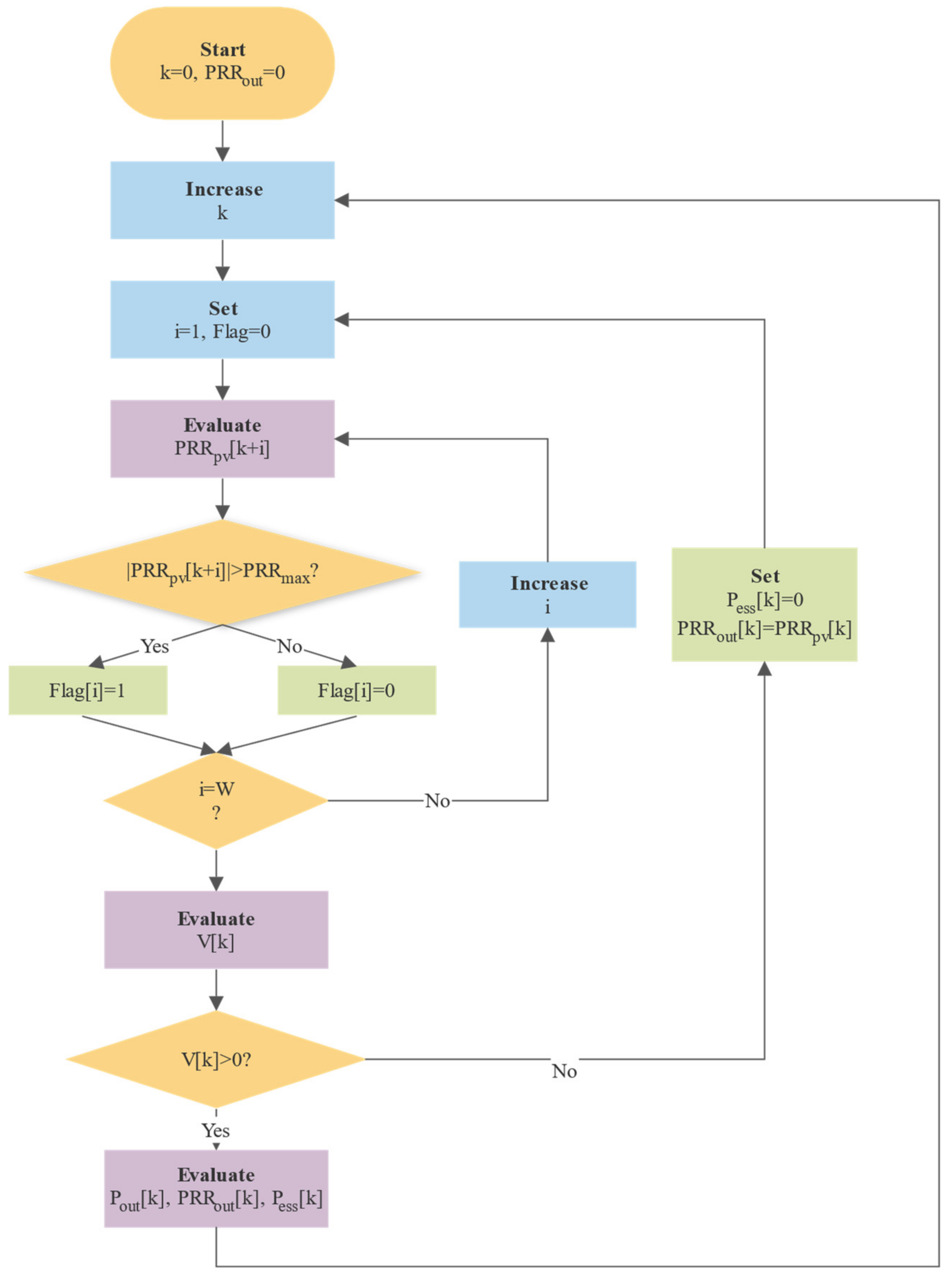
3. Proposed Predictive Dynamic Smoothing PRRC Method
4. Methodology for the Levelized Cost of Storage Estimation
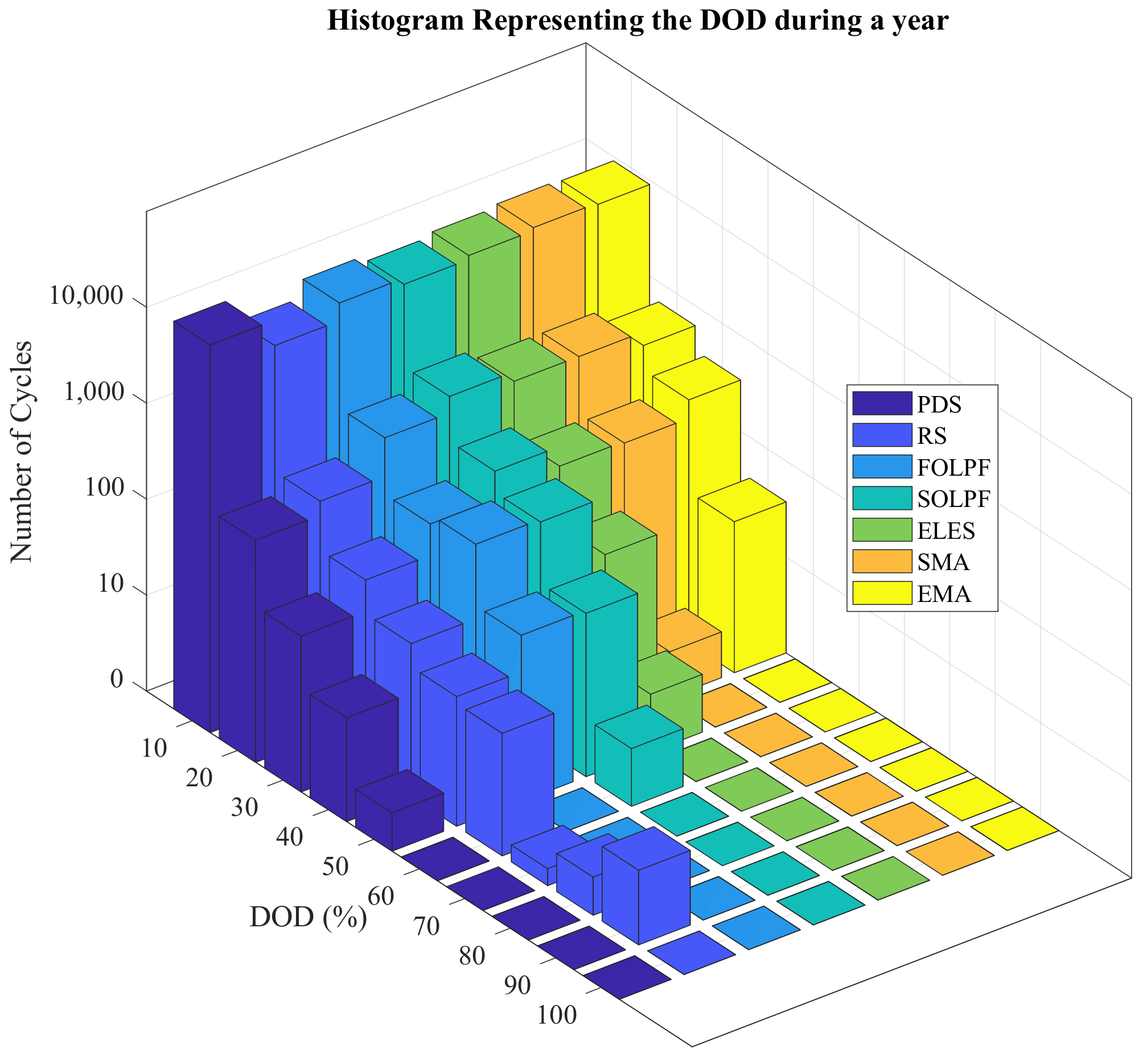
4.1. Battery Degradation Estimation for PRRC
4.2. Levelized Cost of Storage (LCOS) Estimation
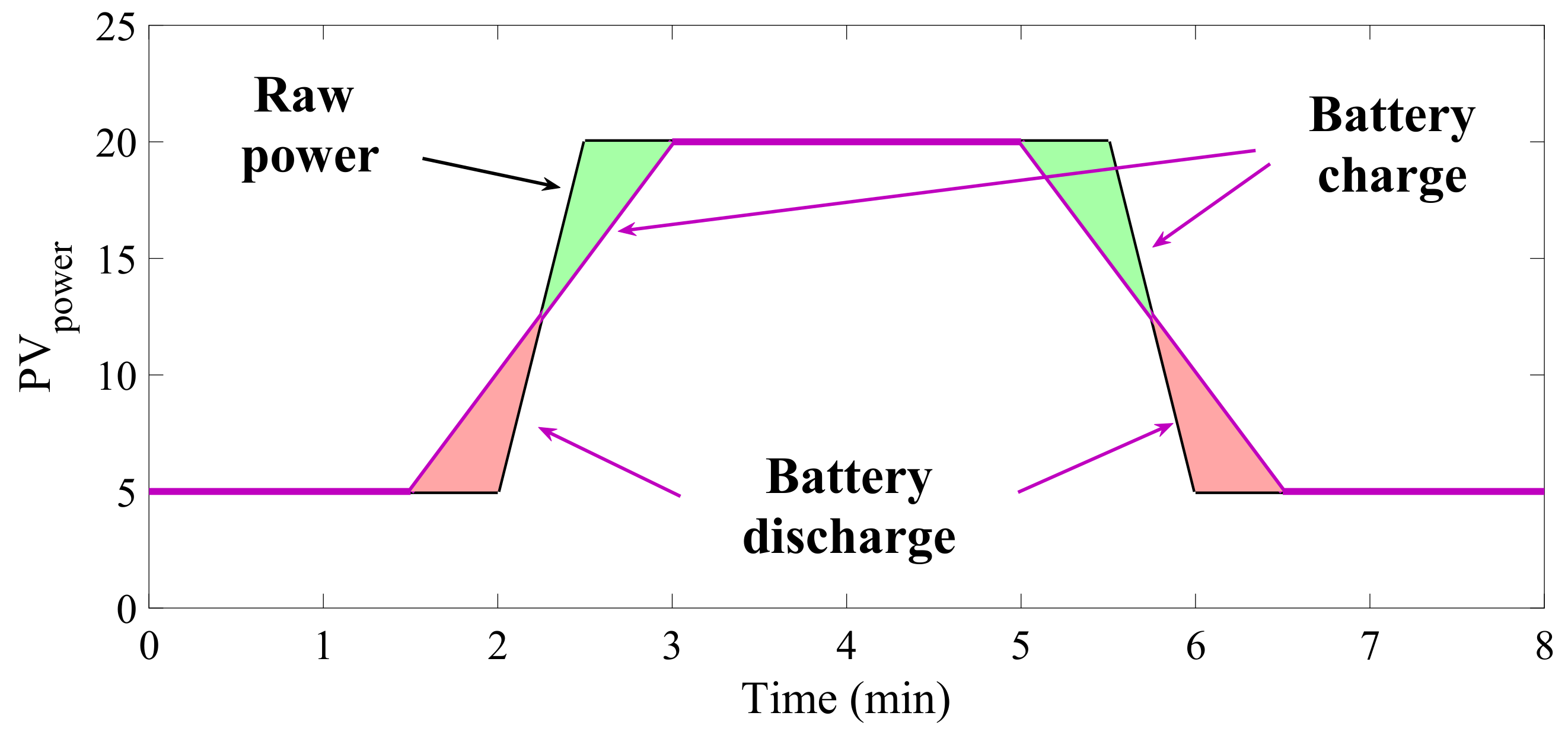
4.3. Ramp Violations
5. Coto Laurel Case Study
5.1. General Description of Coto Laurel Solar Power Plant
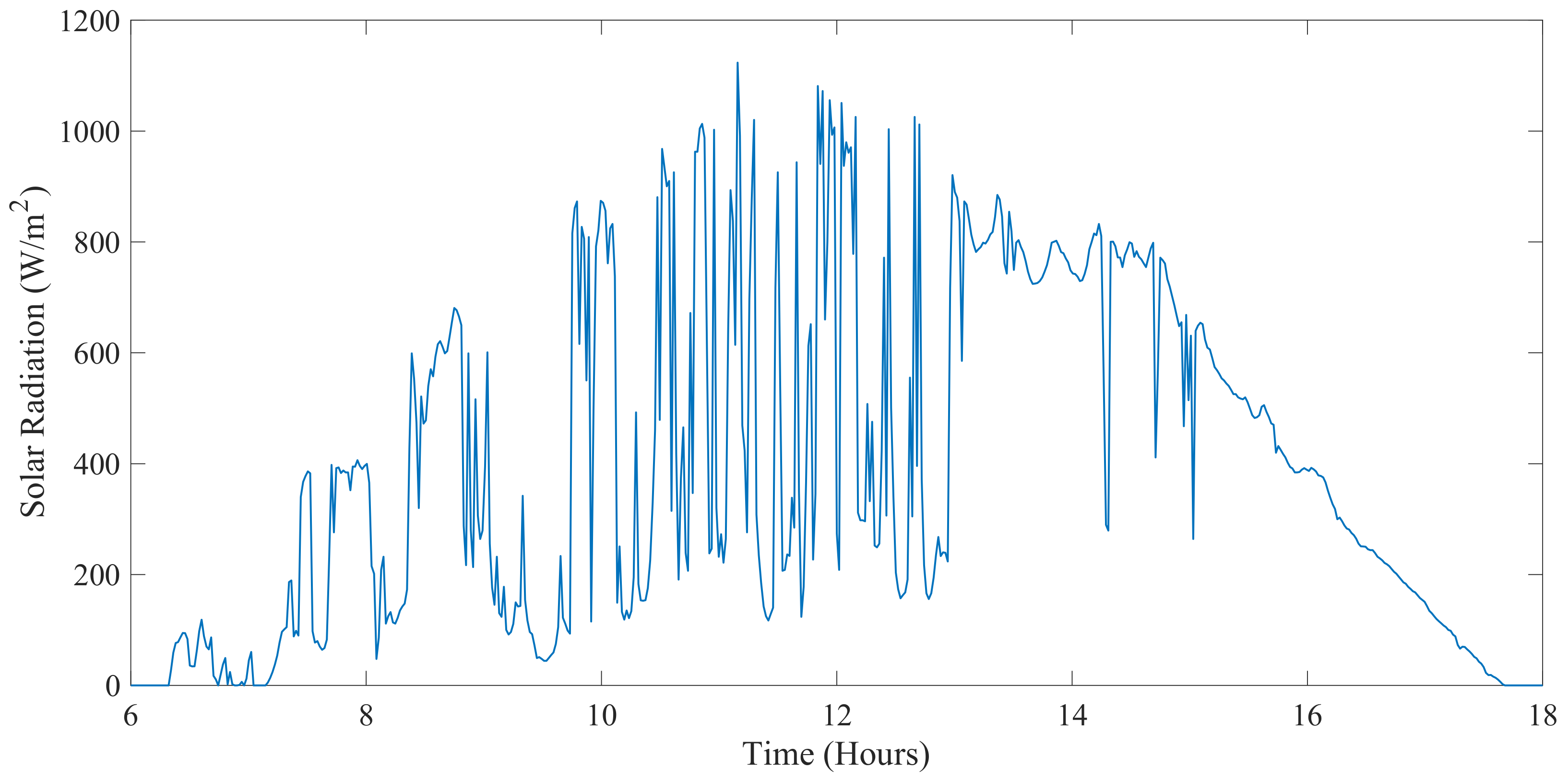
5.2. Environmental Characteristics of Coto Laurel Solar Power Plant
5.3. Proposed Model
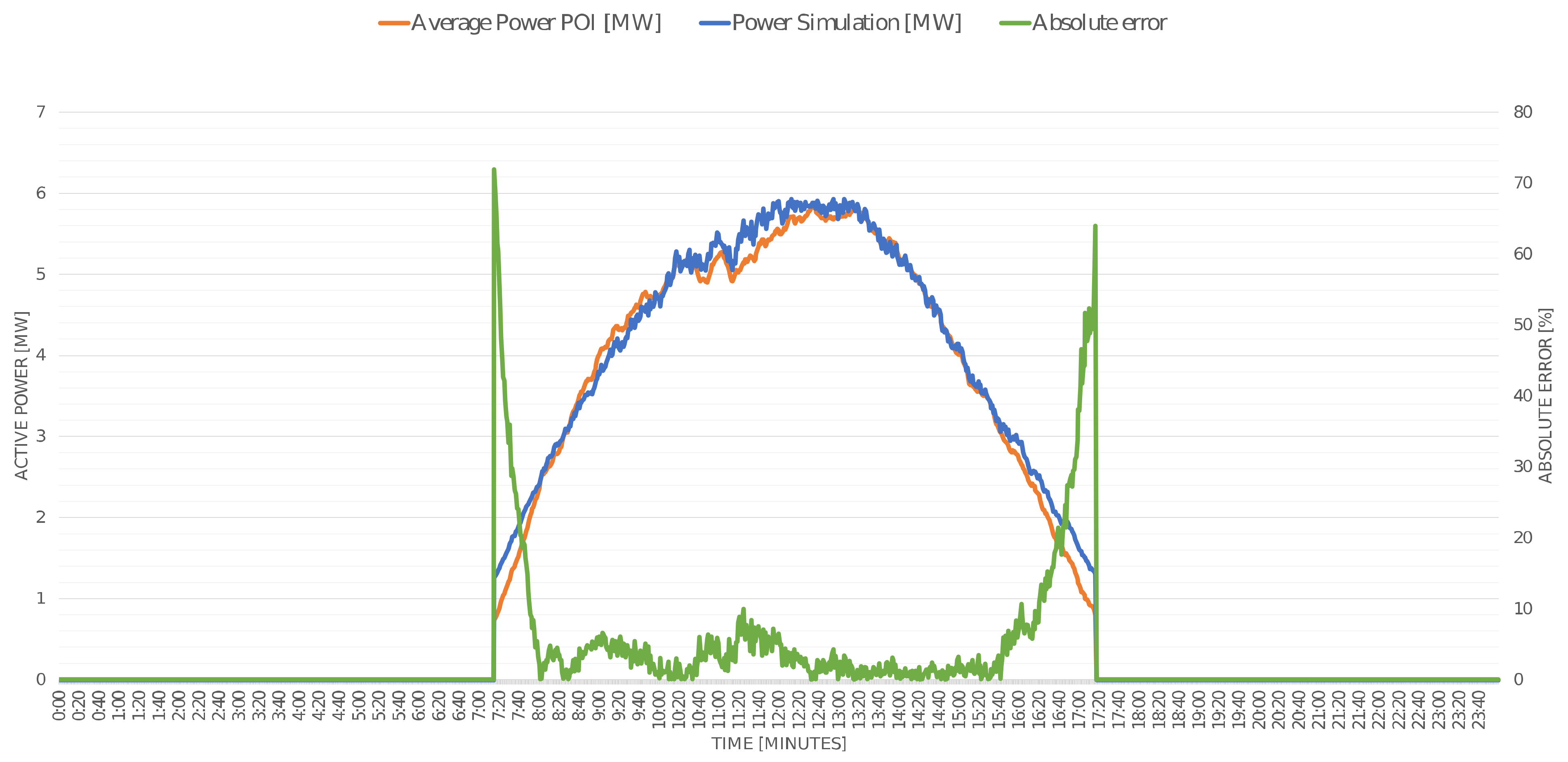
5.4. Model Validation
6. Simulation Results
6.1. First Stage: One Day Evaluation
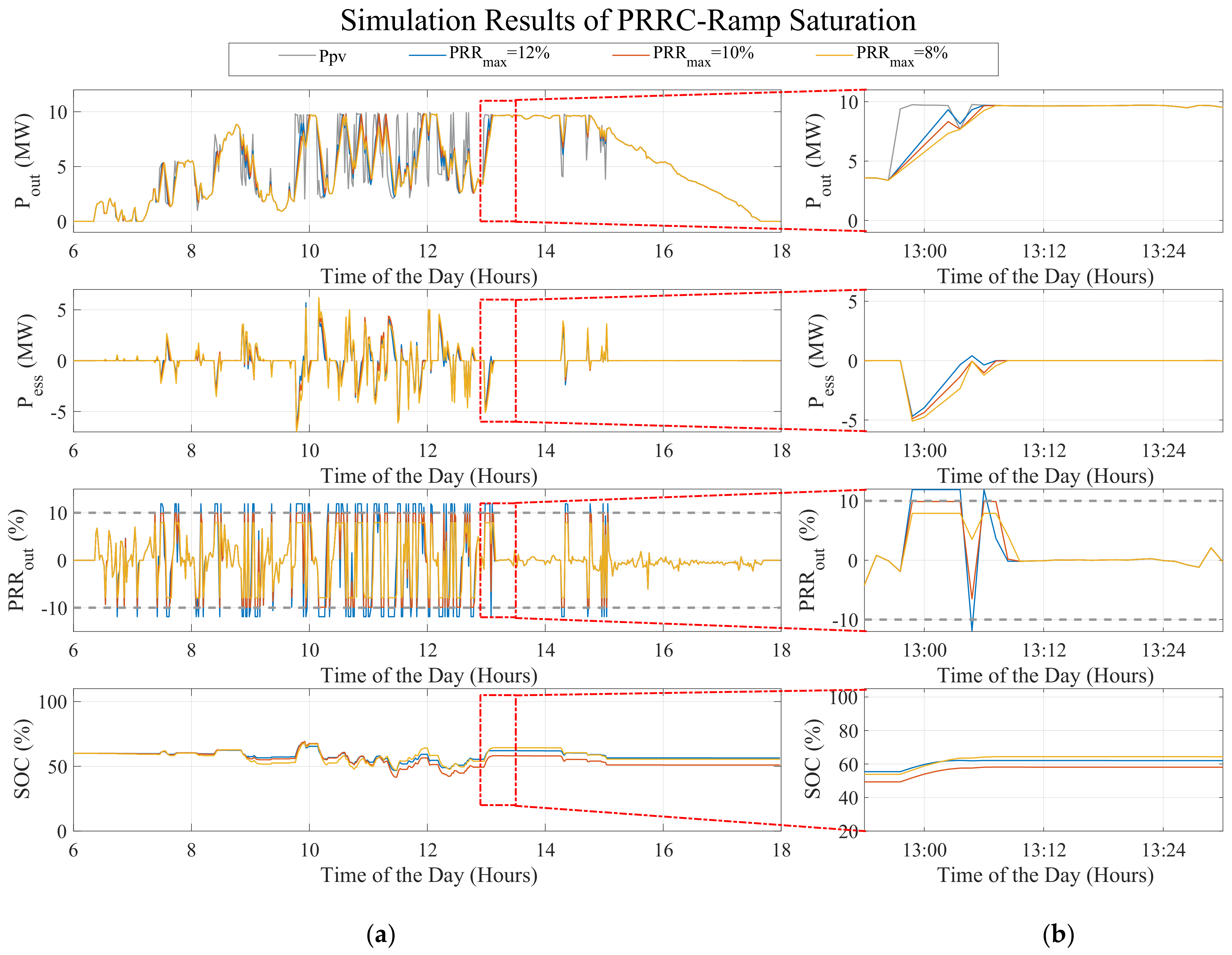
6.1.1. Ramp Saturation Method
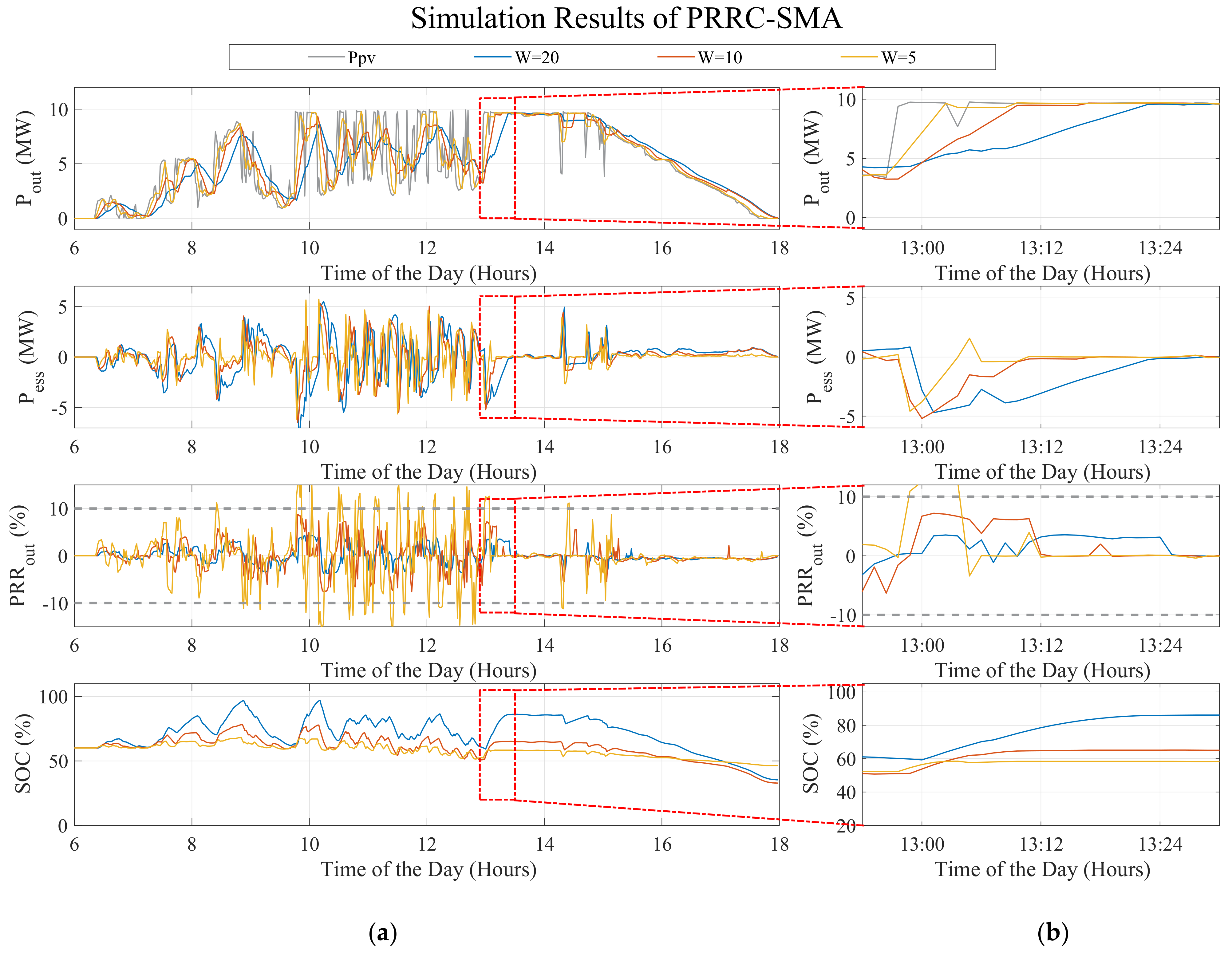
6.1.2. Simple Moving Average (SMA) Method
6.1.3. Exponential Moving Average (EMA) Method
6.1.4. First Order Low-Pass Filter (FOLPF) Method
6.1.5. Second Order Low-Pass Filter (SOLPF) Method
6.1.6. Enhanced Linear Exponential Smoothing (ELES) Method
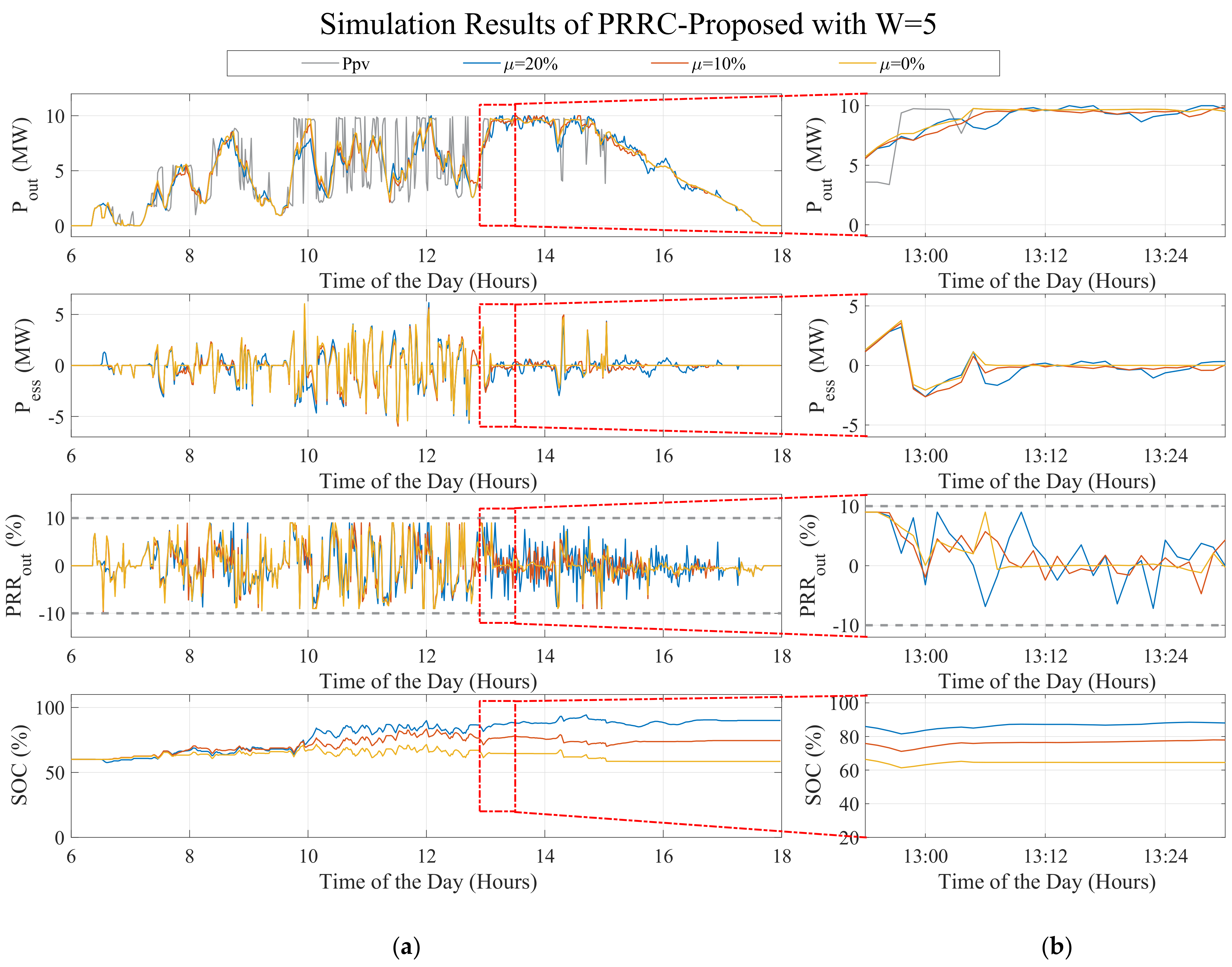
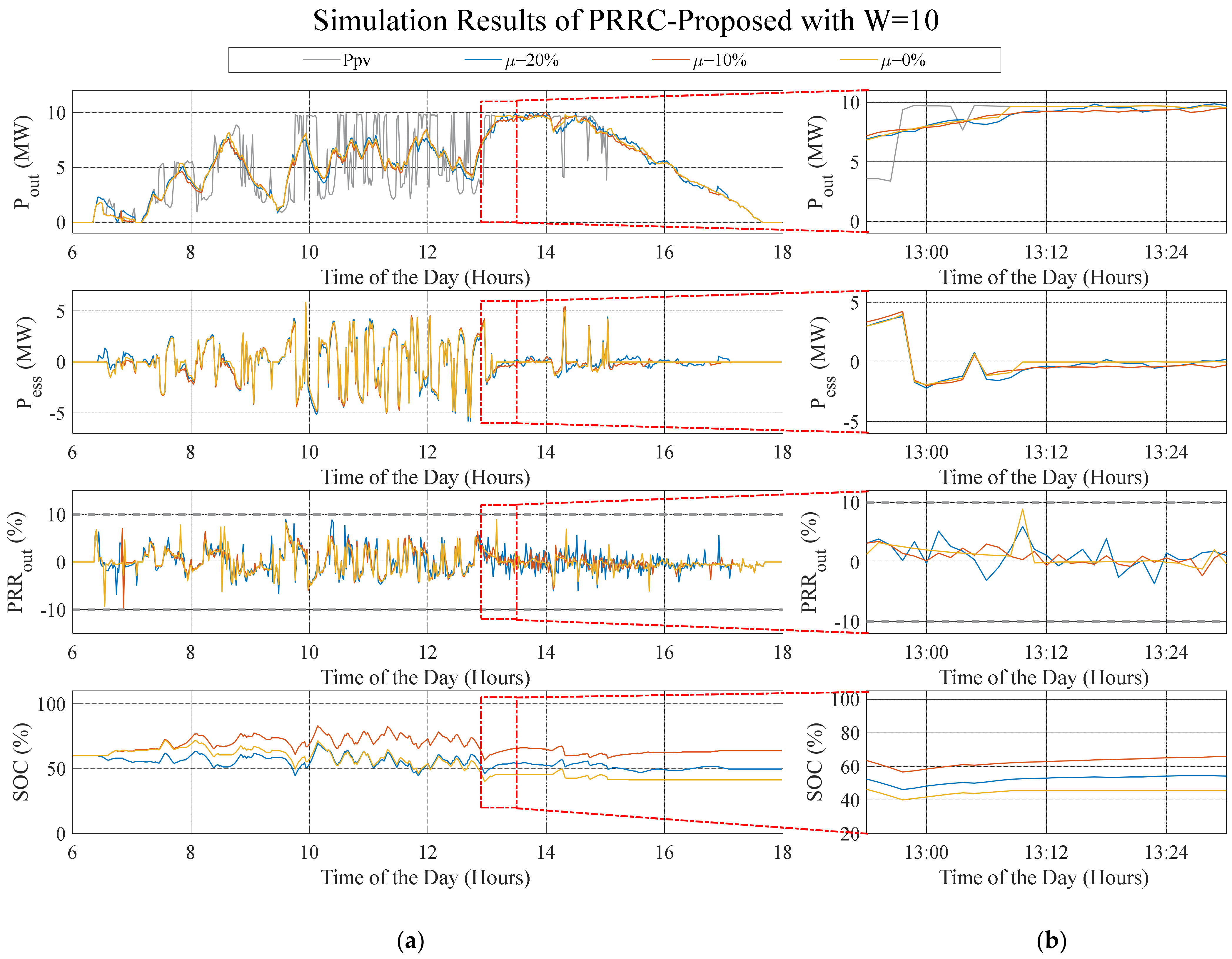
6.1.7. Proposed Predictive Dynamic Smoothing (PDS)
6.2. Economic Analysis through One Year
- RS with a PRRmax of 10%.
- SMA with a window size W = 10.
- EMA with a window size W = 30 and a smoothing factor α = 0.123.
- FOLPF with a sampling period Ts = 60 s and a Tf = 500 s.
- SOLPF with a sampling period of Ts = 60 s, a damping ratio ζ = 0.707, and a natural frequency ωn = 1/25 rad/s.
- ELES with a smoothing factor α = 0.06.
- Proposed PDS with a window size W = 5 and a disturbance coefficient µ = 10%. This coefficient was selected since it represented errors in estimations of about 1 MW, which is reasonable according to the literature presented in Section 3.
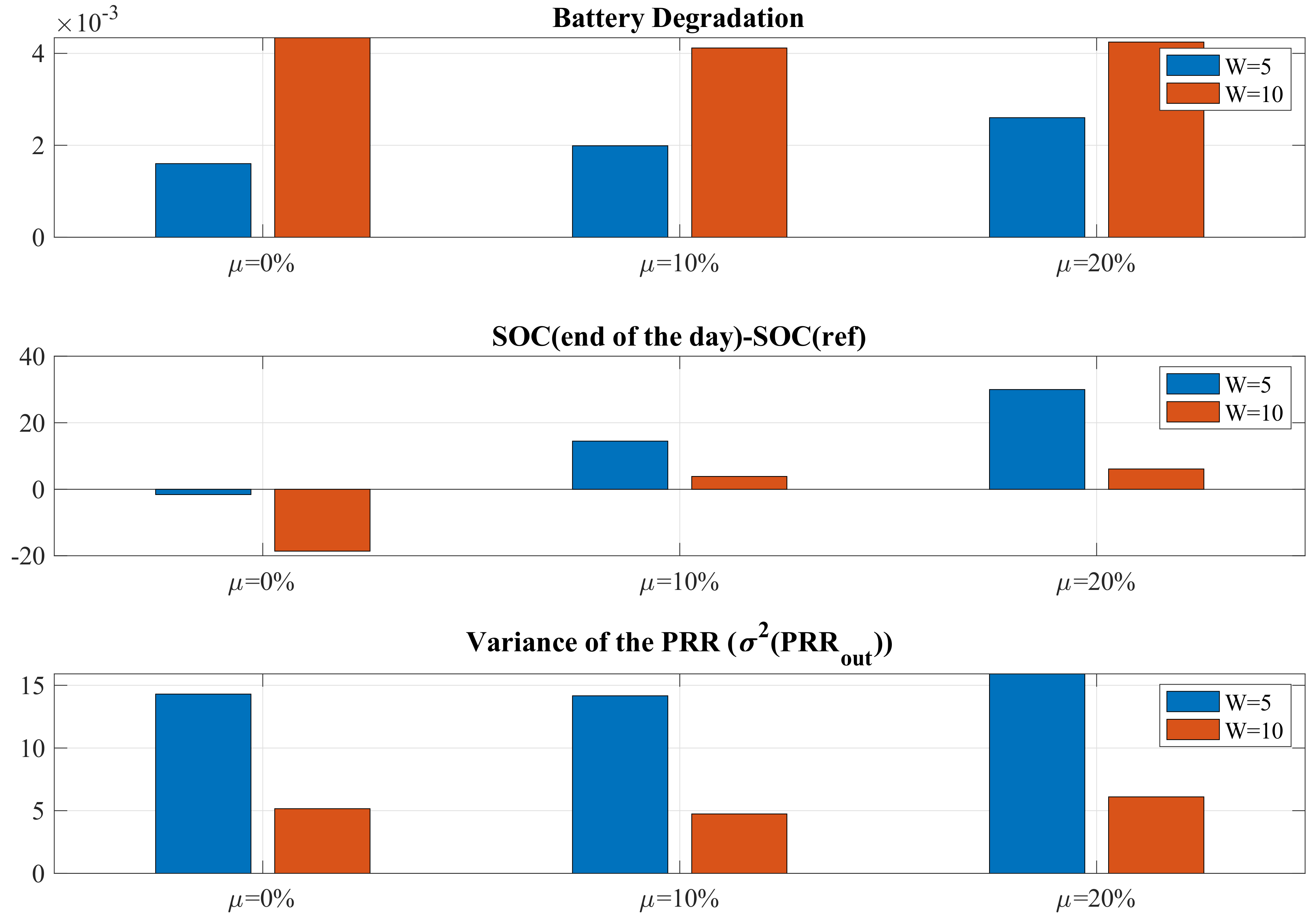
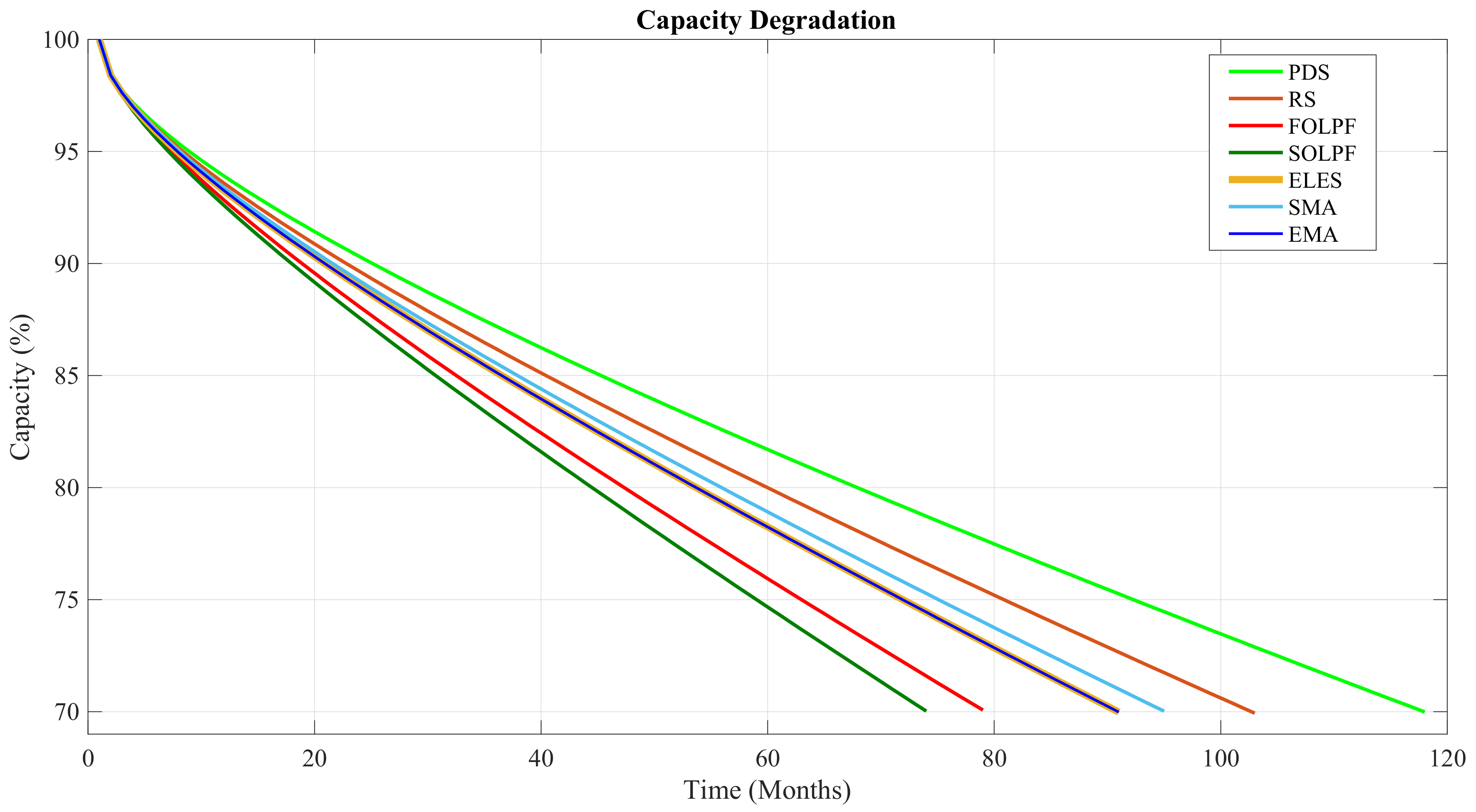
6.2.1. Battery Degradation
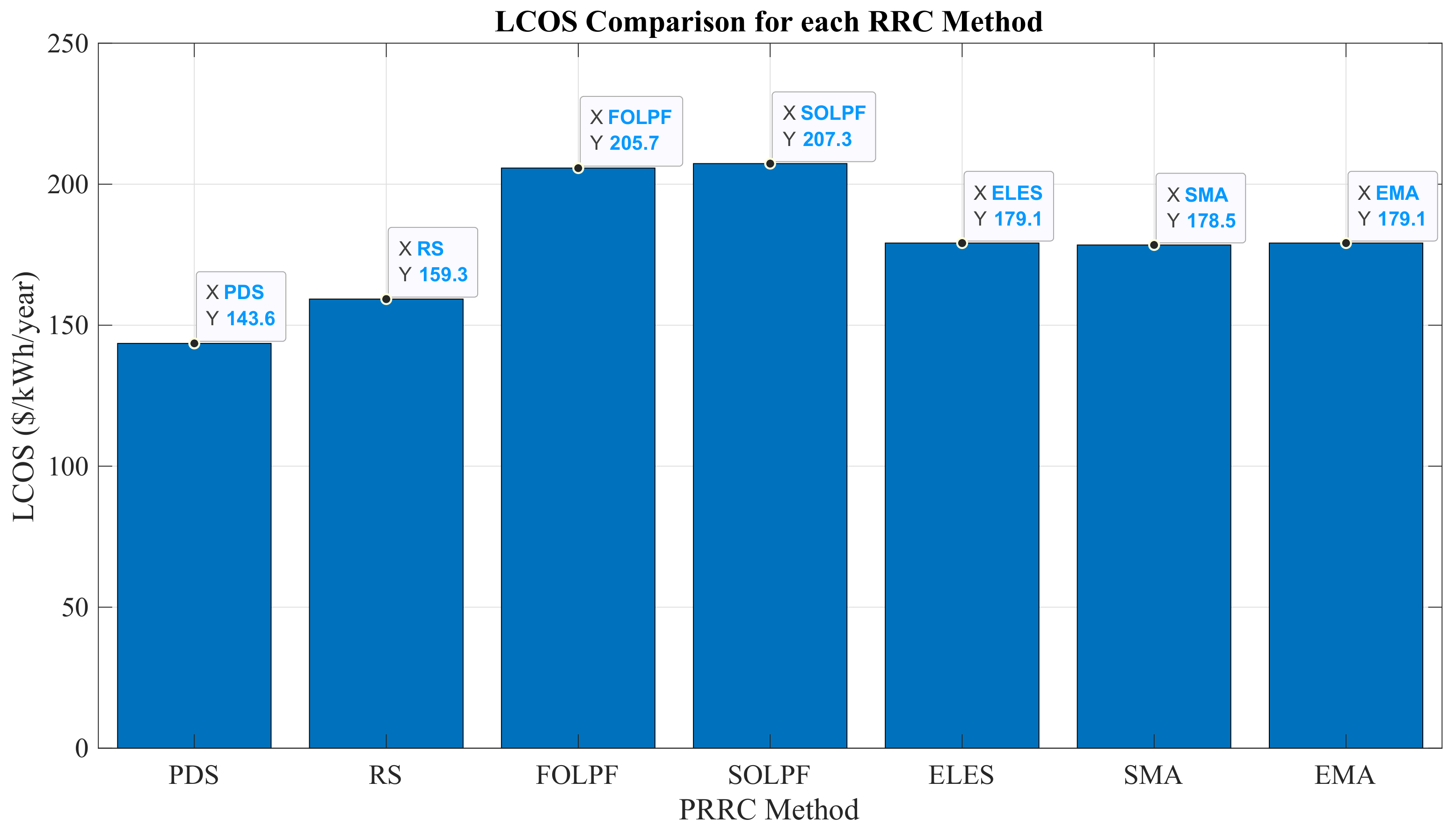
6.2.2. LCOS
6.2.3. Violations
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Puerto Rico Electrical Power Authority. Generation, Consumption, Cost, Income and Customers of the Puerto Rico Electrical System; indicadores.pr: San Juan, PR, USA, 2020. [Google Scholar]
- Puerto Rico Electric Power Authority. SB 1121 Puerto Rico Energy Public Policy Act; Government of Puerto Rico: San Juan, PR, USA, 2020; p. 23.
- Government of Puerto Rico. PREPA Hydroelectric Power Plants Revitalization Project (PRQ2019-2)—Questions and Responses Log; Government of Puerto Rico: San Juan, PR, USA, 2020.
- Puerto Rico Energy Bureau. Final Resolution and Order on the Puerto Rico Electric Power Authority’s Integrated Resource Plan (CEPR-AP-2018-0001); Puerto Rico’s Electric Energy Bureau: San Juan, PR, USA, 2020; p. 179.
- Crǎciun, B.I.; Kerekes, T.; Séra, D.; Teodorescu, R.; Annakkage, U.D. Power Ramp Limitation Capabilities of Large PV Power Plants With Active Power Reserves. IEEE Trans. Sustain. Energy 2017, 8, 573–581. [Google Scholar] [CrossRef]
- Martins, J.; Spataru, S.; Sera, D.; Stroe, D.I.; Lashab, A. Comparative study of ramp-rate control algorithms for PV with energy storage systems. Energies 2019, 12, 1342. [Google Scholar] [CrossRef] [Green Version]
- Elwakil, E.; Hegab, M. Risk Management for Power Purchase Agreements. In Proceedings of the 2018 IEEE Conference on Technologies for Sustainability (SusTech), Long Beach, CA, USA, 11–13 November 2018. [Google Scholar] [CrossRef]
- Puerto Rico Electric Power Authority. Minimum Technical Requirements For Interconnection Of Photovoltaic (Pv) Facilities; Energia.pr.gov: San Juan, PR, USA, 2020; pp. 1–11.
- Beltran, H.; Tomas Garcia, I.; Alfonso-Gil, J.C.; Perez, E. Levelized Cost of Storage for Li-Ion Batteries Used in PV Power Plants for Ramp-Rate Control. IEEE Trans. Energy Convers. 2019, 34, 554–561. [Google Scholar] [CrossRef]
- Belderbos, A.; Delarue, E.; D’haeseleer, W. Calculating the levelized cost of storage? Energy Expect. In Proceedings of the Uncertainty, 39th IAEE International Conference, Beren, Norway, 19–22 November 2016; pp. 1–2. [Google Scholar]
- Hoff, M.; Lin, R. Development and Practical Use of a Levelized Cost of Storage (LCOS) Metric. Available online: https://www.neces.com/wp-content/uploads/2019/08/Development_and_practical_use_of_a_LCOS_031619.pdf (accessed on 27 January 2021).
- Alam, M.J.E.; Muttaqi, K.M.; Sutanto, D. A novel approach for ramp-rate control of solar PV using energy storage to mitigate output fluctuations caused by cloud passing. IEEE Trans. Energy Convers. 2014, 29, 507–518. [Google Scholar] [CrossRef] [Green Version]
- Marcos, J.; de La Parra, I.; García, M.; Marroyo, L. Control strategies to smooth short-term power fluctuations in large photovoltaic plants using battery storage systems. Energies 2014, 7, 6593–6619. [Google Scholar] [CrossRef]
- Solanki, S.G.; Ramachandaramurthy, V.K.; Shing, N.Y.K.; Tan, R.H.G.; Tariq, M.; Thanikanti, S.B. Power smoothing techniques to mitigate solar intermittency. In Proceedings of the 2019 International Conference on Electrical, Electronics and Computer Engineering, UPCON 2019, Aligarh, India, 8–10 November 2019. [Google Scholar]
- Tesfahunegn, S.G.; Ulleberg, Ø.; Vie, P.J.S.; Undeland, T.M. PV fluctuation balancing using hydrogen storage—A smoothing method for integration of PV generation into the utility grid. Energy Procedia 2011, 12, 1015–1022. [Google Scholar] [CrossRef] [Green Version]
- Ellis, A.; Schoenwald, D.; Hawkins, J.; Willard, S.; Arellano, B. PV output smoothing with energy storage. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Austin, TX, USA, 3–8 June 2012; pp. 1523–1528. [Google Scholar]
- Hund, T.D.; Gonzalez, S.; Barrett, K. Grid-tied PV system energy smoothing. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 2762–2766. [Google Scholar]
- Addisu, A.; George, L.; Courbin, P.; Sciandra, V. Smoothing of renewable energy generation using Gaussian-based method with power constraints. Energy Procedia 2017, 134, 171–180. [Google Scholar] [CrossRef]
- Lin, D. Strategy Comparison of Power Ramp Rate Control for Photovoltaic Systems. CPSS Trans. Power Electron. Appl. 2020, 5, 329–341. [Google Scholar] [CrossRef]
- Jamroen, C.; Usaratniwart, E.; Sirisukprasert, S. PV power smoothing strategy based on HELES using energy storage system application: A simulation analysis in microgrids. IET Renew. Power Gener. 2019, 13, 2298–2308. [Google Scholar] [CrossRef]
- Chanhom, P.; Sirisukprasert, S.; Hatti, N. Enhanced linear exponential smoothing technique with minimum energy storage capacity for PV distributed generations. Int. Rev. Electr. Eng. 2014, 9, 1190–1196. [Google Scholar] [CrossRef]
- Usaratniwart, E.; Sirisukprasert, S.; Hatti, N.; Hagiwara, M. A case study in micro grid using adaptive enhanced linear exponential smoothing technique. In Proceedings of the 2017 8th International Conference on Information and Communication Technology for Embedded Systems, IC-ICTES 2017—Proceedings, Chonburi, Thailand, 7–9 May 2017. [Google Scholar]
- Usaratniwart, E.; Sirisukprasert, S. Adaptive enhanced linear exponential smoothing technique to mitigate photovoltaic power fluctuation. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe, Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 712–717. [Google Scholar]
- Liu, H.; Peng, J.; Zang, Q.; Yang, K. Control Strategy of Energy Storage for Smoothing Photovoltaic Power Fluctuations. IFAC-PapersOnLine 2015, 48, 162–165. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T.; Yona, A.; Funabashi, T.; Kim, C.H. Photovoltaic output power fluctuations smoothing methods for single and multiple PV generators. Curr. Appl. Phys. 2010, 10, S265–S270. [Google Scholar] [CrossRef]
- Koiwa, K.; Liu, K.Z.; Tamura, J. Analysis and Design of Filters for the Energy Storage System: Optimal Tradeoff between Frequency Guarantee and Energy Capacity/Power Rating. IEEE Trans. Ind. Electron. 2018, 65, 6560–6570. [Google Scholar] [CrossRef]
- Lin, Z.; Qiu, G.; Wang, G.; Jiang, R. Improved wind power and storage system smoothing control strategy based on RE reinforcement learning and low pass filtering algorithms. In Proceedings of the POWERCON 2014–2014 International Conference on Power System Technology: Towards Green, Efficient and Smart Power System, Chengdu, China, 20–22 October 2014; pp. 1749–1753. [Google Scholar]
- Nikolov, D. Power Ramp Rate Reduction in Photovoltaic Power Plants Using Energy Storage. Master’s Thesis, Aalborg University, Aalborg Øst, Denmark, 2017. [Google Scholar]
- Blaabjerg, F.; Yang, Y.; Ma, K.; Wang, X. Power electronics-the key technology for renewable energy system integration. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications, ICRERA 2015, Palermo, Italy, 22–25 November 2015; pp. 1618–1626. [Google Scholar]
- Yang, Y.; Wang, H.; Blaabjerg, F.; Kerekes, T. A hybrid power control concept for PV inverters with reduced thermal loading. IEEE Trans. Power Electron. 2014, 29, 6271–6275. [Google Scholar] [CrossRef] [Green Version]
- Sangwongwanich, A.; Yang, Y.; Blaabjerg, F. High-performance constant power generation in grid-connected PV systems. IEEE Trans. Power Electron. 2016, 31, 1822–1825. [Google Scholar] [CrossRef] [Green Version]
- Omran, W.A.; Kazerani, M.; Salama, M.M.A. Investigation of methods for reduction of power fluctuations generated from large grid-connected photovoltaic systems. IEEE Trans. Energy Convers. 2011, 26, 318–327. [Google Scholar] [CrossRef]
- Ina, N.; Yanagawa, S.; Kato, T.; Suzuoki, Y. Smoothing of PV system output by tuning MPPT control. Electr. Eng. Jpn. 2005, 152, 10–17. [Google Scholar] [CrossRef]
- Zarina, P.P.; Mishra, S.; Sekhar, P.C. Exploring frequency control capability of a PV system in a hybrid PV-rotating machine-without storage system. Int. J. Electr. Power Energy Syst. 2014, 60, 258–267. [Google Scholar] [CrossRef]
- Chen, X.; Du, Y.; Wen, H.; Jiang, L.; Xiao, W. Forecasting-Based Power Ramp-Rate Control Strategies for Utility-Scale PV Systems. IEEE Trans. Ind. Electron. 2019, 66, 1862–1871. [Google Scholar] [CrossRef]
- Chen, X.; Du, Y.; Xiao, W.; Lu, S. Power ramp-rate control based on power forecasting for PV grid-Tied systems with minimum energy storage. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 2647–2652. [Google Scholar] [CrossRef]
- Lave, M.; Kleissl, J.; Ellis, A.; Mejia, F. Simulated PV power plant variability: Impact of utility-imposed ramp limitations in Puerto Rico. In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 1817–1821. [Google Scholar] [CrossRef]
- Cormode, D.; Cronin, A.D.; Richardson, W.; Lorenzo, A.T.; Brooks, A.E.; Dellagiustina, D.N. Comparing ramp rates from large and small PV systems, and selection of batteries for ramp rate control. In Proceedings of the 2013 IEEE 39th Photovoltaic Specialists Conference (PVSC), Tampa, FL, USA, 16–21 June 2013; pp. 1805–1810. [Google Scholar] [CrossRef]
- Marquez, R.; Pedro, H.T.C.; Coimbra, C.F.M. Hybrid solar forecasting method uses satellite imaging and ground telemetry as inputs to ANNs. Sol. Energy 2013, 92, 176–188. [Google Scholar] [CrossRef]
- Salehi, V.; Radibratovic, B. Ramp rate control of photovoltaic power plant output using energy storage devices. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Stan, A.I.; Teodorescu, R.; Andreasen, S.J. Accelerated lifetime testing methodology for lifetime estimation of lithium-ion batteries used in augmented wind power plants. IEEE Trans. Ind. Appl. 2014, 50, 4006–4017. [Google Scholar] [CrossRef]
- Downing, S.D.; Socie, D.F. Simple rainflow counting algorithms. Int. J. Fatigue 1982, 4, 31–40. [Google Scholar] [CrossRef]
- Safari, M.; Morcrette, M.; Teyssot, A.; Delacourt, C. Life-Prediction Methods for Lithium-Ion Batteries Derived from a Fatigue Approach. J. Electrochem. Soc. 2010, 157, A713. [Google Scholar] [CrossRef]
- Adarme-Mejia, L.M.; Irizarry-Rivera, A.A. Feasibility study of a linear Fresnel Concentrating Solar Power plant located in Ponce, Puerto Rico. In Proceedings of the 2015 North American Power Symposium (NAPS), Charlotte, NC, USA, 4–6 October 2015. [Google Scholar] [CrossRef]




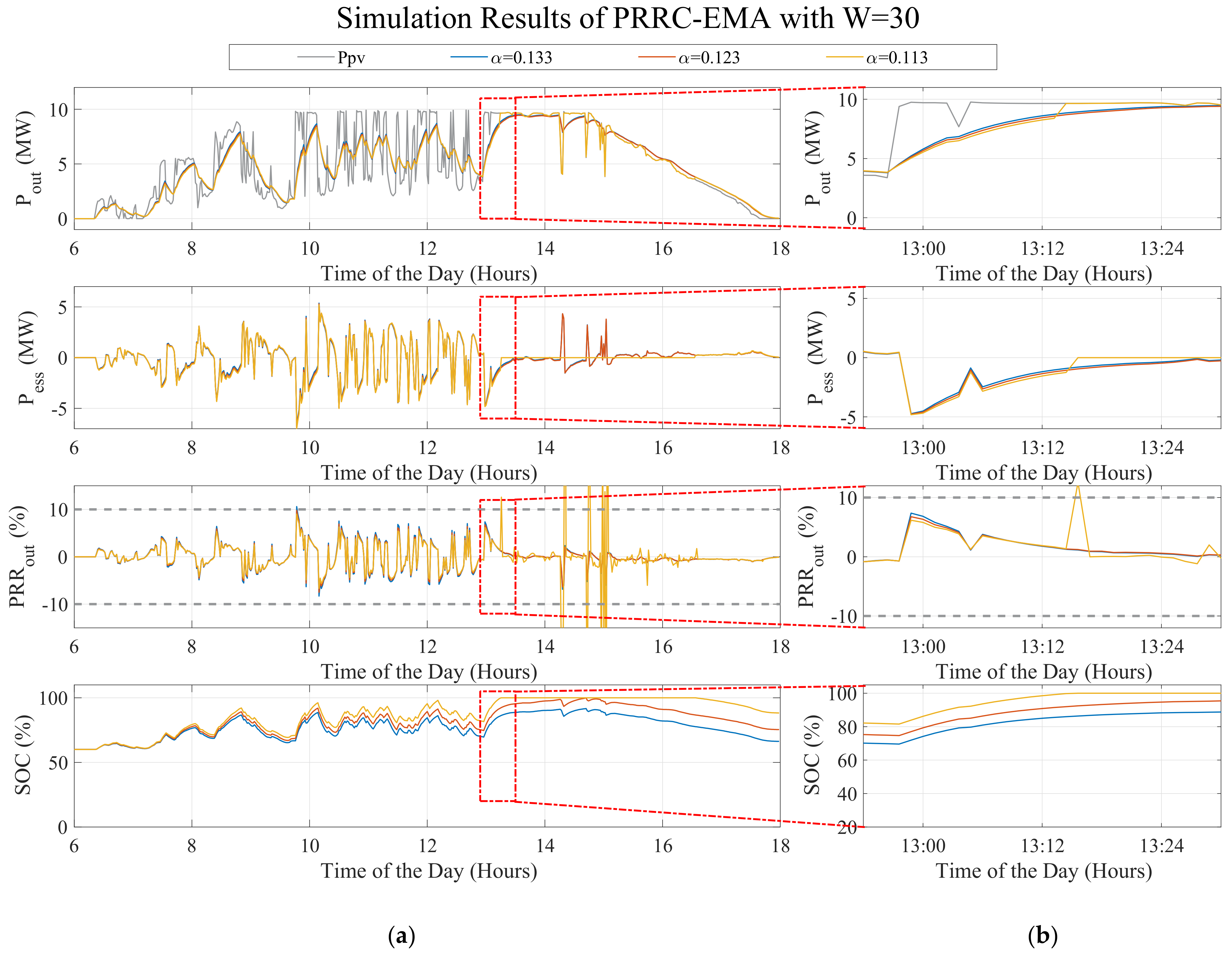
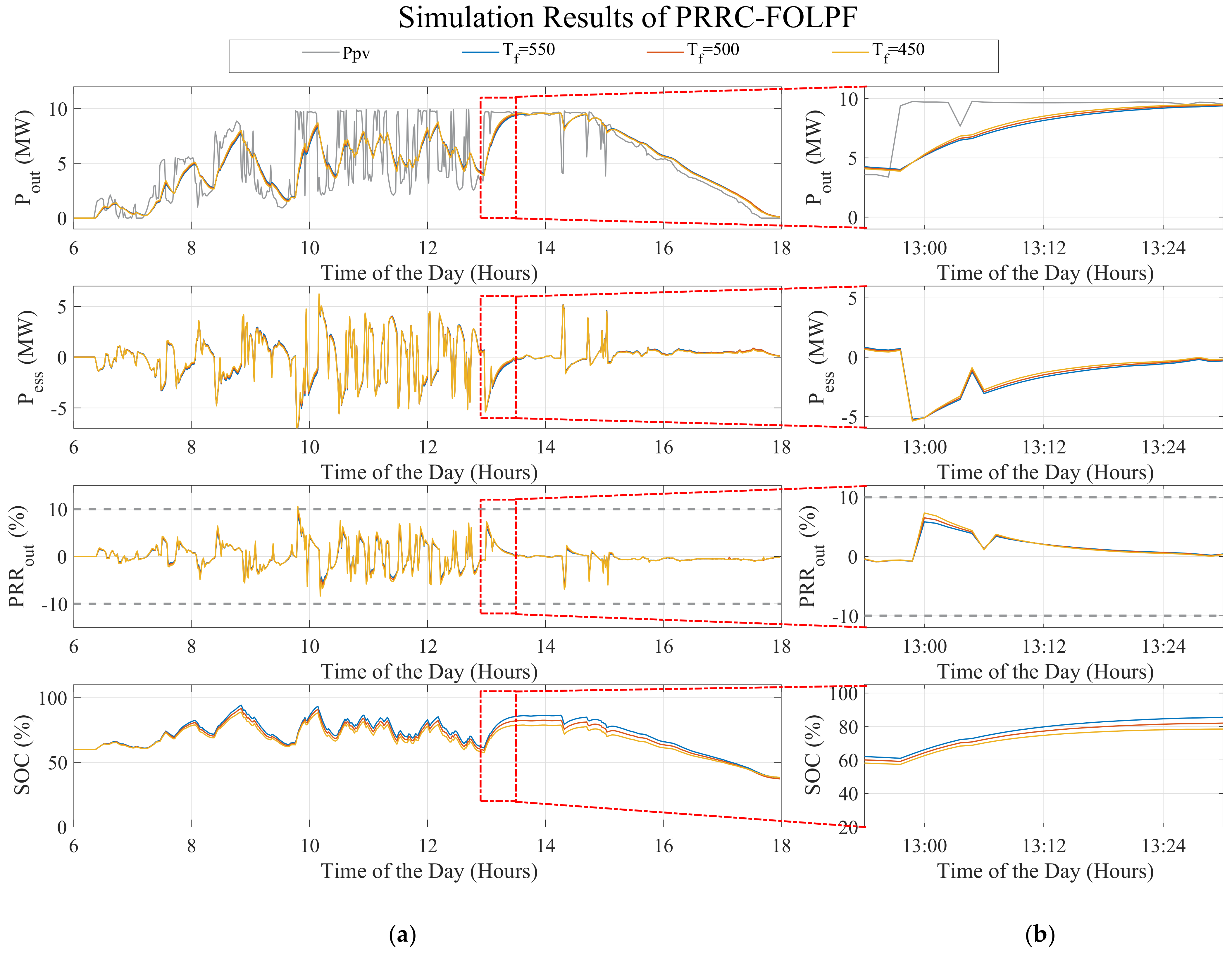
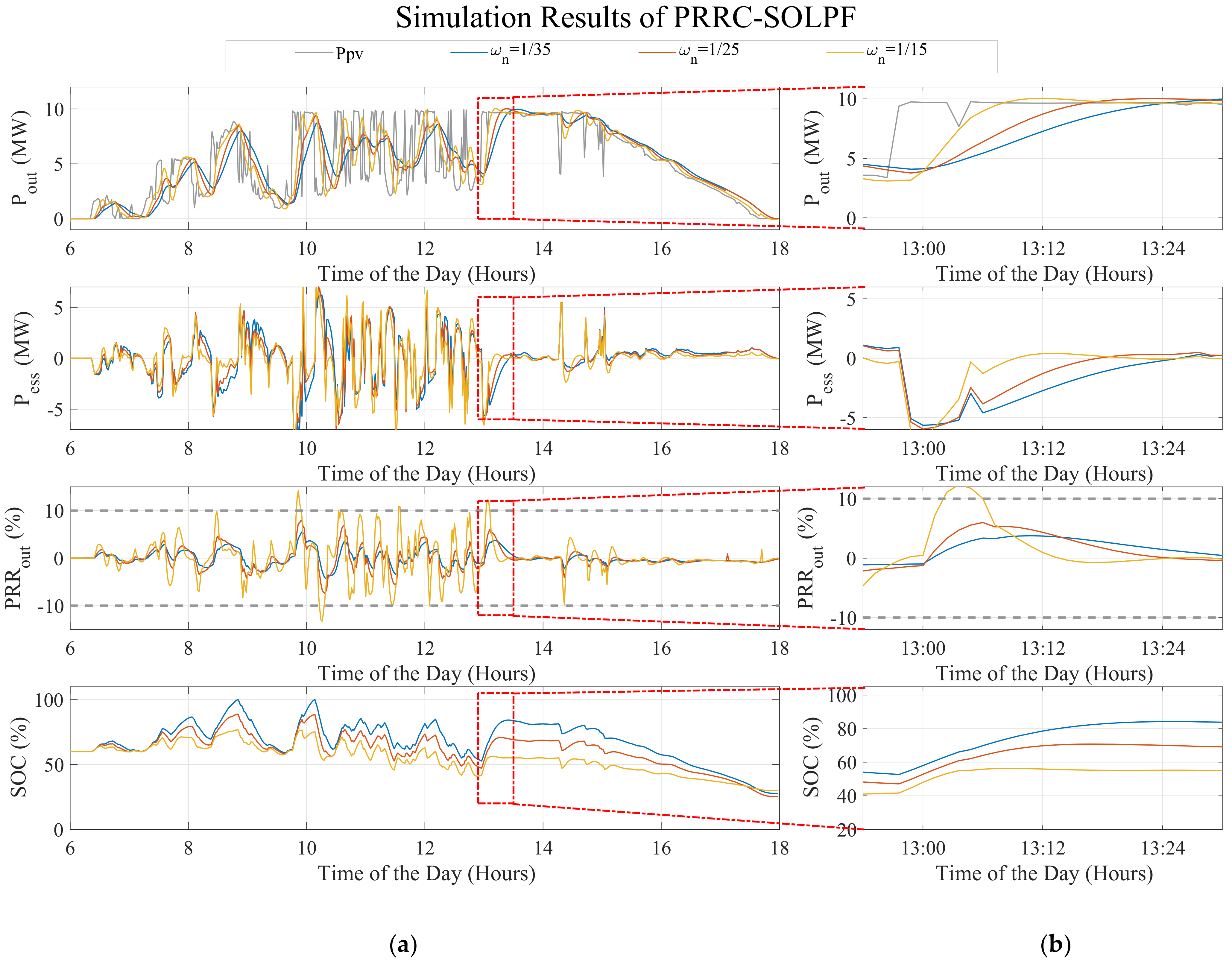
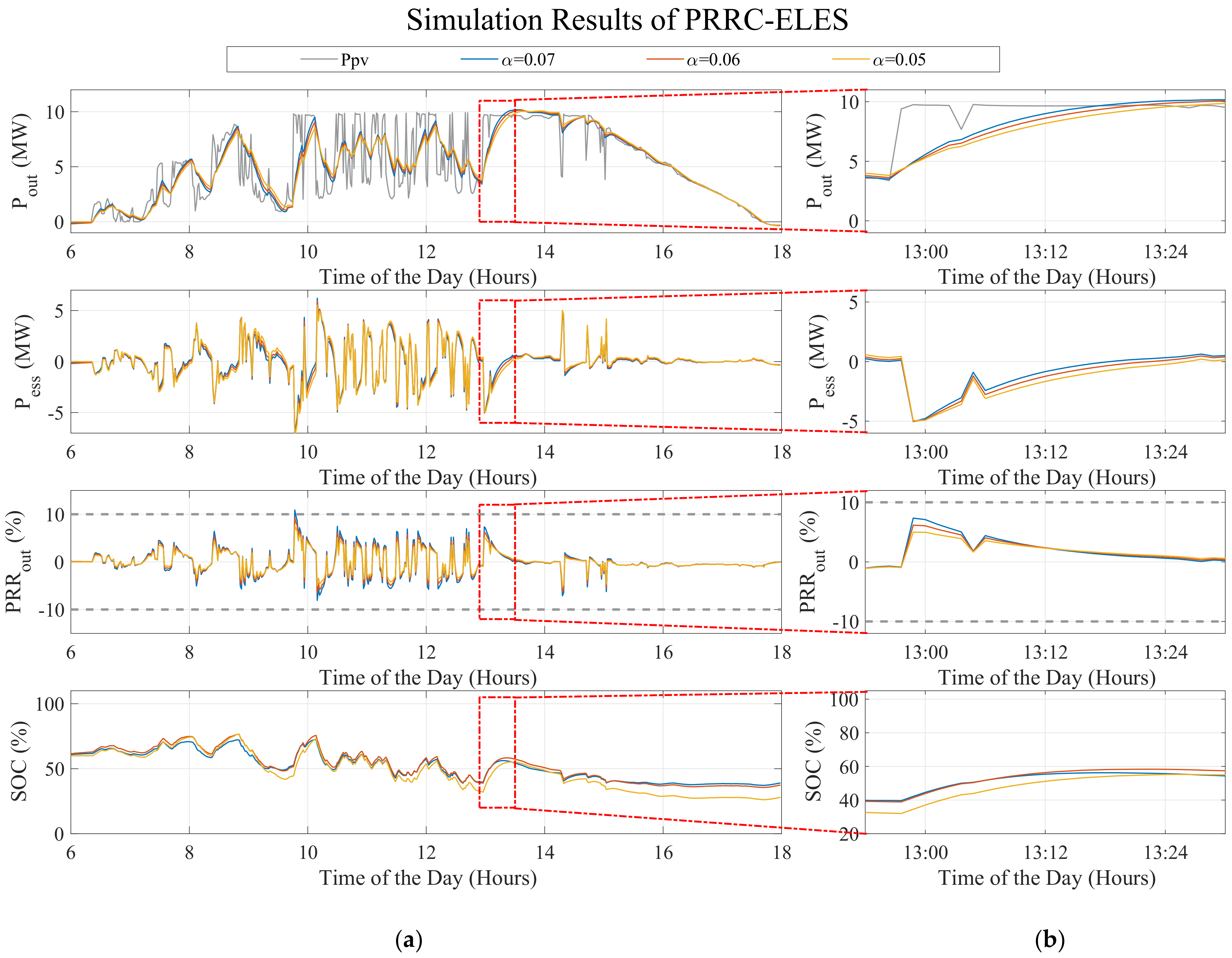

| Battery | Output | DC Power [MW] | Inverter Capacity [kWac] | Feeder | Transf. Capacity [kVA] | Primary-Delta [kV] | Secondary-Yn [V] |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 880 | 3 | 1800 | 13.2 | 360 |
| 2 | 880 | ||||||
| 2 | 1 | 1 | 880 | 3 | 1800 | 13.2 | 360 |
| 2 | 880 | ||||||
| 3 | 1 | 1 | 880 | 3 | 1800 | 13.2 | 360 |
| 2 | 880 |
| Group | PV Capacity [W] | PV Quantity | DC Power [kW] | PowerLimit [kW] | Feeder ID | Transf. Capacity [kVA] | Primary-Delta [kV] | Secondary-Yn [V] |
|---|---|---|---|---|---|---|---|---|
| A1 | 235 | 3408 | 800.88 | 575 | 1 | 1800 | 13.2 | 360 |
| A2 | 235 | 3312 | 778.32 | 555 | 1 | |||
| B1 | 235 | 3480 | 817.8 | 585 | 1 | 1800 | 13.2 | 360 |
| B2 | 235 | 3240 | 761.4 | 545 | 1 | |||
| D | 275 | 3744 | 1029.6 | 695 | 2 | 1800 | 13.2 | 360 |
| G | 275 | 3744 | 1029.6 | 695 | 2 | |||
| E | 275 | 3720 | 1023 | 705 | 2 | 1800 | 13.2 | 360 |
| H | 275 | 3744 | 1029.6 | 705 | 2 | |||
| D-G | 275 | 3864 | 1062.6 | 710 | 2 | 1800 | 13.2 | 360 |
| E-H | 275 | 3864 | 1062.6 | 735 | 2 | |||
| F | 260 | 3720 | 967.2 | 695 | 1 | 800 | 13.2 | 360 |
| J | 260 | 3744 | 973.44 | 695 | 1 | 1800 | 13.2 | 360 |
| F-J | 260 | 3864 | 1004.64 | 710 | 1 | |||
| K | 280 | 3984 | 1115.52 | 790 | 2 | 1800 | 13.2 | 360 |
| L | 280 | 3984 | 1115.52 | 790 | 2 | |||
| = | 55,416 | 14,571.72 | 10,185 |
| Measurement | PRRmax = 8% | PRRmax = 10% | PRRmax = 12% |
|---|---|---|---|
| (%) | 0.0023 | 0.0021 | 0.0014 |
| 0.2349 | 0.2097 | 0.1405 | |
| Violations (mins) | 0 | 0 | 161 |
| SOC (end of the day)-SOC(ref) | −4.5307 | −9.0051 | −3.5554 |
| 22.7312 | 31.9882 | 41.9434 |
| Measurement | W = 5 | W = 10 | W = 20 |
|---|---|---|---|
| (%) | 0.0019 | 0.0052 | 0.0107 |
| 0.1864 | 0.5201 | 1.0685 | |
| Violations (mins) | 64 | 0 | 0 |
| SOC (end of the day) -SOC(ref) | −13.6058 | −27.1991 | −24.6659 |
| 25.3416 | 7.7530 | 2.6601 |
| Measurement | |||
|---|---|---|---|
| (%) | 0.0048 | 0.0053 | 0.0049 |
| 0.4823 | 0.5315 | 0.4927 | |
| Violations (mins) | 13 | 0 | 1 |
| SOC (end of the day) -SOC(ref) | 28.215 | 15.3441 | 6.2242 |
| 25.9067 | 5.3813 | 6.1433 |
| Measurement | |||
|---|---|---|---|
| (%) | 0.0071 | 0.0081 | 0.0085 |
| 0.7117 | 0.8127 | 0.8485 | |
| Violations (mins) | 1 | 0 | 0 |
| SOC (end of the day) -SOC(ref) | −21.6426 | −22.8112 | −21.7886 |
| 6.1622 | 5.1486 | 4.3769 |
| Measurement | |||
|---|---|---|---|
| (%) | 0.0063 | 0.0101 | 0.0136 |
| 0.6286 | 1.0117 | 1.3634 | |
| Violations (mins) | 18 | 0 | 0 |
| SOC (end of the day) -SOC(ref) | −29.9978 | −34.8233 | −32.3034 |
| 14.4757 | 4.6293 | 2.4287 |
| Measurement | |||
|---|---|---|---|
| (%) | 0.0072 | 0.0057 | 0.0046 |
| 0.7206 | 0.5709 | 0.4599 | |
| Violations (mins) | 0 | 0 | 1 |
| SOC (end of the day) -SOC(ref) | −31.949 | −22.593 | −20.975 |
| 3.9163 | 5.3242 | 6.8792 |
| Measurement | |||
|---|---|---|---|
| (%) | 0.0016 | 0.0020 | 0.0026 |
| 0.1591 | 0.1990 | 0.2621 | |
| Violations (mins) | 0 | 0 | 0 |
| SOC (end of the day) -SOC(ref) | −1.5788 | 14.4696 | 29.9847 |
| 14.2955 | 14.1632 | 15.9081 |
| Measurement | |||
|---|---|---|---|
| (%) | 0.0043 | 0.0041 | 0.0042 |
| 0.4340 | 0.4115 | 0.4245 | |
| Violations (mins) | 0 | 0 | 0 |
| SOC (end of the day) -SOC(ref) | −18.594 | 3.8675 | −10.287 |
| 5.1573 | 4.7417 | 6.1070 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patarroyo-Montenegro, J.F.; Vasquez-Plaza, J.D.; Rodriguez-Martinez, O.F.; Garcia, Y.V.; Andrade, F. Comparative and Cost Analysis of a Novel Predictive Power Ramp Rate Control Method: A Case Study in a PV Power Plant in Puerto Rico. Appl. Sci. 2021, 11, 5766. https://doi.org/10.3390/app11135766
Patarroyo-Montenegro JF, Vasquez-Plaza JD, Rodriguez-Martinez OF, Garcia YV, Andrade F. Comparative and Cost Analysis of a Novel Predictive Power Ramp Rate Control Method: A Case Study in a PV Power Plant in Puerto Rico. Applied Sciences. 2021; 11(13):5766. https://doi.org/10.3390/app11135766
Chicago/Turabian StylePatarroyo-Montenegro, Juan F., Jesus D. Vasquez-Plaza, Omar F. Rodriguez-Martinez, Yuly V. Garcia, and Fabio Andrade. 2021. "Comparative and Cost Analysis of a Novel Predictive Power Ramp Rate Control Method: A Case Study in a PV Power Plant in Puerto Rico" Applied Sciences 11, no. 13: 5766. https://doi.org/10.3390/app11135766
APA StylePatarroyo-Montenegro, J. F., Vasquez-Plaza, J. D., Rodriguez-Martinez, O. F., Garcia, Y. V., & Andrade, F. (2021). Comparative and Cost Analysis of a Novel Predictive Power Ramp Rate Control Method: A Case Study in a PV Power Plant in Puerto Rico. Applied Sciences, 11(13), 5766. https://doi.org/10.3390/app11135766









