Metaheuristic Optimized Multi-Level Classification Learning System for Engineering Management
Abstract
1. Introduction
2. Literature Review
3. Methodology
3.1. Decomposition Methods
3.2. Optimization in Machine Learning
3.2.1. Least Squares Support Vector Machine for Classification
3.2.2. Enhanced Firefly Algorithm
Metaheuristic Firefly Algorithm
Chaotic Maps: Generating a Variety of Initial Population and Refining Attractive Values
Adaptive Inertia Weight: Controlling Global and Local Search Capabilities
Lévy Flight: Increasing Movement and Mimicking Insects
3.2.3. Optimized LSSVM Model with Decomposition Scheme
3.3. Performance Measures
3.3.1. Cross-Fold Validation
3.3.2. Confusion Matrix
4. Metaheuristic-Optimized Multi-Level Classification System
4.1. Benchmarking of the Enhanced Metaheuristic Optimization Algorithm
4.2. System Development
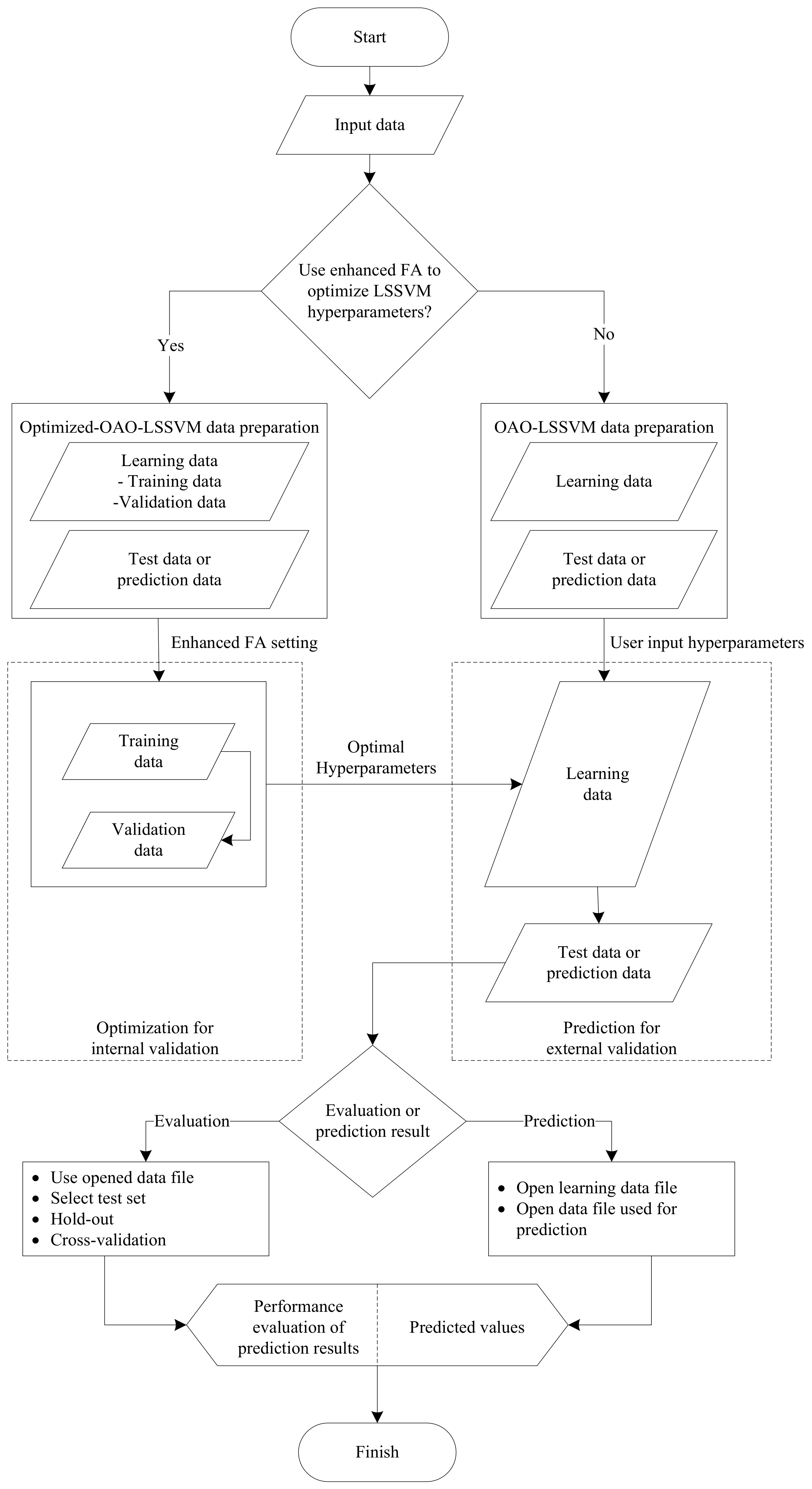
4.2.1. Framework
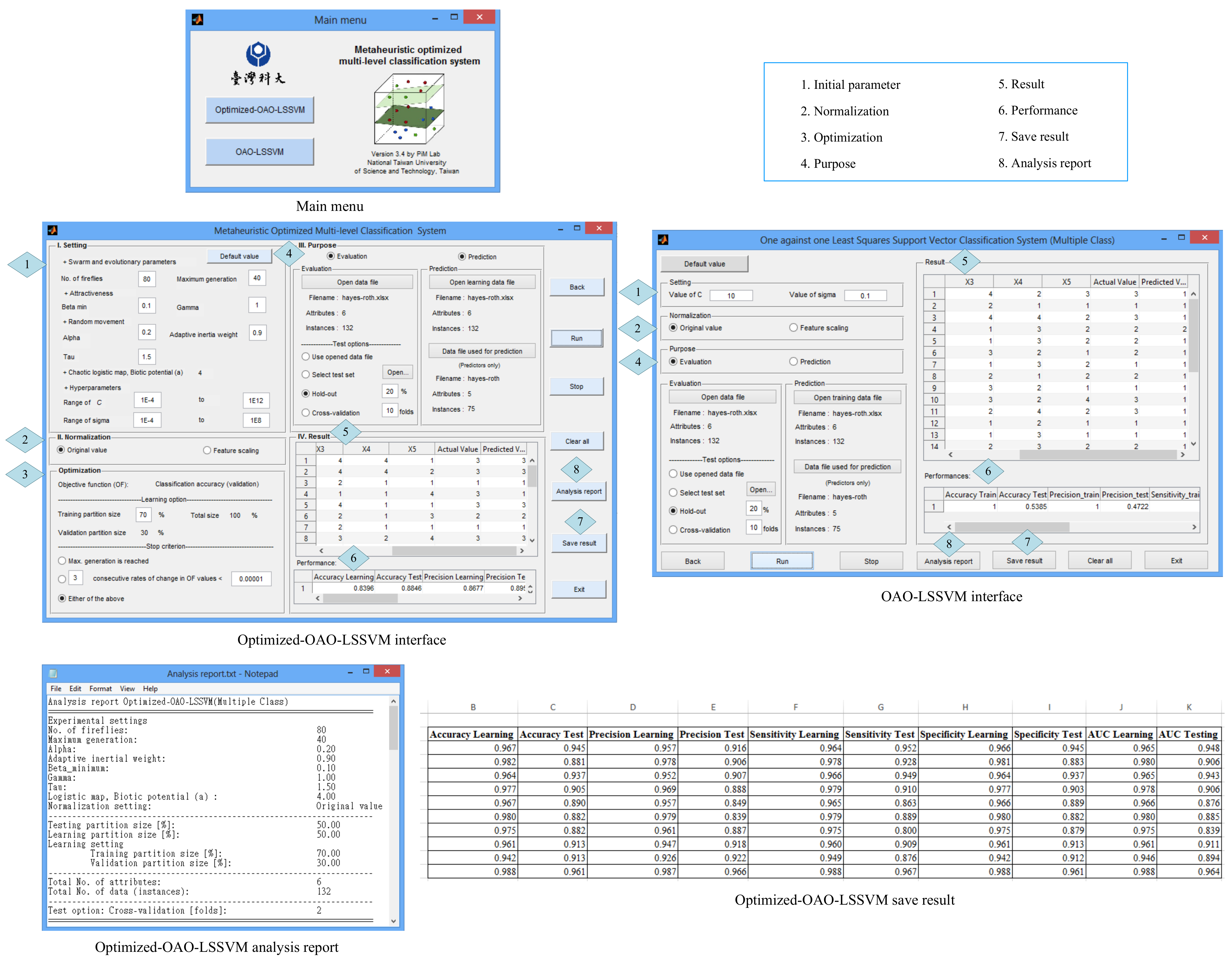
4.2.2. Implementation
5. Engineering Applications
5.1. Binary-Class Problems
5.2. Multi-Level Problems
5.2.1. Case 1—Diagnosis of Faults in Steel Plates
5.2.2. Case 2—Quality of Water in Reservoir
5.2.3. Case 3—Urban Land Cover
5.3. Analytical Results and Discussion
6. Conclusions and Recommendation
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sesmero, M.P.; Alonso-Weber, J.M.; Gutierrez, G.; Ledezma, A.; Sanchis, A. An ensemble approach of dual base learners for multi-class classification problems. Inf. Fusion 2015, 24, 122–136. [Google Scholar] [CrossRef]
- Khaledian, Y.; Miller, B.A. Selecting appropriate machine learning methods for digital soil mapping. Appl. Math. Model. 2020, 81, 401–418. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Wu, D.; Yu, Y.; Tin-Loi, F.; Ma, J.; Gao, W. Machine learning aided static structural reliability analysis for functionally graded frame structures. Appl. Math. Model. 2020, 78, 792–815. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Tiwari, A. Breast cancer diagnosis using Genetically Optimized Neural Network model. Expert Syst. Appl. 2015, 42, 4611–4620. [Google Scholar] [CrossRef]
- Iounousse, J.; Er-Raki, S.; El Motassadeq, A.; Chehouani, H. Using an unsupervised approach of Probabilistic Neural Network (PNN) for land use classification from multitemporal satellite images. Appl. Soft Comput. 2015, 30, 1–13. [Google Scholar] [CrossRef]
- Huang, N.; Xu, D.; Liu, X.; Lin, L. Power quality disturbances classification based on S-transform and probabilistic neural network. Neurocomputing 2012, 98, 12–23. [Google Scholar] [CrossRef]
- Del Vecchio, C.; Fenu, G.; Pellegrino, F.A.; Di Foggia, M.; Quatrale, M.; Benincasa, L.; Iannuzzi, S.; Acernese, A.; Correra, P.; Glielmo, L. Support Vector Representation Machine for superalloy investment casting optimization. Appl. Math. Model. 2019, 72, 324–336. [Google Scholar] [CrossRef]
- Kaefer, F.; Heilman, C.M.; Ramenofsky, S.D. A neural network application to consumer classification to improve the timing of direct marketing activities. Comput. Oper. Res. 2005, 32, 2595–2615. [Google Scholar] [CrossRef]
- Karakatič, S.; Podgorelec, V. Improved classification with allocation method and multiple classifiers. Inf. Fusion 2016, 31, 26–42. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, Z. Seismic damage classification and risk assessment of mountain tunnels with a validation for the 2008 Wenchuan earthquake. Soil Dyn. Earthq. Eng. 2013, 45, 45–55. [Google Scholar] [CrossRef]
- Chou, J.-S.; Hsu, S.-C.; Lin, C.-W.; Chang, Y.-C. Classifying Influential Information to Discover Rule Sets for Project Disputes and Possible Resolutions. Int. J. Proj. Manag. 2016, 34, 1706–1716. [Google Scholar] [CrossRef]
- Hsu, C.-W.; Lin, C.-J. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar] [CrossRef] [PubMed]
- Lorena, A.C.; de Carvalho, A.C.P.L.F.; Gama, J.M.P. A review on the combination of binary classifiers in multiclass problems. Artif. Intell. Rev. 2009, 30, 19. [Google Scholar] [CrossRef]
- Pal, M. Multiclass Approaches for Support Vector Machine Based Land Cover Classification. arXiv 2008, arXiv:0802.2411, 1–16. [Google Scholar]
- Rifkin, R.; Klautau, A. In Defense of One-Vs-All Classification. J. Mach. Learn. Res. 2004, 5, 101–141. [Google Scholar]
- Galar, M.; Fernández, A.; Barrenechea, E.; Bustince, H.; Herrera, F. An overview of ensemble methods for binary classifiers in multi-class problems: Experimental study on one-vs-one and one-vs-all schemes. Pattern Recognit. 2011, 44, 1761–1776. [Google Scholar] [CrossRef]
- Perner, P.; Vingerhoeds, R. Special issue data mining and machine learning. Eng. Appl. Artif. Intell. 2009, 22, 1–2. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; John Wiley and Sons: New York, NY, USA, 1998. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Galar, M.; Fernández, A.; Barrenechea, E.; Herrera, F. DRCW-OVO: Distance-based relative competence weighting combination for One-vs-One strategy in multi-class problems. Pattern Recognit. 2015, 48, 28–42. [Google Scholar] [CrossRef]
- Kang, S.; Cho, S.; Kang, P. Constructing a multi-class classifier using one-against-one approach with different binary classifiers. Neurocomputing 2015, 149, 677–682. [Google Scholar] [CrossRef]
- Balazs, J.A.; Velásquez, J.D. Opinion Mining and Information Fusion: A survey. Inf. Fusion 2016, 27, 95–110. [Google Scholar] [CrossRef]
- Medhat, W.; Hassan, A.; Korashy, H. Sentiment analysis algorithms and applications: A survey. Ain Shams Eng. J. 2014, 5, 1093–1113. [Google Scholar] [CrossRef]
- Yang, X.; Yu, Q.; He, L.; Guo, T. The one-against-all partition based binary tree support vector machine algorithms for multi-class classification. Neurocomputing 2013, 113, 1–7. [Google Scholar] [CrossRef]
- Kim, K.-j.; Ahn, H. A corporate credit rating model using multi-class support vector machines with an ordinal pairwise partitioning approach. Comput. Oper. Res. 2012, 39, 1800–1811. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pham, A.-D. Nature-inspired metaheuristic optimization in least squares support vector regression for obtaining bridge scour information. Inf. Sci. 2017, 399, 64–80. [Google Scholar] [CrossRef]
- Van Gestel, T.; Suykens, J.A.K.; Baesens, B.; Viaene, S.; Vanthienen, J.; Dedene, G.; de Moor, B.; Vandewalle, J. Benchmarking Least Squares Support Vector Machine Classifiers. Mach. Learn. 2004, 54, 5–32. [Google Scholar] [CrossRef]
- Parouha, R.P.; Das, K.N. An efficient hybrid technique for numerical optimization and applications. Comput. Ind. Eng. 2015, 83, 193–216. [Google Scholar] [CrossRef]
- Hanafi, R.; Kozan, E. A hybrid constructive heuristic and simulated annealing for railway crew scheduling. Comput. Ind. Eng. 2014, 70, 11–19. [Google Scholar] [CrossRef]
- Setak, M.; Feizizadeh, F.; Tikani, H.; Ardakani, E.S. A bi-level stochastic optimization model for reliable supply chain in competitive environments: Hybridizing exact method and genetic algorithm. Appl. Math. Model. 2019, 75, 310–332. [Google Scholar] [CrossRef]
- Dabiri, N.; Tarokh, M.J.; Alinaghian, M. New mathematical model for the bi-objective inventory routing problem with a step cost function: A multi-objective particle swarm optimization solution approach. Appl. Math. Model. 2017, 49, 302–318. [Google Scholar] [CrossRef]
- Janardhanan, M.N.; Li, Z.; Bocewicz, G.; Banaszak, Z.; Nielsen, P. Metaheuristic algorithms for balancing robotic assembly lines with sequence-dependent robot setup times. Appl. Math. Model. 2019, 65, 256–270. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, L.; Pan, Q. Queuing search algorithm: A novel metaheuristic algorithm for solving engineering optimization problems. Appl. Math. Model. 2018, 63, 464–490. [Google Scholar] [CrossRef]
- Qingjie, L.; Guiming, C.; Xiaofang, L.; Qing, Y. Genetic algorithm based SVM parameter composition optimization. Comput. Appl. Softw. 2012, 4, 29. [Google Scholar]
- Rastegar, S.; Araújo, R.; Mendes, J. Online identification of Takagi–Sugeno fuzzy models based on self-adaptive hierarchical particle swarm optimization algorithm. Appl. Math. Model. 2017, 45, 606–620. [Google Scholar] [CrossRef]
- Pal, S.K.; Rai, C.S.; Singh, A.P. Comparative study of firefly algorithm and particle swarm optimization for noisy non-linear optimization problems. Int. J. Intell. Syst. Appl. 2012, 4, 50–57. [Google Scholar] [CrossRef]
- Olamaei, J.; Moradi, M.; Kaboodi, T. A new adaptive modified Firefly Algorithm to solve optimal capacitor placement problem. In Proceedings of the 18th Electric Power Distribution Conference, Kermanshah, Iran, 30 April–1 May 2013; pp. 1–6. [Google Scholar]
- Chou, J.-S.; Pham, A.-D. Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Coelho, L.d.S.; Mariani, V.C. Improved firefly algorithm approach applied to chiller loading for energy conservation. Energy Build. 2013, 59, 273–278. [Google Scholar] [CrossRef]
- Chou, J.-S.; Lin, C. Predicting Disputes in Public-Private Partnership Projects: Classification and Ensemble Models. J. Comput. Civ. Eng. 2013, 27, 51–60. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Hoang, N.-D. Risk Score Inference for Bridge Maintenance Project Using Evolutionary Fuzzy Least Squares Support Vector Machine. J. Comput. Civ. Eng. 2014, 28, 04014003. [Google Scholar] [CrossRef]
- Pant, P.; Chatterjee, D. Prediction of clad characteristics using ANN and combined PSO-ANN algorithms in laser metal deposition process. Surf. Interfaces 2020, 21, 100699. [Google Scholar] [CrossRef]
- Noori, N.; Kalin, L.; Isik, S. Water quality prediction using SWAT-ANN coupled approach. J. Hydrol. 2020, 590, 125220. [Google Scholar] [CrossRef]
- Sujith, M.; Jeon, J.-S. Machine Learning–Based Failure Mode Recognition of Circular Reinforced Concrete Bridge Columns: Comparative Study. J. Struct. Eng. 2019, 145, 04019104. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Liu, Y.; Wang, H.; Zhang, H.; Liber, K. A comprehensive support vector machine-based classification model for soil quality assessment. Soil Tillage Res. 2016, 155, 19–26. [Google Scholar] [CrossRef]
- Gholami, R.; Rasouli, V.; Alimoradi, A. Improved RMR Rock Mass Classification Using Artificial Intelligence Algorithms. Rock Mech. Rock Eng. 2013, 46, 1199–1209. [Google Scholar] [CrossRef]
- Liao, Y.; Xu, J.; Wang, W. A Method of Water Quality Assessment Based on Biomonitoring and Multiclass Support Vector Machine. Procedia Environ. Sci. 2011, 10, 451–457. [Google Scholar] [CrossRef]
- Du, S.; Liu, C.; Xi, L. A Selective Multiclass Support Vector Machine Ensemble Classifier for Engineering Surface Classification Using High Definition Metrology. J. Manuf. Sci. Eng. 2015, 137, 011003. [Google Scholar] [CrossRef]
- Polat, K.; Güneş, S. A novel hybrid intelligent method based on C4.5 decision tree classifier and one-against-all approach for multi-class classification problems. Expert Syst. Appl. 2009, 36, 1587–1592. [Google Scholar] [CrossRef]
- Garcia, L.P.F.; Sáez, J.A.; Luengo, J.; Lorena, A.C.; de Carvalho, A.C.P.L.F.; Herrera, F. Using the One-vs-One decomposition to improve the performance of class noise filters via an aggregation strategy in multi-class classification problems. Knowl. Based Syst. 2015, 90, 153–164. [Google Scholar] [CrossRef]
- Zhou, L.; Tam, K.P.; Fujita, H. Predicting the listing status of Chinese listed companies with multi-class classification models. Inf. Sci. 2016, 328, 222–236. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; Gestel, T.V.; Brabanter, J.D.; Moor, B.D.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific: Singapore, 2002. [Google Scholar]
- Khemchandani, R.; Jayadeva; Chandra, S. Regularized least squares fuzzy support vector regression for financial time series forecasting. Expert Syst. Appl. 2009, 36, 132–138. [Google Scholar] [CrossRef]
- Haifeng, W.; Dejin, H. Comparison of SVM and LS-SVM for Regression. In Proceedings of the 2005 International Conference on Neural Networks and Brain, Beijing, China, 13–15 October 2005; pp. 279–283. [Google Scholar]
- Yang, X.-S. Firefly Algorithm; Luniver Press: Bristol, UK, 2008. [Google Scholar]
- Banati, H.; Bajaj, M. Fire Fly Based Feature Selection Approach. Int. J. Comput. Sci. Issues 2011, 8, 473–479. [Google Scholar]
- Fister, I.; Fister, I., Jr.; Yang, X.-S.; Brest, J. A comprehensive review of firefly algorithms. Swarm Evol. Comput. 2013, 13, 34–46. [Google Scholar] [CrossRef]
- Khadwilard, A.; Chansombat, S.; Thepphakorn, T.; Thapatsuwan, P.; Chainate, W.; Pongcharoen, P. Application of Firefly Algorithm and Its Parameter Setting for Job Shop Scheduling. J. Ind. Technol. 2012, 8, 49–58. [Google Scholar]
- Aungkulanon, P.; Chai-ead, N.; Luangpaiboon, P. Simulated Manufacturing Process Improvement via Particle Swarm Optimisation and Firefly Algorithms. In Lectures Notes Engineering and Computer Science; Newswood Limited: Hong Kong, China, 2011. [Google Scholar]
- Aci, M.; İnan, C.; Avci, M. A hybrid classification method of k nearest neighbor, Bayesian methods and genetic algorithm. Expert Syst. Appl. 2010, 37, 5061–5067. [Google Scholar] [CrossRef]
- Chou, J.-S.; Cheng, M.-Y.; Wu, Y.-W. Improving classification accuracy of project dispute resolution using hybrid artificial intelligence and support vector machine models. Expert Syst. Appl. 2013, 40, 2263–2274. [Google Scholar] [CrossRef]
- Lee, Y.; Lee, J. Binary tree optimization using genetic algorithm for multiclass support vector machine. Expert Syst. Appl. 2015, 42, 3843–3851. [Google Scholar] [CrossRef]
- Seera, M.; Lim, C.P. A hybrid intelligent system for medical data classification. Expert Syst. Appl. 2014, 41, 2239–2249. [Google Scholar] [CrossRef]
- Tian, Y.; Fu, M.; Wu, F. Steel plates fault diagnosis on the basis of support vector machines. Neurocomputing 2015, 151, 296–303. [Google Scholar] [CrossRef]
- García-Pedrajas, N.; Ortiz-Boyer, D. An empirical study of binary classifier fusion methods for multiclass classification. Inf. Fusion 2011, 12, 111–130. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2008; p. 128. [Google Scholar]
- Hong, W.-C.; Dong, Y.; Chen, L.-Y.; Wei, S.-Y. SVR with hybrid chaotic genetic algorithms for tourism demand forecasting. Appl. Soft Comput. 2011, 11, 1881–1890. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Talatahari, S.; Alavi, A.H. Firefly algorithm with chaos. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 89–98. [Google Scholar] [CrossRef]
- Li, X.; Niu, P.; Liu, J. Combustion optimization of a boiler based on the chaos and Lévy flight vortex search algorithm. Appl. Math. Model. 2018, 58, 3–18. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence—Volume 2, Montreal, QC, Canada, 20 August 1995; pp. 1137–1143. [Google Scholar]
- Chou, J.-S.; Tsai, C.-F.; Lu, Y.-H. Project dispute prediction by hybrid machine learning techniques. J. Civ. Eng. Manag. 2013, 19, 505–517. [Google Scholar] [CrossRef]
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Jamil, M.; Yang, X.-S. A Literature Survey of Benchmark Functions For Global Optimization Problems. Int. J. Math. Model. Numer. Optim. 2013, 4, 150–194. [Google Scholar]
- Surjanovic, S.; Bingham, D. Virtual Library of Simulation Experiments: Test Functions and Datasets. Available online: http://www.sfu.ca/~ssurjano/optimization.html (accessed on 8 May 2016).
- Sikora, M.; Wróbel, Ł. Application of rule induction algorithms for analysis of data collected by seismic hazard monitoring systems in coal mines. Arch. Min. Sci. 2010, 55, 91–114. [Google Scholar]
- Goh, A.T.C.; Goh, S.H. Support vector machines: Their use in geotechnical engineering as illustrated using seismic liquefaction data. Comput. Geotech. 2007, 34, 410–421. [Google Scholar] [CrossRef]
- Chou, J.-S.; Thedja, J.P.P. Metaheuristic optimization within machine learning-based classification system for early warnings related to geotechnical problems. Autom. Constr. 2016, 68, 65–80. [Google Scholar] [CrossRef]
- Durduran, S.S. Automatic classification of high resolution land cover using a new data weighting procedure: The combination of k-means clustering algorithm and central tendency measures (KMC–CTM). Appl. Soft Comput. 2015, 35, 136–150. [Google Scholar] [CrossRef]
- Chou, J.-S.; Ho, C.-C.; Hoang, H.-S. Determining quality of water in reservoir using machine learning. Ecol. Inform. 2018, 44, 57–75. [Google Scholar] [CrossRef]
- Hydrotech Research Institute of National Taiwan University. Reservoir Eutrophiction Prediction and Prevention by Using Remote Sensing Technique. Water Resources Agency: Taipei, Taiwan, 2005. (In Chinese) [Google Scholar]
- Lichman, M. UCI Machine Learning Repository; University of California, School of Information and Computer Science: Irvine, CA, USA, 2013; Available online: http://archive.ics.uci.edu/ml (accessed on 20 December 2015).
- Wentz, E.A.; Stefanov, W.L.; Gries, C.; Hope, D. Land use and land cover mapping from diverse data sources for an arid urban environments. Comput. Environ. Urban Syst. 2006, 30, 320–346. [Google Scholar] [CrossRef]
- Crone, S.; Guajardo, J.; Weber, R. The impact of preprocessing on support vector regression and neural networks in time series prediction. In Proceedings of the International Conference on Data Mining DMIN’06, Las Vegas, NV, USA, 26–29 June 2006; pp. 37–42. [Google Scholar]
| Group | Parameter | Setting | Purpose |
|---|---|---|---|
| Swarm and metaheuristic settings | Number of fireflies | User defined; default value: 80 | Population number |
| Max generation | User defined; default value: tmax = 40 | Constrain implementation of algorithm | |
| Chaotic logistic map | Random generation; biotic potential η = 4 | Generate initial population with high diversity | |
| Brightness | Objective function | Accuracy | Calculate firefly brightness |
| Attractiveness | βmin | Default value β0 = 0.1 | Minimum value of attractive parameter β |
| Chaotic Gauss/mouse map | Random generation | Automatically tune β parameter | |
| γ | Default value γ = 1 | Absorption coefficient | |
| Random movement | α | Default value α0 = 0.2 | Randomness of firefly movement |
| Adaptive inertia weight | Default value θ = 0.9 | Control the local and global search capabilities of swarm algorithm | |
| Lévy flight | Default value τ = 1.5 | Accelerate the local search by generating new optimal neighborhoods around the obtained best solution |
| Actual Class | |||
|---|---|---|---|
| Positive | Negative | ||
| Predicted class | Positive | True positive (tp) | False negative (fn) |
| Negative | False positive (fp) | True negative (tn) | |
| No. | Benchmark Functions | Dimension | Minimum Value | Maximum Value | Mean of Optimum | Standard Deviation | Total Time (s) |
|---|---|---|---|---|---|---|---|
| 1 | Griewank | 10 | 3.03 × 10−11 | 3.75 × 10−10 | 1.36 × 10−10 | 8.44 × 10−11 | 2.10 × 104 |
| 30 | 7.84 × 10−8 | 2.36 × 10−7 | 1.51 × 10−7 | 4.49 × 10−7 | 1.99 × 104 | ||
| Minimum f(0,…,0) = 0 | 50 | 5.40 × 10−7 | 1.74 × 10−6 | 1.17 × 10−6 | 3.01 × 10−7 | 2.34 × 104 | |
| 2 | Deb 01 | 10 | −1 | −1 | −1 | 4.98 × 10−12 | 1.54 × 104 |
| (5*pi*x) = [−1;1] | 30 | −1 | −8.34 × 10−1 | −9.93 × 10−1 | 3.12 × 10−2 | 1.85 × 104 | |
| Minimum f(0,…,0) = −1 | 50 | −1 | −5.24 × 10−1 | −9.31 × 10−1 | 1.39 × 10−1 | 2.26 × 104 | |
| 3 | Csendes | 10 | 7.04 × 10−11 | 1.06 × 10−5 | 9.57 × 10−7 | 2.09 × 10−6 | 3.55 × 104 |
= [−1; 1] | 30 | 4.39 × 10−6 | 2.39 × 10−3 | 5.07 × 10−4 | 5.66 × 10−4 | 4.27 × 104 | |
| Minimum f(0,…,0) = 0 | 50 | 3.78 × 10−4 | 6.53 × 10−3 | 1.49 × 10−3 | 1.22 × 10−3 | 4.91 × 104 | |
| 4 | De Jong | 10 | 2.80 × 10−12 | 8.65 × 10−12 | 4.82 × 10−12 | 1.59 × 10−12 | 1.50 × 104 |
| = [−5.12; 5.12] | 30 | 7.40 × 10−11 | 3.33 × 10−4 | 1.11 × 10−5 | 6.08 × 10−5 | 1.97 × 104 | |
| Minimum f(0,…,0) = 0 | 50 | 1.39 × 10−4 | 4.45 × 10−2 | 8.07 × 10−3 | 9.66 × 10−3 | 2.37 × 104 | |
| 5 | Alpine 1 | 10 | 6.69 × 10−7 | 5.49 × 10−4 | 2.03 × 10−5 | 9.99 × 10−5 | 1.50 × 104 |
= [−10; 10] | 30 | 6.80 × 10−6 | 7.43 × 10−3 | 5.21 × 10−4 | 1.65 × 10−3 | 2.07 × 104 | |
| Minimum f(0,…,0) = 0 | 50 | 2.43 × 10−5 | 4.95 × 10−3 | 9.43 × 10−4 | 1.42 × 10−3 | 2.34 × 104 | |
| 6 | Sum Squares | 10 | 4.77 × 10−11 | 1.74 × 10−10 | 1.06 × 10−10 | 3.27 × 10−11 | 1.44 × 104 |
= [−10; 10] | 30 | 1.52 × 10−8 | 4.59 × 10−8 | 2.70 × 10−8 | 7.78 × 10−9 | 3.20 × 104 | |
| Minimum f(0,…,0) =0 | 50 | 1.51 × 10−5 | 1.60 × 10−2 | 1.13 × 10−3 | 2.89 × 10−3 | 2.46 × 104 | |
| 7 | Rotated hyper-ellipsoid | 10 | 1.96 × 10−9 | 6.99 × 10−9 | 4.73 × 10−9 | 1.29 × 10−9 | 1.48 × 104 |
= [−65.536; 65.536] | 30 | 4.43 × 10−7 | 1.56 × 10−6 | 1.06 × 10−6 | 3.30 × 10−7 | 2.40 × 104 | |
| Minimum f(0,…,0) = 0 | 50 | 3.80 × 10−5 | 3.37 × 10−3 | 9.75 × 10−4 | 1.10 × 10−3 | 2.23 × 104 | |
| 8 | Xin She Yang 2 | 10 | 5.66 × 10−4 | 5.66 × 10−4 | 5.66 × 10−4 | 4.63 × 10−15 | 1.59 × 104 |
| *exp*[)] = [−2π; 2π] | 30 | 3.51 × 10−12 | 1.06 × 10−11 | 5.24 × 10−12 | 2.09 × 10−12 | 2.32 × 104 | |
| Minimum f(0,…,0) = 0 | 50 | 4.36 × 10−20 | 5.04 × 10−18 | 1.18 × 10−18 | 1.40 × 10−18 | 2.21 × 104 | |
| 9 | Schwefel | 10 | 6.36 × 10−58 | 1.50 × 10−55 | 2.27 × 10−56 | 3.28 × 10−56 | 3.59 × 104 |
| = [−10; 10] | 30 | 3.42 × 10−49 | 4.68 × 10−28 | 1.64 × 10−29 | 8.55 × 10−29 | 4.20 × 104 | |
| Minimum f(0,…,0) =0 | 50 | 7.08 × 10−18 | 3.40 × 10−13 | 2.75 × 10−14 | 6.75 × 10−14 | 4.78 × 104 | |
| 10 | Chung-Reynolds | 10 | 3.95 × 10−19 | 6.84 × 10−18 | 2.74 × 10−18 | 1.63 × 10−18 | 1.47 × 104 |
| = [−100; 100] | 30 | 1.25 × 10−15 | 5.22 × 10−15 | 2.22 × 10−15 | 9.62 × 10−16 | 1.79 × 104 | |
| Minimum f(0,…,0) = 0 | 50 | 1.99 × 10−14 | 1.32 × 10−13 | 5.82 × 10−14 | 2.74 × 10−14 | 2.48 × 104 |
| Parameter | Unit | Max. Value | Min. Value | Mean | Standard Deviation |
|---|---|---|---|---|---|
| Dataset 1—Seismic bumps, 2584 samples, Poland [76] | |||||
| Genergy | N/A | 2,595,650.00 | 100.00 | 90,242.52 | 229,200.51 |
| Gpuls | N/A | 4518.00 | 2.00 | 538.58 | 562.65 |
| Gdenergy | N/A | 1245.00 | −96.00 | 12.38 | 80.32 |
| Gdpuls | N/A | 838.00 | −96.00 | 4.51 | 63.17 |
| Energy | Joule | 402,000.00 | 0.00 | 4975.27 | 20,450.83 |
| Maxenergy | Joule | 400,000.00 | 0.00 | 4278.85 | 19,357.45 |
| Seismic bumps (1 = hazardous state, 2 = not) | N/A | 2 | 1 | ||
| Dataset 2—Soil Liquefaction, 226 samples, U.S.A., China and Taiwan [77] | |||||
| Cone tip resistance (qc) | MPa | 25.00 | 0.90 | 5.82 | 4.09 |
| Sleeve friction ratio (Rf) | % | 5.20 | 0.10 | 1.22 | 1.05 |
| Effective stress (σ’v) | kPa | 215.20 | 22.50 | 74.65 | 34.40 |
| Total stress (σv) | kPa | 274.00 | 26.60 | 106.89 | 55.36 |
| Horizontal ground surface acceleration (amax) | gal | 0.80 | 0.08 | 0.29 | 0.14 |
| Earthquake movement magnitude (Mw) | N/A | 7.60 | 6.00 | 6.95 | 0.44 |
| Soil liquefaction (1 = exists, 2 = not) | N/A | 2 | 1 | ||
| Technique | Cross-Fold Validation | Accuracy (%) | Training and Test Time (s) |
|---|---|---|---|
| Dataset 1—Seismic bumps (2584 samples) | |||
| SFA-LSSVM (original value) | 10 | 93.46 | 355,913.59 |
| SFA-LSSVM (feature scaling) | 10 | 93.96 | 174,328.48 |
| Optimized-OAO-LSSVM (original value) | 10 | 93.42 | 1136.60 |
| Optimized-OAO-LSSVM (feature scaling) | 10 | 93.30 | 717.37 |
| Dataset 2—Soil liquefaction (226 samples) | |||
| SFA-LSSVM (original value) | 10 | 94.31 | 19,884.82 |
| SFA-LSSVM (feature scaling) | 10 | 95.18 | 998.45 |
| Optimized-OAO-LSSVM (original value) | 10 | 93.38 | 57.22 |
| Optimized-OAO-LSSVM (feature scaling) | 10 | 92.93 | 56.14 |
| Parameter | Max. Value | Min. Value | Mean | Standard Deviation |
|---|---|---|---|---|
| Input | ||||
| Edges Y Index | 1 | 0.048 | 0.813 | 0.234 |
| Outside Global Index | 1 | 0 | 0.576 | 0.482 |
| Orientation Index | 1 | −0.991 | 0.083 | 0.501 |
| Edges X Index | 1 | 0.014 | 0.611 | 0.243 |
| Type of Steel_A300 | 1 | 0 | 0.400 | 0.490 |
| Luminosity Index | 1 | −0.999 | −0.131 | 0.149 |
| Square Index | 1 | 0.008 | 0.571 | 0.271 |
| Type of Steel_A400 | 1 | 0 | 0.600 | 0.490 |
| Length of Conveyer | 1794 | 1227 | 1459.160 | 144.578 |
| Minimum of Luminosity | 203 | 0 | 84.549 | 32.134 |
| X Maximum | 1713 | 4 | 617.964 | 497.627 |
| X Minimum | 1705 | 0 | 571.136 | 520.691 |
| Sigmoid of Areas | 1 | 0.119 | 0.585 | 0.339 |
| Edges Index | 1 | 0 | 0.332 | 0.300 |
| Empty Index | 1 | 0 | 0.414 | 0.137 |
| Maximum of Luminosity | 253 | 37 | 130.194 | 18.691 |
| Log of Areas | 51,837 | 0.301 | 22,757.224 | 9704.564 |
| Log Y Index | 42,587 | 0 | 11,636.590 | 7273.127 |
| Log X Index | 30,741 | 0.301 | 9477.470 | 7727.986 |
| Steel Plate Thickness | 300 | 40 | 78.738 | 55.086 |
| Output—Type of fault | N/A | |||
| Pastry (Class 1) | ||||
| ZScratch (Class 2) | ||||
| KScratch (Class 3) | ||||
| Stains (Class 4) | ||||
| Dirtiness (Class 5) | ||||
| Bumps (Class 6) | ||||
| Empirical Models Reported in Primary Works and Single Multi-Class Models | Performance Measure | Improved Accuracy by Optimized-OAO-LSSVM System (%) | |||||
|---|---|---|---|---|---|---|---|
| Dataset | Accuracy (%) | Precision (%) | Sensitivity (%) | Specificity (%) | AUC | ||
| Dataset 1—Diagnosis of faults in steel plates | SMO | 86.357 | 86.400 | 86.300 | 95.300 | 0.908 | 5.191 |
| Multiclass Classifier | 85.726 | 85.700 | 85.600 | 96.000 | 0.908 | 5.884 | |
| Naïve Bayes | 82.334 | 82.300 | 84.440 | 95.960 | 0.902 | 9.608 | |
| Logistic | 86.124 | 86.100 | 86.000 | 97.400 | 0.917 | 5.447 | |
| LibSVM | 31.704 | 31.700 | 10.100 | 89.900 | 0.500 | 65.193 | |
| GS-SVM [65] | 77.800 | - | - | - | - | 14.586 | |
| GA-SVM [65] | 78.000 | - | - | - | - | 14.366 | |
| PSO-SVM [65] | 79.600 | - | - | - | - | 12.610 | |
| OAO-LSSVM | 53.553 | 28.764 | - | 59.148 | - | 41.206 | |
| Optimized-OAO-LSSVM | 91.085 | 89.995 | 90.437 | 91.020 | 0.907 | - | |
| Dataset 2—Quality of water in reservoir | SMO | 75.238 | 75.200 | 77.500 | 85.900 | 0.817 | 19.661 |
| Multiclass Classifier | 85.397 | 85.400 | 86.500 | 94.900 | 0.907 | 8.813 | |
| Naïve Bayes | 76.000 | 76.000 | 78.700 | 99.500 | 0.891 | 18.847 | |
| Logistic | 89.580 | 89.600 | 89.600 | 95.000 | 0.923 | 4.346 | |
| LibSVM | 80.950 | 81.000 | 81.000 | 87.600 | 0.843 | 13.561 | |
| OAO-LSSVM | 92.196 | 90.794 | 90.633 | 92.078 | 0.914 | 1.553 | |
| Optimized-OAO-LSSVM | 93.650 | 92.531 | 93.840 | 93.746 | 0.938 | - | |
| Dataset 3—Urban land cover | SMO | 85.778 | 85.800 | 86.000 | 89.000 | 0.875 | 1.714 |
| Multiclass Classifier | 64.900 | 64.900 | 64.800 | 99.400 | 0.821 | 25.636 | |
| Naïve Bayes | 81.000 | 81.000 | 81.600 | 91.800 | 0.867 | 7.189 | |
| Logistic | 65.926 | 65.900 | 65.900 | 95.300 | 0.806 | 24.461 | |
| LibSVM | 18.370 | 18.400 | 19.000 | 81.400 | 0.502 | 78.951 | |
| k-NN classifier [79] | 80.140 | - | - | - | - | 8.174 | |
| ELM classifier [79] | 84.700 | - | - | - | - | 2.949 | |
| SVM classifier [79] | 84.890 | - | - | - | - | 2.732 | |
| OAO-LSSVM | 18.378 | 11.637 | - | - | - | 78.942 | |
| Optimized-OAO-LSSVM | 87.274 | 87.048 | 89.918 | 87.297 | 0.886 | - | |
| Parameter | Max. Value | Min. Value | Mean | Standard Deviation |
|---|---|---|---|---|
| Input | ||||
| Secchi disk depth (SD) | 8.375 | 0.1 | 1.8605 | 1.1026 |
| Chlorophyll a (Chla) | 151.4 | 0.1 | 7.9216 | 12.2305 |
| Total phosphorus (TP) | 2.0495 | 0.0022 | 0.0677 | 0.214 |
| Output-Reservoir water quality | N/A | |||
| Excellent—Class 1 | ||||
| Good—Class 2 | ||||
| Average—Class 3 | ||||
| Fair—Class 4 | ||||
| Poor—Class 5 | ||||
| Factor/Index | Excellent 1 | Good 2 | Average 3 | Fair 4 | Poor 5 |
|---|---|---|---|---|---|
| Secchi disk depth (SD) | >4.5 | 4.5–3.7 | 3.7–2.3 | 2.3–1.7 | <1.7 |
| Chlorophyll a (Chla) | <2 | 2.0–3.0 | 3.0–7.0 | 7.0–10.0 | >10 |
| Total phosphorus (TP) | <8 | 8–12 | 12–28 | 28–40 | >40 |
| Carlon’s Trophic State Index (CTSI) | <20 | 20–40 | 40–50 | 50–70 | >70 |
| Names of Attributes in the Dataset | Source of Information of the Segments |
|---|---|
| BrdIndx: border index | Shape |
| Area: area in m2 | Size |
| Round: roundness | Shape |
| Bright: brightness | Spectral |
| Compact: compactness | Shape |
| ShpIndx: shape index | Shape |
| Mean_G: green | Spectral |
| Mean_R: red | Spectral |
| Mean_NIR: near Infrared | Spectral |
| SD_G: standard deviation of green | Texture |
| SD_R: standard deviation of red | Texture |
| SD_NIR: standard deviation of near infrared | Texture |
| LW: length/width | Shape |
| GLCM1: gray-level co-occurrence matrix | Texture |
| Rect: rectangularity | Shape |
| GLCM2: another gray-level co-occurrence matrix attribute | Texture |
| Dens: density | Shape |
| Assym: asymmetry | Shape |
| NDVI: normalized difference vegetation index | Spectral |
| BordLngth: border length | Shape |
| GLCM3: another gray-level co-occurrence matrix attribute | Texture |
| Names of the Land Cover in the Dataset | No. of Data Points |
|---|---|
| Trees (Class 1) | 106 |
| Concrete (Class 2) | 122 |
| Shadow (Class 3) | 61 |
| Asphalt (Class 4) | 59 |
| Buildings (Class 5) | 112 |
| Grass (Class 6) | 116 |
| Pools (Class 7) | 29 |
| Cars (Class 8) | 36 |
| Soil (Class 9) | 34 |
| Total | 675 |
| Dataset | Performance Measure | |||||
|---|---|---|---|---|---|---|
| Accuracy (%) | Precision (%) | Sensitivity (%) | Specificity (%) | AUC | ||
| Dataset 1—Diagnosis of faults in steel plates | ||||||
| Original value | 91.085 | 89.995 | 90.437 | 91.020 | 0.907 | |
| Feature scaling | 88.646 | 86.518 | 88.458 | 88.620 | 0.885 | |
| Dataset 2—Quality of water in reservoir | ||||||
| Original value | 93.526 | 92.335 | 94.272 | 93.622 | 0.939 | |
| Feature scaling | 93.650 | 92.531 | 93.840 | 93.746 | 0.938 | |
| Dataset 3—Urban land cover | ||||||
| Original value | 87.274 | 87.048 | 89.918 | 87.297 | 0.886 | |
| Feature scaling | 86.521 | 86.003 | 87.310 | 86.534 | 0.874 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou, J.-S.; Pham, T.T.P.; Ho, C.-C. Metaheuristic Optimized Multi-Level Classification Learning System for Engineering Management. Appl. Sci. 2021, 11, 5533. https://doi.org/10.3390/app11125533
Chou J-S, Pham TTP, Ho C-C. Metaheuristic Optimized Multi-Level Classification Learning System for Engineering Management. Applied Sciences. 2021; 11(12):5533. https://doi.org/10.3390/app11125533
Chicago/Turabian StyleChou, Jui-Sheng, Trang Thi Phuong Pham, and Chia-Chun Ho. 2021. "Metaheuristic Optimized Multi-Level Classification Learning System for Engineering Management" Applied Sciences 11, no. 12: 5533. https://doi.org/10.3390/app11125533
APA StyleChou, J.-S., Pham, T. T. P., & Ho, C.-C. (2021). Metaheuristic Optimized Multi-Level Classification Learning System for Engineering Management. Applied Sciences, 11(12), 5533. https://doi.org/10.3390/app11125533







