Unit Commitment with Ancillary Services in a Day-Ahead Power Market
Abstract
1. Introduction
2. Problem Formulation
- a.
- Load balance
- b.
- Upper and lower limits of unit generation
- c.
- Ramping down/up rate limitations
- d.
- Minimum up/down time
- A.
- AGC limitation
- a
- The AGC demand is esxpresed as
- b.
- The response to the rise/down rate of 3 min can be expressed as
- B.
- RSR limitation
- a
- The RSR demand is expressed as
- b.
- The rise rate of 30 min is expressed as
- C.
- SR limitation
- a
- The SR demand is expressed as
- b.
- The rise rate of 60 min is expressed as
3. Proposed Methodology
- (1)
- unit state—Ui(t) is an integer variable;
- (2)
- generation output: Pi(t) is a continuous variable.
3.1. DPSO
3.2. SQP
- a.
- Update the Hessian matrix
- b.
- Compute quadratic programming, as expressed in Equation (22).
- c.
- Use Line Search and the Merit Function to update system parameters.
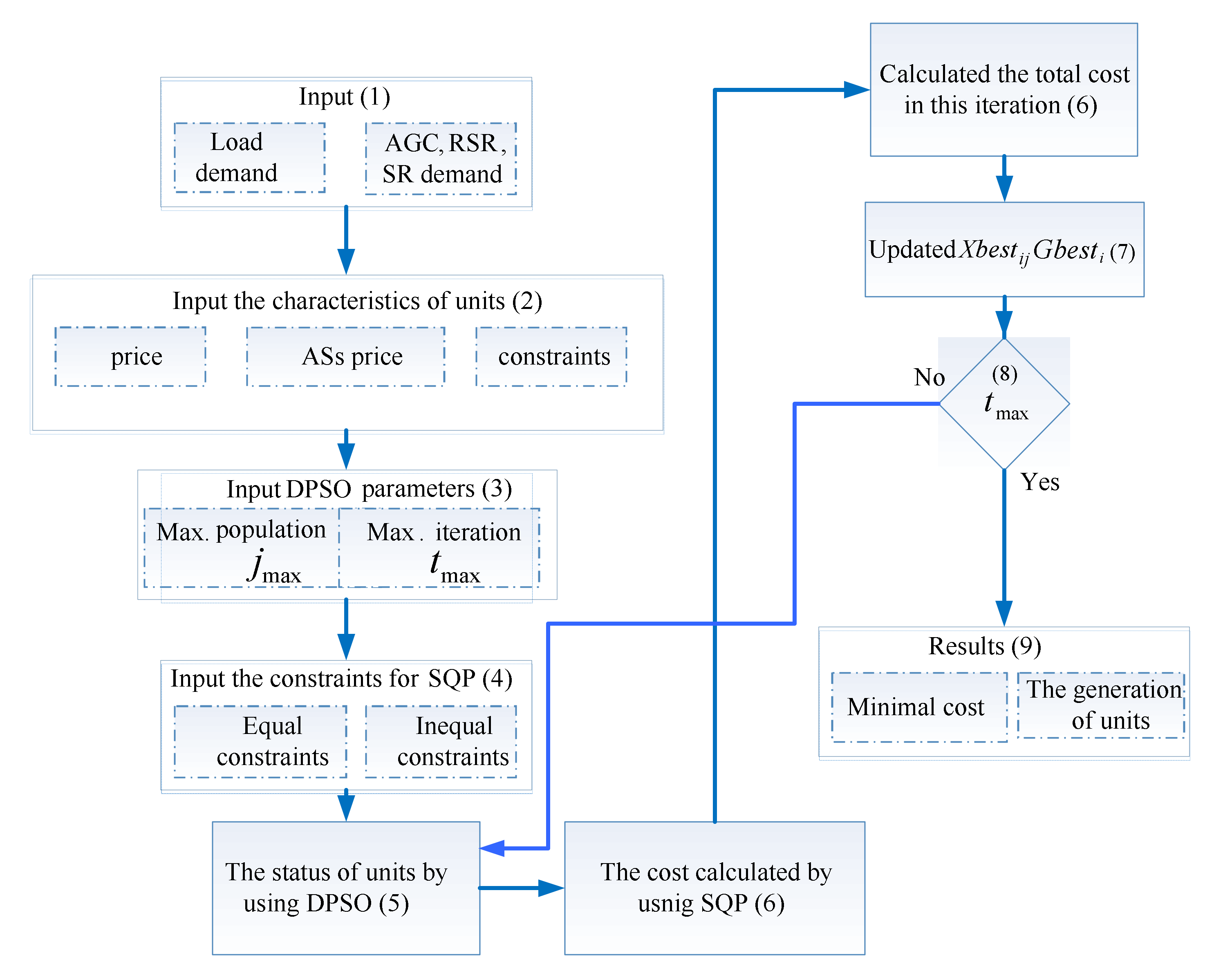
3.3. DPSO-SQP Implementation Procedure
- (1)
- Input the load demand, as well as the AGC, RSR, and SR demands on ancillary services.
- (2)
- Input the operating limits of the units in ancillary services and the costs of electric energy, AGC, RSR, and SR.
- (3)
- Set the maximum population size and maximum number of iterations of DPSO.
- (4)
- Import the equality and inequality constraints into the SQP program.
- (5)
- Initialize the search area, and set the initial position with a local random search.
- (6)
- Copy the initial position to the generated optimum particle position.
- (7)
- Use DPSO to solve the states of units in a state matrix.
- (8)
- Use SQP to compute the generation output of various units, and calculate the total cost.
- (9)
- Update the optimal solutions of and .
- (10)
- Go to (7) for the next generation.
- (11)
- If the preset maximum number of iterations is reached, iteration terminates, otherwise go to (5).
- (12)
- Export the minimum cost and the assigned generation output of various units, including electric energy, AGC, RSR, and SR.
4. Simulation Results
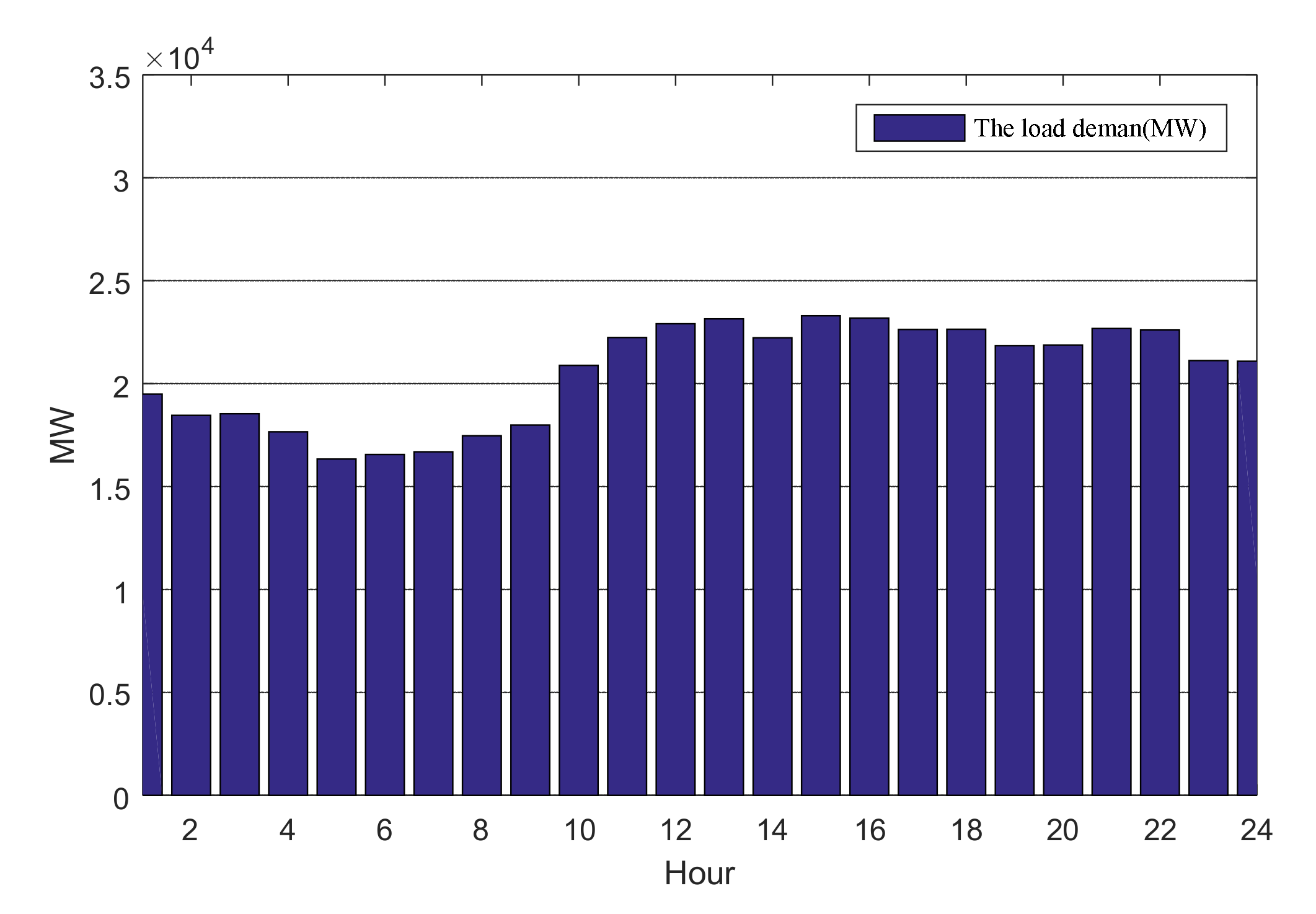
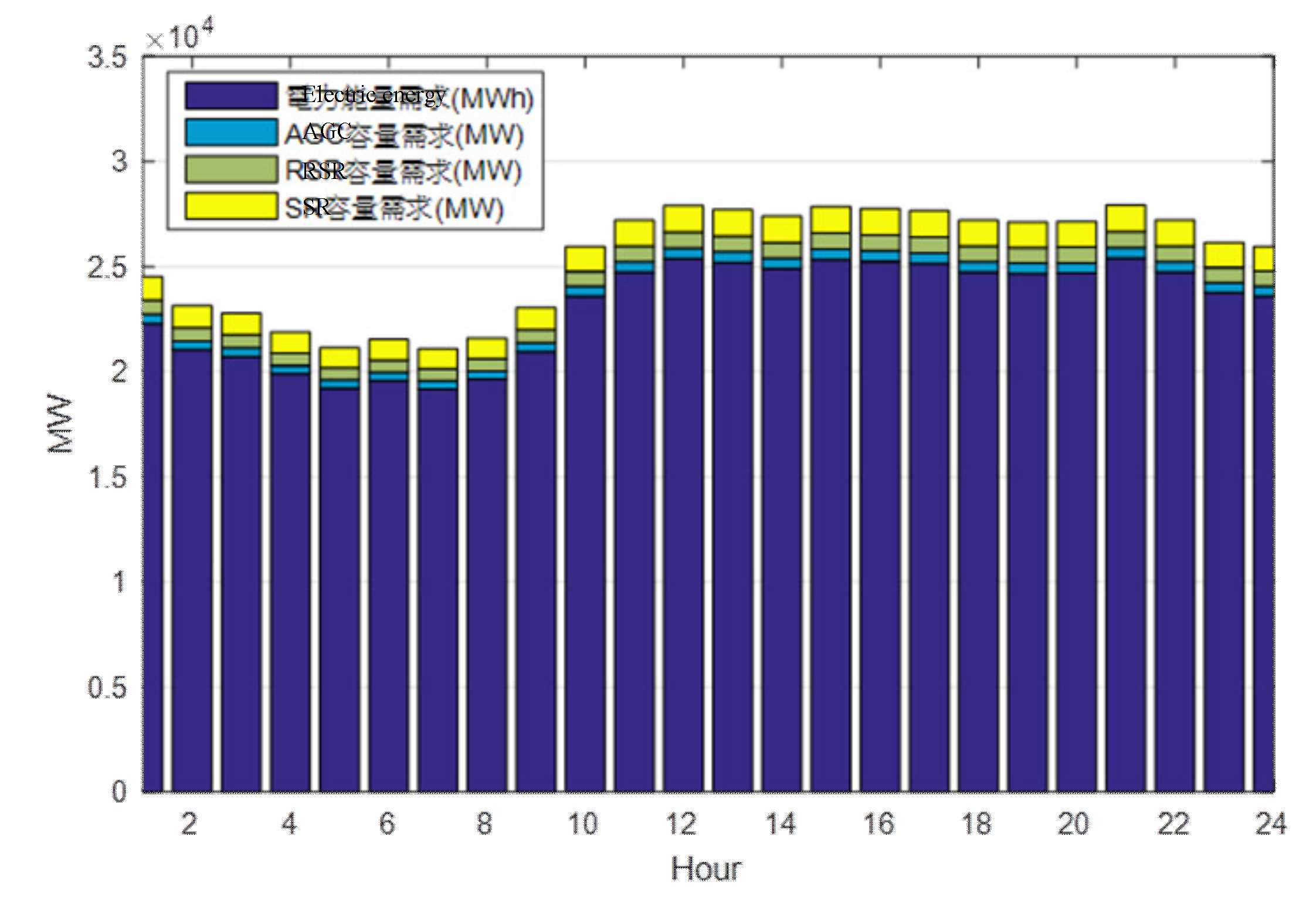
4.1. Unit Commitment with Ancillary Services during Non-Summer
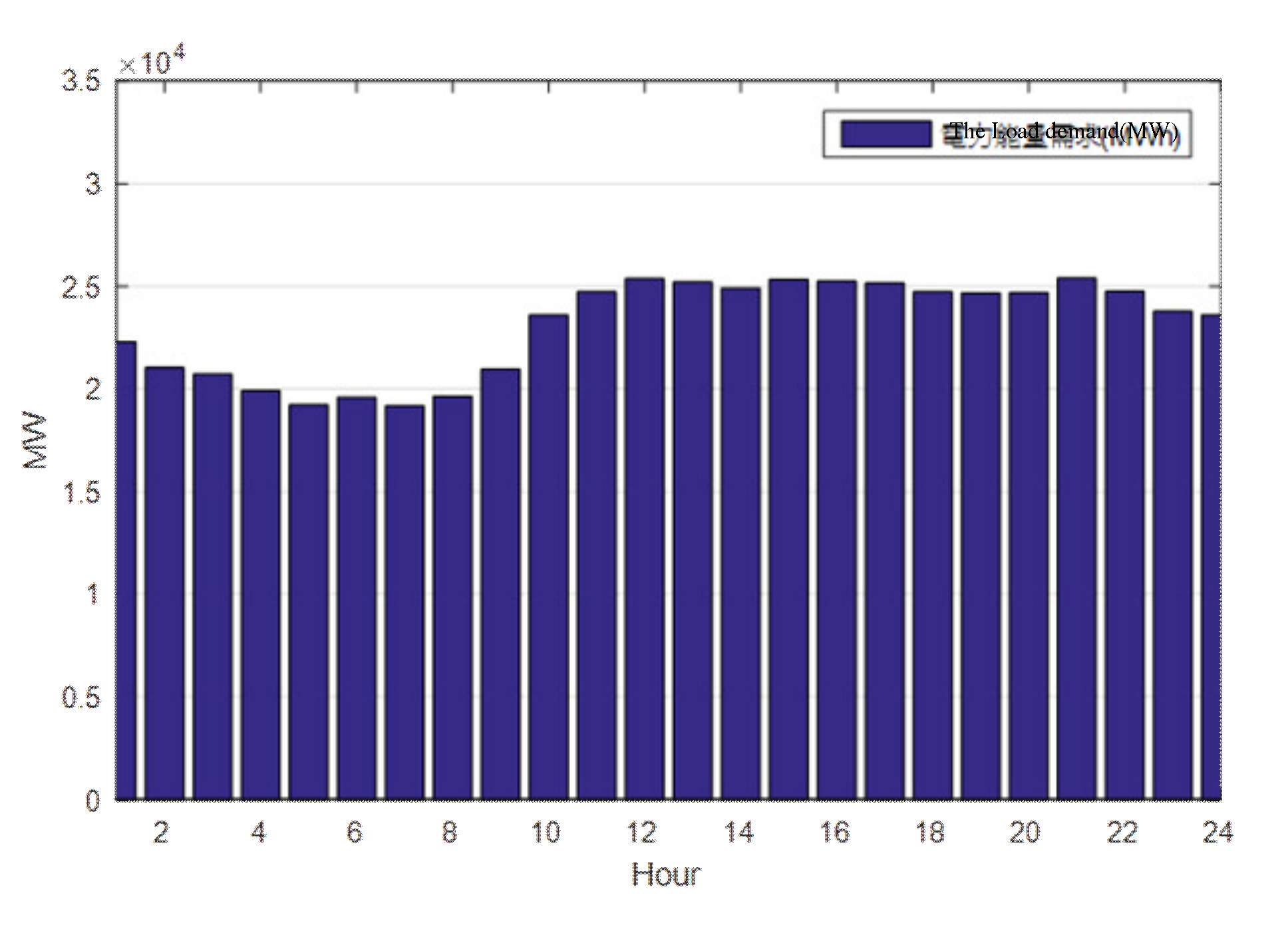
4.2. Unit Commitment in Summer
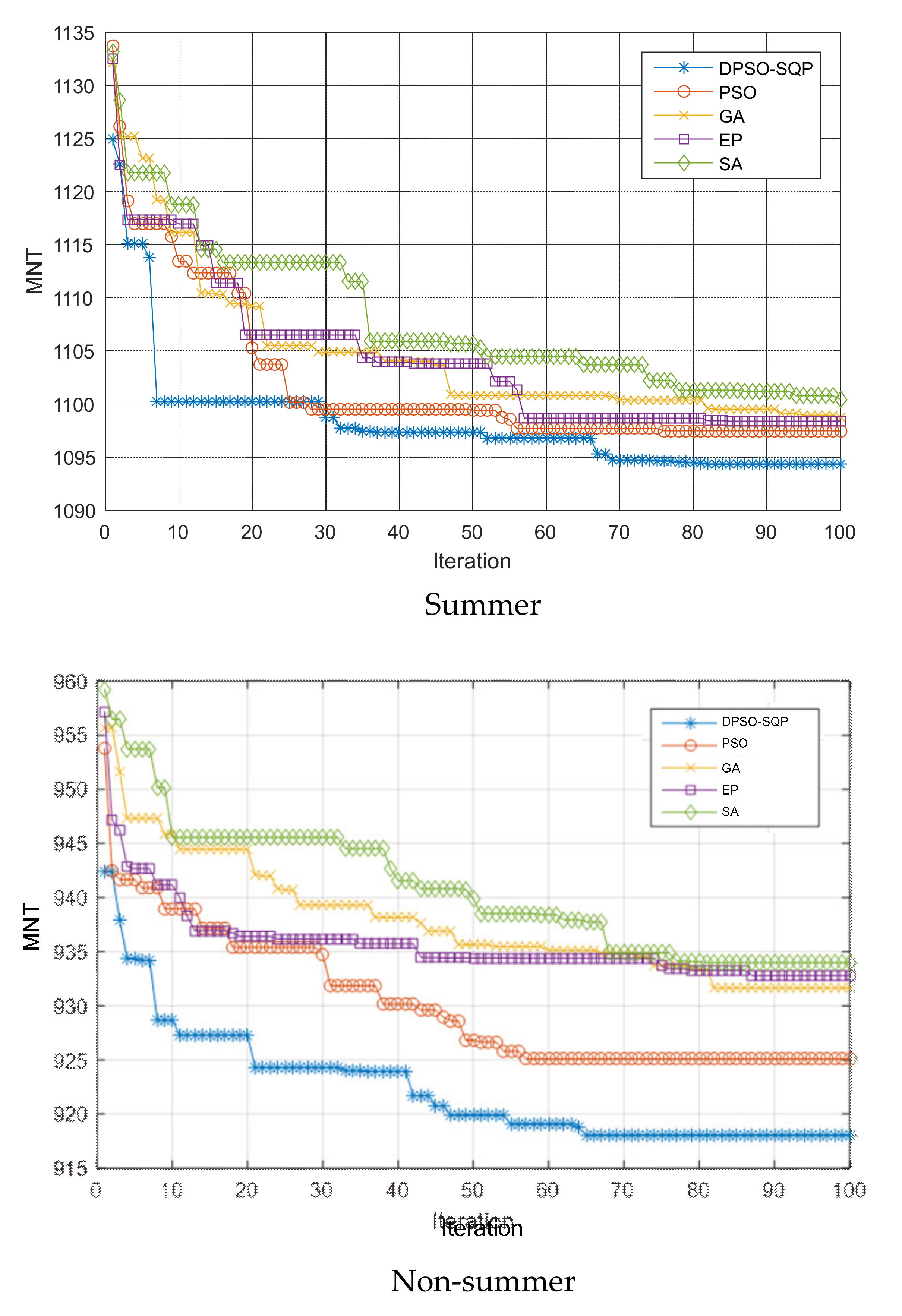
4.3. Convergent Characteristic Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Acronyms | |
| AGC | Automatic Generation Control |
| DPSO | Discrete Particle Swarm Optimization |
| EP | Evolutionary Programming |
| GA | Genetic Algorithm |
| IPPs | Independent Power Producers |
| PSO | Particle Swarm Optimization |
| RSR | Real Spinning Reserve |
| SQP | Sequential Quadratic Programming |
| SR | Supplemental Reserve |
| SA | Simulated Anneal |
| TPC | Taipower Company |
| Constraints | |
| AGC demand in the | |
| Demand reduction value of the -th unit within 3 min | |
| RSR demand in the -th time interval | |
| SR demand in the -th time interval | |
| Minimum up time of the -th unit | |
| Minimum down time of the -th unit | |
| Maximum/minimum power generation limitations of the -th unit | |
| AGC operation of -th unit participating in the -th time interval | |
| RSR operation of -th unit participating in the -th time interval | |
| SR operation of -th unit participating in the -th time interval | |
| Ramp up/down rate limitations of unit | |
| Start and stop time intervals of the continuous shutdown of the unit | |
| Start and stop time intervals of the continuous startup of the unit | |
| Demand rise value of the -th unit within 3 min | |
| Demand rise value of the -th unit within 30 min | |
| Demand rise value of the -th unit within 60 min | |
| Variables | |
| d | Each particle has a d dimension |
| Moving parameter of individual particle value updating | |
| Moving parameter of the particle following the overall value | |
| The fuel cost of unit | |
| The AGC cost of unit | |
| The RSR cost of unit | |
| The SR cost of unit in time interval | |
| The optimal solution in particle swarm after iteration | |
| The power generation of the -th unit in time interval | |
| Uniformly distributed random variables between 0 and 1 | |
| The startup cost | |
| The state of the units in time interval | |
| Velocity of particle | |
| Self-optimal solution of particle after iteration | |
| Position of particle in iteration |
References
- Glover, J.D.; Sarma, M.S. Power System Analysis and Design, 3rd ed.; PWS Publishing Co.: Boston, MA, USA, 1994. [Google Scholar]
- Shahidehpour, M.; Yamin, H.; Li, Z. Market Operations in Electric Power Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Isemonger, A.G. The evolving design of RTO ancillary service markets. Energy Policy 2009, 37, 150–157. [Google Scholar] [CrossRef]
- Sen, S.; Kothari, D.P. Optimal thermal generating unit commitment: A review. Int. J. Electr. Power Energy Syst. 1998, 20, 443–451. [Google Scholar] [CrossRef]
- The Platform for the Taipower Ancillary Service. 2021. Available online: https://billionwatts.com.tw/taipower-business (accessed on 5 June 2020).
- Yuan, X.; Ji, B.; Zhang, S.; Tian, H.; Hou, Y. A new approach for unit commitment problem via binary gravitational search algorithm. Appl. Soft Comput. 2014, 22, 249–260. [Google Scholar] [CrossRef]
- Li, Y.F.; Pedroni, N.; Zio, E. Memetic evolutionary multi-objective optimization method for environmental power unit commitment. IEEE Trans. Power Syst. 2013, 28, 2660–2669. [Google Scholar] [CrossRef]
- Trivedi, A.; Srinivasan, D.; Sharma, D.; Singh, C. Evolutionary multi-objective day-ahead thermal generation scheduling in uncertain environment. IEEE Trans. Power Syst. 2013, 28, 1345–1354. [Google Scholar] [CrossRef]
- Ghadi, M.J.; Baghramian, A.; Imani, M.H. An ICA based approach for solving profit based unit commitment problem market. Appl. Soft Comput. 2016, 38, 487–500. [Google Scholar] [CrossRef]
- Venkatesan, T.; Sanavullah, M.Y. SFLA approach to solve PBUC problem with emission limitation. Int. J. Electr. Power Energy Syst. 2013, 46, 1–9. [Google Scholar] [CrossRef]
- Canizes, B.; Soares, J.; Faria, F.; Vale, Z. Mixed integer non-linear programming and Artificial Neural Network based approach to ancillary services dispatch in competitive electricity markets. Appl. Energy 2013, 108, 261–270. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J. Comparison of security constrained economic dispatch formulations to incorporate reliability standards on demand response resources into Midwest ISO co-optimized energy and ancillary service market. Electr. Power Syst. Res. 2011, 81, 1786–1795. [Google Scholar] [CrossRef]
- Chen, Y.; Leonard, R.; Keyser, M.; Gardner, J. Development of Performance-Based Two-Part Regulating Reserve Compensation on MISO Energy and Ancillary Service Market. IEEE Trans. Power Syst. 2015, 30, 142–155. [Google Scholar] [CrossRef]
- Costa, A.L.; Costa, A. Energy and ancillary service dispatch through dynamic optimal power flow. Electr. Power Syst. Res. 2007, 77, 1047–1055. [Google Scholar] [CrossRef]
- Aghaei, J.; Alizadeh, M.I. Robust n–k contingency constrained unit commitment with ancillary service demand response program. IET Gener. Transm. Distrib. 2014, 8, 1928–1936. [Google Scholar] [CrossRef]
- Charalambous, A.; Hadjidemetriou, L.; Zacharia, L.; Bintoudi, A.D.; Tsolakis, A.C.; Tzovaras, D.; Kyriakides, E. Phase balancing and reactive power support services for Microgrid. Appl. Sci. 2019, 9, 5076. [Google Scholar] [CrossRef]
- Ku, T.T.; Lin, C.H.; Hsu, C.T.; Chen, C.S.; Liao, Z.Y.; Wang, S.D.; Chen, F.F. Enhancement of power system operation by renewable ancillary service. IEEE Trans. Ind. Appl. 2020, 56, 6150–6157. [Google Scholar] [CrossRef]
- Fu, R.; Wu, Y.; Wang, H.; Xie, J. A Distributed Control Strategy For Frequency Regulation In Smart Grids Based On The Consensus Protocol. Energies 2015, 8, 7930–7944. [Google Scholar] [CrossRef]
- Kim, Y.J.; Fuentes, E.; Norford, L.K. Experimental Study of Grid Frequency Regulation Ancillary Service of a Variable Speed Heat Pump. IEEE Trans. Power Syst. 2016, 31, 56. [Google Scholar] [CrossRef]
- Aragon, A.G.; Hernandez, J.H.T.; Alcaraz, G.G. Multi-stage Model for Voltage Control and Reactive Power Ancillary Services Allocation Costs in Electricity Markets. IEEE Lat. Am. Trans. 2015, 13, 2961–2970. [Google Scholar]
- Mingtao, Y.; Zhaoguang, H.; Froylan, S.; Ning, Z. Integrated Power Management of Conventional Units and Industrial Loads in China’s Ancillary Services Scheduling. Energies 2015, 8, 3955–3977. [Google Scholar]
- Menendez, J.; Fernandez, J.M.; Loredo, J. Economic feasibility of undergroud pumped storage hydropower plants providing ancillary service. Appl. Sci. 2020, 10, 3947. [Google Scholar] [CrossRef]
- Lin, C.C. The Quantitative Evaluation and Selection for Ancillary Services of AGC Generators. Master’s Thesis, National Taiwan Technical University, Taipei, Taiwan, 2006. [Google Scholar]
- Chen, Y.P. Cost Allocation of Transmission and Ancillary Service in a Deregulated Poqer System. Master’s Thesis, Ta-Tung University, Taipei, Taiwan, 2009. [Google Scholar]
- Vellasques, E.; Sabourin, R.; Granger, E. DS-DPSO: A dual surrogate approach for intelligent watermarking of bi-tonal document image streams. Expert Syst. Appl. 2013, 40, 5240–5259. [Google Scholar] [CrossRef]
- Rekiaites, G.V.; Ravinpran, A.; Ragsdell, K.M. Engineering Optimization Methods and Applications; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1983; pp. 371–402. [Google Scholar]
- Feng, Z.K.; Niu, J.Z.; Cheng, C.T.; Qin, H.; Jiang, Z.Q. Parallel multi-objective genetic algorithm for short-term economic environmental hydrothermal scheduling. Energies 2017, 10, 163. [Google Scholar] [CrossRef]
- Lau, T.W.; Chung, C.Y.; Wong, K.P.; Chung, T.S.; Ho, S.L. Quantum-inspired evolutionary algorithm approach for unit commitment. IEEE Trans. Power Syst. 2009, 24, 1503–1512. [Google Scholar] [CrossRef]
- Cheng, Z.; Xiong, R.; Wang, K.; Jiao, B. Optimal energy management strategy of a plug-in hybrid electric vehicle based on a particle swarm optimization algorithm. Energies 2015, 8, 3661–3678. [Google Scholar] [CrossRef]
- Wang, K.; Li, X.; Gao, L.; Li, P.; Gupta, S.M. A genetic simulated annealing algorithm for parallel partial disassembly line balancing problem. Appl. Soft Comput. 2021, 107, 107404. [Google Scholar] [CrossRef]
- Wang, Y.H. The Unit Commitment Planning in a Day-Ahead Power Market. Master’s Thesis, Cheng-Shiu University, Kaohsiung, Taiwan, 2017. [Google Scholar]

| Type of Unit | Electric Energy (MWh) | AGC Demand (MWh) | RSR Demand (MWh) | SR Demand (MWh) | |
|---|---|---|---|---|---|
| TPC | Coal-fired unit | 182,400 | 0 | 0 | 0 |
| Gas-fired unit | 204,157 | 5710 | 4943 | 7803 | |
| Oil-fired unit | 3240 | 140 | 0 | 42 | |
| IPP | Coal-fired unit | 74,348 | 0 | 0 | 0 |
| Gas-fired unit | 29,381 | 3995 | 9847 | 16,818 | |
| Total | 493,526 | 9845 | 14,790 | 24,663 | |
| Type of Unit | Electric Energy | AGC Demand | RSR Demand | SR Demand | |
|---|---|---|---|---|---|
| TPC | Coal-fired unit | 36.96% | 0.00% | 0.00% | 0.00% |
| Gas-fired unit | 41.37% | 58.00% | 33.42% | 31.64% | |
| Oil-fired unit | 0.66% | 1.42% | 0.00% | 0.17% | |
| IPP | Coal-fired unit | 15.06% | 0.00% | 0.00% | 0.00% |
| Gas-fired unit | 5.95% | 40.58% | 66.58% | 68.19% | |
| Total | 100.00% | 100.00% | 100.00% | 100.00% | |
| Type of Unit | Electric Energy (MWh) | AGC Demand (MWh) | RSR Demand (MWh) | SR Demand (MWh) | |
|---|---|---|---|---|---|
| TPC | Coal-fired unit | 182,400 | 0 | 0 | 0 |
| Gas-fired unit | 231,638 | 3147 | 4231 | 6580 | |
| Oil-fired unit | 11,895 | 1459 | 1823 | 14,869 | |
| IPP | Coal-fired unit | 74,350 | 0 | 0 | 0 |
| Gas-fired unit | 53,451 | 6435 | 10,551 | 6232 | |
| Total | 553,734 | 11,041 | 16,605 | 27,681 | |
| Type of Unit | Electric Energy | AGC Demand | RSR Demand | SR Demand | |
|---|---|---|---|---|---|
| TPC | Coal-fired unit | 32.94% | 0.00% | 0.00% | 0.00% |
| Gas-fired unit | 41.83% | 28.50% | 25.48% | 23.77% | |
| Oil-fired unit | 2.15% | 13.21% | 10.98% | 53.72% | |
| IPP | Coal-fired unit | 13.43% | 0.00% | 0.00% | 0.00% |
| Gas-fired unit | 9.65% | 58.28% | 63.54% | 22.51% | |
| Total | 100.00% | 100.00% | 100.00% | 100.00% | |
| Non-Summer | Summer | |
|---|---|---|
| Unit commitment with ancillary service | MNT 918.020 | MNT 1094.307 |
| Unit commitment without ancillary service | MNT 900.081 | MNT 1057.450 |
| Gap | MNT 17.939 | MNT 36.857 |
| Summer (NTD) | Non-Summer (NTD) | |
|---|---|---|
| DPSO-SQP | 1,094,306.618 | 918,019.664 |
| PSO | 1,097,463.111 | 925,090.938 |
| GA | 1,098,729.402 | 931,661.242 |
| EP | 1,098,374.348 | 932,800.777 |
| SA | 1,100,455.785 | 933,989.690 |
| Method | DPSO-SQP | PSO | SA | GA | EP | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Item | AET | NRO | AET | NRO | AET | NRO | AET | NRO | AET | NRO | |
| Case | |||||||||||
| Summer | 0.3104 | 36 | 0.3268 | 32 | 0.1828 | 4 | 0.5083 | 2 | 0.5094 | 10 | |
| Non-summer | 4.6384 | 28 | 5.7441 | 24 | 10.956 | 6 | 11.1013 | 5 | 8.6657 | 6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, W.-M.; Yang, C.-Y.; Tsai, M.-T.; Wang, Y.-H. Unit Commitment with Ancillary Services in a Day-Ahead Power Market. Appl. Sci. 2021, 11, 5454. https://doi.org/10.3390/app11125454
Lin W-M, Yang C-Y, Tsai M-T, Wang Y-H. Unit Commitment with Ancillary Services in a Day-Ahead Power Market. Applied Sciences. 2021; 11(12):5454. https://doi.org/10.3390/app11125454
Chicago/Turabian StyleLin, Whei-Min, Chung-Yuen Yang, Ming-Tang Tsai, and Yun-Hai Wang. 2021. "Unit Commitment with Ancillary Services in a Day-Ahead Power Market" Applied Sciences 11, no. 12: 5454. https://doi.org/10.3390/app11125454
APA StyleLin, W.-M., Yang, C.-Y., Tsai, M.-T., & Wang, Y.-H. (2021). Unit Commitment with Ancillary Services in a Day-Ahead Power Market. Applied Sciences, 11(12), 5454. https://doi.org/10.3390/app11125454





