Spindle Thermal Error Prediction Based on LSTM Deep Learning for a CNC Machine Tool
Abstract
1. Introduction
2. Materials and Methods
2.1. ITP Analysis and Experimental Design
2.2. Analysis and Selection of the Temperature Rise Reference Point
2.3. KTP Selection Method
- Step 1:
- Define the clustering threshold ρ.
- Step 2:
- Obtain the correlation coefficient CZ(E, ΔT) between the temperature difference of each unclassified IPT, ΔT, and the actual spindle displacement in the z-direction E.
- Step 3:
- Among the unclassified IPTs, select the temperature point that is the most correlated with the spindle thermal displacement and define it as cluster centroid Ts.
- Step 4:
- Calculate the correlation coefficient CT(Ts, ΔT) between cluster centroid Ts and all other unclassified IPTs, individually.
- Step 5:
- If the correlation coefficient CT(Ts, ΔT) of the unclassified IPTs is larger than the clustering threshold ρ, then they are grouped in a cluster with cluster centroid Ts. Meanwhile, import cluster centroid Ts into a candidate KTP set TK.
- Step 6:
- Repeat Steps 3–5 until all the n–1 ITPs are grouped, resulting in the final candidate KTP set TK = {tk1, tk2, …, tkv}, where v denotes the total number of groups.
- Step 7:
- In the candidate KTP set TK, select KTPs from tk1 to tkr, where r is initially set to 1. Next, establish the prediction model of the thermal displacement of the spindle, the details of which are specified in Section 2.4 and Section 2.5.
- Step 8:
- Use the data from the high-speed spindle rotation experiment to calculate the RMSE between the estimated values and actual values of spindle thermal displacement.
- Step 9:
- Add 1 to r and repeat Steps 6 and 8 until the RMSEs are obtained for all the KTP combinations.
- Step 10:
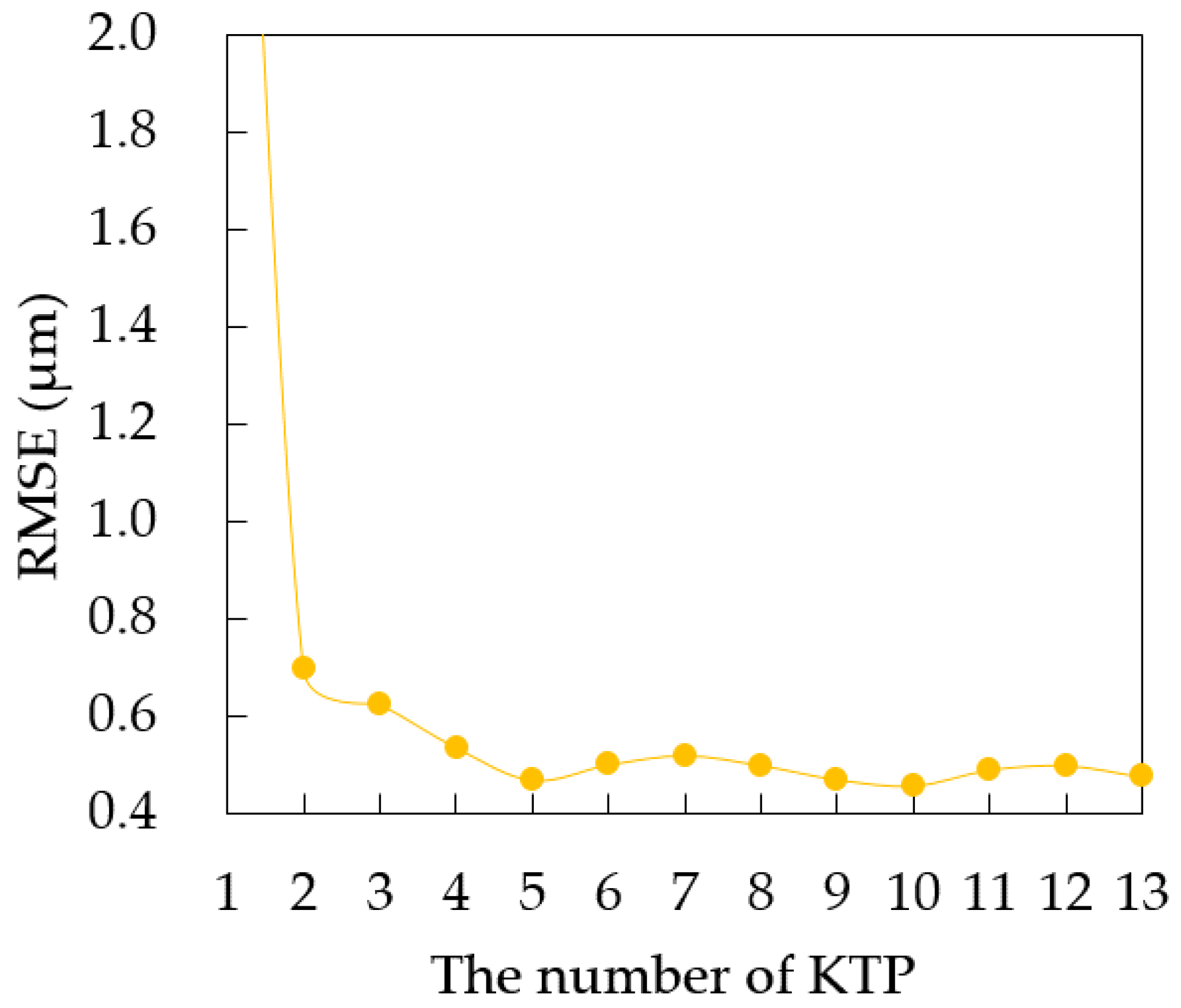
- Adopt the elbow method [33] to plot a graph, in which the x-axis denotes the number of KTP c and the y-axis denotes the RMSE.
- Step 11:
- Identify where the line in a graph is curved without an obvious decrease and relate the point (i.e., the elbow of the curve) to the corresponding c value (i.e., the point where all RMSEs have nearly converged). This value c was defined as the optimal number of KTPs.
2.4. Definition and Normalization of the Modeling Data
2.5. Establishment of a Spindle Thermal Displacement Model in the Z-Direction
3. Experimental Results
3.1. Environment Establishment and Experimental Result Analysis
3.2. Analysis of KTP Combinations
3.3. Model Establishment and Modeling Effect Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| ITP | Initial Temperature Point. |
| KTP | Key Temperature Point. |
| BPNN | BackPropagation Neural Network. |
| RMSE | Root Mean Square Errors |
| ANN | Artificial Neural Network. |
| LSTM | Long Short-Term Memory. |
| MLR | Multiple Linear Regression. |
| RNN | Recurrent Neural Network |
| n | The number of ITPs. |
| ΔT | The temperature differences. |
| The average of temperature. | |
| CZ | The correlation coefficient between ΔT of each ITP and the spindle displacement in the z-direction. |
| A | The number of data. |
| Z | The actual spindle displacement in the z-direction. |
| The average of spindle displacement in the z-direction. | |
| y | The estimated output from the estimation model. |
| Tb | The reference point of the temperature rise. |
| Ts | The cluster centroid. |
| CT | The correlation coefficient between Ts of cluster centroid and the other unclassified IPTs. |
| ρ | The clustering threshold. |
| v | The number of groups. |
| r | The number of KTP. |
| dmax, dmin | The maximum and minimum value in the specified data. |
| xt | The LSTM unit input value of the tth datum. |
| it, Ui, Wi, bi | Denoted as the output, input weight, previous output weight, and bias of the input gate. |
| ft, Uf, Wf, bf | Denoted as the output, input weight, previous output weight, and bias of the forget gate. |
| ot, Uo, Wo, bo | Denoted as the output, input weight, previous output weight, and bias of the output gate. |
| Denoted the current neural output. | |
| Ug, Wg, bg | Denoted as the output, input weight, previous output weight, and bias of the neural. |
| ct | The memory cell output. |
| ht | The LSTM unit output. |
| ITPs | Absolute Cartesian Coordinates (mm) | ITPs | Absolute Cartesian Coordinates (mm) | ITPs | Absolute Cartesian Coordinates (mm) |
|---|---|---|---|---|---|
| T0 | (0, 0, 0) | T16 | (140, −64, 260) | T32 | (0, 280, 270) |
| T1 | (−150, 269, 1040) | T17 | (140, 64, 420) | T33 | (0, −280, 270) |
| T2 | (−150, 269, 780) | T18 | (140, −64, 420) | T34 | (−716, −327, 1190) |
| T3 | (−111, −186, 1040) | T19 | (−616, 327, 840) | T35 | (−616, −780, 1080) |
| T4 | (−111, −186, 780) | T20 | (−616, 327, 600) | T36 | (−185, −554, 70) |
| T5 | (140, 0, 740) | T21 | (−616, 0, 840) | T37 | (−434, 455, 0) |
| T6 | (0, 140, 550) | T22 | (−616, 0, 600) | T38 | (−434, 686, 0) |
| T7 | (140, 0, 420) | T23 | (−616, −327, 840) | T39 | (−434, −686, 0) |
| T8 | (0, −140, 550) | T24 | (−616, −327, 600) | T40 | (−434, −455, 0) |
| T9 | (140, 0, 1180) | T25 | (−616, −764, 830) | T41 | (−388, −217, 580) |
| T10 | (0, 140, 1120) | T26 | (−616, −552, 610) | T42 | (−388, 0, 580) |
| T11 | (−180, 0, 1200) | T27 | (−616, −552, 300) | T43 | (−388, 217, 580) |
| T12 | (0, −140, 1120) | T28 | (−275, 556, 990) | T44 | (−265, 0, 580) |
| T13 | (140, 0, 190) | T29 | (−275, 0, 990) | T45 | (−265, 217, 580) |
| T14 | (140, 0, 1610) | T30 | (−275, −556, 990) | T46 | (1,000, 686, −180) |
| T15 | (140, 64, 260) | T31 | (−716, −327, 1560) | T47 | (140, −64, 380) |
References
- Bryan, J. International Status of Thermal Error Research. CIRP Ann. 1990, 28, 645–656. [Google Scholar] [CrossRef]
- Mayr, J.; Jedrzejewski, J.; Uhlmann, E.; Donmez, M.A.; Knapp, W.; Hartig, F.; Wendt, K.; Moriwaki, T.; Shore, P.; Schmit, R.; et al. Thermal issues in machine tools. CIRP Ann. 2012, 61, 771–791. [Google Scholar] [CrossRef]
- Postlethwaite, S.R.; Allen, J.P.; Ford, D.G. The use of thermal imaging, temperature and distortion models for machine tool thermal error reduction. Proc. Inst. Mech. Eng. 1998, 212, 671–679. [Google Scholar] [CrossRef]
- Kim, H.S.; Jeong, K.S.; Lee, D.G. Design and manufacture of a three-axis ultra-precision CNC grinding machine. J. Mater. Process. Technol. 1997, 71, 258–266. [Google Scholar] [CrossRef]
- Sugishita, H.; Nishiyama, H.; Nagayasu, O.; Shin-nou, T.; Sato, H.; O.-hori, M. Development of Concrete Machining Center and Identification of the Dynamic and the Thermal Structural Behavior. CIRP Ann. 1988, 37, 377–380. [Google Scholar] [CrossRef]
- Spur, G.; Hoffmann, E.; Paluncic, Z.; Benzinger, K.; Nymoen, H. Thermal Behaviour Optimization of Machine Tools. CIRP Ann. 1988, 37, 401–405. [Google Scholar] [CrossRef]
- Tanabe, I.; Takada, K.; Tsutsumi, M. Thermal deformation of machine tool structures using epoxy resin concrete. In Proceedings of the International Machine Tool Design and Research Conference, Manchester, UK, 17–18 September 1986; pp. 245–252. [Google Scholar]
- Sun, L.; Ren, M.; Hong, H.; Yin, Y. Thermal error reduction based on thermodynamics structure optimization method for an ultra-precision machine tool. Int. J. Adv. Manuf. Technol. 2017, 88, 1267–1277. [Google Scholar] [CrossRef]
- Li, K.Y.; Luo, W.J.; Wei, S.J. Machining Accuracy Enhancement of a Machine Tool by a Cooling Channel Design for a Built-in Spindle. Appl. Sci. 2020, 10, 3991. [Google Scholar] [CrossRef]
- Mori, K.; Bergmann, B.; Kono, D.; Denkena, B.; Matsubara, A. Energy efficiency improvement of machine tool spindle cooling system with on–off control. CIRP J. Manuf. Sci. Technol. 2019, 25, 14–21. [Google Scholar] [CrossRef]
- Shi, H.; He, B.; Yue, Y.; Min, C.; Mei, X. Cooling effect and temperature regulation of oil cooling system for ball screw feed drive system of precision machine tool. Appl. Therm. Eng. 2019, 161, 114150. [Google Scholar] [CrossRef]
- Grama, S.N.; Badhe, A.N. A model-based cooling strategy for motorized spindle to reduce thermal errors. Int. J. Mach. Tools Manuf. 2018, 132, 3–16. [Google Scholar] [CrossRef]
- Ramesh, R.; Mannan, M.A. Error compensation in machine tools—A review Part II. Int. J. Mach. Tools Manuf. 2000, 40, 1257–1284. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, W.; Du, C.; Liu, H.; Zhang, J. Dynamic modeling and analysis for gantry-type machine tools considering the effect of axis coupling force on the slider–guide joints’stiffness. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2016, 230, 2036–2046. [Google Scholar] [CrossRef]
- Shen, L.; Ding, X.; Li, T.; Kong, X.; Dong, X. Structural dynamic design optimization and experimental verification of a machine tool. Int. J. Adv. Manuf. Technol. 2019, 104, 3773–3786. [Google Scholar] [CrossRef]
- Lv, Y.; Li, C.; Tang, Y.; Chen, X.; Zhao, X. Towards Lightweight Spindle of CNC Lathe Using Structural Optimization Design for Energy Saving. In Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 220–225. [Google Scholar]
- Li, Y.; Shi, H.; Ji, S.; Liang, F. Thermal Positioning Error Modeling of Servo Axis Based on Empirical Modeling Method. Micromachines 2021, 12, 201. [Google Scholar] [CrossRef]
- Lin, C.J.; Su, X.Y.; Hu, C.H.; Jian, B.L.; Wu, L.W.; Yau, H.T. A Linear Regression Thermal Displacement Lathe Spindle Model. Energies 2020, 13, 949. [Google Scholar] [CrossRef]
- Chen, T.C.; Chang, C.J.; Hung, J.P.; Lee, R.M.; Wang, C.C. Real-Time Compensation for Thermal Errors of the Milling Machine. Appl. Sci. 2016, 6, 101. [Google Scholar] [CrossRef]
- Li, F.; Li, T.; Wang, H.; Jiang, Y. A Temperature Sensor Clustering Method for Thermal Error Modeling of Heavy Milling Machine Tools. Appl. Sci. 2017, 7, 82. [Google Scholar] [CrossRef]
- Miao, E.; Liu, Y.; Liu, H.; Gao, Z.; Li, W. Study on the effects of changes in temperature-sensitive points on thermal error compensation model for CNC machine tool. Int. J. Mach. Tools Manuf. 2015, 97, 50–59. [Google Scholar] [CrossRef]
- Liu, H.; Miao, E.; Wei, X.Y.; Zhuang, X.D. Robust modeling method for thermal error of CNC machine tools based on ridge regression algorithm. Int. J. Mach. Tools Manuf. 2017, 113, 35–48. [Google Scholar] [CrossRef]
- Liu, H.; Miao, E.; Zhuang, X.; Wei, X. Thermal error robust modeling method for CNC machine tools based on a split unbiased estimation algorithm. Int. J. Precis. Eng. 2018, 51, 169–175. [Google Scholar] [CrossRef]
- Pozevalkin, V.; Parfenov, V.; Polyakov, N. Approximation of machine tool experimental thermal characteristics by neural network. J. Phys. Conf. Ser. 2019, 1–6. [Google Scholar] [CrossRef]
- Jian, B.L.; Wang, C.C.; Hsieh, C.T.; Kuo, Y.P.; Houng, M.C.; Yau, H.T. Predicting spindle displacement caused by heat using the general regression neural network. Int. J. Adv. Manuf. Technol. 2019, 104, 4665–4674. [Google Scholar] [CrossRef]
- Jian, B.L.; Guo, Y.S.; Hu, C.H.; Wu, L.W.; Yau, H.T. Prediction of Spindle Thermal Deformation and Displacement Using Back Propagation Neural Network. Sens. Mater. 2020, 32, 431–445. [Google Scholar] [CrossRef]
- Reddy, T.N.; Shanmugaraj, V.; Vinod, P.; Krishna, S.G. Real-time Thermal Error Compensation Strategy for Precision Machine tools. Mater. Today Proc. 2020, 22, 2386–2396. [Google Scholar] [CrossRef]
- Tian, Y.; Pan, G. An Unsupervised Regularization and Dropout based Deep Neural Network and Its Application for Thermal Error Prediction. Appl. Sci. 2020, 10, 2870. [Google Scholar] [CrossRef]
- Yin, Q.; Tan, F.; Chen, H.; Yin, G. Spindle thermal error modeling based on selective ensemble BP neural networks. Int. J. Adv. Manuf. Technol. 2019, 101, 1699–1713. [Google Scholar] [CrossRef]
- Zhou, Z.; Hu, J.; Liu, Q.; Lou, P.; Yan, J.; Hu, J.; Gui, L. The selection of key temperature measurement points for thermal error modeling of heavy-duty computer numerical control machine tools with density peaks clustering. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar] [CrossRef]
- Lou, P.; Liu, N.; Chen, Y.; Liu, Q.; Zhou, Z. The selection of key temperature measuring points for the compensation of thermal errors of CNC machining tools. Int. J. Manuf. Res. 2017, 12, 338–350. [Google Scholar] [CrossRef]
- Abdulshahed, A.M.; Longstaff, A.P.; Fletcher, S. The application of ANFIS prediction models for thermal error compensation on CNC machine tools. Appl. Soft Comput. 2015, 27, 158–168. [Google Scholar] [CrossRef]
- Kodinariya, T.M.; Makwana, P.R. Review on determining number of Cluster in K-Means Clustering. Int. J. Adv. Res. Comput. Sci. Manag. Stud. 2013, 1, 90–95. [Google Scholar]
- ISO. Test Code for Machine Tools-Part 3: Determination of Thermal Effects, Standard ISO/FDIS 230-3; International Organization for Standardization: Geneva, Switzerland, 2001. [Google Scholar]
- OMRON Corporation. Available online: https://automation.omron.com/en/us/products/family/ZX-E (accessed on 21 May 2021).
- MST Corporation. Available online: http://teknikatools.myfactory.space/mk_urun_pdf/2017121391131.pdf (accessed on 20 May 2021).
- Zhanga, C.; Gaoa, F.; Li, Y. Thermal error characteristic analysis and modeling for machine tools due to time varying environmental temperature. Precis. Eng. 2017, 47, 231–238. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W.; Lan, S.; Ni, J.; Wu, W.; Lu, B. A review on spindle thermal error compensation in machine Tools. Int. J. Mach. Tools Manuf. 2015, 95, 20–38. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]


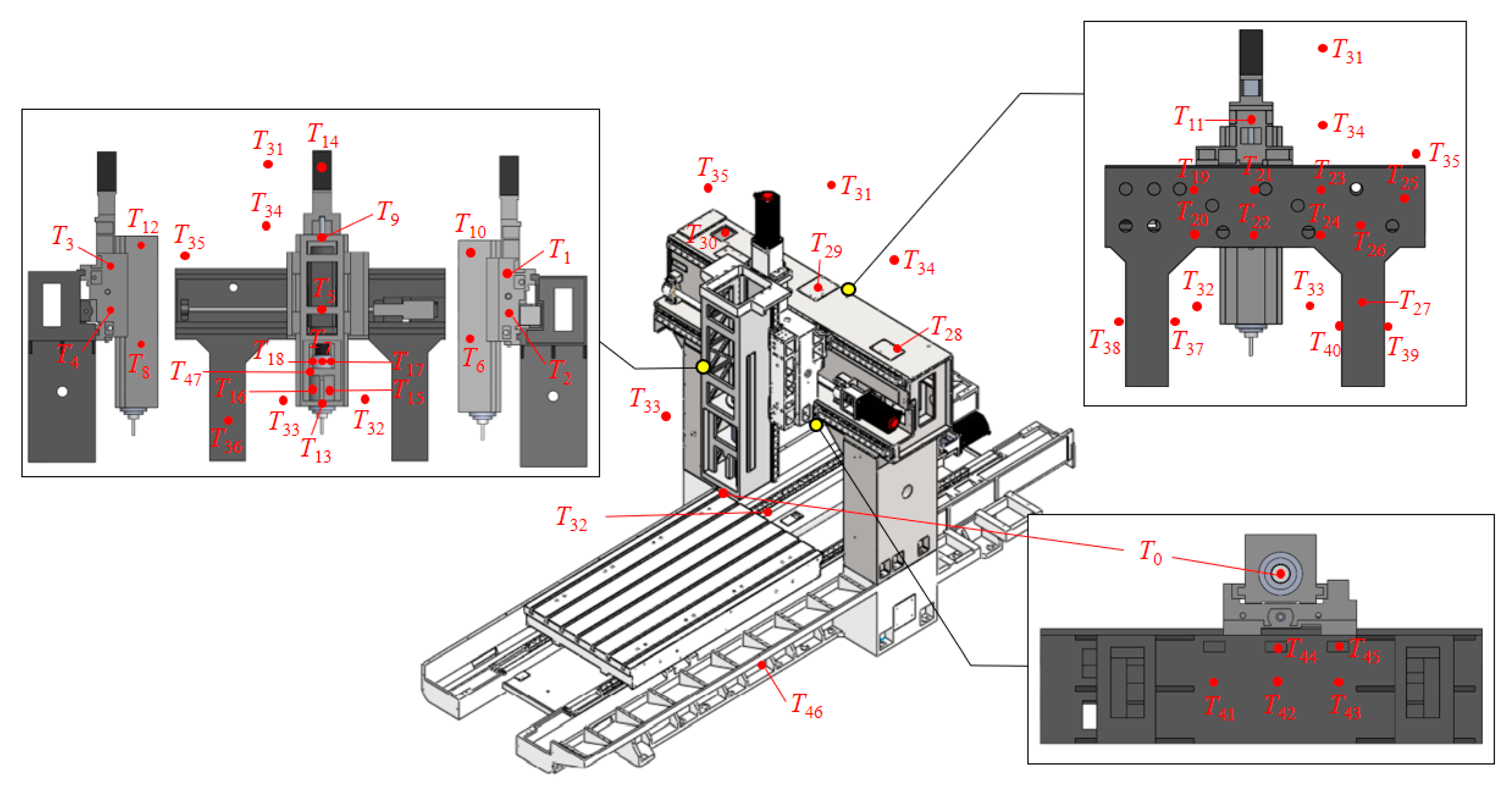



| Position on the Machining Center | Initial Temperature Points (ITPs) |
|---|---|
| Spindle | T1, T2, …, T18 |
| Behind the cross beam | T19, T20, …, T27 |
| Above the cross beam | T28, T29, T30 |
| Environmental temperature | T31, T32, T33, T34, T35 |
| Column | T36, T37, T38, T39, T40 |
| Below the cross beam | T41, T42, T43, T44, T45 |
| Base | T46 |
| Oil chiller inlet | T47 |
| Temperature Point | Variance |
|---|---|
| T46 | 0.491 |
| T39 | 0.532 |
| T36 | 0.535 |
| T40 | 0.573 |
| T19 | 0.586 |
| T20 | 0.591 |
| T43 | 0.593 |
| T28 | 0.596 |
| T34 | 0.601 |
| T2 | 0.606 |
| ITP | Correlation Coefficient Cz |
|---|---|
| T17 | −0.959 |
| T7 | −0.957 |
| T18 | −0.956 |
| T5 | −0.911 |
| T9 | −0.890 |
| ITP | Correlation Coefficient CT |
|---|---|
| T18 | 0.999 |
| T7 | 0.993 |
| T5 | 0.965 |
| T6 | 0.958 |
| T8 | 0.951 |
| T15 | 0.899 |
| T9 | 0.886 |
| T10 | 0.880 |
| T16 | 0.852 |
| T21 | 0.830 |
| ITP | Correlation Coefficient Cz |
|---|---|
| T9 | −0.890 |
| T15 | −0.883 |
| T10 | −0.871 |
| T27 | −0.851 |
| T23 | −0.842 |
| T26 | −0.830 |
| T14 | −0.807 |
| T25 | −0.796 |
| T34 | −0.788 |
| T21 | −0.785 |
| ITP | Correlation Coefficient CT |
|---|---|
| T10 | 0.995 |
| T15 | 0.993 |
| T23 | 0.945 |
| T21 | 0.943 |
| T34 | 0.926 |
| T25 | 0.922 |
| T38 | 0.921 |
| T29 | 0.920 |
| T26 | 0.917 |
| T24 | 0.909 |
| T3 | 0.908 |
| T19 | 0.900 |
| T27 | 0.898 |
| T14 | 0.894 |
| T35 | 0.888 |
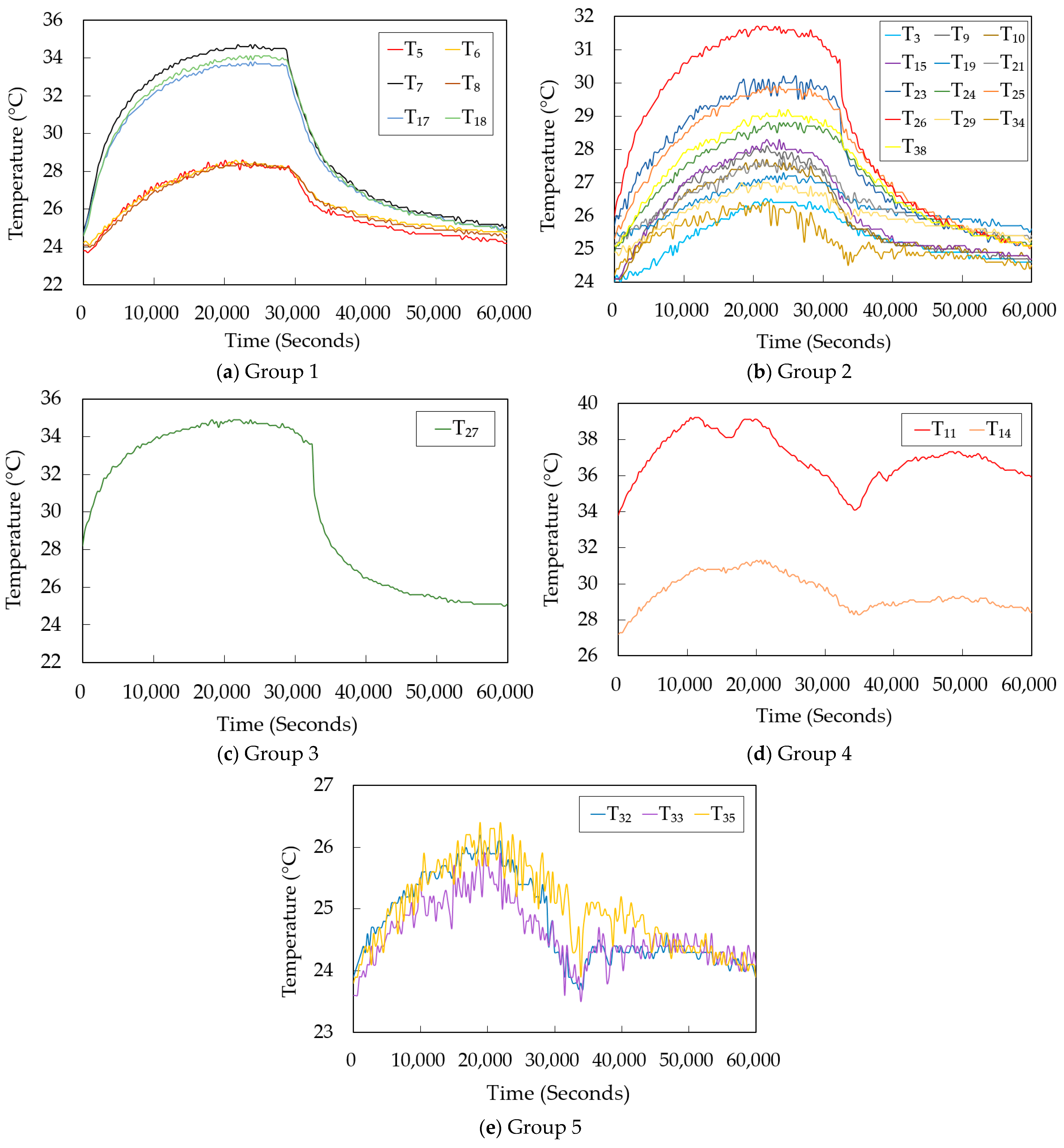
| Group | ITPs | Key Temperature Point (KTP) |
|---|---|---|
| 1 | T5, T6, T7, T8, T17, T18 | T17 |
| 2 | T3, T9, T10, T15, T19, T21, T23, T24, T25, T26, T29, T34, T38 | T9 |
| 3 | T27 | T27 |
| 4 | T11, T14 | T14 |
| 5 | T32, T33, T35 | T32 |
| 6 | T16, T13, T12, | T16 |
| 7 | T4, T20, T22,T28, T30, T37, T40, T41 | T37 |
| 8 | T1, T2 | T1 |
| 9 | T31 | T31 |
| 10 | T47 | T47 |
| 11 | T42, T43, T44, T45 | T42 |
| 12 | T39 | T39 |
| 13 | T36 | T36 |
| Spindle Speed | MLR | BPNN | LSTM |
|---|---|---|---|
| 3000 rpm | 2.716 µm | 0.690 µm | 0.529 µm |
| 6000 rpm | 3.792 µm | 0.828 µm | 0.554 µm |
| 9000 rpm | 4.966 µm | 0.958 µm | 0.625 µm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.-C.; Li, K.-Y.; Tsai, Y.-C. Spindle Thermal Error Prediction Based on LSTM Deep Learning for a CNC Machine Tool. Appl. Sci. 2021, 11, 5444. https://doi.org/10.3390/app11125444
Liu Y-C, Li K-Y, Tsai Y-C. Spindle Thermal Error Prediction Based on LSTM Deep Learning for a CNC Machine Tool. Applied Sciences. 2021; 11(12):5444. https://doi.org/10.3390/app11125444
Chicago/Turabian StyleLiu, Yu-Chi, Kun-Ying Li, and Yao-Cheng Tsai. 2021. "Spindle Thermal Error Prediction Based on LSTM Deep Learning for a CNC Machine Tool" Applied Sciences 11, no. 12: 5444. https://doi.org/10.3390/app11125444
APA StyleLiu, Y.-C., Li, K.-Y., & Tsai, Y.-C. (2021). Spindle Thermal Error Prediction Based on LSTM Deep Learning for a CNC Machine Tool. Applied Sciences, 11(12), 5444. https://doi.org/10.3390/app11125444






