1. Introduction
Bladed-disk vibration has been studied by researchers and designers for more than half a century given the risks posed to turbomachineries, such as aeronautical engines and gas and steam turbines for energy production [
1,
2]. Vibration issues can jeopardize the reliable design of these components, leading, in the worst cases, to catastrophic HCF failures. In this context, an accurate aeromechanical design able to prevent vibration risk is thus required to avoid or reduce the vibration amplitudes of components mainly due to forced response or flutter phenomena [
3]. Despite all of the progress made in this field, the design of more robust and safer bladed disks with respect to HCF vibration is still a challenging task for the designers.
Thanks to the increase of computing resources, more accurate computational methods for aeromechanical study have been applied to a wider part of turbomachinery modules. Such methods are implemented, for instance, to assess the flutter occurrence [
4,
5] and the effect of mistuning and interlocking on the fluid-structure instability conditions [
6,
7] or to compute the aerodynamic forcing that can excite the blade row in regards to the resonance condition in order to evaluate maximum displacements and stresses [
8,
9,
10,
11]. There is a vast literature that addresses the latter phenomenon proposing numerical methodologies [
12,
13] and experimental campaigns [
14] to obtain a deeper insight into the physics and to evaluate the validity of design criteria to lower vibrations.
Forced vibrations of turbomachinery bladed disks are caused by the reciprocal interaction of stationary and rotating components that generate rotating perturbations able to excite specific nodal diameters (ND) of a bladed disk. The most common perturbation sources are related to blade wakes that are convected downstream or pressure potential fields propagating upstream in a multi-row machine [
15]. More recently, it has been proven that acoustic perturbations can also excite blade rows and deserve to be carefully considered in a multi-row environment [
16,
17,
18].
Numerical tools for forced response analysis can be split into CFD solvers able to predict the flow unsteadiness [
19,
20] and FEM codes used to perform modal and harmonic analysis of the excited component [
21]. Such methods can be coupled together or used in a row depending on the type of approach and the complexity of the required simulations. The modern trend in bladed disk design is oriented toward a holistic approach that takes into account aeromechanical aspects together with aerodynamic, thermal and acoustic requirements. For this reason, integrated and fast approaches are preferable for gathering all these aspects in the design loop and are better in a multi-objective optimization procedure [
22].
In this context, this work presents a fast approach to predict the forced response of a bladed disk based on the cyclic symmetry of the component. The approach takes advantage of a dedicated in-house tool able to extract the spinning perturbations acting on the blade row surface from the multi-row URANS solution by means of a temporal and spatial Fourier decomposition. After the forcing decomposition, a second in-house tool was implemented to compute the modal work done by the rotating force acting on the corresponding bladed disk mode shape in order to derive the scaling factor to compute actual oscillating displacements and stresses. The method was conceived for its integration in a CFD environment based on the URANS solver TRAF (developed at the University of Florence) capable of solving the force evaluation for the stator–rotor interaction [
23,
24] and also performing flutter simulations to compute the aerodynamic damping to be added to forced response analyses together with the mechanical contribution [
25].
The presented approach was firstly applied to a dummy test case with cyclic symmetry, and the results in terms of maximum displacement were compared with the ANSYS solution highlighting an excellent agreement both at resonance conditions and far from resonance. After this first validation, a dedicated low-pressure turbine test case was built and used for the further validation of the presented method. The turbine test case consists of a low-pressure stage with an upstream struct (IGV) reproducing a turbine center frame. Rotational speed and blade count are selected so that the IGV wakes excite the rotor on a resonant condition for the first bending mode family while the stator wakes act on the rotor out of resonance again for the first family. Both aerodynamic forcing distributions were considered, and the results are again compared with the ANSYS results. The results are in good agreement, and the sources of slight discrepancies are identified and discussed in the paper.
The comparisons reported in this work validate the implemented strategy to predict the forced response of bladed disks. The method was very cheap in terms of computational requirements and can be easily integrated into an aeromechanical numerical process. Moreover, the implemented tool can be considered ready to be applied in the industrial design loop and to be included in multi-objective optimization processes of turbomachinery bladed disks.
2. Numerical Methods
This section firstly describes the in-house tool conceived for the decomposition of the unsteady forcing resulting from the URANS CFD analyses. Then, the two methods for the forced response analysis of a bladed disk are presented: the implemented tool based on the modal work, and the method available in the ANSYS suite used for validation purposes.
2.1. Unsteady Forcing Decomposition
The unsteady aerodynamic forcing generated by rotor–stator interactions can be extracted from the analyzed bladed disks by means of a proper decomposition of a multi-row URANS solution. A Discrete Fourier Transform (DFT), applied both in time and in space, allows the extraction of the pressure fluctuation components on the blade surfaces in the cyclic symmetry environment typical of turbomachinery bladed disks. To do this, the time-varying pressure fluctuations seen by an airfoil row are firstly decomposed in time by a TRAF code at run-time to extract the harmonic content at selected frequencies (Engine Order, EO) by the following formulation:
in which
h is the time harmonic index (the engine order),
is the discrete equally spaced pressure signal in time and
is the total number of samples.
The resulting complex of Fourier coefficients
extracted on blade surface grid points is further spatially decomposed by the implemented tool along the circumferential direction to determine the rotating perturbation that will excite the corresponding traveling wave mode shape. The time–space Fourier coefficients are extracted along corresponding points on the grid surface as follows:
in which
ℓ is the circumferential order,
is the discrete time Fourier coefficient of the tangential distribution on the blade’s corresponding surface points and
N is the blade count. The circumferential order
ℓ defines the number of rotating lobes, and its sign defines the spinning direction: a positive sign means a downward rotating wave and negative an upward rotating one when looking at the blade-to-blade view with the machine axis from left to right. The latter quantity can be easily converted to nodal diameter ND where the sign has a different definition related to the rotor rotational direction: if positive, it defines a forward rotating wave; if negative, a backward rotating wave.
In the presented time–space decomposition, the circumferential DFT is performed on a coarse down-sampled set of only N samples taken on each blade at corresponding positions (grid points) on the surface. Hence, the extracted rotating pressure components have a number of lobes ranging from to or from to in the case of an odd blade count, as suggested by Nyquist’s theorem. It is clear how this approach also takes into account the aliasing phenomenon experienced by the blade row when excited by a rotating perturbation with a lobe number higher than .
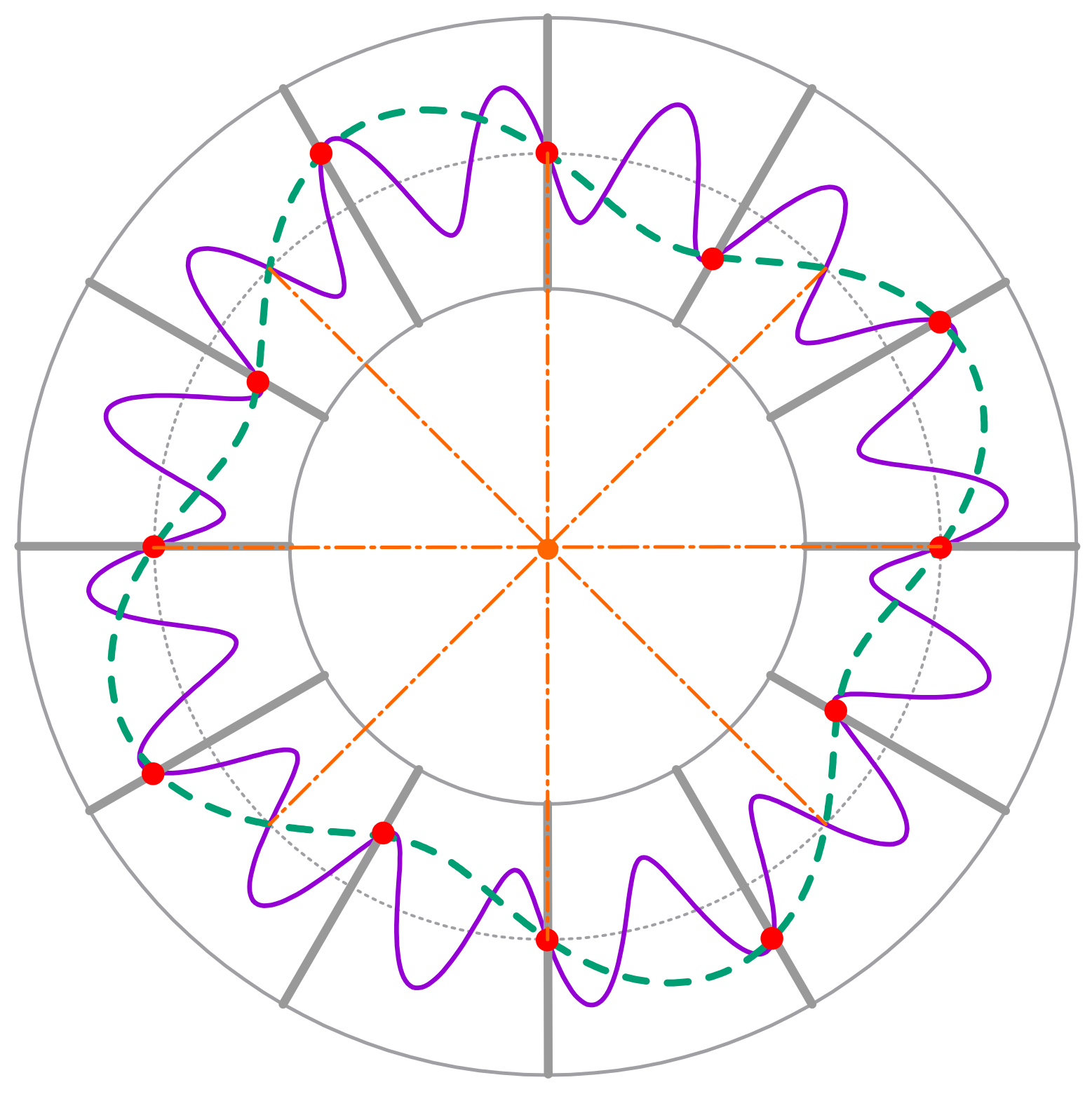
Figure 1 provides a visual representation of a possible excitation scenario, where a rotating perturbation with 16 lobes, represented by the solid violet line, impinges on a row composed by of blades represented by the radial grey segments. The 12 blades experience a 4-lobe perturbation represented by the green dashed line due to the aliasing phenomenon. The orange dash-dot radial lines highlight the resulting four nodal diameters associated with the 4-lobe excitation. The implemented spatial decomposition on the “blade-sampled” corresponding N points along the circumferential direction is thus able to convert the 16-lobe incoming perturbation into the 4-lobe excitation experienced by the blade row, which will finally vibrate as a traveling wave with four nodal diameters.
The implemented post-processor generates the blade surface pressure perturbation maps for each nodal diameter at the selected engine order in a format directly readable by ANSYS.
2.2. Modal Work Approach
The implemented tool, named Tremor (Tool for Response Evaluation by Modal wORk), is capable of computing a forced response analysis of a bladed disk in a cyclic symmetry environment. The tool computes the forced response of a single traveling wave mode shape (defined by the nodal diameter and resulting from a modal cyclic symmetry analysis), excited by the corresponding rotating forcing function, obtained from an unsteady analysis and spatially decomposed to match the nodal diameter of the mode shape.
The forced response evaluation is based on the modal work computation that is integrated on the blade surface CFD mesh, where a nearer point interpolation strategy is used to transfer the blade mode shape from the FEM to the CFD blade surface. The computation of the modal work on the CFD discretization ensures a more accurate result due to the higher density of the CFD mesh.
The tool requires the blade mode shape, the decomposed forcing functions and the total damping as inputs in order to compute the scaling factor to be applied to modal displacements and stresses to obtain actual values. The scaling factor can be computed both in and out of resonance conditions. The modal work approach determines the maximum energy transfer of a rotating pressure perturbation (decomposed on blade corresponding points, as described in the previous section) applied to the corresponding traveling wave mode shape defined by the nodal diameter and is defined as follows:
where
is the modal work,
is the complex conjugate of the modal displacement phasor and
the unsteady aerodynamic pressure phasor.
The modal work approach leads to the computation of the modal force
by the integration of the complex dot product between the complex conjugate of the modal displacements and the forcing function distribution, both evaluated at the cell center for each point of the CFD grid.
The scaling factors can be computed under resonance conditions or not by using the following equation:
where
is the natural angular frequency,
is the angular frequency of interest and
is the damping, which can include the material, mechanical and aerodynamic damping. The scaling factors can be used to scale the modal displacements or stresses in order to obtain the actual values:
where
and
are the modal displacements and stresses from the modal cyclic symmetry analysis, and
is the module of the scaling factor.
2.3. ANSYS Harmonic Analysis
ANSYS mechanical software was used to perform the FEM analyses of the cyclic symmetry for dummy and turbine test cases. The FEM simulations include nonlinear static, pre-stressed modal and harmonic computations for validation of the Tremor tool.
The harmonic forced response analysis in cyclic symmetry was carried out with the mode superposition (MSUP) method, which requires cyclic loading (traveling wave excitation) related to a defined engine order. To solve this analysis, additional commands are directly included in the APDL modal module to provide additional instructions to the solver, including the definition of the cyclic symmetry of the model, pre-processing, solution and post-processing options and rotating-force mapping from the fluid to the solid domain blade skin. The mode superposition method combines the mode shapes, obtained from a previous modal analysis, to calculate the harmonic response. The modal cyclic symmetry analysis can include the pre-stressed state obtained from a static cyclic symmetry analysis. The forcing functions extracted by the tool described in
Section 2.1 have to be mapped on the blade surface of the FEM model before running the harmonic cyclic symmetry analysis.
3. Results and Comparisons
The validation of the tool described in
Section 2.2 was preliminarily performed on a cyclic dummy test case reproducing a simplified bladed disk and finally on an aeronautical LPT (low-pressure turbine) bladed rotor, comparing the displacements computed by Tremor with the values obtained by the harmonic cyclic symmetry analysis performed in ANSYS Mechanical.
For the dummy test case, various arbitrary rotating forcings were imposed to different mode shape families reproducing resonance crossings, whereas when studying the forced response of the bladed rotor, the forcing functions were directly extracted from an unsteady multi-row simulation. The latter test case consists of an IGV (representative of a turbine center frame) and a downstream stage (stator + rotor). In this configuration, the rotor is subjected to the wakes generated by the two upstream static components (IGV and stator) at their blade passing frequencies. In detail, this configuration based on realistic profile geometries was modified in terms of rotor rotation speed and blade count to experience a resonance crossing corresponding to the 1xBPF of the IGV and no crossing for the stator passing frequency at the first bending mode. In this way, the tool can be tested both in resonance and out of resonance conditions. As already mentioned, only the first bending mode family is considered for the validation.
3.1. Dummy Test Case
The preliminary validation of the tool was performed with a dummy test case, which consists of a simplified tuned bladed rotor row with 16 blades. The validation was performed for the first bending mode family comparing the maximum actual displacement obtained by Tremor and ANSYS.
3.1.1. Modal Analysis
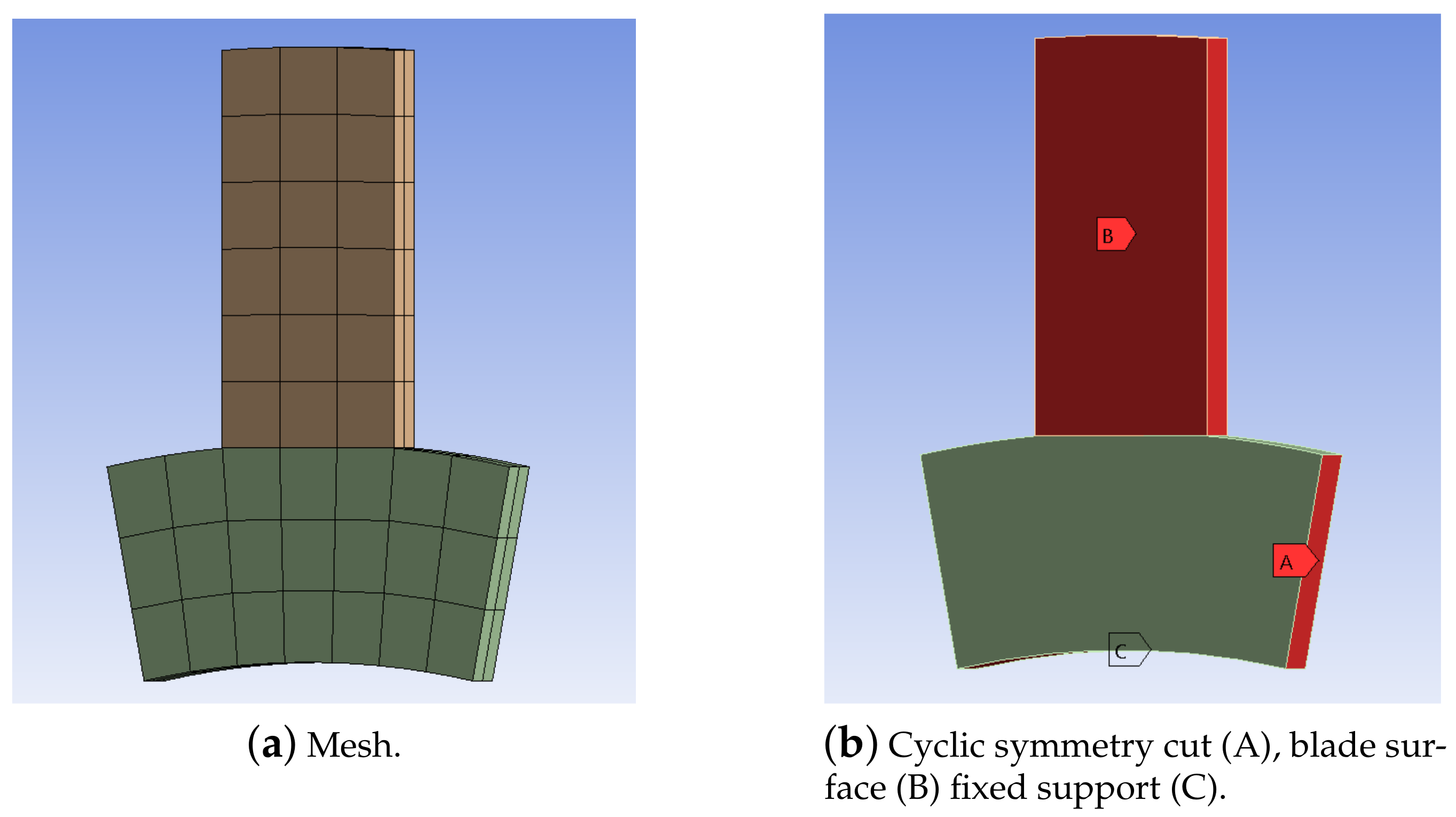
The FEM mesh is very coarse and consists only of 78 hexahedral elements defined by 591 nodes, as shown in
Figure 2a.
The modal analysis with cyclic symmetry was carried out with ANSYS to evaluate the eigenfrequencies and eigenmodes of the system for the first family, neglecting the influence of the thermal load. The disk was fixed at the bottom, and the cyclic symmetry boundary condition at the periodic cuts was applied with the CYCLIC command. Looking at
Figure 2b, a mesh patch (B) was defined to extract the mode shape only on the dummy blade surface, while the applied constraints are the cyclic symmetry (A) and the fixed support (C). The contact between the blade and disk was modeled as bonded.
Moreover, the modal displacements of a pair of points (control nodes) on the cyclic cuts (located at the same axial and radial position and far one-pitch along the circumferential direction) were also extracted to define the direction of the traveling wave between forward and backward for a given nodal diameter solution. The mode shapes on the blade surface and the displacements of two control nodes were exported with the EXPROFILE command. In
Figure 3, the modal displacement contours of the first bending mode for
are shown on the entire dummy blade row.
3.1.2. Forcing Function Distribution
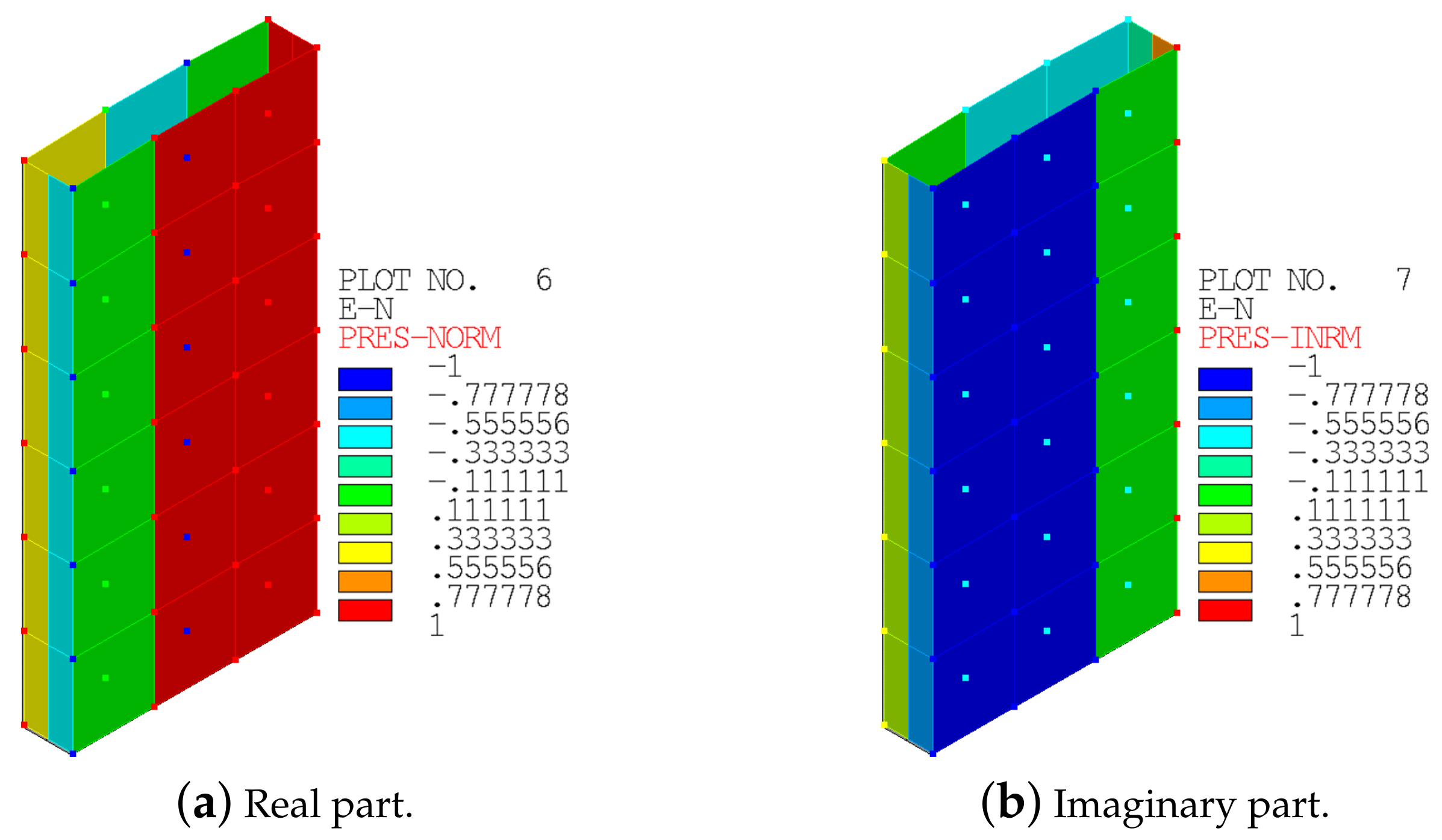
For this simplified case, CFD analyses were not performed, and three arbitrary forcing function distributions of increasing complexity were selected for the validation. These forcing distributions were directly imposed on the nodes representing the blade surface in the FEM model. These load distributions consist of complex pressure values applied to a single or to both faces of the blade. The third and more complex forcing function distribution (case 3) applied on both blade sides is shown in
Figure 4.
3.1.3. Harmonic Analysis with ANSYS
The harmonic cyclic symmetry analyses are performed with ANSYS by using the mode superposition method with the same boundary conditions of the previous modal analysis. Different harmonic analyses were run, keeping the same forcing function to extend the validation to a range of nodal diameters (
). Each forcing function was mapped to the FEM target surface using MAP command before solving the harmonic analysis. The target surfaces and nodes belonging to the FEM model where the pressure mapping is applied are shown in
Figure 5.
An overall damping of 0.01 is included in the model by using the DMPRAT command for all the analyses. The frequency range of the forcing function was set to match the eigenfrequencies of all the first family modes for the different nodal diameters under investigation. The engine order excitation of interest was defined with the CYCFREQ option, taking into account the aliasing phenomenon as well. The amplitude of total deformation over the blade was calculated by the square root of the sum of the squares of the real and the imaginary parts of the computed deformation.
3.1.4. Tremor-ANSYS Comparison
The Tremor program requires the blade mode shape, the control nodes modal displacements and the forcing function distribution for a single traveling wave as inputs. The modal work integration was performed on the CFD blade surface mesh, which is usually finer than the corresponding FEM discretization, ensuring a high computational accuracy. Control nodes were used to select the traveling wave direction of the mode shape and to take the mode complex conjugate in case the analysis of the opposite traveling wave is requested. Moreover, an automatic overlapping of the forcing function on the CFD blade surface was implemented to avoid the manual mapping of the forcing (as required in the ANSYS solver). All these aspects make the tool attractive for its integration in automatic procedures like aeromechanical optimization processes.
For this preliminary validation, the nodal diameters
are considered with the same total damping equal to 0.01. The validation was performed by comparing the maximum amplitude of total deformation between ANSYS and Tremor results in resonance and out of resonance conditions for the different forcing functions. In the resonance condition, Tremor computes the scaling factor by using the natural frequency related to the nodal diameter under investigation. In a tuned system, this excitation acts only on nodal diameters that show a crossing in the interference diagram (ZZENF). The comparison of the maximum amplitude for the more complex forcing function (case 3) at
is reported in
Table 1 shows an excellent agreement, as did the other pressure loads. The additional comparisons are not shown here for the sake of brevity.
The validation is further extended to out-of-resonance conditions, comparing the amplitude of total deformation due to the forcing function at EO = 4 for different nodal diameters, listed in
Table 2. It is clear that the maximum amplitude of total deformation occurs at the crossing (
), whereas when moving away, the amplitude decreases.
The agreement is excellent for out-of-resonance conditions as well, so the tool validation must be extended to a more complex model reproducing a realistic low-pressure turbine bladed rotor.
3.2. LPT Bladed Rotor Test Case
The implemented tool is thus applied to a bladed rotor representative of a low-pressure turbine rotor. The numerical test case consists of an IGV and a downstream stage where the rotor is mounted. This multi-row environment allows the extraction of realistic forcing function due to the IGV and stator wakes from unsteady computation. The validation is performed considering the first bending mode and comparing the displacement computed by Tremor and ANSYS at resonance and out-of-resonance conditions.
3.2.1. FEM Bladed Rotor Model
The original CAD model of the rotor is based on a geometry already studied during the FUTURE European research project from an aeromechanical point of view [
6,
7]. The turbine bladed disk consists of 147 profiles. The mechanical properties of the components are summarized in
Table 3. The blade material is not a typical alloy for low-pressure turbine blade manufacturing, yet the aluminum alloy was chosen during the EU project to lower the blade row frequency in order to trigger free flutter occurrence during an experimental campaign within a cold flow rig [
26].
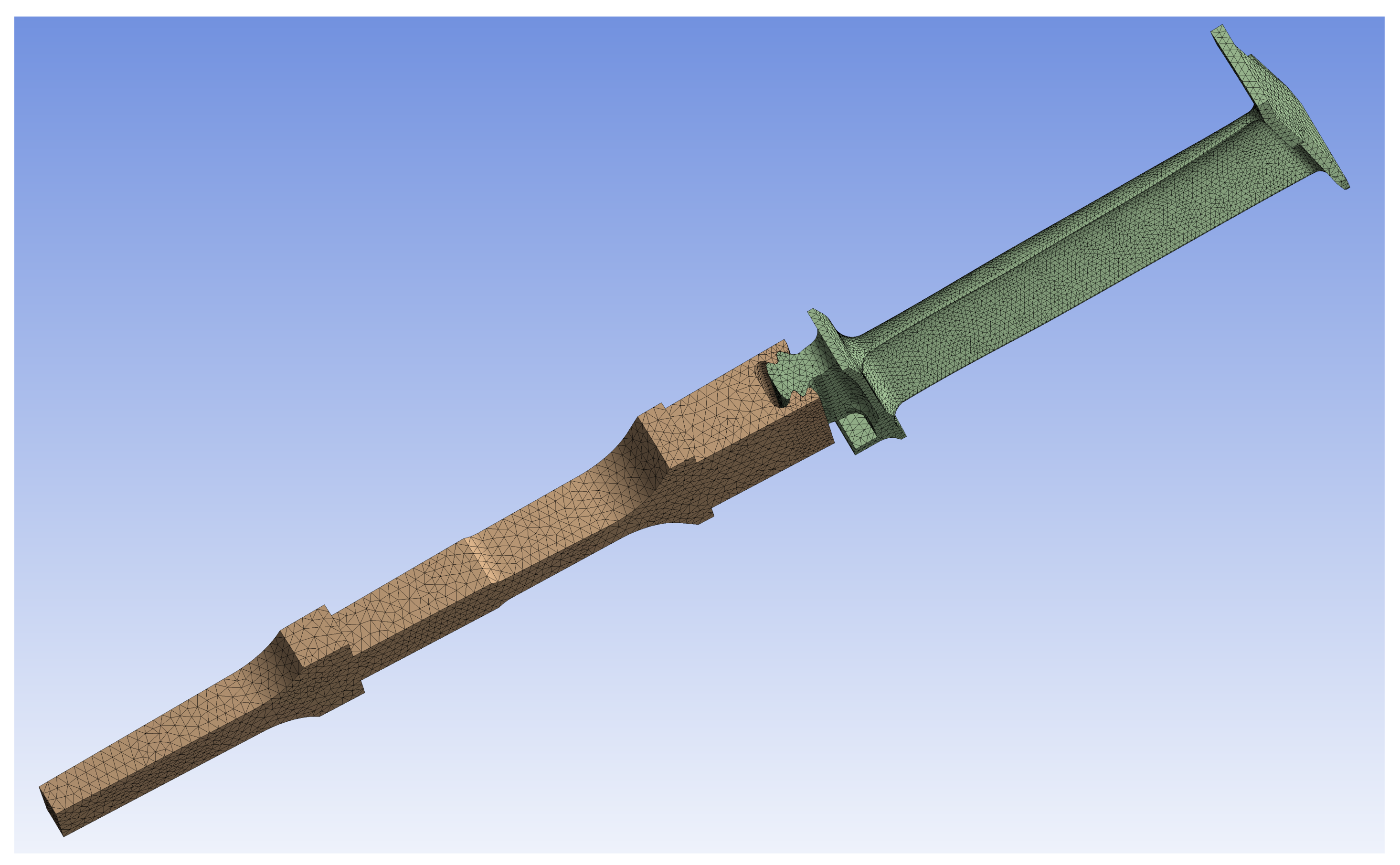
The discretization of the rotor bladed sector was carried out using the mesh generator available in the ANSYS Mechanical software. The number of elements and their minimum size were carefully selected after a sensitivity analysis, with the aim of minimizing computational costs while preserving a good mesh accuracy. A mesh refinement was performed at the blade surface, and the MATCH CONTROL option was used to obtain the mesh matching on the two cuts of the one-pitch sector, where the cyclic symmetry condition was applied. To accurately model the fir-tree attachment between the blade and the disk, a contact region was defined and the mesh is identical at the interface. The contact was modeled as bonded. The final mesh, shown in
Figure 6, consists of around 70,000 10-node tetrahedral structural solid elements (SOLID187). A named selection, including the blade surface, was defined for the mean pressure mapping and the successive extraction of blade mode shapes.
In order to reproduce the constraints of the assembly, the following conditions were chosen and imposed in the FEM model: interlocking constraint at the base of the sector; axial and tangential constraint to reproduce the screw connection between disk and shaft. To perform the FEM analysis, specific commands were included in the modal module in order to define the cyclic symmetry of the model (CYCLIC) and to specify pre-processing (PREP7), solution (SOLU), mapping (MAP) and post-processing (POST1) options.
3.2.2. Pre-Stressed Modal Analysis
The first FEM computation is a static analysis needed for evaluating the pre-stress state of the sector. The influence of the thermal load was neglected, while the centrifugal load was considered by imposing a rotational speed of 3100 rpm. This value is obtained by means of an iterative procedure to obtain a resonance crossing at the 1xBPF of the IGV in the ZZENF diagram.
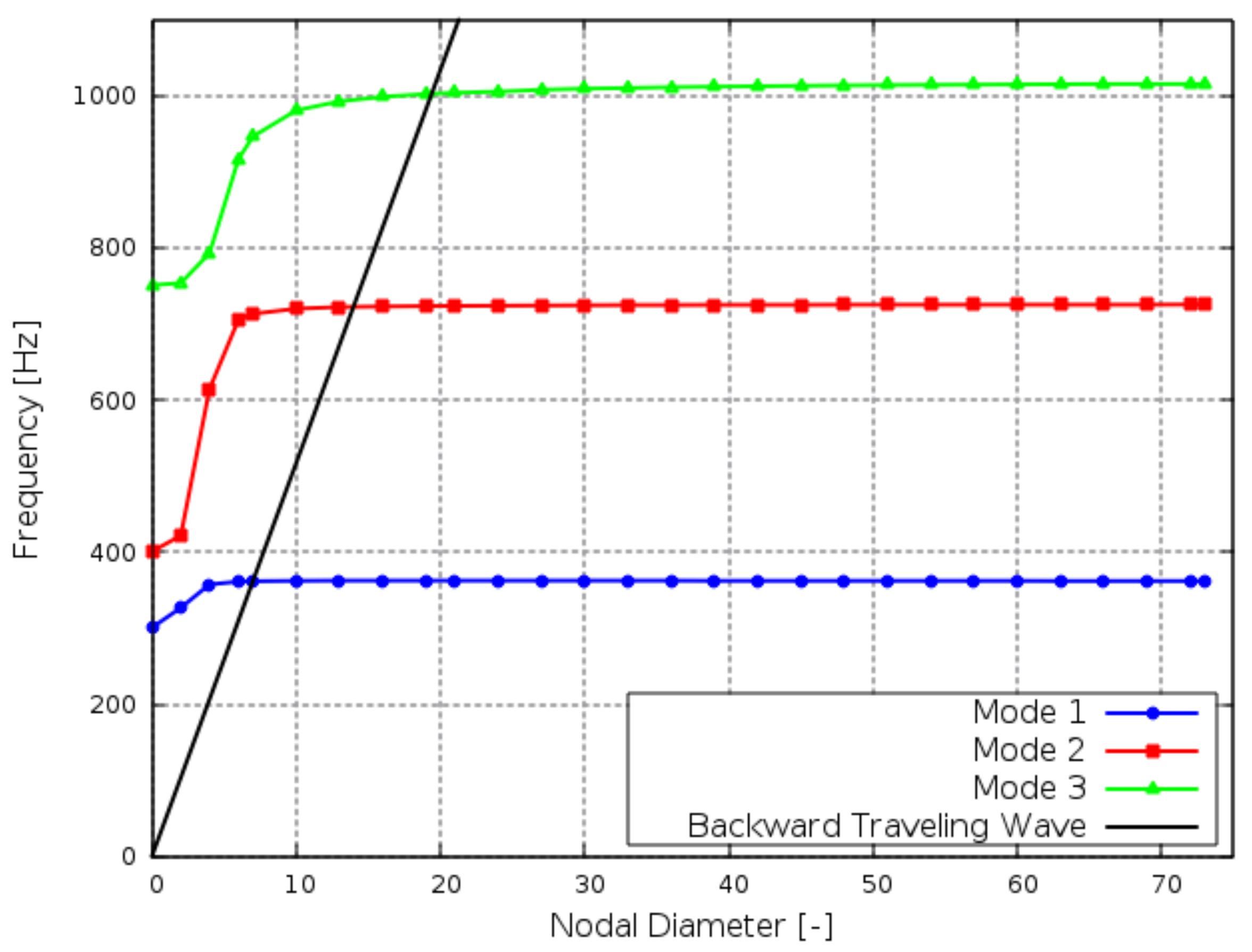
The pre-stressed modal cyclic symmetry analysis was performed to extract only the first three mode families for a selected set of nodal diameters. The modal displacements were extracted at the nodal diameters identified in the ZZENF diagram. The ZZENF diagram for the rotor is shown in
Figure 7, reporting the eigenfrequencies as a function of the nodal diameter for the first three families. The speed line related to the rotational speed of 3100 rpm is reported as well. This diagram allows identifying the potential frequencies where resonances occur.
All three mode families present the typical behavior of bladed rotor systems: at lower nodal diameters, the system shows a relevant disk participation with a sudden frequency increase. Moving to a higher value of nodal diameters, the disk does not participate anymore to the overall deformation that is concentrated to the blade, so there is no more significant difference in the frequency with the variation of nodal diameters. This effect tends to become more evident for high-frequency families.
The validation of the Tremor tool was performed for two forcing distributions, which consider the effect of both IGV and stator wakes on the rotor. In the first case (IGV wake forcing), the resonance crossing occurs at
(backward), where the natural mode frequency corresponds to the first BPF of the IGV (
). In the second case (rotor wake forcing), the first BPF of the stator (
) does not correspond to the mode frequency at
(forward), so this is an out of resonance condition for first mode family, as shown in
Figure 7.
The first family (bending mode) contours for
are shown for the whole system in
Figure 8, where the traveling wave deformation is clearly visible.
The modal displacements for the blade surface points and two control nodes are thus extracted for and .
3.2.3. CFD Multi-Row Model
The CFD domain consists of three blade rows, the IGV, the stator and the rotor, whose blade count (7 IGVs, 126 stators and 147 rotors) allows for the reduction of the computational domain as all the blade counts have a common divisor. The CFD analyses were carried out using the TRAF code, which is a URANS solver for 3D viscous and inviscid flows [
23], developed at the Department of Industrial Engineering of the University of Florence. The discretization of the fluid domain was performed with an in-house meshing tool by stacking the 2D blade-to-blade grids at different span-wise positions.
A structured H-type grid was used for the IGV (232 × 260 × 72 cells in axial, pitch-wise and span-wise directions, respectively) and O-type grids for the stator (432 × 60 × 72 cells along the blade, in pitch-wise and span-wise directions, respectively) and the rotor (432 × 60 × 72).
3.2.4. Unsteady Multi-Row Analysis
The unsteady multi-row analysis allows investigating the interaction between adjacent rows and calculating the unsteady pressure field on the rotor blade surface to be applied in the harmonic analyses. All the computations were performed using the two-equation turbulence model in Wilcox’s high Reynolds formulation. Standard aerodynamic boundary conditions were applied at the inlet and outlet of the computational domain. Inlet conditions were defined by the span-wise distributions of circumferentially averaged total pressure, total temperature and flow angles, while at the outlet, the static pressure span-wise distribution was imposed. The average total temperature and pressure imposed at the inlet are 331.5 K and 76.2 kPa, respectively, as the stage was tested in a cold flow rig. At the stage outlet, a mean static pressure of 41.1 kPa was imposed, leading to a static temperature of 286.3 K.
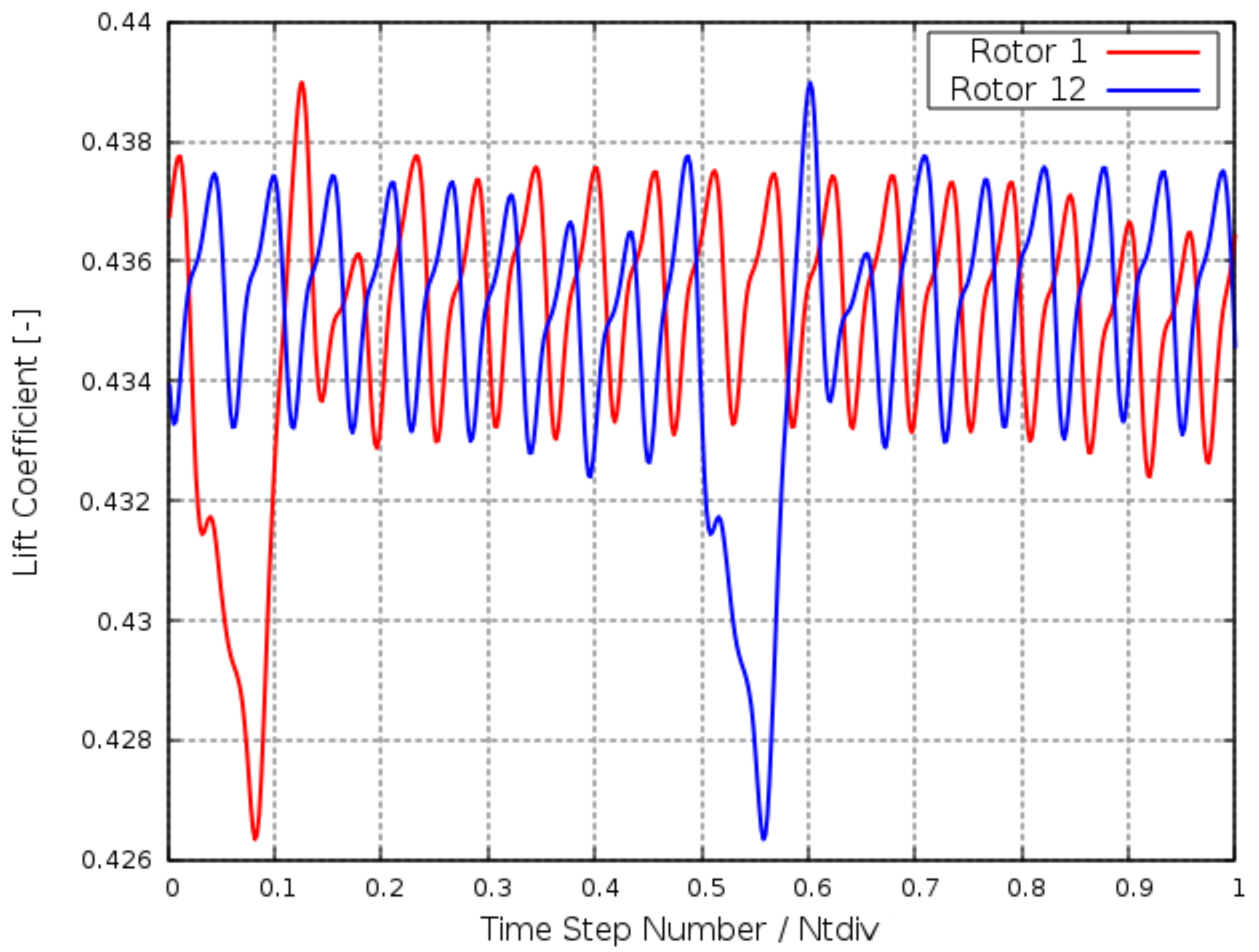
The unsteady multi-row analysis was performed using a dual time-stepping method and the full annulus approach. A reduced computational domain was defined by 1 IGV blade, 18 stator blades, 21 rotor blades representing 1/7 of the entire wheel. To monitor the computation periodicity, a lift coefficient based on the blade surface pressure was stored at each time step for each profile and had to become periodic to ensure the unsteady computation convergence. The rotor lift coefficient is plotted in
Figure 9 for two arbitrarily selected rotor profiles that experience the same time history with a time shift related to their different tangential position. The same unsteady lift time history was experienced by all the 147 rotor profiles with different time shifts. The number of peaks depends on the number of stator blades (and IGV profiles) because the rotating rows undergo the effect of the fixed distortions and vice versa. Indeed, in addition to the 18 peaks caused by stator wakes, it is evident that the presence of a single higher peak due to the IGV wake convected through the stator row and impinged the rotor at EO = 7.
The instantaneous entropy contours on a blade-to-blade surface are shown in
Figure 10 to highlight the typical interaction between adjacent rows due to the wakes. The IGV wake passes through the stator and impinges the rotor blades, adding to the stator wake distortion (
) a further distortion with
. This causes the single highest peak in the lift coefficient shown in
Figure 9.
A run-time temporal DFT on the rotor profiles was activated during the TRAF unsteady run to decompose the time-varying fluctuations at
and
, which correspond to the first BPF of IGV and stator, respectively. Then, the unsteady pressure distribution described by complex Fourier coefficients field acting on the rotor blade surface was circumferentially decomposed in space to extract the rotating perturbations that can excite the corresponding traveling wave mode shapes of the bladed rotor. The in-house post-processor extracts the pressure perturbation at circumferential order
from the
and
from the harmonic at the
, accounting for the aliasing phenomenon. Considering the rotor rotational direction, the circumferential order values were converted to nodal diameters to distinguish between forward and backward traveling waves in ANSYS, so the pressure perturbation is referred to
backward for
and
forward for
.
Figure 11 and
Figure 12 show the amplitude and phase of the unsteady pressure perturbation circumferentially decomposed for
and
, respectively.
Comparing the amplitude maps of the forcing function on the blade, it is possible to observe that the pressure perturbation due to the IGV wake is about an order of magnitude less intense than the one due to the stator wakes, as this row is directly upstream of the rotor. Considering the amplitude of pressure perturbation, the red zones on SS (suction side) in
Figure 12 represent the highest perturbation areas located where the trace of wake impinges the rotor surface. These rotating forcing function distributions on the blade surface were used for the forced response analyses with ANSYS and for Tremor computations.
3.2.5. Aerodynamic Damping Evaluation
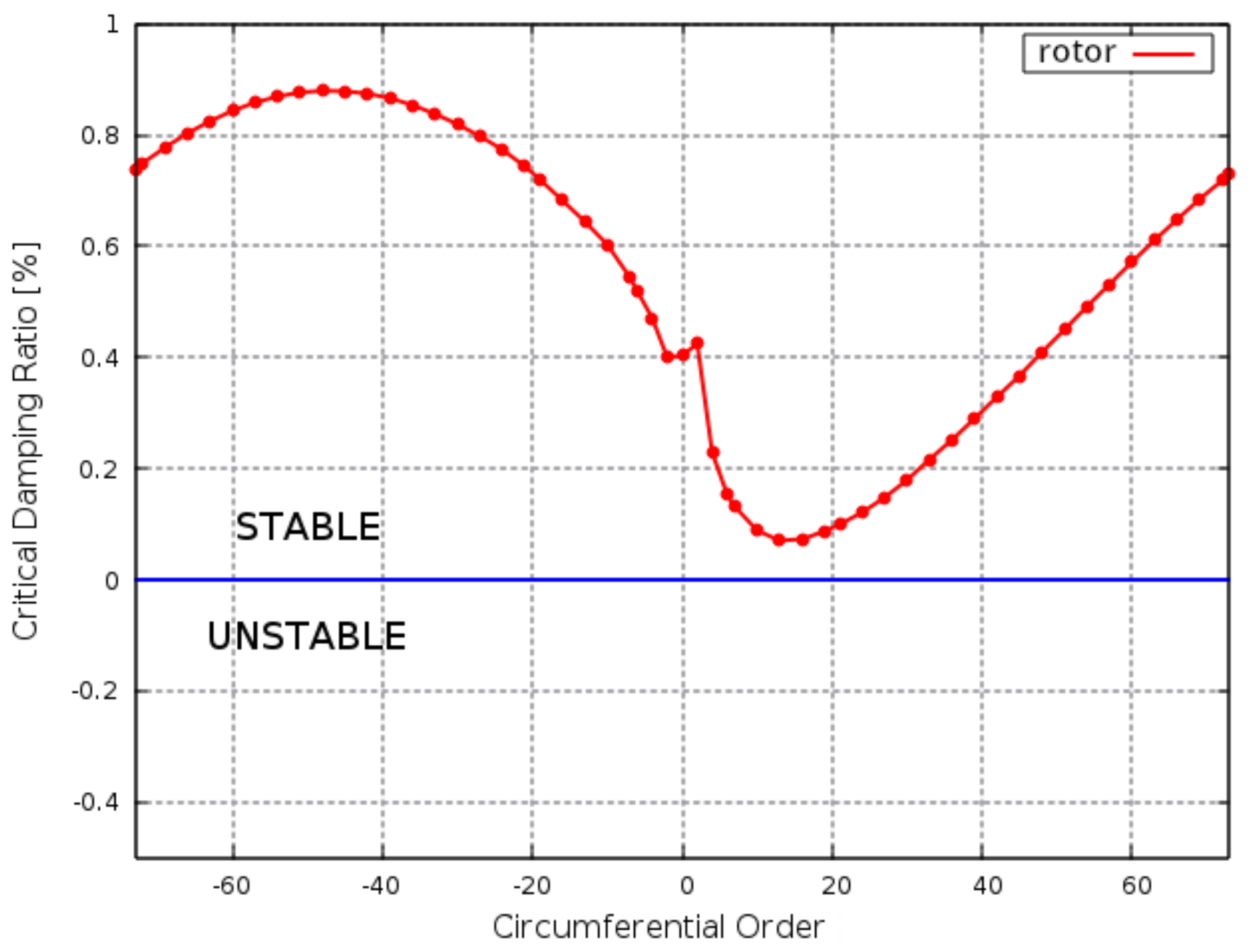
To evaluate the aerodynamic damping to be added to the mechanical contribution for the forced response assessment, a flutter method implemented in TRAF code was used. For the flutter analysis, the solver uses an uncoupled approach with an energy method and phase-lagged approach to calculate the aerodynamic work, from which the aerodynamic damping can be straightforwardly computed. The mode shapes obtained from the modal analysis were transferred to the blade surface in the fluid domain in order to deform the CFD mesh during the unsteady flutter computations. The analysis is based on an unsteady simulation with vibrating blades in a traveling wave manner, so the blade channel must be deformed with the appropriate Inter Blade Phase Angle (IBPA). The aerodynamic damping of the bladed rotor coming from classical flutter simulations in terms of the critical damping ratio as a function of the circumferential order is shown in
Figure 13. The curve for the first bending family is located in the stable zone of the graph, as the aerodynamic damping is always positive above the horizontal zero line that delimits stable and unstable zones. Thus, if the blades start vibrating, it does work on the fluid, and so any oscillation at the first family mode is damped.
The small peak in the curve trend near
is caused by the increase in the frequency values for the first bending mode at lower nodal diameters. This shift is due to the stiffening of the disk, as shown in
Figure 7, which shows a typical trend of a bladed disk mode. The values corresponding to
(
, backward) and
(
, forward) are used as the total damping terms (neglecting the mechanical damping that is usually low for cantilever blades with no connections) in Tremor computations and as a modal damping ratio by using the DMPRAT command in forced response analyses performed by ANSYS.
3.2.6. Harmonic Analysis with ANSYS
Two harmonic cyclic symmetry analyses based on mode superposition were performed to solve the forced response amplitude of the bladed rotor under the effect of wakes due to the IGV and the stator. In detail, the first analysis considers the IGV excitation () as a forcing function, while the second computation accounts for the stator excitation (). For each analysis, the corresponding decomposed pressure perturbation coming from unsteady multi-row analysis and the aerodynamic damping coming from flutter single-row analysis are considered.
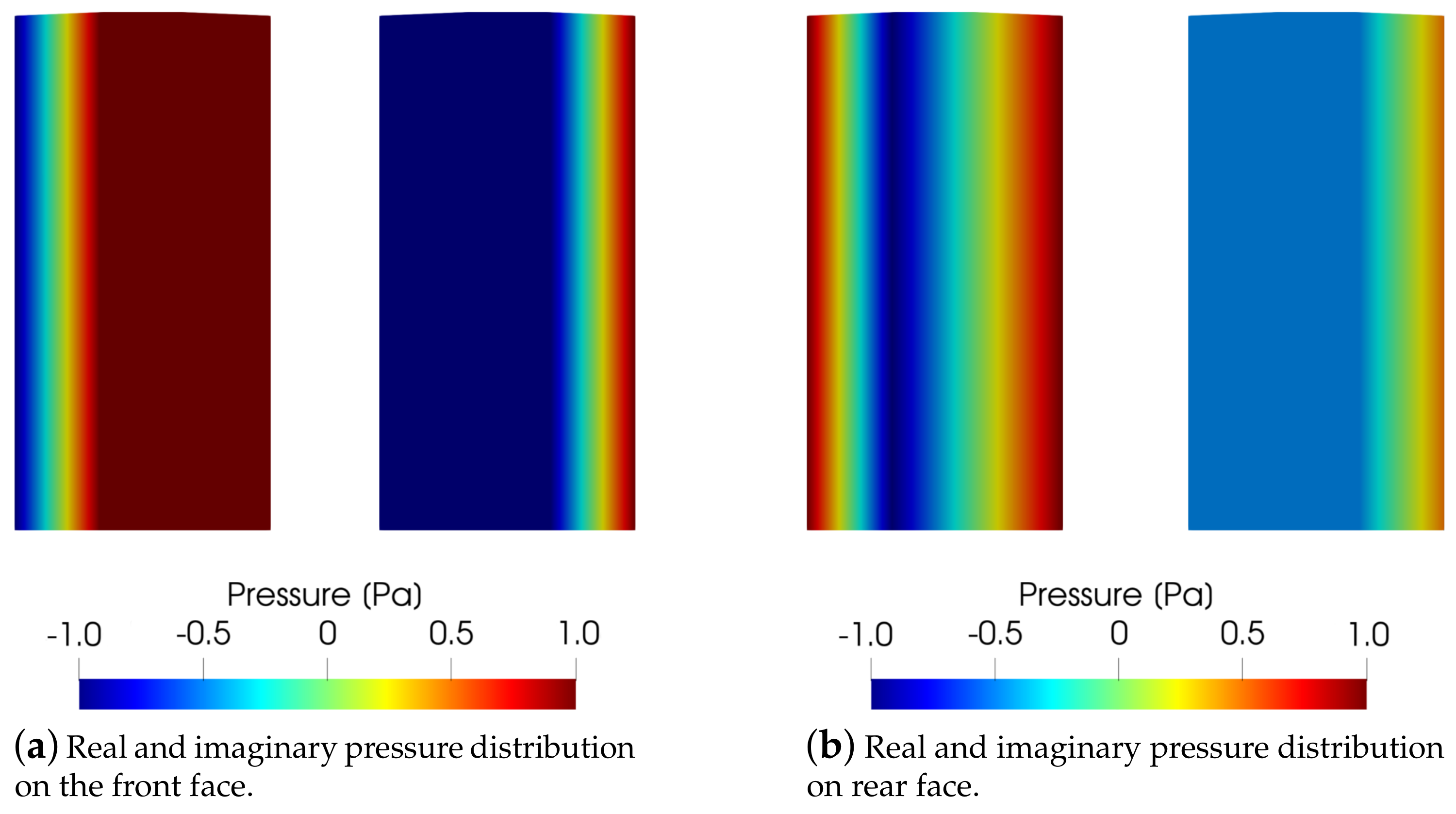
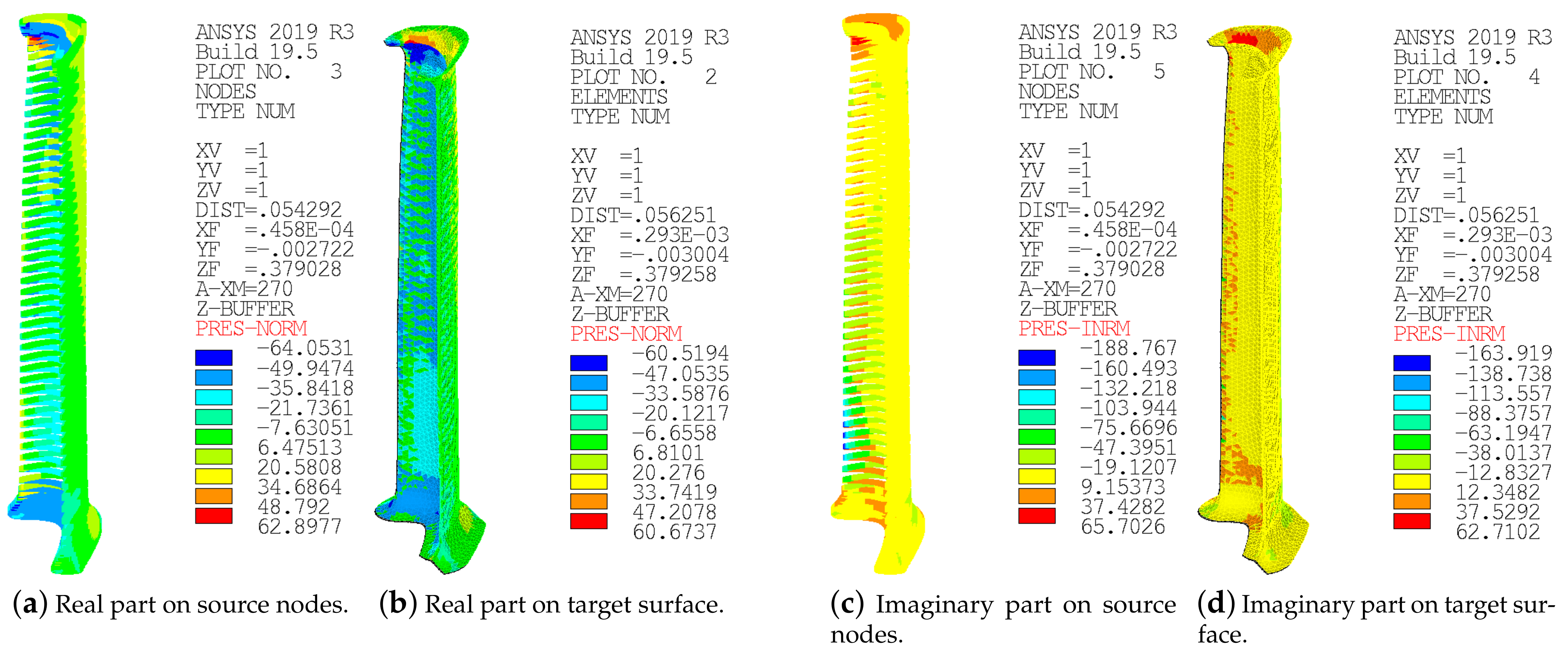
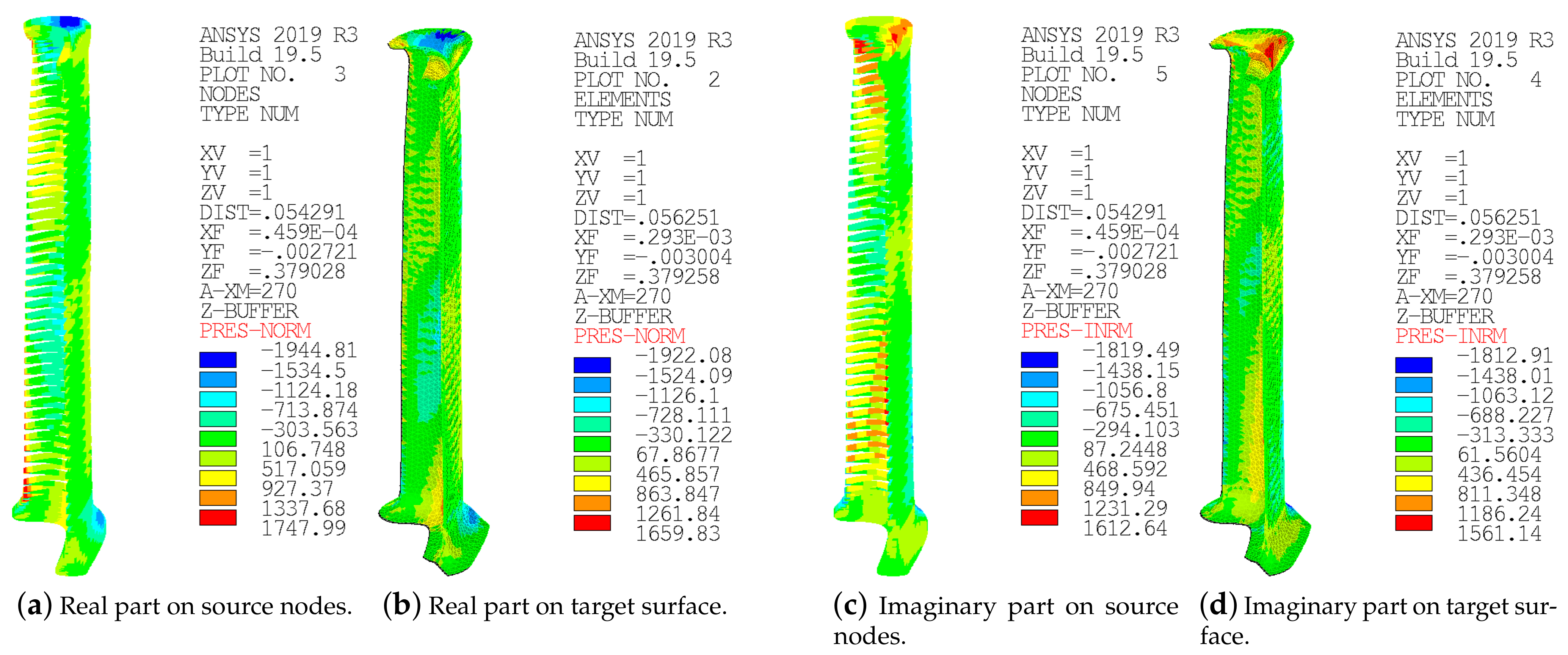
Before solving the harmonic cyclic symmetry analyses, the results of the forcing mapping step have to be discussed, as the transfer of the forcing functions from the fluid to the solid domain represents a key aspect of the validation comparison for this test case. The results of the mapping steps can be checked by using the PLMAP command in terms of target and source pressures. The real and imaginary parts of pressure perturbation are shown in
Figure 14 for
and
Figure 15 for
, representing a portion of the target blade surface and source nodes.
The forcing functions mapped on the FEM blade surface slightly differ from the original ones coming from the fluid domain, not only in the maximum and minimum values but also in the distribution shape. The choice of a different number of nodes for the interpolation in the MAP command does not have a beneficial effect on the mapping results. The discrepancies can be explained by the higher difference in the number of discretization points between FEM and CFD models; in fact, in this exercise, the number of CFD blade surface nodes is more than four times greater than those of the FEM blade surface. This difference justifies the small discrepancies in the mapped pressure on the coarser FEM mesh where the forcing distribution is smoothed, affecting the forced response results. The second reason is the error in the overlapping of the forcing function point cloud with the FEM blade surface. This overlapping procedure is performed by the user in the ANSYS environment, whereas in the Tremor procedure, this aspect is automatically handled by means of an optimization procedure.
The maximum amplitude of the total displacement resulting from the harmonic cyclic symmetry analyses is computed at the frequencies of interest for the first mode family: the peak of the resonance response at 361.67 Hz in the case of IGV excitation, corresponding to in the ZZENF diagram, and the first BPF of the stator (6510 Hz), far from the natural frequency of the first mode family corresponding to with a natural frequency equal to 362.48 Hz.
3.2.7. Tremor–ANSYS Comparison
The Tremor tool was finally used to predict the forced response of the rotor blade due to the IGV and the stator wakes. The modal displacements for and (first family) are provided from the previous modal analysis on the blade surfaces and for the pair of control nodes. The pressure harmonic decomposed in space and time coming from the unsteady multi-row analysis is extracted at and . A roto-translation matrix to transfer the mode displacements from the FEM frame of reference to the CFD one is obtained by means of the open-source CloudCompare program able to find out the rigid transfomation to overlap the FEM surface to the CFD one by means of an optimization procedure. The aerodynamic damping resulting from the flutter analyses is specified for each nodal diameter in the input file.
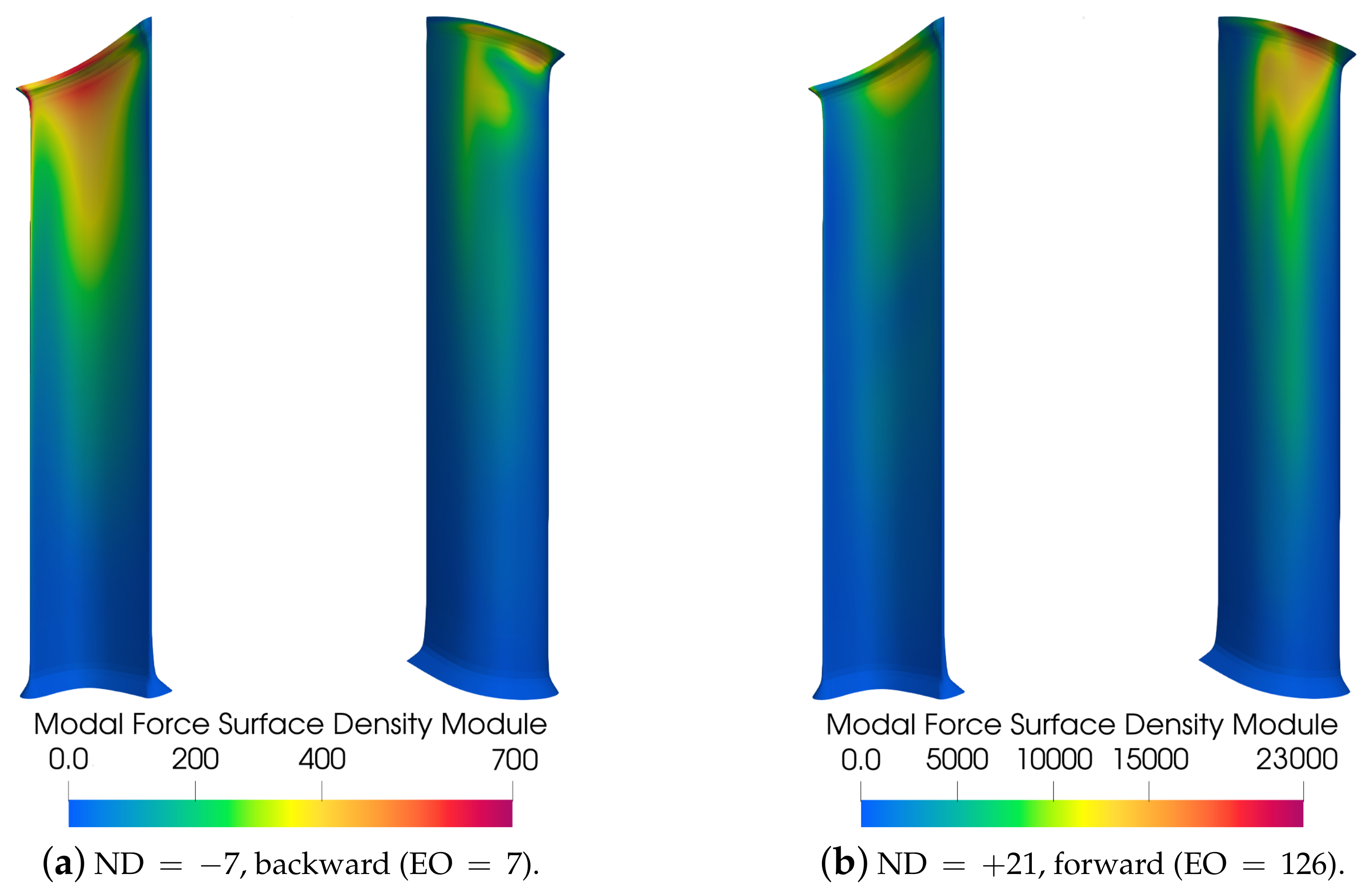
The complex modal forcing distribution is evaluated on cell center points of the CFD blade surface elements to compute the scaling factors to be applied to modal displacements and stresses. The module of the modal force surface density, which is computed as the local modal force contribution divided by the corresponding cell area for each surface cell, is shown in
Figure 16.
Note that the module of this quantity is only useful to qualitatively observe the regions of the blade surface that contribute the most to the overall forced response amplitude; the quantitative comparison must be done separately on the real and imaginary parts of this quantity, which leads to the scaling factor when integrated over the surface and composed together, as shown in Equation (
4). In the case of IGV excitation, the greater values are observed near the tip of the PS (pressure side), where the first bending mode presents higher modal displacements, and on the LE, where the pressure perturbation has a higher amplitude. Considering the stator excitation, this quantity is more than one order of magnitude higher than the other case, and the greater values are observed near the tip on the SS, where the first bending mode presents higher modal displacements and the pressure perturbation is stronger.
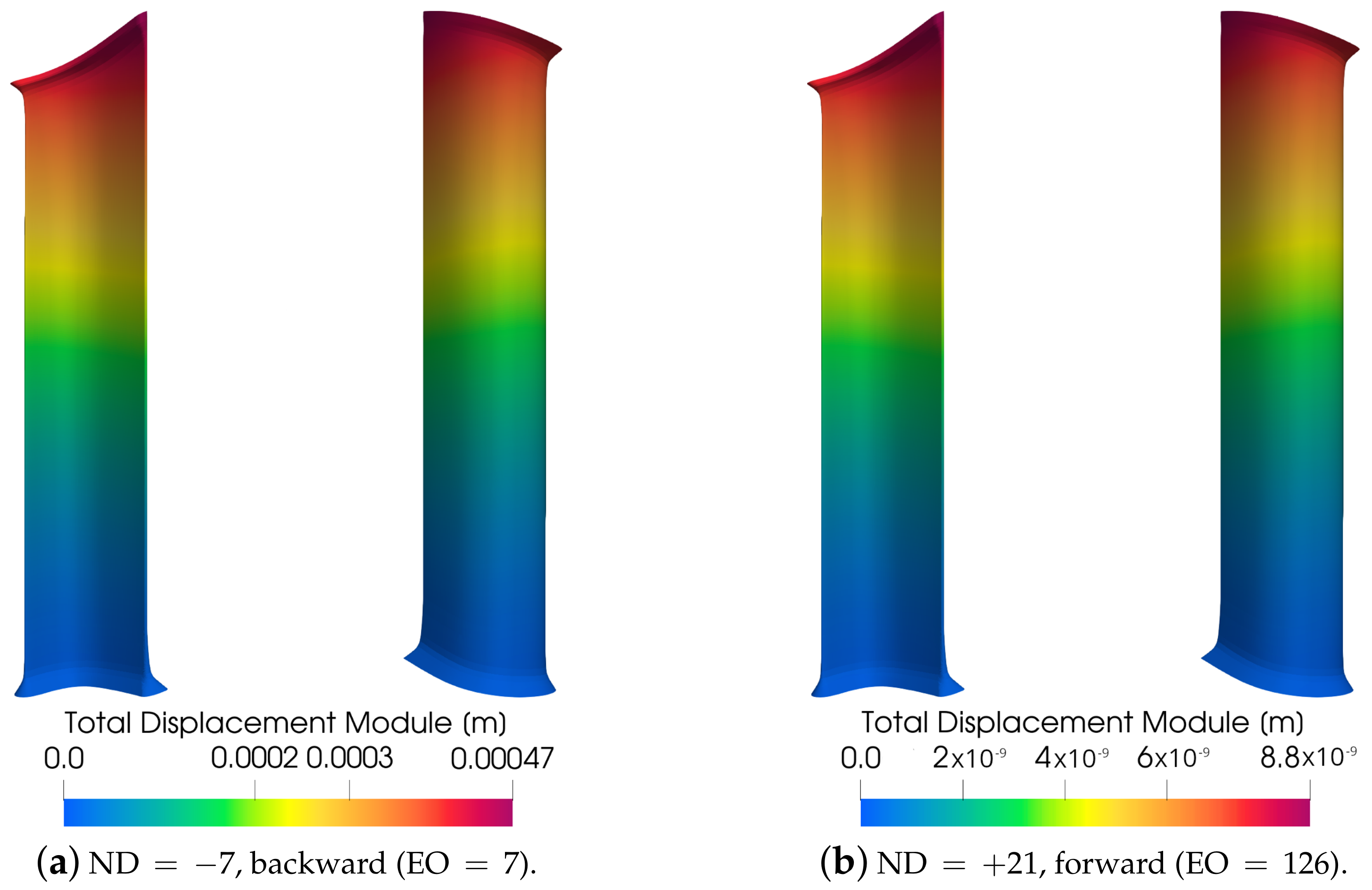
The actual displacements were finally obtained by scaling the modal displacements with the complex scaling factor resulting from the modal work computation. The module of these displacements, i.e., the amplitude of total deformation, which is calculated by the square root of the sum of the squares of the real and the imaginary parts in all directions, is depicted in
Figure 17.
The contours represent the scaling of the first bending mode, and the displacements are almost the same between PS and SS: this further confirms that the mode shape is well transferred from the FEM grid to the CFD one where the scaling factor is computed. The comparison between the harmonic cyclic symmetry analysis in ANSYS and Tremor computations for the first bending mode is listed in
Table 4. For the case of IGV excitation, the validation is performed at the resonance condition for
backward corresponding to 361.67 Hz, while in the case of stator excitation, the results are compared at the 6510 Hz out-of-resonance condition for
forward that exhibits a natural frequency of 362.48 Hz.
The agreement is good for the stator excitation and satisfactory for the IGV excitation. However, the ANSYS results strongly depend on the mapping of the pressure perturbation from the CFD grid to the FEM one. The Tremor tool computes the modal work on the blade surface directly on the CFD discretization without interpolating the forcing function and transferring the blade mode shape, which usually shows a more gradual distribution with respect to the forcing function. It is more likely that the transfer of the forcing functions from CFD to the FEM model can lead to higher transfer errors.
In this case, the great difference in the fluid and solid domain discretization and the small error in the pressure cloud overlapping in the ANSYS environment are the main causes of result discrepancies, which may become more evident depending on the shape of the pressure perturbation. In the case of IGV excitation, for example, it can be seen in
Figure 14 that the peaks of the real and imaginary parts of pressure perturbation at the LE, in particular near the blade tip, are not well interpolated on the FEM grid, so the agreement between the values in
Table 4 has to be considered satisfactory. On the other hand, considering the case of stator excitation, even if there are some differences in the pressure distribution that are still visible, a better agreement between the original and mapped forcing functions is found, leading to a lower discrepancy in the amplitude values. Additionally, the problem due to the mapping performed by the user on the ANSYS environment may depend on the local shape of the surface and, thus, on the position of the nodes used for the interpolation.
As an overall conclusion, the transfer of the blade mode shape from FEM to the CFD blade surface discretization performed by Tremor is not as critical as for the pressure perturbation transfer. Since modal displacements of the blade have similar smooth shapes on PS and SS surfaces, an error on the surface overlapping that can lead to the interpolation of a value from the wrong blade surface (especially in the thinnest zones) is less critical. This is not true for forcing function distributions, which can be very different between the suction and pressure surface, and the interpolation with the wrong surface can cause remarkable errors. Moreover, the interpolation from coarse to fine mesh and the modal work computation on the grid with higher density ensure a higher results accuracy.
4. Conclusions
The paper reports the validation of a numerical method based on a modal work approach to assess the forced response of bladed disks characterized by a cyclic symmetry. The method requires as inputs the forcing function distributions obtained by a time and space Fourier decomposition of an URANS CFD solution and the corresponding traveling wave mode shapes coming from a modal analysis of the cyclic sector. The method can be applied for a crossing on the ZZENF diagram (resonance condition) or for a generic out-of-resonance condition and computes the scaling factor to obtain actual displacements and stresses from modal results.
The method is validated against numerical results obtained by dynamic analysis computed by the ANSYS solver with the same forcing function distributions that come from the decomposition of a URANS solution carried out with the CFD TRAF code. The FEM ANSYS code is also used for the prior modal analysis required by both numerical approaches, while the aerodynamic damping is again computed by the TRAF code with an uncoupled flutter method, which solves the unsteady pressure response of the flow field due to a vibrating blade row. For this exercise, the mechanical damping component is neglected but can be easily included by adding this value to the aerodynamic contribution.
The validation of the method was firstly performed for a dummy test case representative of a bladed disk with cyclic symmetry for different arbitrary forcing distributions that are not subjected to any interpolation procedure. The comparison between Tremor and ANSYS shows an excellent agreement in terms of displacements.
Finally, the validation has been extended to a more realistic test case representative of a low-pressure turbine bladed rotor excited by two different upstream sources: the IGV wakes with low engine order, and the stator wakes. The two spinning forcing functions were extracted from a multi-row unsteady simulation of the IGV and the downstream stage. This test case is based on a rotor geometry already studied during the EU project FUTURE dedicated to flutter and forced response, but the blade count and rotational speed were modified to obtain a resonance condition at the IGV passing frequency and one out of resonance for the stator passing frequency on the first mode family (bending mode). The results show a good agreement between numerical results and pinpoint the source of slight discrepancy in the approximations of the mapped forcing in the ANSYS environment due to a coarse mesh that smooths the pressure distributions and small errors in the overlapping of the forcing point cloud and FEM surface points before the interpolation. This underlines the higher accuracy of Tremor computations that are performed on a finer CFD mesh, where the interpolation of the mode shapes introduces less discrepancy than the interpolation of the forcing on the FEM superficial mesh.
The validation confirms the capability of the presented approach to predict the forced response of a bladed disk. This approach is strictly connected to the CFD framework and only requires a prior modal analysis, making the tool attractive for its use of an integrated multi-objective optimization procedure that is able to include aeromechanical aspects. Future work concerns the extension of the method to intentionally mistuned bladed row configurations.