1. Introduction
Web applications are now considered one of the standard channels in the World Wide Web for representing data and executing service launches. These resources include social media, finance, education, banking, news pages, TV channels, etc. Web applications store sensitive data, which hackers can steal and gain monetary benefits from.
Thus, to identify the vulnerability of web applications, a static analysis explores the web application’s source code [
1]. Static analysis has the potential to observe every possible path in an application through scrutiny of the source code. However, covering all web application paths during testing leads a false positive result [
2,
3]. False positives are results that are safe but are reported to be vulnerabilities, and thus, execution would not occur, despite the type of user input. In addition, researchers have stated that programmers should distinguish which paths can be executed and that the test cases should be implemented on feasible paths only [
4,
5].
A feasible path is defined as any path on which test cases can be executed. Detection of feasible paths can help decrease the false positive rate of the results of static analyses and, thus, further improve the detection rate for different threats. In addition, detecting the same feasible paths (duplicated paths) from test cases more than once provides a false number of threats existing in the program.
Detection of feasible paths can be achieved by generating test cases of the source code to identify the executable paths among the others. Symbolic execution is a basic approach commonly used in various fields, such as software testing and reverse engineering [
6,
7,
8]. The idea is to execute a program with a symbolic representation of inputs instead of concrete values. The symbol signifies symbolic and concrete values that may be understood from the symbol. Some symbolic execution engines have been deployed. Prominent examples are MultiSE [
6], KLEE [
7], and Java PathFinder (Jpf) [
8]. However, all of these studies focused on the intermediate representation (IR) to convert the source code to a simple form for analysis, such as the static single assignment (SSA) form. Nevertheless, there is significant inflation in the IR code, where new constructions correspond to function abstractions. For instance, the code written for the Low-Level Virtual Machine (LLVM) occupies 600 lines, despite the simplicity of the example [
9,
10]. The analysis of this code was time-consuming, as would be the case for similar examples. Meanwhile, Braun et al. [
11] presented an SSA constriction algorithm to produce a minimal and pruned SSA form. They established that the algorithm they designed builds minimal and trimmed SSA form, which helps decrease the instructions in the SSA form to be analyzed.
Therefore, this paper aims to reinforce the improvements in the static analysis results by proposing a new approach for detecting feasible paths based on minimal SSA representation and symbolic execution. The proposed approach was constructed in such a way that it can (i) detect the total quantity of feasible paths in the source code, (ii) avoid detecting duplicated feasible paths, and (iii) decrease the time required to generate the paths. In addition, IR and binary generation tools and libraries are not commonly accessible for all programming languages, such as Hypertext Preprocessor (PHP), thereby significantly reducing the applicability of current symbolic execution systems [
12]. Therefore, our approach was implemented and tested on PHP as the most popular web application technology [
13].
The rest of the paper is structured as follows:
Section 2 provides background information on static analysis and symbolic execution, followed by related studies in
Section 3.
Section 4 elucidates the proposed detection approach of feasible paths.
Section 5 presents the experimental outcomes of the proposed approach and comparisons with related work.
Section 6 highlights the threats to validity.
Section 7 presents the discussion, and
Section 8 concludes this work and introduces our upcoming work.
3. Related Works
In recent years, various approaches have been utilized to detect feasible paths. We point out some works in this section that are pertinent to our study. Directed automated random testing (DART) [
23] was the first concolic testing study used to reduce the number of test cases to generate program paths. The paths are generated randomly based on the type of the variables, and the conditions of each path are stored until the termination of the program. However, DART suffers from a high number of duplicated paths due to the random process of generating the program paths, which leads to producing the same path more than once.
Forms of early works (for example, the Concolic Unit Testing Engine (CUTE) [
24] and execution generated executions (EXE) [
25]) consider the system environment in the assessment by implementing external calls that make use of real and concrete arguments, which constrains the behaviors that they could delve into as compared to an entirely symbolic strategy, which could be impracticable. In the context of an online executor, this selection can lead to having external calls from distinct and well-defined paths of execution that inhibit each other.
Williams et al. [
26] suggested a prototype PathCrawler tool for automated test case creation to meet the paths requirement. It begins with source code instrumentation in order to determine the symbolic execution sequence whenever the code being tested is executed. Subsequently, the instrumented code corresponding to the test scenario is executed until a complete feasible path set has been assessed. However, the tool faces an explosion of paths created due to extensive combinations.
Sen et al. [
6] suggested MultiSE, where symbolic execution comprises incremental merging of the states without the use of auxiliary variables. The fundamental concept behind MultiSE is based on a different state representation, where all variables are mapped to guarded symbolic terms, referred to as a value summary. They implemented their prototype for JavaScript using the Jalangi framework [
27]. However, MultiSE treats each condition separately, which increases the probability of producing duplicate paths, and it does not support web forms.
Cadar et al. [
7] illustrated the LLVM compiler-based KLEE symbolic execution software [
10], which can solve optimization problems and enhance performance by an order of magnitude and process several programs that may otherwise be intractable. Its search heuristics effectively select paths from large sets of paths to obtain high code coverage. KLEE is also a crucial constituent in several ventures and research such as Cloud9 [
28], GKLEE [
29], KLEENet [
30] and Klover [
31]. Nevertheless, the LLVM compiler is based on the algorithm formulated by Cytron et al. [
32]. The compiler is similar to a non-SSA CFG and records the local parameters into memory, which typically are not in SSA form. The results indicated that about a quarter of the instructions created by the front end of the LLVM are in this format.
Havelund and Pressburger [
8] suggested the Java PathFinder (JpF) translator, which translates Java to Promela, the modeling language required for using the Spin model checker. JpF transforms specified Java code to its corresponding Promela version, which may then be processed. The key drawback of this tool is that it cannot be utilized for substantiating any authentic Java application if no non-trivial quantity of work is completed by its user. For the resolution of this issue, Shafiei and Breugel [
33] recommended an extension, jpf-nhandler, of JpF that enables automation of the handling of native methodologies. Automation of the interlinking for the execution of the native code and the model checking of Java code occurs. However, the extension lacks soundness and, as the author of [
33] stated, it is not comprehensive.
Nguyen et al. [
34] proposed a method (CFT4CUnit) for creating static direction-based test cases specific to C functions. Initially, a CFG is created as a C function that comprises the source code, including the inputs, maximum iteration count for loops, and the coverage conditions. Feasible test sequences are then determined using the backtracking technique, a Z3 satisfiability modulo theory (SMT) solver and symbolic execution for traversing the CFG. This technique’s primary drawback is that it is time-intensive when addressing the constraints under a CFG possessing numerous decisive vertices but many fewer infeasible sequences. Nguyen et al. [
12] proposed the SDART tool, which improved upon the DART [
23] tool, along with their prior research [
34] by integrating these techniques with a static test data-producing technique that could determine feasible paths using relatively fewer iterations. The proposed static analysis scheme creates several partial test paths that traverse unvisited branches. Subsequently, test data creation is attempted by traversing these test paths. Traversed branches are marked in order to prevent revisiting the branches more than once.
Table 1 summarizes the most popular symbolic execution studies that aim to detect feasible paths, the methods and tools that their approaches are based on, the limitations of their studies and the programming language used to implement and evaluate their approaches.
To overcome the limitations of previous studies in detecting feasible paths, our proposed approach aims to decrease the time required to detect feasible paths, which was the main issue in the previous studies that used the LLVM compiler [
7,
28,
29,
30,
31]. Some of the previous studies [
23,
24,
25] also missed some feasible paths because of the use of the Simple Theorem Prover (STP). Therefore, the Z3 solver [
36], as a high-performance theorem prover, could be used to solve different complex theorems [
37]. In addition, we present a method to avoid generating duplicated feasible paths by calculating the weight of each path and avoiding the repetition of other paths with the same weight. Based on our knowledge, there is no available study that has been conducted to detect feasible paths in PHP. Therefore, we implemented and evaluated our approach in a PHP environment, which is considered the most common web technology with which to build a web application.
4. Detection Methodology
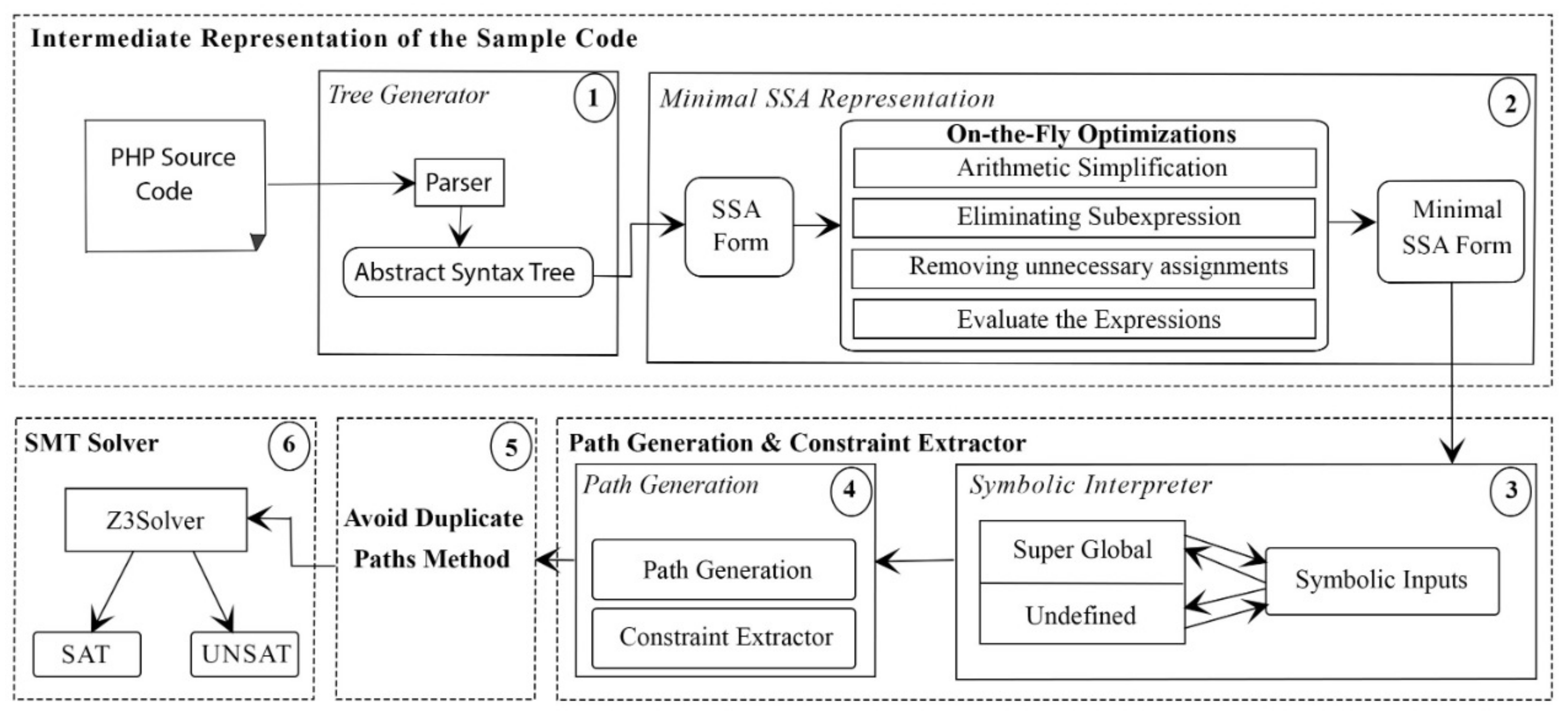
This section presents our proposed approach and algorithm design, including (i) converting the source code to minimal SSA form; (ii) symbolically executing the program with a constraints extractor; (iii) avoiding repeated detection of the same feasible paths among the program paths; and (iv) solving the constraints of each new path.
In this method, the program under test is parsed and converted to an abstract syntax tree (AST). Then, a direct translation from the AST into an SSA-based intermediate representation, which includes optimization of the SSA form to be pruned and the minimal SSA form, is conducted. The second stage starts by assigning symbolic inputs for each superglobal variable (the user input variables) and the undefined variables to represent the variables with unknown values that might affect the path conditions. The path generator algorithm will traverse each block in the SSA form. In each generation, it will flag each path not to be detected again and ensure that all paths were detected once. During the path generation, the conditions inside each path are extracted and stored under that path. The results of path generation and condition extraction are checked again by the introduced method (path weight method) to calculate each path’s weight, and only the paths that have a unique weight are passed to the constraint solver to check their satisfiability (feasible or not) under the given inputs.
Figure 4 shows the full steps of our approach to detect the feasible paths in a PHP source code.
4.1. Parser
The PHP source code should be changed to an intermediate representation, such that it can be converted to SSA format afterward. The structure of the program is indicated by AST; hence, a grammatical and lexical analysis must be performed initially for the source code. In the context of this research, PHP-Parser [
38] was employed for the grammatical and lexical analysis. PHP-Parser produces an AST, which helps immensely with PHP static analysis.
4.2. Minimal and Pruned SSA Form
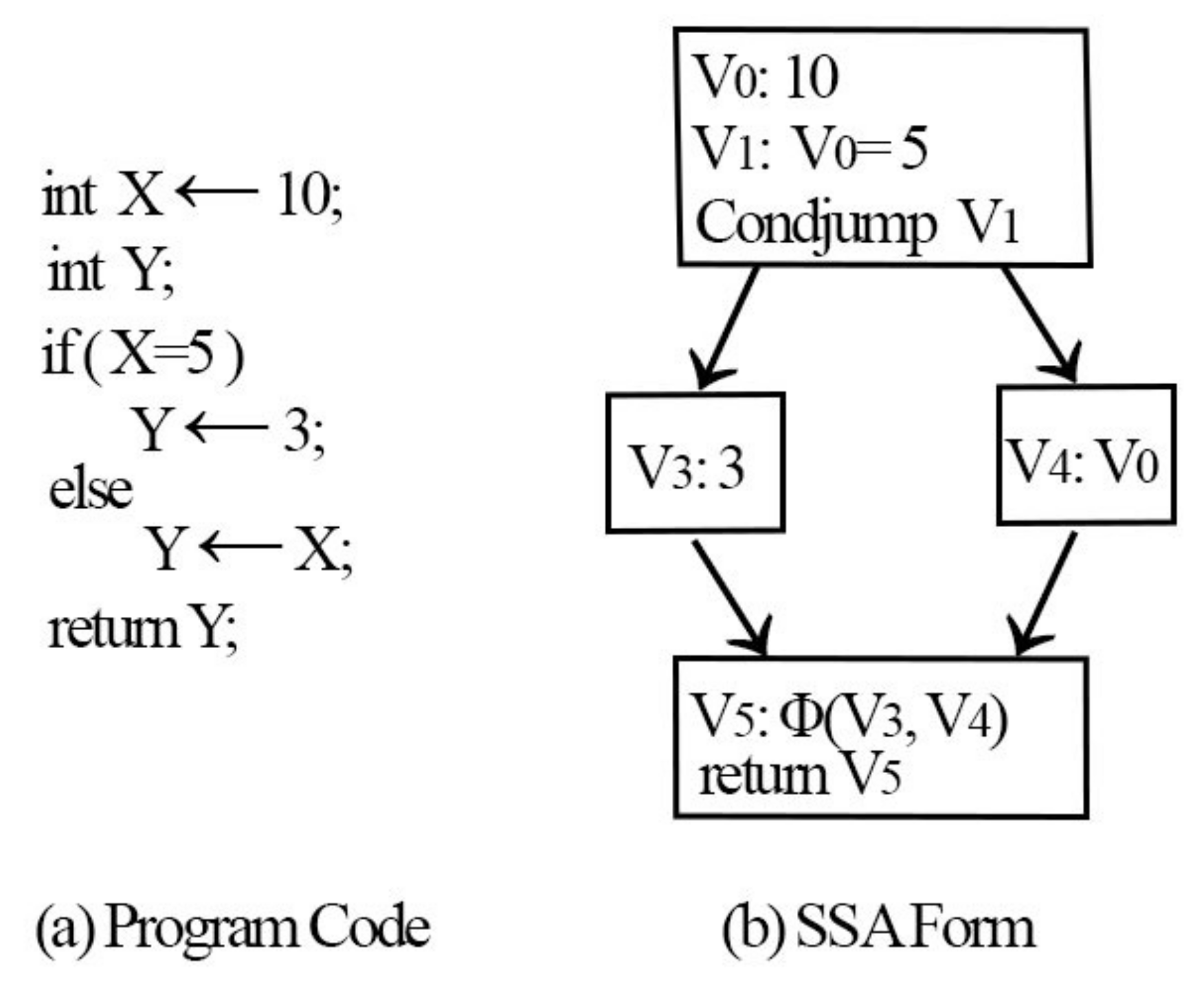
The SSA [
39] form is a property of intermediate representations. This property ensures that each variable is defined and written only once. As a result, programs in SSA form encode explicit data flow relations.
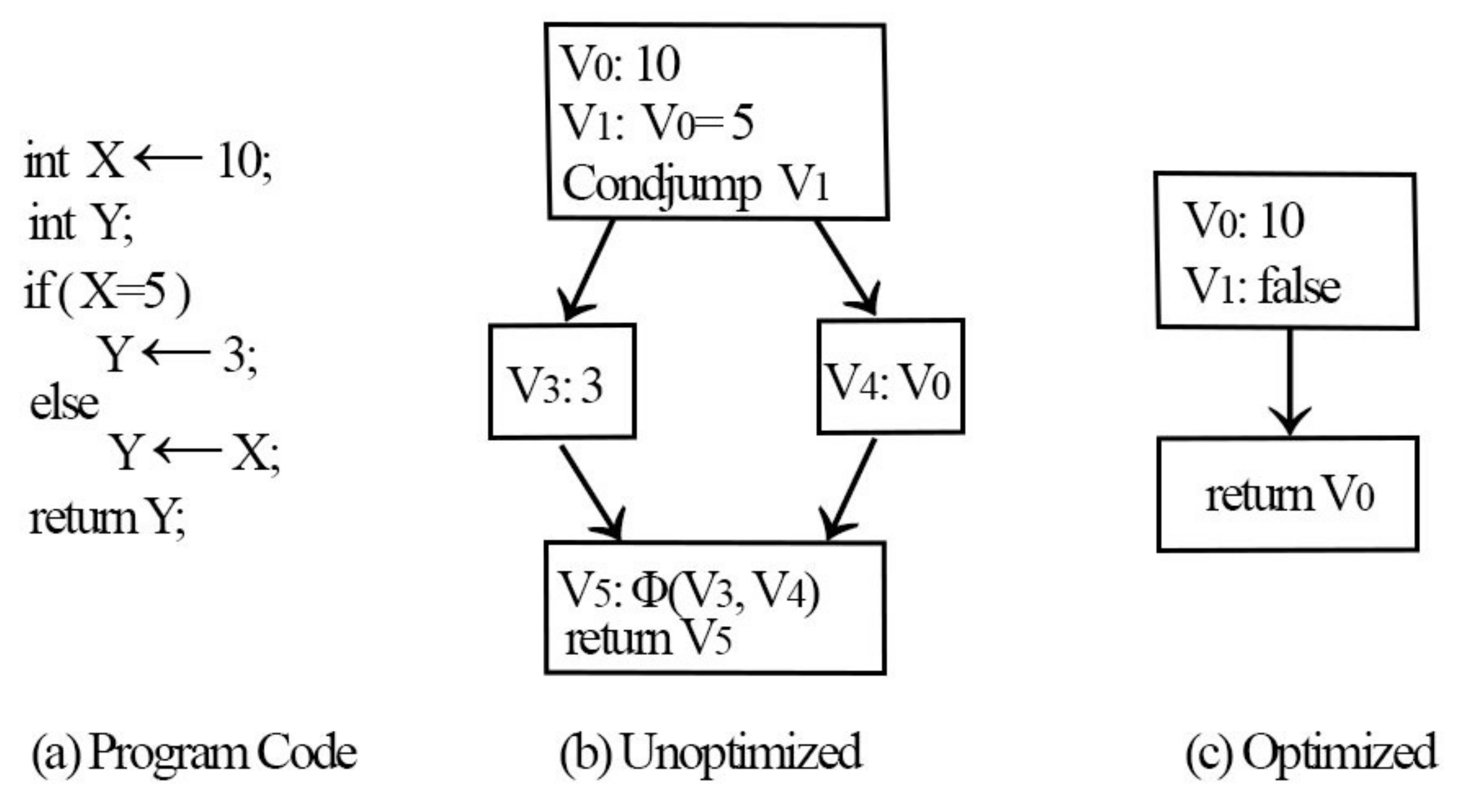
Figure 5 illustrates an example of the SSA form and
function.
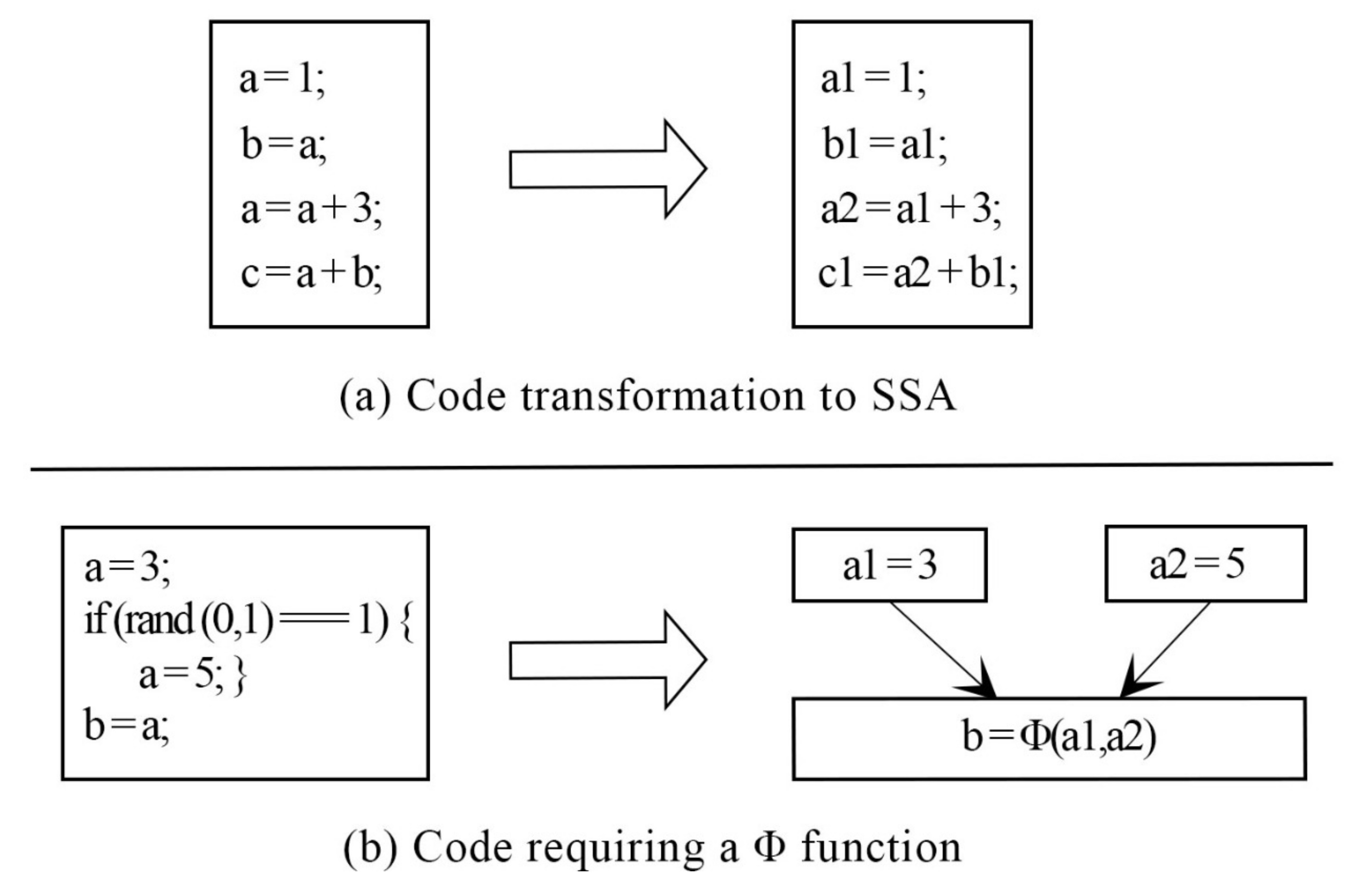
To understand the reasoning behind the SSA representation, a straight-line code is an appropriate way to begin.
Figure 5 shows that a unique name is provided for every assignment made to a variable, and wherever the assignment is used, it is renamed to a new assignment name. The majority of programs comprise join and branch nodes. A unique assignment form referred to as the phi function (
) was used at the join nodes. The operands of the
function represent the assignments to V that reach the join. Any further use of Y is considered a use of V
. The previous variable Y is replaced with new variables V
, V
, and V
. All uses of V
are arrived upon by a single assignment to V
. A single assignment to V
can be found in the complete code, which simplifies the record maintenance process for numerous optimizations.
In this paper, we use the algorithm from Braun et al. [
11] to generate the minimal SSA form, where they used on-the-fly optimizations with an SSA compiler to decrease the number of
functions. Initially, a mathematical simplification is employed where the constructors pertaining to the IR node are subject to peephole optimizations and output simpler nodes wherever feasible. Considering an example, the mathematical expression X–X always amounts to zero. Furthermore, common subexpression removal, reuse of the present values identified using local values, and an evaluation of the constants during compilation are performed—for example,
may be optimized as 6. Finally, the local variables may have unnecessary arguments that must be removed (X = Y is one such example). The SSA form does not require assignments of this form; hence, it is feasible to use the right-hand side value directly. The effectiveness of such optimizations is depicted in
Figure 6.
The minimal static single assignment (MSSA) form before the application of on-the-fly optimizations is depicted in
Figure 6b. When the optimizations are enabled, the initial difference is observed when value V
is constructed. Here, any comparison with zero will return false; therefore, the value is simpler during arithmetic simplification. During the next step, constant propagation converts a comparison with zero returning false. Now, the state at the jump condition is false; therefore, it is feasible to omit the code inside the “then” block. Concerning the “else” block, copy propagation is conducted by assigning V
to Y. Along the same lines, V
vanishes and, ultimately, the code returns V
. The optimized SSA form of the code is illustrated in
Figure 6c. It may be observed from the example that the run-time optimizations suggested by Braun et al. [
11] may potentially reduce the instruction count and
functions in the SSA form. After finding the minimal SSA form of the PHP source code, the next section describes the symbolic execution stage.
4.3. Symbolic Interpreter
During the generation of the SSA form, and once any superglobal variable or any uninitialized variable is detected, we assign a symbolic input for that variable. PHP has several in-built variables called superglobal variables. These variables store the input from the external user, which is unpredictable. Hence, the values are kept symbolic. In the scope of this study, all superglobal variables of the PHP language are considered [
40]. A full symbolic execution assignment algorithm for the symbolic interpreter is shown in Algorithm 1.
| Algorithm 1: Symbolic Interpreter Algorithm. |
![Applsci 11 05384 i001 Applsci 11 05384 i001]() |
For instance, “$name = $_POST[’username’]” points to the value inputted by the external user using the POST technique; hence, the value is not known. Consequently, “$name” is allotted the symbolic value “postsymbolicusername”. Once the symbolic value is assigned for the superglobal variable, this variable is stored in an array so that we can notice if the same superglobal variable is assigned for another variable. Meanwhile, if we detect the use of a variable that has not been defined before, we assign a symbolic value “undefinedsymbolic” for that variable. The complete process of assigning symbolic values to superglobal variables and uninitialized variables is presented in Algorithm 1.
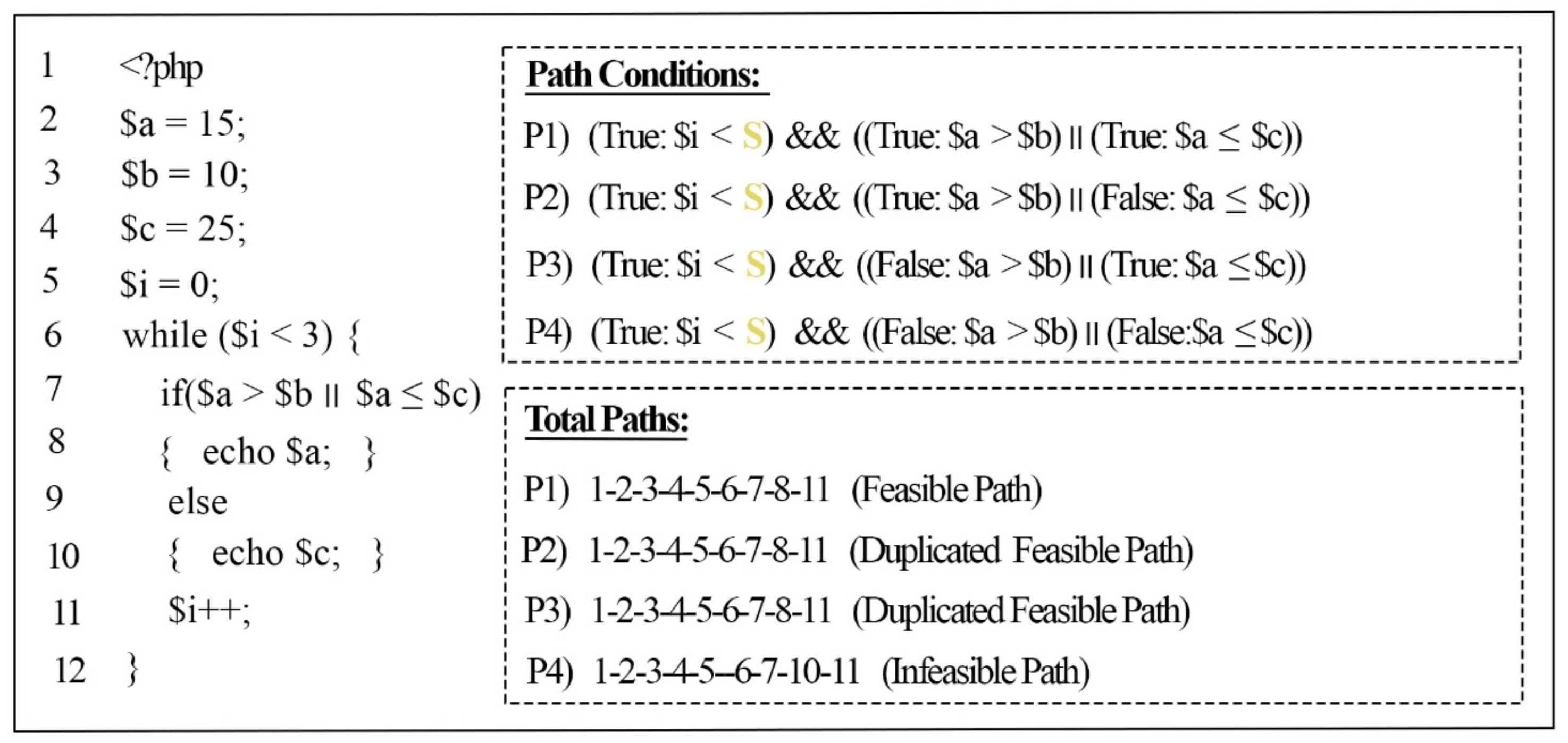
To solve the loop heuristically, we provide a symbolic input for every loop condition variable present in the loop that is being assessed (loop condition), which allows the loop to be evaluated symbolically under the given inputs.
Figure 7 illustrates the previous example code in
Figure 1 with a while loop; this shows the assignment of a symbolic input for the loop condition to be executed symbolically.
The loop in
Figure 7 is defined at Line 6 with the condition (
$i < 3), which means the loop iteration will continue to execute until the condition terminates. In the loop body, a another condition (
$a >
$b ||
$a <
$c) is defined inside the “if” statement at Line 7, which it will execute in each iteration of the loop (3 times during every run of the example program). To avoid the repetition of the loop iteration, a symbolic input (
S) was assigned for the loop condition (
$i < 3). Afterwards, the symbolic loop condition (
$i <
S) was added for each path inside the loop, and the logical operator “AND” (&&) was added to ensure that the path condition of the loop was satisfied and executed at least once.
Since our approach focused on detecting new feasible paths and avoiding duplicated paths, rather than keeping the loop traverse for n number of iterations in the next stage (
Section 4.4), our approach prepared the loop with symbolic inputs. This helped with path generation and constrained the extractor algorithm to connect the symbolic loop condition with the path conditions inside the loop body.
4.4. Path Generation and Constraints Extractor
Each block in the SSA form contains some instructions (i.e., variables, expressions, and conditions) of that block. As the SSA form contains one start block and one end block, it helps to know the start and end points of each path. The complete process of generating the paths and extracting the conditions from the minimal SSA form is presented in Algorithm 2.
The path generator always starts from the first block as an initial block. It will first store the instructions of each block in an array of instructions and those to be used later in the constraint extractor to determine the conditions’ side values. The functions inside the SSA structure are defined as a separate group of blocks. Once the generator finds a function call inside the block, it will move to the function blocks and track the instructions inside that function, and each instruction inside the function is stored in the array of instructions for that path, and the conditions inside that function are also stored in the path conditions. The last block in the function block contains the termination of that function, which will return the generator to the function call instruction.
Each condition contains two or more children based on the condition types (i.e., if and switch). If the generator finds a condition, the generator will choose one of the children it has not yet visited, and the chosen child will be marked as visited. In this way, the generator ensures that it will not follow the same path in the next generation. Each child block will be visited once during the path, and each condition state among the path is stored in the array of conditions. At the termination of the path, a collection of conditions exist in the array of the conditions, and the path generator starts from the first block again to generate a new path.
Since all variables from each block are stored in the array of instructions, the constraint extractor replaces the conditions of both side variables with their concrete values from the array of instructions. For example, a variable
$X was defined with a value of 5, followed by a condition (
$X == 5). The condition has left and right values that must be compared. First, the variable is stored in the array of instructions, and the constraint extractor searches for the condition of the left-side variable in the array of instructions and replaces the variable “
$X” with its concrete value, which is 5. The condition’s right-side variable is a concrete value and, thus, it will not be replaced because it does not exist in the array of instructions for that path. The results of the path generator and constraint extractor are a list of path conditions and their instructions are sent to the Z3 solver to check the satisfiability of these conditions.
| Algorithm 2: Path Generation and Constraints Extractor Algorithm. |
![Applsci 11 05384 i002 Applsci 11 05384 i002]() |
4.5. Avoid Duplicated Feasible Paths
Duplicated paths are related to the branches that contain multiple conditions separated by logical operators (and, or, &&, and ||), as shown in
Figure 1. These branches are split into multiple branches depending on the number of conditions inside them, which gives rise to the possibility of producing numerous paths under the same branches (called duplicated paths). The effects of not addressing these paths are manifested when a sensitive path flow is used to detect a threat in the source code. Duplicating the paths reflects an increase in false alarms in the results (detecting multiple threats in the code whilst all of them are related to one threat). To avoid producing duplicated paths, we introduce a path weight method (PWM) that can avoid generating duplicated paths.
The developed PWM can be implemented in five steps, as follows:
- Step 1:
Assign a unique number to each normal block (non-conditional block) (NB) in the SSA form.
- Step 2:
Count the sum of the NBs assigned a number in the current path and denote it as SNB, where SNB refers to the sum of all NBs in the current path.
- Step 3:
Count the total number of conditional blocks in current path P (denoted as CB).
- Step 4:
Count the total number of logical operators in current path P (denoted as LO).
- Step 5:
Calculate the current path weight W(p) by using the following equation:
The calculation of the current path weight in Equation (
1) is performed by dividing the sum of all blocks’ numbers (SNB) by the difference between the total number of conditional blocks (CB) and the total number of logical operators (LOs) in the current path. The difference between CBs and LOs provides the actual number of CBs without any repetition. The sum of all normal blocks (SNB) is used to give diversity to the weight for each path. Therefore, we can ensure that each path has its own weight, and the same weight is given to the duplicated paths. The PWM’s steps for checking duplicated paths and avoiding them are presented in Algorithm 3.
| Algorithm 3: Avoid Duplicated Paths Algorithm. |
![Applsci 11 05384 i003 Applsci 11 05384 i003]() |
Figure 8 shows the results of the path weight method for the previous example code in
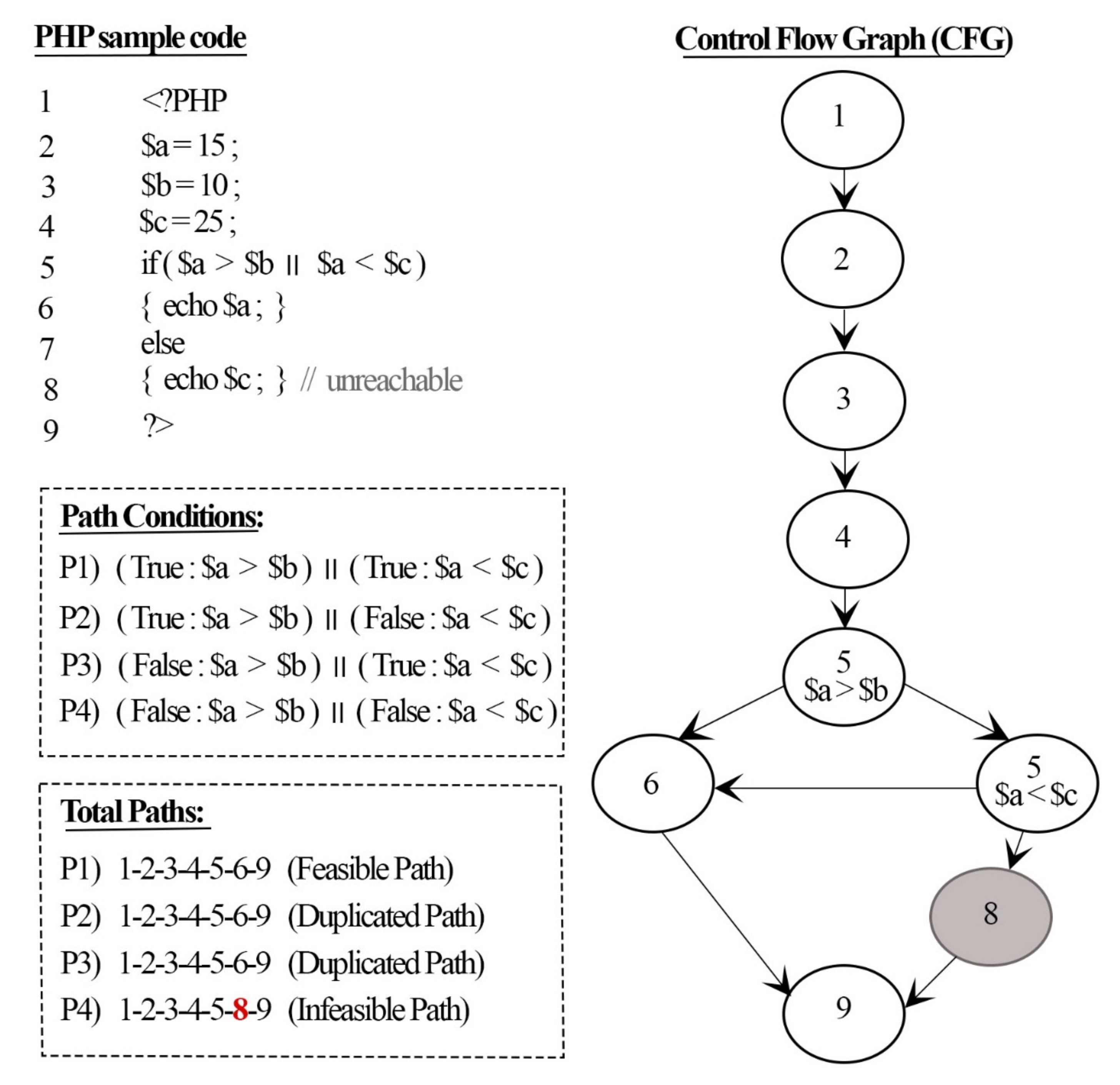
Figure 1. If the path weight has not been detected before (new path), then our approach will proceed to the next step to check its feasibility (such as P1). If our PWM finds a path that has the same weight as that of a path that has been detected previously as a feasible path (such as P2 and P3, which have the same weight (‘7’) as P1), then it will not proceed to the next stage, in which its feasibility is checked, and the path will be considered a duplicated path. However, if our PWM finds a path that has the same weight as that of a path detected previously as an infeasible path (such as P4), then it will proceed to the next stage, in which its feasibility is checked, since the path was not detected as a feasible path before, and there is a chance for the SMT solver to solve these path conditions and consider it as a feasible path.
4.6. Z3 Solver
The Z3 solver is based on the satisfiability modulo theory and was formulated by L. de Moura and N. Bjorner while they were working at Microsoft Research [
36]. The SMT solver works in such a way that when a first-order logic formula is specified, the solver determines if satisfiability is met. Formula f is considered satisfiable if a value that leads to f being true exists. The solver is given inputs regarding the expression and the set of applicable constraints. The solver then attempts to identify a solution applicable under the specified constraints.
The reason behind using Z3 was that it has been established as a high-performance technique for theorem proof [
41]. Additionally, this solver is available for free under the Microsoft Research License Agreement (MSR-LA). Furthermore, it has Application Programming Interfaces (API )s for several languages, which make this tool compatible with several platforms.
Once the path generation produces the condition of each path, it transforms them to the Z3 context based on their guidelines [
36], and the results are sent to the Z3 solver to check satisfiability of those path constraints.
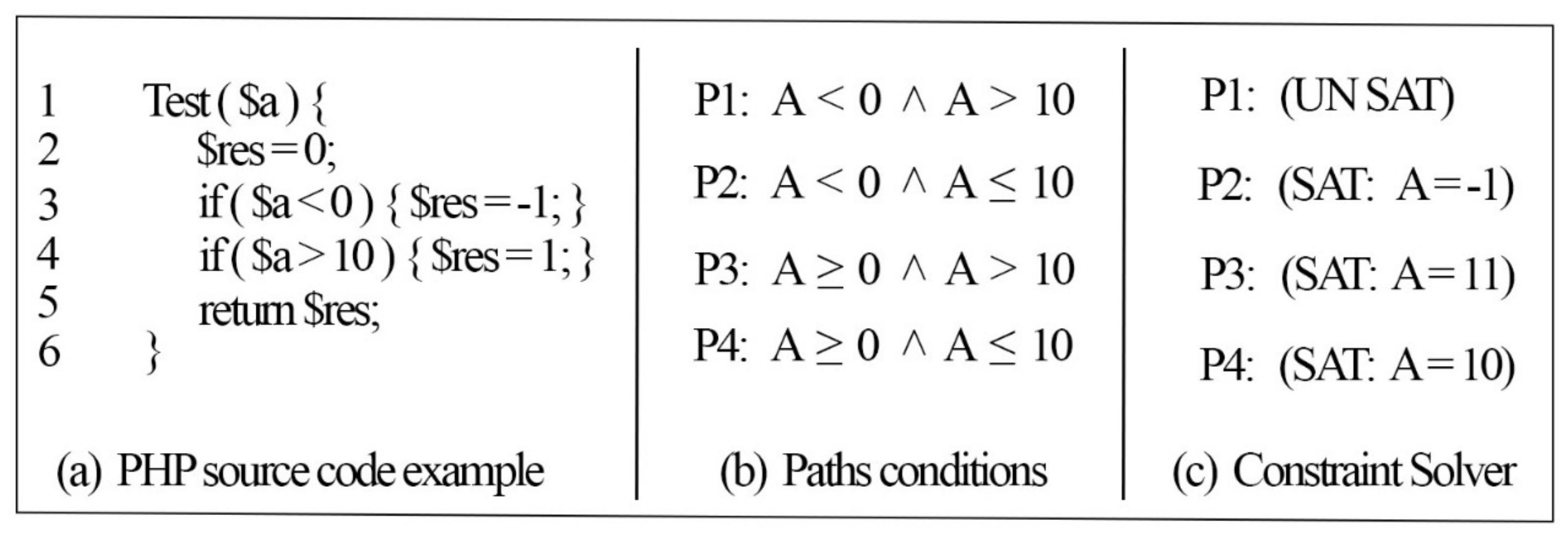
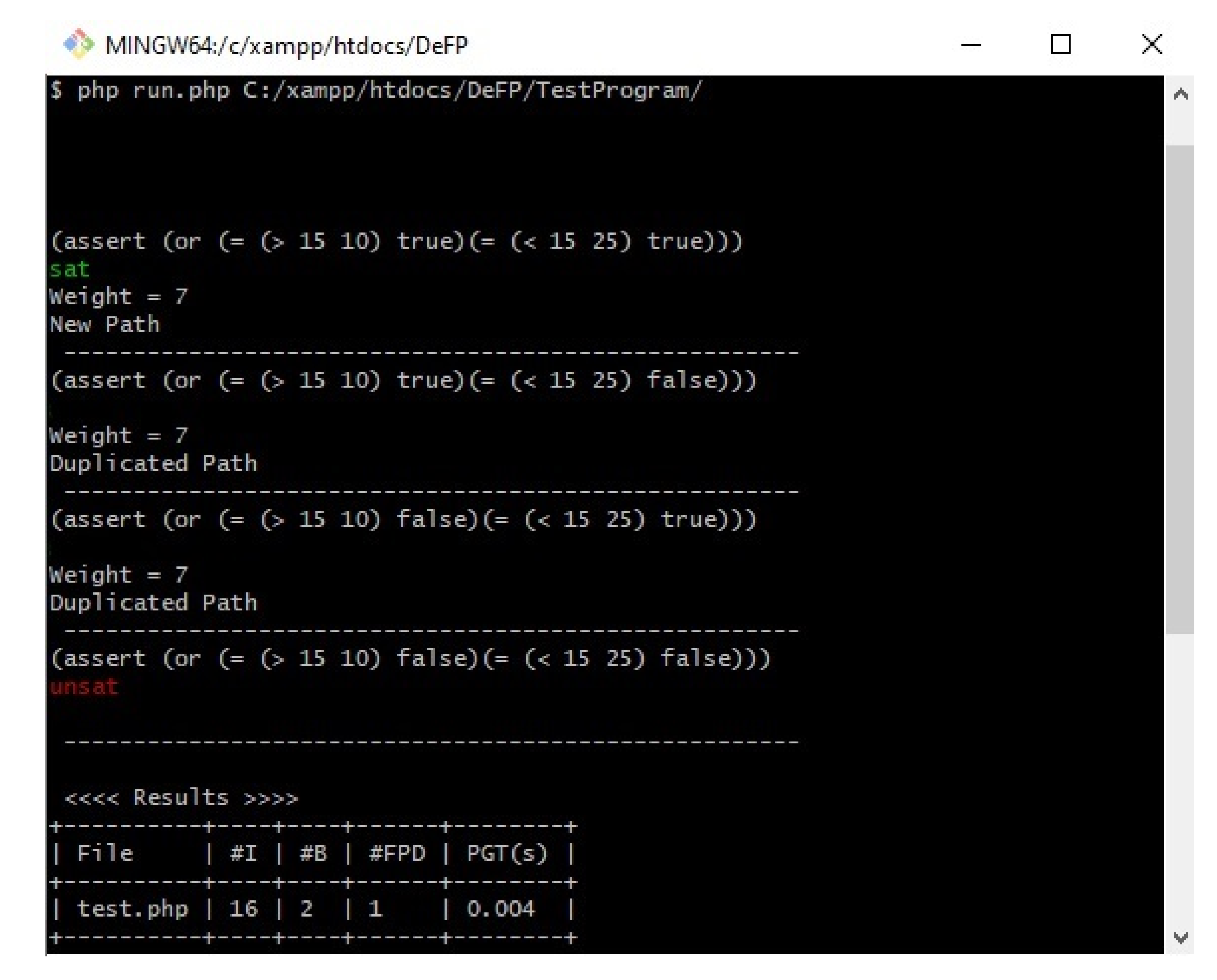
Figure 8 shows the results of our proposed work on the example program in
Figure 1.
The first column in the result table in
Figure 8 shows the file name. The second column shows the number of instructions produced by the minimal SSA algorithm. The third column provides the number of branches analyzed, and the detected feasible paths (new paths) are shown on the fourth column. The last column presents the time (in seconds) required to generate all of the paths, excluding the Z3 solver time.
Figure 8 shows that the first path was checked, and the results indicated that it was satisfiable (sat) under their given inputs. The second and third paths were not checked by Z3solver since they have the same weight as the first path, which was detected as feasible. The fourth path was not satisfied (unsat) by the Z3 solver on the basis of the given inputs. Therefore, it was considered an infeasible path and was not executed at all under the given inputs.
5. Experimental Results and Evaluation
The proposed approach was implemented in PHP, and the implementation followed the architecture in
Figure 4 and the approach presented in the previous sections. The objective of the experimental evaluation was to answer the following questions: (1) Is the proposed approach able to detect the feasible paths and avoid the detection of duplicated paths amongst the test programs (
Section 5.3)? (2) Does the minimal SSA form reduce the time required to generate the paths compared with other studies that used the SSA form (
Section 5.4)? (3) Is the proposed approach able to process a large set of PHP applications (
Section 5.5)?
5.1. The Dataset
The proposed approach focuses on PHP as the most popular web technology for building a web application. To our knowledge, no study has been conducted to detect feasible paths on the basis of PHP. Therefore, we used the same test programs written in C language that were used in related studies [
42,
43,
44,
45,
46,
47,
48,
49,
50,
51]. These programs were rewritten in PHP.
Table 2 presents the characteristics of the test programs, including the number of lines of codes, LoC, the number of branches of each program, B (can be either selection or loop statements, such as IF, IF ELSE, WHILE, FOR and DO), Description, the number of feasible paths (non-duplicated paths), F, and their reference(s), Refs.
The programming language used to write these programs does not affect the results of the programs because target paths are based on the control flow graph; thus, the program does not have a specific statement related to one programming language [
43]. This task is a common practice in testing experiments undertaken by several studies that rewrote these programs in MATLAB [
44,
48]. Others rewrote them in Java [
52,
53,
54]. The source code of each program in C and PHP is publicly available (
https://github.com/Amarashdeh/FP-PHP-C-TestPrograms, accessed on 1 April 2021).
The entire experiment was conducted on the operating platform Windows 10, 8 GB RAM, Intel i5-7200U CPU. PHP version 7.4 was used to build the proposed approach with XAMPP local server version 7.4.
5.2. Performance Evaluation Metrics
The proposed approach started by analyzing the source code to generate an AST. Then, the AST was converted to a minimal SSA form, which is the form that helps to reduce the instructions in the normal SSA form. Two well-defined algorithms were used for the symbolic inputs’ assignments and the path generation including the condition extractor. The entire process of generating the feasible paths was conducted automatically, which means that no human action is needed for generating the path conditions. A path weight method was proposed to avoid detecting duplicated feasible paths. The last stage checks the paths’ conditions by using the Z3 solver. The results of the Z3 solver show the satisfiability of each path and the values of each symbolic input that could satisfy the condition if it is a feasible path.
The proposed approach’s performance was assessed based on the number of feasible paths detected, the number of duplicated paths detected, and the time required to generate paths. “Recall” measures the percentage between the number of feasible paths correctly detected and the actual number of feasible paths existing in the source code. “DuplicatedPathsPercentage” measures the percentage between the number of duplicated paths detected and the total number of paths detected in the program. The precision and recall rates were calculated with Equations (
2) and (
3), respectively.
where
denotes the number of feasible paths detected and
denotes the number of feasible paths that exist in the detected program;
denotes the number of feasible paths detected that are infeasible in reality;
denotes the number of duplicated feasible paths detected.
The evaluation of the time required to generate the paths was performed using the PHP built-in function microtime(), which is a function that returns the current Unix timestamp in microseconds [
55]. By default, microtime() yields a string in the form “msec sec,” where sec is the number of seconds and msec gauges microseconds that have elapsed since sec, which is also stated in seconds. We set up the function at the first stage of generating the SSA form and it ends at the termination of generating the paths.
5.3. Feasible Paths Detection
Table 3 depicts the outcomes of our approach and those of related studies. We compared the proposed approach with the most common engines and tools that are publicly available, such as KLEE [
7] and SDART [
12]. The KLEE engine is the most related work to ours. It uses the SSA form in the LLVM compiler with symbolic execution to detect feasible paths. We selected the latest version of KLEE 2.2, which was released on 7 December 2020. The SDART tool is based on CFT4CUnit [
34] and DART [
23]. It reduces the number of test cases required to generate feasible paths compared with the previously mentioned tools [
23,
34]. The second column in
Table 3 shows the real number of feasible paths (non-duplicated paths) in each program (denoted as #TFP). The third and fourth columns show the KLEE results, where #FD denotes the number of feasible paths detected, and #DFD denotes the number of duplicated feasible paths detected. The fifth and sixth columns show the results of SDART, followed by the proposed approach’s results in the seventh and eighth columns.
Table 3 presents the results of each study on detecting feasible and duplicated paths. Each feasible path generated by each tool was checked to determine whether it is a new path or duplicated from previous detected paths. KLEE detected 45 feasible paths, 10 of which were duplicated. This result means that the number of new feasible paths detected by the KLEE engine was 35. Meanwhile, the SDART tool detected 27 feasible paths, four of which were duplicated. Notably, the four paths were found in the test programs that had more than two conditions at the same branch. The number of new feasible paths detected by SDART was 23. Our approach detected 35 feasible paths without any duplicated paths amongst the results, and all the duplicated paths were addressed and avoided before checking their feasibility.
To answer the first question, we calculated the recall and duplicated path percentages for each study result by using the previously provided metrics (
2) and (
3).
Table 4 shows the recall percentage of each study.
The results of analyzing the test programs in
Table 3 indicate that the proposed approach and KLEE have the same recall percentage (92.1%). The recall rate can reflect the comprehensiveness of the test results. Both approaches adopted the same structure to detect feasible paths. However, our approach reduced the number of instructions in the SSA form by using the minimal SSA form [
11]. Meanwhile, KLEE detected 10 duplicated paths that were detected in the previous test generation. By contrast, our PWM successfully addressed such paths and did not proceed to check their satisfiability in the Z3 solver. SDART’s recall percentage (65.7%) for detecting feasible paths was the lowest in the other studies. The test generation in SDART had an issue in covering the branches that had an infinite loop (fcB2002); it generated 45 test cases, without the ability to cover the last path that is related to the “while” loop. SDART missed 15 feasible paths that were not detected by the test programs. However, SDART was better than KLEE at reducing the number of duplicated paths in the test generation (duplicated path percentage), and the usage of this method shows its efficiency in avoiding duplicated paths under two conditions at the same branch.
5.4. Paths Generation Time
To answer the second question, we compared the proposed approach with KLEE to reflect the reduction in the number of instructions analyzed by the minimal SSA form. KLEE [
7] was implemented as a virtual machine for LLVM. However, the LLVM compiler uses the algorithm of Cytron et al. [
32] to produce the SSA form. The algorithm that we used to generate the minimal SSA form by Braun et al. [
11] reduced the number of instructions in the program.
Table 5 shows the number of instructions (#I) and the time required for each program to generate its paths (T) in seconds. The time shown in
Table 5 excludes the SMT solver’s time to check the satisfiability of each path because many studies have already been conducted to compare the SMT solver’s time and performance [
56,
57,
58].
The comparison of the number of constructed instructions (#I) indicates that the proposed approach generated fewer constructions than KLEE. The number of instructions generated by the programs depends on the LoC of each program and the number of conditions inside each branch. For example, the instructions in programs that have multiple conditions at the same branch (such as ftB2002, tA2008, and ttB2002) are more numerous than those in programs that have one condition inside the same branch. In addition, the results in
Table 4 indicate that the proposed approach reduced the time for generating the paths. The last program (ttB2002) had more branches than the other programs. It had seven branches, five of which contained at least more than two conditions at the same branch. LLVM generated 190 instructions, and KLEE traversed all of these instructions to generate paths in 0.433 s. Meanwhile, our proposed approach generated 155 instructions under the same program and consumed a total of 0.293 s to generate the paths. From these results, we can assume that the proposed approach is efficient at reducing the time required to generate paths.
5.5. Large Scale Programs
Our proposed approach is evaluated with a large set of test cases. This evaluation is carried out to prove that the proposed approach is capable of detecting feasible paths without any duplications from the PHP program. The proposed approach was implemented with 893,575 LoC in 10 WordPress plugins [
59] as shown in
Table 6, where the first column shows the plugins’ names, with the plugin versions tested by each proposed approach in the second column. Column three shows the number of PHP files in each plugin, followed by the line of code (LoC) for each plugin. The number of constructed instructions and analyzed branches are shown in the fifth and sixth columns, respectively. The detected feasible paths (#FD) among each plugin are shown in the seventh column, followed by the detected duplicated feasible paths (#DFD). Lastly, the time required to generate the paths is shown in the last column. We deployed the Cloc (
https://github.com/AlDanial/cloc; accessed on 14 April 2021) tool to count the number of PHP files and LoC in every plugin. Cloc has been utilized in recent studies for similar metrics [
60,
61,
62].
Table 6 shows that the proposed approach detects, in total, 152,669 new feasible paths (Total #FD) within 646.06 s (Total #T(s)), where each path has its own weight (unique weight). It should be noted that the 10 programs consist of a number of strings or pure numerical comparison branches, which belong to data types that can be solved by a constraint solver. Therefore, it is possible to detect a good number of feasible paths using the proposed approach. With regard to the program, i.e., Gallery (a web application allowing users to publish and organize photos in albums), although it contains a large number of branches, the proportion of the constraints that could be solved was not high, owing to the limitations of the constraint solver. Therefore, the proposed approach only detected 2116 paths among the 3093 branches in the Gallery program. In addition, among the analyses of the 10 programs, it was noted that the proposed approach failed to analyze the built-in WordPress functions, i.e., add_action (“list_menu”, function_name), which is quite challenging when it comes to our approach, since it requires an understanding of the built structure of that function in WordPress that can be traversed and analyzed.
On the other hand, if a path is found to possess the same weight as a previous path that has been detected as a feasible path, it is considered a duplicated path. The proposed approach avoided 67,790 duplicated feasible paths (#DFD) among the 10 programs, all which were detected previously as feasible paths. The time required to analyze the instructions and to generate the paths was different in each program based on the number of instructions and conditions that were analyzed.
Since no study has thus far been conducted to detect the feasible paths in PHP, we followed the methods of various studies [
17,
63,
64,
65] to validate the large-scale results by randomly selecting 50 feasible paths from each plugin (detected by the proposed approach) and checking manually whether any of them were duplicated.
Table 7 shows the results when checking for duplications in the detected feasible paths out of the 50 paths that were chosen randomly from each plugin. The first column (program) shows the plugin name, the second column (#FP) shows the number of paths that were chosen randomly for testing, and the third column (#DFP) shows the number of duplicated paths out of the 50 chosen paths.
The chosen feasible paths in
Table 7 were analyzed and we checked whether any duplication existed with the detected feasible paths (i.e., the validation of these paths was implemented by utilizing inputs from Z3Solver to ensure the feasibility of the path). It can be noted that our work successfully accomplished our objective of to producing no duplications in each presented program. This indicates that the proposed work was evaluated accordingly. A sample of the results is shown in
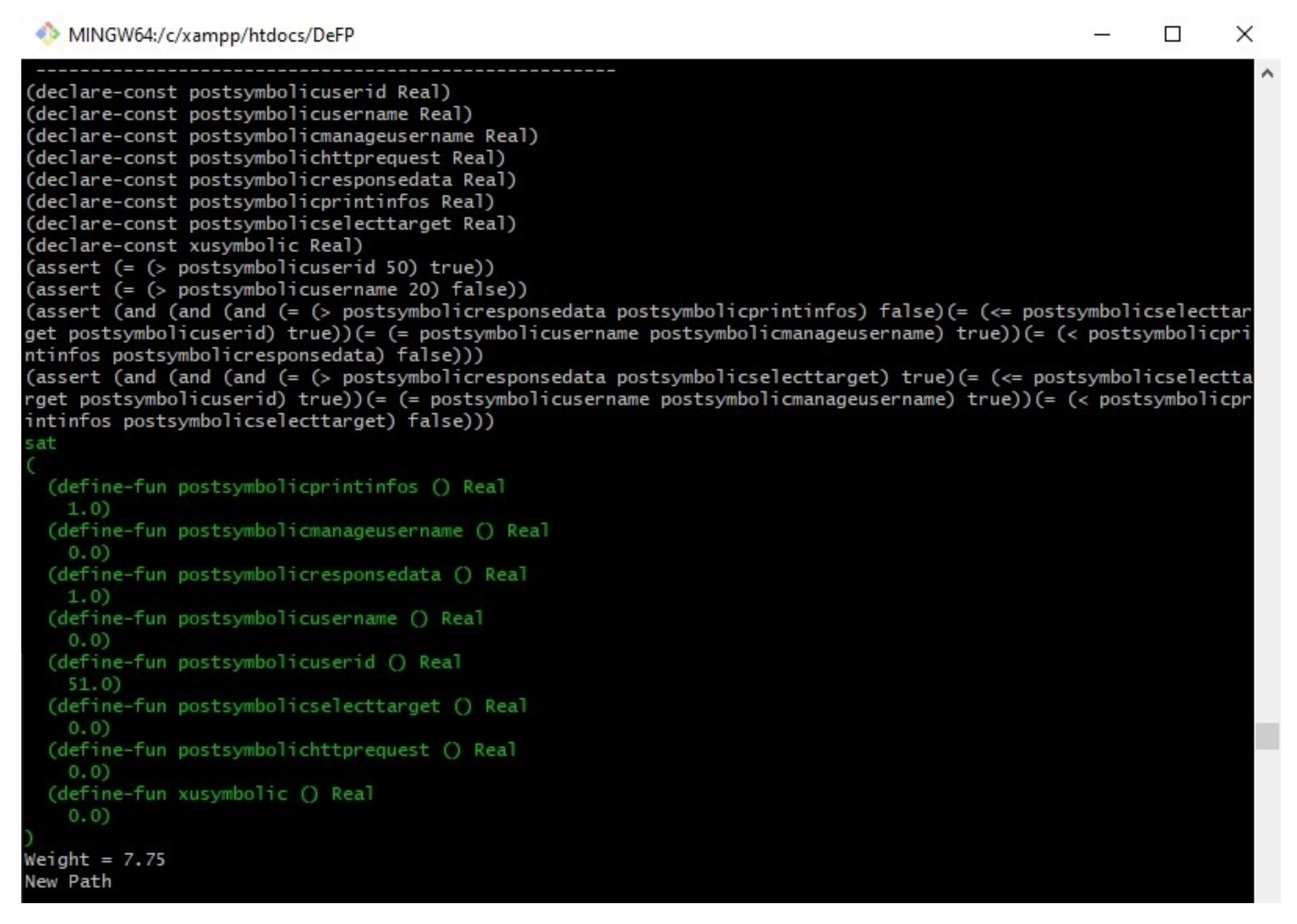
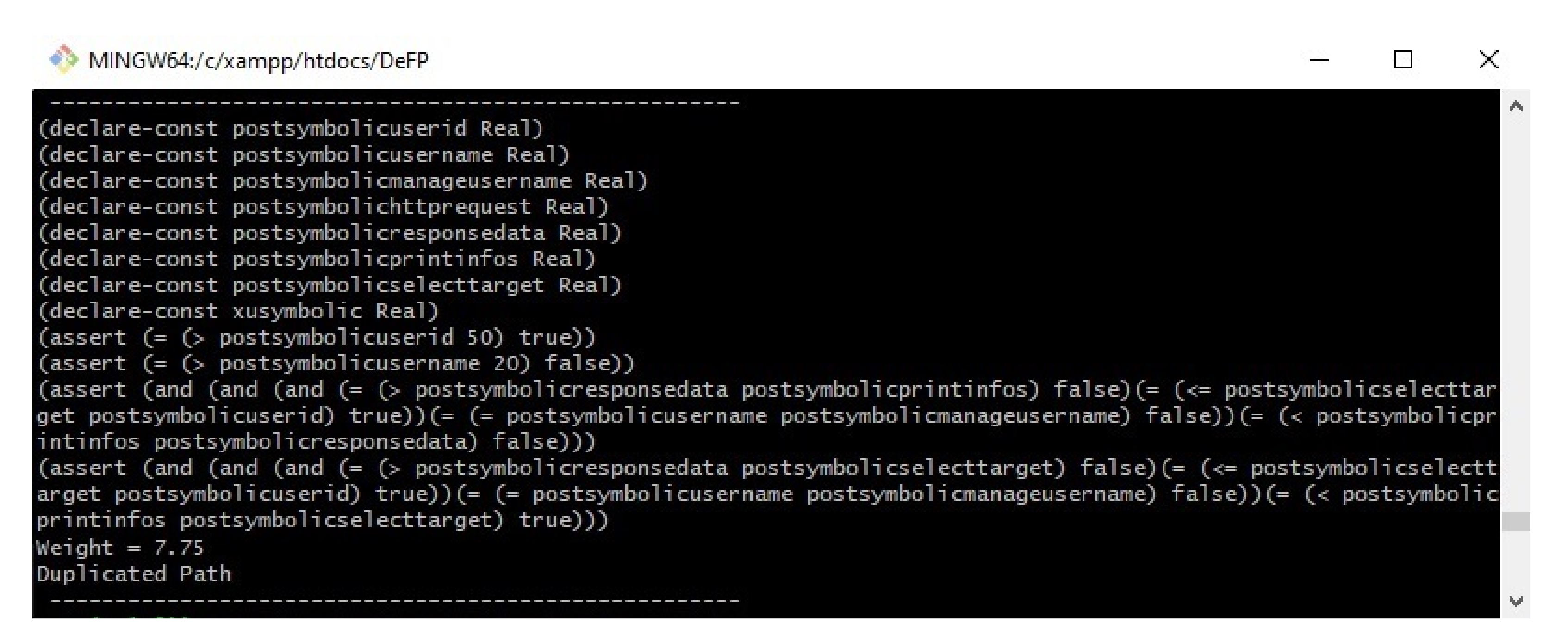
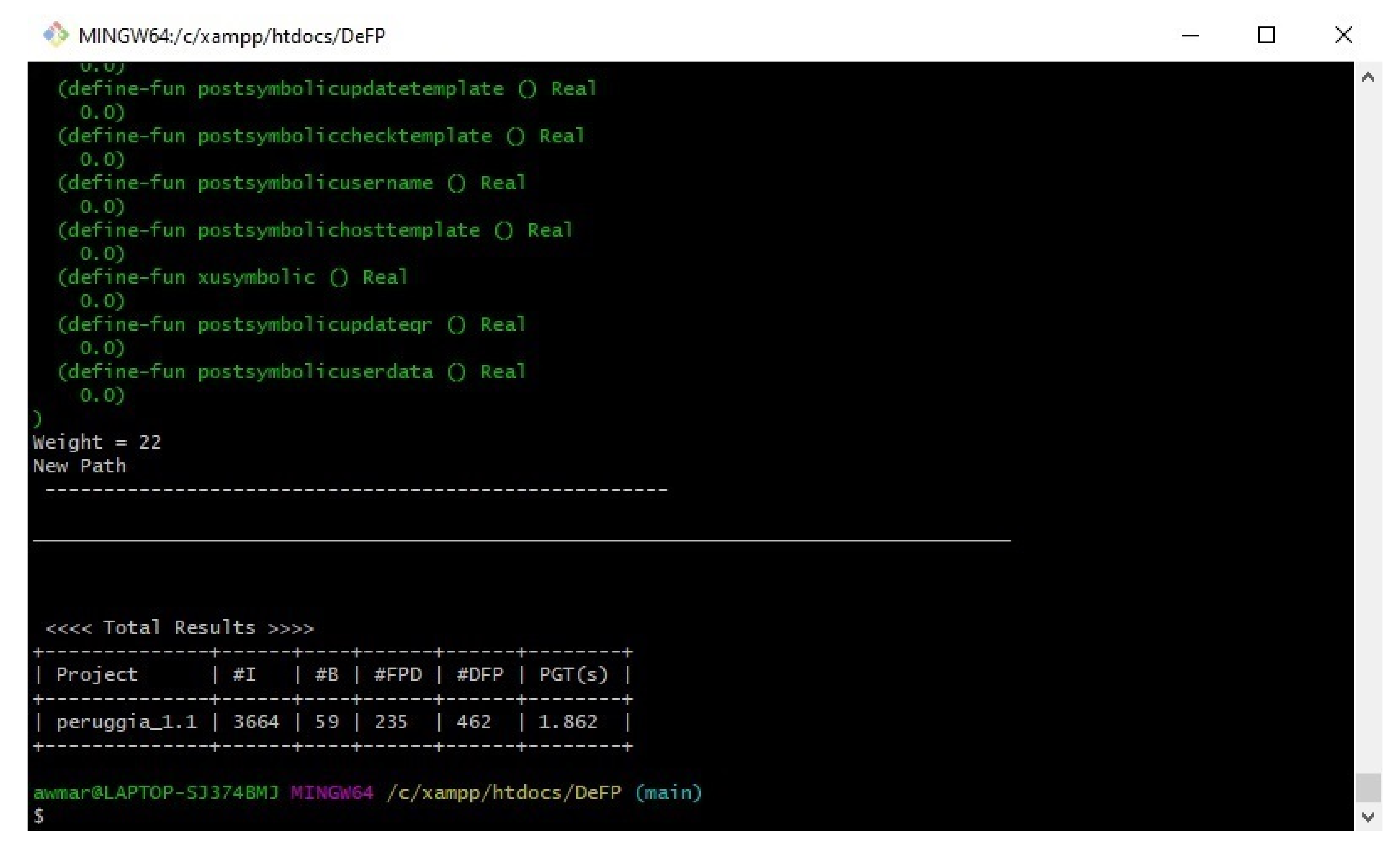
Appendix A (test case of Peruggia).
6. Threats to Validity
While this research demonstrates the effects of minimal SSA representation and avoids duplicated paths in the generation of feasible paths, threats to the validity of certain results remain that the reader should account for when interpreting any outcomes. These threats comprise internal, external, and construct validities, and this section clarifies such problems regarding valid study results.
6.1. Internal Validity
Internal validity threats concern mostly uncontrolled factors that can influence experimental results. The key internal validity threat here lies in probable faults arising in the execution of our strategy. To mitigate this problem, we reviewed our experimental scripts for different feasible path scenarios and cases to ensure correctness before carrying out all experiments.
6.2. Construct Validity
Threats to construct validity mainly involve the relationship between observation and theory, which arise mostly in regard to how performance is measured for the proposed method of generating feasible paths. Test programs were chosen for the evaluation. Moreover, the performance for each feasible path generation strategy was compared via objective metrics such as the amounts of feasible and duplicated paths detected and the time needed for generation.
6.3. External Validity
External validity involves the generalizability of the research findings. Could our approach be implemented with alternative languages effectively? The results indicate that reducing the number of instructions in the SSA form helps decrease the time required to generate the paths. In addition, the proposed method for avoiding duplicated paths has proven its efficiency in avoiding the detection of duplicated paths. In the future, we intend to experiment with various applications written in different languages, which entails creating a minimal SSA form in such languages. Then, the approach could be generalized to several other languages.
The proposed approach in PHP was compared with C-based approaches, where the number of feasible paths and duplicate paths are the same in both languages. The programming language used to write the 7 test programs does not affect the results of the programs because the target paths are based on the control flow graph; thus, the program does not have a specific statement related to one programming language [
43]. However, it would have been better to test the time spent on implementing the paths in each language using the same programming language. The algorithm created by Braun et al. [
11] was previously compared with that of Cytron et al. [
32], and the results indicated that a non-optimized implementation of the algorithm of Braun et al. [
11] is somewhat faster than Cytron et al.’s [
32] algorithm. Therefore, using Braun et al. [
11] algorithm, our results were significantly better than the results obtained using KLEE, as the Braun algorithm helped to reduce the number of instructions to be analyzed and the time required to generate the paths. However, to increase the confidence in the results, in the future, we aim to enhance the proposed approach with other algorithms and provide a full comparison based on PHP (as there are no currently available studies conducted on PHP).
7. Discussion
The proposed approach aims to strengthen studies on detecting feasible paths based on PHP. We selected PHP for two reasons. First, it is widely used in server side web application development, with PHP programs having been used in some 21 million online domains. Second, PHP has long been the left of prior research on the static detection of Internet vulnerabilities, and thus, it has readily available benchmarks. Therefore, the proposed approach would be useful for future studies by implementing their security vulnerability method on the detected feasible paths to help reduce the false positive rate in their results.
To our knowledge, no study has focused on detecting feasible paths in PHP. Thus, we compared our outcomes with related studies that used C language [
7,
66], and the results demonstrate the efficiency of our proposed approach in detecting feasible paths, avoiding the detection of duplicated paths, and reducing the time required to generate paths. Static analysis differs from dynamic analysis in that it can cover 100% of code lines. However, it cannot be conducted on multiple technologies such as PHP, Java, etc. Each approach focuses on one technology and analyzes that technology only.
KLEE [
7] is a symbolic execution tool implemented as a virtual machine for LLVM. Nevertheless, the LLVM compiler uses the algorithm of Cytron et al. [
32] while mimicking non-SSA by placing every local variable into memory, which is typically not in the SSA form. This method comes at the expense of expressing simple definitions and the use of such variables involving memory operations. Around 25% of all instructions shown to be generated by the LLVM front end can be categorized as such. These variables are eliminated by SSA construction immediately following IR construction. The algorithm that we used to generate the minimal SSA form, by Braun et al. [
11], was compared with that of Cytron et al. [
32], and the results indicated that a non-optimized implementation of the algorithm of Braun et al. [
11] is somewhat faster than the heavily optimized implementation of Cytron et al.’s [
32] algorithm within the LLVM compiler. The experimental results of the proposed approach indicate that our approach is more effective than KLEE [
7] in terms of the time required to generate paths amongst program instructions. Furthermore, we introduced a method to avoid detecting duplicated feasible paths.
It is worth mentioning that the proposed approach could be implemented using other programming languages such as C or Java. However, first, this would require finding the minimal SSA representation of those languages by applying on-the-fly optimization to the original SSA form, in a similar manner to the algorithm by Braun et al. [
11]. Then, the symbolic interpreter and path generation could be used to generate the path conditions. In addition, the proposed path weight method proved to be useful to address the duplicated paths and could be implemented using other programming languages to eliminate the duplicated paths.
The limitation of the proposed approach is that it focused only on PHP, because the nature of static analysis is that it can only analyze the source code of one technology at a time. The solution for this issue is to build the proposed approach based on those technologies or to propose an approach based on dynamic analysis. However, using dynamic analysis would mean that 100% of LoC cannot be covered, causing some missing paths to not be detected [
67]. Furthermore, with such dynamic analytical approaches, it might not be possible to acquire a deeper understanding of how an application should behave, which may lead to lower rates of detection.
8. Conclusions
This paper proposed an approach to detect feasible paths based on minimal SSA representation and symbolic execution based on PHP. It starts by parsing the source code to present an AST, followed by converting the AST to minimal SSA form, which is later optimized to produce a minimal SSA form to decrease the number of instructions and the number of functions that would be analyzed. A symbolic input for each superglobal variable and uninitialized variable is assigned, and the paths and the conditions among each path are generated. Furthermore, we introduced a method for avoiding detecting duplicated feasible paths. The path conditions were the target for the Z3 solver to check the satisfiability. To evaluate the proposed approach, we conducted experiments using seven test programs that have been used in the related studies and 10 large scale web applications. The results obtained indicated that the proposed approach improved the time required to generate the paths and avoided detecting duplicated feasible paths. For future works, we plan to implement the proposed approach based on another language such as C or Java. The proposed approach can be improved by implementing it on a multiprocessor or distributed systems, which it will help to decrease the time required to generate the paths, especially for large systems. The proposed method (PWM) has the ability to avoid detection of duplicated feasible paths; thus, it could be combined with other evolutionary algorithms (i.e., as part of the fitness function in genetic algorithms) to reduce the number of iterations that will detect the same feasible paths more than once (duplicated paths). In addition, we will attempt to combine the proposed approach with taint analysis to detect security vulnerability in web applications. We expect the proposed approach to help decrease the false positive and false negative rates of static taint analysis. Moreover, the proposed approach could be extended to export the features of the source code, which could help machine learning algorithms to obtain knowledge on program flaws.