Abstract
In this paper, an improved coyote optimization algorithm (ICOA) is developed for determining control parameters of transmission power networks to deal with an optimal reactive power dispatch (ORPD) problem. The performance of ICOA method is superior to its conventional coyote optimization algorithm (COA) thanks to modifications of two new solution generations of COA. COA uses a center solution to generate an update step size in the first solution generation and produced one new solution by using random factors to diversify the search space in the second solution generation. By tackling the drawbacks of COA, ICOA can reduce control parameters and computation steps, shorten execution time, and provide better results. ICOA is compared to its conventional COA for three standard IEEE systems of 30-, 57-, and 118-buses with continuous and discrete control variables. Moreover, three other algorithms such as water cycle algorithm (WCA), salp swarm algorithm (SSA), and sunflower optimization algorithm (SFOA) have been also implemented for further investigation of the real performance of the proposed method. All the applied methods are metaheuristic algorithms based on population and randomization. The result comparison from the test systems has indicated that ICOA can provide higher solution quality than other methods with reasonable execution time. Therefore, ICOA is a reliable tool for finding optimal solutions of the ORPD problem.
1. Introduction
1.1. Motivation and Incitement
Nowadays, ORPD plays an extremely important role and is acknowledged by the interest of engineers and managers as well as a number of researchers in power system planning and operation areas [1]. The ORPD problem has many complicated constraints and different single objectives [2]. The main target of the ORPD problem is to cut the active power loss on conductors and improve the profile of load voltage, while keeping operating parameters of electric components within allowable ranges. In the ORPD, active power generation of PPs is predetermined, while the voltage of PPs is tuned reasonably. In addition, tap of transformers and generation of capacitors are also tuned for keeping values of reactive power generation of PPs, currents of conductor, and load voltages within allowable operating ranges [3]. Therefore, finding solutions of ORPD is one of the greatest challenges for scientists, and optimization algorithms become believable mathematical tools.
1.2. Literature Review
For reaching the targets of the ORPD problem, various optimization methodologies have been recommended such as deterministic algorithms and metaheuristic algorithms [4]. All of these algorithms comprise original deterministic algorithms, modified deterministic algorithms, original metaheuristic algorithms, modified metaheuristic algorithms, and crossbreed heuristic algorithms. Deterministic algorithms [5,6,7,8] are the earliest proposed methods with the acceptable solution quality and the existence of many handicaps not satisfying readers. Quite the opposite, metaheuristic algorithms such as family line of GA [9,10,11,12,13,14], family line of PSO [15,16,17,18,19,20,21,22,23], family line of DE [24,25,26,27,28], GSA groups [29,30,31], and other methods [32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52] are later proposed for good solution quality.
Methods miming the rule of natural selection or heredities, relating to the terms of genetics, crossover, and mutation selection, are called GA. AGA [9] is a reform of the genetic algorithm. SARCGA has been recommended in [10] by using simulated binary crossover, binary tournament selection, and polynomial mutation distribution of RCGA. In [11], HLGA is an incorporation of loop method and GA in which striking global search characteristic of GA has been used to exploit large solution spaces, whilst the loop method has played a task of search within the predetermined zones found by GA. In [13], authors have solved the ORPD problem by applying standard GA with Roulette wheel-based selection mechanism and improved GA with classification selection mechanism. A new different version, called SGA [14], was introduced in 2018 for handling the ORPD problem considering power-loss minimization only. A different optimization technique, which is called particle swarm optimization, is also not less famous than GA. It includes original PSO [15] and lots of variants such as CLPSO [16], ALC-PSO [17], PSO [18], PSO-IPG [19], HPSO [20], HPSO-ICA [21], PSO-GT [22], and HPSO-TS [23]. HMAPSO is a combination of GA, multiagent system and the excellent characteristic of PSO. Therefore, the method is capable of finding solutions better than other implemented methods such as GA, PSO, HPSO, and MPSO. PSO-IPG [19] is more effective than PSO-AIW, PSO-AAC, SPSO-AAC, PSO-CF, PSO-PG, PSO-SWT, and PSO-PGSWT.
A large DE group consisting of standard DE [24], DE-AS [25], MTLA-DDE [26], QODE [27], and IABC-DE [28] has been reapplied or newly recommended for the ORPD problem. The purpose of such methods is to overcome some shortcomings of DE, such as premature convergence to not very high-quality solutions and easily getting stuck into less effective solutions by improving main stages of DE or combination of DE and other methods with more potential characteristics. In DE-AS [25], authors have modified mutation and selection mechanisms of DE by applying VSMF and PST rule used in the ant system. Using both VSMF and PST has supported the method to achieve not only good solution quality but also avoid consuming time manner better than PSO and DE through IEEE 30-bus system with minimizing power-loss objective function.
In addition to the mentioned method groups, a high number of other methods have been used for solving the ORPD problem via different systems with single objective as well as multiple objectives. These methods are GSA [29,30,31], ACO [32], QOTLBO [33], TLBO [33], GBTLBO [34], MGBTLBO [34], CSA [35], and ICSA [36], HAS [37], CKHA [38], HFA-NMS [39], GWO [40], ABC [41], EMOA [42], DSA [43], ALO [44], ICBO [45], GBBWCA [46], JA [47], MFO [48], MOGWA [49], WOA [50], ABC-FF [51], and CSOA [52]. Among these methods, QOTLBO [33], GBTLBO [34], ICSA [36], HFA-NMS [39], ICBO [45], GBBWCA [46], and ABC-FF [51] are improved versions of original methods in aim to find more promising solutions than those of original methods for the ORPD problem. In [33], authors have reapplied the modified learning technique based on quasi-opposition developed in [53], while the original teaching technique of TLBO has remained unchanged. In [34], GBTLBO and MGBTLBO were constructed by using different modifications on new solution generation techniques. GBTLBO applied the Gaussian mutation technique, while MGBTLBO used both the Gaussian mutation technique and the modified learning technique based on mutation technique (rand/2 mode) of modified DE in [54]. ICSA, which was applied in [36] for the ORPD problem, was first developed in [55] for solving optimization benchmark functions. Compared to original CSA, ICSA used different lower bound and upper bound constraint handling method and reduced one new solution generation. ICSA has been compared to different PSO methods for performance evaluation, but the comparisons with original CSA have not been carried out. Thus, the improvement of ICSA over CSA is still questionable.
In general, authors have tried to develop better optimization algorithms for finding better optimal solutions than those of previously publicized algorithms. Approximately all demonstrations have been based on quality of the most optimal solutions and convergence characteristic of the best run among the number of runs. As compared to previous methods shown in earlier studies, algorithms have not been proved persuasively. The settings of control parameters or the comparisons of control parameters have not been clarified or just have just been analyzed sketchily. Some studies were based on execution time to conclude potential search speed of applied methods; however, they have forgotten that the same methods run on different computers would result in much different computational time.
1.3. Contributions and Paper Organization
In this paper, the concerned ORPD problem with three different standard IEEE systems consisting of 30-, 57-, and 118-buses was solved by ICOA, which was first developed by replacing two lowly effective techniques of standard COA. COA, a novel population-based metaheuristic algorithm, was developed by Juliano and Leandro in 2018 [56]. COA achieved a smaller average, especially for hybrid benchmark functions and cases with high number of variables. However, the real performance of COA for engineering problems such ass ORPD has not been demonstrated persuasively, since there has been no application so far. However, COA has not achieved good results for other problems in engineering, and it has been suggested to be modified [57,58,59]. For the cases of solving benchmark functions, many functions have real optimal solutions with zero values, and construction of COA has produced solutions around the real ones. In fact, in the first generation of each iteration, COA produced center solutions, and then the new solution was newly produced based on the center ones. The center ones are around the middle point of upper and lower boundaries. The feature unintentionally supports COA to exploit the search space, wherein real global optimum solutions are existing for cases of benchmark functions. Unfortunately, the feature is not effective for the ORPD problem because the real optimum solutions of the ORPD problem are not around the center ones. Therefore, the proposed ICOA method applied the first modification on the first generation by canceling center solutions and using the most effective solution so far. The second modification has been proposed due to low efficiency of the second generation. In the second generation, COA produced one new solution for each pack based on randomization, but there must be selection condition for the randomization. Thus, the second generation is time consuming, but its effectiveness is not high. Basically, the feature is appropriate for the case that approximately all current solutions are lumped in local optimum zones. It can be supported to refresh almost all solutions except the best one, resulting in a high possibility of explore other zones effectively and quickly rather than thank to nature ability. Therefore, in the second modification, we have used another strategy for producing such new solutions of each pack. Thanks to the application of two modifications, the proposed ICOA approach can solve ORPD more effectively and robustly than COA in terms of better stabilization of found solutions as well as finding more effective solutions faster. In addition, the proposed ICOA approach is also competed with other applied metaheuristic algorithms including original ones, improved versions of original ones together with other hybrid methods mentioned above. The IEEE 30-, 57-, and 118-bus power systems with three single objectives, being the TPL, TVD, and L index, are used for comparison and conclusion. The main contributions of the study can be summarized as follows:
- Show the structure of conventional COA and indicate its strong points and weak points. Based on found strong and weak points, good features of COA are retained, but bad features are changed by applying modifications,
- Simulate the result for the modified method and its conventional method for all study cases to indicate the impact of modifications on the performance of the proposed method,
- Provide a strong optimization approach to get good solutions for the ORPD problem. Power loss, voltage deviation, and voltage stability of the applied systems become better by the solutions provided by the proposed approach,
- The proposed method can solve the ORPD problem faster than other compared methods.
In addition to the introduction section, the other parts of the paper are as follows: Description of concerned the ORPD problem is shown in Section 2. The original COA and the proposed ICOA method are explained in detail in Section 3. The whole computation procedure of solving the concerned the ORPD problem by using the proposed ICOA approach is given in Section 4. Section 5 shows the comparison of results obtained by the proposed methods and other methods. Finally, the conclusion is given in Section 6. In addition to references, optimal solutions obtained by the proposed ICOA method are also included at the end of the paper.
2. Optimal Reactive Power Dispatch Problem
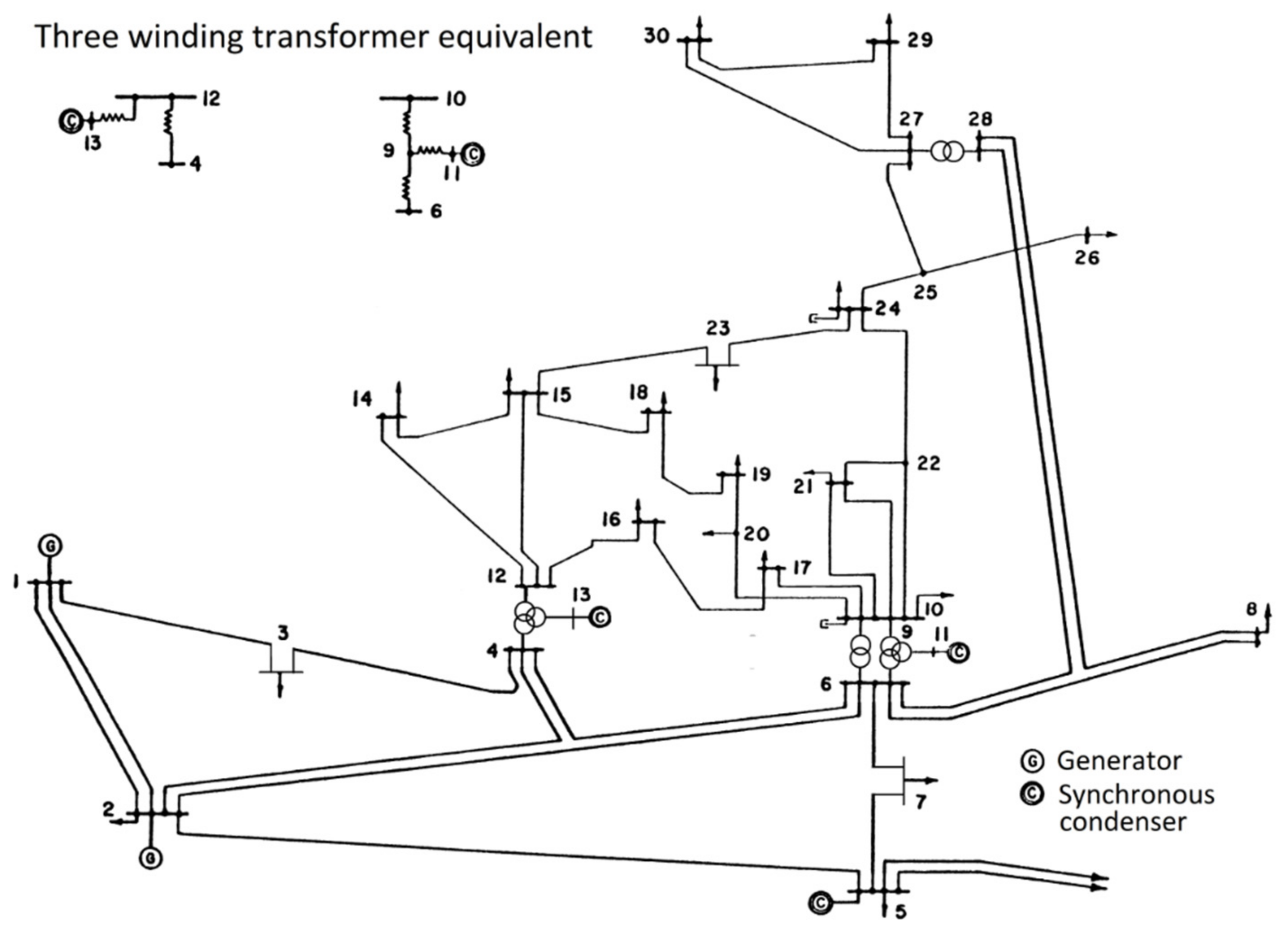
In the ORPD problem, systems with electric components shown in Figure 1 are considered. Due to the given active power generation of power plants, three single objective functions are considered to be minimized, while constraints are strictly imposed on electric components and other factors. Basically, constraints of electric components are represented by inequalities while those of other factors are expressed by equalities. The expression can be observed by using the following mathematical functions:
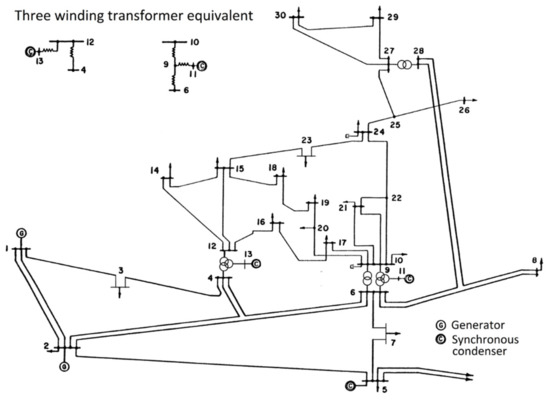
Figure 1.
The IEEE 30-bus power system.
2.1. Objective Functions
Minimization of total active power losses (TPL) in all branches: Total energy losses in transmission power network are significant because current magnitude flowing through conductors are high and the length of transmission lines can be up to hundreds of kilometers. In order to reduce the cost of energy losses, the minimization of total power losses is a unique solution so far. The total power losses can be found by the following formula:
Minimization of total voltage deviation (TVD): In transmission power network, voltage magnitude of load buses and generator buses are the primary concerns for stable operation of the network. The voltage of generators can be controlled by the adjusting exciter, while voltage of loads is dependent on parameters of other components in transmission power network. The good voltage profile is a target of operation of power systems, and it can be achieved by minimizing total voltage deviation. The total voltage deviation is calculated by the model below:
Minimization of voltage stability-L index: In transmission power networks, voltage of load is not stable and fixed at a value due to the change of consumed reactive power and active power. This can lead to different cases of power system status, high voltage, and voltage collapse. Basically, L index is in a range from 0 to 1 in which 0 is the best case and 1 is the worst status of power system. Therefore, the voltage stability enhancement can be achieved if L index is very close to 0 [11]. In order to get the target, L index at each load bus is determined first, and then the highest L index of a bus is selected for minimization. Li index of the ith bus is first calculated by [11]:
Then, L index is determined by choosing Li with the highest value (i.e., L index = max(Li)).
2.2. A Set of Constraints
The set of constraints imposed on the ORPD is described as follows:
Lower bound and upper bound constraints of generators: As explained in Section 2.2, active power output of generators are known and always within lower bound and upper bound. Thus, the control of each generator is only to monitor and adjust reactive power and voltage magnitude within an allowed range. Generators can be working stably if the following rules are always obeyed:
Lower bound and upper bound constraints of shunt capacitor banks: At some buses in transmission power network, shunt capacitor banks are additionally installed with intent to supply reactive power to loads and reduce voltage drop in transmission lines. The reactive power output of shunt capacitor banks must follow the rule below:
In the study, the value of reactive power output of shunt capacitors is classified into two different cases. It is a continuous variable in the first case as long as it is within lower and upper bounds as shown in Equation (6), but it is discrete variable with a step of 100 KVAR in the second case.
Lower bound and upper bound constraints of tap changer of transformers: During the operation of transformers, voltage of secondary side is always controlled by setting tap changer, while voltage of primary side is dependent on current flowing through transmission lines, voltage of generators, and reactive power of shunt capacitor banks. The setting of tap changer of transformer at the bus must obey the following inequality:
Similar to shunt capacitors, tap changer of transformers is also considered to be a continuous variable and discrete variable for two study cases. In the second case, it is constrained by each change step of 0.01 pu.
Capacity constraint of transmission lines: On the contrary to other devices, transmission lines are conductors, which are not imposed on lower bound, but upper bound constraint is strictly supervised. Apparent power flowing through transmission lines should not be higher than its capacity. If the following inequality can be accurately responded, the transmission line is working stably.
Lower bound and upper bound constraints of voltage at load buses: In addition to two objectives regarding voltage such as total voltage deviation and L index, voltage at each load bus is also imposed on lower and upper bounds for the purpose of stable operation of load. The requirement of load bus voltage is as follows:
Power balance constraint at each bus: In addition to constraints from electric components in transmission lines, the ORPD problem also considers active and reactive power balance at each bus as a serious concern due to issues regarding frequency and voltage. Power generated by generator and capacitor, power consumed by load, and power of connected transmission line have the following relationship:
3. The Proposed Coyote Optimization Algorithm
3.1. Original Coyote Optimization Algorithm
In the COA, Coyote community is equally disunited into Npack packs, and each pack contains Ncoyote coyotes. Therefore, the population size is the result of multiplication of Npack and Ncoyote. The initial generation for each pack among the population can be performed by using the following popular model:
where:
where Sold,p is the social condition of the dth coyote in the pth pack corresponding to the ith solution in the pack p. Solmin and Solmax represent upper and lower bounds of the social conditions; xj,min and xj,max are the lowest value and highest value of the jth control variable; and NCV is number of control variables.
The initialization step of COA is ended by the two following tasks: calculate quality of each solution Fitnessd,p, and determine the best solution in each pack, Solbest,p.
In order to produce new social condition for each coyote, COA produces a center condition for each pack that is similar to a center solution, Solcenter,p. The center solution Solcenter,p collects center variables in each pack. Thus, there are two cases for each center variable in the center solution due to the number of coyotes in each pack. For the case of odd number of coyotes, the center variable of the coyote (Ncoyote + 1)/2 is picked up, but for the case of even number of coyotes, the variable of coyote Ncoyote/2 is taken. After determining the center solution for each pack, solutions are newly updated by the following rule:
It is not sure that each variable of new solution always exactly satisfies lower limit xj,min and upper limit xj,max. Thus, each variable must be verified and corrected by using the following equation:
Similar to other metaheuristic algorithms such as PSO, BA, and CSA, COA also uses the selection technique for retaining more effective solutions and abandoning solutions with worse quality. New solutions are evaluated by calculating fitness function, and old solutions are replaced with these new ones in case that fitness function is improved better. The description is mathematically modeled as follows:
For replacing the worst social condition in each pack, COA produces a new social condition, and then its quality is evaluated. In case that its quality is more effective than the worst condition, which is being existed in the pack, the worst one is replaced. Otherwise, the worst condition cannot be eliminated unintentionally. The new condition is also corresponding to a new solution in which the jth variable xj of can be found by the following way:
where and are two variables in two randomly picked solutions; xj,r is the jth variable obtained by randomization within lower and upper bounds. Pro1 and Pro2 are, respectively, the scatter and association probabilities and obtained by:
Before terminating an iteration of search process, COA performs the action of leaving current pack and joining another pack for coyotes. The phenomenon results in the exchange of solutions among available packs. Each two randomly selected solutions in two random packs are exchanged if the following condition is satisfied:
The exchange of solutions among different packs can avoid lumping all solutions into one zone, restricting search space and leading to local optimum easily. However, the effectiveness of the operator is very dependent on the random number and the value of Ncoyote. If Ncoyote is less than 10, the possibility that exchange phenomenon occurs is less than 50%. If Ncoyote is not smaller than 14, the solution exchange certainly takes place.
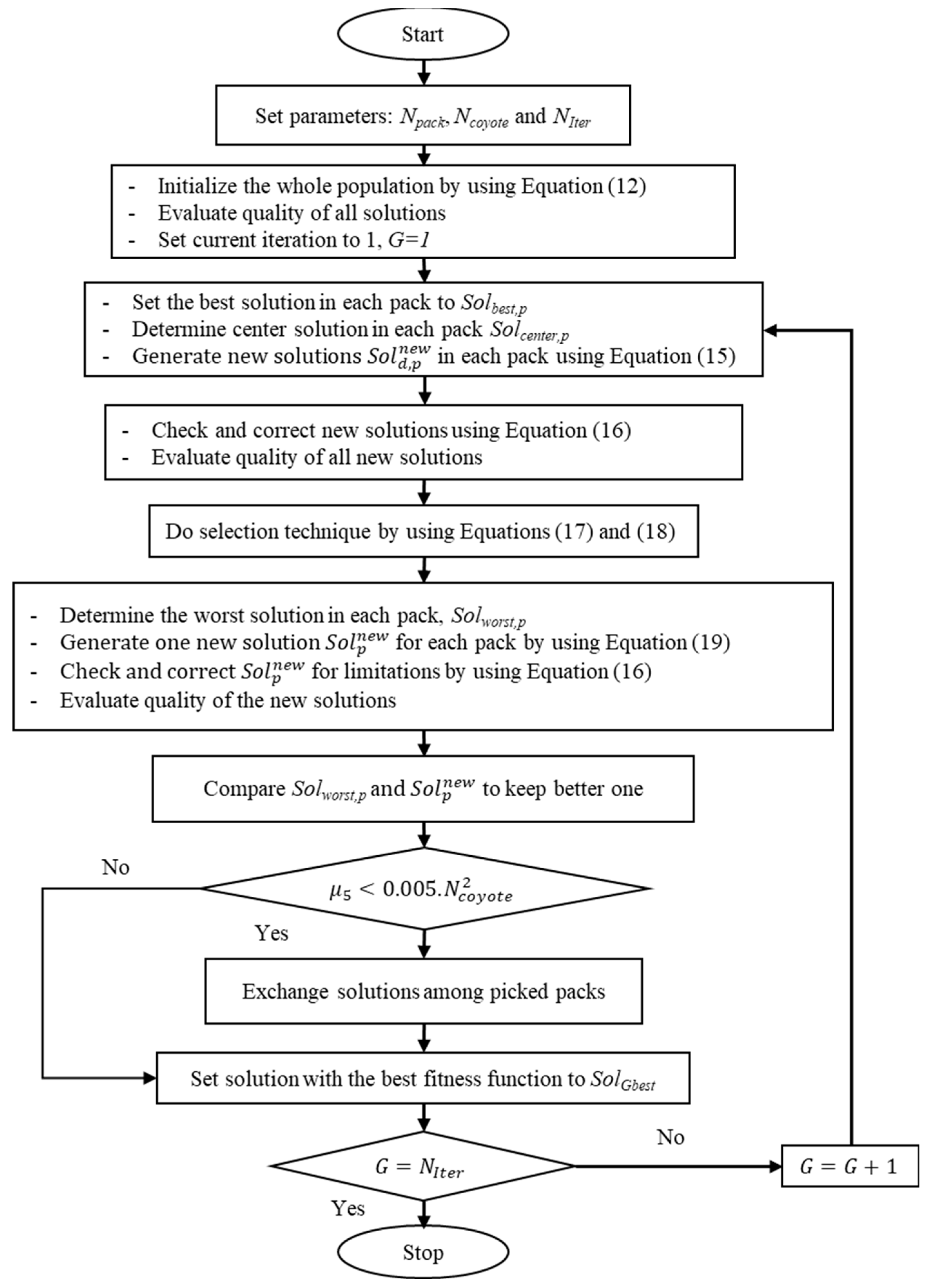
The whole computation process of COA is expressed in Figure 2.
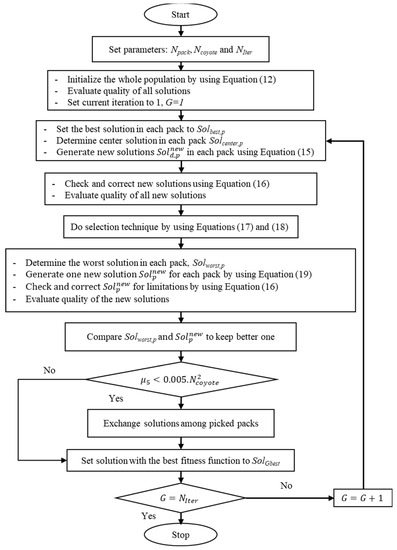
Figure 2.
The flowchart of using COA for solving a typical optimization problem.
3.2. Improved Coyote Optimization Algorithm
In each iteration, the search process of COA is comprised of two new solution generations, in which the first generation produces Npop solutions by using Equation (15) but the second generation produces only one solution by using Equation (19). Thus, there are (Npop + 1) new solutions for each iteration, and there are [(Npop + 1)*NIter] new solutions for one run. The information indicates that if the function of the two equations is ineffective or insignificantly effective, the best optimal solution of COA is of very low quality, and the considered optimization problem has been solved unsuccessfully. Consequently, in the paper, we have investigated the performance of the two methods of producing new solutions and proposed two new methods for the two major new solution generations. The new methods are presented and explained in the following sections.
3.2.1. The First Modification
In the first modification, we focus on the function of Equation (15) with intent to produce new solutions with higher quality. As seen from Equation (15), COA has employed a center solution Solcenter,p for each pack p to update new solutions because in natural behavior of coyote, a center tendency or a center social condition of all coyotes can lead to a better new social condition for each coyote in the flock. Each coyote can find new social conditions more effectively by using the center social condition from the whole population. However, center variables are impossible to form a promising solution. Furthermore, the use of the center variables, which are in charge of producing new solutions in Equation (15), is completely ineffective. Center variables included in one solution, and a center social condition are totally different in the nature phenomenon and in math. However, the method was successful in [56] in dealing with benchmark optimization functions, because many functions have optimal solutions with “0 value” variables. It should be noted that the “0 value” solutions are in the middle of the lower bound and upper bound of variables. Unintentionally, center solution is very useful for finding “0 value” solutions. Unlikely, the manner is not useful for the ORPD problem, because the optimal solutions of the ORPD problem are not around the center ones. Consequently, we suggest the model in Equation (15) should be changed by replacing center solution with a global best solution, which has been found so far. The search is performed as follows:
The equation can take advantage of the information exchange between current solutions and the so-far best solution. By using the modification, COA can take several advantages as follows:
- Reduce determination of Npack center solutions for Npack: The task of finding center solutions uses high simulation time, because it is comprised of many steps such as ranking each variable for the whole population and determining center variables from result of rank. The advantage is highly significant for large scale problem such as the ORPD problem due to high number of control variables and high population size.
- Many new solutions with high quality are found: The superiority can reduce the number of iterations, reducing the number of iterations, but the best optimal solution is still much more effective than that found by origin COA method.
The performance of the first modification is investigated by comparing the original COA and COA with the first modification, called COA1.
3.2.2. The Second Modification
In the second modification, we concentrate on the performance of the second new solution generation, which is accomplished by using Equation (19) above. The review on Equation (19) can indicate that the use of and has the same function, because the former is taken from a random solution and the latter is also taken from anther random one among the population. Thus, the conditions of (μ4 < Pro1) and (μ4 < Pro1 + Pro2) are meaningless, but they result in more computation steps and time-consuming aspect. In addition, Equation (19) uses random variables within lower and upper bounds in the case that the two conditions above are denied completely. Some variables in the new solution are taken from two random solutions, while rest of variables in the new solution are randomly produced. Clearly, the combination is not from certain and believable arguments. Thus, in the second modification, we propose using the following model for finding one new solution for each pack.
By using the modification, COA can take advantages as follows:
- 1.
- Reduce the calculation of Pro1 and Pro2.
- 2.
- Reduce two conditions: μ4 < Pro1 and μ4 < Pro1 + Pro2.
- 3.
- Reduce random generation of variable xj,r in Equation (19).
- 4.
- Shorten simulation time due to the reduction of three tasks above.
- 5.
- Npack solutions with high quality are produced: The advantages can enable to reduce the number of iterations, leading to shorter simulation time, but the best optimal solution is still much more effective than that of original COA method.
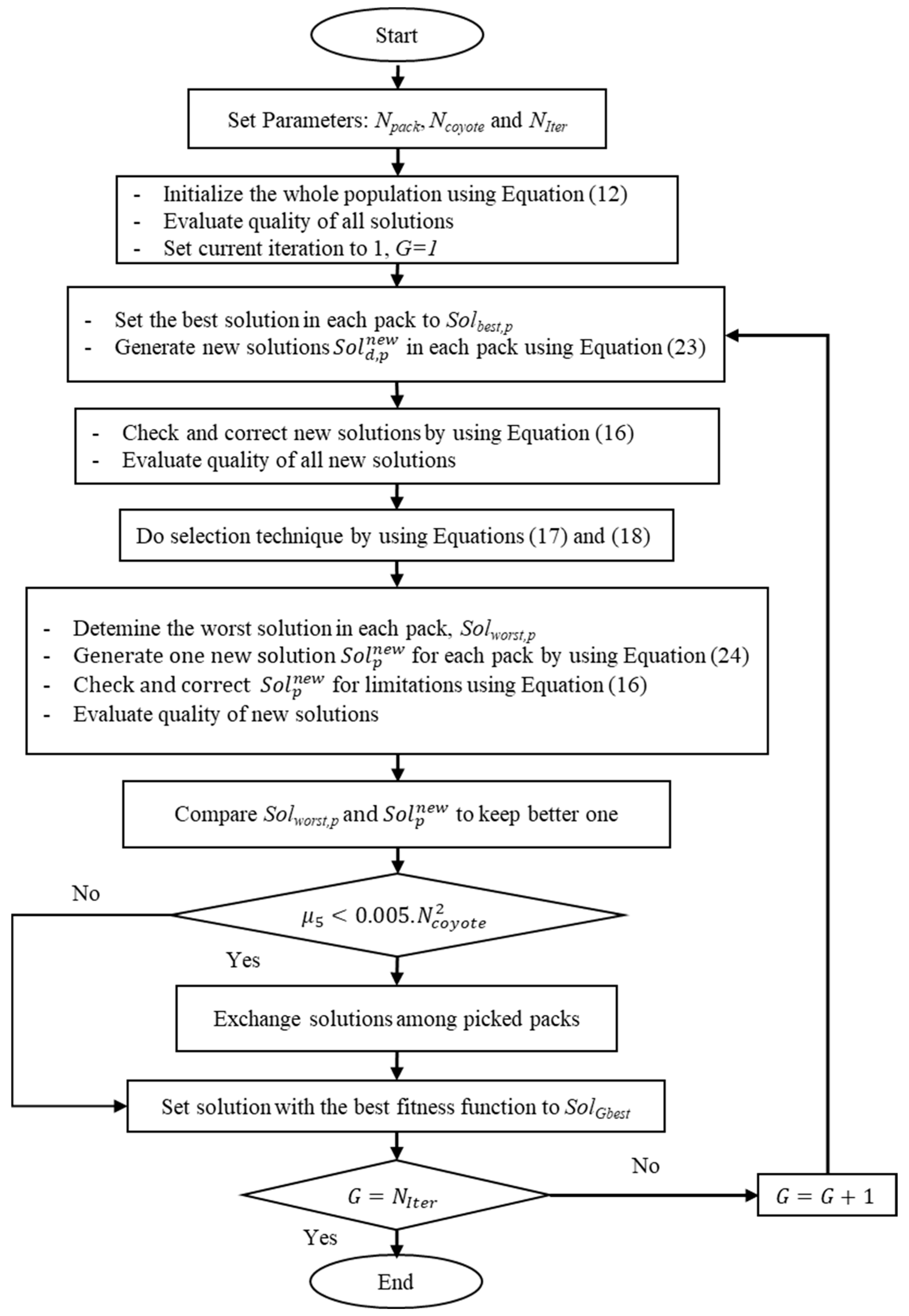
The whole computation process of the proposed ICOA approach is given in Figure 3.
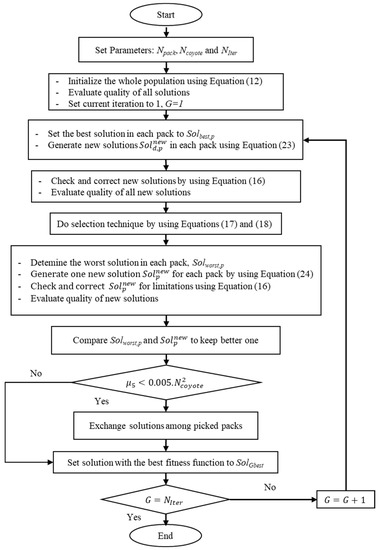
Figure 3.
The flowchart of using the proposed ICOA approach for a typical optimization problem.
4. Solving the Typical ORPD Problem by Using the Proposed ICOA Method
4.1. Population Initialization
In order to carry out the optimal solution search program of the proposed ICOA method, the first step is to produce a set of initial solutions, called population. On the contrary to other metaheuristic algorithms, ICOA as well as COA have Npack packs, and there are Ncoyote particles in each. Thus, the initial population generation is executed for each pack as the following model.
In the equation above, Solmin and Solmax are the minimum and maximum values of control variables of the ORPD problem and can be represented as below:
Finding solutions of the ORPD problem is also supported by using Matpower program for obtaining remaining variables, which are different from control variables available in solution Sold,p. Each solution Sold,p is transferred to Matpower program for running, and then a set of dependent variables is obtained, consisting of apparent flow through each transmission line Sbranch,ij, reactive power output of generators QGen,has, and voltage of load buses Vload,i. The three variables are imposed on inequality constraints (4), (8), and (9), and the three constraints are of course included in fitness function. However, other inequality constraints (5)–(7) together with two equality constraints (10) and (11) are not taken into account in fitness function. In fact, VGen,has and TTi accompanied with Qcap,has are control variables, which are considered in each social condition of coyotes. Thus, such variables’ boundaries are always monitored and corrected within their limits, as shown in Section 4.3 below. In another side, equality constraints (10) and (11) have been taken into account in the Newton–Raphson method, which is run in Matpower program. Consequently, before calculating fitness function, such three dependent variables are checked and penalized as follows:
As a result, fitness function for evaluating quality of solutions can be constructed by the following equation:
After having fitness function, the solution with the lowest fitness function in each pack is set to local optimal solution Solbest,p, and the best solution among all packs is set to the global best solution SolGbest.
4.2. Processes of Newly Updated Solutions
The proposed ICOA method updates new solutions two times. In the first time, Ncoyote solutions in Npack packs are newly produced by using Equation (23), but only one solution in each pack is updated for the second time by using Equation (24). As mentioned in Section 3, and are, respectively, new solutions in the first and the second updated solution processes.
4.3. Correction of Violation of New Solutions
After each updated solution process, correction is executed for handling violation of all control variables. The conventional method that has been applied so far is called boundary constraint handling method. By using the method, control variables are assigned to lower bound/upper bound if they are less/higher than lower/upper bound. Namely, the method can be implemented by the following models:
4.4. Termination of Iterative Search Algorithm
At the end of each iteration, one solution with the lowest fitness function is identified and set to the so-far best solution. In case that the current iteration is the last iteration, the so-far best solution is the best optimal solution for the run, and it is stored as a candidate. After finishing a predetermined number of runs, we have a set of candidates, and the best candidate is found by determining the lowest fitness function. On the other hand, the performance of the proposed method is also judged via minimum, average, and maximum fitness function values together with the standard deviation of the number of runs. Consequently, the termination condition of each run is dependent on the maximum number of iterations while the termination condition of each study case is dependent on the maximum number of runs. The maximum number of iterations NIter is determined based on the number of control variables, which is dependent on the sizing of considered systems. The maximum number of runs Nrun is selected depending on both the performance of implemented methods and the sizing of considered systems. Normally, finding high-quality solutions for small-scale systems is much easier and faster than for larger-scale systems. In dealing with three standard IEEE systems with 30, 57, and 118 buses, the proposed ICOA can find high-quality solutions by using Nrun = 50. Therefore, the selection is adopted for the purpose of reducing simulation time.
4.5. The Entire Computation Procedure
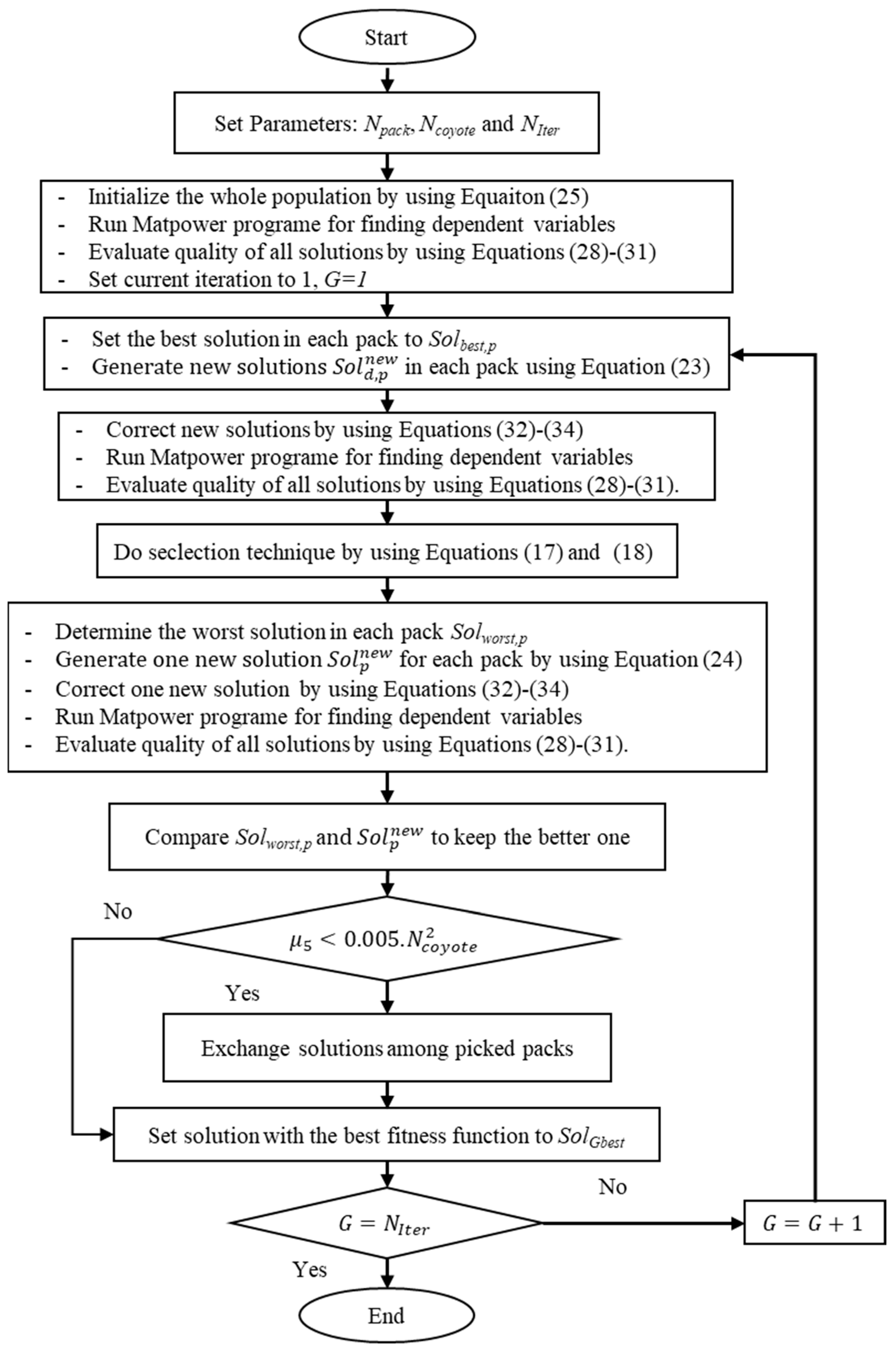
Finding ORPD problem solutions can be successfully accomplished by applying the flowchart in Figure 4.
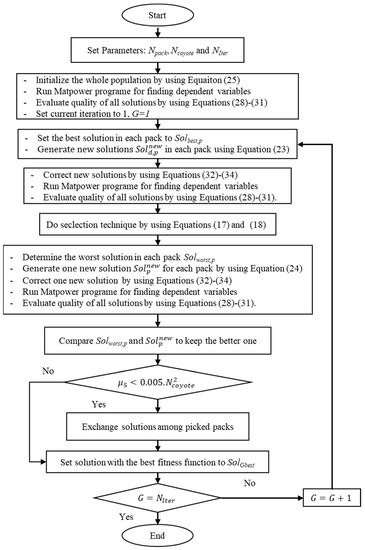
Figure 4.
The flowchart of solving the ORPD problem by using the proposed ICOA method.
5. Numerical Results
The efficiency of the proposed ICOA method has been simulated by using three standard tests with the IEEE 30-bus, IEEE 57-bus, and IEEE 118-bus systems considering three single-objective functions consisting of power-loss minimization, total-voltage deviation, and L index. The optimal solution search program of the proposed method has been coded on MATLAB program language and executed on a personal computer with a 2.4 GHz processor and a 4 GB RAM. In addition to comparisons with other methods available in previously published studies, we have also employed other state-of-the-art and popular methods such as salp swarm algorithm (SSA) [60], sunflower optimization algorithm (SFOA) [61], water cycle algorithm (WCA) [62], standard coyote optimization algorithm (COA) [56], improved coyote optimization algorithm with the first modification (COA1), and improved coyote optimization algorithm with the second modification (COA2). For finding optimal solutions, each method has been run 50 times in independent trials for each objective of each system. The setting of the adjustment parameters of the proposed method and other ones as well as test cases are summarized in Table 1.

Table 1.
The description of study cases and control parameter selection.
It is noted that for each study system corresponding to each objective, the proposed ICOA has been run two different cases as mentioned in Section 2.
Case 1: All control variables are set to continuous variables (CV).
Case 2: Reactive power output of shunt capacitors and tap changer of transformers are set to discrete variables (DV) in which a change step of reactive power output is 0.1 MVAR and that of tap changer is 0.01 pu.
The two cases are indicated in each comparison table because it is very important in evaluating the performance of methods. Basically, methods using continuous variables tend to obtain smaller fitness function than using discrete variables. For comparison with other implemented methods, we run ICOA and these methods with continuous variables only.
5.1. Performance Comparison Criteria for Different Methods
In the evaluation of the performance of optimization tools, while solving ORPD problem solutions, the sole key factor that has been used to point out the performance of compared methods is the best optimal solution reflected via fitness function [23,24]. Some of the previous studies [19,61] have used more comparison factors such as execution time in seconds, but computers, which have been used for simulation, have not been mentioned. It is obvious that computers with a higher processor spend less time for the same condition of control parameters or Matlab code. There is also another view point about the comparison of performance depending on the setting of adjustment parameters [64]. The higher population size and number of iterations can produce the higher number of new solutions, but it takes a long time to find optimal solutions. However, the statement is not completely accurate because there are some methods with complicated and time-consuming computation steps, although these methods and other ones produce the same number of new solutions for per iteration and per run. The simplest example for demonstrating the point is the comparison between PSO and DE. The two methods produce a set of new solutions equaling population size per iteration, and the same number of new solutions per run, but PSO has a smaller number of computation steps and simpler computation steps than those of DE. PSO updates velocity and position for all particles at the same time, leading to short simulation time, but DE must perform mutation for one solution by one solution, and then the crossover operation must be conducted. Thus, DE tends to spend longer simulation time.
Consequently, we suggest applying acceptably clear and fair comparison criteria for the evaluation of the performance of the proposed method and other ones. We focus on the following main issues:
The best optimal solution: The best optimal solution comparison can point out the robustness of the method. The method with the better solution is considered to be stronger in the search process.
The solution search speed: It is also a very important factor for providing an accurate assessment of methods performance. A method with better solutions but with much longer simulation time is not a method with more potential. A method that finds better solutions and uses shorter simulation time is considered to be a better method, if the time comparison is carried out in the same conditions such as the same program language, the same program way, and the same computer. However, the expected conditions are hardly ever reached. For dealing with the issue, studies in [64,65] have proposed different comparison criteria for evaluating the optimal solution search speed of compared methods. Authors [64] have suggested a persuasive argument in regard to Npop and NIter that the two factors directly influence the performance of implemented methods. The setting with higher values for the two factors can improve optimal solutions considerably, but convergence process to these solutions is time consuming and vice versa. Thus, they have suggested that the total number of newly produced solutions Nspr or the number of quality solution evaluations over one run Nsqe should be employed as the main comparison factor. Methods with the same or smaller number of quality solution evaluations but finding better optimal solutions become more powerful methods. Due to the suggestion, we construct different Nsqe for different compared methods as follows:
The three abovementioned formulas are applied for different methods with a different number of generations and different number of new solutions per generation. Formula (35) can calculate the number of solution quality evaluations for methods producing the number of new solutions equaling population size such as PSO, DE, SSA, GWO, BBO, etc. Formula (36) provides the number of solution quality evaluations for methods having two generations per iteration, and there is a population size of new solutions per generation such as ABC, TLBO, QOTLBO, CSA, etc. The model of Formula (37), which is applied for COA and the proposed method, is different than that of (35) and (36), because COA and ICOA have different search procedures than other methods. (Ncoyote.Npack) is the number of quality solution evaluations for the first generation, while Npack is the number of solution quality evaluations for the second generation. On the other hand, (Ncoyote.Npack) is equal to population size, and Formula (37) can be rewritten as follows:
With the form, if we set (Ncoyote.Npack) equally to the population size of other methods, COA and the proposed ICOA method produce a higher number of new solutions and spend more time than other methods with Formula (35) but the two methods produce a smaller number of new solution and use a shorter time for evaluating solution than other methods with Formula (36).
Although unlikely, the authors in [65] have suggested using computation time for fair comparison of performance. They did not consider Nsqe, but they did consider the processor of computers as a strict factor. They have defined a time index of the compared method has, Tii by using the following model:
In Equation (39), GHi and GH (in GHz) are the processor of computers, which have been used to run the compared method has and the proposed method. Simtimei and Simtime (in second) are the simulated time of the compared method has and the proposed method. According to the viewpoint of the authors, the compared method has is slower than the proposed method if Tii is higher than 1 and vice versa.
The stable search ability: The stable search ability is not the most important factor for evaluating the performance of method, but it can be used for further investigation in the case that two compared methods have the same optimal solution and the same search speed. Normally, the stability of the solution search is reflected via the average fitness of all runs. On the other hand, a better comparison can be made if the best fitness of all runs is plotted in the same figure. For comparison with other methods available in previous studies, we compare the average, but for implemented methods in the study, we plot all runs in the same figure, and a clear view can point out which method is superior to others. The applied comparison criteria cannot provide a fair comparison with the accuracy of 100%, but a general comparison with acceptable accuracy can be useful for concluding the performance of the proposed method as compared to other ones.
5.2. Testing Performance of COA and ICOA on Different Adjustment Parameters
In the section, we have presented the result obtained by COA and the proposed ICOA method by setting different values to the number of coyotes in each pack Ncoyote and the number of packs Npack. The task aims to find the most appropriate values for the two adjustment control parameters, Ncoyote and Npack, so that the proposed ICOA can get the highest performance with the best objective and the fastest search ability. In addition, a comparison of performance between COA and the proposed method as setting the same parameter was also investigated.
The considered ORPD problem is a complicated problem, and it takes optimization tools very much time to find optimal solutions due to the function of Matpower program. For judging the quality of one solution, the program must be run for dependent variables, and then fitness function can be calculated. Thus, the number of new solutions produced in each iteration Nspi and the number of new solutions produced in each run Nspr are criteria for comparing the search speed of different applied methods. We have set different values (2, 3, 4, 5) to Npack and the values of Ncoyote have been 9, 6, 4, and 3, accordingly. Although the different setting results in different population size, Npop = 18, 18, 16, 15, Nspi = 20 is the same for all settings excluding the case of Npack = 3 and Ncoyote = 6 with Nspi = 21. Over 50 runs, the best, average, and worst fitness values together with the standard deviation and average execution time are reported in Table 2, Table 3 and Table 4 for TPL, TVD, and L index objectives, respectively. The best fitness values from the three tables can reveal the small impact of the two control parameters on the performance of the proposed ICOA, once the difference between the smallest best value and the highest best value is very tiny. For instance, the smallest power loss and the highest power loss are 4.5128 and 4.5238 MW. Similarly, the two values for TVD objective and L index objective are 0.0888 and 0.9833 pu, and 0.1242 and 0.1250 pu, respectively. However, there is a coincidence among the three cases since the smallest best fitness are found by the setting of Ncoyote = 4 and Npack = 4, and the highest best fitness are found by the selection of Ncoyote = 9 and Npack = 2. Clearly, a small number of packs could not produce promising quality solutions. However, it does not mean that a high number of packs is a good selection for a better comparison if the number of coyotes is not high enough. The setting of Ncoyote = 3 and Npack = 5 could not achieve the best result among all settings. In addition, the survey of standard deviation can show the best stability of search by setting Ncoyote = 9 and Npack = 2, while the second-best search stability is recorded by setting Ncoyote = 4 and Npack = 4. The best performance and the second-best stability can lead to a conclusion that the setting of Ncoyote = 4 and Npack = 4 is the most appropriate parameters for the IEEE 30-bus, and they are also applied for the IEEE 57-bus and 118-bus systems.

Table 2.
Results found by the proposed ICOA approach for TPL objective of the IEEE 30-bus system.

Table 3.
Results found by the proposed ICOA approach for TVD objective of the IEEE 30-bus system.

Table 4.
Results found by the proposed ICOA approach for L index objective of the IEEE 30-bus system.
In regard to comparisons with COA method, the results of the proposed method are more favorable since almost all minimum values of the proposed methods are less than those of COA method, and the success rate (SR) of the proposed method is always higher than SR of COA. In fact, with different setting cases for Ncoyote and Npack, COA found different minimum TPL values to be 4.789, 4.682, 4.5777, and 4.595 MW, while those from ICOA are, respectively, 4.5178, 4.5154, 4.5128, and 4.5238 MW. The numbers indicate that the proposed method could reach less TPL by 0.2712, 0.1666, 0.0649, and 0.0712 MW, which are corresponding to the improvement level of 5.66%, 3.558%, 1.418%, and 1.55%. The improvement level of ICOA over COA is, respectively, 25.11%, 22.29%, 27.86%, and 21.69% for TVD case and is, respectively, 5.02%, 4.67%, and 0.72% for L index case. Clearly, the proposed ICOA approach could find a better optimal solution than COA for the same settings of control parameters. In relation to capability of handling constraints, the proposed method reported SR with 100% for TPL case and TVD case, and SR with 98% for L index case while COA successfully handled the system with SR less than 100%. Namely, SR is 92% for TPL case, 90% for TVD case, and 76% for L index case.
5.3. Investigation of the Proposed Method’s Performance on the IEEE 30-Bus System
In the section, the results obtained by the proposed ICOA for the standard IEEE 30-bus system are compared to those from other implemented methods consisting of WCA, SSA, SFOA, COA, COA1, and COA2, and other methods available in previous studies. As mentioned in Section 5.1 above, the best optimal solution with the lowest fitness function is the first comparison factor for concluding the effectiveness of methods. Secondly, Nsqe and Ti are the second factor for concluding the search speed of the proposed method. Finally, the average fitness of all runs is compared to other existing methods, and 50 runs of all implemented methods are plotted in the same figure for comparison of search stability. All the values regarding the three factors are reported in Table 5, Table 6 and Table 7 for TPL, TVD, and L index objectives. The minimum TPL in Table 5 shows that the proposed ICOA method can find the best solution for the case of continuous variables and discrete variables. The power loss of ICOA is the lowest value with 4.5128 MW for the case of continuous variables and 4.5138 MW for the case of discrete variables, while the best power loss in other studies is much higher.

Table 5.
Result comparison of TPL for the IEEE 30-bus system.

Table 6.
Result comparison of TVD objective for the IEEE 30-bus system.

Table 7.
Result comparison of L index for the IEEE 30-bus system.
For the case of continuous variables, the study [23] employed three methods in which the best one, HPSO-TS, found the most promising solution with 4.5213 MW. The study [19] implemented eight improved PSO approaches, and the best one determined the best solution with 4.52560 MW. The study [50] employed three methods in which the best one reported 4.5943 MW for power loss. Clearly, the proposed method found the best solution with 4.5128 MW, while the second-best method, GSA [29], reported 4.51431 MW, and the worst method, TS [23], reported 4.9203 MW. The further comparison indicates that the proposed ICOA method can improve the result from 0.01% to 8.3%. For the case of discrete variables, the study [37] employed three methods in which the best HAS method reported 4.9059 MW. The best ALO method among four applied methods in [44] reported 4.59 MW, while that of JA [47] was 4.5495 MW. Clearly, these methods found less effective solutions than the proposed method, and the improvement of result from the proposed method over other ones was from 0.79% to 8.6%.
The comparison with six other implemented methods also indicates the outstanding performance of the proposed method. The best power loss of WCA, SSA, SFOA, COA, COA1, and COA2 are 4.58218, 4.7175, 4.7364, 4.5777, 4.5340, and 4.5328 MW, which are higher than that of the proposed method by 0.068, 0.204, 0.222, 0.064, 0.020, and 0.019 MW corresponding to the improvement of 1.488%, 4.314%, 4.696%, 1.392%, 0.441%, and 0.415%. Clearly, COA1 and COA2 can improve the result relatively well as compared with COA, while the improvement of the proposed method over COA is highly significant. Thus, it can lead to a conclusion that the proposed ICOA method is really highly effective for minimizing TPL objective of the IEEE 30-bus system.
For comparison of the TVD objective shown in Table 6, all compared methods have considered only continuous values for all control parameters. Therefore, the comparison is only carried out for continuous variables. However, we have also reported obtained results from the proposed method for the case of discrete variables.
As seen from Table 6, the best TVD of the proposed method, which is 0.0888 pu, is better than that of six other implemented methods and almost all methods in other studies excluding GSA [29] and QOTLBO [33], which reported 0.0676 and 0.0856 pu. Because taking control variables included generator voltages, tap setting of transformers, and power output of shunt capacitor banks of GSA and QOTLBO as the input parameters to run the Matpower program, the recalculated value of TVD is equal to 0.18622 and 0.10313 pu. Clearly, the two recalculated values are much higher than 0.0888 pu from the proposed method. The comparisons with other remaining methods imply that the proposed method can improve the best optimal solution quality from 0.45% to 57%, and the improvement is 27.2% as compared to COA method. Consequently, it can lead to a conclusion that the proposed method is very robust for finding solutions of the IEEE 30-bus system with TVD objective.
According to Table 7 showing result comparison of L index objective, GSA in [29] for the case of continuous variables and four methods in [44] for the case of discrete variables reported the best results with the lowest L index, approximately 0.11 pu, while that of the proposed method is 0.1242 and 0.12437 pu, corresponding to continuous and discrete variables, respectively. However, the recalculated value of L index is 0.1247 and 0.1241 pu for GSA and ALO, which are higher and approximately equal to that of the proposed method. The verification of reported solutions from PSO-IPG [19] and QOTLBO [33] confirms that the two methods have reported accurate solutions; however, the two methods have the same solution quality with the proposed ICOA method. As compared to other remaining methods, the L index values indicate the proposed method can find the optimal solution with the improvement up to 17.1% and that value is 0.8% as compared to the COA method. Thus, the proposed method can find the solution with the same quality as other leading methods for the case of L index optimization for the IEEE 30-bus system.
For the comparison of solution search speed, the values of Nsqe and Ti are also summarized in Table 5, Table 6 and Table 7. Table 5 indicates that the proposed method is ranked the fastest method together with six other implemented methods by spending 2000 solution quality evaluations, while the values from other methods in other studies are 4000, 8000, 10,000, 15,000, 18,000, 20,000, and 75,000. For comparison of converted simulation time Ti, the proposed is faster than other methods approximately from 1.3 times to 15 times. Similarly, Table 6 and Table 7 also display the strong search speed of the proposed method once other methods have used Nsqe = 4000, 10,000, 20,000, and 75,000 for TVD objective and Nsqe = 4000, 8000, 10,000, 20,000, and 25,000 for L index objective. Accordingly, the proposed method is faster than these compared methods approximately from 1.6 to 3.5 times for TVD objective and approximately from 2 to 11 times for L index objective. All in all, the proposed method is more powerful than other compared methods available in previous studies in terms of solution search speed.
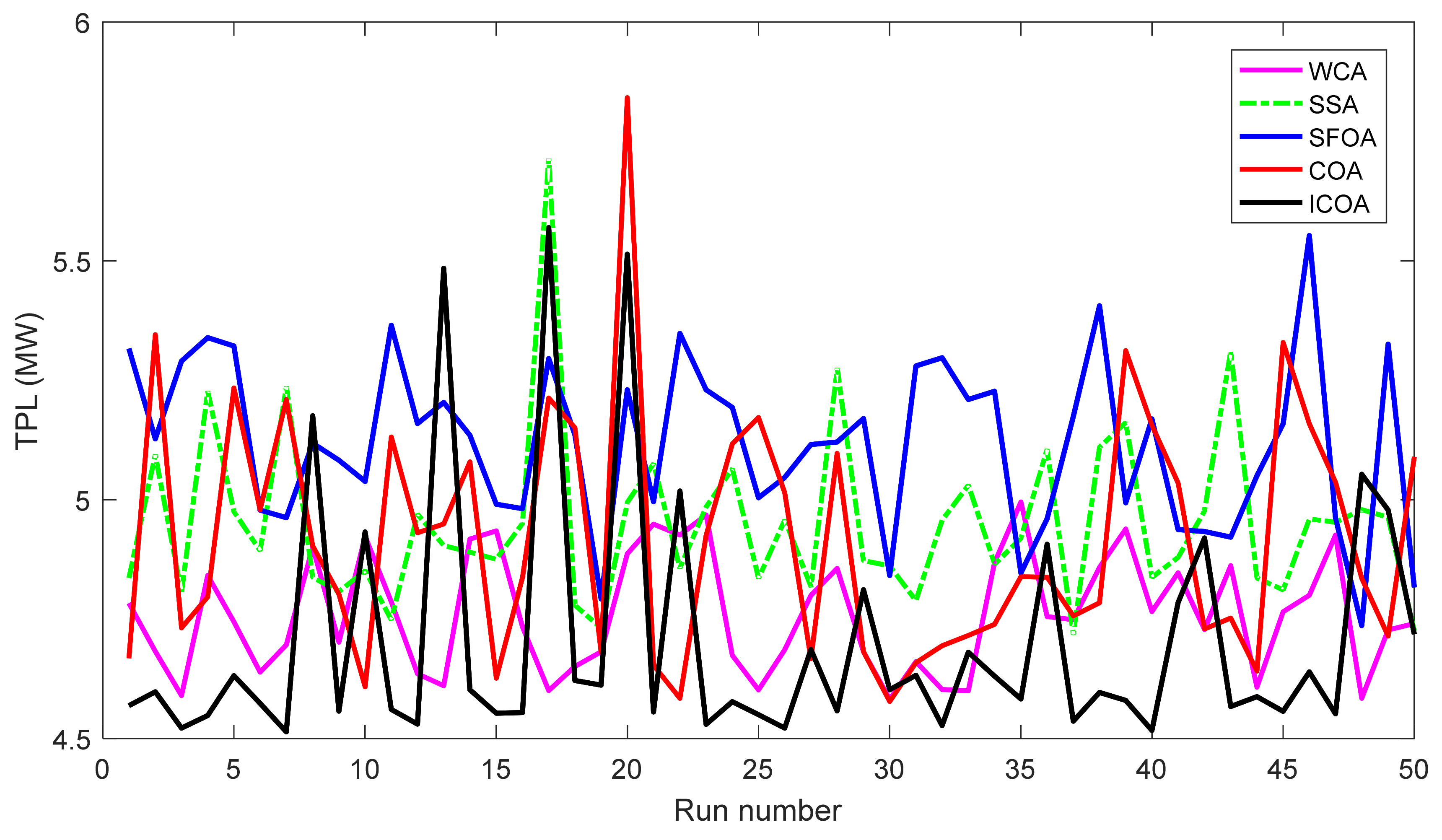
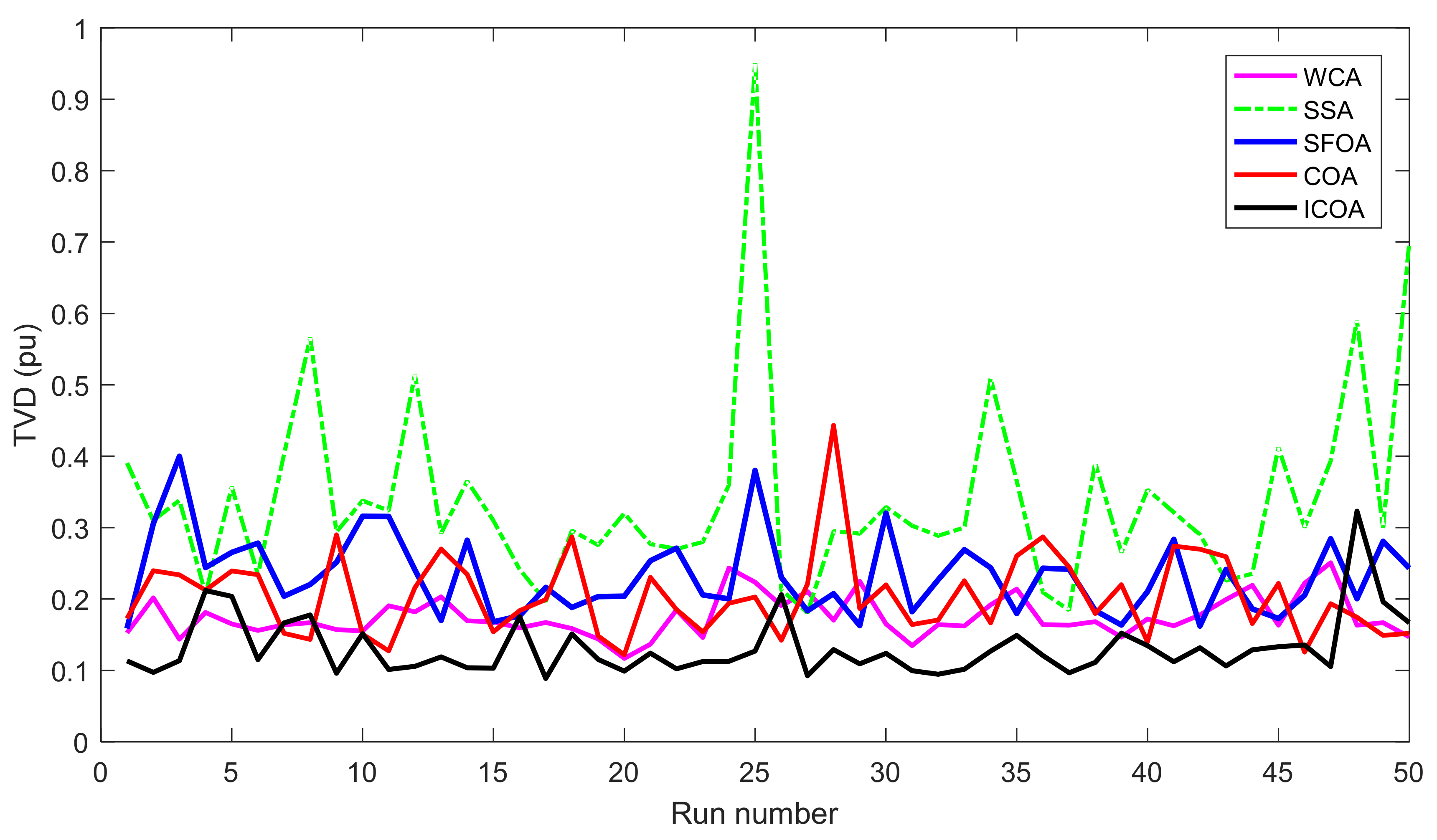
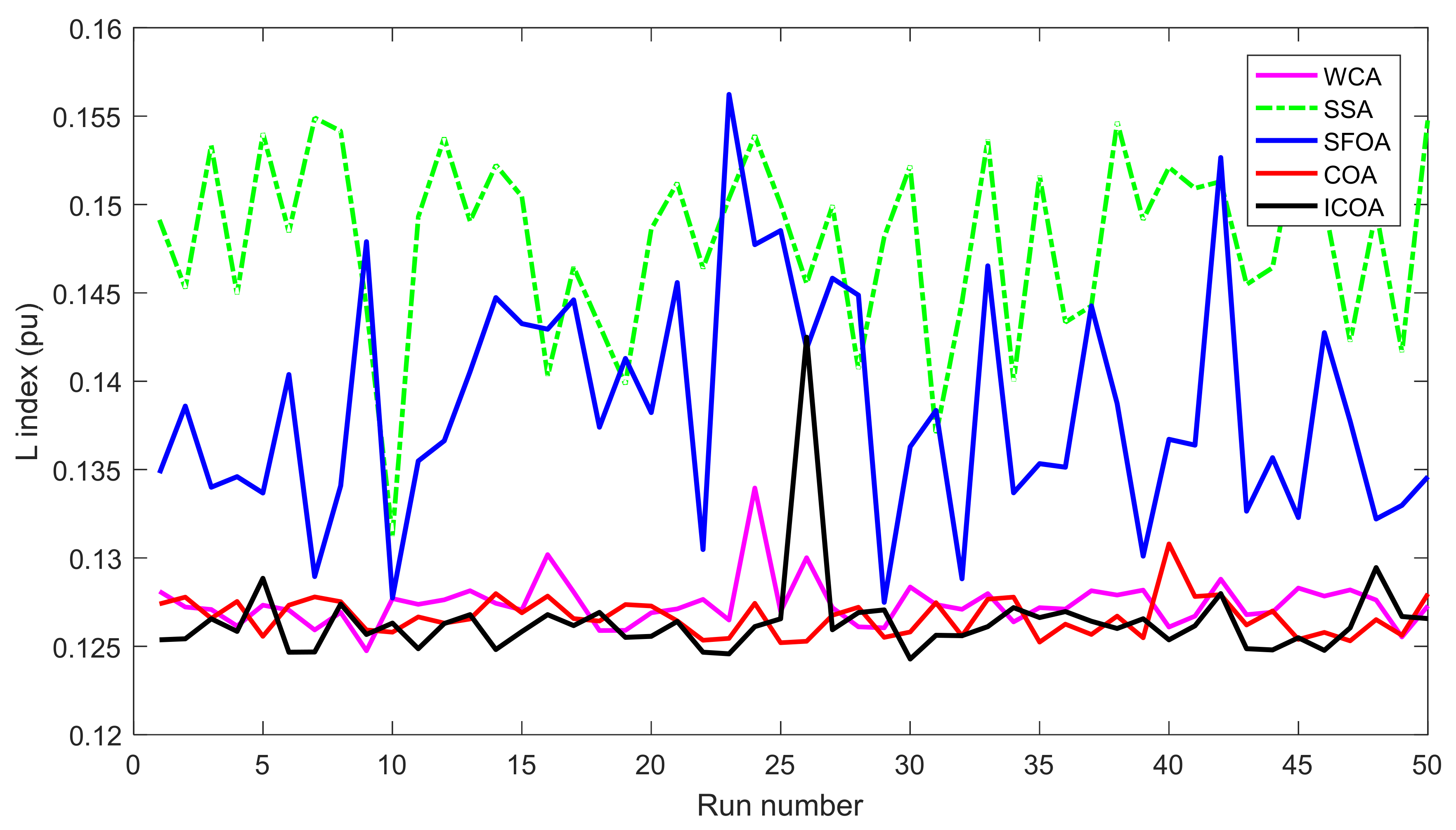
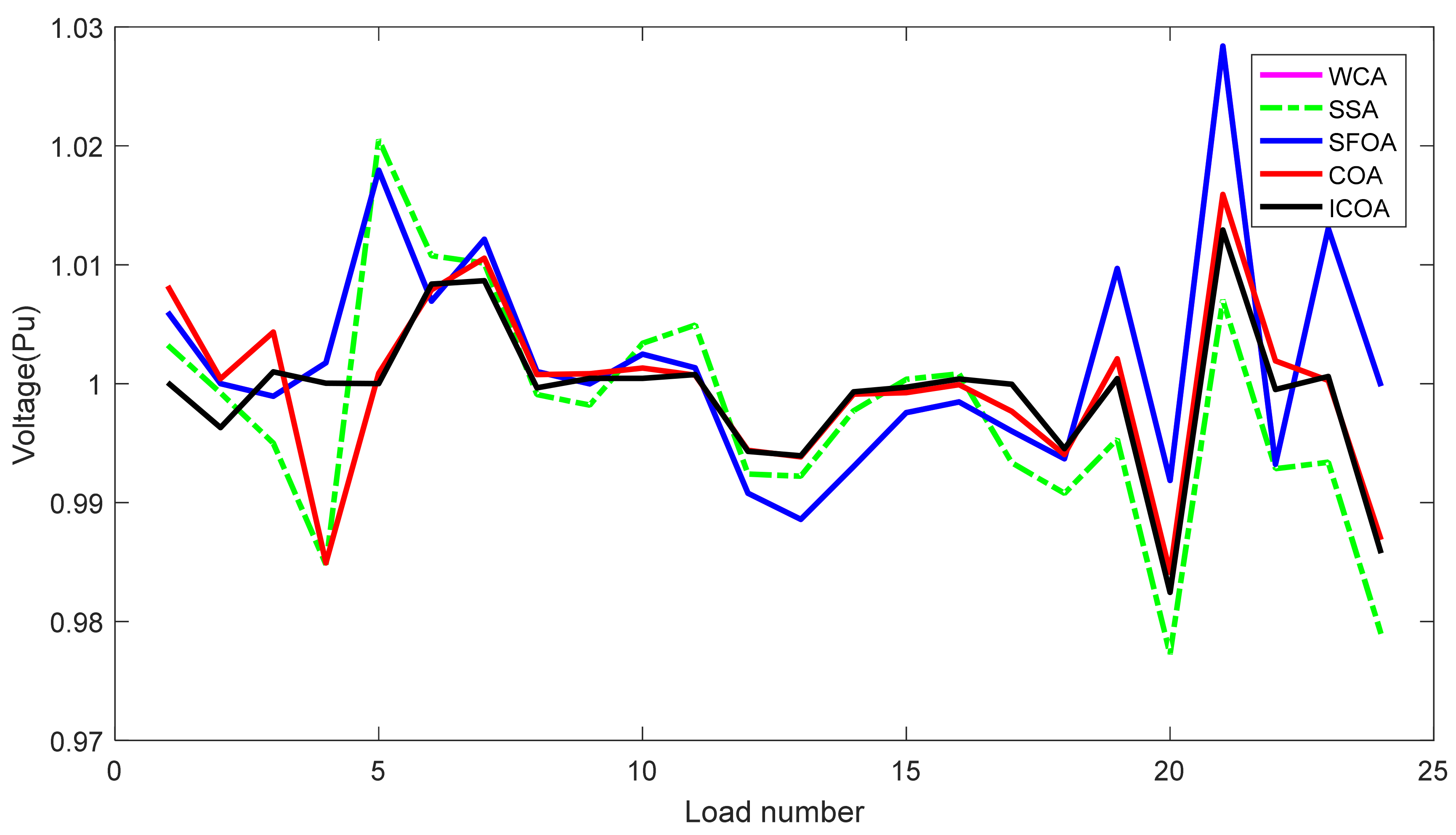
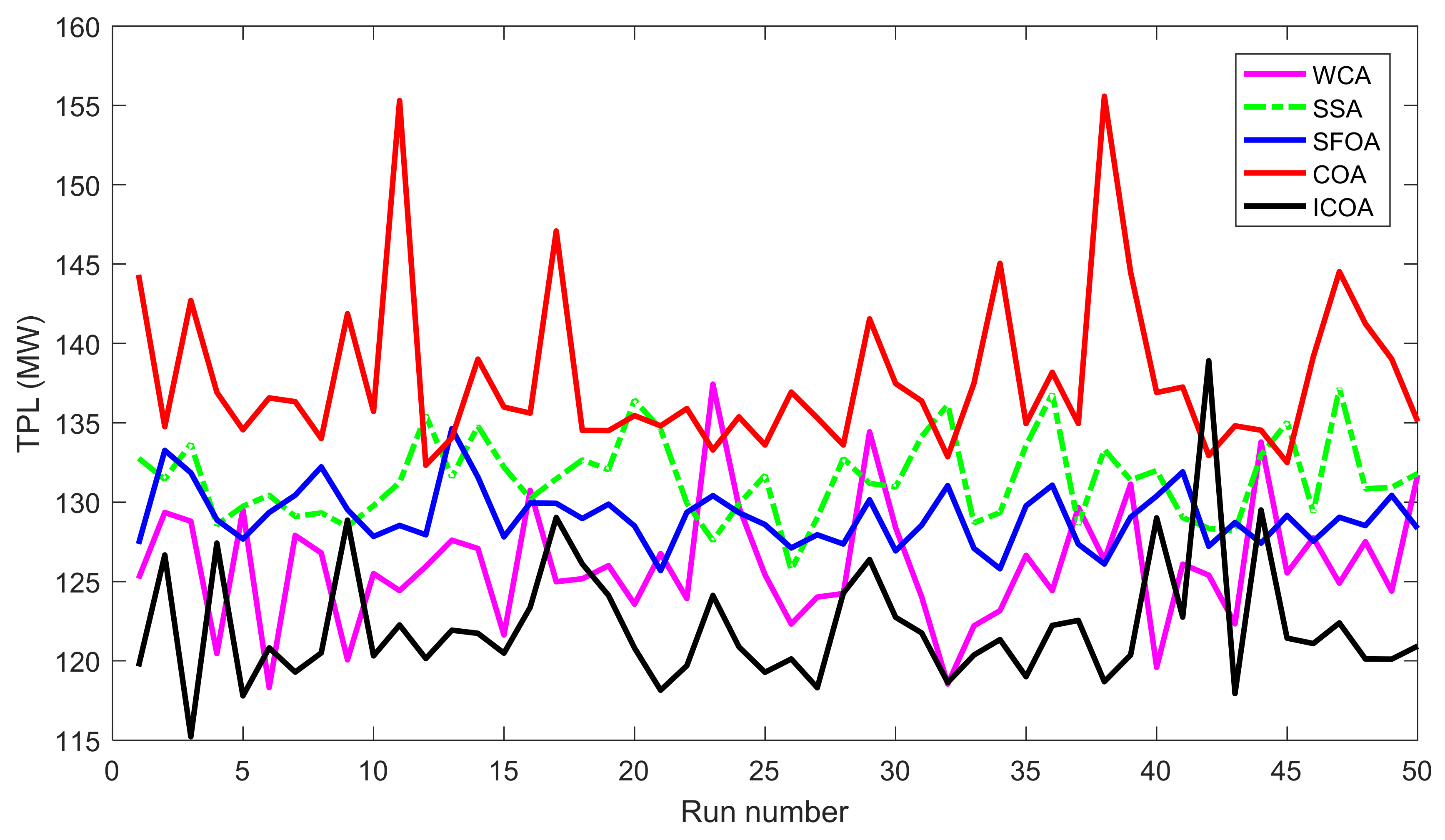
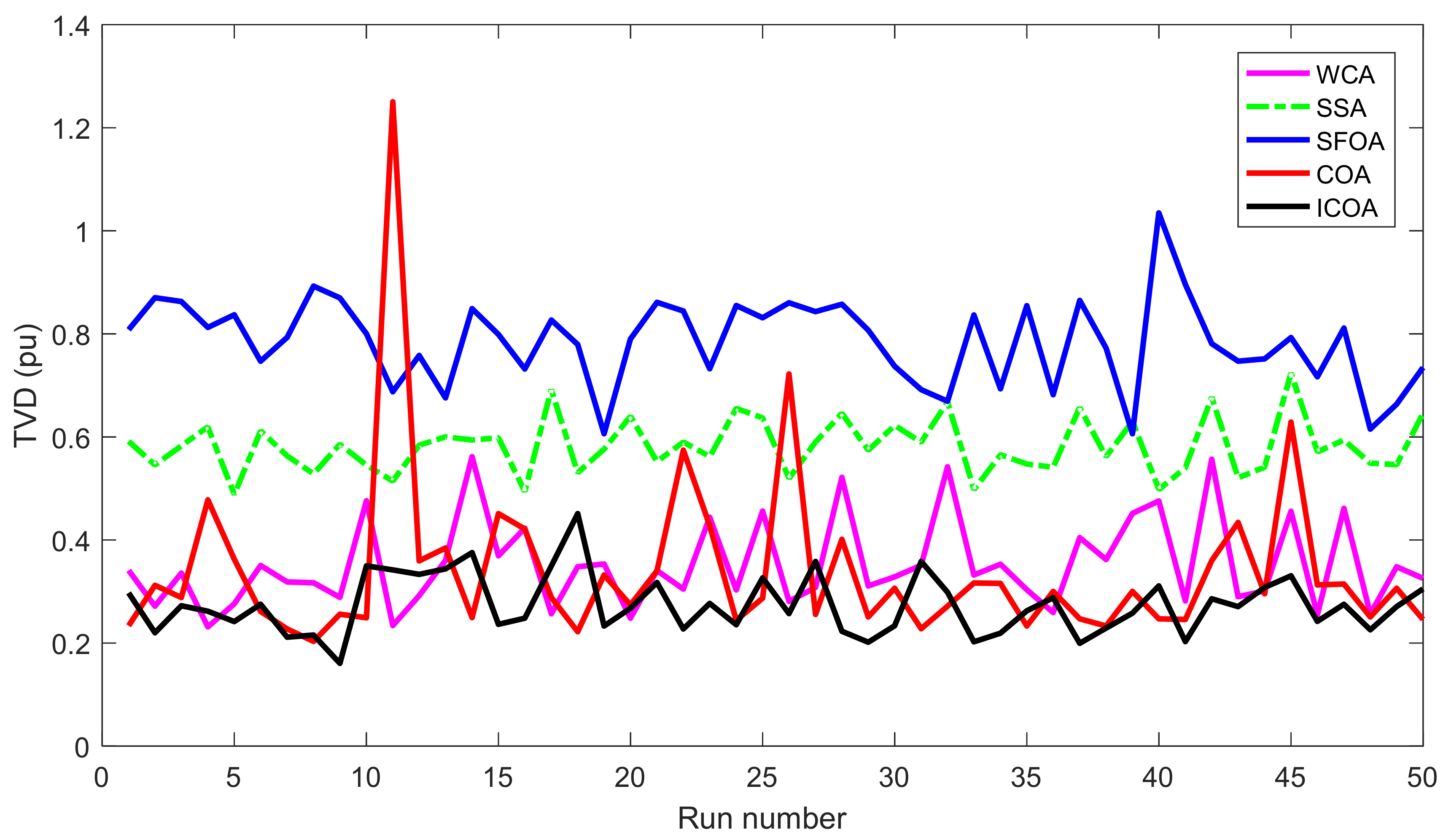
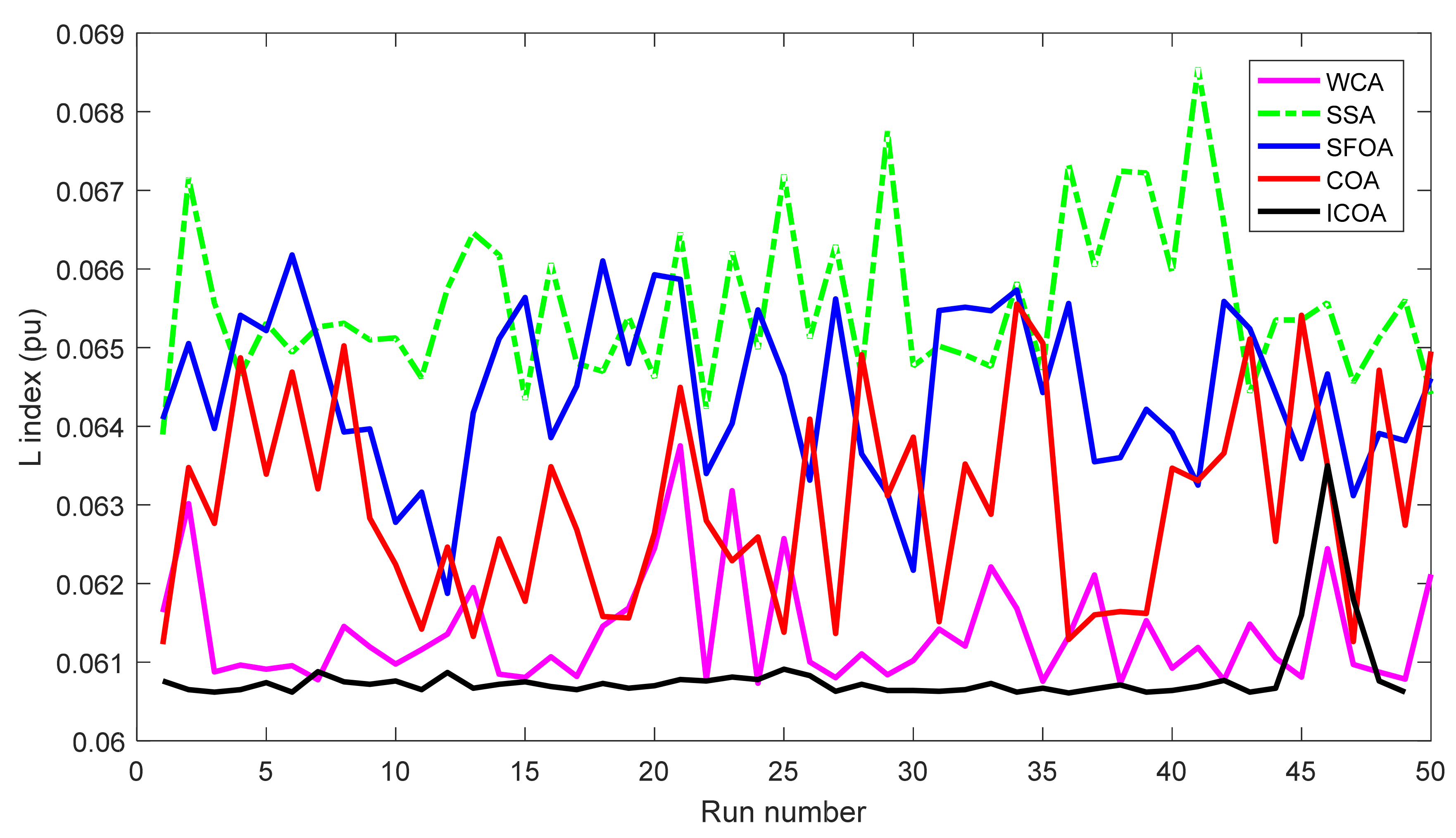
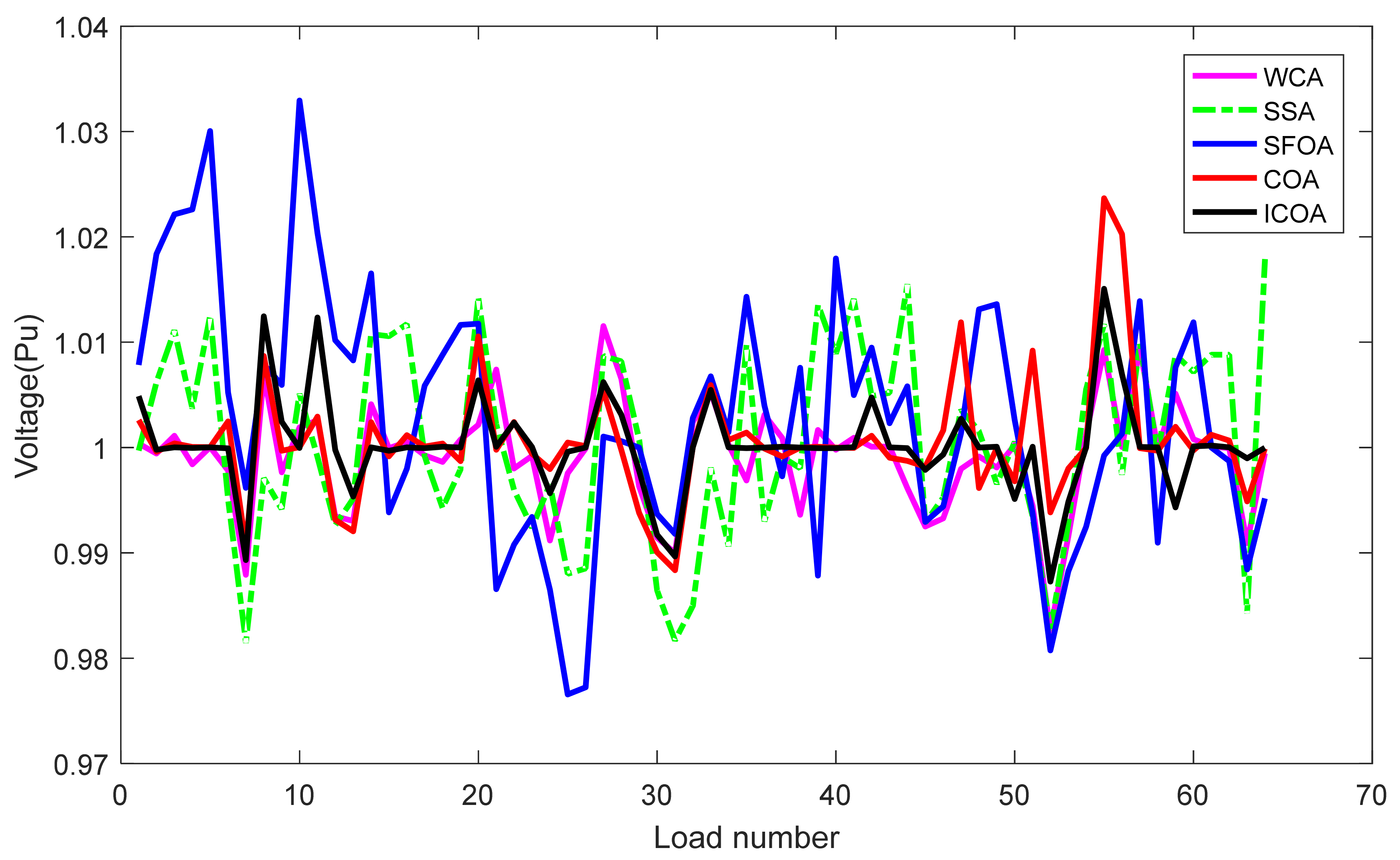
Compared to other implemented methods, the proposed method and these methods have approximately the same search speed due to the same setting of adjustment parameters; however, the proposed method has converged to optimal solutions with high quality, while others have not yielded the achievement. As shown in Section 5.2, the proposed method has reached a success rate of up to 100% for TPL and TVD cases and 98% for L index case, while the implemented methods have not reached the same success rate. For TPL case, only WCA has achieved SR with 100%, while SSA and SFOA have reached SR with 89% and 87%. SR of the three methods was, respectively, 100%, 92%, and 93% for TVD case and was, respectively, 90%, 78%, and 81% for L index case. Clearly, the proposed method is more capable of handling all constraints of the IEEE 30-bus system. One again, the conclusion can be confirmed via the best fitness of 50 runs plotted in Figure 5, Figure 6 and Figure 7 for TPL, TVD, and L index objective, respectively. In Figure 5, all applied methods have high fluctuations, but only the proposed ICOA reaches many better solutions with less power loss than other methods. In Figure 6 and Figure 7, the proposed ICOA has smaller fluctuation than other methods, and it also find solutions with much lower values of TVD and L index than others. Clearly, the figures show that the proposed method is more stable than other ones for finding solutions, since almost all solutions from the proposed method have lower fitness than other methods. Figure 8 shows the voltage of all loads for TVD objective. It is noted in the figure that voltage of loads closest to 1.0 pu is the best, with the smallest deviation, because 1.0 is an expected value. Voltage from the first load to the 24 loads indicates that the proposed method always keeps a small deviation with the expected voltage 1.0 pu. Thus, the proposed ICOA has the best value of TVD, as shown in Table 6 and Figure 6.
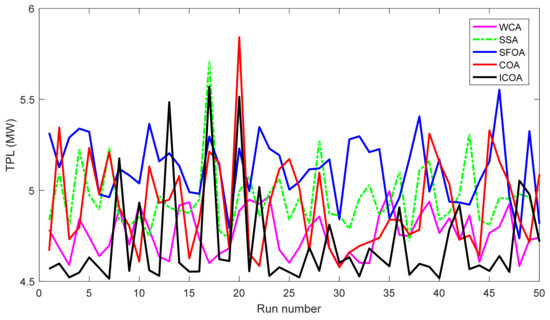
Figure 5.
TPL of 50 runs obtained by compared methods for the IEEE 30-bus system.
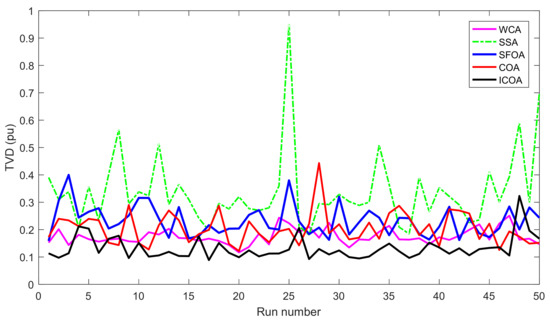
Figure 6.
TVD of 50 runs obtained by compared methods for the IEEE 30-bus system.
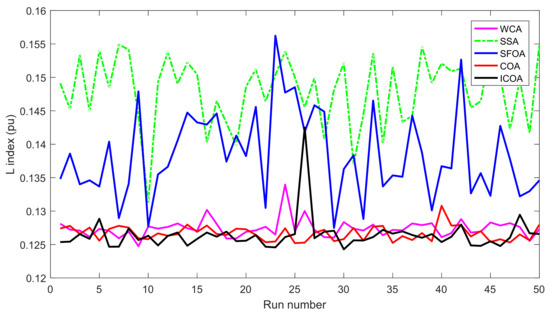
Figure 7.
L index of 50 runs obtained by compared methods for the IEEE 30-bus system.
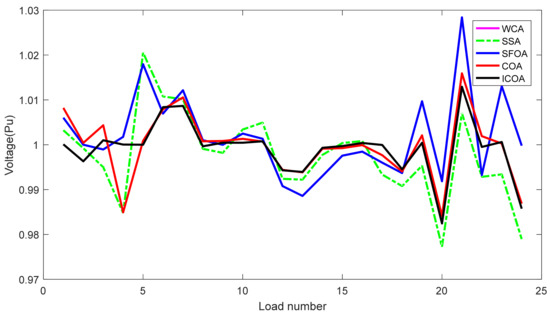
Figure 8.
Voltage of loads obtained by the compared methods for the IEEE 30-bus system.
Optimal solutions obtained by the proposed method for IEEE 30-bus system are given in Table A1 in Appendix A.
5.4. Investigation of the Proposed Method’s Performance on IEEE 57-Bus System
In this section, three different objectives of the IEEE 57-bus are considered to be optimized. Table 8, Table 9 and Table 10 show the information comparisons of all compared approaches with the proposed ICOA approach for TPL, TVD, and L index optimization. For the three objective comparisons, all the compared methods in other studies have been run only by setting control variables to continuous values. Thus, the comparisons with these methods and four other implemented methods are only performed for the case of continuous variables. However, all results obtained by the proposed methods for the case of discrete variables are also reported.

Table 8.
Result comparison of TPL for the IEEE 57-bus system.

Table 9.
Result comparison of TVD for the IEEE 57-bus system.

Table 10.
Result comparison of L index for the IEEE 57-bus system.
For the comparison with four implemented WCA, SSA, SFOA, and COA approaches, the high performance of the proposed ICOA approach can be identified clearly and exactly, since approximately all results from the proposed ICOA approach are superior to those from these methods. The proposed approach can reduce TPL to 22.376 MW, while the four methods found the best solutions with 26.0402, 25.3854, 26.6541, and 24.5358 MW. Clearly, the proposed approach can obtain less TPL than these methods by 3.6642, 3.0094, 4.2781, and 2.1598 MW. Similarly, the proposed ICOA approach continues to be more effective than these methods for TVD optimization and L index optimization, since the best TVD and the best L index are, respectively, less than these methods by 0.126, 0.335, 0.186, and 0.066 pu, and 0.02721, 0.03831, 0.03141, and 0.02401 pu. The values can result in the improvement level of the proposed ICOA approach over these methods. Namely, the improvement for TVD is 20.790%, 55.346%, 30.772%, and 10.907% and for L index is 10.81%, 15.22%, 12.47%, and 9.5%, respectively. The analysis of the best TPL, TVD, and L index can confirm the high efficiency of the proposed approach as compared to the four implemented methods. For judging the stabilization of search ability of the proposed approach, the average for 50 runs of the three optimization cases is compared among all methods.
For TPL optimization, the averages of the proposed approach and these ones are 24.9062 MW, and 26.5319, 27.0306, 28.4249, and 26.8983 MW. Similarly, these values for TVD optimization are 0.7436, 0.7913, 1.1736, 0.9975, and 0.8198 pu and for L index are 0.25169, 0.2789, 0.29, 0.2831, and 0.2757 pu. It can be realized that the search process of the proposed approach is more stable than the approaches.
The performance of the proposed ICOA approach is also evaluated effectively and strongly as comparisons with other approaches are carried out and analyzed. In fact, the proposed ICOA approach can find out more effective optimal solutions than almost all methods for TPL optimization and all methods for TVD optimization. Only MOGWA [49] has shown TPL of 21.171 MW, which is less than that of the proposed ICOA approach; however, the verification implies that the optimal solution has not been shown in the study [49]. Other comparisons with the second-best solution and the worst solution indicate that the proposed ICOA approach can reduce TPL from 0.894 to 3.264 MW, corresponding to the improvement level from 3.99% to 14.59%. The proposed ICOA approach also finds less TVD than others from 0.0433 to 0.1258 pu, corresponding to the improvement level from 7.16% to 20.79%. The average of 50 runs found by the proposed ICOA approach is less than almost all methods excluding ALC-PSO [17]. However, it should be pointed out that the method has used a much higher value for Nsqe than the proposed ICOA approach. Namely, Nsqe is 30,000 for ALC-PSO [17] but 6000 for the proposed ICOA approach. The reported values of Ti also lead to the same manner, since the proposed method can be faster than other methods by approximately 15–62 times for TPL optimization and approximately 21 times for TVD optimization. Consequently, there are enough evidences consisting of the best optimal solution, the best stabilization of search, and the fastest search ability to conclude that the proposed ICOA approach is the most effective solution for the ORPD problem with IEEE 57-bus system.
Optimal solutions obtained by the proposed method for IEEE 57-bus system are given in Table A2 in Appendix A.
5.5. Investigation of the Proposed Method’s Performance on the IEEE 118-Bus System
In this section, the proposed ICOA is applied for the purpose of reducing TPL, improving voltage profile, and enhancing voltage stabilization of the IEEE 118-bus system. In addition, the application of SSA, WCA, SFOA, COA, COA1, and COA2 methods for the system is also accomplished for further investigation of performance. The main comparison data consisting of minimum fitness, average fitness, Nsqe, and Ti together with others are reported in Table 11 for TPL objective, in Table 12 for TVD objective, and in Table 13 for L index objective. Other compared methods have set control variables to continuous values only and ignored the case of discrete values. Thus, analysis as well as discussion on results is only performed for the case of continuous variables. However, results from the proposed method for the case of discrete values are also reported in each comparison table.

Table 11.
Comparison of results obtained from the IEEE 118-bus system with power-loss optimization.

Table 12.
Comparison of results obtained from the IEEE 118-bus system with voltage deviation optimization.

Table 13.
Comparison of results obtained from the IEEE 118-bus system with voltage stabilization index optimization.
Comparisons of minimum and average fitness values among the proposed and implemented SSA, WCA, SFOA, COA, COA1, and COA2 methods shows that the proposed method is more effective in finding the best optimal solutions and more stable in the whole search process because the two values of the proposed method are less than those of these implemented ones for three objectives. The same values of Nsqe and Ti confirm that all methods have been run on the same conditions and fair comparisons have been executed. Nevertheless, the proposed method is always superior to the methods, as observed in Figure 9, Figure 10 and Figure 11. Approximately all runs of the proposed method could find better quality solutions for different objectives, and the fluctuations of the search process are very small, but very high fluctuations can be seen from the curves of other ones. Moreover, Figure 12 shows that nearly all loads of ICOA have voltage approximate with the reference value, 1 pu, while those from other ones are very different than 1 pu. The reported SR values in the three tables are useful for demonstrating the high potential of dealing with complicated constraints of the proposed method. For the three study cases, the proposed method handled all constraints as successfully as/more successfully than WCA, but its capability of dealing with constraints was better than other ones, especially much better than COA.
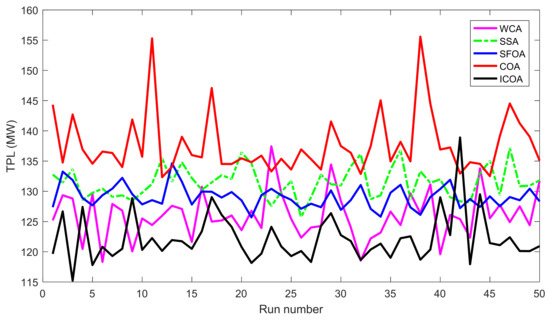
Figure 9.
TPL of 50 runs obtained by different methods for the IEEE 118-bus system.
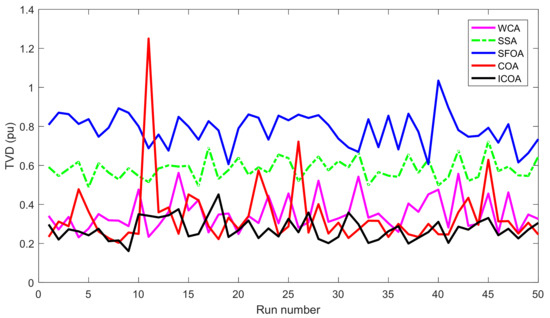
Figure 10.
TVD of 50 runs obtained by different methods for the IEEE 118-bus system.
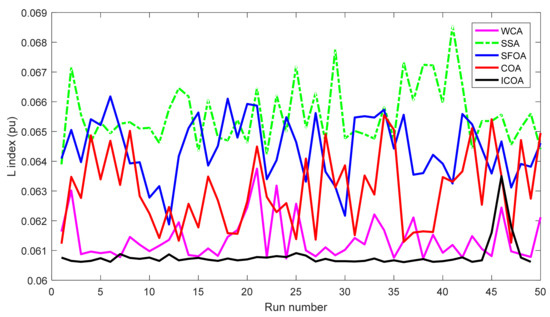
Figure 11.
L index of 50 runs obtained by different methods for the IEEE 118-bus system.
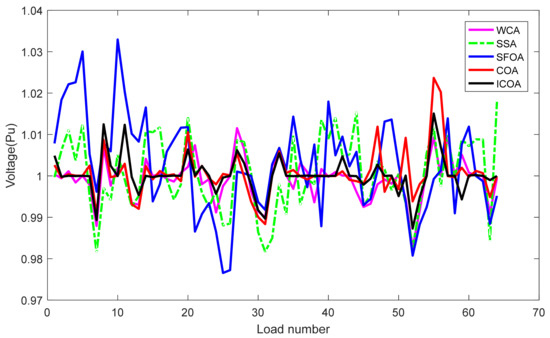
Figure 12.
The voltage of all loads obtained by five implemented methods.
The comparisons with other existing methods available in other studies can point out that the proposed method has a worse result than PSO-IPG [19], SARCGA [10], and QOTLBO [33] for TPL objective, and three PSO methods in [19] consisting of PSO-SWT, PSO-PGSWT, and PSO-IPG for L index objective. Nevertheless, it needs to confirm that not all the methods are really superior to the proposed method for the two objective functions. The verification of reported solutions can lead to the conclusion that SARCGA is not a real effective method, because there was no solution reported in [10]. QOTLBO [33] is only more effective than the proposed method for TPL objective but it is less effective for two cases of TVD and L index objectives. However, it should be noted that QOTLBO used a higher number of solution quality evaluations, 10,000, while that of the proposed method was only 8000. Thus, it can be said that the proposed method is more effective than QOTLBO.
Among the rest of methods in [19], PSO-IPG is more effective than the proposed method for two cases of TPL and L index objective, but it is less effective than the proposed method for TVD objective. PSO-SWT and PSO-PGSWT used the same number of solution quality evaluations as the proposed method, but the two methods found less effective solutions for two cases of TPL and TVD objectives. However, it should be noted that these methods in [19] were run by setting upper bound of the load bus voltage to 1.1 pu, while the proposed method and other ones were run on the bound of 1.05 pu. Thus, we have continued to implement the proposed method by assigning the upper bound of load bus voltage to 1.1 pu. All results obtained for three single objectives are shown in Table 14. It can be seen that the best TPL, TVD, and L index from the method for the same comparison condition with methods in [19] (i.e., continuous variables, the same upper bound of load bus voltage of 1.1 pu) are 111.2344 MW, 0.1561 pu, and 0.5678 pu; meanwhile, these values of the best PSO-IPG method in [19] are 115.06 MW, 0.162 pu, and 0.0568 pu. Clearly, the proposed ICOA method can improve performance of up to 3.32% for TPL objective and 3.64% for TVD objective over PSO-IPG, while the proposed method has the same optimal solution quality with PSO-IPG for L index case. For comparison with other methods shown in Table 11, Table 12 and Table 13, the improvement level of the proposed method can be from 0.37% to 12.93% for TPL objective, from 0.93% to 92.82% for TVD, and from 0.15% to 56.33% for L index.

Table 14.
Results obtained by the proposed method from the IEEE 118-bus system.
All methods in [19] were run by setting Npop = 40 and NIter = 200 corresponding to Nsqe = 8000, which is similar to that of the proposed method but their execution time was reported completely differently. For instance, the simulation time for TPL objective was approximately about 95 s. However, for TVD objectives, some methods reported about 75 s, and some other methods reported about 50 s, whilst one method, PSO-PGSWT, reported over 110 s. For L index, simulation time was over 110 s for five methods, but it was under 60 s for three other ones. The unreasonable issue is that methods using pseudogradient search reported the shortest time, even though pseudogradient search is complicated and it takes more time to determine the better direction for velocity. The comparisons of search speed easily led to the conclusion that the search speed of the proposed method is ranked in the leading method group, with once only methods in [19] having been executed for solving the IEEE 118-bus system by setting the same number of solution quality evaluations, which is less than that of all other methods. By considering Ti, it can be indicated that Ti of other methods is higher than 1, i.e., they were slower to converge to their optimal solutions. Consequently, it can conclude that the proposed method is effective for solving the IEEE 118-bus system.
6. Conclusions
This paper has presented an ICOA with intent to enhance convergence speed to the global optimum solution with the lowest value of fitness function as solving different systems of reactive power dispatch problem. The proposed method has been developed successfully in dealing with all constraints of the problem and in finding promising solutions with higher quality than those of the standard coyote optimization algorithm. In terms of the optimal solution search function for a general optimization problem, the implementation of the proposed method is simpler than that of COA, because the determination of center solutions in each pack is no longer essential in the proposed method and the offspring generation process is suggested to be changed in the proposed method. In COA, finding center solutions is time consuming, and the quality of center solutions is low, while offspring determination also needs high simulation time due to the process of finding control variables one by one. About the result comparison for the three IEEE power systems for the ORPD problem, each of two modifications was demonstrated to be more effective than the original procedure of COA via the comparisons of COA1 (COA with the first modification) and COA2 (COA with the second modification) with the standard COA. All the best optimal solutions from the two modified versions have better quality than those of COA for all objectives of three power systems. Furthermore, the success rate of the proposed method is always higher than that of COA. As compared to other methods consisting of implemented methods such as WCA, SSA, and SFOA, and other existing methods available in previous studies, the performance of the proposed method was thoroughly evaluated by focusing on three comparison criteria: the best optimal solution quality, the search speed, and the stabilization. The proposed method found more promising results than all methods for the IEEE 30-bus system in terms of better quality of the best optimal solution, faster search speed with the lower number of solution quality evaluations, and good stabilization. For the IEEE 57-bus and IEEE 118-bus systems, the proposed ICOA approach was more effective than all other methods. Consequently, it indicated that the proposed method is a powerful optimization tool for dealing with the ORPD problem, and it can be one of the most effectively alternative methods for other optimization problems in power systems.
Author Contributions
The contributions of L.C.K. are methodology, software, and writing—original draft preparation. C.T.H. contributed to the writing—review and editing, and funding acquisition. T.T.N. contributed to the method, supervision, and editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work belongs to the project grant number B2020-SPK-02 funded by Ministry of Education and Training, and hosted by Ho Chi Minh City University of Technology and Education, Vietnam.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data of the study are taken from [63].
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ABC | Artificial Bee Colony algorithm |
| ABC-FF | ABC with firefly algorithm |
| ACO | Ant Colony Optimization |
| AGA | Adaptive genetic algorithm |
| ALC-PSO | PSO with an aging leader and challengers |
| ALO | Ant lion optimizer |
| BA | Bat algorithm |
| CKHA | Chaotic krill herd algorithm |
| CLPSO | Comprehensive learning particle swarm optimization |
| COA | Coyote optimization algorithm |
| CSA | Cuckoo search algorithm |
| CSOA | Crow search optimization algorithm |
| DE | Differential evolution |
| DE-AS | Combination of differential evolution and ant system method |
| DSA | Differential search algorithm |
| EMOA | Exchange market optimization algorithm |
| GA | Genetic algorithm |
| GBBWCA | Gaussian barebones water cycle algorithm |
| GBTLBO | Gaussian barebones-based TLBO algorithm |
| GSA | Gravitational search algorithm |
| GWO | Gray wolf optimizer |
| HFA-NMS | Hybrid Nelder–Mead simplex-based firefly algorithm |
| HLGA | Hybrid loop genetic algorithm |
| HMAPSO | Hybrid multiagent particle swarm optimization |
| HPSO | Hybrid PSO |
| HPSO-ICA | Hybrid PSO and imperialist competitive algorithms |
| HPSO-TS | Hybridization of PSO and Tabu search method |
| HAS | Harmony search algorithm |
| IABC-DE | Incorporation of chaotic artificial bee colony algorithm and differential evolution |
| ICA | Imperialist competitive algorithms |
| ICBO | Improved Colliding Bodies optimization |
| ICOA | Improved coyote optimization algorithm |
| ICSA | Improved CSA |
| JA | Jaya algorithm |
| KHA | Krill herd algorithm |
| MFO | Moth-flame optimization technique |
| MGBTLBO | modified GBTLBO |
| MOGWA | Multiobjective grey wolf algorithm |
| MPSO | Modified Particle swarm optimization |
| MTLA-DDE | Hybrid modified teaching learning technique and double differential evolution algorithm |
| ORPD | Optimal reactive power dispatch |
| PPs | Power plants |
| PSO | Particle swarm optimization |
| HPSO | Hybrid PSO |
| PSO-AAC | PSO with adaptive acceleration coefficients |
| PSO-AIW | PSO with adaptive inertia weight |
| PSO-CF | PSO with constriction factor |
| PSO-GT | Combination of PSO and graph theory |
| PSO-IPG | PSO with pseudogradient theory and constriction factor |
| PSO-PG | PSO with pseudogradient theory |
| PSO-PGSWT | PSO-SWT with pseudogradient theory |
| PSO-SWT | PSO with the trade-off of stochastic weight |
| PST | Probabilistic state transition |
| QODE | Quasi-oppositional differential evolution |
| QOTLBO | Quasi-oppositional teaching learning-based optimization |
| RCGA | Real coded genetic algorithm |
| SARCGA | Self-adaptive real coded genetic algorithm |
| SFOA | Sunflower optimization algorithm |
| SGA | Specialized genetic algorithm |
| SPSO-AAC | Self-adaptive PSO with adaptive acceleration coefficients |
| SR | Success rate |
| SSA | Salp swarm algorithm |
| Std. dev. | Standard deviation |
| TLBO | Teaching learning-based optimization |
| TPL | Total active power losses |
| TS | Tabu search method |
| TVD | Total voltage deviation |
| VSMF | Variable scaling mutation factor |
| WCA | Water cycle algorithm |
| WOA | Whale optimization algorithm |
| Nomenclature | |
| : | Fitness function of new solution and old solution d in the pth pack |
| G | Current iteration |
| Glineij, Blineij | Real element and imaginary element of admittance of branch ij |
| NB | Number of all buses in considered power system |
| Ncoyote | Number of coyotes in each pack |
| NC | Number of shunt capacitor banks |
| NG | Number of generators |
| NIter | The largest iteration |
| NL | Number of all loads |
| Npack | Number of packs |
| Npop | Number of coyotes in all packs |
| Nrun | Number of runs |
| Nspi | Number of new solutions produced per iteration |
| Nspr | Number of new solutions produced per run |
| Nsqe | Number of quality solution evaluations |
| NT | Number of transformers |
| PGen,i, QGen,i | Active power and reactive power generated by generator at bus i |
| Pload,i, Qload,i | Active power and reactive power consumed by load at bus i |
| Qcap,i | Reactive power generated by shunt capacitor banks at bus i |
| Qcap,i,min, Qcap,i,max | The lowest and highest reactive power generated by shunt capacitor banks at bus i |
| QGen,i,min, QGen,i,max | The lowest and highest reactive power generated by generators at bus i |
| Sbranch,ij | Apparent power flow through branch ij |
| Sbranch,ij,max | Apparent power flow capacity of branch ij |
| Solbest,p, Solworst,p | The best solution and the worst solution in the pack p |
| Solbest,r1, Solbest,r2, Solbest,r3, Solbest,r4 | The best solutions in all packs picked up randomly |
| Solcenter,p | The center solution in the pack p |
| Sold | The dth solution in population |
| SolGbest | The best solution in the population |
| The new solution in the pack p | |
| Solr1,p, Solr2,p | Two randomly picked solutions in the pth pack |
| TTi,min, TTi,max | The lowest and highest tap changers of transformers at bus i |
| Vexpected | Expected voltage magnitude, 1.0 pu |
| VGeni,min, VGeni,max | Lower and upper limitations of voltage magnitude of generators at bus i |
| Vi, Vj | Magnitude of voltage at buses i and j |
| Vload,i | Voltage magnitude of load at the bus i |
| Vload,i,min, Vload,i,max | The lowest and highest voltage magnitude of loads at bus i |
| Yij | Shunt admittance of branch ij |
| μ1, μ2, μ3, μ4, μ5, μ6, μ7 | Random numbers in range from 0 to 1 |
| αi, αj | Phase angles of voltage at bus i and bus j |
| ϕ1, ϕ 2, ϕ 3 | Penalty factors in fitness function |
Appendix A

Table A1.
Optimal solutions obtained by ICOA for the IEEE 30-bus system.
Table A1.
Optimal solutions obtained by ICOA for the IEEE 30-bus system.
| Case | Continuous Variables | Discrete Variables | ||||
|---|---|---|---|---|---|---|
| Input/Control Variables | Minimize Power Loss | Minimize Vol. Dev. | Minimize L Index | Minimize Power Loss | Minimize Vol. Dev. | Minimize L Index |
| VG1 (pu) | 1.1 | 1.0143 | 1.1 | 1.1 | 1.0135 | 1.1 |
| VG2 | 1.0943 | 1.0109 | 1.0962 | 1.0945 | 1.0102 | 1.0954 |
| VG5 | 1.0747 | 1.0192 | 1.0996 | 1.075 | 1.0193 | 1.1 |
| VG8 | 1.0766 | 1.0103 | 1.0918 | 1.077 | 1.0103 | 1.0928 |
| VG11 | 1.1 | 0.9843 | 1.0997 | 1.1 | 0.9864 | 1.1 |
| VG13 | 1.1 | 1.0099 | 1.1 | 1.1 | 1.0089 | 1.1 |
| QC10 (MVAR) | 5 | 5.0000 | 0.0129 | 5 | 5 | 0 |
| QC12 | 5 | 2.9662 | 5 | 5 | 3.1 | 5 |
| QC15 | 5 | 5.0000 | 4.9194 | 5 | 5 | 5 |
| QC17 | 5 | 0.0000 | 0.1459 | 5 | 0 | 2.7 |
| QC20 | 3.9845 | 4.9880 | 4.6736 | 3.8 | 5 | 5 |
| QC21 | 5 | 5.0000 | 0 | 5 | 5 | 0 |
| QC23 | 2.4693 | 5.0000 | 0 | 2.6 | 5 | 0 |
| QC24 | 5 | 5.0000 | 5 | 5 | 5 | 5 |
| QC29 | 2.1955 | 5.0000 | 0 | 2.5 | 5 | 0 |
| T11 | 1.0434 | 0.9980 | 0.9822 | 1.04 | 1.00 | 0.99 |
| T12 | 0.9 | 0.9002 | 0.9 | 0.9 | 0.90 | 0.9 |
| T15 | 0.9794 | 0.9830 | 0.9801 | 0.98 | 0.98 | 0.99 |
| T36 | 0.965 | 0.9782 | 0.9588 | 0.97 | 0.98 | 0.96 |

Table A2.
Optimal solutions obtained by ICOA for the IEEE 57-bus system.
Table A2.
Optimal solutions obtained by ICOA for the IEEE 57-bus system.
| Case | Continuous Variables | Discrete Variables | ||||
|---|---|---|---|---|---|---|
| Input/Control Variables | TPL Optimization | TVD Optimization | L Index Optimization | TPL Optimization | TVD Optimization | L Index Optimization |
| VG1 (pu) | 1.1 | 1.0249 | 1.0728 | 1.0999 | 0.991 | 1.0329 |
| VG2 | 1.0979 | 0.9802 | 1.0412 | 1.0968 | 0.994 | 1.0258 |
| VG3 | 1.0858 | 1.0190 | 1.0534 | 1.0815 | 1.0075 | 1.0090 |
| VG6 | 1.0792 | 0.9991 | 1.0836 | 1.0777 | 1.0046 | 1.0568 |
| VG8 | 1.0978 | 1.0218 | 1.0690 | 1.0954 | 1.019 | 1.0488 |
| VG9 | 1.0794 | 1.0260 | 1.0840 | 1.0767 | 1.0387 | 1.0599 |
| VG12 | 1.0753 | 1.0022 | 1.0857 | 1.0735 | 1.0282 | 1.0537 |
| QC18 (MVAR) | 10 | 0 | 8.8363 | 10 | 7 | 9.9000 |
| QC25 | 5.9 | 5.9000 | 0.0001 | 5.9 | 5.9 | 0.6000 |
| QC53 | 6.3 | 6.3000 | 1.4086 | 6.3 | 3 | 0 |
| T19 | 1.1 | 1.0594 | 0.9109 | 1.1 | 1.03 | 0.9000 |
| T20 | 0.9315 | 0.9315 | 0.9845 | 0.95 | 0.97 | 1.0200 |
| T31 | 1.0298 | 0.9723 | 1.1000 | 1.03 | 0.97 | 1.0300 |
| T35 | 0.9553 | 1.0354 | 0.8815 | 0.97 | 0.9 | 0.9000 |
| T36 | 0.9581 | 0.9600 | 0.9135 | 0.94 | 1.07 | 0.8800 |
| T37 | 1.0041 | 0.9036 | 0.9303 | 1.01 | 1.03 | 0.9200 |
| T41 | 0.9761 | 0.9000 | 0.9670 | 0.98 | 0.95 | 0.9800 |
| T46 | 0.9399 | 0.9059 | 0.8972 | 0.94 | 0.92 | 0.9000 |
| T54 | 1.0204 | 0.9923 | 0.8670 | 1.02 | 0.8 | 0.8000 |
| T58 | 0.9736 | 1.0005 | 0.9593 | 0.97 | 0.99 | 0.9600 |
| T59 | 0.9569 | 0.9002 | 0.9577 | 0.96 | 1 | 0.9400 |
| T65 | 0.9683 | 0.9653 | 0.9776 | 0.97 | 1.04 | 1.0500 |
| T66 | 0.933 | 1.0141 | 0.8858 | 0.93 | 0.81 | 0.8700 |
| T71 | 0.9652 | 0.9002 | 0.9637 | 0.97 | 1.02 | 1.0200 |
| T73 | 1.1 | 0.9913 | 1.0149 | 1.1 | 1.06 | 1.0900 |
| T76 | 1.0065 | 1.0249 | 1.0872 | 1.01 | 0.95 | 1.1000 |
| T80 | 0.9767 | 0.9802 | 0.9900 | 0.98 | 1 | 0.9900 |

Table A3.
Optimal solution obtained by ICOA for TPL objective of the IEEE 118-bus power system with the case of continuous variables.
Table A3.
Optimal solution obtained by ICOA for TPL objective of the IEEE 118-bus power system with the case of continuous variables.
| Input/Control Variables | Value | Input/Control Variables | Value | Input/Control Variables | Value |
|---|---|---|---|---|---|
| VG1 (pu) | 1.0268 | VG62 | 1.042 | VG113 | 1.0419 |
| VG4 | 1.0491 | VG65 | 1.0572 | VG116 | 1.0492 |
| VG6 | 1.0378 | VG66 | 1.068 | QC5 (MVAR) | 0 |
| VG8 | 1.0371 | VG69 | 1.0783 | QC34 | 9.5094 |
| VG10 | 1.041 | VG70 | 1.0457 | QC37 | 0 |
| VG12 | 1.0356 | VG72 | 1.0387 | QC44 | 10 |
| VG15 | 1.0309 | VG73 | 1.0404 | QC45 | 4.6391 |
| VG18 | 1.0341 | VG74 | 1.0346 | QC46 | 0 |
| VG19 | 1.0305 | VG76 | 1.0333 | QC48 | 13.1049 |
| VG24 | 1.0422 | VG77 | 1.0502 | QC74 | 1.0051 |
| VG25 | 1.0826 | VG80 | 1.0601 | QC79 | 19.9991 |
| VG26 | 1.0794 | VG85 | 1.0516 | QC82 | 20 |
| VG27 | 1.0372 | VG87 | 1.0541 | QC83 | 4.5755 |
| VG31 | 1.0293 | VG89 | 1.0634 | QC105 | 1.0771 |
| VG32 | 1.0316 | VG90 | 1.045 | QC107 | 5.9685 |
| VG34 | 1.0409 | VG91 | 1.0462 | QC110 | 0.7361 |
| VG36 | 1.0382 | VG92 | 1.056 | T 8 (pu) | 0.9847 |
| VG40 | 1.0141 | VG99 | 1.0491 | T 32 | 1.043 |
| VG42 | 1.0183 | VG100 | 1.0521 | T36 | 0.9841 |
| VG46 | 1.0362 | VG103 | 1.0383 | T 51 | 0.9883 |
| VG49 | 1.0543 | VG104 | 1.0283 | T 93 | 0.9785 |
| VG54 | 1.0258 | VG105 | 1.022 | T 95 | 1.0061 |
| VG55 | 1.0232 | VG107 | 1.0076 | T 102 | 0.9217 |
| VG56 | 1.0239 | VG110 | 1.0169 | T 107 | 0.9389 |
| VG59 | 1.0476 | VG111 | 1.0245 | T 127 | 0.9751 |
| VG61 | 1.0447 | VG112 | 1.0016 | ||

Table A4.
Optimal solution obtained by ICOA for TVD objective of the IEEE 118-bus power system with the case of continuous variables.
Table A4.
Optimal solution obtained by ICOA for TVD objective of the IEEE 118-bus power system with the case of continuous variables.
| Input/Control Variables | Value | Input/Control Variables | Value | Input/Control Variables | Value |
|---|---|---|---|---|---|
| VG1 (pu) | 1.0024 | VG62 | 1.009 | VG113 | 0.9973 |
| VG4 | 0.9899 | VG65 | 0.984 | VG116 | 0.9942 |
| VG6 | 0.9921 | VG66 | 1.0046 | QC5 (MVAR) | −36.195 |
| VG8 | 0.9931 | VG69 | 0.982 | QC34 | 0.4873 |
| VG10 | 0.9894 | VG70 | 0.9669 | QC37 | −24.8748 |
| VG12 | 1.0146 | VG72 | 1.0548 | QC44 | 9.8991 |
| VG15 | 1.0102 | VG73 | 1.0274 | QC45 | 9.6248 |
| VG18 | 0.9729 | VG74 | 1.0254 | QC46 | 5.7702 |
| VG19 | 1.0353 | VG76 | 1.0131 | QC48 | 0.029 |
| VG24 | 1.0217 | VG77 | 1.0127 | QC74 | 7.6541 |
| VG25 | 0.9661 | VG80 | 1.0148 | QC79 | 0.3241 |
| VG26 | 0.97 | VG85 | 1.0115 | QC82 | 19.8856 |
| VG27 | 1.0068 | VG87 | 1.0054 | QC83 | 9.9122 |
| VG31 | 1.0032 | VG89 | 1.0076 | QC105 | 0.9221 |
| VG32 | 1.0036 | VG90 | 1.0911 | QC107 | 0.4846 |
| VG34 | 1.0043 | VG91 | 0.9554 | QC110 | 0.7378 |
| VG36 | 1.0003 | VG92 | 0.9986 | T 8 (pu) | 0.9631 |
| VG40 | 1.0117 | VG99 | 1.0954 | T 32 | 1.0507 |
| VG42 | 0.9937 | VG100 | 1.0373 | T36 | 1.0058 |
| VG46 | 1.0437 | VG103 | 0.9517 | T 51 | 0.9923 |
| VG49 | 1.0006 | VG104 | 1.0771 | T 93 | 0.9419 |
| VG54 | 1.0234 | VG105 | 0.981 | T 95 | 1.0164 |
| VG55 | 0.9934 | VG107 | 1.0824 | T 102 | 1.041 |
| VG56 | 1.0163 | VG110 | 1.0192 | T 107 | 1.0865 |
| VG59 | 1.0662 | VG111 | 0.9656 | T 127 | 0.9708 |
| VG61 | 0.9939 | VG112 | 1.0682 | ||

Table A5.
Optimal solution obtained by ICOA for L index objective of the IEEE 118-bus power system with the case of continuous variables.
Table A5.
Optimal solution obtained by ICOA for L index objective of the IEEE 118-bus power system with the case of continuous variables.
| Input/Control Variables | Value | Input/Control Variables | Value | Input/Control Variables | Value |
|---|---|---|---|---|---|
| VG1 (pu) | 0.9631 | VG62 | 1.0448 | VG113 | 1.0456 |
| VG4 | 0.9979 | VG65 | 1.0665 | VG116 | 0.9985 |
| VG6 | 0.9766 | VG66 | 0.9506 | QC5 (MVAR) | −21.7949 |
| VG8 | 0.95 | VG69 | 0.9516 | QC34 | 0.0016 |
| VG10 | 1.0959 | VG70 | 0.96 | QC37 | −24.4039 |
| VG12 | 0.978 | VG72 | 1.0241 | QC44 | 7.2981 |
| VG15 | 0.9846 | VG73 | 1.1 | QC45 | 3.8457 |
| VG18 | 0.98 | VG74 | 0.9631 | QC46 | 10 |
| VG19 | 0.9965 | VG76 | 1.0128 | QC48 | 0.0079 |
| VG24 | 1.0489 | VG77 | 1.0384 | QC74 | 7.4084 |
| VG25 | 1 | VG80 | 1.0183 | QC79 | 6.8455 |
| VG26 | 1.0999 | VG85 | 1.053 | QC82 | 19.8649 |
| VG27 | 1.0188 | VG87 | 1.052 | QC83 | 10 |
| VG31 | 1.0149 | VG89 | 0.9634 | QC105 | 5.8526 |
| VG32 | 1.0137 | VG90 | 0.9571 | QC107 | 0.1586 |
| VG34 | 1.0596 | VG91 | 0.9718 | QC110 | 1.0895 |
| VG36 | 1.0261 | VG92 | 0.9501 | T 8 (pu) | 0.9 |
| VG40 | 1.0352 | VG99 | 1.0989 | T 32 | 1.0989 |
| VG42 | 1.0969 | VG100 | 0.995 | T36 | 0.9 |
| VG46 | 1.1 | VG103 | 1.0955 | T 51 | 1.0054 |
| VG49 | 1.0444 | VG104 | 0.9615 | T 93 | 0.9989 |
| VG54 | 0.9623 | VG105 | 1.0286 | T 95 | 1.0989 |
| VG55 | 1.0373 | VG107 | 0.95 | T 102 | 1.077 |
| VG56 | 0.9961 | VG110 | 0.9539 | T 107 | 0.9759 |
| VG59 | 0.9501 | VG111 | 0.9549 | T 127 | 1.053 |
| VG61 | 0.9678 | VG112 | 0.9502 | ||

Table A6.
Optimal solution obtained by ICOA for TPL objective of the IEEE 118-bus power system with the case of discrete variables.
Table A6.
Optimal solution obtained by ICOA for TPL objective of the IEEE 118-bus power system with the case of discrete variables.
| Input/Control Variables | Value | Input/Control Variables | Value | Input/Control Variables | Value |
|---|---|---|---|---|---|
| VG1 (pu) | 1.0277 | VG62 | 1.0408 | VG113 | 1.0427 |
| VG4 | 1.0483 | VG65 | 1.0597 | VG116 | 1.0477 |
| VG6 | 1.0395 | VG66 | 1.0689 | QC5 (MVAR) | 0 |
| VG8 | 1.0347 | VG69 | 1.0761 | QC34 | 10.1 |
| VG10 | 1.0434 | VG70 | 1.0387 | QC37 | 0 |
| VG12 | 1.037 | VG72 | 1.0323 | QC44 | 10 |
| VG15 | 1.0326 | VG73 | 1.0402 | QC45 | 4.6 |
| VG18 | 1.0321 | VG74 | 1.0322 | QC46 | 0 |
| VG19 | 1.0299 | VG76 | 1.0296 | QC48 | 6.3 |
| VG24 | 1.0453 | VG77 | 1.0505 | QC74 | 0.8 |
| VG25 | 1.0766 | VG80 | 1.0617 | QC79 | 6.7 |
| VG26 | 1.0901 | VG85 | 1.052 | QC82 | 20 |
| VG27 | 1.0344 | VG87 | 1.047 | QC83 | 4.4 |
| VG31 | 1.0257 | VG89 | 1.0631 | QC105 | 7.2 |
| VG32 | 1.0332 | VG90 | 1.0439 | QC107 | 4.1 |
| VG34 | 1.0376 | VG91 | 1.0466 | QC110 | 1.5 |
| VG36 | 1.0356 | VG92 | 1.0562 | T 8 (pu) | 0.98 |
| VG40 | 1.0188 | VG99 | 1.0479 | T 32 | 1.05 |
| VG42 | 1.0239 | VG100 | 1.0506 | T36 | 0.98 |
| VG46 | 1.0332 | VG103 | 1.0405 | T 51 | 0.99 |
| VG49 | 1.0554 | VG104 | 1.0305 | T 93 | 0.98 |
| VG54 | 1.0258 | VG105 | 1.0268 | T 95 | 1 |
| VG55 | 1.023 | VG107 | 1.0132 | T 102 | 0.9 |
| VG56 | 1.025 | VG110 | 1.0196 | T 107 | 0.94 |
| VG59 | 1.0495 | VG111 | 1.0281 | T 127 | 0.97 |
| VG61 | 1.047 | VG112 | 1.0026 | ||

Table A7.
Optimal solution obtained by ICOA for TVD objective of the IEEE 118-bus power system with the case of discrete variables.
Table A7.
Optimal solution obtained by ICOA for TVD objective of the IEEE 118-bus power system with the case of discrete variables.
| Input/Control Variables | Value | Input/Control Variables | Value | Input/Control Variables | Value |
|---|---|---|---|---|---|
| VG1 (pu) | 1.0025 | VG62 | 1.0095 | VG113 | 0.9974 |
| VG4 | 0.9897 | VG65 | 0.9831 | VG116 | 0.9975 |
| VG6 | 0.9922 | VG66 | 1.0041 | QC5 (MVAR) | −36.2 |
| VG8 | 0.9929 | VG69 | 0.95 | QC34 | 0.5 |
| VG10 | 0.9895 | VG70 | 0.9669 | QC37 | −24.9 |
| VG12 | 1.0146 | VG72 | 1.0554 | QC44 | 9.9 |
| VG15 | 1.0099 | VG73 | 1.0274 | QC45 | 9.6 |
| VG18 | 0.9785 | VG74 | 1.0367 | QC46 | 5.8 |
| VG19 | 1.0354 | VG76 | 1.0131 | QC48 | 0 |
| VG24 | 1.0218 | VG77 | 1.0127 | QC74 | 7.7 |
| VG25 | 0.9662 | VG80 | 1.0149 | QC79 | 0.3 |
| VG26 | 0.965 | VG85 | 1.0115 | QC82 | 19.9 |
| VG27 | 1.0072 | VG87 | 1.0054 | QC83 | 9.9 |
| VG31 | 1.0031 | VG89 | 1.0075 | QC105 | 0.9 |
| VG32 | 1.0031 | VG90 | 1.0913 | QC107 | 0.5 |
| VG34 | 1.0042 | VG91 | 0.9513 | QC110 | 0.7 |
| VG36 | 1.0003 | VG92 | 0.9986 | T 8 (pu) | 0.96 |
| VG40 | 1.0114 | VG99 | 1.0981 | T 32 | 1.05 |
| VG42 | 0.9937 | VG100 | 1.0371 | T36 | 1.01 |
| VG46 | 1.0438 | VG103 | 0.9517 | T 51 | 0.99 |
| VG49 | 1.0006 | VG104 | 1.077 | T 93 | 0.94 |
| VG54 | 1.0234 | VG105 | 0.981 | T 95 | 1.02 |
| VG55 | 0.9939 | VG107 | 1.0824 | T 102 | 1.04 |
| VG56 | 1.0162 | VG110 | 1.019 | T 107 | 1.09 |
| VG59 | 1.0669 | VG111 | 0.9688 | T 127 | 0.97 |
| VG61 | 0.9938 | VG112 | 1.0682 | ||

Table A8.
Optimal solution obtained by ICOA for L index objective of the IEEE 118-bus power system with the case of discrete variables.
Table A8.
Optimal solution obtained by ICOA for L index objective of the IEEE 118-bus power system with the case of discrete variables.
| Input/Control Variables | Value | Input/Control Variables | Value | Input/Control Variables | Value |
|---|---|---|---|---|---|
| VG1 (pu) | 0.9529 | VG62 | 1.0389 | VG113 | 1.0491 |
| VG4 | 0.9972 | VG65 | 1.0693 | VG116 | 1.0024 |
| VG6 | 0.9765 | VG66 | 0.9502 | QC5 (MVAR) | −22.2 |
| VG8 | 0.95 | VG69 | 0.9507 | QC34 | 0 |
| VG10 | 1.0972 | VG70 | 0.9574 | QC37 | −24.4 |
| VG12 | 0.9783 | VG72 | 1.0244 | QC44 | 7.1 |
| VG15 | 0.9862 | VG73 | 1.1 | QC45 | 4.1 |
| VG18 | 0.9801 | VG74 | 0.9544 | QC46 | 10 |
| VG19 | 0.9965 | VG76 | 1.0191 | QC48 | 0 |
| VG24 | 1.0449 | VG77 | 1.0379 | QC74 | 7.4 |
| VG25 | 0.9991 | VG80 | 1.0184 | QC79 | 7.1 |
| VG26 | 1.0999 | VG85 | 1.0534 | QC82 | 19.9 |
| VG27 | 1.0159 | VG87 | 1.0623 | QC83 | 10 |
| VG31 | 1.015 | VG89 | 0.9635 | QC105 | 7.8 |
| VG32 | 1.0238 | VG90 | 0.9663 | QC107 | 0 |
| VG34 | 1.0596 | VG91 | 0.9769 | QC110 | 1.2 |
| VG36 | 1.0361 | VG92 | 0.95 | T 8 (pu) | 0.9 |
| VG40 | 1.0355 | VG99 | 1.1 | T 32 | 1.1 |
| VG42 | 1.0956 | VG100 | 0.9968 | T36 | 0.9 |
| VG46 | 1.1 | VG103 | 1.093 | T 51 | 1.02 |
| VG49 | 1.0444 | VG104 | 0.9611 | T 93 | 1.01 |
| VG54 | 0.9617 | VG105 | 1.0286 | T 95 | 1.1 |
| VG55 | 1.0372 | VG107 | 0.95 | T 102 | 1.06 |
| VG56 | 0.9956 | VG110 | 0.9535 | T 107 | 0.98 |
| VG59 | 0.9501 | VG111 | 0.9513 | T 127 | 1.05 |
| VG61 | 0.9682 | VG112 | 0.9507 | ||
References
- Awad, N.H.; Ali, M.Z.; Mallipeddi, R.; Suganthan, P.N. An efficient differential evolution algorithm for stochastic OPF based active-reactive power dispatch problem considering renewable generators. Appl. Soft Comput. 2019, 76, 445–458. [Google Scholar] [CrossRef]
- Sayah, S. Modified differential evolution approach for practical optimal reactive power dispatch of hybrid AC-DC power systems. Appl. Soft Comput. 2018, 73, 591–606. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vu Quynh, N.; Duong, M.Q.; Van Dai, L. Modified differential evolution algorithm: A novel approach to optimize the operation of hydrothermal power systems while considering the different constraints and valve point loading effects. Energies 2018, 11, 540. [Google Scholar] [CrossRef]
- Murray, A.; Engelmann, A.; Hagenmeyer, V.; Faulwasser, T. Hierarchical distributed mixed-integer optimization for reactive power dispatch. IFAC-PapersOnLine 2018, 51, 368–373. [Google Scholar] [CrossRef]
- Da Costa, G.R.M. Modified Newton method for reactive dispatching. Int. J. Electr. Power Energy Syst. 2002, 24, 815–819. [Google Scholar] [CrossRef]
- Venkatesh, B.; Sasadivam, G.; Khan, M.A. Towards on-line optimal reactive power scheduling using ANN memory model based method. In Proceedings of the Power Engineering Society 1999 Winter Meeting, New York, NY, USA, 31 January–4 February 1999; Volume 2, pp. 844–848. [Google Scholar] [CrossRef]
- Rezania, E.; Shahidehpour, S.M. Real power loss minimization using interior point method. Int. J. Electr. Power Energy Syst. 2001, 23, 45–56. [Google Scholar] [CrossRef]
- Grudinin, N. Reactive power optimization using successive quadratic programming method. IEEE Trans. Power Syst. 1998, 13, 1219–1225. [Google Scholar] [CrossRef]
- Cao, Y.J.; Wu, Q.H. Optimal reactive power dispatch using an adaptive genetic algorithm. In Proceedings of the Second International Conference on Genetic Algorithms in Engineering Systems, Glasgow, UK, 2–4 September 1997; pp. 117–122. [Google Scholar] [CrossRef]
- Subbaraj, P.; Rajnarayanan, P.N. Optimal reactive power dispatch using self-adaptive real coded genetic algorithm. Electr. Power Syst. Res. 2009, 79, 374–381. [Google Scholar] [CrossRef]
- Alam, M.S.; De, M. Optimal reactive power dispatch using hybrid loop-genetic based algorithm. In Proceedings of the Power Systems Conference (NPSC) IEEE, Bhubaneswar, India, 19–21 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Rayudu, K.; Yesuratnam, G.; Jayalaxmi, A. Improving voltage stability by optimal reactive power dispatch based on genetic algorithm and linear programming technique. In Proceedings of the International Conference on IEEE: Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 1357–1362. [Google Scholar] [CrossRef]
- Văduva, A.M.; Bulac, C. New evolutionary algorithm method for solving optimal reactive power dispatch problem. In Proceedings of the 2016 International Conference on IEEE on Applied and Theoretical Electricity (ICATE), Craiova, Romania, 6–8 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Villa-Acevedo, W.; López-Lezama, J.; Valencia-Velásquez, J.A. A novel constraint handling approach for the optimal reactive power dispatch problem. Energies 2018, 11, 2352. [Google Scholar] [CrossRef]
- Kanatip, R.; Keerati, C. Probabilistic optimal power flow considering load and solar power uncertainties using particle swarm optimization. GMSARN Int. J. 2021, 15, 37–43. [Google Scholar]
- Mahadevan, K.; Kannan, P.S. Comprehensive learning particle swarm optimization for reactive power dispatch. Appl. Soft Comput. 2010, 10, 641–652. [Google Scholar] [CrossRef]
- Singh, R.P.; Mukherjee, V.; Ghoshal, S.P. Optimal reactive power dispatch by particle swarm optimization with an aging leader and challengers. Appl. Soft Comput. 2015, 29, 298–309. [Google Scholar] [CrossRef]
- Reddy, P.L.; Yesuratnam, G. PSO based optimal reactive power dispatch for voltage profile improvement. In Proceedings of the Power, Communication and Information Technology Conference (PCITC) on IEEE, Bhubaneswar, India, 15–17 October 2015; pp. 361–366. [Google Scholar] [CrossRef]
- Polprasert, J.; Ongsakul, W.; Dieu, V.N. Optimal reactive power dispatch using improved pseudo-gradient search particle swarm optimization. Electr. Power Compon. Syst. 2016, 44, 518–532. [Google Scholar] [CrossRef]
- Dieu, V.N.; Nguyen, T.P.; Nguyen, K.D. Multi-objective security constrained optimal active and reactive power dispatch using hybrid particle swarm optimization and differential evolution. GMSARN Int. J. 2018, 12, 84–117. [Google Scholar]
- Mehdinejad, M.; Mohammadi-Ivatloo, B.; Dadashzadeh-Bonab, R.; Zare, K. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms. Int. J. Electr. Power Energy Syst. 2016, 83, 104–116. [Google Scholar] [CrossRef]
- Kaur, D.; Lie, T.T.; Nair, N.K.; Valles, B. An optimal reactive power dispatch (ORPD) for voltage security using particle swarm optimization (PSO) in graph theory. In Proceedings of the 2016 IEEE International Conference on Sustainable Energy Technologies (ICSET), Hanoi, Vietnam, 14–16 October 2016; pp. 25–30. [Google Scholar] [CrossRef]
- Sahli, Z.; Hamouda, A.; Bekrar, A.; Trentesaux, D. Reactive power dispatch optimization with voltage profile improvement using an efficient hybrid algorithm. Energies 2018, 11, 2134. [Google Scholar] [CrossRef]
- El Ela, A.A.; Abido, M.A.; Spea, S.R. Differential evolution algorithm for optimal reactive power dispatch. Electr. Power Syst. Res. 2011, 81, 458–464. [Google Scholar] [CrossRef]
- Huang, C.M.; Huang, Y.C. Combined differential evolution algorithm and ant system for optimal reactive power dispatch. Energy Procedia 2012, 14, 1238–1243. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghanbarian, M.M.; Ghavidel, S.; Rahmani, S.; Moghaddam, E.M. Modified teaching learning algorithm and double differential evolution algorithm for optimal reactive power dispatch problem: A comparative study. Inf. Sci. 2014, 278, 231–249. [Google Scholar] [CrossRef]
- Basu, M. Quasi-oppositional differential evolution for optimal reactive power dispatch. Int. J. Electr. Power Energy Syst. 2016, 78, 29–40. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Li, Z. Reactive power optimization using hybrid CABC-DE algorithm. Electr. Power Compon. Syst. 2017, 45, 980–989. [Google Scholar] [CrossRef]
- Duman, S.; Sönmez, Y.; Güvenç, U.; Yörükeren, N. Optimal reactive power dispatch using a gravitational search algorithm. IET Gener. Transm. Distrib. 2012, 6, 563–576. [Google Scholar] [CrossRef]
- Babu, M.R.; Lakshmi, M. Gravitational search algorithm based approach for optimal reactive power dispatch. In Proceedings of the Second International Conference on IEEE on Science Technology Engineering and Management (ICONSTEM), Chennai, India, 30–31 March 2016; pp. 360–366. [Google Scholar] [CrossRef]
- Chen, G.; Liu, L.; Zhang, Z.; Huang, S. Optimal reactive power dispatch by improved GSA-based algorithm with the novel strategies to handle constraints. Appl. Soft Comput. 2017, 50, 58–70. [Google Scholar] [CrossRef]
- Rayudu, K.; Yesuratnam, G.; Jayalaxmi, A. Ant colony optimization algorithm based optimal reactive power dispatch to improve voltage stability. In Proceedings of the 2017 International Conference on IEEE on Circuit, Power and Computing Technologies (ICCPCT), Kollam, India, 20–21 April 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Mandal, B.; Roy, P.K. Optimal reactive power dispatch using quasi-oppositional teaching learning based optimization. Int. J. Electr. Power Energy Syst. 2013, 53, 123–134. [Google Scholar] [CrossRef]
- Ghasemi, M.; Taghizadeh, M.; Ghavidel, S.; Aghaei, J.; Abbasian, A. Solving optimal reactive power dispatch problem using a novel teaching-learning-based optimization algorithm. Eng. Appl. Artif. Intell. 2015, 39, 100–108. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z. Cuckoo Search Algorithm as an optimizer for Optimal Reactive Power Dispatch problems. In Proceedings of the 2017 3rd International Conference on IEEE on Control, Automation and Robotics, Nagoya, Japan, 24–26 April 2017; pp. 735–739. [Google Scholar] [CrossRef]
- An, N.H.T.; Dieu, V.N.; Nguyen, T.T.; Kien, V.T. One rank cuckoo search algorithm for optimal reactive power dispatch. GMSARN Int. J. 2015, 73, 82 . [Google Scholar]
- Khazali, A.H.; Kalantar, M. Optimal reactive power dispatch based on harmony search algorithm. Int. J. Electr. Power Energy Syst. 2011, 33, 684–692. [Google Scholar] [CrossRef]
- Mukherjee, A.; Mukherjee, V. Solution of optimal reactive power dispatch by chaotic krill herd algorithm. IET Gener. Transm. Distrib. 2015, 9, 2351–2362. [Google Scholar] [CrossRef]
- Rajan, A.; Malakar, T. Optimal reactive power dispatch using hybrid Nelder-Mead simplex based firefly algorithm. Int. J. Electr. Power Energy Syst. 2015, 66, 9–24. [Google Scholar] [CrossRef]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef]
- Rayudu, K.; Yesuratnam, G.; Jayalaxmi, A. Artificial Bee Colony algorithm for optimal reactive power dispatch to improve voltage stability. In Proceedings of the 2016 International Conference on IEEE on Circuit, Power and Computing Technologies (ICCPCT), Nagercoil, India, 18–19 March 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Rajan, A.; Malakar, T. Exchange market algorithm based optimum reactive power dispatch. Appl. Soft Comput. 2016, 43, 320–336. [Google Scholar] [CrossRef]
- Abaci, K.; Yamaçli, V. Optimal reactive-power dispatch using differential search algorithm. Electr. Eng. 2017, 99, 213–225. [Google Scholar] [CrossRef]
- Mouassa, S.; Bouktir, T.; Salhi, A. Ant lion optimizer for solving optimal reactive power dispatch problem in power systems, engineering science and technology. An. Int. J. 2017, 3, 885–895. [Google Scholar] [CrossRef]
- Anbarasan, P.; Jayabarathi, T. Optimal reactive power dispatch problem solved by an improved colliding bodies optimization algorithm. In Proceedings of the 2017 IEEE International Conference on IEEE on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Heidari, A.A.; Abbaspour, R.A.; Jordehi, A.R. Gaussian bare-bones water cycle algorithm for optimal reactive power dispatch in electrical power systems. Appl. Soft Comput. 2017, 57, 657–671. [Google Scholar] [CrossRef]
- Barakat, A.F.; El-Sehiemy, R.A.; Elsaid, M.; Osman, E. Solving reactive power dispatch problem by using JAYA optimization Algorithm. Int. J. Eng. Res. Afr. Trans Tech Publ. 2018, 36, 12–24. [Google Scholar] [CrossRef]
- Mei, R.N.S.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017, 59, 210–222. [Google Scholar] [CrossRef]
- Nuaekaew, K.; Artrit, P.; Pholdee, N.; Bureerat, S. Optimal reactive power dispatch problem using a two-archive multi-objective grey wolf optimizer. Expert Syst. Appl. 2017, 87, 79–89. [Google Scholar] [CrossRef]
- Ben oualid Medani, K.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electric Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Shareef, S.M.; Rao, R.S. Optimal reactive power dispatch under unbalanced conditions using hybrid swarm intelligence. Comput. Electr. Eng. 2018, 69, 183–193. [Google Scholar] [CrossRef]
- Meddeb, A.; Amor, N.; Abbes, M.; Chebbi, S. A novel approach based on crow search algorithm for solving reactive power dispatch problem. Energies 2018, 11, 3321. [Google Scholar] [CrossRef]
- Tizhoosh, H. Opposition-based learning: A new scheme for machine intelligence. In Proceeding of the International Conference on Computational Intelligence for Modelling Control and Automation, Vienna, Austria, 28–30 November 2005. [Google Scholar] [CrossRef]
- Neri, F.; Tirronen, V. Recent advances in differential evolution: A survey and experimental analysis. Artif. Intell. Rev. 2010, 33, 61–106. [Google Scholar] [CrossRef]
- Ahmed, S.T.; Amr, A.B.; Ibrahim, F.A. One rank cuckoo search algorithm with application to algorithmic, trading systems optimization. Int. J. Comput. Appl. 2013, 64, 30–37. [Google Scholar] [CrossRef]
- Pierezan, J.; Coelho, L.D.S. Coyote optimization algorithm: A new metaheuristic for global optimization problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC) IEEE, Busan, Korea, 27–28 June 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Pham, T.D.; Nguyen, T.T.; Dinh, B.H. Find optimal capacity and location of distributed generation units in radial distribution networks by using enhanced coyote optimization algorithm. Neural Comput. Appl. 2021, 33, 4343–4371. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Nguyen, T.T.; Nguyen, N.A.; Duong, T.L. A novel method based on coyote algorithm for simultaneous network reconfiguration and distribution generation placement. Ain Shams Eng. J. 2021, 12, 665–676. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Pham, T.D.; Kien, L.C.; Van Dai, L. Improved coyote optimization algorithm for optimally installing solar photovoltaic distribution generation units in radial distribution power systems. Complexity 2020. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Gomes, G.F.; da Cunha, S.S.; Ancelotti, A.C. A sunflower optimization (SFO) algorithm applied to damage identification on laminated composite plates. Eng. Comput. 2018, 1–8. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110, 151–166. [Google Scholar] [CrossRef]
- MATPOWER 4.1 IEEE 30-Bus, IEEE 57-Bus and 118-Bus Test System. Available online: http://www.pserc.cornell.edu/matpower (accessed on 12 May 2021).
- Mernik, M.; Liu, S.H.; Karaboga, D.; Crepinšek, M. On clarifying misconceptions when comparing variants of the artificial bee colony algorithm by offering a new implementation. Inf. Sci. 2015, 291, 115–127. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, L.; Yuan, Y.; Zhang, Y.; Yang, B. A modified differential evolution approach for dynamic economic dispatch with valve-point effects. Energy Convers. Manag. 2008, 49, 3447–3453. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).