Smart Topology Optimization Using Adaptive Neighborhood Simulated Annealing
Abstract
:1. Introduction
2. Simulated Annealing
3. Topology Optimization
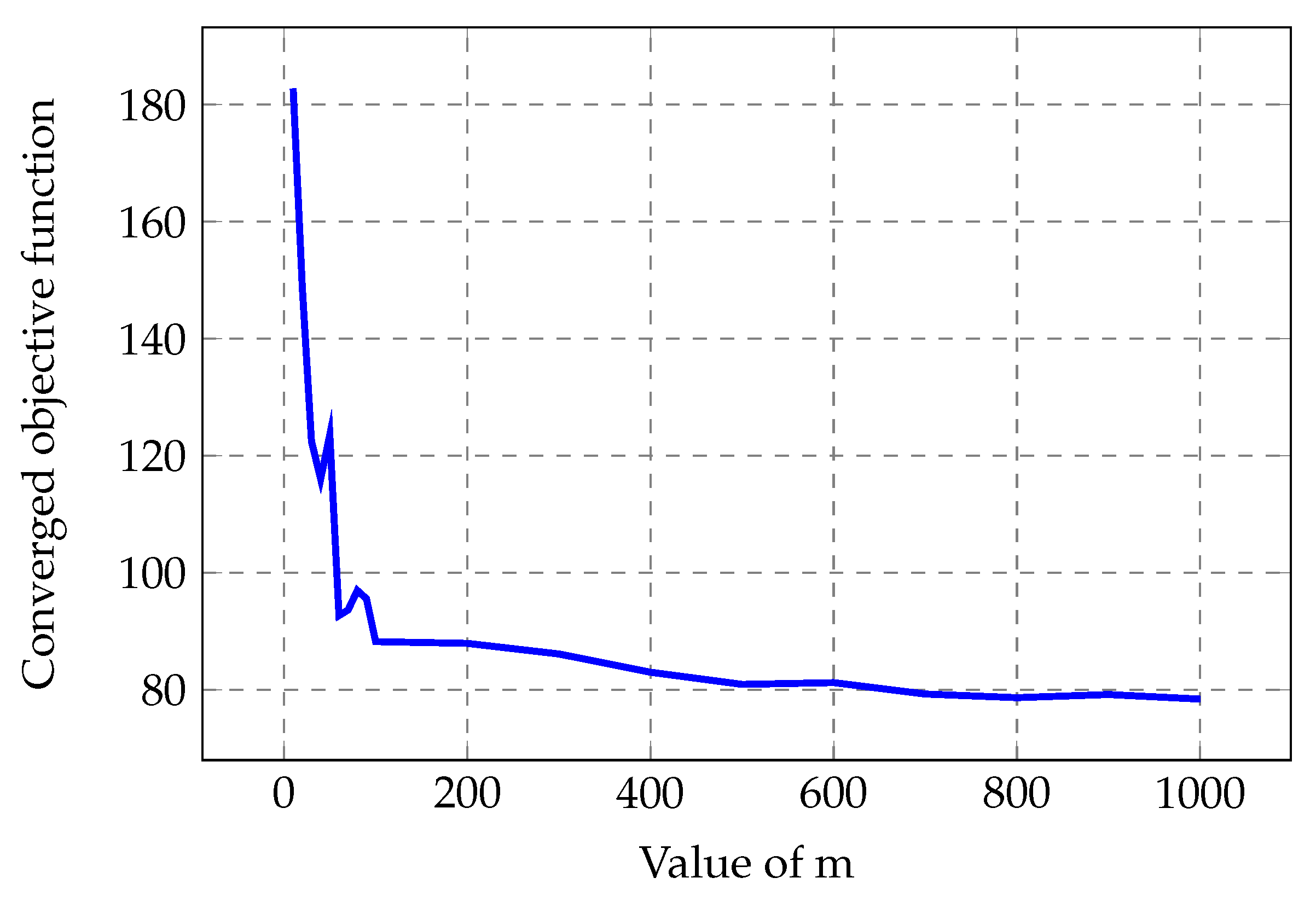
4. SA in TO
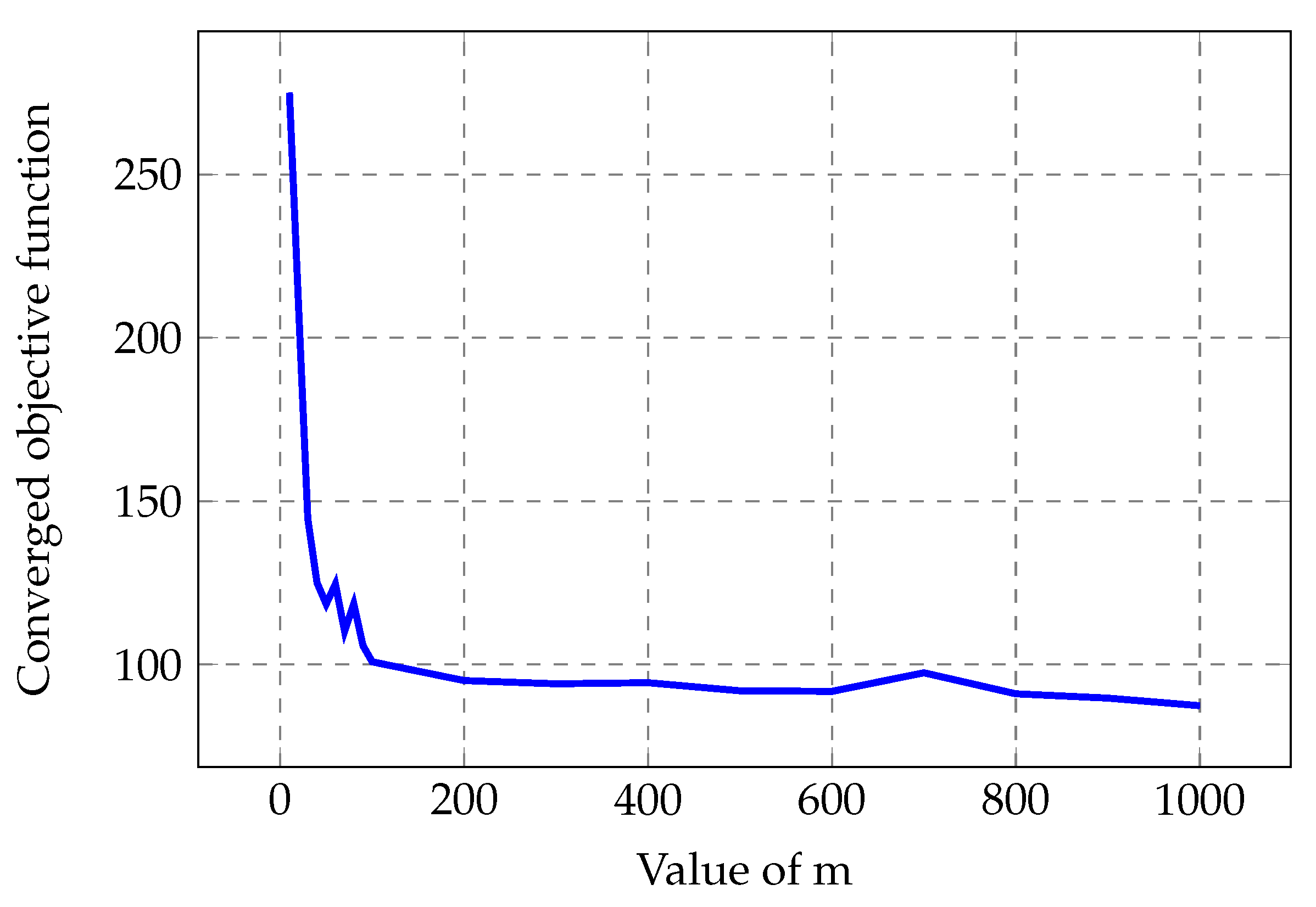
5. Results
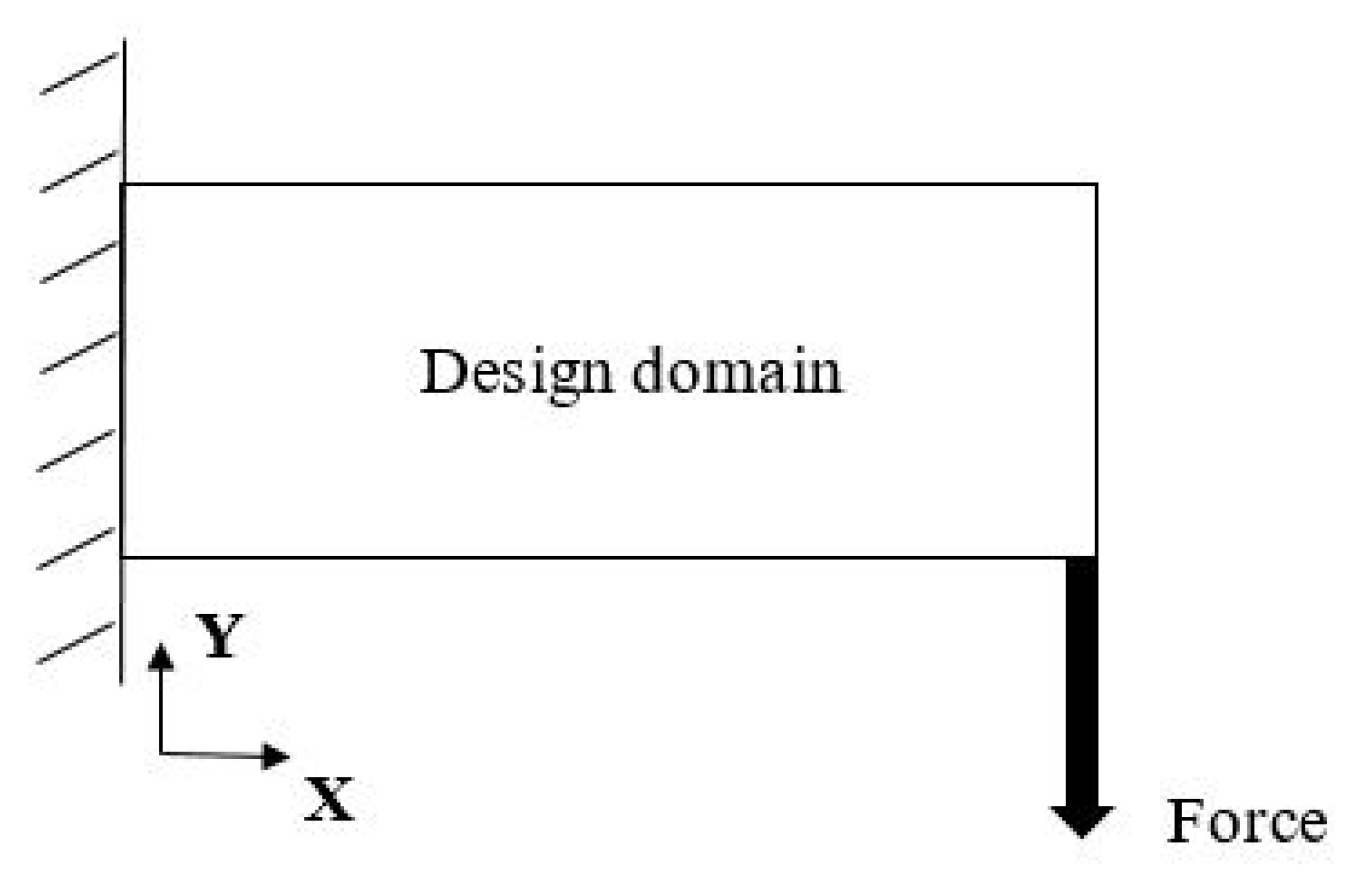
5.1. Cantilever Problem
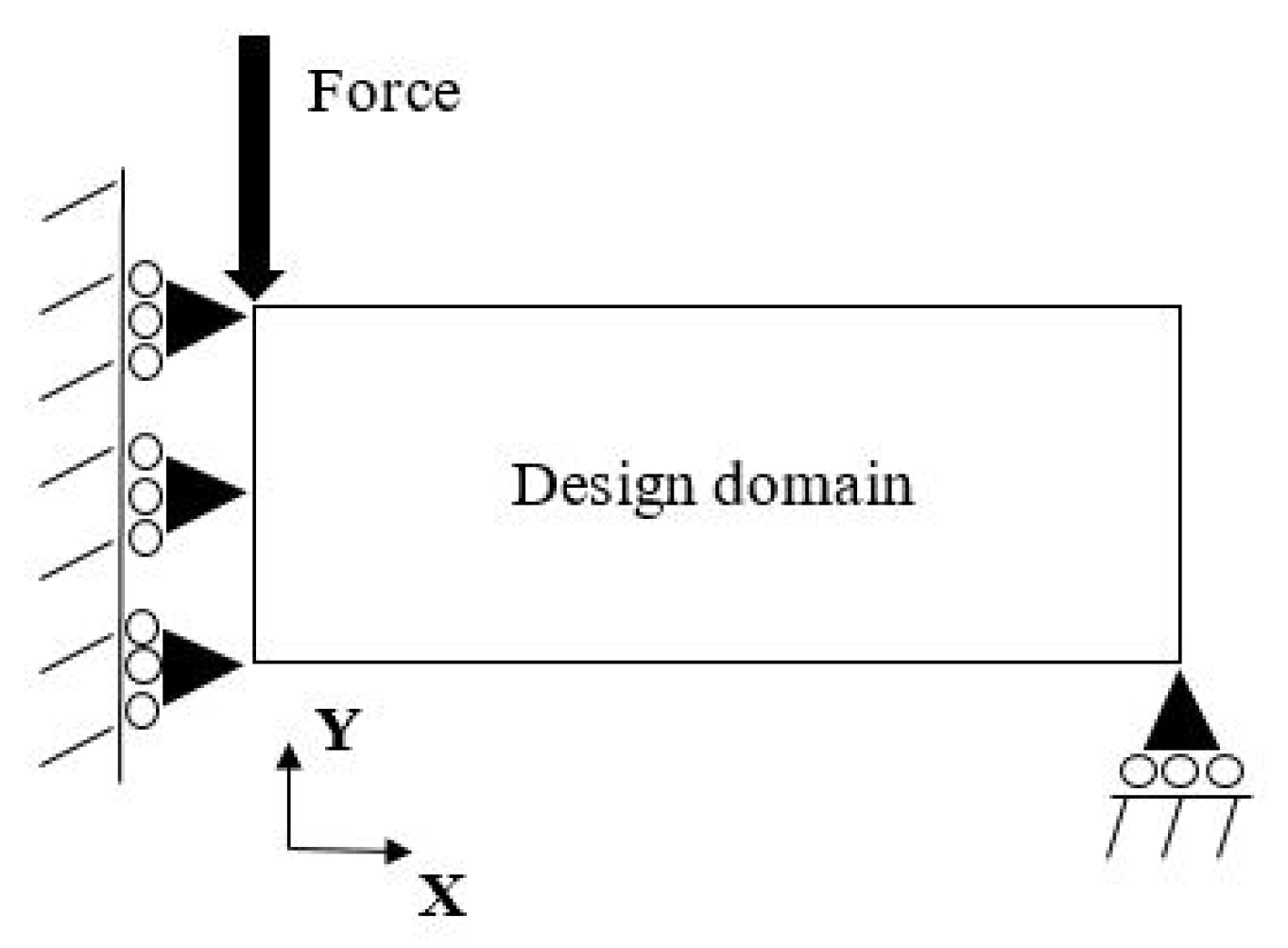
5.2. MBB Problem
5.3. Heat Conduction Problem
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| TO | Topology Optimization |
| SA | Simulated Annealing |
| OC | Optimally Criteria |
| SIMP | Solid Isotropic Materials with Penalization |
| MMA | Method of Moving asymptotes |
| GA | Genetic Algorithm |
References
- Marchesi, T.R.; Lahuerta, R.D.; Silva, E.C.N.; Tsuzuki, M.S.G.; Martins, T.C.; Barari, A.; Wood, I. Topologically optimized diesel engine support manufactured with additive manufacturing. IFAC-PapersOnLine 2015, 28, 2333–2338. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Rozvany, G. The SIMP method in topology optimization-theoretical background, advantages and new applications. In Proceedings of the 8th Symposium on Multidisciplinary Analysis and Optimization, Long Beach, CA, USA, 6–8 September 2000; p. 4738. [Google Scholar]
- Huang, X.; Xie, M. Evolutionary Topology Optimization of Continuum Structures: Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Sigmund, O. A 99 line topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2001, 21, 120–127. [Google Scholar] [CrossRef]
- Andreassen, E.; Clausen, A.; Schevenels, M.; Lazarov, B.S.; Sigmund, O. Efficient topology optimization in MATLAB using 88 lines of code. Struct. Multidiscip. Optim. 2011, 43, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Liu, K.; Tovar, A. An efficient 3D topology optimization code written in Matlab. Struct. Multidiscip. Optim. 2014, 50, 1175–1196. [Google Scholar] [CrossRef] [Green Version]
- Jankovics, D.; Gohari, H.; Tayefeh, M.; Barari, A. Developing topology optimization with additive manufacturing constraints in ANSYS®. IFAC-PapersOnLine 2018, 51, 1359–1364. [Google Scholar] [CrossRef]
- Sigmund, O. On the usefulness of non-gradient approaches in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 589–596. [Google Scholar] [CrossRef]
- Munk, D.J.; Vio, G.A.; Steven, G.P. Topology and shape optimization methods using evolutionary algorithms: A review. Struct. Multidiscip. Optim. 2015, 52, 613–631. [Google Scholar] [CrossRef]
- Chapman, C.D. Structural Topology Optimization via the Genetic Algorithm. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1994. [Google Scholar]
- Hajela, P.; Lee, E.; Lin, C.Y. Genetic algorithms in structural topology optimization. In Topology Design of Structures; Springer: Berlin/Heidelberg, Germany, 1993; pp. 117–133. [Google Scholar]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Rutenbar, R.A. Simulated annealing algorithms: An overview. IEEE Circuits Devices Mag. 1989, 5, 19–26. [Google Scholar] [CrossRef]
- Najafabadi, H.R.; Goto, T.G.; Martins, T.C.; Barari, A.; Tsuzuki, M.S. Multi-objective topology optimization using simulated annealing method. In Proceedings of the International Conference on Geometry and Graphics, São Paulo, Brazil, 18–22 January 2021; pp. 343–353. [Google Scholar]
- Bureerat, S.; Limtragool, J. Structural topology optimisation using simulated annealing with multiresolution design variables. Finite Elem. Anal. Des. 2008, 44, 738–747. [Google Scholar] [CrossRef]
- Garcia-Lopez, N.; Sanchez-Silva, M.; Medaglia, A.; Chateauneuf, A. A hybrid topology optimization methodology combining simulated annealing and SIMP. Comput. Struct. 2011, 89, 1512–1522. [Google Scholar] [CrossRef]
- Martins, T.C.; Tsuzuki, M.S.G. Rotational placement of irregular polygons over containers with fixed dimensions using simulated annealing and no-fit polygons. J. Braz. Soc. Mech. Sci. 2008, 30, 205–212. [Google Scholar] [CrossRef] [Green Version]
- Martins, T.C.; Tsuzuki, M.S.G. Simulated annealing applied to the rotational polygon packing. IFAC (IFAC-PapersOnline) 2006, 12, 475–480. [Google Scholar]
- Sato, A.K.; Martins, T.C.; Tsuzuki, M.S.G. Rotational placement using simulated annealing and collision free region. IFAC Proc. Vol. 2010, 43, 234–239. [Google Scholar] [CrossRef]
- Martins, T.C.; Camargo, E.D.L.B.; Lima, R.G.; Amato, M.B.P.; Tsuzuki, M.S.G. Electrical impedance tomography reconstruction through Simulated Annealing with incomplete evaluation of the objective function. In Proceedings of the 33rd IEEE EMBC, Boston, MA, USA, 30 August–1 September 2011; pp. 7033–7036. [Google Scholar]
- Martins, T.C.; Tsuzuki, M.S.G. Simulated annealing with partial evaluation of objective function applied to electrical impedance tomography. IFAC Proc. Vol. 2011, 44, 4989–4994. [Google Scholar] [CrossRef] [Green Version]
- Tavares, R.S.; Martins, T.C.; Tsuzuki, M.S.G. Electrical impedance tomography reconstruction through aimulated annealing using a new outside-in heuristic and GPU parallelization. J. Physics: Conf. Ser. 2012, 407, 012015. [Google Scholar]
- Martins, T.C.; Tsuzuki, M.S.G. Electrical impedance tomography reconstruction through simulated annealing with total least square error as objective function. In Proceedings of the 34th IEEE EMBC, San Diego, CA, USA, 28 August 28–1 September 2012; pp. 1518–1521. [Google Scholar]
- Martins, T.C.; Tsuzuki, M.S.G. Electrical impedance tomography reconstruction through simulated annealing with multi-stage partially evaluated objective functions. In Proceedings of the 35th IEEE EMBC, Osaka, Japan, 3–7 July 2013; pp. 6425–6428. [Google Scholar]
- Martins, T.C.; Fernandes, A.V.; Tsuzuki, M.S.G. Image reconstruction by electrical impedance tomography using multi-objective simulated annealing. In Proceedings of the IEEE 11th ISBI, Beijing, China, 29 April–2 May 2014; pp. 185–188. [Google Scholar]
- Martins, T.C.; Tsuzuki, M.S.G. EIT image regularization by a new multi-objective simulated annealing algorithm. In Proceedings of the 37th IEEE EMBC, Milano, Italy, 25–29 August 2015; pp. 4069–4072. [Google Scholar]
- Martins, T.C.; Tsuzuki, M.S.G.; Camargo, E.D.L.B.D.; Lima, R.G.; Moura, F.S.D.; Amato, M.B.P. Interval simulated annealing applied to electrical impedance tomography image reconstruction with fast objective function evaluation. Comput. Math Appl. 2016, 72, 1230–1243. [Google Scholar] [CrossRef]
- Martins, T.C.; Tsuzuki, M.S.G. Investigating anisotropic EIT with simulated annealing. IFAC-PapersOnLine 2017, 50, 9961–9966. [Google Scholar] [CrossRef]
- Ueda, E.K.; Tsuzuki, M.S.G.; Takimoto, R.Y.; Sato, A.K.; Martins, T.C.; Miyagi, P.E.; Rosso, R.S.U., Jr. Piecewise Bézier curve fitting by multiobjective simulated annealing. IFAC-PapersOnLine 2016, 49, 49–54. [Google Scholar] [CrossRef]
- Ueda, E.K.; Tsuzuki, M.S.; Barari, A. Piecewise Bézier curve fitting of a point cloud boundary by simulated annealing. In Proceedings of the 2018 13th IEEE International Conference on Industry Applications (INDUSCON), Sao Paulo, Brazil, 12–14 November 2019; pp. 1335–1340. [Google Scholar]
- Ueda, E.K.; Barari, A.; Sato, A.K.; Tsuzuki, M.S.G. Detection of defected zone using 3D scanning data to repair worn turbine blades. In Proceedings of the 21st IFAC World Congress, Berlin, Germany, 12–17 July 2020; pp. 10666–10670. [Google Scholar]
- Černý, V. Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm. J. Optim. Theory Appl. 1985, 45, 41–51. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Martins, T.C.; Tsuzuki, M.S.G. Placement over containers with fixed dimensions solved with adaptive neighborhood simulated annealing. Pol. Acad. Sci. Tech. 2009, 57, 273–280. [Google Scholar] [CrossRef] [Green Version]
- Deng, S.; Suresh, K. Multi-constrained topology optimization via the topological sensitivity. Struct. Multidiscip. Optim. 2015, 51, 987–1001. [Google Scholar] [CrossRef]
- Ueda, E.K.; Sato, A.K.; Martins, T.C.; Takimoto, R.Y.; Rosso, R.S.U., Jr.; Tsuzuki, M.S.G. Curve approximation by adaptive neighborhood simulated annealing and piecewise Bézier curves. Soft Comput. 2020, 24, 18821–18839. [Google Scholar] [CrossRef]
- Tavares, R.S.; Sato, A.K.; Martins, T.C.; Lima, R.G.; Tsuzuki, M.S.G. GPU acceleration of absolute EIT image reconstruction using simulated annealing. Biomed. Signal. Process. Control 2019, 52, 445–455. [Google Scholar] [CrossRef]






| Volume Fraction | Compliance from [6] | Compliance from the Method Proposed Herein |
|---|---|---|
| 0.5 | 70.41 | 73.71 |
| 0.6 | 60.43 | 61.42 |
| 0.7 | 53.95 | 54.97 |
| 0.8 | 49.68 | 50.21 |
| 0.9 | 46.84 | 47.10 |
| Volume Fraction | Compliance from [6] | Compliance from the Method Proposed Herein |
|---|---|---|
| 0.5 | 77.42 | 80.87 |
| 0.6 | 66.73 | 68.55 |
| 0.7 | 59.69 | 60.72 |
| 0.8 | 54.55 | 55.60 |
| 0.9 | 51.31 | 51.95 |
| Volume Fraction | Compliance from [8] | Compliance from the Proposed Method |
|---|---|---|
| 0.5 | 250.75 | 224.56 |
| 0.6 | 211.83 | 196.44 |
| 0.7 | 189.88 | 182.27 |
| 0.8 | 180.18 | 173.51 |
| 0.9 | 170.89 | 169.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
R. Najafabadi, H.; G. Goto, T.; Falheiro, M.S.; C. Martins, T.; Barari, A.; S. G. Tsuzuki, M. Smart Topology Optimization Using Adaptive Neighborhood Simulated Annealing. Appl. Sci. 2021, 11, 5257. https://doi.org/10.3390/app11115257
R. Najafabadi H, G. Goto T, Falheiro MS, C. Martins T, Barari A, S. G. Tsuzuki M. Smart Topology Optimization Using Adaptive Neighborhood Simulated Annealing. Applied Sciences. 2021; 11(11):5257. https://doi.org/10.3390/app11115257
Chicago/Turabian StyleR. Najafabadi, Hossein, Tiago G. Goto, Mizael S. Falheiro, Thiago C. Martins, Ahmad Barari, and Marcos S. G. Tsuzuki. 2021. "Smart Topology Optimization Using Adaptive Neighborhood Simulated Annealing" Applied Sciences 11, no. 11: 5257. https://doi.org/10.3390/app11115257
APA StyleR. Najafabadi, H., G. Goto, T., Falheiro, M. S., C. Martins, T., Barari, A., & S. G. Tsuzuki, M. (2021). Smart Topology Optimization Using Adaptive Neighborhood Simulated Annealing. Applied Sciences, 11(11), 5257. https://doi.org/10.3390/app11115257









